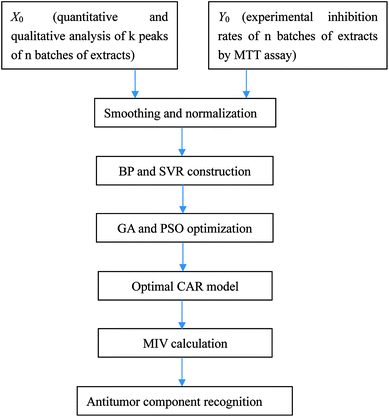
Open Access Article
Open Access ArticleAntitumor component recognition from the Aconiti Lateralis Radix Praeparata and Glycyrrhizae Radix et Rhizoma herb pair extract by chemometrics and mean impact value†
Hailiu Fan,
Jianbang Xuan,
Xinyun Du,
Ningzhi Liu and
Jianlan Jiang *
*
Key Laboratory of Systems Bioengineering, Ministry of Education, School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, P. R. China. E-mail: jljiang@tju.edu.cn; Tel: +86-022-2740-0388
First published on 27th November 2018
Abstract
The purpose of this research is to recognize the active antitumor components from the mixed pair extract of Aconiti Lateralis Radix Praeparata (Fuzi in Chinese) and Glycyrrhizae Radix et Rhizoma (Gancao in Chinese) using chemometrics and mean impact value (MIV) methods. Firstly, 30 common components of 31 different samples were analyzed quantitatively and qualitatively by HPLC-UV and UPLC-Q-TOF tandem mass spectrometry, respectively. Meanwhile, MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) assays were used to test the inhibition activities of the 31 different samples against HeLa cells. Then a back propagation (BP) neural network, support vector regression (SVR), and two optimization algorithms – genetic algorithm (GA) and particle swarm optimization (PSO) – were applied to construct composition–activity relationship (CAR) models for the Fuzi–Gancao extract. Based on the optimal CAR model, the MIV was introduced to evaluate the contribution of each individual component to the anticancer efficacy of the extract. Results indicated that the SVR-PSO model best depicted the complex relationship between the chemical composition and the inhibition effect of a Fuzi–Gancao extract. The 30 common components were ranked by their absolute MIVs, and the top 8, which corresponded to peaks 17, 25, 22, 13, 23, 28, 5, and 7 in the chromatogram, were tentatively deemed to be the main antitumor components. The integrated strategy shows a novel and efficient approach to understanding the potential contributions of components from complicated herbal medicines, and the identified results suggest certain directions for screening and research into new antitumor drugs.
1. Introduction
Recently, herbal medicines (HMs) have appeared more and more attractive owing to their shining advantages of favorable cure effects, mild action, low levels of side effects and rich sources.1 Especially for malignant and chronic diseases like cancer, HMs can tend to have remarkable therapeutic effects.2 As we all know, HMs contain various compounds, which provide the material basis of the excellent curative effect of HMs. However, at present, most scientific research on HMs just focuses on one or a small number of ingredients that are usually present in high amounts, while some other low level components, which may also have potent bioactivity or can promote efficacy, are overlooked intentionally or unintentionally.In order to find out as much as possible about the therapeutic constituents of HMs, it is necessary to study the relationship between chemical composition and the therapeutic effect of the HMs, and chemometrics makes it possible to establish a composition–activity relationship (CAR) model. The CAR model can be used to predict the pharmaceutical activities of crude medicines according to chemical component information. Moreover, when combined with a variable relevance analysis method like mean impact value (MIV), the model can evaluate the bioactivities of the contained constituents, improving the efficiency of drug discovery. Some achievements have been made by this strategy, demonstrating its effectiveness.3–5 To date, various algorithms have been applied to CAR model construction. However, since HMs contain a wide variety of compounds and complicated mutual interactions exist among these components, the commonly used linear models like multiple linear regression analysis (MLR) usually do not fit the practical situation very well. By contrast, nonlinear algorithms like the back propagation (BP) neural network and support vector regression (SVR) are more suitable for explaining the CAR of HMs.6–8 BP is one of the most widely used neural networks, and it usually consists of three parts: an input layer, a hidden layer and an output layer. There are a certain number of neurons in each layer, which are involved in two processes, namely signal forward propagation and error back propagation, to adjust the weight and bias of each neuron to achieve functional approximation.9 SVR solves nonlinear problems by increasing the dimensions of the input data. In theory, a kernel function is utilized to map the input data to a high-dimensional characteristic space, converting the linearly non-separable data to linear separable data, and a linear regression function is established in the space to describe the relationship.10,11 BP and SVR have been successfully applied to quality prediction and evaluation for some herbal medicines.12–15
Furthermore, the performance of CAR models can be markedly improved after parameter optimization.16,17 The genetic algorithm (GA) and particle swarm optimization (PSO) algorithm are two commonly used parameter optimization methods. GA is derived from the combination of natural selection and genetic inheritance, and it searches for the best optimal solution by selection, crossover and mutation like biological evolution.18 PSO is a kind of swarm intelligence algorithm, inspired by the foraging behavior of a biotic population, and it has many attractive traits such as easy operation, few adjustment parameters and fast convergence rates.19
Aconiti Lateralis Radix Praeparata (Fuzi in Chinese) and Glycyrrhizae Radix et Rhizoma (Gancao in Chinese) used to concurrently appear in classical Chinese medicine prescriptions for the treatment of rheumatoid arthritis and joint pain.20,21 Fuzi, the processed lateral roots of Aconitum carmichaelii Debeaux, has been in officinal use for a long time having various biological activities like analgesic, anti-inflammation, antidepressant, antihyperglycemic and cardiovascular protective effects.22–24 Gancao, the dried roots and stolons of Glycyrrhiza uralensis Fisch., is one of the most frequently used herbal medicines all over the world, and in addition to its pharmaceutical use, it often serves as an additive in herbal formulations to improve solubility, increase effects and alleviate toxicity.25,26 Recently, some researchers have reported that both Fuzi and Gancao possess favorable antitumor effects.27–29 However, the study of the antitumor constituents of the Fuzi–Gancao herb pair is extremely insufficient. As illustrated in Fig. 1, the present research makes use of a BP neural network and SVR to explore the CAR of the aqueous extract of the Fuzi–Gancao herb pair, and uses MIV to find out the main active antitumor components in this extract.
2. Materials and methods
2.1. Chemicals and plant materials
HPLC-grade methanol and acetonitrile were both purchased from Concord Technology Co., Ltd. (Tianjin, China). Ammonium acetate (HPLC ≥ 98%) and glacial acetic acid (HPLC ≥ 99.8%) were both purchased from Tianjin Kemiou Chemical Reagent Co., Ltd. (Tianjin, China). Water was supplied by a Milli-Q water purification system (Millipore, Bedford, MA, USA). Lappaconitine hydrobromide (HPLC ≥ 98%) was purchased from Nanjing SenBeiJia Biological Technology Co., Ltd. (Nanjing, China). Roswell Park Memorial Institute (RPMI) 1640 culture medium and trypsin were both purchased from Invitrogen Gibco Company (Gaithersburg, MD, USA). Fetal bovine serum (FBS) was purchased from Beijing Dingguo Changsheng Biotechnology Co., Ltd. (Beijing, China). Sodium chloride injection (0.9%) was purchased from China Otsuka Pharmaceutical Co., Ltd. (Tianjin, China). MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) and dimethyl sulfoxide (DMSO) were purchased from Sigma-Aldrich Co. LLC. (Santa Clara, USA). HeLa cells were provided by Logistics University of People's Armed Police Force (Tianjin, China).A total of 31 batches of raw Fuzi and Gancao from different places in China were collected and authenticated by Professor Tiejun Zhang from the Tianjin Institute of Pharmaceutical Research, and all voucher specimens are deposited at our laboratory.
2.2. Preparation of the extract
Dried medicinal slices of the two herbal medicines were accurately weighed, to give 20.00 g for Fuzi and 30.00 g for Gancao, and they were mixed in a 1000 mL round-bottom flask. The mixture was soaked in 600 mL water for 30 minutes and then extracted using a reflux device at 100 °C for 2 hours. The mixture was immediately filtered when the extraction was over. The filter liquor was concentrated under vacuum at 75 °C until the weight change in one minute was no more than 0.1 g, to obtain the extract sample, which was stored at 4 °C for next use.2.3. Preparation of internal standard solution and sample solution
Lappaconitine hydrobromide served as the internal standard (IS). Lappaconitine hydrobromide (6.3 mg) was dissolved in water in a 10 mL volumetric flask using an ultra-sonicator, and diluted with water to obtain a concentration of 630 μg mL−1 of IS stock solution. IS stock solution (1 mL) was diluted with water in a 5 mL volumetric flask to 126 μg mL−1, to give the IS solution, which was stored at 4 °C for next use.Precisely weighed extract (0.2 g) (see Section 2.2) was dissolved in water in a 5 mL volumetric flask using an ultra-sonicator, and then centrifuged at 7000 rpm for 10 minutes. Thereafter, an accurately measured amount of supernatant liquor (1.0 mL) was taken out and mixed thoroughly with an equal volume of IS solution. The mixture was filtered through a 0.22 μm nylon membrane, to give a sample solution for the following qualitative and quantitative analysis.
2.4. HPLC-UV instruments and conditions
A Waters e2695 high performance liquid chromatography (HPLC) Alliance system (Waters, Milford, MA, USA) consisting of a quaternary gradient pump, an online vacuum degasifier, an autosampler, and a column heating compartment, was used to separate the extract components and these separated components were then detected by a connected 2489 ultraviolet-visible (UV) detector. An Empower 3.0 workstation (Waters, Milford, MA, USA) was used for data acquisition and processing.Chromatographic separation was fulfilled using a Waters Symmetry C18 column (4.6 × 250 mm, 5 μm) operated at 30 °C. The mobile phase was composed of 0.1% (v/v) glacial acetic acid and 5 mmol L−1 ammonium acetate aqueous solution (A) and acetonitrile (B). A linear gradient elution pattern was adopted keeping a constant flow rate of 0.4 mL min−1, and the following elution program was used: 0–5 min, 5–5% B; 5–15 min, 5–10% B; 15–55 min, 10–26% B; 55–70 min, 26–27% B; 70–80 min, 27–30% B; 80–120 min, 30–46% B. The injection volume was 10 μL and the detection wavelength was set at 254 nm.
2.5. UPLC-Q-TOF instruments and conditions
An Agilent 1290 ultra-performance liquid chromatography (UPLC) Infinity system (Agilent Technologies, Palo, Alto, CA, USA), connected to a Bruker microTOF-Q II (Bruker Daltonics, Bremen, Germany) quadrupole time-of-flight mass spectrometer (Q-TOF-MS) with an electrospray ion source (ESI) was used for the qualitative identification of the components.The separation conditions for UPLC were the same as those listed in Section 2.4. MS detection of the separated components was conducted in positive ion mode with a scan range from 100 m/z to 980 m/z. The other detailed conditions for MS analysis were as follows: the capillary voltage was set at 4.5 kV and the end plate offset voltage was −0.5 kV. The collision cell radio frequency was 100.0 Vpp and the nebulizer pressure was 0.12 MPa. The temperature of the dry heater was 190 °C and the flow rate of dry gas was 6.0 L min−1. System control and data analysis were accomplished using a DataAnalysis 4.0 workstation (Bruker Daltonics, Bremen, Germany).
2.6. Antitumor efficacy test on the extract
MTT assays were performed to test the proliferation inhibition effects of the herb pair extracts of Fuzi–Gancao on the HeLa cervical cancer cell line. Three groups, namely a medicated group (all given the same amount of drug), a negative group not treated with drug solution, and a blank control group given only culture medium, were tested in parallel. Briefly, a certain amount of the prepared extract (see Section 2.2) was dissolved in sodium chloride (0.9%) by ultrasound and then centrifuged at 7000 rpm for 10 minutes. The supernatant liquor was filtered using a 0.22 μm nylon membrane, and the subsequent filtrate was used as the mother solution (concentration 200 mg mL−1 in terms of crude Fuzi). An accurately measured amount of mother solution (240 μL) was diluted with culture medium to 2 mL, to give a pharmaceutical medium of 24 mg mL−1 in terms of crude Fuzi. Monolayer HeLa cells were digested with 0.25% trypsin and inoculated at a concentration of 5 × 103 cells per well into 96-well plates containing RPMI 1640 complete medium and 10% FBS, and cultured at 37 °C, with saturated humidity, and 5% CO2. After 24 hours, 100 μL of pharmaceutical medium was added into each well so that the final concentrations of crude Fuzi and Gancao in the cultivation system were 12 mg mL−1 and 18 mg mL−1, respectively, and then the cell culture was continued, keeping the conditions unchanged. After a further 48 hours, the supernatant culture solution was removed and 50 μL of MTT solution (1 mg mL−1) was added into each well for generating formazan, and then the cell culture was continued as before. After 4 hours, the cultivation system was centrifuged and the supernatant liquor was discarded. Following this, 150 μL of DMSO solution was added into each well and the plate was slightly shaken until the generated formazan was dissolved thoroughly. The optical density (OD) of each well was measured using a Sunrise absorbance microplate reader (Tecan, Phoenix, CA, USA) at 490 nm, and the inhibition rate was calculated according to eqn (1). All experiments were repeated three times and the average value was calculated as the final inhibition rate of the sample.
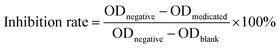 | (1) |
2.7. Model construction
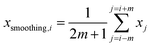 | (2) |
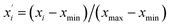 | (3) |
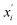 and xi are normalized data and raw data, respectively; and xmax and xmin are the maximum and minimum of each raw variable, respectively.
and xi are normalized data and raw data, respectively; and xmax and xmin are the maximum and minimum of each raw variable, respectively.In general, SVR includes two methods, ε-SVR and ν-SVR, and the only difference between them is that the insensitive loss function ε is artificially set for the former whereas it is automatically adapted for the latter.31 Although ε-SVR is simple and convenient, the manual selection of an appropriate value for ε is not always easy, and ν-SVR usually gives a better performance owing to its flexible changeability, so ν-SVR was adopted in this paper. The gauss radial basis function eqn (5) was used as the kernel function in this research due to its good learning and generalization ability.32 Moreover, the penalty parameter C and kernel function parameter g significantly impact the model reliability and should be optimized. In this research, GA was utilized to optimize the parameters of both the BP model and the SVR model, and PSO was used only to optimize the SVR model.
n = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m m
| (4) |
| K(xi − xj) = exp(−γ‖xi − xj‖2), γ > 0 | (5) |
In this study, 31 different samples were assigned to two groups at random; 20 samples were used as a training set to create and train the CAR model, while the other 11 samples were used as a test set to examine the predictive ability of the established CAR model for unknown data. The root mean square error (RMSE) and correlation coefficient (R) were used to evaluate the accuracy and reliability of the developed CAR model:
 | (6) |
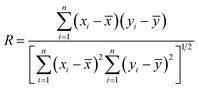 | (7) |
2.8. Mean impact value
The mean impact value (MIV), originally put forward by Dombi in 1995 to characterize the variation of weight matrix of neurons in a neural network, is regarded as one of the most important indicators reflecting the effect of each independent variable on dependent variables.33 In this research, MIVs were used to evaluate the bioactivities of the constituents in the samples based on the developed CAR model. The calculation process can briefly be described as follows: each independent variable (xj) is assigned new values, plus and minus 10%, to obtain two new input data sets, X(j)1([x1, x2, …, 1.1xj, …, xk]) and X(j)2([x1, x2, …, 0.9xj, …, xk]), which are presently imported to the optimal CAR model to give the two corresponding predicted inhibition rates, Y(j)1 and Y(j)2. The difference between the Y(j)1 and Y(j)2 values is called the impact value (IV), and is caused by the variation of the independent variable, xj. The MIV of xj is worked out through dividing the difference value by the sample number. The absolute MIV for each independent variable stands for the contribution of that constituent to the inhibition activity of the Fuzi–Gancao extract on HeLa cells.Matlab R2013b software (MathWork Inc., Natick, MA, USA) integrated with a ga toolbox and a libsvm-3.1 toolbox was used as a platform for all of the above computer aided operations, including data preprocessing, CAR model training, and MIV calculation.
3. Results and discussion
3.1. HPLC-UV method development and validation
In order to acquire as much chemical composition information about the Fuzi–Gancao extract as possible, and to achieve the best separation of the contained constituents, the chromatographic column, detection wavelength, composition and flow rate of the mobile phase, column temperature, and elution program were all optimized; the optimum separation was fulfilled by the HPLC-UV conditions described in Section 2.4.To ensure the effectiveness and reliability of the developed HPLC-UV method, the precision, stability and reproducibility of the method were validated. The precision experiment was carried out by analyzing the same sample six times in succession. To validate intra-day stability, the same sample was analyzed at 0 h, 4 h, 8 h, 12 h and 24 h. For reproducibility, six different samples from the same extract were prepared and analyzed using the established method. For all of these experiments, the relative retention time (RRT) and relative peak area (RPA) of 30 common chromatographic peaks were measured using the IS as the reference peak, and then relative standard deviations (RSDs) of RRTs and RPAs of each of the 30 peaks were calculated. As shown in Table 1, the RSDs of the RRTs and RPAs of all of the characteristic peaks were no more than 5% in the experiments for precision, stability and reproducibility. This means that the developed HPLC-UV method is feasible and dependable, and the samples are stable for 24 hours.
3.2. HPLC analysis
When developing the HPLC method, several detection wavelengths were tested; at 254 nm, the chromatographic peaks had relatively moderate responses and better peak resolutions than at other wavelengths. Thus, 254 nm was chosen as the detection wavelength for the Fuzi–Gancao extract. Using the developed HPLC method, a representative fingerprint of the Fuzi–Gancao extract was acquired and is shown in Fig. 2, which contains more than 70 chromatographic peaks. Among these peaks, some peaks existed in all or most of the 31 batches of Fuzi–Gancao extract; they were marked as common peaks and investigated, while some other peaks only existed in some of the batches of Fuzi–Gancao extract, and they were not investigated in this paper. By aligning the fingerprints of 31 batches of samples using the Similarity Evaluation System for Chromatographic Fingerprint of TCM by the Chinese Pharmacopoeia Commission, as marked in Fig. 2, 30 characteristic peaks were identified as common peaks.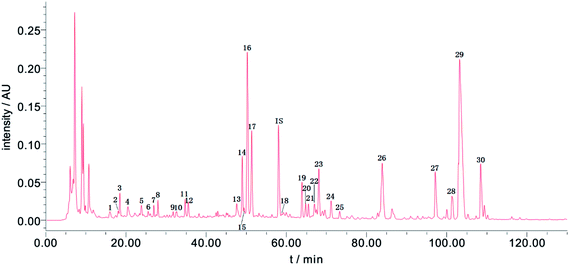 | ||
| Fig. 2 A representative HPLC-UV fingerprint of Fuzi–Gancao extract. The 30 marked chromatographic peaks were determined as common peaks in 31 batches of Fuzi–Gancao extract. | ||
RPAs of the 30 common peaks from all batches of the samples were measured and the data are listed in Table S1.† It can be seen that the contents of the chemical compounds in the different samples differed hugely. Taking peak 16 for instance, among the 31 batches of samples, the minimum RPA was 0.177 in sample 6 while the maximum RPA was 7.424 in sample 22. This is not an exception but a general case. These conspicuous differences usually result from various factors like the growing environment, harvesting time, post-processing and so on. These very different chemical compositions provide a solid material data basis for constructing a high-quality CAR model.
3.3. Peak identification by tandem mass spectrometry
A prepared sample that contained all the marked chromatographic peaks was subjected to UPLC-Q-TOF, and the 30 common peaks were tentatively characterized according to the m/z values of the parent ions and characteristic fragment ions in MS and MS/MS spectra, in comparison with those data in the published literature. The detailed identification information is listed in Table 2, and the structural formulas are shown in Fig. S1.†| No. | tR/min | MS | MS/MS | Error (ppm) | Formula | Identification |
|---|---|---|---|---|---|---|
| 1 | 16.8 | 394.5073[M + H]+ | 376.2489, 358.2396, 340.2323, 328.2262, 322.2198 | 4 | C22H35NO5 | Chuanfumine |
| 2 | 21.2 | 440.2661[M + H]+ | 422.2511, 408.4881 | −4 | C23H37NO7 | 9-Hydroxysenbusine A |
| 3 | 21.7 | 378.4667[M + H]+ | 360.2534, 342.2443, 332.2296, 300.7898 | −0.9 | C22H35NO4 | KaraKoline |
| 4 | 22.7 | 486.4962[M + H]+ | 468.2523, 454.2445, 436.2346, 422.2274, 404.2056 | −2.4 | C24H39NO9 | Mesaconine |
| 5 | 24.0 | 424.4683[M + H]+ | 406.2590, 388.2472, 374.2306 | −0.8 | C23H37NO6 | Senbusine A/B |
| 6 | 25.3 | 408.5207[M + H]+ | 390.2637, 372.2516, 358.2383, 340.2322 | −4.9 | C23H37NO5 | Isotalatizidine |
| 7 | 26.6 | 500.5257[M + H]+ | 482.2795, 468.2628, 450.2505, 436.2210, 418.2287 | 0.9 | C25H41NO9 | Aconine |
| 8 | 27.7 | 358.4685[M + H]+ | 340.2277, 322.2143 | 5.8 | C22H31NO3 | Songorine |
| 9 | 30.7 | 470.4375[M + H]+ | 438.2501, 420.2327, 406.2375, 388.2110 | −1.2 | C24H39NO8 | Hypaconine |
| 10 | 31.3 | 454.5523[M + H]+ | 436.2706, 418.2640, 404.2458, 386.2331 | −4.7 | C24H39NO7 | Fuziline |
| 11 | 33.4 | 438.5300[M + H]+ | 420.2749, 402.2658, 388.2500, 370.2386, 356.2235 | −1.3 | C24H39NO6 | Neoline |
| 12 | 34.9 | 450.4916[M + H]+ | 432.2742, 422.2562, 414.2669, 404.2507, 390.2517 | −2.7 | C25H39NO6 | Kondelfin |
| 13 | 47.2 | 464.5773[M + H]+ | 432.2741, 414.2627, 400.2456, 372.2519, 358.2419, 340.2204, 322.2145 | 3.9 | C26H41NO6 | 14-Acetyltalatizamine |
| 14 | 48.5 | 257.2084[M + H]+ | 137.0216, 119.0490 | 1.2 | C15H12O4 | Liquiritigenin |
| 15 | 49.2 | 606.5307[M + H]+ | 588.2766, 574.2666, 556.2552, 542.2361, 524.2215, 506.2155 | 0.3 | C31H43NO11 | 14-Benzoyl-10-hydroxymesaconine |
| 16 | 49.8 | 551.1760[M + H]+ | 419.1353, 257.2213, 137.0227, 119.0501 | 1.8 | C26H30O13 | Liquiritin apioside |
| 17 | 50.9 | 419.1329[M + H]+ | 257.1971, 137.0237, 119.0496 | 1.9 | C21H22O9 | Liquiritin |
| 18 | 58.8 | 590.6342[M + H]+ | 572.2874, 558.2707, 540.2597, 526.2448, 508.2342, 494.2155 | 0.8 | C31H43NO10 | Benzoylmesaconine |
| 19 | 63.4 | 604.6657[M + H]+ | 586.3044, 572.2835, 554.2715, 540.2547, 522.2469 | 0.6 | C32H45NO10 | Benzoylaconine |
| 20 | 64.5 | 543.5424 | — | — | — | Unknown |
| 21 | 65.5 | 419.1369[M + H]+ | 389.9859, 239.0720, 137.0219 | 5.5 | C21H22O9 | Isoliquiritin |
| 22 | 67.3 | 574.7080[M + H]+ | 542.2746, 510.2440, 492.2435, 478.2282 | −1.8 | C31H43NO9 | Benzoylhypaconine |
| 23 | 68.2 | 269.2086[M + H]+ | 237.0521, 169.0647 | 1.7 | C16H12O4 | Formononetin |
| 24 | 71.6 | 855.6927[M + K]+ | 679.3701, 503.3346, 485.3246, 467.3159, 449.3103 | 0.1 | C42H64O16 | Licorice saponin J2 |
| 25 | 73.1 | 558.5207[M + H]+ | 540.2869, 526.2824, 508.2663 | 2.2 | C31H43NO8 | 14-Benzoyl-deoxyaconine |
| 26 | 85.1 | 469.5422[M + H]+ | 379.2757 | −0.4 | C30H44O4 | Glabrolide |
| 27 | 97.3 | 839.4065[M + H]+ | 663.3755, 487.3440, 469.3316, 451.3204 | −0.7 | C42H62O17 | Licorice saponin G2 |
| 28 | 101.2 | 487.3388[M + H]+ | 469.3329, 451.3196, 439.3216, 423.3244, 405.3087 | −1.9 | C30H46O5 | 24-Hydroxy glycyrrhetinic acid |
| 29 | 103.4 | 823.4108[M + H]+ | 647.3800, 471.3416, 453.3373, 435.3268 | 2.7 | C42H62O16 | Glycyrrhizic acid |
| 30 | 108.1 | 453.5640[M + Na]+ | 257.1911, 217.1702, 204.1916 | 0.4 | C22H22O9 | Ononin |
For these chromatographic peaks of interest, there is only one component (peak 20) that has not been identified. According to the identification results, 18 components (peaks 1–13, 15, 18, 19, 22, 25) belong to Fuzi, which comprise three types of alkaloids, diester diterpenoid alkaloids (DDA), monoester diterpenoid alkaloids (MDA) and alkylolamine diterpenoid alkaloids (ADA); and the other 11 components originate from Gancao, containing two kinds of compounds, flavonoids and saponins.
3.4. Antitumor efficacy of Fuzi–Gancao extract
In our previous study, an extract of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 (weight ratio) of Fuzi and Gancao showed a noticeable antitumor effect. In this paper, the inhibition rates on HeLa cells of 31 batches of samples were measured by MTT assays, as listed in Table S2.† As is shown in Fig. 3, most samples could strongly prevent the growth of HeLa cells. At the same weight ratio (2
1.5 (weight ratio) of Fuzi and Gancao showed a noticeable antitumor effect. In this paper, the inhibition rates on HeLa cells of 31 batches of samples were measured by MTT assays, as listed in Table S2.† As is shown in Fig. 3, most samples could strongly prevent the growth of HeLa cells. At the same weight ratio (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
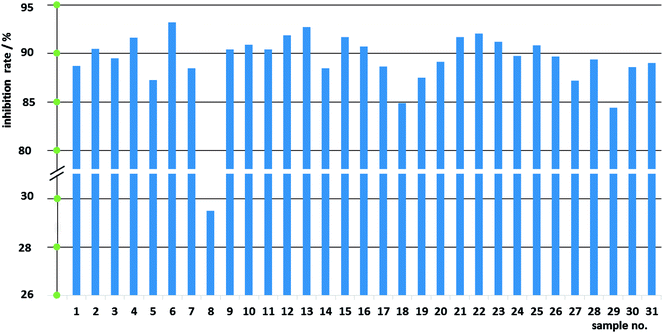
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) of Fuzi and Gancao and the same dose of 15 mg mL−1 (with respect to crude Fuzi), different samples exerted obviously different inhibition effects against HeLa cells: the lowest and the highest inhibition rates were 29.50% (sample 8) and 93.21% (sample 6), respectively. The significant differences in anticancer efficacy among the 31 different samples work in concert with the diverse chemical compositions, and imply that these data are suited to the construction of a CAR model.
3) of Fuzi and Gancao and the same dose of 15 mg mL−1 (with respect to crude Fuzi), different samples exerted obviously different inhibition effects against HeLa cells: the lowest and the highest inhibition rates were 29.50% (sample 8) and 93.21% (sample 6), respectively. The significant differences in anticancer efficacy among the 31 different samples work in concert with the diverse chemical compositions, and imply that these data are suited to the construction of a CAR model.
3.5. Model comparison and selection
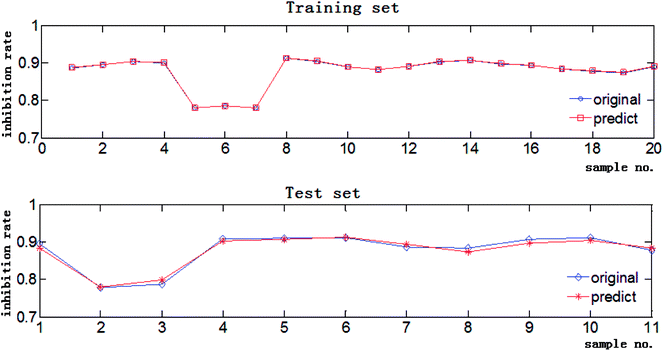
The data in Tables S1 and S2† were used to create the independent variable matrix X31×30 and the dependent variable matrix Y31×1, and three models were constructed by different algorithms to fit the relationship between these two groups of data. The RPAs of the 30 concerned chromatographic peaks were imported to Matlab and the corresponding inhibition rates of the extracts were the theoretical output values of the CAR model. The RMSE and R of the training set and test set of the three investigative models are listed in Table 3. For the training set, the three models have the same R values, and BP-GA and SVR-PSO have similar RMSEs that are both much lower than the RMSE of SVR-GA, suggesting that the former two models have better fitting precision than SVR-GA. For the test set, the RMSEs of BP-GA and SVR-PSO are still nearly the same and lower than that of SVR-GA, however the R of SVR-PSO is far higher than that of BP-GA, indicating that SVR-PSO has the stronger prediction and generalization capability. Comparatively speaking, SVR-PSO performs best in describing the complicated composition–activity relationship for the Fuzi–Gancao extract. The predictive regression curves of the training set and test set by the SVR-PSO model with best C = 14.3265 and best g = 0.1 are shown in Fig. 4. Clearly, the predicted values correspond with the original experimental inhibition rates very well in both the training set and the test set, indicating that the established SVR-PSO model combines high fitting accuracy with good generalization capability and is capable of describing the relationship between chemical composition and pharmacological activity of Fuzi–Gancao extract.3.6. Antitumor component recognition by MIV
Based on the superior SVR-PSO model, the MIV method was employed to identify the active antitumor components from the Fuzi–Gancao extract. MIVs of the 30 common peaks from the 31 different samples were acquired as described in Section 2.8 and the 30 peaks were then ranked by their absolute MIVs, as shown in Table 4. A higher absolute MIV means that the corresponding component contributes more to the inhibition effect of the Fuzi–Gancao extract on HeLa cells, and therefore, the top 8 components (peaks 17, 25, 22, 13, 23, 28, 5, 7) are temporarily deemed to possess good antitumor activity.| Peak | Absolute MIV | Ranking | Peak | Absolute MIV | Ranking |
|---|---|---|---|---|---|
| a MIV: mean impact value. | |||||
| 1 | 0.0008 | 28 | 16 | 0.0015 | 25 |
| 2 | 0.0102 | 15 | 17 | 0.0424 | 1 |
| 3 | 0.0042 | 19 | 18 | 0.0109 | 14 |
| 4 | 0.0016 | 24 | 19 | 0.0012 | 26 |
| 5 | 0.0184 | 7 | 20 | 0.0160 | 9 |
| 6 | 0.0008 | 29 | 21 | 0.0009 | 27 |
| 7 | 0.0169 | 8 | 22 | 0.0293 | 3 |
| 8 | 0.0137 | 10 | 23 | 0.0247 | 5 |
| 9 | 0.0002 | 30 | 24 | 0.0042 | 20 |
| 10 | 0.0022 | 23 | 25 | 0.0315 | 2 |
| 11 | 0.0113 | 13 | 26 | 0.0028 | 22 |
| 12 | 0.0121 | 11 | 27 | 0.0072 | 16 |
| 13 | 0.0284 | 4 | 28 | 0.0238 | 6 |
| 14 | 0.0060 | 17 | 29 | 0.0029 | 21 |
| 15 | 0.0120 | 12 | 30 | 0.0051 | 18 |
The top 8 components are liquiritin, 14-benzoyl-deoxyaconine, benzoylhypaconine, 14-acetyltalatizamine, formononetin, 24-hydroxy glycyrrhetinic acid, senbusine A/B and aconine. Of these, five components (peaks 25, 22, 13, 5, 7) are from Fuzi and three components (peaks 17, 23, 28) are from Gancao. Among the 8 components, there are not only high level components like formononetin (peak 23), but also lower level components like 14-benzoyl-deoxyaconine (peak 25). Indeed, the ranking of 14-benzoyl-deoxyaconine is even higher than that of formononetin, meaning that the recognition results do not rely on the component content, which is beneficial for finding those low level compounds with high activity. Most of the recognized components have been confirmed to have prominent anti-tumor efficacy in the published literature. For example, liquiritin (peak 17) is a major flavonoid constituent in Glycyrrhizae Radix and it was found that liquiritin could effectually suppress the proliferation and migration of human gastric cancer cells which are resistant to cisplatin, and, furthermore, the combined therapy of liquiritin and cisplatin exhibited potent inhibition activity against cisplatin-resistant gastric cancer cells through multiple pathways.34 Moreover, the component corresponding to peak 22 was identified as benzoylhypaconine, which has been reported to possess selective cytotoxicity against the MGC80 gastric cancer cell line with a low IC50 value of 24.7 μg mL−1.35
4. Conclusions
An integrated strategy was efficiently applied to recognize antitumor components from a mixed extract of Fuzi–Gancao. Firstly, desirable separation was fulfilled by HPLC for the constituent ingredients in the Fuzi–Gancao extract, and 30 common chromatographic peaks from 31 different samples were analyzed quantitatively and qualitatively. Secondly, three CAR models were established using different algorithms to interpret the relationship between the chemical composition and the antitumor effect of the Fuzi–Gancao extracts, and the SVR-PSO model stood out after consideration of the fitting precision and prediction ability. Furthermore, the antitumor activities of the 30 identified compounds were evaluated by MIV, and 8 components with high absolute MIVs were identified as promising anticancer compounds. This proposed strategy provides an attractive approach to the identification of potent antitumor compounds. It will benefit drug-discovery from herbal medicines, and the identified compounds provide a reference for early antitumor pharmaceutical screening.Conflicts of interest
The authors declare no competing financial interest.Non-standard abbreviations
| BP | Back propagation |
| CAR | Composition–activity relationship |
| GA | Genetic algorithm |
| MIV | Mean impact value |
| MLR | Multiple linear regression |
| PSO | Particle swarm optimization |
| RPA | Relative peak area |
| RRT | Relative retention time |
| SVR | Support vector regression |
Acknowledgements
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.References
- Y. L. Zhang, Y. Liang and C. W. He, Anticancer activities and mechanisms of heat-clearing and detoxicating traditional Chinese herbal medicine, Chin. Med., 2017, 12 DOI:10.1186/s13020-017-0140-2
.
- T. Basu, A. Mallik and N. Mandal, Evolving importance of anticancer research using herbal medicine: a scientometric analysis, Scientometrics, 2017, 110, 1375–1396 CrossRef
.
- Y. P. Huang, Z. W. Wu, R. H. Su, G. H. Ruan, F. Y. Du and G. K. Li, Current application of chemometrics in traditional Chinese herbal medicine research, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2016, 1026, 27–35 CrossRef CAS PubMed
.
- C. Chen, J. Yuan, X. J. Li, Z. B. Shen, D. H. Yu, J. F. Zhu and F. L. Zeng, Chemometrics-Based Approach to Feature Selection of Chromatographic Profiles and its Application to Search Active Fraction of Herbal Medicine, Chem. Biol. Drug Des., 2013, 81, 688–694 CrossRef CAS PubMed
.
- H. Q. Li, W. Zhang, Y. Chen, Y. M. Guo, G. Z. Li and X. X. Zhu, A novel multi-target regression framework for time-series prediction of drug efficacy, Sci. Rep., 2017, 7 DOI:10.1038/srep40652
.
- N. Xin, X. F. Gu, H. Wu, Y. Z. Hu and Z. L. Yang, Application of genetic algorithm-support vector regression (GA-SVR) for quantitative analysis of herbal medicines, J. Chemom., 2012, 26, 353–360 CrossRef CAS
.
- P. D. Harrington, Automated support vector regression, J. Chemom., 2017, 31 DOI:10.1002/cem.2867
.
- G. C. M. Patel, A. K. Shettigar, P. Krishna and M. B. Parappagoudar, Back propagation genetic and recurrent neural network applications in modelling and analysis of squeeze casting process, Appl. Soft Comput., 2017, 59, 418–437 CrossRef
.
- P. Baldi and P. Sadowski, A theory of local learning, the learning channel, and the optimality of backpropagation, Neural Netw., 2016, 83, 51–74 CrossRef PubMed
.
- A. J. Smola and B. Scholkopf, A tutorial on support vector regression, Stat. Comput., 2004, 14, 199–222 CrossRef
.
- L. Douha, N. Benoudjit, F. Douak and F. Melgani, Support Vector Regression in Spectrophotometry: An Experimental Study, Crit. Rev. Anal. Chem., 2012, 42, 214–219 CrossRef CAS
.
- H. Baba, J. Takahara and H. Mamitsuka, In Silico Predictions of Human Skin Permeability using Nonlinear Quantitative Structure-Property Relationship Models, Pharm. Res., 2015, 32, 2360–2371 CrossRef CAS PubMed
.
- M. Clavaud, Y. Roggo, K. Degardin, P. Y. Sacre, P. Hubert and E. Ziemons, Global regression model for moisture content determination using near-infrared spectroscopy, Eur. J. Pharm. Biopharm., 2017, 119, 343–352 CrossRef PubMed
.
- W. Shi, C. Zhang, D. S. Zhao, L. L. Wang, P. Li and H. J. Li, Discovery of Hepatotoxic Equivalent Combinatorial Markers from Dioscorea bulbifera tuber by Fingerprint-Toxicity Relationship Modeling, Sci. Rep., 2018, 8 DOI:10.1038/s41598-017-18929-z
.
- Y. B. Sun, L. Chen, B. S. Huang and K. L. Chen, A Rapid Identification Method for Calamine Using Near-Infrared Spectroscopy Based on Multi-Reference Correlation Coefficient Method and Back Propagation Artificial Neural Network, Appl. Spectrosc., 2017, 71, 1447–1456 CrossRef CAS PubMed
.
- P. Tsirikoglou, S. Abraham, F. Contino, C. Lacor and G. Ghorbaniasl, A hyperparameters selection technique for support vector regression models, Appl. Soft Comput., 2017, 61, 139–148 CrossRef
.
- H. Kaneko and K. Funatsu, Fast optimization of hyperparameters for support vector regression models with highly predictive ability, Chemom. Intell. Lab. Syst., 2015, 142, 64–69 CrossRef CAS
.
- Q. X. Yang, M. Wang, H. B. Xiao, L. Yang, B. K. Zhu, T. D. Zhang and X. Y. Zeng, Feature selection using a combination of genetic algorithm and selection frequency curve analysis, Chemom. Intell. Lab. Syst., 2015, 148, 106–114 CrossRef CAS
.
- Y. D. Zhang, S. H. Wang and G. L. Ji, A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications, Math. Probl. Eng., 2015, 2015 DOI:10.1155/2015/931256
.
- Y. Yang, X. J. Yin, H. M. Guo, R. L. Wang, R. Song, Y. Tian and Z. J. Zhang, Identification and comparative analysis of the major chemical constituents in the extracts of single Fuzi herb and Fuzi–Gancao herb-pair by UFLC-IT-TOF/MS, Chin. J. Nat. Med., 2014, 12, 542–553 CAS
.
- J. M. Zhang, W. Liao, Y. X. He, Y. He, D. Yan and C. M. Fu, Study on intestinal absorption and pharmacokinetic characterization of diester diterpenoid alkaloids in precipitation derived from Fuzi–Gancao herb-pair decoction for its potential interaction mechanism investigation, J. Ethnopharmacol., 2013, 147, 128–135 CrossRef CAS PubMed
.
- H. C. Yan, H. D. Qu, L. R. Sun, S. J. Li, X. O. Cao, Y. Y. Fang, W. Jie, J. C. Bean, W. K. Wu, X. H. Zhu and T. M. Gao, Fuzi polysaccharide-1 produces antidepressant-like effects in mice, Int. J. Neuropsychopharmacol., 2010, 13, 623–633 CrossRef CAS PubMed
.
- J. Han, P. Tan, Z. Y. Li, Y. Wu, C. Li, Y. Wang, B. B. Wang, S. Zhao and Y. G. Liu, Fuzi Attenuates Diabetic Neuropathy in Rats and Protects Schwann Cells from Apoptosis Induced by High Glucose, PLoS One, 2014, 9 DOI:10.1371/journal.pone.0086539
.
- D. D. Zhao, J. Wang, Y. J. Cui and X. F. Wu, Pharmacological effects of Chinese herb aconite (Fuzi) on cardiovascular system, J. Tradit. Chin. Med., 2012, 32, 308–313 CrossRef PubMed
.
- R. Yang, L. Q. Wang, B. C. Yuan and Y. Liu, The Pharmacological Activities of Licorice, Planta Med., 2015, 81, 1654–1669 CrossRef CAS PubMed
.
- B. Sun, X. B. Wang, R. L. Cao, Q. Zhang, Q. Liu, M. F. Xu, M. Zhang, X. B. Du, F. T. Dong and X. Z. Yan, NMR-based metabonomics study on the effect of Gancao in the attenuation of toxicity in rats induced by Fuzi, J. Ethnopharmacol., 2016, 193, 617–626 CrossRef PubMed
.
- Q. Zhang, X. Chen, Y. J. Luo, H. P. Ren and T. K. Qiao, Fuzi Enhances Anti-Tumor Efficacy of Radiotherapy on Lung Cancer, J. Cancer, 2017, 8, 3945–3951 CrossRef PubMed
.
- C. K. Lee, K. K. Park, S. S. Lim, J. H. Y. Park and W. Y. Chung, Effects of the licorice extract against tumor growth and cisplatin-induced toxicity in a mouse xenograft model of colon cancer, Biol. Pharm. Bull., 2007, 30, 2191–2195 CrossRef CAS
.
- K. Fukuchi, N. Okudaira, K. Adachi, R. Odai-Ide, S. Watanabe, H. Ohno, M. Yamamoto, T. Kanamoto, S. Terakubo, H. Nakashima, Y. Uesawa, H. Kagaya and H. Sakagami, Antiviral and Antitumor Activity of Licorice Root Extracts, In Vivo, 2016, 30, 777–785 CrossRef CAS PubMed
.
- K. Amasyali and N. M. El-Gohary, A review of data-driven building energy consumption prediction studies, Renewable Sustainable Energy Rev., 2018, 81, 1192–1205 CrossRef
.
- Q. H. Hu, S. G. Zhang, Z. X. Xie, J. S. Mi and J. Wan, Noise model based v-support vector regression with its application to short-term wind speed forecasting, Neural Netw., 2014, 57, 1–11 CrossRef PubMed
.
- Z. Ramedani, M. Omid, A. Keyhani, S. Shamshirband and B. Khoshnevisan, Potential of radial basis function based support vector regression for global solar radiation prediction, Renewable Sustainable Energy Rev., 2014, 39, 1005–1011 CrossRef
.
- Y. R. Zeng, Y. Zeng, B. Choi and L. Wang, Multifactor-influenced energy consumption forecasting using enhanced back-propagation neural network, Energy, 2017, 127, 381–396 CrossRef
.
- F. Wei, X. Jiang, H. Y. Gao and S. H. Gao, Liquiritin induces apoptosis and autophagy in cisplatin (DDP)-resistant gastric cancer cells in vitro and xenograft nude mice in vivo, Internet J. Oncol., 2017, 51(5), 1383–1394 CrossRef CAS PubMed
.
- J. Q. Zhao, Y. M. Wang, S. Wang, J. Dang, Y. P. Shi, L. J. Mei and Y. D. Tao, A new isocoumarin from the aerial parts of Aconitum gymnandrum, Nat. Prod. Res., 2016, 30, 1746–1752 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra07911k |
| This journal is © The Royal Society of Chemistry 2018 |