Open Access Article
Open Access ArticleInk-injected dual-band antennas based on graphene flakes, carbon nanotubes and silver nanowires†
Haochuan Qiu ab,
Houfang Liu*ab,
Xiufeng Jiaab,
Xiao Liuab,
Yuxing Liab,
Tianyu Jiangab,
Benkuan Xiongab,
Yi Yangab and
Tian-ling Ren
ab,
Houfang Liu*ab,
Xiufeng Jiaab,
Xiao Liuab,
Yuxing Liab,
Tianyu Jiangab,
Benkuan Xiongab,
Yi Yangab and
Tian-ling Ren *ab
*ab
aInstitute of Microelectronics, Tsinghua University, Beijing 100084, China. E-mail: hfliu@tsinghua.edu.cn; RenTL@tsinghua.edu.cn
bTsinghua National Laboratory for Information Science and Technology, Tsinghua University, Beijing 100084, China
First published on 7th November 2018
Abstract
The transition from the current 4th generation mobile networks (4G) to the next generation, known as 5th generation mobile networks (5G), is expected to occur within the next decade. To provide greater network speed, capacity and better coverage, the wireless broadband technologies need to update traditional antennas for high frequency and millimeter wavelengths. In this study, meander line dipole antennas produced by direct ink-injecting technology have been successfully designed, fabricated and characterized, where the ink-injecting technology may open new routes to the fabrication of wireless antenna applications. An accurate electromagnetic numerical analysis model for the proposed meander line antenna is also developed. The designed dual-band antenna based on graphene flakes and Ag nanowires can operate from 1.2 GHz up to the 1.5 GHz band and from 3.2 GHz up to the 3.8 GHz band with |S11| > 10 dB for wireless communications applications. Different mixtures by mass ratio of aqueous dispersions of CNTs and Ag nanowires (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 10
1, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 20
1, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are also prepared to investigate the influence of the network structure on the performance of the meander line antennas.
1) are also prepared to investigate the influence of the network structure on the performance of the meander line antennas.
Introduction
5th generation mobile networks (5G) are defined as the next major phase of mobile telecommunications standards beyond the current 4G technologies, because of their innovative applicability for smart wearables, autonomous cars, the Internet of Things (IoT) and virtual/augmented reality.1–3 Driven by low time-to-market and on-demand manufacturing, besides high-speed-data propagation and energy-saving capability, the antennas, as one of the key points of wireless communications, have been transforming to allow flexibility, reconfiguration and easy fabrication. As emerging materials, graphene flakes (GFs), carbon nanotubes (CNTs) and Ag nanowires (NWs-Ag) have great advantages for antenna application, such as good bio-compatibility, and electrical and mechanical properties. In recent years, numerous methods have been proposed for the fabrication of these materials in antenna applications, such as inkjet printing,4 transfer,7 cutting operations by milling machines5 and injecting liquid metal into microfluidic channels.6 For example, CNTs hardened by resin infiltration were printed on both sides of the substrate and then cut by a milling machine to obtain a multiband antenna.5 A CNT-sheet patch antenna was proposed with CNT sheets laminated on the Teflon substrate or transferred to Kapton tape.7 A wideband microwave antenna with highly conductive graphene was demonstrated with graphene-oxide/graphene composite annealed at 900 °C to achieve low ohmic resistance.8 A stretchable radio frequency antenna was realized with liquid metal (EGaIn alloy) enclosed in elastomeric microfluidic channels, but there still existed the problem of leakage.9 However, there are few reports about the direct evaluation of the materials of GFs, CNTs and NWs-Ag in RF antenna applications under the same fabrication process. Further, a customizable fabrication method for RF antenna also needs to be developed.In this paper, dual-band meander line antennas based on GFs, CNTs and NWs-Ag are achieved for radiolocation at the 1.3 GHz band and 5G at the 3.4 GHz band. The fabrications of antennas are done by a direct ink-injecting method on PDMS substrates with ξr = 2.67 and a thickness d = 1.5 mm, which are molded with a 3D printed acrylonitrile-butadiene-styrene copolymer (ABS). The return loss and radiation patterns are experimentally characterized and numerically simulated by a Vector Network Analyzer (VNA), Ansoft HFSS and Advanced Design System (ADS), respectively. The validated excellent performance of the prototype dual-band meander line antennas suggests that antennas based on GFs, CNTs and NWs-Ag can be manufactured by a direct ink-injected process.
Experimental section
Sample preparation
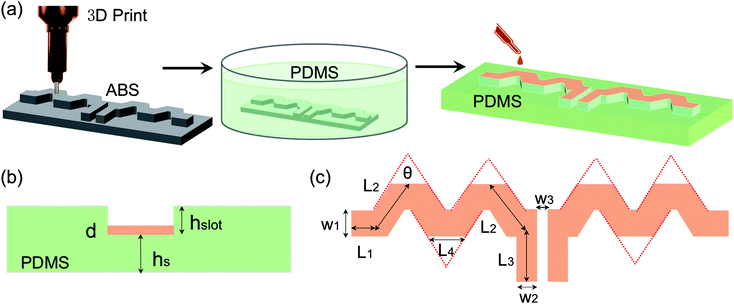
Fig. 1(a) illustrates the schematic preparation process for GFs, CNTs and NWs-Ag dual-band meander line antennas on a transparent and flexible PDMS substrate, with relative permittivity ξr = 2.67, loss tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 0.37,10 thickness hs = 1.5 mm and slot depth hslot = 1 mm, as shown in Fig. 1(b). As shown in Fig. 1(a), the designed ABS mold is fabricated using a 3D printing technique and then placed in a container fully filled with PDMS liquid (Dow Corning SYLGARD 184). The samples are dried at 60 °C in air for 30 min before lifting the PDMS off from the mold. The shape of the meander line dipole antenna is transferred from the ABS mold to the PDMS substrate with meander slots. The GFs, metallic CNTs (Me-CNTs), silver nanowires (NWs-Ag) and semi-CNTs/NWs-Ag complex film were prepared from droplets of water solutions of 0.15 wt% into PDMS slots. Here, the diameters of the GFs range from 0.5 to 5 μm with a thickness of 0.5 to 3 nm, the diameters of the Me-CNTs range from 1.2 to 1.7 nm with a length of 300 nm to 5 μm, the diameters of the semi-CNTs range from 1 to 2 nm with a length of 5 to 30 μm and the diameters of the silver nanowires are 30 nm with a length of 20 μm to 60 μm (Nanjing XFNANO Materials TECH Co., Ltd.). The CNT–silver nanowire complex water solution is prepared by mixing aqueous dispersions of semi-CNTs and aqueous dispersions of NWs-Ag with mass ratios (MR) = 1
δ = 0.37,10 thickness hs = 1.5 mm and slot depth hslot = 1 mm, as shown in Fig. 1(b). As shown in Fig. 1(a), the designed ABS mold is fabricated using a 3D printing technique and then placed in a container fully filled with PDMS liquid (Dow Corning SYLGARD 184). The samples are dried at 60 °C in air for 30 min before lifting the PDMS off from the mold. The shape of the meander line dipole antenna is transferred from the ABS mold to the PDMS substrate with meander slots. The GFs, metallic CNTs (Me-CNTs), silver nanowires (NWs-Ag) and semi-CNTs/NWs-Ag complex film were prepared from droplets of water solutions of 0.15 wt% into PDMS slots. Here, the diameters of the GFs range from 0.5 to 5 μm with a thickness of 0.5 to 3 nm, the diameters of the Me-CNTs range from 1.2 to 1.7 nm with a length of 300 nm to 5 μm, the diameters of the semi-CNTs range from 1 to 2 nm with a length of 5 to 30 μm and the diameters of the silver nanowires are 30 nm with a length of 20 μm to 60 μm (Nanjing XFNANO Materials TECH Co., Ltd.). The CNT–silver nanowire complex water solution is prepared by mixing aqueous dispersions of semi-CNTs and aqueous dispersions of NWs-Ag with mass ratios (MR) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 10
1, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. Finally, all the samples were dried at 80 °C for 15 min in a vacuum to eliminate the influence of water.
1, respectively. Finally, all the samples were dried at 80 °C for 15 min in a vacuum to eliminate the influence of water.
Characterization
The SEM images of GFs, CNTs and NWs-Ag are observed using Raith e-line plus SEM. The X-ray photoelectron spectra (XPS) of GFs and Me-CNTs are measured by ESCALAB 250Xi (Thermo Fisher Scientific). The return losses are measured with an Agilent PNA-X series N5242A network analyzer. The radiation patterns were obtained in an anechoic chamber.Results and discussions
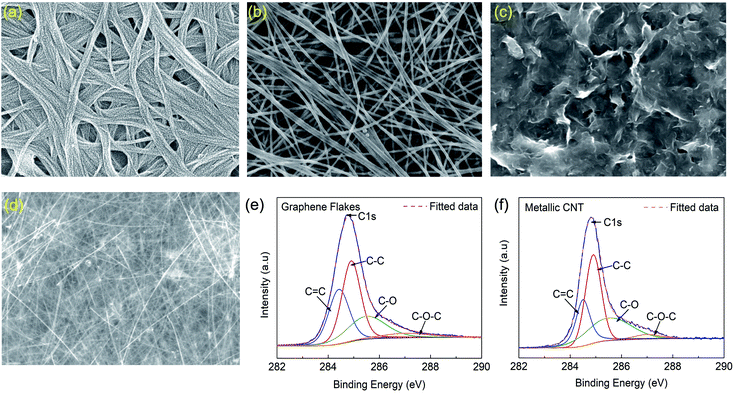
The antenna is designed as a meander line dipole antenna, which can significantly reduce the size of the dipole antennas.11 Due to the cancellation of the opposite polarity of currents between two adjacent meandering sections,12,13 folding the elements in the meander line structure produces a resonant frequency much lower than that of a single-element antenna of equal length. To obtain the resonant frequency of radiolocation at the 1.3 GHz band and 5G at the 3.4 GHz band, the geometric dimensions of the designed antenna are shown in Fig. 1(c). As can be seen, the detailed parameters of the meander-line antenna are shown in Table S1.† The corners of the antenna usually cause discontinuity of current density accumulation of charge, which induces extra inductance and capacitance. Therefore, in order to reduce the discontinuous reactance of the antenna, the corners marked with red dashed lines in Fig. 1(c) are chamfered at an angle θ. The length and width of the cutout region were optimized to achieve better impedance matching. To connect the antenna to a vector network analyzer (VNA), epoxy resin conductive Ag adhesive is used to connect the SMA connector with the antenna.GFs, CNTs and NWs-Ag have emerged as good candidates for lightweight, durable, 5G and radiolocation antennas, due to their unique physical and electrical properties, such as corrosion resistance, weight saving, reliability and enhanced electrical characteristics.14–16 The microstructures of Me-CNTs, NWs-Ag, GFs, and a semi-CNTs/NWs-Ag complex were investigated using Raith e-line plus SEM, as presented in Fig. 2(a)–(d). The graphene has its typical multilayer sheet structure and the typical sheet size is shown in Fig. 2(c). The MR of semi-CNTs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NWs-Ag = 5
NWs-Ag = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; it is well mixed and has a typical length, as shown in Fig. 2(d).
1; it is well mixed and has a typical length, as shown in Fig. 2(d).
Fig. 2(e) and (f) show X-ray photoelectron spectra (XPS) for GFs and Me-CNTs. The charge correction has been used and the XPS spectra were also calibrated relative to C 1s at 284.8 eV. The C–C peak was set to 284.9 eV all over the spectra. It is clear that the sums (pink dashed lines) of four peaks at 284.3 eV (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 284.9 eV (C–C), 285.5 eV (C–O) and 287.0 eV (C–O–C) are accurately fitted with the deconvoluted C 1s spectra of graphene flakes, which are in good agreement with previous reports.17–19 Based on the XPS survey spectra, the atomic ratio between C and O can be estimated from
C), 284.9 eV (C–C), 285.5 eV (C–O) and 287.0 eV (C–O–C) are accurately fitted with the deconvoluted C 1s spectra of graphene flakes, which are in good agreement with previous reports.17–19 Based on the XPS survey spectra, the atomic ratio between C and O can be estimated from 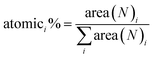 and
and 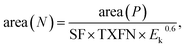 where area (N)i is the normalized area of different specific spectra, area (P) is the area of different specific spectra, SF is the sensitivity factor, TXFN is the transmission function and Ek is the kinetic energy19 (see concrete parameters in ESI, Table S2†). Hence, the C/O ratio for GFs is calculated as C/O = 8.1
where area (N)i is the normalized area of different specific spectra, area (P) is the area of different specific spectra, SF is the sensitivity factor, TXFN is the transmission function and Ek is the kinetic energy19 (see concrete parameters in ESI, Table S2†). Hence, the C/O ratio for GFs is calculated as C/O = 8.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is almost equal to that for reduced GO (C/O ∼ 8–14).20 These results indicate that the GFs and Me-CNTs both have high conductivities, due to a lower content of oxygen and a high number of sp2 carbon bonds. In addition, the XPS spectra of GFs and CNTs did not contain any elements except C and O, indicating the absence of impurities; the survey spectra have been provided in Fig. S2† as proof (see ESI, Fig. S2†).
1, which is almost equal to that for reduced GO (C/O ∼ 8–14).20 These results indicate that the GFs and Me-CNTs both have high conductivities, due to a lower content of oxygen and a high number of sp2 carbon bonds. In addition, the XPS spectra of GFs and CNTs did not contain any elements except C and O, indicating the absence of impurities; the survey spectra have been provided in Fig. S2† as proof (see ESI, Fig. S2†).
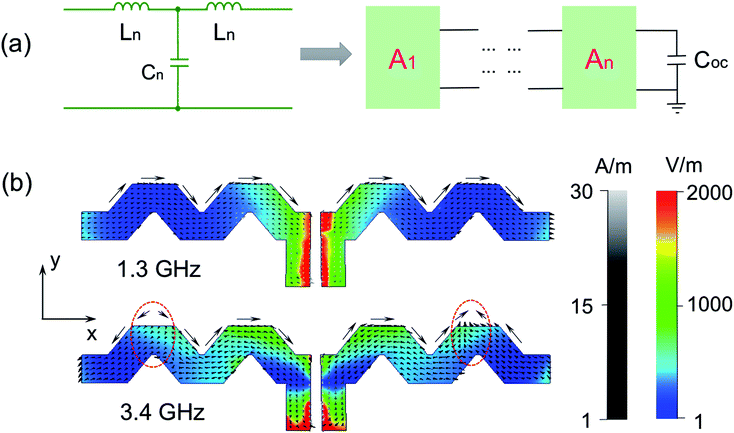
One great limitation of the antenna is that GFs and CNTs have a relatively higher surface resistance than that of metal. Therefore, it was designed with a relatively large strip width to reduce the resistance of the antenna. The radiation efficiency (ηr) of the antenna can be maximized by an increase in radiation resistance (Rr) or a decrease in loss resistance (Rl), following the basics of antenna theory: ηr = Rr/(Rr + Rl).21 The radiations always occur at the right-angle bends and the straight segments. The overall equivalent circuit is shown in Fig. 3(a). The designed antenna consists of straight elements and bends, which are considered as distributed transmission lines. The lumped parameter equivalent to straight elements can be represented by a T-equivalent network, as shown in Fig. 3(a). The equivalent lumped inductance Ln and capacitance Cn can be also described as 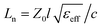 and
and 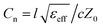 .22
.22
Numerical analysis based on the finite element method is used to design and optimize the design structure of the antennas. Here, for example, in simulations the conductivity of the GFs is calculated as σ = 1/(dRsquare) = 2.5 × 104 S m−1 with a thickness of d = 10 μm (see ESI, Table S1†). The current distributions are evaluated to understand the performance of the antennas. Fig. 3(b) shows the surface current and electric field distribution at resonant frequencies of 1.3 GHz and 3.4 GHz for the designed meander line dipole antenna. The electric field distributions are almost symmetric on the antenna and then cause symmetric distributions of the surface current. The currents are concentrated at the corners of the antenna, which cause a discontinuity in current and extra discontinuity inductance. At 1.3 GHz, the current distribution is along the +x direction, as shown in Fig. 3(b). On the other hand, the current distribution at 3.4 GHz is quite different (see ESI, Fig. S1†). The current direction in the middle part (+x) is opposite to that of the left and right edges (−x), which results in a reduction in the total electrical length.
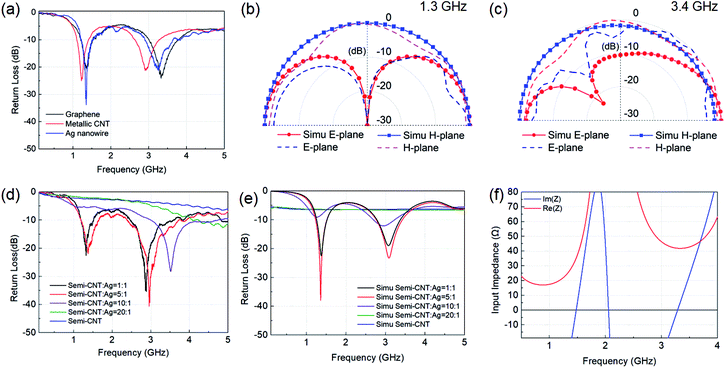
As an important aspect of antenna characterization, the return loss |S11|, characterized by an Agilent PNA-X series N5242A network analyzer, represents the input power acceptance level of the antenna.23 Normally, an optimized antenna with return loss |S11| > 10 dB is acceptable for use at a desired frequency.24,25 Antennas were bonded to SMAs with a typical impedance of 50 Ω and connected with the network analyzer. Fig. 4(a) shows the measured return loss |S11| of the antennas based on GFs, CNTs and NWs-Ag from 100 MHz to 5 GHz. Dual-band modes are obtained for all of the antennas. The frequency band for |S11| > 10 dB is from 1.1 GHz to 1.4 GHz, and from 2.6 GHz to 3.3 GHz for the Me-CNTs antenna, from 1.2 GHz to 1.5 GHz for the NWs-AG antenna and from 3.2 GHz to 3.8 GHz for the GFs antenna, which means a wideband performance.
As shown in Table 1, the −10 dB bandwidths for GFs antenna are 316 MHz (1.3 GHz) and 773 MHz (3.4 GHz), 316 MHz (1.3 GHz) and 750 MHz (3.4 GHz) for the NWs-Ag antenna, and 314 MHz (1.3 GHz) and 640 MHz (3.4 GHz) for the Me-CNTs antenna. As shown in Table S4 (see ESI†), compared with other dipole antennas, our proposed GFs antenna has good performance with dual band and bandwidths of 316 MHz/773 MHz at 1.3 GHz/3.4 GHz, which can be used in radiolocation and 5G communication. Further details of the radiation properties of the antennas, including the resonant frequency and radiation efficiency, are summarized in Table 1. The efficiency can also be calculated from ηr = G/D, where G and D are the gain and directivity of the antenna, respectively.26 The measured efficiency of the graphene flakes antenna can reach 69% at 1.3 GHz and 52% at 3.4 GHz. Due to the increment in input resistance induced by the skin effect, the efficiency at 1.3 GHz is higher than that at 3.4 GHz, or for the GFs and Me-CNTs antennas. In comparison to NWs-Ag and Me-CNTs, the cost of graphene flakes is much lower, and the manufacturing process is relatively simple and scalable. These results indicate that the graphene-flakes dual-band antenna has great potential for low-cost and high-performance wireless communication.
| Material | NWs-Ag | Graphene flakes | Me-CNTs |
|---|---|---|---|
| Size mm2 | 75 × 20 | 75 × 20 | 75 × 20 |
| 1.3 GHz bandwidth | 316 MHz | 316 MHz | 314 MHz |
| 3.4 GHz bandwidth | 750 MHz | 773 MHz | 640 MHz |
| 1.3 GHz efficiency | 75% (Simu: 82%) | 69% (Simu: 75%) | 71% (Simu: 78%) |
| 3.4 GHz efficiency | 62% (Simu: 72%) | 52% (Simu: 64%) | 58% (Simu: 67%) |
It is reported that the lumped inductance of strips consists of magnetic inductance (LM) and kinetic inductance (LK). LM is the sum of self-inductance and mutual inductance, which are determined by the structure of the device, while LK is related to material alone.27 As shown in Fig. 4(a), the resonant frequency, which is related to lumped impedance, of Me-CNTs and NWs-Ag antennas shifted to slightly lower values compared with GFs. The simulation, based on the conductivity of graphene, of the Z parameter is shown in Fig. 4(f). At resonant frequency f0, the imaginary part of the Z parameter Im(Z) = 0 with the real part of the Z parameter Re(Z) = 35.3 Ω at 1.3 GHz and Re(Z) = 42 Ω at 3.4 GHz. This is probably because of the difference in carrier density and kinetic inductance, which may cause the change in Im(Z) of the antenna and further influence resonant frequencies. The measured and simulated normalized radiation patterns of the graphene flakes antenna in the E-plane and H-plane are shown in Fig. 4(b) and (c). Both at 1.3 GHz and at 3.4 GHz, the radiation patterns are almost omnidirectional in the H-plane, which is of most interest for wireless communication systems. The radiation pattern of the E-plane at 1.3 GHz is a typical dipole-like radiation pattern and at 3.4 GHz, influenced by the meander line structure, it has a mushroom-like radiation pattern.
Different MR of semi-CNTs/NWs-Ag complex (MRCNT:Ag = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 10
1, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) antennas are also prepared on the PDMS substrate with hs = 1.5 mm. The test results of |S11| are presented in Fig. 4(d). The performance of the semi-CNTs antenna causes a mismatch in impedance due to the low conductivity in Table S3 (see ESI†), as shown in Fig. 4(d). With the increment in MRCNT:Ag, the resonant frequency of the antennas increases. For example, when MRCNT:Ag = 10
1) antennas are also prepared on the PDMS substrate with hs = 1.5 mm. The test results of |S11| are presented in Fig. 4(d). The performance of the semi-CNTs antenna causes a mismatch in impedance due to the low conductivity in Table S3 (see ESI†), as shown in Fig. 4(d). With the increment in MRCNT:Ag, the resonant frequency of the antennas increases. For example, when MRCNT:Ag = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the |S11| becomes less than 5 dB at 1.4 GHz, and the resonant frequency shifts from 2.8 GHz, compared with MRCNT:Ag = 1
1, the |S11| becomes less than 5 dB at 1.4 GHz, and the resonant frequency shifts from 2.8 GHz, compared with MRCNT:Ag = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, to 3.55 GHz. When MRCNT:Ag increases to 20
1, to 3.55 GHz. When MRCNT:Ag increases to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the resonant frequency shifts to a higher value with the |S11| > 10 dB band from 4.5 GHz to 8 GHz (not shown here). Based on the tested square resistance in Table S3,† the simulation results are presented in Fig. 4(e). Note that the change in the ohmic resistance has little influence on the resonant frequency. NWs-Ag in the complex plays an important part in current transportation, due to the higher conductivity than that of semi-CNTs. The simulation result, as shown in Fig. 4(e), is obtained by using the same geometry but different measured conductivity of MRCNT:Ag, which means only the conductivity is changed while the current pass is the same as for pure materials (GFs, NWs-Ag and Me-CNTs) in the simulation. The simulation results indicate that the change in conductivity could not explain the shift in resonant frequency and the change in bandwidth observed in the experiment. To explain the shift, input impedance is shown in Fig. 4(f). At resonant frequency f0, the imaginary part of the Z parameter Im(Z) = 0. The discontinuous distribution of NWs-Ag can cause unevenly distributed currents, which contribute to extra parasitic inductance and capacitance; meanwhile, the NWs-Ag could also introduce extra kinetic inductance and further change the input impedance. With the increment in MRCNT:Ag, the distribution of the Z parameter is tuned, and hence the resonant frequency is changed. That is, the higher the MRCNT:Ag, the higher the resonant frequency measured. Therefore, the resonant frequency of the antennas can be monitored via the change in the MR of semi-CNTs and NWs-Ag.
1, the resonant frequency shifts to a higher value with the |S11| > 10 dB band from 4.5 GHz to 8 GHz (not shown here). Based on the tested square resistance in Table S3,† the simulation results are presented in Fig. 4(e). Note that the change in the ohmic resistance has little influence on the resonant frequency. NWs-Ag in the complex plays an important part in current transportation, due to the higher conductivity than that of semi-CNTs. The simulation result, as shown in Fig. 4(e), is obtained by using the same geometry but different measured conductivity of MRCNT:Ag, which means only the conductivity is changed while the current pass is the same as for pure materials (GFs, NWs-Ag and Me-CNTs) in the simulation. The simulation results indicate that the change in conductivity could not explain the shift in resonant frequency and the change in bandwidth observed in the experiment. To explain the shift, input impedance is shown in Fig. 4(f). At resonant frequency f0, the imaginary part of the Z parameter Im(Z) = 0. The discontinuous distribution of NWs-Ag can cause unevenly distributed currents, which contribute to extra parasitic inductance and capacitance; meanwhile, the NWs-Ag could also introduce extra kinetic inductance and further change the input impedance. With the increment in MRCNT:Ag, the distribution of the Z parameter is tuned, and hence the resonant frequency is changed. That is, the higher the MRCNT:Ag, the higher the resonant frequency measured. Therefore, the resonant frequency of the antennas can be monitored via the change in the MR of semi-CNTs and NWs-Ag.
Conclusion
In conclusion, novel direct ink-injected meander line dipole antennas based on graphene flakes, CNTs and silver nanowires were successfully designed, fabricated and tested. The shape of the antennas was transferred from the 3-D printing ABS mold to the PDMS substrate with meander slots. The return losses and radiation patterns of the antennas were characterized with dual bands of 1.3 GHz for radiolocation and 3.4 GHz for 5G applications as a proof of concept. The simulated and measured results indicate that these antennas show excellent performance with radiation efficiency up to nearly 80% for the NWs-Ag antenna. The antennas of GFs, Me-CNTs and NWs-Ag have similar dual-band performance and wide bandwidth, but Me-CNTs and NWs-Ag have lower resonant frequency than GFs, which is caused by the different kinetic inductances of different materials. At the same time, semi-CNTs/Ag nanowire complex antennas with different mass ratios were also studied. With the increment in MR, the resonant frequency shifts to a higher frequency, probably due to extra parasitic inductance, capacitance and kinetic inductance induced by the discontinuous distribution of Ag nanowires. The presented results show that the ink-injected dipole antennas have great potential for the applications of radiolocation and 5G.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by National Natural Science Foundation (61574083, 61434001, 11674373), National Key R&D Program (2016YFA0200400), National Basic Research Program (2015CB352101), Special Fund for Agroscientific Research in the Public Interest (201303107) of China, Opening Fund of Key Laboratory of Silicon Device Technology, Chinese Academy of Sciences, and Research Fund from Beijing Innovation Center for Future Chip. The authors are also thankful for the support of Open Research Fund Program of the State Key Laboratory of Low-Dimensional Quantum Physics (KF201715) and Independent Research Program (2014Z01006) of Tsinghua University.References
- F. Akyildiz and J. M. Jornet, IEEE Wirel. Commun., 2010, 17, 58–63 Search PubMed.
- F. Boccardi, R. W. Heath, A. Lozano, T. L. Marzetta and P. Popovski, IEEE Communications Magazine, 2014, 52, 74–80 Search PubMed.
- A. Lamminen, K. Arapov, S. Gijsbertus de With, S. Haque, H. G. O. Sandberg, H. Friedrich and V. Ermolov, IEEE Trans. Microwave Theory Tech., 2001, 49, 2331–2335 CrossRef.
- Z. Hamouda, J.-L. Wojkiewicz, A. A. Pud, L. Kone, B. Belaabed, S. Bergheul and T. Lasri, IEEE Trans. Antennas Propag., 2017, 16, 5864–5867 Search PubMed.
- S. D. Keller, A. I. Zaghloul, V. Shanov, M. J. Schulz, D. B. Mast and N. T. Alvarez, IEEE Trans. Antennas Propag., 2014, 62, 48–55 Search PubMed.
- A. Mehdipour, I. D. Rosca, A. Razik Sebak and C. W. Trueman, IEEE Antennas Wirel. Propag. Lett., 2010, 9, 891–894 Search PubMed.
- M. Kubo, X. F. Li, C. Kim, M. Hashimoto, B. J. Wiley, D. Ham and G. M. Whitesides, Adv. Mater., 2010, 22, 2749–2752 CrossRef CAS PubMed.
- R. G. Song, Q. L. Wang, B. Y. Mao, Z. Wang, D. L. Tang, B. Zhang, J. W. Zhang, C. G. Liu, D. P. He, Z. Wu and S. C. Mu, Carbon, 2018, 130, 164–169 CrossRef CAS.
- M. D. Dickey, R. C. Chiechi, R. J. Larsen, E. A. Weiss, D. A. Weitz and G. M. Whitesides, Adv. Funct. Mater., 2008, 18, 1097–1104 CrossRef CAS.
- A. Hassan, S. Ali, J. Bae and C. H. Lee, Appl. Phys. A, 2016, 122, 1–7 CrossRef CAS.
- C. W. P. Huang, A. Z. Elsherbeni, J. J. Chen and C. E. Smith, Journal of Electromagnetic Waves and Applications, 1999, 13, 1649–1651 CrossRef.
- J. W. Wu, C. R. Lin and J. H. Lu, Microwave Opt. Technol. Lett., 2004, 41, 380–382 CrossRef.
- Z. Elsherbeni, C. P. Huang and C. E. Smith, IEEE-APS Conference on Antennas and Propagation for Wireless Communications, 2000, pp. 17–20 Search PubMed.
- T. T. Tung, S. J. Chen, C. Fumeaux and D. Losic, J. Mater. Chem. C, 2016, 4(45), 10620 RSC.
- L. N. Song, A. C. Myers, J. J. Adams and Y. Zhu, ACS Appl. Mater. Interfaces, 2014, 6, 4248–4253 CrossRef CAS PubMed.
- I. Puchades, J. E. Rossi, C. D. Cress, E. Naglich and B. J. Landi, ACS Appl. Mater. Interfaces, 2016, 8, 20986–20992 CrossRef CAS PubMed.
- M. S. Strano, C. A. Dyke, M. L. Usrey, P. W. Barone, M. J. Allen, H. W. Shan, C. Kittrell, R. H. Hauge, J. M. Tour and R. E. Smalley, Science, 2003, 301, 1519–1522 CrossRef CAS PubMed.
- D. V. Kosynkin, A. Higginbotham, A. Sinitskii, J. R. Lomeda, A. B. Dimiev and K. Price, Nature, 2009, 458, 872–876 CrossRef CAS PubMed.
- T. I. T. Okpalugo, P. Papakonstantinou, H. Murphy, J. McLaughlin and N. M. D. Brown, Carbon, 2005, 43, 153–157 CrossRef CAS.
- H. J. Shin, K. K. Kim, A. Benayad, S. Yoon, H. Park, I. Jung, M. H. Jin, H.-Ky. Jeong, J. M. Kim, J.-Y. Choi and Y. H. Lee, Adv. Funct. Mater., 2009, 19, 1987–1992 CrossRef CAS.
- D. M. Pozar and B. Kaufman, IEEE Trans. Antennas Propag., 1988, 1, 136–139 CrossRef.
- C. A. Balanis, Antenna Theory Analysis and Design, John Wiley & Sons, Hoboken, 3rd edn, 2005 Search PubMed.
- H. Schantz, The Art and Science of Ultra-Wideband Antennas, ArtechHouse, Incorporated, 1st edn, 2005, p. 291 Search PubMed.
- A. M. Hussain, F. A. Ghaffar, S. I. Park, J. A. Rogers, A. Shamim and M. M. Hussain, Adv. Funct. Mater., 2015, 25, 6565–6575 CrossRef CAS.
- T. Inui, H. Koga, M. Nogi, N. Komoda and K. Suganuma, Adv. Mater., 2015, 27, 1112–1116 CrossRef CAS PubMed.
- H. Choo, R. Rogers and H. Ling, IEEE Trans. Antennas Propag., 2005, 7, 2328–2332 Search PubMed.
- J. Kang, Y. Matsumoto, X. Li, J. Jiang, X. Xie, K. Kawamoto, M. Kenmoku, J. H. Chu, W. Liu, J. Mao, K. Ueno and K. Banerjee, Nature Electronics, 2018, 1, 46–51 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra08018f |
| This journal is © The Royal Society of Chemistry 2018 |