Open Access Article
Open Access ArticleMesoscopic simulations of temperature-dependent anchoring and wetting behavior at aqueous–liquid crystal interfaces in the presence of a rod–coil amphiphilic monolayer
Zunmin Zhang ac,
Hongxia Guo
ac,
Hongxia Guo *ab and
Erik Nies*c
*ab and
Erik Nies*c
aBeijing National Laboratory for Molecular Sciences, Joint Laboratory of Polymer Sciences and Materials, State Key Laboratory of Polymer Physics and Chemistry, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: hxguo@iccas.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
cDivision of Polymer Chemistry and Materials, Department of Chemistry, KU Leuven, Celestijnenlaan 200F, B-3001 Heverlee, Belgium. E-mail: erik.nies@kuleuven.be
First published on 18th December 2018
Abstract
Dissipative particle dynamics simulations have been applied to study the temperature dependent anchoring and wetting behavior of thermotropic liquid crystals (LCs) in the presence of a rod–coil amphiphilic monolayer at the aqueous–LC interface. Upon cooling in the nematic phase, a thermally-induced anchoring transition from homeotropic through tilted to planar has been observed. The growth and propagation of smectic order from the interfaces to the bulk nematic LCs are demonstrated to be mainly responsible for this novel transition sequence. In particular, when a complete smectic layer in the amphiphile monolayer is induced around the bulk transition of nematic–smectic-A, the propagation of homeotropic alignment fails instantly and a unique planar anchoring configuration is formed instead. While heating towards the isotropic phase, simulation results show that the nematic–isotropic transition of confined LCs is slightly shifted to a higher temperature, and a nematic wetting layer with homeotropic alignment appears in the rod block monolayer when the bulk LCs is isotropic. Our systematic simulations throughout the whole phase regimes of LCs provide important molecular-level insight into how the coupling between the ordering of LCs and adsorbents and their temperature dependencies affect the anchoring behavior in this complex system, which should be instrumental in the rational design and application of advanced LC-based biosensors with optimal operating temperature range.
1. Introduction
It is well known that thermotropic liquid crystals (LCs) near interfaces exhibit a preferred direction of alignment that extends into the bulk over macroscopic distances, a phenomenon defined as surface anchoring. Generally, depending on the molecular details of the surface, the alignment of LCs may be parallel to the interface (planar anchoring), normal to the interface (homeotropic anchoring), or at some acute angle to the interface (tilted anchoring). Recently, considerable attention has been paid to the anchoring behavior at the interfaces between LCs and immiscible aqueous phases,1–4 since this type of interface exhibits a unique deformable and fluid nature, and consequently provides a novel platform for studying the molecular assembly and specific biomolecular recognition events. For example, the adsorption and organization of amphiphiles (e.g. surfactants,5–7 lipids,8,9 polymers,10 etc.) at aqueous–LC interfaces strongly influence the orientational ordering of LCs, which further has been exploited in the study of, e.g., enzymatic reactions,8 protein binding events,11 DNA hybridization.12 Additionally, the anchoring transition of LCs induced by these molecular-level events can be readily visualized in real time due to the optical birefringence properties, which presents new opportunities for the creation of fast and inexpensive chemical and biological sensors.1–4As a consequence of these promising applications, intensive efforts have been devoted to understanding the underlying mechanism. Previous studies by Abbott and co-workers5–7 have shown that upon the addition of amphiphiles in aqueous phase, some of them adsorb at the interface and trigger the LC phase to undergo a continuous orientational transition, from planar through tilted to homeotropic. The interfacial concentration, conformational property and tail organization of amphiphiles have been observed to be important in directing the homeotropic alignment. The principle qualitatively drawn from these experiments is that, with increasing the amphiphile coverage, the amphiphile monolayer is packed more densely and orderly with the amphiphile tails stretching further, which allows the deeper penetration of LC molecules into the amphiphile monolayer and in turn induces homeotropic anchoring. Our simulation study13 has further revealed that the tails of amphiphiles may act as an interfacial orientation field in dictating the orientational ordering of LCs, which is in the same spirit as the conclusions of Bahr.14,15 Moreover, recent work also suggests that the ordering of LCs also has a significant effect on the interfacial assembly of amphiphiles.16–22 For example, molecular simulation study by some of us19 has shown that with an increase of amphiphiles at interface, the perpendicular penetration of LCs in monolayer as well as the stronger coupling between LCs and amphiphile tails, promote the lateral ordering transition from liquid-expanded to liquid-condensed phase in the resulting mixed monolayer. Very recently, in LC nanodroplets decorated with surfactants, a liquid-crystal phase (nematic or smectic) is found to induce much richer nanophases with morphologies dependent on surfactant concentration and temperature, including circular, striped and worm-like patterns.20–22
In view of the fact that both the orientational ordering of bulk thermotropic LCs23 and the lateral ordering of amphiphile monolayers at isotropic interfaces (i.e., air–water and liquid–liquid)24 are sensitive to temperature, we thus expect that the thermal effects are also to remarkably influence the anchoring behavior of LCs at heterogeneous system such as aqueous–LC interface. Actually, there have been several experimental and theoretical studies aimed at exploring the temperature-driven anchoring transitions of LCs in contact with solid substrates, wherein the alignment of LCs was found to change from planar to homeotropic and vice versa continuously or discontinuously with temperature.25–30 In contrast with these solid interfaces, the lateral mobility of amphiphiles adsorbed at the aqueous–LC interfaces could be substantially improved, which facilitates the spontaneous reorganization of amphiphile monolayers at a given temperature. From a perspective of the strong coupling between amphiphiles and LCs, thus a rich thermally-induced anchoring behavior is expected to emerge at aqueous–LC interface. We have to note that, although the surfactant-laden LC nanodroplet provides a robust aqueous–LC interface for the discovery of new classes of nanophases of amphiphiles,20–22 the small and highly-curved interface is supposed to distort the propagation of the interfacial coupling of surfactant–LC into the bulk LCs, hence it may not be a viable platform for a direct examining of the thermally-induced anchoring behavior at aqueous–LC interfaces for potential applications.
In case of the great promise of this type of LC-based detectors, a deeper understanding of the molecular-level mechanisms for the temperature-induced anchoring transitions is not only interesting from a fundamental point of view but also instrumental in facilitating its advanced applications. As a computationally efficient method for probing the large-scale cooperative behavior in particularly complex systems, dissipative particle dynamics (DPD) simulation technique in combination with generic coarse-grained models are employed in this paper to investigate the basic mechanism of how the temperature affects the anchoring behavior of LCs at the aqueous–LC interfaces laden with rod–coil amphiphiles. Actually, our previous work13 has already demonstrated the rationality and efficiency of this model system in studying the anchoring behavior, i.e., a rich anchoring transition sequence is successfully reproduced by tuning an individual interaction parameter for the repulsion between the mesogens and the rod blocks of amphiphiles, which is essentially playing a role of changing the chemical constitution of amphiphilic molecules or mesogens. As an succeeding application of our coarse-grained models for this interfacial system,13 by fixing the above repulsion parameter and the amphiphile interfacial coverage, here we mainly explore the temperature dependent anchoring behavior. In the low-temperature nematic phase while cooling the homeotropic sample, we observe a rich thermally-induced anchoring transition sequence from homeotropic through tilted to planar. The simulations suggest that this behavior arises from the growth and propagation of a smectic order in the nematic phase with decreasing temperature. Whereas, when the bulk LCs is heated to the high-temperature isotropic state, the orientational wetting, a phenomenon closely related to surface anchoring that occurs above the nematic–isotropic bulk phase transition temperature at surfaces, is also probed when the bulk LCs is heated to the high-temperature isotropic state. It is worthy to mention that the temperature-dependent anchoring transitions produced in this study qualitatively agree well with some experimental observations. Therefore, the simplified coarse-grained models we developed capture the essential physics of the experimentally observed anchoring behavior of LCs at aqueous–LC interfaces, which will continue to provide useful guidelines for the rational design of advanced LC-based biosensor in a wide parameter range including temperature, interaction parameters, system composition, molecular architecture, and so on.
2. Simulation method and models
As a particle-based mesoscopic simulation technique, DPD has been successfully applied to study various complex fluids.31–37 In the method, each DPD particle represents a cluster of atoms or molecules, and the corresponding dynamics is governed by Newton's second law of motion. The total force acting between two particles is usually expressed as a sum of a conservation force, a dissipative force and a random force within a selected cutoff radius rc. The conservation force is a soft repulsion given by:
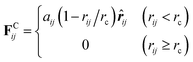 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |rij|. The other two forces act together as a thermostat, which maintains an equilibrium temperature for the simulated system:
|rij|. The other two forces act together as a thermostat, which maintains an equilibrium temperature for the simulated system:| FijD = −γωD(rij) (vij·rij)rij, (rij < rc) | (2) |
| FijR = σωR(rij)θijΔt−1/2rij, (rij < rc) | (3) |
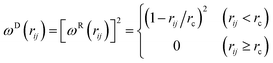 | (4) |
In order to generate a correct equilibrium Gibbs–Boltzmann distribution, the dissipative and random forces must satisfy the fluctuation–dissipation theorem given by the conditions:
| ωD(rij) = [ωR(rij)]2, σ2 = 2γkBT | (5) |
In the following we will briefly review the simulation models introduced by some of us earlier.13 It is worth to stress that as the rod blocks exhibit a much higher orientational order at the interface than the flexible tails of conventional amphiphiles and can further act as the ordering interface field,13 a kind of rod–coil amphiphilic molecule is chosen. Like our earlier work, there are three kinds of molecular species in the present model system, including the rod-like mesogens (M7), rod–coil amphiphiles (R10C7) and water molecules (C1), as schematically shown in Fig. 1a. The subscript, such as in M7, refers to the number of DPD beads in the molecule or the block. For more details about the choice of bead number for each individual molecule we also refer to ref. 13. Note that three types of beads (M, R and C) are considered in our simulation systems. All beads have same size and mass and interact with the aforementioned soft repulsive potential. Hence the system is characterized by six repulsion parameters, which describe the mutual incompatibility of mesogens, water, heads and tails of amphiphiles. Following the earlier settings,13 aRR = aCC = aMM = 20ε and aCM = aCR = 40ε are chosen. It is worth to mention that in the present study ε = 1 is considered as the unit of energy. The cut-off distance and bead mass are also set as the reduced units, that is rc = m = 1. Then the reduced temperature unit is defined as ε/kB and the scale of time is given by (mrc2/ε)1/2. Particularly, to mimic the strong affinity between the mesogens and the rod blocks of amphiphiles, a relatively weak repulsive parameter aMR = 10 is applied in the current study. With this favorable interaction, it has been demonstrated that the ordered rod blocks tend to orient along the interface normal and in turn act as an interfacial orientation field to align mesogens with a homeotropic anchoring at a given temperature T = 0.50.13
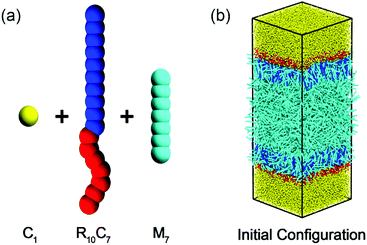 | ||
| Fig. 1 Schematic representation of (a) the molecular structures of water (C1), rod–coil amphiphiles (R10C7) and mesogens (M7), and (b) the initial configuration of simulated systems. | ||
Both the mesogens and amphiphiles are modelled as bead-spring chains, wherein the spring potential is defined as Ubond = 0.5kbond(r − req)2 with kbond = 100 and req = 2/3, Two additional potentials are applied for the mesogen and the rod block of the amphiphile to keep their rod-like structures:23 an extra bond potential between the first and last bead, Ubondex = 0.5kbond[r − (n − 1)req]2 with kex = 500 and a bond bending potential, Uϕ = 0.5kϕ(ϕ − π)2 with kϕ = 30. It should be noted that with these set of parameters, the bulk mesogens (M7) could undergo a nematic–isotropic (N–I) phase transition at 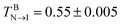 and a nematic–smectic-A (N–SmA) phase transition at
and a nematic–smectic-A (N–SmA) phase transition at 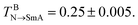 23 Obviously, such a substantially wide temperature window of the nematic phase allows us to systematically explore the complex thermally-induced anchoring behavior of nematic LCs at aqueous–LC interfaces with a fine resolution.23
23 Obviously, such a substantially wide temperature window of the nematic phase allows us to systematically explore the complex thermally-induced anchoring behavior of nematic LCs at aqueous–LC interfaces with a fine resolution.23
All simulations are performed in a rectangular box (Lx = Ly = 22.0, Lz ≈ 61.0) with a bead number density of ρ = 4.0, involving 9000 mesogens, 776 rod–coil amphiphiles and 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water beads. Accordingly, the surfactant coverage at the interface is roughly fixed at ρs = NR10C7/(LxLy) ≈ 0.8. In addition, the periodic boundary conditions are applied in all three directions, effectively creating a film of confined mesogens periodic in x− and y− directions but imposing nano-confinement in the z− direction by the rod–coil amphiphiles and water. We started our simulations from an initial state consisting of two neighboring slabs of water and disordered LCs with rod–coil amphiphiles randomly dispersed at the two water–LC interfaces, as schematically illustrated in Fig. 1b. After equilibration at temperature of T = 0.50, the well-defined homeotropic anchoring of nematic LCs could be obtained, which is then gradually cooled and heated through the bulk phase transitions of N–SmA and N–I with a resolution of ΔT = 0.01 respectively in order to investigate the temperature effect on the anchoring behavior.
000 water beads. Accordingly, the surfactant coverage at the interface is roughly fixed at ρs = NR10C7/(LxLy) ≈ 0.8. In addition, the periodic boundary conditions are applied in all three directions, effectively creating a film of confined mesogens periodic in x− and y− directions but imposing nano-confinement in the z− direction by the rod–coil amphiphiles and water. We started our simulations from an initial state consisting of two neighboring slabs of water and disordered LCs with rod–coil amphiphiles randomly dispersed at the two water–LC interfaces, as schematically illustrated in Fig. 1b. After equilibration at temperature of T = 0.50, the well-defined homeotropic anchoring of nematic LCs could be obtained, which is then gradually cooled and heated through the bulk phase transitions of N–SmA and N–I with a resolution of ΔT = 0.01 respectively in order to investigate the temperature effect on the anchoring behavior.
The orientational ordering of the mesogens and the rod blocks of amphiphiles was quantified by the diagonalization of the ordering tensor, defined as
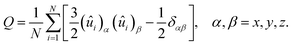 | (6) |
3. Results and discussion
3.1 Anchoring transition upon cooling
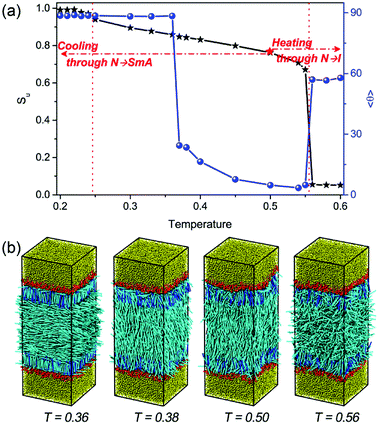
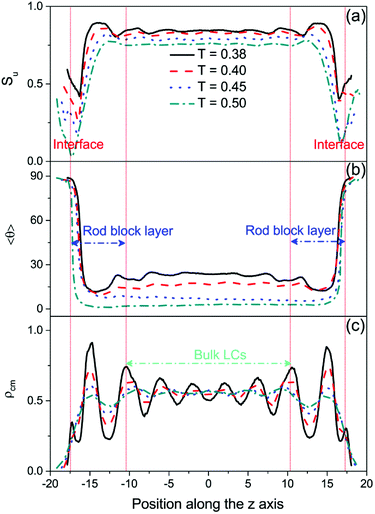
Numerous DPD simulations have been performed in this study to thoroughly examine the alignment and arrangement of bulk LCs at different temperatures. Fig. 2 presents the temperature dependent orientational order parameter and director tilt angle of mesogens locating at the bulk center. It is clear that there is a rich anchoring behavior with varying the temperature.As can be seen from Fig. 2a, while cooling in the nematic phase, the director tilt angle 〈θ〉 of the bulk mesogens gradually increases from 2.72° at T = 0.50 to 23.65° at T = 0.37, indicating a continuous anchoring transition of homeotropic-to-tilted. It is worthwhile to note that this transition is found to be reversible without any thermal hysteresis. To the best of knowledge, this kind temperature-dependent anchoring behavior has never been reported on aqueous–LC interfaces. However, a similar continuous homeotropic-to-tilted transition was once reported experimentally on solid substrates,25,26 and the underlying mechanism was qualitatively explained on the basis of the different dependence on temperature of four competing interactions at the interfaces, i.e. dispersion interactions, steric interactions, dipolar interactions and electrostatic interactions.25 In order to yield a deeper understanding of this novel thermally-induced anchoring transition, the detailed organization of four typical anchoring configurations at different temperatures is examined carefully. As clearly exhibited in Fig. 3(a and b), the orientational order parameter of the bulk LCs (approximately located at −10.5 < rz < 10.5) increases from 0.758 ± 0.003 at T = 0.50 to 0.844 ± 0.003 at T = 0.38 with a subsequent cooling process, accompanied by a gradual deviation of its orientation from the interface normal to 〈θ〉 = 23.65°. More importantly, it is very interesting to further observe that periodic oscillations in the density profile of mesogens, originating from the rod block monolayer and quickly decaying into the bulk LCs, start to appear at T = 0.50 and strengthens with decreasing the temperature, as shown in Fig. 3c. During this transition, the layer spacing of this unexpected translational ordering measured from the peak–peak distance is also found to decrease slightly from 4.62 to 4.18, roughly satisfying a condition of d = dSmA × cos(〈θ〉) with dSmA = 4.62 being the smectic-A layer spacing.23 Accordingly, it is reasonable to conclude that a surface-induced smectic order appears and grows in the nematic LC phase upon cooling, and simultaneously shifts from smectic-A-like to smectic-C-like, which may play a crucial role in this continuous homeotropic-to-tilted anchoring transition.
In fact, the influence of smectic short-range order on the anchoring transition has been investigated previously on solid substrates.27–30 Although most of studies have shown that the growth of surface-induced smectic order in the nematic phase prefers to drive a alignment transition from planar or tilted to homeotropic,27–29 an inverse transition reminiscent of our findings was once achieved by Barbero and Komitov30 due to the appearance of smectic-C-like order at the solid surface. In view of the absence of smectic-C phase for the studied mesogens (M7) in bulk,23 the formation of the smectic-C-like order may be associated with the confinement. Intuitively, due to the mismatch between the length of mesogens and the z-dimension of simulated system, the smectic-A phase of confined LCs is not likely to be formed with the layers parallel to the aqueous–LC interfaces. Upon cooling, the growth of the smectic-A order in nematic phase is supposed to be distorted by the dimensional mismatch of the confinement, and instead mesogens have to tilt adopting a smectic-C-like order for effective packing, leading to a continuous homeotropic-to-tilted anchoring transition. These results are partly consistent with a prior molecular simulation study that an unusual smectic-C ordering was found in the vicinity of grooved surfaces.38 However, it is not evident that the transitions reported here will be found at unconfined interfaces or in the macroscopic systems described in literature.2 For comparison, the thickness of the confined LCs sample in those experiments is usually thousands of times the length of liquid crystal molecules, and consequently the effect of dimensional mismatch is negligible.
In addition, it should be pointed out that regardless of the anchoring states there is a very thin planar anchoring layer in the vicinity of the aqueous–LC interface, as clearly shown in the director tilt angle profile in Fig. 3b. Our previous study13 has demonstrated that a few penetrated mesogens within the rod block monolayer prefer to lie down on the interface so as to effectively reduce the interfacial tension.39–41 It is found that the aqueous–LC interface becomes more flat and smooth with lowering the temperature, and the thin planar anchoring layer is confirmed at lower temperature by the appearance of a weak peak near the interface (located at rz ∼ ±17.30) shown in the density profiles in Fig. 3c.
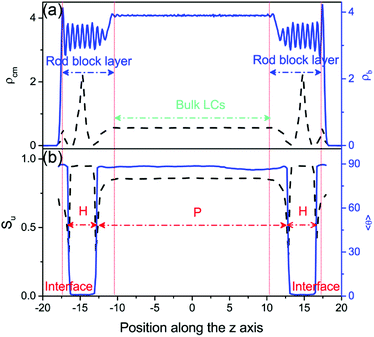
Upon further cooling toward the N–SmA bulk phase transition, a discontinuous anchoring transition of tilted-to-planar occurs, indicated by a sudden increase of the tilt angle of bulk mesogens from 24.5° at T = 0.37 to 88.5° at T = 0.36 (see Fig. 2a). The visual snapshot of the corresponding configuration in Fig. 2b vividly displays that one homeotropic layer within each rod block monolayer is formed in this unique planar anchoring. As exhibited in Fig. 4a, the homeotropic layer structure was confirmed by a sharp peak in the density profile for the center of mass of mesogens. Seven strong oscillations shown in the bead density profile of Fig. 4a, corresponding to seven beads in the mesogen chain, further demonstrated the highly ordered arrangement of mesogens with homeotropic alignment. Accordingly, a much higher orientational order parameter (Su almost equal 1.0) with a much smaller tilt angle is observed in the region of the homeotropic layer (Fig. 4b). Besides that, it has to be mentioned that no significant in-layer positional ordering is observed. These characteristic structural features suggest that a complete smectic-A layer with homeotropic alignment is formed within the rod block monolayer at T = 0.36, while the bulk LCs are still in the nematic phase. In the light of the weaker repulsive interactions between the rod blocks and mesogens, the mesogens prefer to penetrate into the rod block monolayer, leading to a local density increase of 15%. Therefore, the formation of the homeotropic layer should be largely attributed to the increased local density and the presence of the longer rod block, which are well known to shift the N–SmA phase transition to higher temperature.42–45 In addition, since the length of rod block (LR = 6.0) is 1.5 times the mesogen length (LM = 4.0), the rod block monolayer cannot provide enough space for the formation of a second smectic layer. As a result, the rest of mesogens have to comply with the orientation of bulk LCs and adopt the planar anchoring in order to minimize the distortion of the director. Note that a weak biaxiality is observed for these planar aligning mesogens near the homeotropic layer, which quickly vanishes in the bulk LCs.
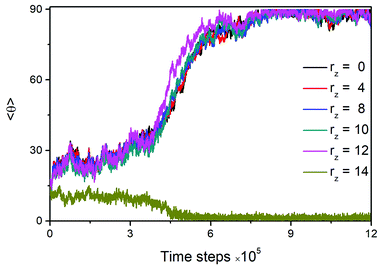
Detailed examinations of the dynamic behavior have also been performed to understand this tilted-to-planar anchoring transition. As typically illustrated in Fig. 5, the time evolution of the director tilt angle for mesogens in different slabs along the interface normal is monitored. It is found that upon cooling, a phase separation of mesogens occurs within the rod block monolayer, as reflected in the completely opposite variation of the mesogen orientation for the slabs located at rz = 12.0 and 14.0. Around 4.5 × 105 time steps, one smectic layer (rz = 14.0) of mesogens with homeotropic alignment is formed, and then mesogens exchange with this layer is found to be no longer available. Subsequently, the other mesogens (rz = 12.0) in the rod block monolayer start to gradually orient parallel to the interface, and this orientation adjustment quickly propagates into the bulk LCs. Given such dynamic behavior, it is thought that the formation of the homeotropic smectic layer may effectively act as a hard wall preventing other mesogens to penetrate, in consideration of the poor inter-layer diffusion of smectic-A phase, consequently driving the formation of planar anchoring in bulk. The underlying mechanism is apparently in the same sprit as discussed in a theoretical study of the planar anchoring induced by the very high surfactant coverage at a solid surface.46 Similar planar anchoring states induced by the temperature-dependent condensed phase of surfactant monolayers have also been experimentally studied at the aqueous–LC interface18 or at the air–LC interface.47
Below the temperature of N–SmA bulk phase transition, it is worthwhile to note that the unique planar anchoring observed in the low-temperature nematic phase remains unchanged but an unexpected smectic-C structure is formed instead of the smectic-A phase in bulk. As typically shown in Fig. 6, the director of the bulk mesogens is clearly different with the normal direction of smectic layer. Intuitively, this behavior should also be associated with the confinement nature of liquid crystals located between the aqueous–LC interfaces.
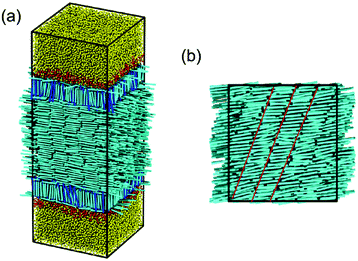 | ||
| Fig. 6 Snapshots of (a) the typical anchoring configuration in the smectic phase (T = 0.21) and (b) the top view of the corresponding bulk LC (locating between −10.5 < rz < 10.5) in the same sample. | ||
3.2 Wetting behavior upon cooling
While heating toward the N–I bulk phase transition, as shown in Fig. 2, the orientational ordering of the bulk LCs weakens gradually, but the homeotropic anchoring remains unchanged until the isotropic phase is formed at T = 0.56. In comparison with the pure LC system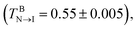 23 it is interesting to find that the N–I transition is slightly shifted to a higher temperature, which may be attributed to the presence of surfactant-coated interfaces.48,49 At the temperatures above this transition, despite the bulk LC is in the isotropic state, the rod blocks still exhibit a pronounced orientational ordering with the direction perpendicular to the interface, owing to its larger aspect ratio. Consequently, a nematic wetting layer with homeotropic alignment is induced by the ordered rod blocks at the aqueous–LC interface. As illustrated in Fig. 7, for example, along the interface normal the orientational order parameter profile for the wetting layer at T = 0.56 displays a peak-like shape with a maximum value (Su = 0.65) in the middle of the rod block monolayer. Close to the aqueous phase, the homeotropic penetrating mesogens are distorted largely as the immiscible interface favors the planar anchoring, leading to a decrease of the order parameter. Near to the bulk isotropic LCs, the orientational ordering quickly decreases and decays to zero beyond the rod block monolayer. In addition, it should be noted that with further increasing temperature the nematic wetting layer rapidly loses its ordering, and the amphiphile monolayer at the aqueous–LC interface gradually becomes unstable and collapses at T = 0.61.
23 it is interesting to find that the N–I transition is slightly shifted to a higher temperature, which may be attributed to the presence of surfactant-coated interfaces.48,49 At the temperatures above this transition, despite the bulk LC is in the isotropic state, the rod blocks still exhibit a pronounced orientational ordering with the direction perpendicular to the interface, owing to its larger aspect ratio. Consequently, a nematic wetting layer with homeotropic alignment is induced by the ordered rod blocks at the aqueous–LC interface. As illustrated in Fig. 7, for example, along the interface normal the orientational order parameter profile for the wetting layer at T = 0.56 displays a peak-like shape with a maximum value (Su = 0.65) in the middle of the rod block monolayer. Close to the aqueous phase, the homeotropic penetrating mesogens are distorted largely as the immiscible interface favors the planar anchoring, leading to a decrease of the order parameter. Near to the bulk isotropic LCs, the orientational ordering quickly decreases and decays to zero beyond the rod block monolayer. In addition, it should be noted that with further increasing temperature the nematic wetting layer rapidly loses its ordering, and the amphiphile monolayer at the aqueous–LC interface gradually becomes unstable and collapses at T = 0.61.
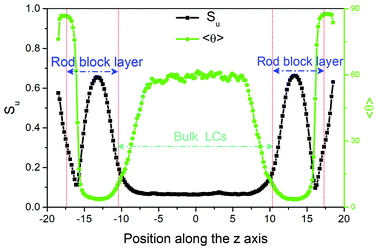 | ||
| Fig. 7 Profiles of the orientational order parameter Su and the director tilt angle 〈θ〉 of mesogens along the interface normal direction (z axis) for a disordered configuration at T = 0.56. | ||
4. Conclusions
In this paper, DPD simulations have been performed to systematically investigate the effect of temperature on the anchoring and wetting behavior at the aqueous–LC interfaces laden with rod–coil amphiphiles. Upon cooling toward the N–SmA bulk phase transition, we have observed a continuous anchoring transition of homeotropic-to-tilted, which can be attributed to the growth and propagation of a smectic order from the interfaces to the bulk LCs with decreasing the temperature. Further cooling the sample, a real smectic layer is found to be formed within each rod block monolayer, which effectively acts as a hard wall preventing other mesogens to penetrate, and consequently triggers a discontinuous anchoring transition from tilted to planar alignment at T = 0.36. Below the temperature of N–SmA bulk phase transition, an unexpected smectic-C structure with planar anchoring is induced instead of the smectic-A phase in bulk due to the confinement nature of liquid crystals located between the aqueous–LC interfaces. In addition, the orientational wetting behavior has also been studied by heating the homeotropic sample into the isotropic phase. The simulation results show that in this confined system the N–I phase transition is slightly shifted to a higher temperature, and an orientational wetting layer with the homeotropic alignment is observed in the rod block monolayer when the bulk LC is in the isotropic phase.Clearly these findings provide molecular insights into the underlying mechanism of how the coupling between the ordering of liquid crystals and adsorbents and their temperature dependence affect the anchoring and wetting behavior at aqueous–LC interfaces. Relevant information is important for optimizing the role of temperature in the rational design and application of advanced LC-based biosensor.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the National Key Research and Development Program of China (2016YFB1100800), NSF of China (20874110 and 20674093) and KU Leuven for a postdoctoral grant (GOA/10/04). The simulations have been performed on the supercomputing center of CAS and the VIC3 and ThinKing HPC supercomputers of KU Leuven (part of the VSC (Flemish Supercomputer Centre)).References
- S. J. Woltman, G. D. Jay and G. P. Crawford, Nat. Mater., 2007, 6, 929–938 CrossRef CAS PubMed.
- N. A. Lockwood, J. K. Gupta and N. L. Abbott, Surf. Sci. Rep., 2008, 63, 255–293 CrossRef CAS.
- Y. Bai and N. L. Abbott, Langmuir, 2010, 27, 5719–5738 CrossRef PubMed.
- A. M. Lowe and N. L. Abbott, Chem. Mater., 2012, 24, 746–758 CrossRef CAS PubMed.
- J. M. Brake and N. L. Abbott, Langmuir, 2002, 18, 6101–6109 CrossRef CAS.
- J. M. Brake, A. D. Mezera and N. L. Abbott, Langmuir, 2003, 19, 6436–6442 CrossRef CAS.
- N. A. Lockwood, J. J. de Pablo and N. L. Abbott, Langmuir, 2005, 21, 6805–6814 CrossRef CAS PubMed.
- J. M. Brake, M. K. Daschner, Y.-Y. Luk and N. L. Abbott, Science, 2003, 302, 2094–2097 CrossRef CAS PubMed.
- J.-S. Park and N. L. Abbott, Adv. Mater., 2008, 20, 1185–1190 CrossRef CAS.
- M. I. Kinsinger, M. E. Buck, M.-V. Meli, N. L. Abbott and D. M. Lynn, J. Colloid Interface Sci., 2010, 341, 124–135 CrossRef CAS PubMed.
- J. M. Brake and N. L. Abbott, Langmuir, 2007, 23, 8497–8507 CrossRef CAS PubMed.
- A. D. Price and D. K. Schwartz, J. Am. Chem. Soc., 2008, 130, 8188–8194 CrossRef CAS PubMed.
- Z. Zhang and H. Guo, Soft Matter, 2012, 8, 5168–5174 RSC.
- C. Bahr, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 030702(R) CrossRef PubMed.
- C. Bahr, Phys. Rev. Lett., 2007, 99, 057801 CrossRef PubMed.
- J. K. Gupta, M.-V. Meli, S. Teren and N. L. Abbott, Phys. Rev. Lett., 2008, 100, 048301 CrossRef PubMed.
- J. K. Gupta and N. L. Abbott, Langmuir, 2009, 25, 2026–2033 CrossRef CAS PubMed.
- A. D. Price, J. Ignes-Mullol, M. Angels Vallve, T. E. Furtak, Y.-A. Lo, S. M. Malone and D. K. Schwartz, Soft Matter, 2009, 5, 2252–2260 RSC.
- Y.-T. Ouyang and H.-X. Guo, Chin. J. Polym. Sci., 2014, 32, 1298–1310 CrossRef CAS.
- T. Inokuchi and N. Arai, Mol. Simul., 2017, 43, 1218–1226 CrossRef CAS.
- V. Tomar, S. I. Hernandez, N. L. Abbott, J. P. Hernandez-Ortiz and J. J. de Pablo, Soft Matter, 2012, 8, 8679–8689 RSC.
- J. A. Moreno-Razo, E. J. Sambriski, N. L. Abbott, J. P. Hernández-Ortiz and J. J. de Pablo, Nature, 2012, 485, 86 CrossRef CAS PubMed.
- Z. M. Zhang and H. X. Guo, J. Chem. Phys., 2010, 133, 144911 CrossRef PubMed.
- W.-X. Shi and H.-X. Guo, J. Phys. Chem. B, 2010, 114, 6365–6376 CrossRef CAS PubMed.
- S. Dhara, J. K. Kim, S. M. Jeong, R. Kogo, F. Araoka, K. Ishikawa and H. Takezoe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 060701 CrossRef PubMed.
- J. S. Patel and H. Yokoyama, Nature, 1993, 362, 525–527 CrossRef CAS.
- H. V. Känel, J. D. Litster, J. Melngailis and H. I. Smith, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 24, 2713–2719 CrossRef.
- D. V. Sai, T. A. Kumar, W. Haase, A. Roy and S. Dhara, J. Chem. Phys., 2014, 141, 044706 CrossRef PubMed.
- T. Shioda, B. Wen and C. Rosenblatt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 041706 CrossRef PubMed.
- G. Barbero and L. Komitov, J. Appl. Phys., 2009, 105, 064516 CrossRef.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Espanol and P. B. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- Z. Bai and H. Guo, Polymer, 2013, 54, 2146–2157 CrossRef CAS.
- M. Huang and H. Guo, Soft Matter, 2013, 9, 7356–7368 RSC.
- Z. Zhang, T. Li and E. Nies, Macromolecules, 2014, 47, 5416–5423 CrossRef CAS.
- Z. Zhang, E. Henry, G. Gompper and D. A. Fedosov, J. Chem. Phys., 2015, 143, 243145 CrossRef PubMed.
- J. Stelzer, P. Galatola, G. Barbero and L. Longa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 477–480 CrossRef CAS.
- B. Y. Drovetsky, A. J. Liu and C. H. Mak, J. Chem. Phys., 1999, 111, 4334–4342 CrossRef CAS.
- M. P. Allen, Chem. Phys. Lett., 2000, 331, 513–518 CrossRef CAS.
- A. J. McDonald, M. P. Allen and F. Schmid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 63, 010701 CrossRef.
- J. T. Brown, M. P. Allen, E. Martín del Río and E. d. Miguel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 57, 6685–6699 CrossRef CAS.
- R. Lukač and F. J. Vesely, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 2000, 352, 249–256 CrossRef.
- M. Roushdy, Mol. Cryst. Liq. Cryst., 2006, 457, 151–160 CrossRef CAS.
- G. Cinacchi, L. Mederos and E. Velasco, J. Chem. Phys., 2004, 121, 3854–3863 CrossRef CAS PubMed.
- M. J. Uline, S. Meng and I. Szleifer, Soft Matter, 2010, 6, 5482–5490 RSC.
- X. Feng, A. Mourran, M. Moller and C. Bahr, Soft Matter, 2012, 8, 9661–9668 RSC.
- H. Yokoyama, J. Chem. Soc., Faraday Trans. 2, 1988, 84, 1023–1040 RSC.
- E. Cañeda-Guzmán, J. A. Moreno-Razo, E. Díaz-Herrera and E. J. Sambriski, Mol. Phys., 2013, 112, 1149–1159 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |