Open Access Article
Open Access ArticleExploring the mechanism of the Pd-catalyzed spirocyclization reaction: a combined DFT and experimental study†
Ivan
Franzoni‡
 a,
Hyung
Yoon‡
a,
Hyung
Yoon‡
 a,
José-Antonio
García-López
a,
José-Antonio
García-López
 b,
Amalia Isabel
Poblador-Bahamonde
*c and
Mark
Lautens
*a
b,
Amalia Isabel
Poblador-Bahamonde
*c and
Mark
Lautens
*a
aDavenport Research Laboratories, Department of Chemistry, University of Toronto, 80 St. George St., Toronto, Ontario M5S 3H6, Canada. E-mail: mlautens@chem.utoronto.ca
bDepartamento de Química Inorgánica, Universidad de Murcia, Campus de Espinardo, 30100 Murcia, Spain. E-mail: joangalo@um.es
cDepartment of Organic Chemistry, University of Geneva, 30 Quai Ernest Ansermet, 1211 Geneva, Switzerland. E-mail: Amalia.pobladorbahamonde@unige.ch
First published on 8th December 2017
Abstract
The mechanism of the palladium-catalyzed spirocyclization of acrylamides has been investigated by density functional theory and experimental studies. The results support a mechanistic pathway that proceeds via oxidative addition, intramolecular carbopalladation, C–H bond activation, and migratory insertion sequence. The M06L/def2-TZVPP//BP86/6-31G(d,p)/LANL2DZ level of theory used and the inclusion of solvent effects provide results in good agreement with the experimental data. The C–H bond activation step proceeds via a concerted outer-sphere metallation deprotonation mechanism that explains the absence of a measurable kinetic isotopic effect. The subsequent intermolecular migratory insertion of arynes is significantly faster than the insertion of internal alkynes. Furthermore, the regioselectivities calculated in the case of unsymmetrical reactants are remarkably close to the experimental values. Evaluation of the potential energy surfaces for specific substrates provides an explanation for the lack of product formation observed experimentally. Finally, the computational and experimental analyses of potential side reactions are also presented and support the initially proposed mechanism.
Introduction
The application of transition metal catalysts in the activation of traditionally inert C–H bonds has advanced significantly and currently represents a recurrent strategy for the construction of carbon–carbon (C–C) and carbon–heteroatom (C–Y) bonds.1 This approach has opened the possibility to tackle the synthesis of complex molecules based on new disconnections by utilizing simple and inactivated starting materials in a step- and atom-economical fashion.2 Although substrate prefunctionalization is not required, the installation of a suitable directing group (DG) is necessary in most cases to guide the metal center toward a specific C–H bond in a regioselective manner (Scheme 1a).3,4 The development of (removable) DGs based on tethered substituted quinolines, pyridines, amides and cyano groups has allowed the intramolecular selective activation and functionalization of C–H bonds in proximal and even distal positions (e.g. meta- and para-positions in aromatic groups and γ- and δ-positions in alkyl chains).5,6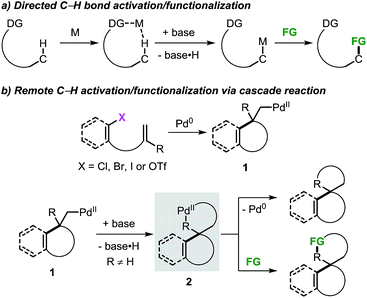 | ||
| Scheme 1 Remote C–H bond activation and functionalization strategies with the use of directing groups or as a part of a domino process. | ||
The combination of the palladium-catalyzed intramolecular Mizoroki–Heck reaction and C–H bond activation in a domino process has been exploited as a valuable alternative for the selective functionalization of remote unactivated C–H bonds within the molecular framework (Scheme 1b).7,8 In this approach, a low-valent palladium catalyst undergoes oxidative addition into a carbon–(pseudo)halogen (C–X) bond followed by intramolecular carbopalladation of a tethered unsaturated moiety. This sequence generates σ-alkylpalladium(II) intermediate 1, where the metal center is now placed in proximity to a formerly remote C–H bond. In the absence of β-hydrogen atoms or nucleophilic species,9 regioselective C–H bond activation could occur to give the spirocyclic palladacycle 2. This complex could undergo C–C bond-forming reductive elimination or, in the presence of suitable reactants, further evolve by functionalization of the C–Pd bond.
Inspired by the pioneering work of Grigg10 and Larock,11 our groups12–16 and others17 have explored this class of transformations for the synthesis of valuable spirocyclic scaffolds containing heterocyclic cores (Scheme 2). These structural motifs have attracted considerable interest due to their occurrence in pharmaceuticals, biologically active, and natural products.18 In 2014, Shi and co-workers reported the application of this approach in the synthesis of indoline derivatives.19 Recently, our group disclosed the use of an intramolecular Heck reaction and C–H bond activation cascade for the divergent synthesis of two classes of compounds via the intermediacy of a single spirocyclic palladacycle (Scheme 2a).12 The use of the bulky t-Bu3P ligand promoted the direct C–C bond-forming reductive elimination providing benzofused cyclobutane derivatives. Alternatively, in the presence of alkyl iodides and a N-heterocyclic carbene (NHC) ligand, Catellani-type products were obtained. Following this work, the reactivity of this class of palladacycle intermediates was further explored resulting in the development of several methodologies to access spirooxindoles and spirodihydrobenzofuranes. In 2016, we independently reported the palladium-catalyzed spirocyclization reaction via an intramolecular C–H bond activation and aryne migratory insertion sequence (Scheme 2b).13,14 Extension of this approach to the use of α-diazocompounds15 and internal alkynes16 as terminating reagents was recently reported by our groups (Scheme 2c and d).
 | ||
| Scheme 2 Synthesis of spiro-heterocycles via palladium-catalyzed remote C–H bond activation and functionalization cascade reactions. | ||
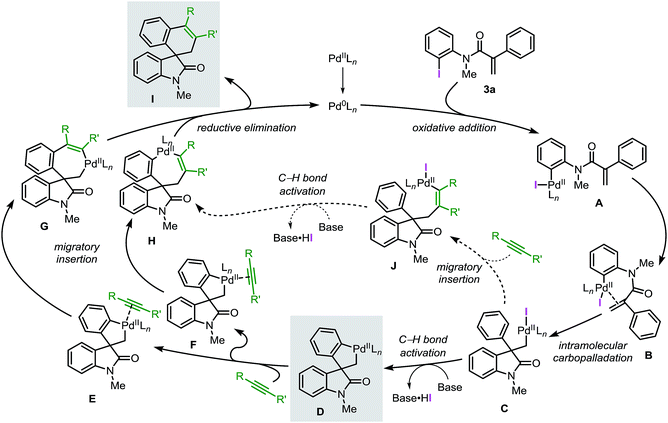
Based on the collective results obtained in these studies, a plausible mechanism for the Pd-catalyzed spirocyclization reaction of unsaturated reagents is presented in Fig. 1.
Initially, the low-valent active catalyst oxidatively adds to the starting material 3a to form intermediate A. Coordination of the tethered double bond functionality to the metal center gives B followed by an intramolecular carbopalladation to generate neopentyl intermediate C. The lack of β-hydrogen atoms and the conformational flexibility of C allow the metal center to be placed in proximity of an ortho C(sp2)–H bond of the phenyl ring. This orientation facilitates a base mediated C–H bond activation process and formation of the spirocyclic palladacycle intermediate D. Ligand exchange at the metal center provides either intermediate E or F where the unsaturated substrate (aryne or alkyne) coordinates to the palladium atom trans with respect to either the C(sp3)–Pd or the C(sp2)–Pd bond, respectively. Subsequent migratory insertion generates intermediates G or H, which finally undergo C–C bond-forming reductive elimination, releasing product I and the active catalyst. In an alternative scenario, migratory insertion of the unsaturated reactant in C precedes the C(sp2)–H bond activation step to eventually generate complex Hvia intermediate J.
Recently, the García-López group reported a detailed study on the organometallic intermediates involved in this reaction.20 Several key species were synthesized and fully characterized by nuclear magnetic resonance and single-crystal X-ray crystallography. Furthermore, the reactivities of these species were evaluated and the role of ligands and bases were studied providing additional insights into the reaction mechanism.
Herein, we report a complementary computational and experimental study on the mechanism of the palladium-catalyzed spirocyclization reaction. Our results support the initially proposed mechanism (Fig. 1) and provide new insights into key steps of the catalytic cycle. Two possible pathways for the C–H bond activation step were computed and the equilibration of several species was studied. Analysis of the migratory insertion step for diverse unsaturated reactants was evaluated and correlated with experimental data. The theoretical results obtained in this study, as well as experimental findings were compared to obtain a comprehensive and realistic overview of the underlying mechanism of these reactions. We anticipate that these results will aid the design of new catalysts, new substrates and novel approaches to extend the applicability of the palladium-catalyzed spirocyclization reactions in the synthesis of other important classes of spirocyclic compounds.
Computational details
The computational studies were performed using acrylamide 3a as a substrate. This compound was demonstrated to be reactive under both sets of reaction conditions (benzyne and alkyne insertion reactions) and it was successfully employed in the synthesis and isolation of the fully characterized palladacycle complex 11. All geometries were fully optimized in gas phase at the BP86 level21 of theory without any constraints, at 298 K and 1 atm using a fine integration grid. The Berny algorithm was used for geometry optimizations.22 The standard double-ζ basis set (LANL2DZ)23 and effective core potentials (ECPs)23c,d were used for Pd, Cs and heavy halogen atoms whereas for the other atoms (C, H, O, N, P and F) the 6-31G(d,p) Pople basis set was used.24 Frequency calculations were performed at the same level for all intermediates and transition states to confirm minima (no imaginary frequencies) and first order saddle points (one imaginary frequency representing the desired reaction coordinate), respectively. Furthermore, transition states were confirmed by either intrinsic reaction coordinates (IRC)25 or quick reaction coordinate (QRC) calculations.26 The latter calculations were performed by small manual displacement (0.05–0.10 Bohr) of the geometry on the vibration of the imaginary frequency followed by regular optimization. Single point energies were calculated on the optimized structures at 298 K and 1 atm at the M06L level of theory,27 a method in which dispersion effects are included in the parameterization scheme. The Karlsruhe triple-ζ Gaussian basis set def2-TZVPP was used for all atoms.28 Solvent effects were assessed through the integral equation formalism variant of the polarizable continuum model (IEFPCM)29 with default parameters for toluene and UFF radii. Evaluation of other functionals, basis sets, implicit models to describe solvent effects, and with or without addition of the Grimme's D3 dispersion30 provided qualitative consistent results. Solution phase zero-point corrected energies, enthalpies and Gibbs free energies were obtained by adding the respective gas-phase thermodynamic contributions to the single-point solution phase energies. Relative Gibbs free energies are reported in kcal mol−1 and were converted to 1 M standard state by addition of 1.89 kcal mol−1 to all species (according to RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(c/c0) at 298 K). Relative enthalpies are presented in parenthesis. All energies are quoted relative to the energy of 3a, and the following nomenclature will be used in the discussion: ΔG relative energy with respect to 3a; ΔΔG difference between relative energies; ΔG‡ activation energies; and ΔΔG‡ difference between activation energies. The fully detailed energy profiles inclusive of all the intermediates not presented in the text are presented in the ESI.† All calculations were performed by using the Gaussian09 package, revision D.01.31 Figures were created with CLYview32 and all H atoms were omitted for clarity except for the H atoms involved in the C–H bond activation process. Root-mean-square deviation (RMSD) of atomic positions values were calculated using ICM Molsoft Browser Software. Representative geometrical parameters are also reported (Å, degrees).
ln(c/c0) at 298 K). Relative enthalpies are presented in parenthesis. All energies are quoted relative to the energy of 3a, and the following nomenclature will be used in the discussion: ΔG relative energy with respect to 3a; ΔΔG difference between relative energies; ΔG‡ activation energies; and ΔΔG‡ difference between activation energies. The fully detailed energy profiles inclusive of all the intermediates not presented in the text are presented in the ESI.† All calculations were performed by using the Gaussian09 package, revision D.01.31 Figures were created with CLYview32 and all H atoms were omitted for clarity except for the H atoms involved in the C–H bond activation process. Root-mean-square deviation (RMSD) of atomic positions values were calculated using ICM Molsoft Browser Software. Representative geometrical parameters are also reported (Å, degrees).
Results and discussion
Oxidative addition and intramolecular carbopalladation steps
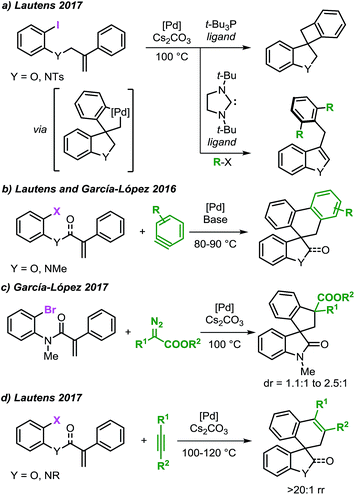
Our investigation started by the computational analysis of the initial steps of the reaction, namely the oxidative addition and the intramolecular carbopalladation steps (Fig. 2).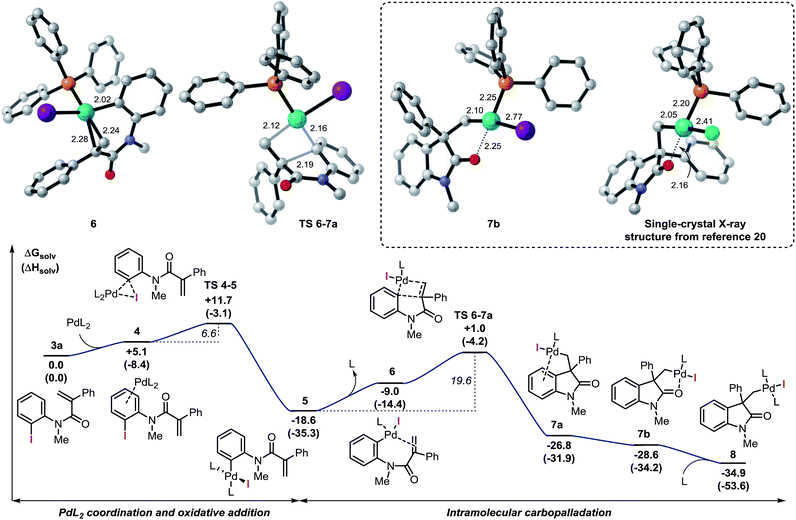 | ||
| Fig. 2 Free energy profile for the oxidative addition and intramolecular carbopalladation steps and selected computed structures (L = Ph3P). Comparison between the computed structure for intermediate 7b and the related single-crystal X-ray structure from ref. 20. | ||
Coordination of the palladium catalyst to the aromatic ring of 3a provides intermediate 4 (ΔG = +5.0 kcal mol−1) which undergoes an oxidative addition process to generate 5 (ΔG = −18.6 kcal mol−1). This step requires only 6.6 kcal mol−1 and the two intermediates are connected by TS 4–5 (ΔG = +11.7 kcal mol−1), which models a concerted three-membered process. In 2006, Norrby and co-workers reported a detailed computational study on the oxidative addition of triphenylphosphine–palladium complexes to haloarenes.33a The authors found that low-coordinated palladium species such as [Pd(Ph3P)S], where S is a molecule of a coordinating solvent, would be more reactive than palladium complexes with two or more phosphine ligands. Furthermore, Vidossich et al. studied by means of explicit solvent molecular dynamic simulation the equilibration of [Pd(Ph3P)nSm] species in toluene suggesting that a bare [Pd(Ph3P)] promptly coordinates to a molecule of solvent.33d Attempts to locate a transition state analogous to TS 4–5 where only one ligand is placed on the metal center were unsuccessful in our case. The results obtained in this analysis suggest that the potential energy surface for the oxidative addition step of a [Pd(Ph3P)] species to substrate 3a would be particularly flat in a non-coordinating solvent such as toluene. Although this circumstance renders the search of transition states particularly challenging, it also suggests that a mono-ligated palladium catalyst may indeed provide a lower energy pathway for this step.
Decoordination of one ligand in 5, provides an empty coordination site on palladium that allows the interaction with the tethered alkene to generate intermediate 6 (ΔG = −9.0 kcal mol−1) with an overall destabilization of 9.6 kcal mol−1. Intramolecular migratory insertion of the unsaturated moiety into the Pd–C bond leads to intermediate 7a (ΔG = −26.8 kcal mol−1) where the metal center coordinates to the fused aromatic ring of the newly formed oxindole core. The overall process requires 19.6 kcal mol−1 and is modeled by TS 6–7a (ΔG = +1.0 kcal mol−1).
Among the different conformers of 7a, a lower energy structure 7b (ΔG = −28.6 kcal mol−1) was found where the palladium atom coordinates to the oxygen atom of the carbonyl functionality. Of note, this structure closely resembles the X-ray structure previously reported (Fig. 2).20 In order to compare the geometrical features of these structures, the structure of intermediate 7b-Cl was optimized after replacement of the iodine atom in 7b with a chlorine atom (see ESI†). Key bond distances and bond angles in these structures are presented in Table 1. Comparison of the bond distances between the metal atom and the four ligands in the reported X-ray crystal structure and the optimized intermediate 7b-Cl provides a mean standard deviation (SD) of 0.061 Å. These bond distances are expected to be only marginally influenced by solid-state packing effects thus highlighting the accuracy of the BP86/6-31G(d,p) method used in geometry optimizations. Aware that these solid-state packing effects could significantly affect the torsion angles of the phosphine ligand and of the phenyl moiety, we found that the root-mean-square deviation (RMSD) of atomic positions between the two structures still provides a remarkable correlation with a value of 0.760 Å (see ESI†).34 Coordination of a phosphine ligand in 7b gives the more stable bis-ligated intermediate 8 (ΔG = −34.9 kcal mol−1). This complex is characterized by a distorted square planar geometry around the metal center (P–Pd–P = 148.5; C–Pd–I = 157.2) due to the steric hindrance of the two ligands in trans relative arrangement and the iodine atom. The equilibration between 7a, 7b, and 8 in solution has been previously studied by means of 1H NMR techniques (Scheme 3).20 A solution of 8, prepared by independent synthesis, in deuterated chloroform at room temperature was analyzed by 1H NMR at different times. After the initial formation of a new species, tentatively attributed to intermediate 7a, significant formation of 7b with concomitant generation of triphenylphosphine oxide was observed (no free phosphine was detectable after 11 h). These experimental results seem to be in discordance with our computational study, where the bis-ligated complex 8 is thermodynamically more stable than 7a and 7b. A closer analysis of the data obtained in this 1H NMR study reveals that after 5 h, a substantial amount of triphenylphosphine oxide is formed and its concentration increases over time along with formation of 7b. The irreversible formation of triphenylphosphine oxide would reduce the concentration of free ligand in solution, thus providing the necessary thermodynamic driving force for the formation of the higher energy intermediate 7b instead of the more stable bis-ligated intermediate 8.
| 7b | 7b-Cl | X-ray | |
|---|---|---|---|
| Pd–X | 2.770 | 2.469 | 2.408 |
| Pd–P | 2.252 | 2.248 | 2.196 |
| Pd–O | 2.247 | 2.249 | 2.162 |
| Pd–C | 2.097 | 2.083 | 2.050 |
| C–Pd–O | 81.0 | 81.0 | 81.7 |
| O–Pd–X | 89.4 | 91.1 | 92.5 |
| X–Pd–P | 95.4 | 92.7 | 91.0 |
| P–Pd–C | 94.1 | 95.0 | 95.0 |
| L–Pd–O | 174.8 | 175.6 | 173.1 |
| C–Pd–X | 169.9 | 171.8 | 173.8 |
 | ||
| Scheme 3 NMR studies on the equilibration between 7a, 7b, and 8 from ref. 20 (L = Ph3P). Computed structure for intermediate 8. | ||
C–H bond activation step and formation of the spirocyclic palladacycle intermediate
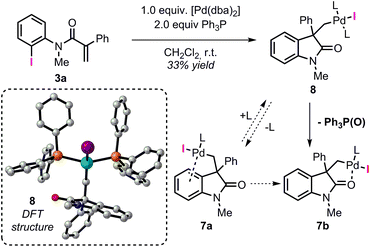
The analysis of the potential energy surface for the base mediated C–H bond activation step provides two possible pathways (Fig. 3). In the first scenario, ligand exchange on intermediate 8 generates the carbonate complex 9 (ΔG = −42.3 kcal mol−1). A subsequent concerted inner-sphere metallation deprotonation mechanism could occur generating the corresponding spirocyclic complex 11 (ΔG = −41.4 kcal mol−1).35 This process requires 25.8 kcal mol−1 and it is modeled by TS 9–11 (ΔG = −16.5 kcal mol−1). This transition state is characterized by a shortening of the Pd–C(sp2) distance and concomitant abstraction of the hydrogen atom by the carbonate base bound to the metal center. Furthermore, during this process, the large cesium ion interacts with the oxygen atom in the carbonyl group of the oxindole ring (for other examples in which the cation is included in the transitions state for C–H activation processes, see ref. 36). An alternative pathway for the formation of palladacycle 11 was computed. Interaction between the carbonate base and 8 generates intermediate 10 (ΔG = −38.9 kcal mol−1) where the iodine ligand still binds to the metal center. A concerted outer-sphere metallation deprotonation mechanism follows and requires 14.2 kcal mol−1. The corresponding transition state TS 10–11 (ΔG = −24.7 kcal mol−1) models the formation of the Pd–C(sp2) bond with concomitant abstraction of the hydrogen atom by the carbonate base that does not directly interact with the palladium atom. Agostic-type structures with pre-coordination of the C(sp2)–H bond to the metal center prior to the C–H bond activation were not observed either by conformational search nor by IRC/QRC calculations. This type of interaction has been proposed to polarize the C–H bond, thus facilitating the deprotonation step and has been found in related computational studies.36 The overall results shown in Fig. 3 suggest that a base mediated concerted outer-sphere metallation deprotonation mechanism is thermodynamically (ΔΔG = −8.2 kcal mol−1) and kinetically (ΔΔG‡ = −11.6 kcal mol−1) favored over the previously reported inner-sphere type pathway for this type of reaction.12 These computational results are further corroborated by a number of experimental results. In the development of a palladium-catalyzed spirocyclization reaction based on a C(sp2)–H bond activation and benzyne migratory insertion sequence, our groups independently demonstrated that CsF, a salt that is used for the in situ generation of aryne reactants, is an effective replacement of Cs2CO3 as a base in this reaction. Since fluoride ions would not be able to coordinate to the metal center and promote hydrogen abstraction, this observation suggests the viability of an outer-sphere type C–H bond activation process in our system. The feasibility of such process is also computationally supported by the successful optimization of a transition state resembling the structural features of TS 10–11 where the carbonate base was replaced with CsF (see ESI†). Furthermore, we found that replacement of the hydrogen atoms in the non-halogenated phenyl ring of 3a with deuterium does not provide any measurable kinetic isotope effect (KIE),14 which suggests that C–H bond activation is not the rate-limiting step in the catalytic cycle. Since the subsequent insertion of arynes is a fast process (vide infra), the absence of a KIE is not compatible with the highly energy demanding inner-sphere type C–H bond activation mechanism (ΔG‡ = 25.8 kcal mol−1) thus supporting the alternative outer-sphere type mechanism (ΔG‡ = 14.2 kcal mol−1). | ||
| Fig. 3 Free energy profiles of the alternative pathways for the base mediated C–H bond activation step and selected computed structures (L = Ph3P). | ||
The spirocyclic palladacycle 11 (ΔG = −41.4 kcal mol−1) is characterized by a distorted square planar geometry around the metal center due to the cis arrangement of the two phosphine ligands. We previously reported the synthesis and characterization of 11, and demonstrated the viability of this intermediate in this class of reactions.14,16Table 2 summarizes the key structural features of the computed and the single-crystal X-ray structure of 11. In analogy to the case of intermediate 7b-Cl, there is a remarkable similarity in both the key Pd–R distances, with a SD of 0.058 Å, and in the overall structure with a RMSD of 0.375 Å (see ESI†). Decoordination of a ligand trans to either the C(sp2) or the C(sp3) atoms in 11 provides a significant increase in energy of the resulting 14-electron complexes (ΔG = −26.1 and −26.6 kcal mol−1, respectively). Since the spirocyclization reaction of aryne substrates is carried out in a toluene/acetonitrile mixture,13,14 we envisioned that replacement of a phosphine ligand in 11 by coordination a molecule of MeCN would be possible (Scheme 4, top). The relative energies of the resulting intermediates 11a and 11a′ show higher energy species in both cases (ΔG = −31.9 and −31.4 kcal mol−1, respectively) with a slight preference for the substitution of the phosphine ligand trans of the C(sp2)–Pd bond. Attempts to detect these type of intermediates by 1H NMR analysis of a solution of 11 in MeCN-d3 were inconclusive. However, treatment of 11 with one equivalent of xylylisocyanide (XylNC) provides a single isomeric species that was attributed to 11b (Scheme 4, bottom).20 Indeed, replacement of a phosphine ligand with a XylNC molecule provides the two more stable structures 11b and 11b′ (ΔG = −43.9 and −43.2 kcal mol−1, respectively) being 11b thermodynamically favored with respect to 11b′ and the original palladacycle 11.
| 11 (DFT) | 11 (X-ray) | |
|---|---|---|
| Pd–C(sp3) | 2.098 | 2.076 |
| Pd–C(sp2) | 2.095 | 2.076 |
| Pd–P1 | 2.438 | 2.358 |
| Pd–P2 | 2.414 | 2.335 |
| C(sp2)–Pd–P2 | 93.6 | 92.1 |
| P2–Pd–P1 | 98.9 | 97.0 |
| P1–Pd–C(sp3) | 90.2 | 91.2 |
| C(sp2)–Pd–C(sp3) | 77.5 | 79.9 |
| C(sp2)–Pd–P2 | 167.2 | 170.2 |
| C(sp3)–Pd–P1 | 169.8 | 171.4 |
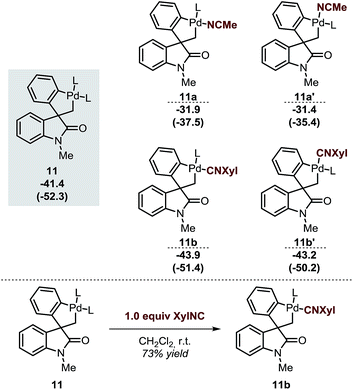 | ||
| Scheme 4 Relative energies of different analogues of 11 after replacement of a ligand by a solvent molecule (top, L = Ph3P) and experimental result from ref. 20 (bottom). | ||
Regioselectivity of the migratory insertion step
We next studied the migratory insertion step in the spirocyclic palladacycle intermediate 11 for the case of benzyne 12a (Fig. 4). According to the general mechanism presented in Fig. 1, a ligand substitution on 11 could generate either 13a or 13b (ΔG = −50.6 and −51.4 kcal mol−1, respectively). In 13a the benzyne ligand 12a binds to the metal center in a trans position with respect to the C(sp3) atom whereas in 13b it binds in trans to the C(sp2) atom. Although the formation of 13b is slightly favored thermodynamically (ΔΔG = −0.8 kcal mol−1) the subsequent migratory insertion step is kinetically favored for intermediate 13a (ΔΔG‡ = −1.8 kcal mol−1) following a classic Curtin-Hammet scenario.37 This trend is maintained in all the cases presented in this work, therefore, only the profiles involving migratory insertions into the Pd–C(sp2) bond of 11 will be discussed here (see ESI† for the profiles of selected cases of migratory insertions into the Pd–C(sp3) bond). The corresponding transition states TS 13a–14a (ΔG = −45.6 kcal mol−1) and TS 13b–14b (ΔG = −43.8 kcal mol−1) model a planarization of the benzyne ring with respect to the phenyl moiety during the formation of the C(sp2)–(Csp2) and the C(sp2)–(Csp3) bonds, respectively. The two isomers 14a and 14b (ΔG = −92.4 and −92.2 kcal mol−1, respectively) are characterized by a remarkable thermodynamic stability and to be almost isoenergetic. The geometry of these intermediates facilitates the subsequent C–C bond-forming reductive elimination process (ΔG‡ = 5.3 and 2.9 kcal mol−1, respectively). Transition states TS 14a–15 and TS 14b–15 (ΔG = −87.1 and −89.3 kcal mol−1, respectively) model a shortening of the C(sp2)–(Csp3) and C(sp2)–(Csp2) distances, respectively, and the concomitant migration of the palladium atom on the adjacent π-aromatic system to form the spirooxindole complex 15 (ΔG = −131.4 kcal mol−1). Final ligand-assisted decoordination of the catalyst releases the final product 16 (ΔG = −144.6 kcal mol−1) and regenerates the [Pd(Ph3P)2] active catalyst. In an attempt to isolate or detect any intermediate 13–15 in the reaction mixture, preformed palladacycle 11 was treated with benzyne generated in situ at room temperature but only product 16 was detected.20 In agreement with this experiment, the low activation energies and the remarkable exergonic nature for the migratory insertion and the C–C bond-forming reductive elimination steps suggest that the concentration of any of the unstable intermediates 13–15 would be extremely low in catalytic and stoichiometric conditions.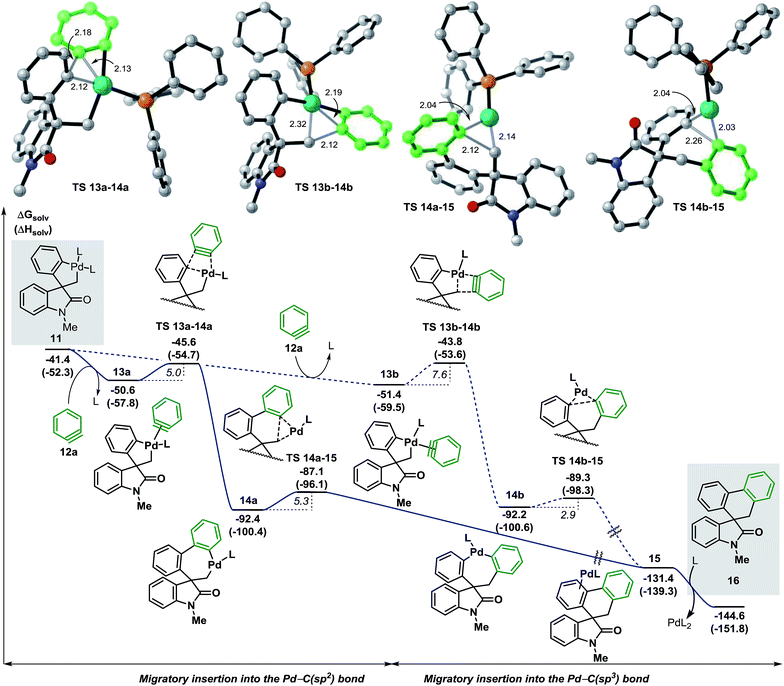 | ||
| Fig. 4 Free energy profile for the migratory insertion step with benzyne 12a and transition state structures (L = Ph3P). | ||
Evaluation of the potential energy surface for the migratory insertion of the unsymmetrical 3-methoxy substituted benzyne 12b is presented in Fig. 5. In this case, the unsymmetrical aryne 12b introduces a new regioselective element, based on the different relative positions of the methoxy substituent with respect to the spirocyclic core of the oxindole moiety. Coordination of 12b to 11 generates either 17a (ΔG = −46.7 kcal mol−1) or 17b (ΔG = −46.0 kcal mol−1). The methoxy group in intermediate 17a points toward the phosphine ligand whereas in 17b this substituent points toward the oxindole backbone (Fig. 6).
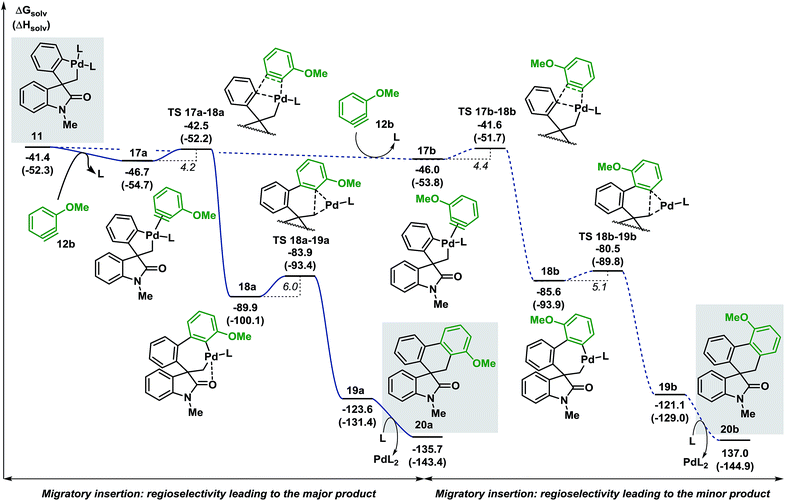 | ||
| Fig. 5 Computed Gibbs free energy profile explaining the regioselectivity of the migratory insertion of 3-methoxy substituted benzyne 12b (L = Ph3P). | ||
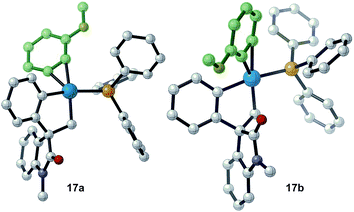 | ||
| Fig. 6 Computed structure for intermediates 17a and 17b highlighting the different orientations of the methoxy substituent. | ||
In analogy to 12a, insertion of the substituted aryne in 17a and 17b is a fast process (ΔG‡ = 4.2 and 4.4 kcal mol−1, respectively). The relative energy of the corresponding transition states TS 17a–18a and TS 17b–18b (ΔG = −42.5 and −41.6 kcal mol−1, respectively) favors the formation of 18a (ΔG = −89.9 kcal mol−1) over 18b (ΔG = −85.6 kcal mol−1). Subsequent C(sp2)–C(sp3) bond-forming reductive elimination proceeds viaTS 18a–19a and TS 18b–19b (ΔG = −83.9 and −80.5 kcal mol−1, respectively) to generate the two isomeric complexes 19a and 19b (ΔG = −123.6 and −121.1 kcal mol−1, respectively). Decoordination of the catalyst ultimately releases the two compounds 20a and 20b (ΔG = −135.7 and −137.0 kcal mol−1, respectively). The reaction between 3a and 3-methoxy benzyne 12b carried out under the standard reaction conditions14 affords the desired spirooxindoles products 20a and 20b in a mixture 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (see ESI†). The experimental ratio (3
1 (see ESI†). The experimental ratio (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is in good agreement with the calculated theoretical ratio (ΔΔG = 0.9 kcal mol−1, corresponding to a 3.6
1) is in good agreement with the calculated theoretical ratio (ΔΔG = 0.9 kcal mol−1, corresponding to a 3.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio at 80 °C) in favor of the same isomer 20a.38
1 ratio at 80 °C) in favor of the same isomer 20a.38
Reactivity and regioselectivity for the migratory insertion of alkynes
In order to examine the regioselectivity of the reaction with other unsaturated compounds, we selected less reactive π-systems such as unsymmetrical internal alkynes.16 Indeed, minor adjustments of the reaction conditions allowed the generation of the desired spirocyclic products in excellent regioselectivity (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The computational analysis of the migratory insertion step for methyl 3-phenylpropiolate 12c is presented in Fig. 7.39
1). The computational analysis of the migratory insertion step for methyl 3-phenylpropiolate 12c is presented in Fig. 7.39
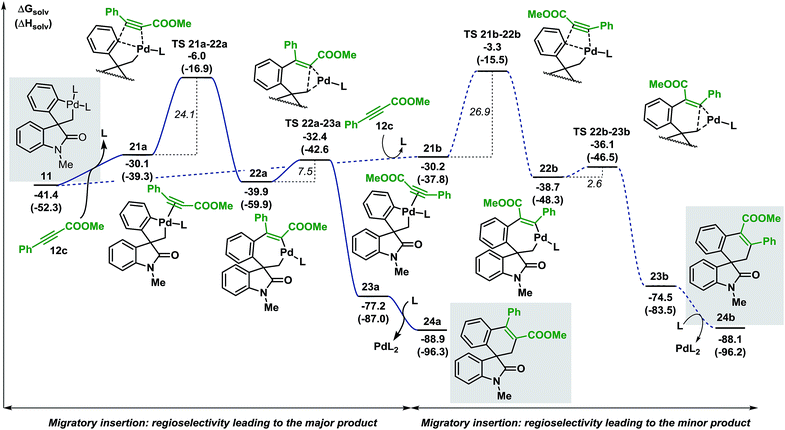 | ||
| Fig. 7 Computed Gibbs free energy profile explaining the regioselectivity of the migratory insertion of methyl 3-phenylpropiolate 12c (L = Ph3P). | ||
Coordination of the alkyne 12c to the palladium atom in 11 provides the two isomeric structures 21a and 21b (ΔG = −30.1 and −30.2 kcal mol−1, respectively). Migratory insertion takes place and the formation of a new C(sp2)–C(sp2) bond is modeled by transition states TS 21a–22a and TS 21b–22b (ΔG = −6.0 and −3.3 kcal mol−1, respectively) to generate intermediates 22a and 22b (ΔG = −39.9 and −38.7 kcal mol−1, respectively). The energies required for these insertion processes (ΔG‡ = 24.1 and 26.9 kcal mol−1, respectively) are significantly higher (>15 kcal mol−1) than the activation energies calculated in the case of arynes. This result reflects the higher temperatures required for the insertion of internal alkynes compared to arynes (100 °C vs. 80 °C). The following C(sp2)–C(sp3) bond-forming reductive elimination step is modeled by TS 22a–23a and TS 22b–23b (ΔG = −32.4 and −36.1 kcal mol−1, respectively) and requires 7.5 and 2.6 kcal mol−1, respectively. Final decoordination of the palladium complex from intermediates 23a and 23b (ΔG = −77.2 and −74.5 kcal mol−1, respectively) releases the corresponding products 24a and 24b (ΔG = −88.9 and −88.1 kcal mol−1, respectively). Of note, the kinetic theoretical ratio of 24a and 24b at 100 °C is 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, a value in good agreement with the ratios obtained experimentally (>20
1, a value in good agreement with the ratios obtained experimentally (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).
1).
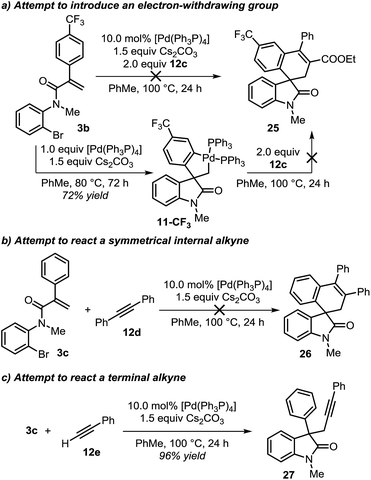
During the evaluation of the scope of this transformation, we found that introduction of an electron-withdrawing group on the pendant aromatic ring failed to generate the corresponding spirooxindole product 25 (Scheme 5a).16
Furthermore, when palladacycle 11-CF3 was successfully synthesized by independent synthesis, its reaction with internal alkyne 12d did not generate the expected product 26. Analysis of the alkyne migratory insertion step in complex 11-CF3 provides an activation energy only 2.6 kcal mol−1 higher than for the insertion in 21a (see ESI†). These results and experimental observations suggest that the low stability of complex 11-CF3 under the reaction conditions, in combination with a slower migratory insertion step, could be responsible for the lack of product formation. In other experiments, we found that the reaction of internal symmetrical alkynes such as 12d did not generate the expected product 26 (Scheme 5b).16 The energetics of the migratory insertion step for alkyne 12d was evaluated (see ESI†). The computed activation energy (ΔG‡ = 32.2 kcal mol−1) is 8.1 kcal mol−1 higher than for the insertion of unsymmetrical alkyne 12c (ΔG‡ = 24.1 kcal mol−1) supporting a particularly slow insertion step. The anticipated low rate for this insertion process, along with the kinetic stability of the active catalyst, may explain the lack of product formation in this case. In addition to these experiments, in an attempt to react substrate 3c with phenylacetylene 12e, we observed exclusive formation of the known compound 27 instead of the expected spirocyclic product (Scheme 5c). The computational analysis for the formation of this Sonogashira-type compound 27 is shown in Fig. 8.
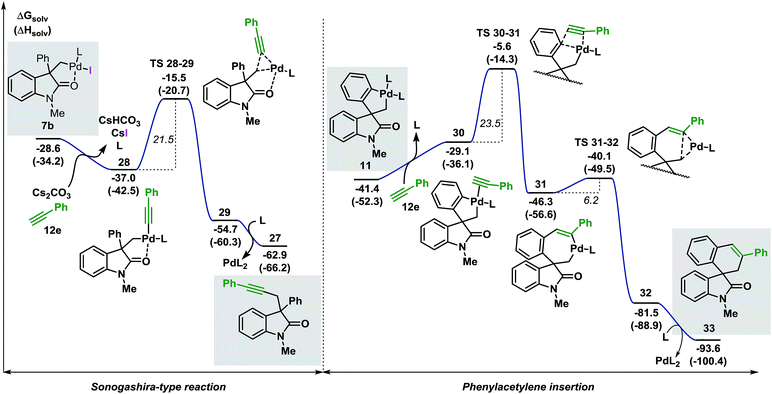 | ||
| Fig. 8 Comparison between the free energy profiles for the Sonogashira-type reaction (left side) and the migratory insertion reaction (right side) with terminal alkyne 12e (L = Ph3P). | ||
The base present in the reaction media facilitates a ligand exchange process in intermediate 7b to generate the organometallic species 28 (ΔG = −37.0 kcal mol−1).40 Ensuing C(sp3)–(Csp) bond-forming reductive elimination generates intermediate 29 (ΔG = −54.7 kcal mol−1) where the palladium atom coordinates to the alkyne moiety. This step requires 21.5 kcal mol−1 and is modeled by TS 28–29 (ΔG = −15.5 kcal mol−1). Interaction between the oxygen atom of the carbonyl functionality and the metal center was observed during the whole transformation. Decoordination of the catalyst releases the final product 27 (ΔG = −62.9 kcal mol−1). The alternative migratory insertion pathway starts with a ligand exchange process on palladacycle 11 to form intermediate 30 (ΔG = −29.1 kcal mol−1). Insertion of the alkyne ligand into the C(sp2)–Pd bond requires 23.5 kcal mol−1 and the corresponding transition state TS 30–31 (ΔG = −5.6 kcal mol−1) connects 30 to the resulting seven-membered palladacycle 31 (ΔG = −46.3 kcal mol−1). Final C(sp2)–C(sp3) bond-forming reductive elimination is modeled by TS 31–32 (ΔG = −40.1 kcal mol−1) and, upon decoordination of the catalyst, generates the expected product 33 (ΔG = −93.6 kcal mol−1). Comparison between the two possible pathways shows that the Sonogashira-type reaction on intermediate 7b is kinetically and thermodynamically favoured over the anticipated migratory insertion process (ΔΔG‡ = −2.0 kcal mol−1 and ΔΔG = −9.9 kcal mol−1, respectively). This result is in agreement with the experimental data where the reaction between 3c and the terminal alkyne 12e under the standard reaction conditions provides product 27 exclusively.
Experimental studies on the alternative migratory insertion/C–H bond activation sequence
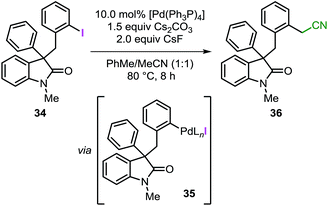
As mentioned in the introduction, intermediate C in Fig. 1 may undergo migratory insertion with the unsaturated reactant prior to the C–H bond activation step. In order to establish the feasibility of this sequence, substrate 34 was independently synthesized and submitted to the standard reaction conditions (Table 3). Oxidative addition of the low-valent catalyst into the reactive C(sp2)–I bond would generate intermediate 35 (analogous to intermediate J in Fig. 1).41 In the presence of a base, 35 could undergo intramolecular C–H bond activation on the unsubstituted phenyl ring to eventually form the spirooxindole 16, corresponding to the product obtained for the reaction of 3a with a benzyne precursor. Unexpectedly, the reaction of 34 provided compound 36 exclusively with the remaining mass balance represented by unreacted starting material (Table 3, entry 1). Product 36 presumably derives from the reaction between intermediate 35 (generated in situ) and the acetonitrile co-solvent. Indeed, the reaction carried out in pure toluene did not afford any product but only full recovery of starting material (Table 3, entry 2). Exclusion of either the palladium catalyst or the base also resulted in unreacted starting material (Table 3, entry 3 and 4). Of note, compound 36 has never been detected in any catalytic reaction during the optimization or the evaluation of scope of the spirocyclization reaction with arynes.14 These collective observations suggest that the alternative pathway initially proposed, where migratory insertion take places before the C–H bond activation step, is unlikely to be operative in the system under study. Unfortunately, attempts to carry out a computational analysis for this alternative mechanism provided a scenario inconsistent with the experimental results (see ESI†).Conclusions
The mechanism of the palladium-catalyzed spirocyclization of acrylamides with arynes and alkynes has been investigated by means of density functional theory calculations coupled with experimental studies. Our results show an excellent agreement between theoretical and experimental data and support the initially postulated mechanism for this reaction proceeding via a C–H bond activation and migratory insertion sequence. The most favorable pathway, based on the results of this study, is presented in Fig. 9.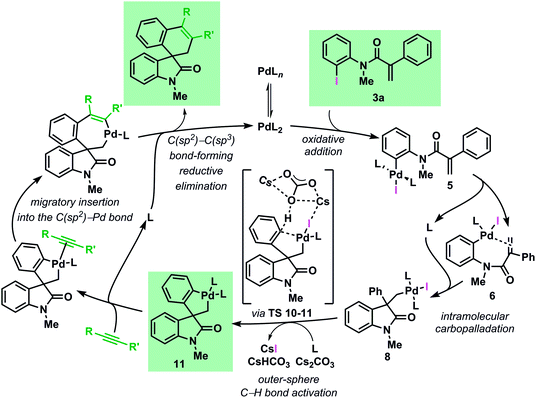 | ||
| Fig. 9 Catalytic cycle for the computed most favourable pathway for the Pd-catalyzed spirocyclization reaction (L = Ph3P). | ||
Investigation of the early stages of the reaction supports the existence of several species in equilibrium and comparisons between the computed and the single-crystal X-ray structures of some of these intermediates show a remarkable similarity. The intramolecular migratory insertion was found to be the rate determining step in the formation of the palladacycle intermediate 11. The C–H bond activation step is found to proceed via a concerted outer-sphere metallation deprotonation mechanism. This scenario is supported by kinetic measurements and by evaluation of other bases. Furthermore, ligand dissociation and exchange in the experimentally isolated palladacycle 11 was studied. The analysis of the migratory insertion step revealed that the process is consistently favored for the insertion into the C(sp2)–Pd bond in all the cases and it originates the observed stereoselectivities via kinetic control. The differences in the energies obtained in the case of aryne and alkyne reactants correlate to the different sets of experimental conditions. Furthermore, the calculated regioselectivities for the insertion of unsymmetrical unsaturated reactants are in excellent agreement with the experimental ratio previously reported. Finally, experimental data provide evidence that the alternative mechanism where the migratory insertion process precedes the C–H activation step is not operative under the standard reaction conditions.
Conflicts of interest
The authors declare no conflict of interests.Acknowledgements
We are grateful for financial support from the Natural Sciences and Engineering Research Council (NSERC), the University of Toronto (U of T), the University of Geneva (U of G) and Alphora Research Inc. I. F. thanks the Collaborative Research and Training Experience (Create ChemNET) program for a postdoctoral fellowship. H. Y. thanks the Ontario Graduate Scholarship (OGS) program for funding. We thank Dr Marcus Wegmann (U of T), Nicolas Zeidan (U of T), José F. Rodríguez (U of T), and Egor Larin (U of T) for proofreading the manuscript and for discussions. We thank Dr Marco van Woerden (Van Woerden Consultancy) for the preparation of Python scripts used for data analysis. We also thank Carmine Chiancone (U of G) for technical support.Notes and references
- For selected reviews and references therein, see: (a) F. Shi and R. C. Larock, in C–H Activation, ed. J.-Q. Yu and Z. Shi, Springer, Heidelberg, 2010, pp. 123–164 Search PubMed; (b) R. Giri, B.-F. Shi, K. M. Engle, N. Maugel and J.-Q. Yu, Chem. Soc. Rev., 2009, 38, 3242 RSC; (c) T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147 CrossRef CAS PubMed; (d) O. Baudoin, Chem. Soc. Rev., 2011, 40, 4902 RSC; (e) T. Gensch, M. N. Hopkinson, F. Glorius and J. Wencel-Delord, Chem. Soc. Rev., 2016, 45, 2900 RSC; (f) H. M. L. Davies and D. Morton, J. Org. Chem., 2016, 81, 343 CrossRef CAS PubMed; (g) J. F. Hartwig, J. Am. Chem. Soc., 2016, 138, 2 CrossRef CAS PubMed; (h) X.-S. Xue, P. Ji, B. Zhou and J.-P. Cheng, Chem. Rev., 2017, 117, 8622 CrossRef CAS PubMed; (i) Y. Yang, J. Lan and J. You, Chem. Rev., 2017, 117, 8787 CrossRef CAS PubMed; (j) J. R. Hummel, J. A. Boerth and J. A. Ellman, Chem. Rev., 2017, 117, 9163 CrossRef CAS PubMed.
- For selected reviews and references therein, see: (a) K. Godula and D. Sames, Science, 2006, 312, 67 CrossRef CAS PubMed; (b) D. Alberico, M. E. Scott and M. Lautens, Chem. Rev., 2007, 107, 174 CrossRef CAS PubMed; (c) L. McMurray, F. O'Hara and M. J. Gaunt, Chem. Soc. Rev., 2011, 40, 1885 RSC; (d) J. Ye and M. Lautens, Nat. Chem., 2015, 7, 863 CrossRef CAS PubMed; (e) N. Della Ca', M. Fontana, E. Motti and M. Catellani, Acc. Chem. Res., 2016, 49, 1389 CrossRef PubMed.
- For selected reviews and references therein, see: (a) X. Chen, K. M. Engle, D.-H. Wang and J.-Q. Yu, Angew. Chem., Int. Ed., 2009, 48, 5094 CrossRef CAS PubMed; (b) R. Giri, S. Thapa and A. Kafle, Adv. Synth. Catal., 2014, 356, 1395 CrossRef CAS; (c) C. Liu, J. Yuan, M. Gao, S. Tang, W. Li, R. Shi and A. Lei, Chem. Rev., 2015, 115, 12138 CrossRef CAS PubMed; (d) Z. Chen, B. Wang, J. Zhang, W. Yu, Z. Liu and Y. Zhang, Org. Chem. Front., 2015, 2, 1107 RSC; (e) Y. Park, Y. Kim and S. Chang, Chem. Rev., 2017, 117, 9247 CrossRef CAS PubMed.
- For selected examples and references therein, see: (a) J. J. Topczewski, P. J. Cabrera, N. I. Saper and M. S. Sanford, Nature, 2016, 531, 220 CrossRef CAS PubMed; (b) Z. Zhang, K. Tanaka and J.-Q. Yu, Nature, 2017, 543, 538 CrossRef CAS PubMed.
- For selected examples and references therein, see: (a) D. Leow, G. Li, T.-S. Mei and J.-Q. Yu, Nature, 2012, 486, 518 CrossRef CAS PubMed; (b) R.-Y. Tang, G. Li and J.-Q. Yu, Nature, 2104, 507, 215 CrossRef PubMed; (c) X.-C. Wang, W. Gong, L.-Z. Fang, R.-Y. Zhu, S. Li, K. M. Engle and J.-Q. Yu, Nature, 2015, 519, 334 CrossRef CAS PubMed; (d) Y. Xu, M. C. Young, C. Wang, D. M. Magness and G. Dong, Angew. Chem., Int. Ed., 2016, 55, 9084 CrossRef CAS PubMed; (e) K. Hong, H. Park and J.-Q. Yu, ACS Catal., 2017, 7, 6938 CrossRef CAS PubMed.
- For selected reviews and references therein, see: (a) I. Franzoni and C. Mazet, Org. Biomol. Chem., 2014, 12, 233 RSC; (b) R. Sharma, K. Thakur, R. Kumar, I. Kumar and U. Sharma, Catal. Rev.: Sci. Eng., 2015, 57, 345 CrossRef CAS; (c) H. J. Davis and R. J. Phipps, Chem. Sci., 2017, 8, 864 RSC.
- For selected examples and references therein, see: (a) M. Sickert, H. Weinstabl, B. Peters, X. Hou and M. Lautens, Angew. Chem., Int. Ed., 2014, 53, 5147 CAS; (b) O. Baudoin, Acc. Chem. Res., 2017, 50, 1114 CrossRef CAS PubMed.
- For selected reviews and references therein, see: (a) J. He, M. Wasa, K. S. L. Chan, Q. Shao and J.-Q. Yu, Chem. Rev., 2017, 117, 8754 CrossRef CAS PubMed; (b) V. P. Mehta and J.-A. García-López, ChemCatChem, 2017, 9, 1149 CrossRef CAS.
- For selected examples, see: (a) B. Seashore-Ludlow and P. Somfai, Org. Lett., 2012, 14, 3858 CrossRef CAS PubMed; (b) X. Liu, X. Ma, Y. Huang and Z. Gu, Org. Lett., 2013, 15, 4814 CrossRef CAS PubMed; (c) Z. Liu, Y. Xia, S. Zhou, L. Wang, Y. Zhang and J. Wang, Org. Lett., 2013, 15, 5032 CrossRef CAS PubMed; (d) M.-B. Zhou, X.-C. Huang, Y.-Y. Liu, R.-J. Song and J.-H. Li, Chem.–Eur. J., 2014, 20, 1843 CrossRef CAS PubMed; (e) D. D. Vachhani, H. H. Butani, N. Sharma, U. C. Bhoya, A. K. Shan and E. V. Van der Eycken, Chem. Commun., 2015, 51, 14862 RSC; (f) C. Shen, R.-R. Liu, R.-J. Fan, Y.-L. Li, T.-F. Xu, J.-R. Gao and Y.-X. Jia, J. Am. Chem. Soc., 2015, 137, 4936 CrossRef CAS PubMed; (g) W. Kong, Q. Wang and J. Zhu, Angew. Chem., Int. Ed., 2016, 55, 9714 CrossRef CAS PubMed; (h) H. Yoon, Y. J. Jang and M. Lautens, Synthesis, 2016, 48, 1483 CrossRef CAS; (i) D. A. Petrone, M. Kondo, N. Zeidan and M. Lautens, Chem.–Eur. J., 2016, 22, 5684 CrossRef CAS PubMed.
- (a) B. Burns, R. Gridd, V. Santhakumar, V. Sridharan, P. Stevenson and T. Worakum, Tetrahedron, 1992, 48, 7297 CrossRef CAS; (b) R. Grigg, J. M. Sansano, V. Santhakumar, V. Sridharan, R. Thangavelanthum, M. Thornton-Pett and D. Wilson, Tetrahedron, 1997, 53, 11803 CrossRef CAS; (c) P. Fretwell, R. Grigg, J. M. Sansano, V. Sridharan, S. Sukirthalingam, D. Wilson and J. Redpath, Tetrahedron, 2000, 56, 7525 CrossRef CAS.
- Q. Huang, A. Fazio, G. Dai, M. A. Campo and R. C. Larock, J. Am. Chem. Soc., 2004, 126, 7460 CrossRef PubMed.
- J. Ye, Z. Shi, T. Sperger, Y. Yasukawa, C. Kingston, F. Schoenebeck and M. Lautens, Nat. Chem., 2017, 9, 361 CrossRef CAS PubMed.
- M. Pérez-Gómez and J.-A. García-López, Angew. Chem., Int. Ed., 2016, 55, 14389 CrossRef PubMed.
- H. Yoon, A. Lossouarn, F. Landau and M. Lautens, Org. Lett., 2016, 18, 6324 CrossRef CAS PubMed.
- M. Pérez-Gómez, S. Hernández-Ponte, D. Bautista and J.-A. García-López, Chem. Commun., 2017, 53, 2842 RSC.
- H. Yoon, M. Rölz, F. Landau and M. Lautens, Angew. Chem., Int. Ed., 2017, 56, 10920 CrossRef CAS PubMed.
- For selected examples, see: (a) O. René, D. Lapointe and K. Fagnou, Org. Lett., 2009, 11, 4560 CrossRef PubMed; (b) R. T. Ruck, M. A. Huffman, M. M. Kim, M. Shevlin, W. V. Kandur and I. W. Davies, Angew. Chem., Int. Ed., 2008, 47, 4711 CrossRef CAS PubMed; (c) Z. Lu, C. Hu, J. Guo, J. Li, Y. Cui and Y. Jia, Org. Lett., 2010, 12, 480 CrossRef CAS PubMed; (d) T. Piou, L. Neville and J. Zhu, Org. Lett., 2012, 14, 3760 CrossRef CAS PubMed; (e) T. Piou, L. Neville and J. Zhu, Angew. Chem., Int. Ed., 2012, 51, 11561 CrossRef CAS PubMed; (f) T. Piou, A. Bunescu, Q. Wang, L. Neville and J. Zhu, Angew. Chem., Int. Ed., 2013, 52, 12385 CrossRef CAS PubMed; (g) M. Wang, X. Zhang, Y.-X. Zhuang, Y.-H. Xu and T.-P. Loh, J. Am. Chem. Soc., 2015, 137, 1341 CrossRef CAS PubMed; (h) Z.-Y. Gu, C.-G. Liu, S.-Y. Wang and S.-J. Ji, Org. Lett., 2016, 18, 2379 CrossRef CAS PubMed; (i) T. Yao and D. He, Org. Lett., 2017, 19, 842 CrossRef CAS PubMed; (j) S. Tong, A. Limouni, Q. Wang, M.-X. Wang and J. Zhu, Angew. Chem., Int. Ed., 2017, 56, 14192 CrossRef CAS PubMed; (k) C. Shao, Z. Wu, X. Ji, B. Zhou and Y. Zhang, Chem. Commun., 2017, 53, 10429 RSC.
- (a) B. M. Trost and M. K. Brennan, Synthesis, 2009, 18, 3003 CrossRef; (b) J. E. M. N. Klein and R. J. K. Taylor, Eur. J. Org. Chem., 2011, 6821 CrossRef CAS; (c) G. S. Singh and Z. Y. Desta, Chem. Rev., 2012, 112, 6104 CrossRef CAS PubMed; (d) L. K. Smith and I. R. Baxendale, Org. Biomol. Chem., 2015, 13, 9907 RSC; (e) W. Kong, Q. Wang and J. Zhu, J. Am. Chem. Soc., 2015, 137, 16028 CrossRef CAS PubMed; (f) B. V. S. Reddy, P. N. Nair, A. Antony and N. Srivastava, Eur. J. Org. Chem., 2017, 5484 CrossRef.
- H. Zheng, Y. Zhu and Y. Shi, Angew. Chem., Int. Ed., 2014, 53, 11280 CrossRef CAS PubMed.
- M. Pérez-Gómez, L. Navarro, I. Saura-Llamas, D. Bautista, M. Lautens and J.-A. García-López, Organometallics, 2017, 36, 4465 CrossRef.
- (a) J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800 CrossRef; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef; (c) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CAS.
- X. Li and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 835 CrossRef CAS PubMed.
- (a) T. H. Dunning Jr and P. J. Hay, Modern Theoretical Chemistry, ed. H. F. Schaefer III, Plenum, New York, 1997, vol. 3 Search PubMed; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS; (c) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284 CrossRef CAS; (d) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299 CrossRef CAS.
- (a) A. D. MacLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639 CrossRef; (b) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363 CrossRef CAS; (b) H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918 CrossRef CAS PubMed; (c) H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61 CrossRef CAS PubMed.
- J. M. Goodman and M. A. Silva, Tetrahedron Lett., 2003, 44, 8233 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, Sherbrooke, Quebec, Canada, 2009, http://www.cylview.org Search PubMed.
- (a) M. Ahlquist, P. Fristrup, D. Tanner and P.-O. Norrby, Organometallics, 2006, 25, 2066 CrossRef CAS; (b) M. Ahlquist and P.-O. Norrby, Organometallics, 2007, 26, 550 CrossRef CAS. for a related study, see also: (c) W.-J. Sun, W. Chu, L.-J. Yu and C.-F. Jiang, Chin. J. Chem. Phys., 2010, 23, 175 CrossRef CAS. for a study on the speciation of [Pd(Ph3P)4] in aromatic solvents, see: (d) P. Vidossich, G. Ujaque and A. Llledos, Chem. Commun., 2014, 50, 661 RSC.
- Evaluation of this RMSD was performed by comparison of the single crystal X-ray structure from ref. 20 and the mirror image (i.e. the opposite enantiomer) of 7b-Cl.
- The structure of the IRC/QRC intermediates which follows the C–H bond activation step are presented in the ESI.† These structures are not included in the discussion herein due to the inaccuracy of DFT methods to describe salts that in the experimental conditions are present as solids and not as isolated molecules.
- For a comprehensive review and reference therein, see: D. L. Davies, S. A. Macgregor and C. L. McMullin, Chem. Rev., 2017, 117, 8649 CrossRef CAS PubMed.
- J. I. Seeman, Chem. Rev., 1983, 83, 83 CrossRef CAS.
- For experimental and computational studies of the reactivity of unsymmetrical arynes in the absence of transition metals, see: (a) P. H.-Y. Cheong, R. S. Paton, S. M. Bronner, G.-Y. J. Im, N. K. Garg and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 1267 CrossRef CAS PubMed; (b) J. M. Medina, J. L. Mackey, N. K. Garg and K. H. Houk, J. Am. Chem. Soc., 2014, 136, 15798 CrossRef CAS PubMed.
- In the original publication, ethyl 3-phenylpropiolate was used experimentally.
- Ligand exchange in the more stable intermediate 8 is possible but the resulting trans arrangement of the two carbon substituents would not allow direct C–C bond-forming reductive elimination. This would require an initial ligand dissociation and isomerization to form 28.
- The reactivity of this bond was confirmed by coupling compound 34 with p-tolylboronic acid under standard Suzuki-Miyaura reaction conditions utilizing [Pd(Ph3P)4] as catalyst (see ESI†).
Footnotes |
| † Electronic supplementary information (ESI) available: Additional potential energy profiles, additional experimental data, Cartesian coordinates and energies for all intermediates and transition states are given. See DOI: 10.1039/c7sc04709f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |