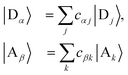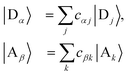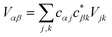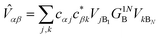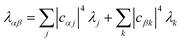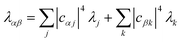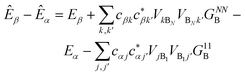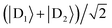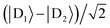DOI:
10.1039/C8SC00053K
(Edge Article)
Chem. Sci., 2018,
9, 2942-2951
Generalised Marcus theory for multi-molecular delocalised charge transfer
Received
5th January 2018
, Accepted 11th February 2018
First published on 13th February 2018
Abstract
Although Marcus theory is widely used to describe charge transfer in molecular systems, in its usual form it is restricted to transfer from one molecule to another. If a charge is delocalised across multiple donor molecules, this approach requires us to treat the entire donor aggregate as a unified supermolecule, leading to potentially expensive quantum-chemical calculations and making it more difficult to understand how the aggregate components contribute to the overall transfer. Here, we show that it is possible to describe charge transfer between groups of molecules in terms of the properties of the constituent molecules and couplings between them, obviating the need for expensive supermolecular calculations. We use the resulting theory to show that charge delocalisation between molecules in either the donor or acceptor aggregates can enhance the rate of charge transfer through a process we call supertransfer (or suppress it through subtransfer). The rate can also be enhanced above what is possible with a single donor and a single acceptor by judiciously tuning energy levels and reorganisation energies. We also describe bridge-mediated charge transfer between delocalised molecular aggregates. The equations of generalised Marcus theory are in closed form, providing qualitative insight into the impact of delocalisation on charge dynamics in molecular systems.
1 Introduction
Theories of charge-transfer rates underpin our understanding of a wide variety of chemical reactions and charge-transport processes, not only in chemistry, but also in biology and materials science.1–4 In most of the well-studied cases, the charge is being transferred from one molecule to another. However, in many systems—including organic semiconductors,5,6 the reaction centres of photosynthetic organisms,7,8 inorganic coordination complexes,9 and conductive metal–organic frameworks (MOFs)10—the charge to be transferred is delocalised across multiple donor molecules (or is to be received by states delocalised over multiple acceptor molecules). The usual theoretical approaches can be applied to these cases if the donor or acceptor aggregates are treated as single supermolecules, but doing so is often computationally prohibitive, requires a complete re-calculation if any part is changed, and, most importantly, offers limited qualitative insight into how the component molecules and the interactions between them affect the inter-aggregate charge transfer.
Although delocalisation in charge transfer has been studied extensively, most studies have focused on cases of delocalisation between the donor and acceptor, as opposed to delocalisation within donor or acceptor aggregates. In particular, donor–acceptor delocalisation is critical to understanding adiabatic electron transfer, as first emphasised by Hush,11,12 and extended by numerous authors since.13–15 For example, intervalence transitions in mixed-valence compounds are a clear manifestation of delocalisation between two molecules.16
Here, we study the problem of charge transfer from one delocalised molecular aggregate to another. In order to be able to speak of two distinct aggregates, we assume that the coupling between the aggregates (i.e., between any donor molecule and any acceptor molecule) is small compared to the strength of their coupling to the environment. Furthermore, to ensure that charges within either aggregate (or both) are delocalised among the constituent molecules, we assume that the couplings between the molecules are stronger than their coupling to the environment.
Because the overall donor–acceptor coupling is weak, the charge transfer will be incoherent, i.e., with no coherence between the donor and acceptor states. Apart from the delocalisation within the aggregates, this situation is described by non-adiabatic electron transfer, which we take as our starting point. Although we will follow convention in calling it Marcus theory17 (MT), the standard expression for non-adiabatic charge transfer between one donor D and one acceptor A was derived by Levich and Dogonadze:18
| | 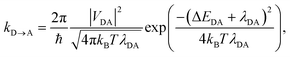 | (1) |
where, at temperature
T, three parameters control the transfer rate: the donor–acceptor electronic coupling,
VDA, determined by the overlap of their electronic wavefunctions; the reorganisation energy,
λDA, which is the energy required to reorganise the environment from equilibrium about the reactant to equilibrium about the product without changing the electronic state; and the energy difference between the final and initial states, Δ
EDA.
Here, we show that it is possible to generalise non-adiabatic MT to describe charge transfer between molecular aggregates in terms of the properties of individual molecules and couplings between them. Our theory is both computationally cheap – avoiding the need for supramolecular quantum-chemical simulations – and offers intuitive insight into how the charge transfer rates are affected by changes to molecules in either aggregate.
Our approach is inspired by developments in Förster resonance energy transfer (FRET), which describes the exciton transfer rate between two chromophores and is, like MT, derived from second-order perturbation theory in the donor–acceptor coupling. Sumi developed generalised FRET (gFRET) to describe the transfer of excitons between delocalised aggregates in photosynthetic antenna complexes,19,20 and his approach has since been used to study exciton transfer in a wide range of molecular aggregates.21–23 Following Sumi, we name our theory ‘generalised Marcus theory’ (gMT).
MT also allows a description of bridge-mediated charge transfer, where the donor and acceptor are not directly coupled, but a coupling between them is mediated by intervening ‘bridge’ molecules, whose states are sufficiently high in energy to prevent actual charge transfer from the donor to the bridge.1–3 A bridge enables charge transfer to occur over longer distances, although the rate typically decreases exponentially with the number of bridge elements. After deriving gMT in Section 2.1, we show that it is also easily extended to describe bridge-assisted charge transfer between delocalised aggregates in Section 2.2.
2 Results
2.1 Generalised Marcus theory
We generalise Marcus theory by considering an aggregate of ND donor molecules and an aggregate of NA acceptor molecules, with each molecule coupled to an independent environment of thermalised harmonic oscillators. Three approximations make it possible to define two distinct aggregates (Fig. 1): first, the coupling between molecules in each aggregate is much stronger than their coupling to the environment, ensuring that the delocalised eigenstates of each aggregate are the appropriate basis for perturbation theory; second, the system-environment coupling is much stronger than the inter-aggregate coupling, implying that inter-aggregate charge transfer is incoherent (hopping); and third, because we assume each site is coupled to its own environment, no environmental mode connects a donor and an acceptor molecule. Where applicable, we follow the derivation of multi-chromophoric FRET (MC-FRET),24 which reduces to generalised FRET in the appropriate limit. While gFRET can also be derived using Fermi's golden rule,25 we used a time-dependent derivation because some of our intermediate results may be useful in more general contexts.
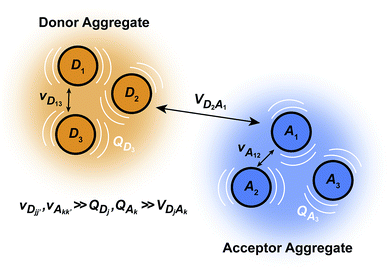 |
| | Fig. 1 The model system for generalised Marcus theory. The model describes charge transfer between two delocalised aggregates if the couplings v between molecules constituting the donor (or acceptor) are strong compared to the coupling to the environment Q, while the couplings V between molecules in the donor with those in the acceptor are relatively weak. | |
The full Hamiltonian is H = H0D + H0A + HC + HDE + HAE + HE, and we introduce each term here as well as in Fig. 1. The donor-aggregate and acceptor-aggregate Hamiltonians are, respectively,
| | 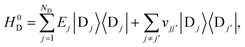 | (2) |
| | 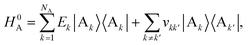 | (3) |
where |D
j〉 and |A
k〉 are the states where the charge is localised on molecules D
j and A
k respectively. Throughout this work we index donor sites with
j and acceptor sites with
k:
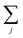
should be read as a sum over only the donor sites, and
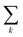
only over acceptors. The donor and acceptor molecules have site energies
Ej and
Ek, and intra-aggregate couplings are
vjj′ (in the donor) and
vkk′ (in the acceptor).
We refer to the eigenstates of H0D and H0A as the aggregate basis, being, respectively, 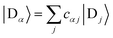 and
and 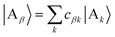 , with energies Eα and Eβ. Similar to site indices j and k, index α is consistently used to denote only donor eigenstates, and β acceptor eigenstates.
, with energies Eα and Eβ. Similar to site indices j and k, index α is consistently used to denote only donor eigenstates, and β acceptor eigenstates.
Inter-aggregate coupling is described by the Hamiltonian
| | 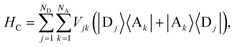 | (4) |
where
Vjk is the coupling between the
jth donor and
kth acceptor molecules.
The environment is described by a set of harmonic oscillators:
| | 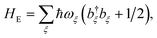 | (5) |
where
ωξ is the frequency of the
ξth environment mode, with creation operator
b†ξ. We can also write
HE =
HED +
HEA, with the environment modes partitioned between those that couple to donor and acceptor molecules.
The donor-environment and acceptor-environment interaction Hamiltonians are, respectively,
| | 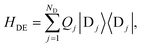 | (6) |
| | 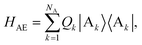 | (7) |
with
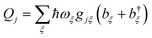
, where
gjξ is the dimensionless coupling of the
ξth environment mode to the charged
jth donor molecule, relative to the uncharged state.
Qk is defined analogously. The assumption of a local environment means that, for a fixed
ξ, only one of
gjξ can be non-zero.
The charge-transfer rate is the rate of change of the charge population on the acceptor,
| | 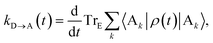 | (8) |
where
ρ(
t) is the density matrix of the system, and Tr
E is the trace over the environmental modes. As detailed in the Appendix,
kD→A can be calculated using second-order perturbation theory in
HC and, because we assumed separable environments, generates a time-dependent transfer rate
| | 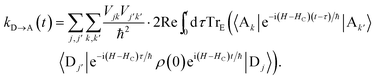 | (9) |
To proceed, we consider the rate in the aggregate basis. The requirement that Vjk be weaker than all other couplings means that the donor aggregate will relax to a thermal state faster than the charge transfer. In other words, we assume that the initial density operator of the system ρ(0) will, before charge transfer takes place, relax to a state ρth in which both the donor and acceptor aggregates are in equilibrium with their own environments (see Appendix for details). This gives a time-independent transfer rate,
| | 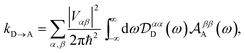 | (10) |
where
| | 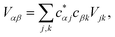 | (11) |
| | 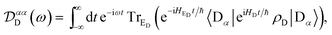 | (12) |
| | 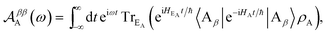 | (13) |
and where
ρth is split into donor and acceptor components,
ρth =
ρD ⊗
ρA. Because the donor-environment coupling is weak, the thermal state of the donor will approximately factorise to
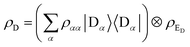
, where the electronic population distribution is
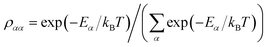
and the thermal environment is
ρED = exp(−
HED/
kBT)/Tr
ED(exp(−
HED/
kBT)). The thermal state of the acceptor is
ρA =
ρEA = exp(−
HEA/
kBT)/Tr
EA(exp(−
HEA/
kBT)). Finally, we have also written
HD =
H0D +
HDE +
HED, and similarly for
HA.
Eqn (10)–(13) are analogous to the MC-FRET treatment of delocalised exciton transfer.24 In particular, the rate of MC-FRET depends on the (weighted) overlap of the donor emission spectrum with the acceptor absorption spectrum, which resembles the form of eqn (10). However, in gMT, eqn (12) describes the spectrum of charge disassociation from the donor and eqn (13) the charge association spectrum for the acceptor. Furthermore, the inter-aggregate coupling in eqn (10) is determined by the overlap of electronic wavefunctions, while in MC-FRET the couplings are from the interactions of transition dipole moments.
Evaluating eqn (12) and (13) for independent harmonic environments gives (see Appendix for details)
| | 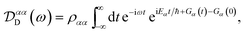 | (14) |
| | 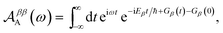 | (15) |
with the lineshape function
| | 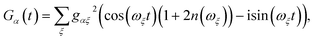 | (16) |
and
Gβ(
t) analogously defined. For a thermally populated environment, the occupation of environmental modes is given by the Bose–Einstein distribution
n(
ν) = (exp(
ħν/
kBT) − 1)
−1.
The preceding equations are appropriate at a wide range of temperatures and environmental spectral densities. Although we could stop here, to obtain a clear comparison with MT, we now make two additional approximations that are also made in deriving ordinary Marcus theory. To do so, we assume that the spectral density 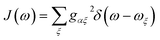 goes rapidly to zero beyond a cut-off frequency ωc. Then, we first assume the high-temperature limit kBT ≫ ħωc, so that n(ν) ≈ kBT/ħν ≫ 1, giving
goes rapidly to zero beyond a cut-off frequency ωc. Then, we first assume the high-temperature limit kBT ≫ ħωc, so that n(ν) ≈ kBT/ħν ≫ 1, giving
| | 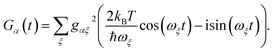 | (17) |
Second, MT also assumes the slow-nuclear-mode limit, in which the charge-transfer occurs faster than the characteristic timescales of the environment:
t ≪ 1/
ωc ≲ 1/
ωξ. With
ωξt ≪ 1, we expand the trigonometric functions in
eqn (17) to leading order:
| | 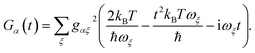 | (18) |
We now define the reorganisation energy for the donor sites as 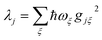 , and similarly for the acceptor sites, λk. The change of basis
, and similarly for the acceptor sites, λk. The change of basis 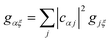 gives the reorganisation energy of aggregate eigenstates
gives the reorganisation energy of aggregate eigenstates
| | 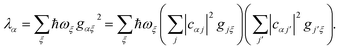 | (19) |
Since each site has an independent environment, no mode
ξ couples to two different sites (
gjξgj′ξ =
gjξ2δjj′), giving
| | 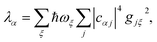 | (20) |
and similarly for
λβ.
Substituting eqn (18) and (20) into eqn (14) and (15) we find
| | 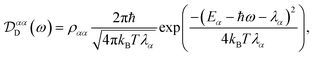 | (21) |
| | 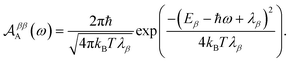 | (22) |
Consequently, the overlap integral in
eqn (10) becomes
| | 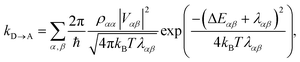 | (23) |
where Δ
Eαβ =
Eβ −
Eα and
λαβ =
λα +
λβ, demonstrating that gMT takes the same form as MT, with all parameters defined analogously to—and expressible in terms of—their site-basis counterparts. These results are also summarised in
Table 1, and in the limit of a single-molecule donor and single-molecule acceptor,
eqn (23) reduces to the ordinary MT rate,
eqn (1). The ability to recast gFRET in a form analogous to
eqn (23) (
ref. 26) further illustrates the deep similarities between charge and exciton transfer.
Table 1 The equations of generalised Marcus theory (gMT) and bridge-mediated gMT have the same form as ordinary Marcus theory, provided that relevant parameters are replaced as provided in this table. Eα and Eβ are the eigenstates of the donor and acceptor aggregate Hamiltonians, H0D and H0A respectively. Bridge-mediated gMT contains a bridge of N sites, with site B1 coupling to the donor aggregate and BN to the acceptor. The couplings VjB1 and VkBN are the coupling of the jth donor site to B1, and the coupling of the kth acceptor site to BN, respectively. Green's function GB, given by eqn (37), describes transport through the bridge
|
|
Marcus theory |
Generalised Marcus theory |
Bridge-mediated generalised Marcus theory |
| Donor & acceptor indices |
Sites |Dj〉, |Ak〉 |
Eigenstates 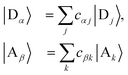 |
Eigenstates 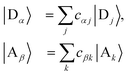 |
| Electronic coupling |
V
jk
|
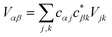
|
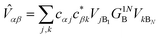
|
| Reorganisation energy (separable environments) |
λ
j
+ λk |
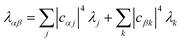
|
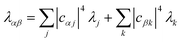
|
| Energy difference (ΔE) |
E
Ak − EAj |
E
β
− Eα |
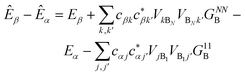
|
2.2 Generalised bridge-mediated charge transfer
Like MT, gMT can be expanded to include the case where the coupling between the donor and the acceptor aggregates is not direct, but is instead mediated by a bridge consisting of higher-lying states of intervening molecules. We consider a bridge of N molecules, each modelled as a single site, where the donor molecules only couple to the first bridge state, B1, the acceptor molecules only couple to the last bridge state, BN, and each bridge molecule only couples to its two nearest neighbours in the chain, as shown in Fig. 2. Usually, the bridge site energies EBl are considered energetically distinct from the donor and acceptor aggregates, i.e.,| | | (EBk − EBl), |VBlBl+1| ≪ EBl − Eα/β, | (24) |
where VBlBl+1 are the intra-bridge couplings and Eα/β is the characteristic energy of donor and acceptor eigenstates (for concreteness, it could be taken as the highest eigenvalue of either H0D or H0A).
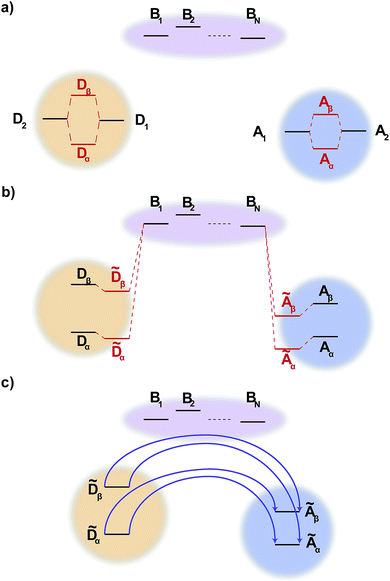 |
| | Fig. 2 Generalised bridge-assisted charge transfer, shown with two donor molecules, D1 and D2, two acceptor molecules, A1 and A2, and N bridge molecules, B1, …, BN. (a) The eigenstates of each aggregate are calculated. (b) The energies of these eigenstates are then perturbed by the coupling to the bridge (perturbation of the bridge levels is neglected, see text). (c) Charge transfer occurs directly between donor and acceptor aggregate eigenstates, assisted by virtual bridge states. | |
We define the donor–bridge–acceptor Hamiltonian HDBA = HB + H0D + HDB + H0A + HAB using H0D and H0A as above and adding the bridge Hamiltonian HB and the coupling of the bridge to the donor, HDB, and acceptor, HAB,
| | 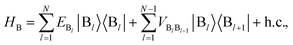 | (25) |
| | 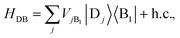 | (26) |
| | 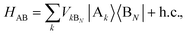 | (27) |
where |B
l〉 is the state of a charge being located on bridge site B
l.
Instead of thinking of B1 and BN as coupling to donor and acceptor sites, we can also consider them as coupling to the aggregate eigenstates. In the aggregate basis, HDBA becomes
| | 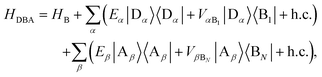 | (28) |
where
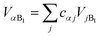
and
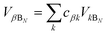
.
We calculate the rate of charge transfer from each donor eigenstate |Dα〉 to each acceptor eigenstate |Aβ〉 independently, using the mathematics already established for single-site bridge-mediated transfer.27 In other words, instead of considering the entire donor–bridge–acceptor system, we consider separately the subspace of each donor and acceptor eigenstate with the bridge,
| | | HDBA(α,β) = HB + Eα|Dα〉〈Dα| + VαB1|Dα〉〈B1| + h.c. + Eβ|Aβ〉〈Aβ| + VβBN|Aβ〉〈BN| + h.c. | (29) |
We denote the lowest-eigenvalue eigenvector of
HDBA(
α,
β) as
dDBA = (
dα,
dB1, …,
dBN,
dβ), with eigenvalue
EDBA.
Since (HDBA(α,β) − IEDBA)dDBA = 0, we find that
| | | (Eα − EDBA)dα + VαB1dB1 = 0, | (30) |
| | | (Eβ − EDBA)dβ + VβBNdBN = 0. | (31) |
The values of
dB1 and
dBN can be found by considering the bridge subspace, (
HB −
IEDBA)
dB = −(
VB1αdα, 0, …, 0,
VBNβdβ) where
dB consists of the bridge elements of
dDBA in the same order. The solution of this equation is
dB =
GB(
VB1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αdα
αdα, 0, …, 0,
VBNβdβ), using Green's function
GB = (
IEDBA −
HB)
−1.
By substituting this solution for dB1 and dBN into eqn (30) and (31), we find
| | (Êα − EDBA)dα + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) αβdβ = 0, αβdβ = 0, | (32) |
| | (Êβ − EDBA)dβ + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) βαdα = 0, βαdα = 0, | (33) |
where
Ê are the perturbed energies of aggregate eigenstates due to coupling with the bridge,
| | | Êα = Eα + VαB1G11BVB1α, | (34) |
| | | Êβ = Eβ + VβBNGNNBVBNβ, | (35) |
and
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif)
is the effective coupling between the donor and acceptor eigenstates, mediated by the bridge,
| | ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) αβ = VαB1G1NBVBNβ. αβ = VαB1G1NBVBNβ. | (36) |
To find the Green's function, we expand GB in terms of a Dyson series. Because |VBlBl+1| is small (see eqn (24)), we keep only the lowest-order term,27
| | | G1NB = (EDBA − EB1)−1VB1B2(EDBA − EB2)−1VB2B3 ×... × (EDBA − EBN−1)−1VBN−1BN(EDBA − EBN)−1. | (37) |
While
EDBA is an eigenvalue of the entire donor–bridge–acceptor system, we are only interested in the donor/acceptor subspace. Because
EBl −
Eα/β is large relative to inter-site couplings and energy differences (
eqn (24)), we can approximate
EDBA −
EBl ≈
Eα/β −
EB, for average bridge energy
EB. This allows us to simplify
eqn (36) using the geometric mean of the bridge couplings
VBB,
| | 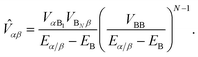 | (38) |
As in ordinary bridge-assisted charge transfer, the effective coupling decays exponentially with bridge length because
VBB <
Eα/β −
EB (
eqn (24)). Substituting
eqn (34)–(37) into
eqn (23), we have the rate of bridge-assisted gMT:
| | 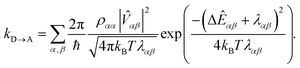 | (39) |
3 Discussion
The summary of results in Table 1 shows that gMT—whether bridged or not—follows the same functional form as ordinary Marcus theory. This allows intuition gained from studying MT to continue to be useful when studying aggregates instead of single molecules (provided that the parameters are redefined as shown in Table 1). Further, gMT allows known values of relevant parameters (couplings, energy differences, and reorganisation energies) of individual molecules to be used to calculate the effective parameters for aggregates, saving computational time by avoiding expensive supramolecular quantum-chemical simulations.
However, the presence of delocalisation in aggregates leads to significant differences between MT and gMT. We can analyse the influence of delocalisation on charge transfer by separating its impact on the electronic and nuclear components of the MT rate.
The gMT electronic coupling factor 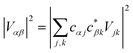 includes a coherent sum involving electronic amplitudes in each of the donor and acceptor aggregates, allowing both constructive and destructive interference to affect the transfer rate. If the interferences is constructive, leading to enhanced transfer rates, we call the effect supertransfer, and if it is destructive, subtransfer, borrowing terminology from the similar problem of MC-FRET.28
includes a coherent sum involving electronic amplitudes in each of the donor and acceptor aggregates, allowing both constructive and destructive interference to affect the transfer rate. If the interferences is constructive, leading to enhanced transfer rates, we call the effect supertransfer, and if it is destructive, subtransfer, borrowing terminology from the similar problem of MC-FRET.28
For illustration, we consider an aggregate of two identical coupled donors, D1 and D2, with a charge delocalised between them in the 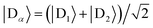 state. The donors are coupled to a single acceptor A with strengths VD1A and VD2A respectively. If we were to apply Marcus theory between each donor and the acceptor independently, we would expect a transfer rate proportional to the square of each coupling,
state. The donors are coupled to a single acceptor A with strengths VD1A and VD2A respectively. If we were to apply Marcus theory between each donor and the acceptor independently, we would expect a transfer rate proportional to the square of each coupling, 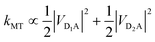 , with the factors of 1/2 indicating the population on each donor. However, this naive approach fails to include coherent effects of the superposition. These are treated correctly by gMT, which predicts a transfer rate of
, with the factors of 1/2 indicating the population on each donor. However, this naive approach fails to include coherent effects of the superposition. These are treated correctly by gMT, which predicts a transfer rate of 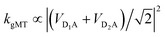 . The presence of rate-enhancement due to supertransfer is apparent if VD1A = VD2A, which implies kgMT = 2kMT. In contrast, if the two transfer pathways interfere destructively, VD1A = −VD2A, gMT predicts subtransfer with kgMT = 0. We refer to states that enhance the charge-transfer rate through supertransfer as bright, while those that retard it as dark, in analogy to the terms used in the literature on superradiance.29 The relative populations of the bright and dark states will strongly influence the rate of charge transfer in delocalised systems.
. The presence of rate-enhancement due to supertransfer is apparent if VD1A = VD2A, which implies kgMT = 2kMT. In contrast, if the two transfer pathways interfere destructively, VD1A = −VD2A, gMT predicts subtransfer with kgMT = 0. We refer to states that enhance the charge-transfer rate through supertransfer as bright, while those that retard it as dark, in analogy to the terms used in the literature on superradiance.29 The relative populations of the bright and dark states will strongly influence the rate of charge transfer in delocalised systems.
Supertransfer is also sensitive to the system's geometry. Changing the distance and orientations between donors and acceptors will affect the electronic wavefunction overlaps due to the exponential decay of electronic wavefunctions with distance, consequently modifying the electronic couplings. To explore the consequences of this geometric sensitivity, we consider a model consisting of two donor molecules transferring a unit of charge to an acceptor molecule, shown in Fig. 3. These calculations demonstrate that rate enhancement/retardation is weakest when the acceptor is co-linear with the donors. This is because the farther donor is so far away that the acceptor is only affected by the nearer donor. The impact is most significant when the acceptor is equidistant from the two donors, where supertransfer from the bright state amplifies the transfer rate by a factor of two, while the dark state provides no transfer.
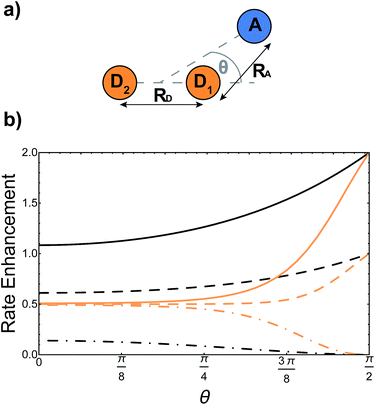 |
| | Fig. 3 Example of generalised Marcus theory (gMT) and supertransfer, showing only the impact of electronic component |Vαβ|2 on the charge transfer rate. (a) Geometric arrangement of two donors and one acceptor, changing from collinear (θ = 0) to an isosceles triangle (θ = π/2). (b) Rates of charge transfer from the donors to the acceptor are displayed as ratios of the rate that would be found if only donor D1 were present and the charge initially localised on it. Black and orange lines indicate, respectively, geometries with RA = 3RD or RA = RD (at a constant RA = 5 Å). In both cases, the rates are computed for three initial donor states: the bright state 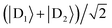 (solid), the dark state (solid), the dark state 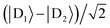 (dot-dashed), and the fully mixed state of |D1〉 and |D2〉 (dashed). These three states are obtained as ground states of the donor Hamiltonian by assuming VD1D2 = −100 meV (bright), VD1D2 = 100 meV (dark), or VD1D2 = 0 meV (mixed). The transfer rates are independent of RA and RD when θ reaches π/2, where both donors are equidistant from the acceptor. At that point, constructive interference ensures that the transfer from the bright state is twice as fast as it would be from either site alone, while transfer from the dark state is completely suppressed by destructive interference caused by the opposite signs of the wavefunction at D1 and D2. The difference between the two geometries is apparent at smaller θ. When RD is large compared to RA (orange), the rate is half the single-site rate for all initial states, indicating that the acceptor is interacting primarily with D1 until θ becomes considerable. By contrast, when both donors are close enough to the acceptor to interact with it strongly (black), supertransfer and subtransfer can occur at all values of θ, resulting in rate enhancements different from 0.5 at all angles. Other calculation parameters: VDA(r) = 50 meV (dot-dashed), and the fully mixed state of |D1〉 and |D2〉 (dashed). These three states are obtained as ground states of the donor Hamiltonian by assuming VD1D2 = −100 meV (bright), VD1D2 = 100 meV (dark), or VD1D2 = 0 meV (mixed). The transfer rates are independent of RA and RD when θ reaches π/2, where both donors are equidistant from the acceptor. At that point, constructive interference ensures that the transfer from the bright state is twice as fast as it would be from either site alone, while transfer from the dark state is completely suppressed by destructive interference caused by the opposite signs of the wavefunction at D1 and D2. The difference between the two geometries is apparent at smaller θ. When RD is large compared to RA (orange), the rate is half the single-site rate for all initial states, indicating that the acceptor is interacting primarily with D1 until θ becomes considerable. By contrast, when both donors are close enough to the acceptor to interact with it strongly (black), supertransfer and subtransfer can occur at all values of θ, resulting in rate enhancements different from 0.5 at all angles. Other calculation parameters: VDA(r) = 50 meV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(1 − r/2 Å). exp(1 − r/2 Å). | |
We can compare these results with gFRET, the analogous theory of excitation-energy transfer between molecular aggregates.24 Bright and dark states also exist in gFRET, but exciton transfer is not as sensitive to small changes in the separation between molecules. While the transfer rate in gMT is determined by the overlap of electronic wavefunctions, which decay exponentially with distance, the MC-FRET rate depends on the coupling of transition dipole moments, which decays with the cube of the distance. In addition, both gMT and gFRET are strongly affected by the relative orientations of the molecules. The orientational dependence of gFRET is easier to predict, especially in the large-separation limit where it can be represented by the interaction of two dipoles. By contrast, the orientational dependence of electronic couplings depends on the shape of the orbitals, which varies from molecule to molecule. Given that the geometric dependence of gFRET can lead to substantially different outcomes in light-harvesting complexes,22,23 the stronger dependence of gMT on geometry provides an opportunity to engineer molecular systems that perform charge transfer better than single sites.
The nuclear factor in gMT (also referred to as the Franck–Condon weighted density), (4πkBTλαβ)−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(ΔEαβ + λαβ)2/4kBTλαβ), has several features in common with ordinary MT. For example, for a fixed λαβ, the nuclear factor is maximised when −ΔEαβ = λαβ, and the inverted regime is possible when −ΔEαβ > λαβ. However, the nuclear term also possesses features not predicted by ordinary MT, allowing for both enhancement or retardation of the transfer rate.
exp(−(ΔEαβ + λαβ)2/4kBTλαβ), has several features in common with ordinary MT. For example, for a fixed λαβ, the nuclear factor is maximised when −ΔEαβ = λαβ, and the inverted regime is possible when −ΔEαβ > λαβ. However, the nuclear term also possesses features not predicted by ordinary MT, allowing for both enhancement or retardation of the transfer rate.
The nuclear factor depends on two energies, ΔEαβ and λαβ, which are affected by delocalisation in different ways. On the one hand, ΔEαβ is the difference between eigenvalues of H0D and H0A. If the extent of delocalisation in, say, the donor is increased, Eα will not change dramatically, remaining close (up to several times the intermolecular coupling) to a value of typical site energies. On the other hand, λαβ is reduced by delocalisation. Since 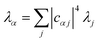 , for a state purely localised on j, λα = λj. However, in a fully delocalised state
, for a state purely localised on j, λα = λj. However, in a fully delocalised state 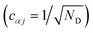 of ND identical donors (λj = λ), the reorganisation energy is decreased ND-fold:
of ND identical donors (λj = λ), the reorganisation energy is decreased ND-fold:
| | 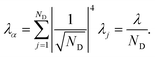 | (40) |
In general, the reduction is by a factor equal to the inverse participation ratio
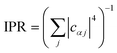
. A reduction in
λ leads to an exponential narrowing of both
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ααD
ααD(
ω) and
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββA
ββA(
ω). Therefore, because the charge-transfer rate depends on the overlap of the two spectra (
eqn (10)), the reduction in
λ will reduce the transfer rate between most pairs of eigenstates, the exception being ones where Δ
Eαβ = −
λαβ.
The presence of different processes affecting the nuclear factor means that delocalisation can have a complicated effect on the charge-transfer rate, even apart from supertransfer. Critical to the rate is the relative size of ΔEαβ and λαβ, because of the rate's exponential sensitivity to (ΔEαβ + λαβ)2. The different effects are illustrated with another example, shown in Fig. 4a, where acceptor A is strongly coupled to donor D1, whose site energy and reorganisation energy are such that the transfer from D1 to A is very slow (−ΔED1A ≫ λD1A). Another donor D2 is then introduced, but is weakly coupled to A due to its distance. A naive application of classical MT might suggest that, because D2 hardly interacts with A, it would serve to only steal charge density from D1, reducing the already slow transfer rate. Generalised MT, however, shows that it is possible to choose the energy and reorganisation energy of D2, as well as its coupling to D1, so that a coherent superposition between D1 and D2 will enhance the total transfer rate above what is possible with either D1 or D2 alone. This is true even if supertransfer is neglected, as shown in Fig. 4b and c. Indeed, for two donors, supertransfer can enhance the rate by at most a factor of two, while there is no limit to how much the nuclear factor can be enhanced by judiciously tuning ΔEαβ and λαβ to minimise (ΔEαβ + λαβ)2. This result shows that even if an unfavourable donor must be used in a donor–acceptor system (for whatever reason), another donor can be added to tune the nuclear term's contribution to the charge transfer rate.
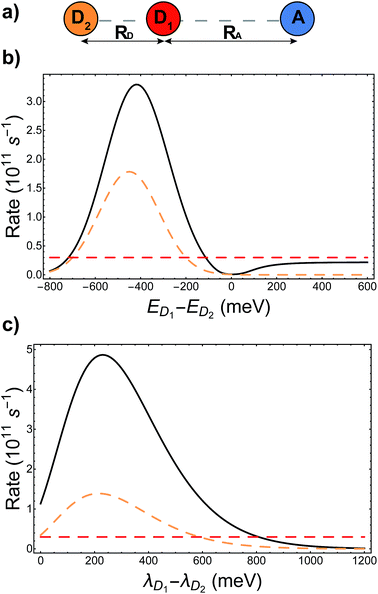 |
| | Fig. 4 Tuning energy offsets and reorganisation energies can enhance charge-transfer rates beyond what is possible with either donor site alone. (a) Two donors and one acceptor in a collinear geometry, with different colours (orange/red) indicating inequivalent donors. (b) Energetic detuning: the charge transfer rate from the aggregate to the acceptor (solid line) is compared to the rate if only D1 (dashed red) or D2 (dashed orange) were present, as a function of the energy difference between D1 and D2. Even with the effects of supertransfer removed (the aggregate rate is shown divided by the electronic supertransfer enhancement of 1.42), energetic tuning can make the aggregate transfer faster than would be possible with either donor alone. In particular, the presence of D2, which itself is weakly coupled to A, can enhance the transfer rate above the rate from D1 alone. (c) Reorganisation energies: plot as in (b), but the rates are shown as a function of the difference in reorganisation energies between D1 and D2. Here as well, adding D2 with a favourable reorganisation energy can enhance the rate above what is possible with either donor alone. Calculation parameters: VD1D2 = −37 meV, VD1A = 18 meV, VD2A = 2.5 meV, λA = 200 meV, λD1 = 150 meV, ED1 = 700 meV, EA = 0 meV, kBT = 25 meV. In addition, (b) uses λD2 = 150 meV and (c) has ED2 = 600 meV. | |
Our results also extend gMT to treat bridge-mediated charge transfer, showing that the usual equations still apply when considering delocalised aggregates. Indeed, including the effects of bridge-mediated charge transfer on gMT does not qualitatively change the effects of supertransfer and energetic tuning, except that the coherent effects depend on the geometry of the donor aggregate with respect to the first bridge molecule, and the acceptor aggregate with respect to the last. In particular, the results shown in Fig. 3 and 4 would remain unchanged if the couplings were mediated by a bridge.
4 Conclusion
The theory presented in this work is the first description of charge transfer between delocalised molecular aggregates. Therefore, we anticipate that it will have broad applications in fields where charge transfer and electronic coherence intersect, including organic photovoltaics, photosynthesis, and inorganic complexes.
The major prediction of gMT is that delocalisation within an aggregate can significantly affect charge transfer rates through two mechanisms: supertransfer and nuclear tuning. The first is a consequence of the constructive interferences of charge-transfer pathways, while the latter is the ability of a charge-transfer rate to be modified by adjusting effective energy levels and reorganisation energies by delocalising electronic states over different molecules.
Both of these predictions are suited to being tested experimentally. The simplest approach would be to construct covalently linked donors and acceptors in geometries that approximate those in Fig. 3 and 4. Tuning the couplings and energy levels through chemical modification would permit the adjustment of the parameters relevant for gMT, allowing the theory to be tested.
In this work, we restricted ourselves to deriving the delocalised generalisation of the simplest Marcus-theory formula. We are confident that many of the subsequent advances that have occurred in charge-transfer theory can also be incorporated as extensions to gMT. Indeed, our derivation is more general than the final result, and some of the approximations needed to derive an MT-like equation (e.g., high temperature, slow environmental modes) can be omitted and more general intermediate results used directly (e.g., eqn (10)–(13)). Although it is not clear whether a simple, closed-form expression could be derived, a number of improvements to gMT can be envisaged, including adiabatic charge transfer, quantum-mechanical vibrational corrections,30 coherent multistep charge transfer,31 shared intra-aggregate environmental modes,32 and off-diagonal system-environment couplings. Inspiration could also be taken from advances in MC-FRET to obtain generalisations able to treat system-environment entanglement or other parameter regimes outside the approximations used here.25,33,34
5 Appendix
Here we give the full derivation of eqn (14) and (15) from eqn (8), indexing the sum with k′′ for future convenience:| | 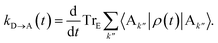 | (41) |
Since the inter-aggregate coupling HC is weak compared to all other terms in H, we take it as a perturbation. Taking H0 = H − HC, and using tildes to denote the interaction picture, we write ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) C(t) = eiH0t/ħHCe−iH0t/ħ and express
C(t) = eiH0t/ħHCe−iH0t/ħ and express 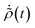 to second order in perturbation theory:
to second order in perturbation theory:
| | 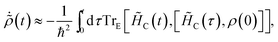 | (42) |
where [·,·] is the commutator, and Tr
E is the trace over the environment degrees of freedom. Substituting into
eqn (41),
| | 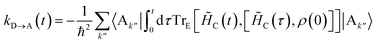 | (43) |
| | 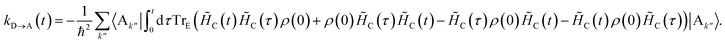 | (44) |
Since the charge is initially on the donor aggregate,
ρ(0)|A
k′′〉 = 〈A
k′′|
ρ(0) = 0, the first two terms vanish, giving
| | 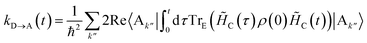 | (45) |
| | 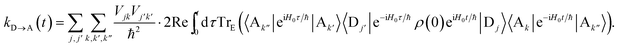 | (46) |
Using the cyclic property of the trace gives
| | 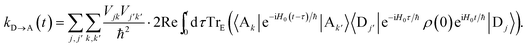 | (47) |
Defining
τ′ =
t −
τ, we can write
| | 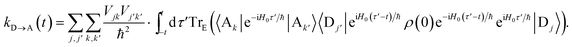 | (48) |
To simplify further, we consider the term eiH0(τ′−t)/ħρ(0)e−iH0(τ′−t)/ħ, which describes the time-evolution of the donor aggregate (because H0 induces no donor–acceptor transitions). Because the aggregate-environment coupling is much stronger than the inter-aggregate coupling, the donor aggregate will thermalise with the environment on timescales much shorter than the charge-transfer timescale. Therefore, for times t much longer than the donor thermalisation time (but much shorter than the charge-transfer time), we can consider the long-time limit,
| | 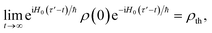 | (49) |
where for a large, weakly coupled environment, the state
ρth =
ρD ⊗
ρA, of donor and acceptor aggregates independently thermalised with their own environments, is independent of
ρ(0). In this limit, we may also extend the limits of integration in
eqn (48) to infinity to give a time-independent rate:
| | 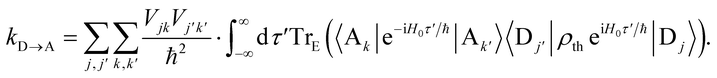 | (50) |
Writing HD = H0D + HDE + HED and HA = H0A + HAE + HEA and using Plancherel's theorem, we can rewrite eqn (50) as
| | 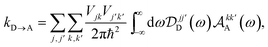 | (51) |
| | 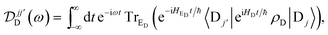 | (52) |
| | 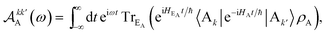 | (53) |
where we have renamed
τ′ to
t. Changing to the aggregate basis,
eqn (51) becomes
| | 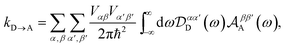 | (54) |
| | 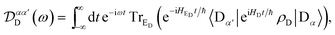 | (55) |
| | 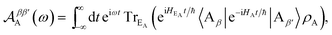 | (56) |
Eqn (54) reduces to eqn (10) if ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) αα′D and
αα′D and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ′A can be assumed to be diagonal in the aggregate basis. In general, this is not the case, because HDE and HAE do not commute with H0D and H0A respectively. However, it is an appropriate approximation in the limit, assumed here, of weak system-environment coupling, where the environment does not significantly perturb the thermal equilibrium of the system. The same approximation was considered and discussed in detail in the context of MC-FRET,24,25 where it can be used to reduce the excitonic analogue of eqn (54) to a diagonal version. Of course, eqn (54) can be used directly, at the cost of intuitive parallels with MT being obscured.
ββ′A can be assumed to be diagonal in the aggregate basis. In general, this is not the case, because HDE and HAE do not commute with H0D and H0A respectively. However, it is an appropriate approximation in the limit, assumed here, of weak system-environment coupling, where the environment does not significantly perturb the thermal equilibrium of the system. The same approximation was considered and discussed in detail in the context of MC-FRET,24,25 where it can be used to reduce the excitonic analogue of eqn (54) to a diagonal version. Of course, eqn (54) can be used directly, at the cost of intuitive parallels with MT being obscured.
Eqn (12) and (13) can be evaluated in the particular case of a thermalised environment of independent harmonic oscillators to yield eqn (14) and (15). Assuming that ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) αα′D and
αα′D and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ′A are diagonal is equivalent to assuming that the electronic Hamiltonians commute with the environmental ones, meaning that exp(iHDt/ħ) = exp(iH0Dt/ħ)exp(i(HDE + HED)t/ħ), so that eqn (12) becomes
ββ′A are diagonal is equivalent to assuming that the electronic Hamiltonians commute with the environmental ones, meaning that exp(iHDt/ħ) = exp(iH0Dt/ħ)exp(i(HDE + HED)t/ħ), so that eqn (12) becomes
| | 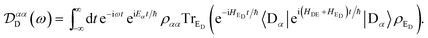 | (57) |
The Hamiltonian
HDE +
HED can be diagonalised using the polaron transformation, which describes the displacement of the environment oscillators by the presence of a charge:
| | 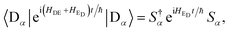 | (58) |
where
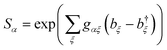
. Using this fact in
eqn (57) gives
| |  | (59) |
In eqn (59), the contributions of different aggregate eigenstates are explicitly uncoupled, meaning that the equation takes, for a particular α, the same form that occurs in the derivation of ordinary, single-site MT. Therefore, the trace can be evaluated for a harmonic environment using standard techniques (e.g., Section 6.8.1 of ref. 3), giving eqn (14).
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
We thank Tom Stace and the UQ Node EQuS Theory Group for helpful comments on the manuscript. We were supported by the Westpac Bicentennial Foundation through a Westpac Research Fellowship, by the Australian Research Council through a Discovery Early Career Researcher Award (DE140100433) and the Centre of Excellence for Engineered Quantum Systems (CE110001013), and by an Australian Government Research Training Program (RTP) Scholarship.
References
- R. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS.
-
V. May and O. Kühn, Charge and Energy Transfer in Molecular Systems, Wiley-VCH, Weinheim, Germany, 3rd edn, 2011 Search PubMed.
-
J. Jortner and M. Bixon, Advances in Chemical Physics, 1999, vol. 106–107 Search PubMed.
- S. Few, J. M. Frost and J. Nelson, Phys. Chem. Chem. Phys., 2015, 17, 2311–2325 RSC.
-
A. Köhler and H. Bässler, Electronic Processes in Organic Semiconductors: An Introduction, John Wiley & Sons, 2015 Search PubMed.
- J. P. Allen and J. C. Williams, FEBS Lett., 1998, 438, 5–9 CrossRef CAS PubMed.
-
R. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley Blackwell, Chichester, UK, 2nd edn, 2014 Search PubMed.
- D. M. D'Alessandro and F. R. Keene, Chem. Rev., 2006, 106, 2270–2298 CrossRef PubMed.
- D. M. D'Alessandro, J. R. R. Kanga and J. S. Caddy, Aust. J. Chem., 2011, 64, 718 CrossRef.
- N. S. Hush, J. Chem. Phys., 1958, 28, 962–972 CrossRef CAS.
- N. S. Hush, Trans. Faraday Soc., 1961, 57, 557 RSC.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS.
- D. V. Matyushov and G. A. Voth, J. Phys. Chem. A, 2000, 104, 6470–6484 CrossRef CAS.
- J. E. Subotnik, S. Yeganeh, R. J. Cave and M. A. Ratner, J. Chem. Phys., 2008, 129, 244101 CrossRef PubMed.
- N. S. Hush, Prog. Inorg. Chem., 1967, 8, 12 Search PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966 CrossRef CAS.
- V. Levich and R. Dogonadze, Dokl. Akad. Nauk SSSR, 1959, 124, 123–126 CAS.
- H. Sumi, J. Phys. Chem. B, 1999, 103, 252–260 CrossRef CAS.
- H. Sumi, Chem. Rec., 2001, 1, 480–493 CrossRef CAS PubMed.
- G. Scholes, X. Jordanides and G. Fleming, J. Phys. Chem. B, 2001, 105, 1640–1651 CrossRef CAS.
- S. Baghbanzadeh and I. Kassal, J. Phys. Chem. Lett., 2016, 7, 3804–3811 CrossRef CAS PubMed.
- S. Baghbanzadeh and I. Kassal, Phys. Chem. Chem. Phys., 2016, 18, 7459–7467 RSC.
- S. Jang, M. Newton and R. Silbey, Phys. Rev. Lett., 2004, 92, 218301 CrossRef PubMed.
- J. Ma and J. Cao, J. Chem. Phys., 2015, 142, 094106 CrossRef PubMed.
- L. Cleary and J. Cao, New J. Phys., 2013, 15, 125030 CrossRef.
-
A. Nitzan, Chemical Dynamics in Condensed Phases, Oxford University Press, Oxford, UK, 2006 Search PubMed.
- S. Jang and Y.-C. Cheng, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 84–104 CrossRef CAS.
- A. Fruchtman, R. Gómez-Bombarelli, B. W. Lovett and E. M. Gauger, Phys. Rev. Lett., 2016, 117, 203603 CrossRef PubMed.
- J. Ulstrup and J. Jortner, J. Chem. Phys., 1975, 63, 4358–4368 CrossRef CAS.
- A. Kuznetsov and J. Ulstrup, Electrochim. Acta, 2000, 45, 2339–2361 CrossRef CAS.
- T. Renger and R. A. Marcus, J. Chem. Phys., 2002, 116, 9997–10019 CrossRef CAS.
- J. Ma, J. Moix and J. Cao, J. Chem. Phys., 2015, 142, 094107 CrossRef PubMed.
- J. M. Moix, J. Ma and J. Cao, J. Chem. Phys., 2015, 142, 094108 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a and
Ivan
Kassal
a and
Ivan
Kassal
 *ab
*ab
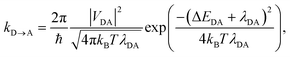
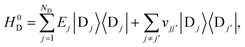
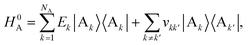
 should be read as a sum over only the donor sites, and
should be read as a sum over only the donor sites, and  only over acceptors. The donor and acceptor molecules have site energies Ej and Ek, and intra-aggregate couplings are vjj′ (in the donor) and vkk′ (in the acceptor).
only over acceptors. The donor and acceptor molecules have site energies Ej and Ek, and intra-aggregate couplings are vjj′ (in the donor) and vkk′ (in the acceptor).
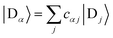 and
and 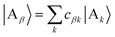 , with energies Eα and Eβ. Similar to site indices j and k, index α is consistently used to denote only donor eigenstates, and β acceptor eigenstates.
, with energies Eα and Eβ. Similar to site indices j and k, index α is consistently used to denote only donor eigenstates, and β acceptor eigenstates.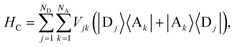
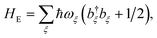
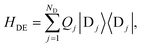
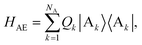
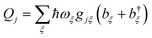 , where gjξ is the dimensionless coupling of the ξth environment mode to the charged jth donor molecule, relative to the uncharged state. Qk is defined analogously. The assumption of a local environment means that, for a fixed ξ, only one of gjξ can be non-zero.
, where gjξ is the dimensionless coupling of the ξth environment mode to the charged jth donor molecule, relative to the uncharged state. Qk is defined analogously. The assumption of a local environment means that, for a fixed ξ, only one of gjξ can be non-zero.
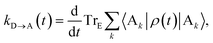
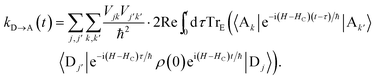
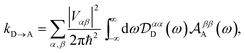
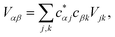
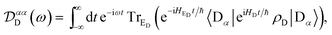
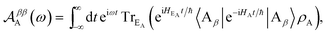
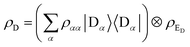 , where the electronic population distribution is
, where the electronic population distribution is 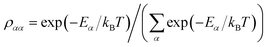 and the thermal environment is ρED = exp(−HED/kBT)/TrED(exp(−HED/kBT)). The thermal state of the acceptor is ρA = ρEA = exp(−HEA/kBT)/TrEA(exp(−HEA/kBT)). Finally, we have also written HD = H0D + HDE + HED, and similarly for HA.
and the thermal environment is ρED = exp(−HED/kBT)/TrED(exp(−HED/kBT)). The thermal state of the acceptor is ρA = ρEA = exp(−HEA/kBT)/TrEA(exp(−HEA/kBT)). Finally, we have also written HD = H0D + HDE + HED, and similarly for HA.
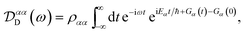
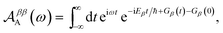
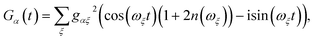
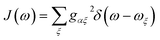 goes rapidly to zero beyond a cut-off frequency ωc. Then, we first assume the high-temperature limit kBT ≫ ħωc, so that n(ν) ≈ kBT/ħν ≫ 1, giving
goes rapidly to zero beyond a cut-off frequency ωc. Then, we first assume the high-temperature limit kBT ≫ ħωc, so that n(ν) ≈ kBT/ħν ≫ 1, giving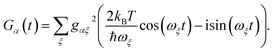
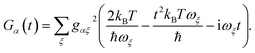
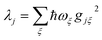 , and similarly for the acceptor sites, λk. The change of basis
, and similarly for the acceptor sites, λk. The change of basis 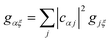 gives the reorganisation energy of aggregate eigenstates
gives the reorganisation energy of aggregate eigenstates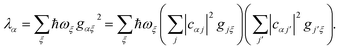
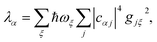
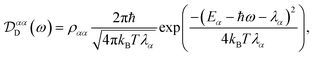
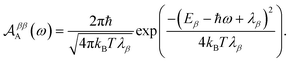
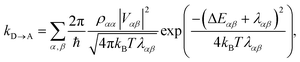
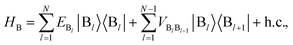
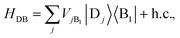
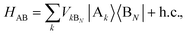
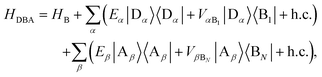
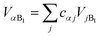 and
and 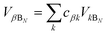 .
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αdα, 0, …, 0, VBNβdβ), using Green's function GB = (IEDBA − HB)−1.
αdα, 0, …, 0, VBNβdβ), using Green's function GB = (IEDBA − HB)−1.
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) αβdβ = 0,
αβdβ = 0,![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) βαdα = 0,
βαdα = 0,![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is the effective coupling between the donor and acceptor eigenstates, mediated by the bridge,
is the effective coupling between the donor and acceptor eigenstates, mediated by the bridge,![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) αβ = VαB1G1NBVBNβ.
αβ = VαB1G1NBVBNβ.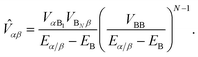
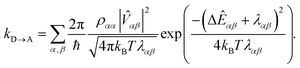
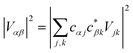 includes a coherent sum involving electronic amplitudes in each of the donor and acceptor aggregates, allowing both constructive and destructive interference to affect the transfer rate. If the interferences is constructive, leading to enhanced transfer rates, we call the effect supertransfer, and if it is destructive, subtransfer, borrowing terminology from the similar problem of MC-FRET.28
includes a coherent sum involving electronic amplitudes in each of the donor and acceptor aggregates, allowing both constructive and destructive interference to affect the transfer rate. If the interferences is constructive, leading to enhanced transfer rates, we call the effect supertransfer, and if it is destructive, subtransfer, borrowing terminology from the similar problem of MC-FRET.28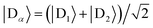 state. The donors are coupled to a single acceptor A with strengths VD1A and VD2A respectively. If we were to apply Marcus theory between each donor and the acceptor independently, we would expect a transfer rate proportional to the square of each coupling,
state. The donors are coupled to a single acceptor A with strengths VD1A and VD2A respectively. If we were to apply Marcus theory between each donor and the acceptor independently, we would expect a transfer rate proportional to the square of each coupling, 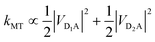 , with the factors of 1/2 indicating the population on each donor. However, this naive approach fails to include coherent effects of the superposition. These are treated correctly by gMT, which predicts a transfer rate of
, with the factors of 1/2 indicating the population on each donor. However, this naive approach fails to include coherent effects of the superposition. These are treated correctly by gMT, which predicts a transfer rate of 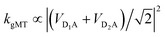 . The presence of rate-enhancement due to supertransfer is apparent if VD1A = VD2A, which implies kgMT = 2kMT. In contrast, if the two transfer pathways interfere destructively, VD1A = −VD2A, gMT predicts subtransfer with kgMT = 0. We refer to states that enhance the charge-transfer rate through supertransfer as bright, while those that retard it as dark, in analogy to the terms used in the literature on superradiance.29 The relative populations of the bright and dark states will strongly influence the rate of charge transfer in delocalised systems.
. The presence of rate-enhancement due to supertransfer is apparent if VD1A = VD2A, which implies kgMT = 2kMT. In contrast, if the two transfer pathways interfere destructively, VD1A = −VD2A, gMT predicts subtransfer with kgMT = 0. We refer to states that enhance the charge-transfer rate through supertransfer as bright, while those that retard it as dark, in analogy to the terms used in the literature on superradiance.29 The relative populations of the bright and dark states will strongly influence the rate of charge transfer in delocalised systems.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(ΔEαβ + λαβ)2/4kBTλαβ), has several features in common with ordinary MT. For example, for a fixed λαβ, the nuclear factor is maximised when −ΔEαβ = λαβ, and the inverted regime is possible when −ΔEαβ > λαβ. However, the nuclear term also possesses features not predicted by ordinary MT, allowing for both enhancement or retardation of the transfer rate.
exp(−(ΔEαβ + λαβ)2/4kBTλαβ), has several features in common with ordinary MT. For example, for a fixed λαβ, the nuclear factor is maximised when −ΔEαβ = λαβ, and the inverted regime is possible when −ΔEαβ > λαβ. However, the nuclear term also possesses features not predicted by ordinary MT, allowing for both enhancement or retardation of the transfer rate.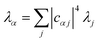 , for a state purely localised on j, λα = λj. However, in a fully delocalised state
, for a state purely localised on j, λα = λj. However, in a fully delocalised state 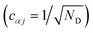 of ND identical donors (λj = λ), the reorganisation energy is decreased ND-fold:
of ND identical donors (λj = λ), the reorganisation energy is decreased ND-fold: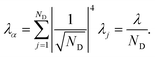
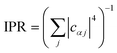 . A reduction in λ leads to an exponential narrowing of both
. A reduction in λ leads to an exponential narrowing of both ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ααD(ω) and
ααD(ω) and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββA(ω). Therefore, because the charge-transfer rate depends on the overlap of the two spectra (eqn (10)), the reduction in λ will reduce the transfer rate between most pairs of eigenstates, the exception being ones where ΔEαβ = −λαβ.
ββA(ω). Therefore, because the charge-transfer rate depends on the overlap of the two spectra (eqn (10)), the reduction in λ will reduce the transfer rate between most pairs of eigenstates, the exception being ones where ΔEαβ = −λαβ.
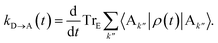
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) C(t) = eiH0t/ħHCe−iH0t/ħ and express
C(t) = eiH0t/ħHCe−iH0t/ħ and express 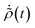 to second order in perturbation theory:
to second order in perturbation theory: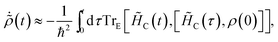
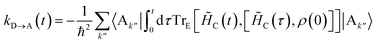
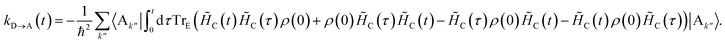
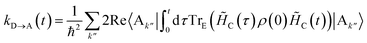
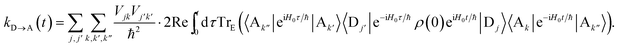
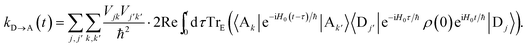
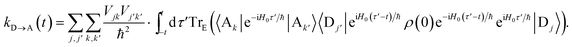
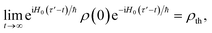
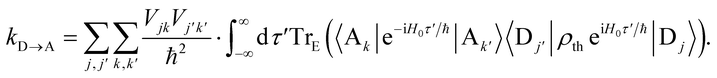
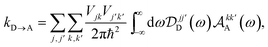
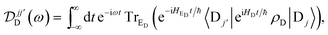
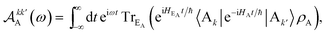
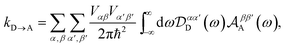
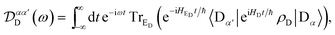
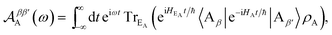
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) αα′D and
αα′D and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ′A can be assumed to be diagonal in the aggregate basis. In general, this is not the case, because HDE and HAE do not commute with H0D and H0A respectively. However, it is an appropriate approximation in the limit, assumed here, of weak system-environment coupling, where the environment does not significantly perturb the thermal equilibrium of the system. The same approximation was considered and discussed in detail in the context of MC-FRET,24,25 where it can be used to reduce the excitonic analogue of eqn (54) to a diagonal version. Of course, eqn (54) can be used directly, at the cost of intuitive parallels with MT being obscured.
ββ′A can be assumed to be diagonal in the aggregate basis. In general, this is not the case, because HDE and HAE do not commute with H0D and H0A respectively. However, it is an appropriate approximation in the limit, assumed here, of weak system-environment coupling, where the environment does not significantly perturb the thermal equilibrium of the system. The same approximation was considered and discussed in detail in the context of MC-FRET,24,25 where it can be used to reduce the excitonic analogue of eqn (54) to a diagonal version. Of course, eqn (54) can be used directly, at the cost of intuitive parallels with MT being obscured.![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) αα′D and
αα′D and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ′A are diagonal is equivalent to assuming that the electronic Hamiltonians commute with the environmental ones, meaning that exp(iHDt/ħ) = exp(iH0Dt/ħ)exp(i(HDE + HED)t/ħ), so that eqn (12) becomes
ββ′A are diagonal is equivalent to assuming that the electronic Hamiltonians commute with the environmental ones, meaning that exp(iHDt/ħ) = exp(iH0Dt/ħ)exp(i(HDE + HED)t/ħ), so that eqn (12) becomes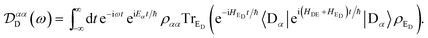
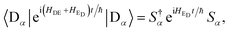
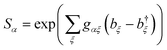 . Using this fact in eqn (57) gives
. Using this fact in eqn (57) gives