Open Access Article
Open Access ArticleUltrafast interligand electron transfer in cis-[Ru(4,4′-dicarboxylate-2,2′-bipyridine)2(NCS)2]4− and implications for electron injection limitations in dye sensitized solar cells†
Belinda
Pettersson Rimgard
a,
Jens
Föhlinger
 a,
Jonas
Petersson
a,
Marcus
Lundberg
a,
Jonas
Petersson
a,
Marcus
Lundberg
 ab,
Burkhard
Zietz
a,
Ann Marie
Woys
c,
Stephen A.
Miller
c,
Michael R.
Wasielewski
ab,
Burkhard
Zietz
a,
Ann Marie
Woys
c,
Stephen A.
Miller
c,
Michael R.
Wasielewski
 *c and
Leif
Hammarström
*c and
Leif
Hammarström
 *a
*a
aDepartment of Chemistry – Ångström Laboratory, Uppsala University, Box 523, SE75120 Uppsala, Sweden. E-mail: leif.hammarstrom@kemi.uu.se
bDepartment of Biotechnology, Chemistry and Pharmacy, Università di Siena, Via A. Moro 2, 53100 Siena, Italy
cDepartment of Chemistry, Argonne-Northwestern Solar Energy Research (ANSER) Center, Northwestern University, Evanston, Illinois 60208-3113, USA. E-mail: m-wasielewski@northwestern.edu
First published on 13th August 2018
Abstract
Interligand electron transfer (ILET) of the lowest metal-to-ligand charge transfer (MLCT) state of N712 (cis-[Ru(dcb)2(NCS)2]4−, where dcb = 4,4′-dicarboxylate-2,2′-bipyridine) in a deuterated acetonitrile solution has been studied by means of femtosecond transient absorption anisotropy in the mid-IR. Time-independent B3LYP density functional calculations were performed to assign vibrational bands and determine their respective transition dipole moments. The transient absorption spectral band at 1327 cm−1, assigned to a symmetric carboxylate stretch, showed significant anisotropy. A rapid anisotropy increase (τ1 ≈ 2 ps) was tentatively assigned to vibrational and solvent relaxation, considering the excess energy available after the excited singlet–triplet conversion. Thereafter, the anisotropy decayed to zero with a time constant τ2 ≈ 240 ps, which was assigned to the rotational correlation time of the complex in deuterated acetonitrile. No other distinctive changes to the anisotropy were observed and the amplitude of the slow component at time zero agrees well with that predicted for a random mixture of MLCT localization on either of the two dcb ligands. The results therefore suggest that MLCT randomization over the two dcb ligands occurs on the sub-ps time scale. This is much faster than proposed by previous reports on the related N3 complex [Benkö et al., J. Phys. Chem. B, 2004, 108, 2862, and Waterland et al., J. Phys. Chem. A, 2001, 105, 4019], but in agreement with that found by Wallin and co-workers [J. Phys. Chem. A, 2005, 109, 4697] for the [Ru(bpy)3]2+ (bpy = 2,2′-bipyridine) complex. This suggests that electron injection from the excited dye into TiO2 in dye-sensitized solar cells is not limited by ILET.
1 Introduction
Dye sensitized solar cells (DSSCs) have since their introduction in the early 90's been viewed as promising devices for solar energy conversion into renewable electricity and more recently also fuels.1–3 The well-known, high performance DSSCs have often utilized ruthenium based dyes, where N3 (Ru(dcb)2(NCS)2, dcb = 4,4′-dicarboxylic acid-2,2′-bipyridine) and its derivative N719 (Fig. 1) have been for many years the gold standard.1 For that reason their excited state dynamics, such as the electron injection into semiconductors, have received much attention.4–22 The excitation of this class of ruthenium based dyes forms a MLCT state where the charge density transfers from the Ru center to the dcb ligands.23–25 For N3 and N719 the HOMO has a significant density on NCS ligands making the transition a mixed [Ru/NCS]-to-[dcb] charge transfer.26,27 Whether the MLCT excitation is localized on one ligand or is delocalized over multiple ligands has been a long debated controversy. In [Ru(bpy)3]2+ intersystem crossing to a triplet MLCT state occurs in less than 100 fs,28–34 and several studies suggest that a 3MLCT state localized on one bpy ligand is formed on a sub-ps time scale.28,29,35 It is often believed that solvent stabilization is the cause for this localization on a single ligand. The localized MLCT state may then undergo interligand electron transfer (ILET), i.e. charge transfer between the two dcb ligands in the N3 family. ILET would cause a random mixture of charge localized MLCT states to form, independent on which ligand the initial excitation localized the charge. This process is a much less studied topic with little consensus on its time scale (see below).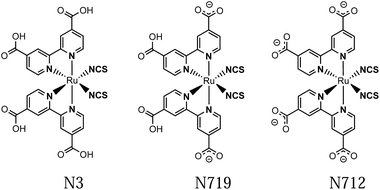 | ||
| Fig. 1 Structures of the N3 dye and its semi- and fully deprotonated derivatives: N719 and N712. This study concerns N712, which was obtained as the (TBA)4 salt. | ||
Many studies of N3 and its derivatives, including experiments with a complete electrolyte mimicking the conditions of a complete solar cell, have shown predominantly ultrafast (sub-ps) electron injection into TiO2.4–16,19,20 Meanwhile, others report exclusively, or predominantly, slower injection, on the time scale of ps to ns.17,18,21,36,37 If only one of the dcb ligands binds to TiO2, and ILET is slow compared to electron injection, then ILET may become a rate limiting factor. Other undesirable quenching processes could then compete with injection, consequently lowering the efficiency of the cell. One study reported that ca. 60% of the injection occurred with a 50 fs time constant, suggesting injection from the 1MLCT state, while ca. 40% injection occurred from the thermalized 3MLCT state with time constants in the ps regime.10 It was also suggested that the slow injection occurred in dyes where the initial excitation formed a localized MLCT state on a non-binding dcb ligand, and that the injection rate was limited by slow ILET.15 In general, slow ILET could limit the function of molecular assemblies that are based on electron transfer from Ru-polypyridine dyes.
A complicating factor for direct measurements of the ILET process in solution is that structurally identical ligands give identical spectroscopic signals in isotropic measurements. One readily available technique to circumvent this problem is anisotropic (polarized) transient absorption measurements. In a pump-probe experiment, the sample is excited and monitored with polarized light, and signals are recorded for both parallel and perpendicular polarizations of the two beams. These signals are used to construct the anisotropy, for which the extreme values for a random orientation of the molecules are given by the excited and probed transition dipole moments being either fully parallel (0.4) or perpendicular (−0.2) to each other. ILET, as well as the rotation of the entire molecule, will randomize the direction of the localized MLCT transition dipole moment relative to the polarization of the pump light and the observed anisotropy decays towards zero (see the more detailed description in Section 3.1).
ILET in [Ru(bpy)3]2+,31,38–42 [Os(bpy)3]2+,43–46 and other homoleptic and heteroleptic metal-polypyridyl complexes47–52 have been studied, both with spectroscopic measurements (isotropic as well as anisotropic) and with calculations. An ILET time constant of 47 ps and 130 ps, respectively, was reported for [Ru(bpy)3]2+ and [Os(bpy)3]2+ in MeCN.38 Further studies however contradict these results. A study on the osmium complex conducted by Shaw et al. showed a much more rapid randomization of the localized MLCT state between three bpy ligands, with a time constant of 8 ps.45,46 Similarly for the ruthenium complex, Wallin et al. reported a sub-ps time scale for ILET, before complete thermal relaxation (ILET from hot vibrational states is here referred to as ILETH), possibly already in the 1MLCT state.39 The sub-ps randomization for [Ru(bpy)3]2+ has been confirmed in a more recent paper by Stark et al. by anisotropic as well as isotropic measurements.42 They further studied heteroleptic complexes [Ru(bpy)3−n(phen)n]2+ (n = 1, 2; phen = 1,10-phenanthroline), and found that ILET from a fully thermalized MLCT state (ILETT) occurs on a 10 ps time scale, as shown by the rise of the isotropic absorption of the reduced bpy ligand. The explanation for the two observed ILET time constants is that the excess energy available at early times, before significant losses by vibrational relaxation, allows ILETH to occur as an activationless process between the degenerate MLCT states leading to a sub-ps time constant. As the MLCT state thermalizes, the ILETT barrier crossing becomes activated which results in a slower process (∼10 ps).
To our knowledge there have only been three reported studies of ILET in N3, which have been made by means of femtosecond transient absorption anisotropy measurements in the visible region, probing the electronic transitions of the molecule.15,53,54 All these studies assumed that excitation creates an initial excited state that is localized on one dcb ligand. Thus, with an initial photoselection of a localized MLCT transition, the anisotropy will decrease as ILET randomizes the MLCT over all ligands. On this basis, Waterland et al. reported an ILET time constant of 1.5 ns in methanol,53 which is much slower than the reported values for [Os(bpy)3]2+ and [Ru(bpy)3]2+ above. This depolarization mechanism occurred in parallel with molecular rotation, reported as rrot = 400 ps. The value for ILET of 1.5 ns is thus strongly dependent on the accuracy of the rotational correlation lifetime of 400 ps. Benkö et al. reported an ILET time constant of about 20 ps,15 in sharp contrast to the 1.5 ns obtained by Waterland. The results by Benkö et al. were based on a TA anisotropy value that increased in magnitude, from −0.07 to −0.09 at 850 nm, during the proposed ILET process. At 850 nm there is neither ground state bleaching nor stimulated emission, and the randomization of the MLCT state between identical ligands can only lead to a loss in the magnitude of the ESA anisotropy signal, never an increase. Instead it is likely that 850 nm is at the isosbestic point of two ESA signals with transition dipole moments in different directions and that their relative TA magnitudes change on the time scale of ca. 10 ps because of vibrational and solvent relaxation. Indeed, relaxation processes in Ru(II)-polypyridyl complexes are typically observed on this time scale by the resulting changes in the isotropic spectra.29,39,53 While the result by Waterland et al. therefore seems to be the preferable of the two studies, the reported ILET is unexpectedly slow compared to the results for [Ru(bpy)3]2+ and [Os(bpy)3]2+. Probing the electronic transitions in the visible region has the disadvantage that there are several overlapping absorption bands, and the direction of the transition dipole moments is not always clear. Here we therefore set out to probe the vibrational transitions in the IR region that are narrow and less congested. There has been no previously reported study of ILET in N3-type dyes that probes the vibrational transitions. The electron density on the dcb ligand should affect the carboxylate vibration, because an increased electron density is expected to downshift the vibrational frequency. The carboxylate IR bands and their anisotropic transient absorption should therefore be good reporters on the localization of the MLCT excitation.
2 Materials and methods
2.1 Vibrational frequencies and prediction of the anisotropy
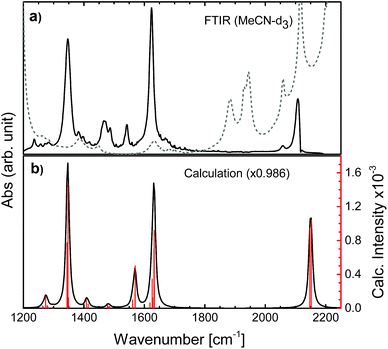
Time-independent DFT calculations were performed to establish the magnitude of the anisotropy associated with the initial charge localized MLCT state (localized) compared to that of the random mixture of the two possible MLCT states (randomized). The optimization and frequency calculations were performed for both the singlet ground state (S0) and the first triplet state (T1) using Gaussian 09 (revision D.01).55 The calculations were performed using the B3LYP functional56–59 and the DGDZVP basis set.60,61 The B3LYP functional has been used previously for similar metal centred systems62–64 with success and the basis set was deemed sufficient based on the computational cost and the incorporation of polarized double-ζ functions which are essential for the orbital mixing and response to the molecular environment. To incorporate solvation effects the polarizable continuum model65,66 (PCM) was used for both states. The calculations excluded symmetry to avoid the rotation of the molecule to simplify the analysis, and the vibrational transition dipole moment derivatives were determined. The electronic transition dipole moment was estimated by a vector bisecting one of the dcb ligands running through the metal center. The resulting FTIR spectra of the singlet and the triplet state were simulated from the frequency calculations using GaussView 5.0.8, a bandwidth of 12 cm−1 (FWHM) and a step size of 3 cm−1, to mimic the conditions of the experimental results and resolution.2.2 Femtosecond transient absorption spectroscopy with an IR-probe
The N712 sample was used as received (Solaronix, Ruthenizer 535-4TBA). The absorbance at the excitation wavelength of 650 nm was ca. 0.3. The UV-vis is shown in Fig. S6† and the FTIR spectrum in Fig. 2 and S7.† The sample path length was 500 μm, set by using a Teflon spacer between two 2 mm thick CaF2 windows (Crystran). All experiments were done in deuterated acetonitrile (MeCN-d3) purchased from Sigma-Aldrich without further purification.Femtosecond visible pump and mid-IR probe transient absorption anisotropy spectroscopy was performed both at Uppsala University (UU) and at Northwestern University (NU). The 1.5 mJ, 45 fs output of a 3(UU)/1(NU) kHz Ti:sapphire amplifier (Libra-USP-HE, Coherent/Spitfire Pro, Spectra-Physics) was split into two separate commercial optical parametric amplifiers (TOPAS Prime/TOPAS-C, Light Conversion), which generates the visible pump (650 nm) and the mid-IR probe (1000–4000 cm−1). Prior to reaching the sample, the probe beam was split into a probe and a reference beam using a wedged ZnSe window. The pump beam was focused onto the sample forming a ∼230/70 μm spot size and its intensity was attenuated to approximately 1 mW. At UU only the probe passes through the sample, while at NU both the probe and the reference do; however only the probe interacts with the photoexcited volume. The probe and reference beams were dispersed by using a commercial monochromator (iHR320/Triax 190, HORIBA Jobin Yvon) equipped with a 50/75 grooves per mm grating and detected on a dual array, 2 × 64 pixel mercury cadmium telluride detector (InfraRed Associates, Inc). The instrument response function for the experiments was approximately 300 fs. Anisotropy experiments were performed by running two separate measurements: parallel and perpendicular pump and probe polarizations altered by the use of a half-wave plate. To avoid possible artefacts due to the ZnSe wedge or the spectrometer, the polarization of the pump beam was rotated between experiments rather than the probe. The absence of sample degradation was confirmed by repeated steady-state UV-vis and FTIR measurements. Amplitude rescaling was performed in order to normalize parallel and perpendicular intensities at longer times (>2 ns), in agreement with previously reported procedures.53
3 Results and discussion
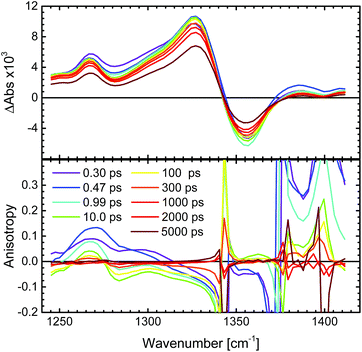
The N3 complex and its semi- and fully deprotonated forms N719 and N712 (see Fig. 1) all have strong ground state IR absorptions as reported.68–70 In the IR region, however, the solvent interference must be kept low. The mentioned ILET studies of the N3 family have been performed in acetonitrile, methanol and ethanol, which have strong overlapping absorbance in the desired IR region. This problem was circumvented by regarding fully deuterated solvents, of which MeCN-d3 showed the smallest disturbance in the considered carboxylate stretching regions and was therefore utilized.71 In order to obtain a stronger and cleaner IR band as well as to achieve a large transient anisotropy, we chose to study the more symmetrical complex N712 with four carboxylates rather than carboxylic acids as in N3. The interpretation of the experimental results was aided by calculations of the vibrational bands and their respective transition dipole moments in the ground state as well as the lowest triplet state. Thus, we predict the anisotropy for both the MLCT state that remains on the photoselected ligand and for the state where the charge is randomly distributed on either of the two dcb ligands.3.1 Anisotropy definition
The anisotropy of a transient absorption spectral band can be predicted from the relative angle between the transition dipole moment of excitation and the probed transitions according to eqn (1).72 The cosine of the angle between the vectors (here excitation and vibrational transition dipole moments) can be replaced by the dot product of the normalized vectors by using basic linear algebra.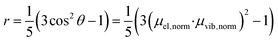 | (1) |
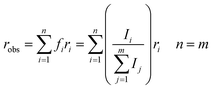 | (2) |
From eqn (1) and (2), the initial anisotropies (r0) for the localized and the randomized MLCT state were predicted. The anisotropy of the localized MLCT state originating from the initial photoselection is calculated from eqn (1) by the dot product of the dipole moment vectors determined computationally. The prediction of the anisotropy for the randomized MLCT state requires the use of eqn (2), which includes weighting of the two sources of anisotropy. Here the intensities of the corresponding carboxylate stretches on the two dcb ligands were used.
The experimental transient anisotropy is calculated from the transient absorption measurements according to eqn (3).
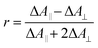 | (3) |
When several overlapping absorption bands are present the observed anisotropy will be the sum of all contributing anisotropies weighted by their corresponding ΔA values (isotropic spectrum), in accordance with eqn (2). Generally, the transient absorption anisotropy is given by eqn (4), where the contributions from ground state bleaching (GSB), excited state absorption (ESA) and stimulated emission (SE) are shown explicitly.31
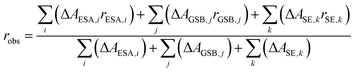 | (4) |
In the IR transient spectrum there is no SE (ΔASE = 0) and GSB is usually well separated from the ESA (compare to Fig. 3 and 6). Note that close to isosbestic points between the GSB and ESA, the denominator in eqn (4) goes towards zero, and the anisotropy goes towards infinity. This is observed in the present experiments (Fig. 6), as well as in earlier studies in both visible and IR regions.39,73 At later times the anisotropy will decrease towards zero as the molecule rotates with a rate depending on the used solvent.
3.2 Computational section
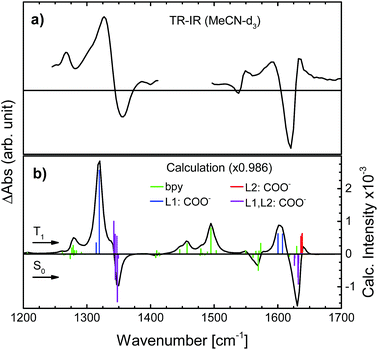
To determine the active vibrational modes and their transition dipole moments, time-independent DFT calculations were performed for the singlet ground state and the first triplet excited state. It is assumed that the observed anisotropy is associated with the 3MLCT rather than the 1MLCT, due to rapid (<100 fs) intersystem crossing.28–34Considering that the observed anisotropy is the sum of all contributing anisotropies in the system, having fewer overlapping bands simplifies the analysis. The determination of the lowest triplet excited state vibrational frequencies allowed for the construction of the difference spectrum which is relevant to establish regions of fewer overlapping bands between the two electronic states (S0 and T1). The observed transient signals in the symmetrical stretch region of N712 as well as the asymmetric stretch are compared to the calculated difference spectrum (see Fig. 3). According to the calculations, the carboxylate stretches show dominant peaks in the excited state just like in the ground state (Fig. 3). In Fig. 3a, the excited state absorption in the region of the ground state symmetric COO− stretch shows an intense peak at 1327 cm−1, a downshift by 20 cm−1 compared to the experimental ground state FTIR. This peak is assigned, with additional computational support, to the symmetric COO− stretch in the 3MLCT state. The peak at 1590 cm−1 in the transient spectrum, assigned to the asymmetric stretch, is downshifted by roughly 30 cm−1 compared to the FTIR spectrum. In addition to these ESA peaks, there is one located around 1267 cm−1 experimentally and 1279 cm−1 computationally. This peak and several other peaks in between 1400 and 1575 cm−1 are associated with the vibrations of the bpy rings. In these regions many overlapping bands make them unsuitable for further analysis. We primarily focus on the carboxylate symmetric stretch due to its intense excited state absorption with little overlap between neighboring peaks, relative to that of the asymmetric stretch.
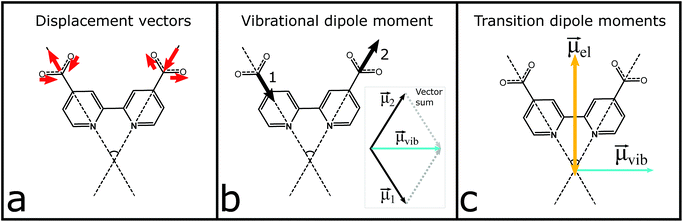
The vibrational modes of the S0 and T1 state in the carboxylate stretching regions can be found in the ESI.† The transient 1327 cm−1 vibration has been associated with the computed vibrational mode 1319 cm−1 (scaled, see the ESI†). The mode involves both carboxylates on the formally reduced dcb ligand on which the MLCT state is localized. The carboxylates stretch symmetrically, but with an anti-phase as illustrated in Fig. 4. This greatly influences the sign of the anisotropy, because the resulting vibrational transition dipole moment depends on the individual carboxylate vibrations as shown in Fig. 4b. The resulting transition dipole moment of the anti-phase symmetric stretch is shown as a blue arrow in Fig. 4c and in Fig. 5. The corresponding vibrational dipole moment of the carboxylates on the spectator dcb ligand, L2, is shown in Fig. 5 in magenta. The ESA band for this mode is shifted to higher wavenumbers (Fig. 3) and does not interfere with the analysis (see the ESI† for mode 1347 cm−1, scaled). The mode has a much lower intensity compared to the L1 centered symmetric stretch and additionally shows some activity even on the L1 bpy-ring.
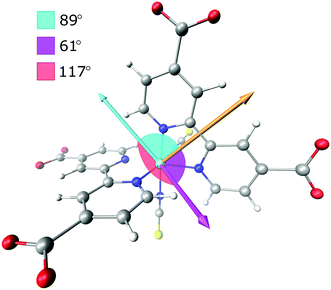
The normalized electronic and vibrational transition dipole moments were used to determine the anisotropy for the localized and the randomized MLCT state. The vectors and the calculations are given in the ESI.† The resulting initial anisotropies, r0, are listed in Table 1, where the localized MLCT state presents an r0 corresponding to the lower limit for a disordered solution, −0.20. This means that the angle between the excitation and vibrational dipole moments is close to 90° as already established visually in Fig. 4 and 5. For a randomized state the computations predict r0 = −0.13, which is based on the weighted sum of the respective anisotropies associated with each dcb ligand. Corrections for possible GSB overlap results in slightly less negative predicted anisotropy values (see the ESI†).
| MLCT state | Localized | Randomized | Experimental |
|---|---|---|---|
| r 0 | −0.20 | −0.13 | −0.095 |
3.3 Experimental transient mid-IR absorption anisotropy
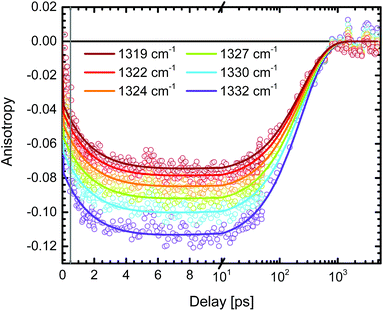
In order to minimize the excess excitation energy, hence limiting the number of possible transitions, N712 was excited at the red edge of the MLCT absorption band, 650 nm. The ground state UV-vis absorption is shown in Fig. S6.†The transient experiments as depicted in Fig. 6 result in an anisotropy close to infinity in the proximity of the isosbestic point, 1340 cm−1, but at the ESA maximum, 1327 cm−1, the 3MLCT band dominates and the signal is not significantly affected by the ground state bleaching. Fitting the anisotropy trace at various wavelengths through global analysis in the region of the symmetric stretch, as seen in Fig. 7, results in two time constants: 1.8 ps and 241 ps. The analysis was restricted to the frequencies that showed sufficiently good fitting with the mentioned time constants and had the least amount of error in the measurement (error analysis in the ESI†). The short time constant has a positive amplitude (0.04 at 1327 cm−1) associated with an increase of the anisotropy magnitude. The reason for this is not clear. We note, however, that the vibrational relaxation of 3MLCT states in Ru(II)-polypyridine complexes is often seen on the 1–5 ps time scale,31,74,75 which would be consistent with the observed lifetime as well as the time constants found for the isotropic traces by global analysis (see the ESI†). Even though the excitation was performed in the tail band of the MLCT, the singlet–triplet conversion causes a non-thermalized state to form, meaning that the vibrational population distribution will change with time as the system equilibrates. At early times, different effects may reduce the anisotropy magnitude compared to the values calculated and measured for the thermalized 3MLCT state, for example vibrational coupling to other modes. We emphasize that MLCT randomization cannot explain an increase in the magnitude of the anisotropy (see above), meaning that ILET cannot be the origin of the fast component. A longer time constant of ∼240 ps (amplitude at 1327 cm−1: −0.095) leads to a loss of anisotropy. This time constant compares to the reported rotational correlation times for N3 in methanol (400 ps (ref. 53)) but is in this case smaller, probably due to the lack of hydrogen bonding in MeCN and therefore a presumed smaller solvent cage.76 Time-resolved photoluminescence studies verified the observed rotational correlation time with excellent agreement (see the ESI†).
The amplitude of the slow 240 ps component is −0.095 at 1327 cm−1. This value agrees well with the r0 value predicted for a thermally relaxed randomized 3MLCT state (see Table 1). The localized state, originating from the photoselection, is instead predicted to result in r0 = −0.20. For our data to be consistent with that prediction, it would require a 20° error between the pump and probe. The relative angle between the pump and probe can be excluded as a source of such a significant error, as shown by the reference measurement of 9-cyanoanthracene (see ESI,† Section 2). Moreover, the influence of possible probe laser fluctuations was estimated to a mere ±0.004 difference in the anisotropy (see the ESI†). The magnitude of the anisotropy also verifies that the assumption of a localized excitation, compared to that of a delocalized in between the dcb ligands, is legitimate. A delocalized excitation in between the dcb ligands would lead to equal anisotropies for the localized and the randomized state and it would not be useful to study this system. Furthermore, the predicted value of anisotropy would be −0.03, which is much lower in magnitude than the experimental value. The findings therefore suggest that N712 undergoes ultrafast ILET forming a randomized MLCT state from an initially localized excitation. This clearly contradicts the conclusions by Benkö et al. and Waterland and Kelley,15,53 for the N3 dye.
For experimental reasons the present study used the deprotonated complex N712 instead of N3, and deuterated acetonitrile instead of ethanol or methanol, but we do not believe that these differences can explain the large discrepancies in the conclusions of these studies. First, Benkö et al. and Waterland and Kelly strongly disagree on the time scale of ILET for N3 in the respectively used alcohols. As already pointed out in the Introduction, the ∼20 ps process reported by Benkö et al. led to an increase in the anisotropy magnitude, which is inconsistent with a randomization process between identical ligands (ILET), and can instead be explained by an artefact from overlapping ESA bands. The τ ≈ 1.5 ns reported by Waterland and Kelly is much longer than the rotational correlation time of the entire complex. They based their result on an extrapolation of data to times after complete rotational randomization, which makes it very sensitive to inaccuracies in the rotational time constant. Also, they probed in a region of overlapping absorption bands, which adds uncertainty to predicted anisotropy values, and is something the present study avoided by probing a certain IR band. Thus, we believe that the present results are more reliable regarding the time scale of ILET in this family of complexes.
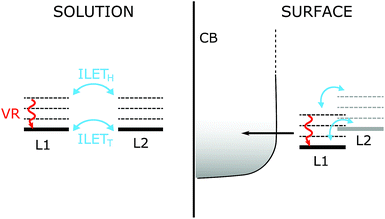
Our results compare well with those for [Ru(bpy)3]2+ in acetonitrile by Wallin et al., who reported that the MLCT state was randomized over all ligands on a time scale shorter than 300 fs.39 The randomization time scale is so short that it must have involved ILET from hot states (ILETH), as illustrated in Fig. 8 (left panel), and possibly also the 1MLCT. According to Stark et al. (see the Introduction), further ILET in the thermalized 3MLCT state (ILETT) may be slower,42 but as the MLCT state is already randomized this cannot be detected by anisotropy measurements. The behavior of N712 seems to be very similar and it is therefore likely that N712 also experiences randomization before thermal relaxation and intersystem crossing.
3.4 Relevance to electron injection in TiO2
Our present results are in agreement with previous work by Wallin et al. where ILET was shown to occur on an ultrafast time scale for [Ru(bpy)3]2+ in solution.39 Therefore, the MLCT localization is randomized over the bipyridine ligands before the 3MLCT state has thermally relaxed. We believe that it is unlikely that ILET limits electron injection so that it would be responsible for the slow (ps) injection component reported for the N3 family of dyes on TiO2. ILETH, which is ultrafast, is likely to become slower in a gradual fashion as the MLCT state thermalizes, developing a barrier for ILETT.42 To observe a ∼10 ps time scale for injection limited by ILET, the thermal relaxation of the hot MLCT state would have to be much faster than the ultrafast component of injection (50 fs), so that a MLCT population on the remote dcb ligand remains as a result of the formed barrier. In the more likely event that the relaxation is much slower than 50 fs, injection and ILET would occur during the MLCT relaxation. With ILETH being much faster than ∼10 ps, the MLCT state would be depleted before thermal relaxation is complete. Similar considerations could be extrapolated to molecular donor–acceptor complexes based on Ru(II)-polypyridyl dyes, in cases where electron transfer occurs on time scales similar to or faster than thermal relaxation.In solar cells, carboxylates of both dcb ligands are involved in binding to the TiO2 surface, as indicated by FTIR studies and calculations.68,70,77 This removes the need for ILET to achieve 100% ultrafast injection. In the fraction of dyes where only one of the dcb ligands is bound to TiO2 (proximal ligand), see Fig. 8, the MLCT state of that dcb ligand should be lower in energy than that of the deprotonated remote dcb, because of both electrostatic effects and electronic coupling to the conduction band. This would create a driving force for ILET to the proximal ligand and thus decrease the ILETT barrier. Therefore, ILET may be even less of a limitation than what could be predicted from its time scale in solution. The situation is different when ILET to the proximal ligand is significantly uphill. Typically, a rapid MLCT equilibrium between the proximal and remote ligand is established, and the kinetics follows a pre-equilibrium model.78–80 ILET can then limit the overall electron transfer process, but that is not because of a small frequency factor for ILET, but because the Boltzmann population of MLCT on the proximal ligand is small.
4 Conclusions
The interligand electron transfer (ILET) of N712 (cis-[Ru(4,4′-dicarboxylate-2,2′-bipyridine)2(NCS)2]4−) in deuterated acetonitrile has been studied by means of femtosecond transient absorption anisotropy in the mid-IR. By observing the vibrational transitions in the IR region rather than the electronic transitions in the UV-vis region the potential problem of overlapping absorption bands was avoided. This allowed for a better comparison with predicted anisotropies. First, it was concluded that the initial anisotropy value for the anti-phase symmetric carboxylate stretch (−0.095) is inconsistent with the predicted value had the initial excitation been delocalized over both dcb ligands (−0.03). This suggests that the initial excitation is localized on a single dcb ligand. Second, it was concluded that ILET is rapid, occurring on a sub-ps time scale. Thus, before a thermally relaxed 3MLCT state is formed (∼5 ps), the 3MLCT state is randomly localized on either of the two dcb ligands, irrespective of which ligand was involved in the initial excitation. The system has lost all memory of the initial photoselection, so that further ILET in the thermally relaxed MLCT state cannot be probed by anisotropy measurements. Our results are in sharp contrast to previous reports from transient anisotropy studies of the N3 family, which suggested ILET on much longer time scales (τ ≈ 20 ps (ref. 15) and 1.5 ns (ref. 53), respectively). Instead, our results agree with the results by Wallin et al., who reported sub-ps randomization of the MLCT state in [Ru(bpy)3]2+.39 Our results suggest that ILET is not likely to limit electron injection in dye-sensitized solar cells based on these dye complexes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Knut and Alice Wallenberg Foundation and The Swedish Energy Agency #43599-1. Research at Northwestern University was supported as part of the ANSER Center, an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basis Energy Sciences (BES), under Award #DE-SC0001059 (transient IR spectroscopy).References
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- W. J. Youngblood, S.-H. A. Lee, Y. Kobayashi, E. A. Hernandez-Pagan, P. G. Hoertz, T. A. Moore, A. L. Moore, D. Gust and T. E. Mallouk, J. Am. Chem. Soc., 2009, 131, 926–927 CrossRef CAS PubMed.
- D. L. Ashford, M. K. Gish, A. K. Vannucci, M. K. Brennaman, J. L. Templeton, J. M. Papanikolas and T. J. Meyer, Chem. Rev., 2015, 115, 13006–13049 CrossRef CAS PubMed.
- Y. Tachibana, J. E. Moser, M. Grätzel, D. R. Klug and J. R. Durrant, J. Phys. Chem., 1996, 100, 20056–20062 CrossRef CAS.
- Y. Tachibana, S. A. Haque, I. P. Mercer, J. R. Durrant and D. R. Klug, J. Phys. Chem. B, 2000, 104, 1198–1205 CrossRef CAS.
- C. Bauer, G. Boschloo, E. Mukhtar and A. Hagfeldt, J. Phys. Chem. B, 2001, 105, 5585–5588 CrossRef CAS.
- Y. Tachibana, S. A. Haque, I. P. Mercer, J. E. Moser, D. R. Klug and J. R. Durrant, J. Phys. Chem. B, 2001, 105, 7424–7431 CrossRef CAS.
- D. Kuciauskas, J. E. Monat, R. Villahermosa, H. B. Gray, N. S. Lewis and J. K. McCusker, J. Phys. Chem. B, 2002, 106, 9347–9358 CrossRef CAS.
- J. Kallioinen, G. Benkö, V. Sundström, J. E. Korppi-Tommola and A. P. Yartsev, J. Phys. Chem. B, 2002, 106, 4396–4404 CrossRef CAS.
- G. Benkö, J. Kallioinen, J. E. Korppi-Tommola, A. P. Yartsev and V. Sundström, J. Am. Chem. Soc., 2002, 124, 489–493 CrossRef.
- J. B. Asbury, N. A. Anderson, E. Hao, X. Ai and T. Lian, J. Phys. Chem. B, 2003, 107, 7376–7386 CrossRef CAS.
- G. Benkö, P. Myllyperkiö, J. Pan, A. P. Yartsev and V. Sundström, J. Am. Chem. Soc., 2003, 125, 1118–1119 CrossRef PubMed.
- R. Katoh, A. Furube, T. Yoshihara, K. Hara, G. Fujihashi, S. Takano, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2004, 108, 4818–4822 CrossRef CAS.
- J. Kallioinen, G. Benkö, P. Myllyperkiö, L. Khriachtchev, B. Skårman, R. Wallenberg, M. Tuomikoski, J. Korppi-Tommola, V. Sundström and A. P. Yartsev, J. Phys. Chem. B, 2004, 108, 6365–6373 CrossRef CAS PubMed.
- G. Benkö, J. Kallioinen, P. Myllyperkiö, F. Trif, J. E. Korppi-Tommola, A. P. Yartsev and V. Sundström, J. Phys. Chem. B, 2004, 108, 2862–2867 CrossRef.
- B. Wenger, M. Grätzel and J.-E. Moser, J. Am. Chem. Soc., 2005, 127, 12150–12151 CrossRef CAS PubMed.
- P. Myllyperkiö, G. Benkő, J. Korppi-Tommola, A. P. Yartsev and V. Sundström, Phys. Chem. Chem. Phys., 2008, 10, 996–1002 RSC.
- S. E. Koops, B. C. O'Regan, P. R. Barnes and J. R. Durrant, J. Am. Chem. Soc., 2009, 131, 4808–4818 CrossRef CAS PubMed.
- M. Pellnor, P. Myllyperkiö, J. Korppi-Tommola, A. Yartsev and V. Sundström, Chem. Phys. Lett., 2008, 462, 205–208 CrossRef CAS.
- J. Teuscher, J.-D. Décoppet, A. Punzi, S. M. Zakeeruddin, J.-E. Moser and M. Grätzel, J. Phys. Chem. Lett., 2012, 3, 3786–3790 CrossRef CAS PubMed.
- M. Juozapavicius, M. Kaucikas, S. D. Dimitrov, P. R. Barnes, J. J. van Thor and B. C. O'Regan, J. Phys. Chem. C, 2013, 117, 25317–25324 CrossRef CAS.
- M. Juozapavicius, M. Kaucikas, J. J. van Thor and B. C. O'Regan, J. Phys. Chem. C, 2012, 117, 116–123 CrossRef.
- A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. l. Belser and A. Von Zelewsky, Coord. Chem. Rev., 1988, 84, 85–277 CrossRef CAS.
- S. Ardo and G. J. Meyer, Chem. Soc. Rev., 2009, 38, 115–164 RSC.
- K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655–2686 CrossRef CAS PubMed.
- J. E. Monat, J. H. Rodriguez and J. K. McCusker, J. Phys. Chem. A, 2002, 106, 7399–7406 CrossRef CAS.
- J.-F. Guillemoles, V. Barone, L. Joubert and C. Adamo, J. Phys. Chem. A, 2002, 106, 11354–11360 CrossRef CAS.
- N. H. Damrauer, G. Cerullo, A. Yeh, T. R. Boussie, C. V. Shank and J. K. McCusker, Science, 1997, 275, 54–57 CrossRef CAS PubMed.
- J. K. McCusker, Acc. Chem. Res., 2003, 36, 876–887 CrossRef CAS PubMed.
- A. Cannizzo, F. van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Angew. Chem., Int. Ed., 2006, 45, 3174–3176 CrossRef CAS PubMed.
- A. T. Yeh, C. V. Shank and J. K. McCusker, Science, 2000, 289, 935–938 CrossRef CAS PubMed.
- A. J. Atkins and L. González, J. Phys. Chem. Lett., 2017, 8, 3840–3845 CrossRef CAS PubMed.
- A. C. Bhasikuttan, M. Suzuki, S. Nakashima and T. Okada, J. Am. Chem. Soc., 2002, 124, 8398–8405 CrossRef CAS PubMed.
- J. B. Asbury, R. J. Ellingson, H. N. Ghosh, S. Ferrere, A. J. Nozik and T. Lian, J. Phys. Chem. B, 1999, 103, 3110–3119 CrossRef CAS.
- D. W. Thompson, A. Ito and T. J. Meyer, Pure Appl. Chem., 2013, 85, 1257–1305 CAS.
- S. A. Haque, E. Palomares, B. M. Cho, A. N. Green, N. Hirata, D. R. Klug and J. R. Durrant, J. Am. Chem. Soc., 2005, 127, 3456–3462 CrossRef CAS PubMed.
- L. J. Antila, P. Myllyperkiö, S. Mustalahti, H. Lehtivuori and J. Korppi-Tommola, J. Phys. Chem. C, 2014, 118, 7772–7780 CrossRef CAS.
- R. Malone and D. Kelley, J. Chem. Phys., 1991, 95, 8970–8976 CrossRef CAS.
- S. Wallin, J. Davidsson, J. Modin and L. Hammarström, J. Phys. Chem. A, 2005, 109, 4697–4704 CrossRef CAS PubMed.
- M.-E. Moret, I. Tavernelli, M. Chergui and U. Rothlisberger, Chem.–Eur. J., 2010, 16, 5889–5894 CrossRef CAS PubMed.
- D. A. Hoff, R. Silva and L. G. Rego, J. Phys. Chem. C, 2011, 115, 15617–15626 CrossRef CAS.
- C. W. Stark, W. J. Schreier, J. Lucon, E. Edwards, T. Douglas and B. Kohler, J. Phys. Chem. A, 2015, 119, 4813–4824 CrossRef CAS PubMed.
- J. Pogge and D. Kelley, Chem. Phys. Lett., 1995, 238, 16–24 CrossRef CAS.
- J. Cushing, C. Butoi and D. Kelley, J. Phys. Chem. A, 1997, 101, 7222–7230 CrossRef CAS.
- G. B. Shaw, C. L. Brown and J. M. Papanikolas, J. Phys. Chem. A, 2002, 106, 1483–1495 CrossRef CAS.
- G. B. Shaw, D. J. Styers-Barnett, E. Z. Gannon, J. C. Granger and J. M. Papanikolas, J. Phys. Chem. A, 2004, 108, 4998–5006 CrossRef CAS.
- T. Yabe, L. Orman, D. Anderson, S. C. Yu, X. Xu and J. B. Hopkins, J. Phys. Chem., 1990, 94, 7128–7132 CrossRef CAS.
- A. C. Benniston, A. Harriman, C. Pariani and C. A. Sams, J. Phys. Chem. A, 2007, 111, 8918–8924 CrossRef CAS PubMed.
- J. T. Hewitt, P. J. Vallett and N. H. Damrauer, J. Phys. Chem. A, 2012, 116, 11536–11547 CrossRef CAS PubMed.
- R. Ghosh and D. K. Palit, Phys. Chem. Chem. Phys., 2014, 16, 219–226 RSC.
- T. Mukuta, N. Fukazawa, K. Murata, A. Inagaki, M. Akita, S. Tanaka, S.-y. Koshihara and K. Onda, Inorg. Chem., 2014, 53, 2481–2490 CrossRef CAS PubMed.
- D. J. Liard, M. Busby, I. R. Farrell, P. Matousek, M. Towrie and A. Vlček, J. Phys. Chem. A, 2004, 108, 556–567 CrossRef CAS.
- M. Waterland and D. Kelley, J. Phys. Chem. A, 2001, 105, 4019–4028 CrossRef CAS.
- C. Olsen, M. Waterland and D. Kelley, J. Phys. Chem. B, 2002, 106, 6211–6219 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Can. J. Chem., 1992, 70, 560–571 CrossRef CAS.
- C. Sosa, J. Andzelm, B. C. Elkin, E. Wimmer, K. D. Dobbs and D. A. Dixon, J. Phys. Chem., 1992, 96, 6630–6636 CrossRef CAS.
- O. Kitao and H. Sugihara, Inorg. Chim. Acta, 2008, 361, 712–728 CrossRef CAS.
- M. K. Nazeeruddin, F. De Angelis, S. Fantacci, A. Selloni, G. Viscardi, P. Liska, S. Ito, B. Takeru and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 16835–16847 CrossRef CAS PubMed.
- O. A. Borg, S. S. Godinho, M. J. Lundqvist, S. Lunell and P. Persson, J. Phys. Chem. A, 2008, 112, 4470–4476 CrossRef CAS PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- M. Koch, R. Letrun and E. Vauthey, J. Am. Chem. Soc., 2014, 136, 4066–4074 CrossRef CAS PubMed.
- M. K. Nazeeruddin, R. Humphry-Baker, P. Liska and M. Grätzel, J. Phys. Chem. B, 2003, 107, 8981–8987 CrossRef CAS.
- M. K. Nazeeruddin, S. Zakeeruddin, R. Humphry-Baker, M. Jirousek, P. Liska, N. Vlachopoulos, V. Shklover, C.-H. Fischer and M. Grätzel, Inorg. Chem., 1999, 38, 6298–6305 CrossRef CAS PubMed.
- F. Schiffmann, J. VandeVondele, J. Hutter, R. Wirz, A. Urakawa and A. Baiker, J. Phys. Chem. C, 2010, 114, 8398–8404 CrossRef CAS.
- N. L. McNiven and R. Court, Appl. Spectrosc., 1970, 24, 296–300 CrossRef.
- J. R. Lakowicz, Principles of fluorescence spectroscopy, Springer Science & Business Media, 2013 Search PubMed.
- H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498–1517 CrossRef CAS PubMed.
- M. Myrick, R. Blakley, M. DeArmond and M. Arthur, J. Am. Chem. Soc., 1988, 110, 1325–1336 CrossRef CAS.
- R. Lomoth, T. Häupl, O. Johansson and L. Hammarström, Chem.–Eur. J., 2002, 8, 102–110 CrossRef CAS.
- D. Chakrabarty, A. Chakraborty, D. Seth and N. Sarkar, J. Phys. Chem. A, 2005, 109, 1764–1769 CrossRef CAS PubMed.
- V. Shklover, Y. E. Ovchinnikov, L. Braginsky, S. Zakeeruddin and M. Grätzel, Chem. Mater., 1998, 10, 2533–2541 CrossRef CAS.
- L. A. Kelly and M. A. J. Rodgers, J. Phys. Chem., 1995, 99, 13132–13140 CrossRef CAS.
- L. F. Cooley, C. E. L. Headford, C. M. Elliott and D. F. Kelley, J. Am. Chem. Soc., 1988, 110, 6673–6682 CrossRef CAS.
- M. L. A. Abrahamsson, H. B. Baudin, A. Tran, C. Philouze, K. E. Berg, M. K. Raymond-Johansson, L. Sun, B. Åkermark, S. Styring and L. Hammarström, Inorg. Chem., 2002, 41, 1534–1544 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational section: optimized structures and vibrational modes, and calculation of predicted anisotropy. Reference: 9-cyanoanthracene. Characterization: UV-vis and FTIR spectrum. Transient spectroscopy: parallel and perpendicular pump-probe transient spectra. See DOI: 10.1039/c8sc00274f |
| This journal is © The Royal Society of Chemistry 2018 |