Open Access Article
Open Access ArticleA flexible, redox-active macrocycle enables the electrocatalytic reduction of nitrate to ammonia by a cobalt complex†
Song
Xu
 a,
Daniel C.
Ashley
a,
Daniel C.
Ashley
 b,
Hyuk-Yong
Kwon
b,
Hyuk-Yong
Kwon
 b,
Gabrielle R.
Ware
c,
Chun-Hsing
Chen
a,
Yaroslav
Losovyj
a,
Xinfeng
Gao
a,
Elena
Jakubikova
b,
Gabrielle R.
Ware
c,
Chun-Hsing
Chen
a,
Yaroslav
Losovyj
a,
Xinfeng
Gao
a,
Elena
Jakubikova
 *b and
Jeremy M.
Smith
*b and
Jeremy M.
Smith
 *a
*a
aDepartment of Chemistry, Indiana University, 800 E. Kirkwood Ave., Bloomington, Indiana 47401, USA. E-mail: smith962@indiana.edu
bDepartment of Chemistry, North Carolina State University, 2620 Yarbrough Dr., Raleigh, NC 27695, USA. E-mail: ejakubi@ncsu.edu
cDepartment of Chemistry, St. Edward's University, 3001, South Congress, Austin, Texas 78704, USA
First published on 15th May 2018
Abstract
The cobalt macrocycle complex [Co(DIM)Br2]+ (DIM = 2,3-dimethyl-1,4,8,11-tetraazacyclotetradeca-1,3-diene) is an electrocatalyst for the selective reduction of nitrate to ammonia in aqueous solution. The catalyst operates over a wide pH range and with very high faradaic efficiency, albeit with large overpotential. Experimental investigations, supported by electronic structure calculations, reveal that catalysis commences when nitrate binds to the two-electron reduced species CoII(DIM−), where cobalt and the macrocycle are each reduced by a single electron. Several mechanisms for the initial reduction of nitrate to nitrite were explored computationally and found to be feasible at room temperature. The reduced DIM ligand plays an important role in these mechanisms by directly transferring a single electron to the bound nitrate substrate, activating it for further reactions. These studies further reveal that the DIM macrocycle is critical to nitrate reduction, specifically its combination of redox non-innocence, hydrogen-bonding functionality and flexibility in coordination mode.
Introduction
The Haber–Bosch process, which was developed in the early 20th century, made ammonia available on an industrial scale.1 About 80% of Haber–Bosch ammonia currently produced goes to fertilizers, which are estimated to support almost half of the planet's population.2 As a consequence of the large increase in food production over the last century, the quantity of nitrogen in the global cycle has doubled, with humans currently responsible for about half of all fixed nitrogen. The enormous scale of ammonia production is associated with huge energy demands and a large carbon footprint, primarily due to the need to generate hydrogen from fossil fuels.3–5Only a few percent of all the nitrogen used as fertilizer is finally consumed as food protein, with most of it lost to the environment. For example, microorganisms in the soil oxidize nitrogen fertilizers to various nitrogen oxides that escape into the environment, either through volatilization into the atmosphere or runoff into waterways.6 This movement of human-produced nitrogen, termed the “Nitrogen Cascade”,7 affects atmospheric, terrestrial and aquatic systems.8 One molecule of reactive nitrogen can have multiple effects during its lifetime in the cascade before it is finally denitrified or fossilized. Since fertilizer nitrogen may have a decades-long residence time in agricultural soils,9 these cascading effects are likely to persist for the long term.
The nitrate ion in particular has significant cascading effects. Nitrate runoff from agricultural fields leads to eutrophication of waterways and cyanobacteria growth, whose death and decay results in hypoxia, where other aquatic species cannot survive.8 The resulting dead zones are associated with significant economic10 and environmental11 consequences. The number of dead zones worldwide has approximately doubled every decade since the 1960's to currently stand at over 400.12 Nitrate runoff may also result in the contamination of aquifers and consequently drinking water, with potentially serious threats to human health,13e.g. blue baby syndrome, increased risk of non-Hodgkin's lymphoma and other cancers.14
Since biological denitrification processes are overwhelmed by anthropogenic nitrate,15,16 there is an opportunity to develop new methods for recycling nitrate by reducing it to useful or benign compounds. Nitrate reduction is a multielectron, multiproton process, but has received significantly less attention than related transformations such as CO2 reduction.17–22 While thermodynamically favorable, there are unique challenges associated with selective nitrate reduction. The low charge density and delocalized electronic structure make nitrate a poor substrate, and consequently it binds catalysts more weakly than most other ligands, including other ions commonly found in aqueous solutions. Additionally, multiple reduction products are possible, some of which have very similar reduction potentials (Table 1).
| Half reaction | E 0 (V vs. SCE) |
|---|---|
| NO3− + 2H+ + 2e− → NO2− + H2O | 0.591 |
| NO3− + 4H+ + 3e− → NO(g) + 2H2O | 0.714 |
| NO3− + 8H+ + 6e− → NH3OH+ + 2H2O | 0.483 |
| NO3− + 10H+ + 8e− → NH4+ + 3H2O | 0.631 |
| 2NO3− + 10H+ + 8e− → N2O(g) + 5H2O | 0.872 |
| 2NO3− + 12H+ + 10e− → N2(g) + 6H2O | 1.002 |
Although nitrate can be electrochemically reduced on heterogeneous metal electrodes,24 catalysis is plagued by high overpotentials and low product selectivity. Moreover, catalytic activity and selectivity is strongly dependent on the electrolyte composition and pH.15,16 In this context, the amenability of molecular complexes to rational design makes them attractive for creating electrocatalysts having improved selectivity and greater efficiency. However there are few examples of molecular electrocatalysts for nitrate reduction,25–29 and very little is known about their reaction mechanisms. While a number of examples of stoichiometric conversions of nitrate by homogeneous metal complexes suggest the importance of hydrogen donor functionalities for nitrate activation,30,31 these results do not provide guidelines for designing electrocatalysts that are selective for nitrate reduction.
The most well-investigated electrocatalyst is [Co(cyclam)Cl2]+, which produces hydroxylamine as the principal reduction product. However, this catalyst is only operative in highly concentrated hydroxide solution, only active on heavy metal electrodes and operates at large overpotentials.32–34 While this complex can be incorporated into modified electrodes, electrocatalysis still requires strongly basic media and large overpotentials.35–37 In this light, we were intrigued to discover an overlooked report on the electrocatalytic reduction of nitrate38 by [Co(DIM)Br2]+ (DIM = 2,3-dimethyl-1,4,8,11-tetraazacyclotetradeca-1,3-diene).39 These initial studies demonstrated that catalysis occurs in aqueous solution with glassy carbon electrodes and that ammonia is the sole product of reduction. Nitrite and hydroxylamine were also electrocatalytically reduced to ammonia, suggesting these substrates could be ligands for intermediates in nitrate reduction, however no further insight into the details of the reaction mechanism or the origin of substrate selectivity were reported.
In this paper, we present a combined experimental and computational investigation into electrocatalytic nitrate reduction by [Co(DIM)Br2]+. In addition to full structural and spectroscopic characterization, including aqueous speciation of the complex, we have investigated mechanisms for cleaving the first N–O bond of nitrate. Combined with experimentally-calibrated electronic structure calculations, these results provide insight into the key factors played by the macrocycle in facilitating nitrate reduction, as well as suggest strategies for the design of improved nitrate reduction electrocatalysts.
Results and discussion
Synthesis and characterization
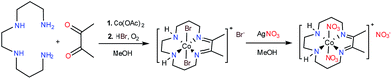
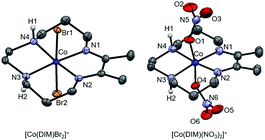
The green cobalt(III) complex, [Co(DIM)Br2]+, was prepared according to the literature procedure39 (Scheme 1) and fully characterized using modern spectroscopic methods. The molecular structure of [Co(DIM)Br2]+, as determined by single crystal X-ray diffraction (Fig. 1) reveals the anticipated structure. Thus, the cobalt ion is in the plane of the four macrocycle N donors with the coordination sphere completed by the two axial bromide ligands. The amine donors of the DIM macrocycle are in an anti configuration with the amine protons oriented in opposite directions. The DFT-optimized geometries show similar structural features (see Tables S3 and S4†).The 1H NMR spectrum of [Co(DIM)Br2]+ in CD3OD solution shows ten resonances between 0 and 10 ppm, as expected for a diamagnetic Co(III) complex (Fig. S1 and S2†) and consistent with the solid state structure. It is notable that the protons on each methylene group in [Co(DIM)Br2]+ are inequivalent. The methyl groups resonate as a singlet at δ 2.78 pm. The protons on the amine donors, which resonate as a broad singlet at δ 6.02 ppm, exchange with deuterium from CD3OD over the course of several hours.
The electrochemical properties of [Co(DIM)Br2]+ in nonaqueous solution were investigated in NBu4PF6/MeCN, with all potentials referenced to Fc+/Fc. The cyclic voltammogram of [Co(DIM)Br2]+ shows two reversible processes with E1/2 = −0.44 V (ΔEp = 74 mV) and −1.31 V (ΔEp = 76 mV), respectively (Fig. 2, −0.03 V and −0.90 V vs. SCE). Calibrating the peak current for these two couples against a ferrocene standard suggests that each of these two waves corresponds to a single electron process. The first process is expected to be the Co(III)/Co(II) couple, and this is corroborated by DFT calculations, where the metal-centered reduction is calculated at −0.15 V (vs. SCE) in excellent agreement with experiment. The reversibility of the second process strongly implicates a ligand-based reduction. While it was not possible to characterize the second reduction computationally due to bromide dissociation in the course of the geometry optimization, additional computational results on related Co–DIM complexes40 support the assignment of the second reduction as the ligand based Co(II)–DIM/Co(II)–DIM(-I) couple. Details on issues regarding this reduction are discussed in the ESI.† Importantly then, [Co(DIM)Br2]+ has the capacity to reduce substrates by two electrons, with one electron provided by the metal and the other by the macrocyclic ligand (see below).
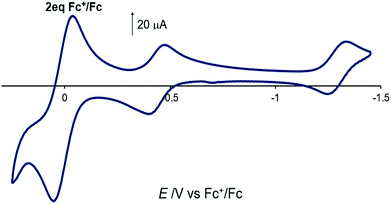 | ||
| Fig. 2 Cyclic voltammogram of [Co(DIM)Br2]+ in acetonitrile solution. 2 equiv. of ferrocene is used as reference. GC electrode, 100 mM NBu4PF6, scan rate = 100 mV s−1. | ||
Reaction of [Co(DIM)Br2]+ with AgNO3 provides the brown complex [Co(DIM)(NO3)2]+ (Scheme 1). The molecular structure of [Co(DIM)(NO3)2]+ shows similar features to that of [Co(DIM)Br2]+. Perhaps surprisingly, there is no evidence for intramolecular H-bonding between the nitrate ligand and the amine protons of the DIM ligand in the solid state (Fig. 1), with the shortest N–H⋯O distance over 2.8 Å. The 1H NMR spectrum of [Co(DIM)(NO3)2]+ in CD3OD is similar to that of [Co(DIM)Br2]+ but with slightly different chemical shifts (Fig. S6†).
Aqueous speciation
Since the 1H NMR of [Co(DIM)Br2]+ in D2O shows evidence for multiple species, we first investigated the aqueous speciation of [Co(DIM)(NO3)2]+, where it is anticipated that both of the weakly binding NO3− ligands41 would be substituted by H2O. Indeed, the conductivity of an aqueous solution of [Co(DIM)(NO3)2]+ is larger than expected for a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte (638 S cm2 mol−1)42 indicating that in addition to replacement of both nitrate ligands, a coordinated aqua ligand is also largely deprotonated. As suggested by the conductivity measurements, dissolving [Co(DIM)(NO3)2]+ in water leads to a decrease in the solution pH, consistent with proton loss from the aqua ligands. The 1H NMR spectrum of [Co(DIM)(NO3)2]+ in D2O is consistent with this proton transfer being fast on the 1H NMR timescale. The acidity of the aqua ligands was determined by pH titration in aqueous solution, providing pKa estimates of ca. 5 for deprotonation of the first bound water and ca. 9.0 for the second.43 While the aqueous speciation of [Co(DIM)Br2]+ is complicated by equilibria involving the bromide ligands, analogous studies reveal that this complex also forms [Co(DIM)(OH)(OH2)]2+ at moderate pH and [Co(DIM)(OH)2]+ at very basic pH (see ESI†). Electronic structure calculations are reasonably consistent with these conclusions, although it is not clear whether both anions have necessarily dissociated at lower pHs (see below).
1 electrolyte (638 S cm2 mol−1)42 indicating that in addition to replacement of both nitrate ligands, a coordinated aqua ligand is also largely deprotonated. As suggested by the conductivity measurements, dissolving [Co(DIM)(NO3)2]+ in water leads to a decrease in the solution pH, consistent with proton loss from the aqua ligands. The 1H NMR spectrum of [Co(DIM)(NO3)2]+ in D2O is consistent with this proton transfer being fast on the 1H NMR timescale. The acidity of the aqua ligands was determined by pH titration in aqueous solution, providing pKa estimates of ca. 5 for deprotonation of the first bound water and ca. 9.0 for the second.43 While the aqueous speciation of [Co(DIM)Br2]+ is complicated by equilibria involving the bromide ligands, analogous studies reveal that this complex also forms [Co(DIM)(OH)(OH2)]2+ at moderate pH and [Co(DIM)(OH)2]+ at very basic pH (see ESI†). Electronic structure calculations are reasonably consistent with these conclusions, although it is not clear whether both anions have necessarily dissociated at lower pHs (see below).
In contrast to the electrochemical behavior in acetonitrile (see above), the cyclic voltammogram of [Co(DIM)(NO3)2]+ in aqueous solution shows a single, irreversible reduction with Ep,c = −1.075 V vs. SCE.44 This wave becomes quasi-reversible, with the appearance of an oxidative wave at very fast scan rates (ca. 2000 mV s−1) and is pH independent over the range 3.5–10.1 (Fig. 3 and S13†). These results suggest that single electron reduction of the complex under aqueous conditions is accompanied by loss of an aqua or hydroxide ligand.
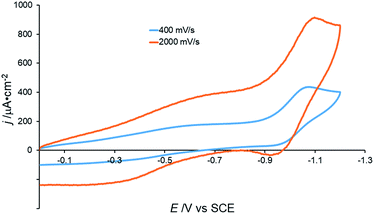 | ||
| Fig. 3 Cyclic voltammograms of 0.5 mM [Co(DIM)(NO3)2]+ under different scan rates. GC electrode, 50 mM Na2SO4, pH = 6.3. | ||
Computed speciation
DFT calculations were performed to evaluate the speciation of [Co(DIM)Br2]+ and [Co(DIM)(NO3)2]+ in water (Fig. 4). For both compounds, replacement of one axial ligand with water is modestly uphill by ∼3–4 kcal mol−1. The resulting monoaqua complexes have calculated pKas of 6.2 and 3.4 for [Co(DIM)(H2O)Br]2+ and [Co(DIM)(H2O)(NO3)]2+, respectively. Compared to the measured pKas of ∼5 this is a good agreement, as both complexes are predicted to be weak acids.45 An alternative interpretation for the first pKas of these complexes is that the ligand substitution equilibria are strongly coupled to the deprotonation process, and hence the pKa should be calculated for the entire thermodynamic process of ligand exchange followed by proton loss (also indicated in Fig. 4). This approach results in first pKas of 9.2 and 5.7 for [Co(DIM)Br2]+ and [Co(DIM)(NO3)2]+, respectively, leading to a worse agreement for the former and a better agreement for the latter.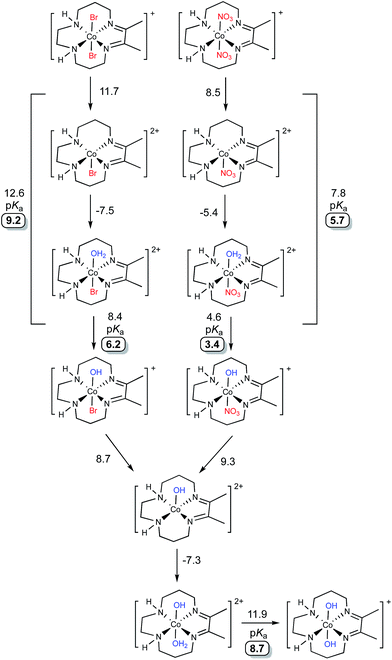 | ||
| Fig. 4 Calculated speciation pathways of [Co(DIM)Br2]+ (top) and [Co(DIM)(NO3)2]+ (bottom). All energies are reported as solvated free energies in kcal mol−1. Calculated pKa values are highlighted. | ||
The subsequent monohydroxo complexes can undergo a second ligand exchange for a water molecule. The identity of the ligand (nitrate vs. bromide) has virtually no effect on the ligand exchange, which is associated with a small energetic cost of ∼1–2 kcal mol−1. The resultant complex, [Co(DIM)(H2O)(OH)]2+, has a larger calculated pKa than either of the monohydroxo complexes at 8.7, consistent with the experimental measurements. As before, the ligand exchange can be considered to be directly involved in the deprotonation equilibria which results in slightly higher calculated pKas of ∼10 for each complex (not indicated in Fig. 4). Significantly, whether these ligand exchange equilibria are considered part of the deprotonation process or not, each approach results in a qualitative agreement with the experimental observation of two weakly acidic protons. As will be shown below, these speciation predictions are also consistent with the experimentally observed peak potentials.
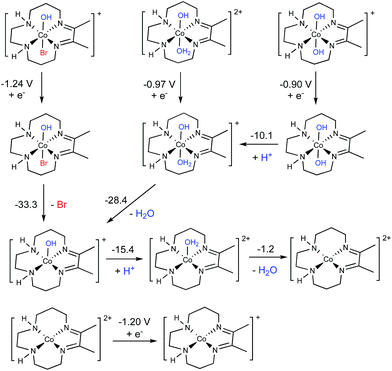
Computational evaluation of active catalyst
A thorough computational investigation of possible speciation/reduction pathways in solution was performed to determine which complexes show reduction potentials consistent with the experimentally observed peak potential at approximately −1.0 V. Note that the electronic structure calculations are only capable of accurately determining the value of E1/2, which is experimentally gauged by averaging the cathodic and anodic peak potentials of a reversible process. Thus, the calculations cannot be used to directly match the peak potentials determined from an irreversible process. It is, however, reasonable to assume that the calculated values of E1/2 should be similar to the observed peak potentials, and this is what was considered. Full square schemes showing different permutations of ligand loss/binding and reduction are shown in Fig. S21 through S29,† but here we only highlight the most important results in Fig. 5.Out of all complexes investigated, only three had calculated reduction potentials similar to −1.0 V (see Fig. 5): [Co(DIM)(OH)Br]+/0 (−1.24 V), [Co(DIM)(OH2)OH]2+/1+ (−0.97 V) and [Co(DIM)(OH)2]+/0 (−0.90 V). While [Co(DIM)(OH)2]+/0 exhibits metal-based reduction, reductions of [Co(DIM)(OH)Br]+/0 and [Co(DIM)(OH2)OH]2+/1+ are assigned as ligand-based (see the ESI for a more detailed discussion†). All three compounds are predicted to behave the same upon reduction, undergoing a series of protonations and ligand losses to eventually form the four-coordinate [Co(DIM)]2+ complex, which is best-described as Co(II). This complex is calculated to be reduced at −1.20 V vs. SCE. This is more negative than the observed peak potential at −1.0 V, but within the error of our method and close enough to suggest that it may also occur at a similar potential to the first reduction.
In summary, based on the experimentally-calibrated computational description of the aqueous speciation and electrochemical properties, we propose that four-coordinate, square-planar [Co(DIM)]+ is the active catalyst for nitrate reduction. This conclusion is consistent with the experimental speciation experiments, and clearly identifies the nature of the complex that enters the catalytic cycle.
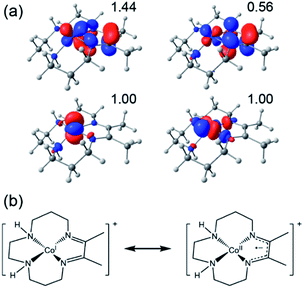
The redox capabilities of DIM distinguish it from the less effective cyclam ligand (although other redox-active ligands can still result in ineffective catalysts, see ESI†), and hence this electronic structure feature may play an important role in Co(DIM)'s enhanced catalytic activity. While [Co(DIM)]+ is formally a Co(I) complex, like every other doubly reduced Co(DIM) species calculated in this study, it has significant Co(II)–DIM(-I) character. Numerous spin-states were examined, and the lowest energy spin-state found corresponds to a HS Co(II) ion antiferromagnetically (AF) coupled to the monoanionic DIM(-I) ligand, leading to an overall triplet (S = 1). This state is referred to as the AF-triplet (AF-T) state. The assignment was confirmed with natural orbital (NO) analysis (Fig. 6), which identifies four NOs with occupation numbers different from 0.0 and 2.0. Several other electronic states examined (a conventional triplet and AF-coupled singlet states with two singly occupied NOs, and a quintet state) lie within 3 kcal mol−1 of the AF-T state. These states also have significant spin density on the DIM ligand, and can be described with the same formal oxidation states.
Electrocatalytic NO3− reduction
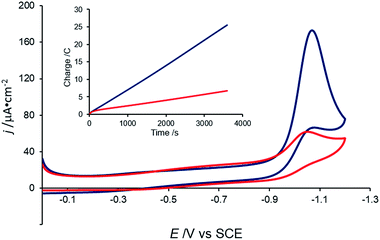
Consistent with the previous report,38 a catalytic current with an onset potential of ca. −0.90 V vs. SCE is observed when the CV of 0.5 mM [Co(DIM)Br2]+ is measured in the presence of 10 mM aqueous nitrate (Fig. 7). Under these conditions, the current reaches a plateau at ca. −1.08 V vs. SCE. This catalytic wave is observed at the same potential as the irreversible wave in the absence of nitrate, and corresponds to an overpotential of ca. 1.2 V vs. SCE (E(NO3−/NH3) = 0.29 V vs. SCE at pH 4.6). The catalytic current is observed at pH values above ca. 3.5 (ref. 46) and below pH ca. 10.1. Importantly, the CV of [Co(DIM)(NO3)2]+ shows the same electrochemical behavior under these conditions (Fig. S12†), suggesting that both cobalt complexes access the same active species upon reduction. It is notable that this current is only observed at slow scan rates (<20 mV s−1). Catalysis is not observed in buffered solutions, even with “non-coordinating” buffers (e.g. PIPBS),47 likely due to the weak binding ability of the nitrate substrate.Controlled-potential electrolysis (CPE) of a 100 mM nitrate solution at −1.05 V vs. SCE shows that the charge passed is greater in the presence of [Co(DIM)Br2]+ than in its absence (Fig. 7, inset). During the course of electrolysis, the pH of an unbuffered solution increases from 3.5 to 12.3, consistent with H+ consumption during the reduction of NO3−. Ammonia was determined to be the product of NO3− reduction, with a faradaic efficiency of 97%, as quantified by the indophenol test,48 with no evidence for the formation of NH2OH.49
A number of experiments have been undertaken to exclude the possibility of heterogeneous or nanoparticle catalysts (Fig. S15–S18†).50,51 No new bands are observed in the optical spectrum following electrolysis, suggesting that the formation of nanoparticles is unlikely, which is further supported by the results of dynamic light scattering measurements. There is also no evidence for the formation of a heterogeneous electrocatalytic deposit on the electrode surface. The catalytic current does not increase over successive cyclic voltammetric (CV) scans, which would be expected for the formation of a catalytic deposit. While XPS measurements suggest that small quantities of cobalt-containing material are adsorbed on the electrode surface, these species are not catalytically active, as revealed by a rinse test. Thus, all available evidence points to a homogeneous molecular catalyst for nitrate reduction.52
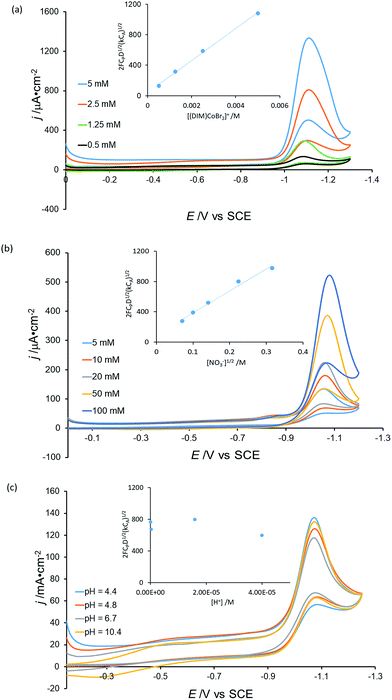
To elucidate further mechanistic details of nitrate reduction, electrocatalysis was conducted with variable catalyst ([Co(DIM)Br2]+) (Fig. 8a), substrate (NaNO3) (Fig. 8b) and H+ (Fig. 8c) concentrations. The current dependence on [Co(DIM)Br2]+ and NO3− concentration was determined using the foot of the wave (FOWA) analysis,53,54 providing first-order dependencies for the catalyst and substrate, consistent with the second-order rate law:
| rate = k[Co][NO3−] |
Interestingly, the analysis reveals that there is no dependence on the proton concentration, suggesting that the required proton transfer steps occur after the rate determining step.55
Mechanism of nitrate reduction
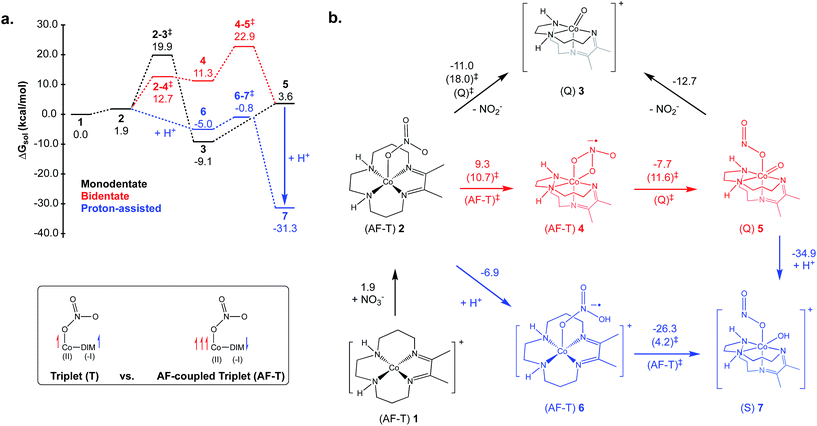
There are many potential mechanisms through which [Co(DIM)]+ could mediate the reduction of nitrate to ammonia, and an exhaustive study is beyond the scope of this manuscript. Instead, a preliminary mechanistic analysis is presented examining several simple mechanisms involved in the initial nitrate-to-nitrite reduction as shown in the reaction coordinate diagram and corresponding mechanistic cycle in Fig. 9. Starting from the active catalyst (complex 1), binding nitrate is thermodynamically easy. This results in formation of the five-coordinate mononitrate 2. The ground state electronic structure of 2 is an AF-triplet state as described for [Co(DIM)]+ above. This can be compared to the more typical triplet state (T) which consists of a LS Co(II) ferromagnetically coupled to the DIM radical anion (Fig. 9, inset). Note there are two other electronic structures deriving from these configurations: the quintet state (Q) is a HS Co(II) ferromagnetically coupled to the DIM ligand and the AF-singlet (AF-S) is a LS Co(II) AF-coupled to the DIM ligand. The closed-shell singlet alternative (S) was always higher in energy and usually possessed an unstable wavefunction. Fig. 9 displays the lowest energy spin state of each structure (indicated next to each structure). The energetics of the alternative spin states are shown in Fig. S30–S32.† Fig. S33† illustrates the various electronic states considered and how they can facilitate nitrate reduction to nitrite.From 2 it is possible to transfer electrons to bound nitrate to form free nitrite and what is formally a Co(III) oxo species 3, a process which is downhill by 11.0 kcal mol−1 (monodentate mechanism; see black pathway in Fig. 9). Based on Mulliken spin and NO analysis, complex 3 can be described as a Co(II) oxyl radical (see Fig. S34†). This oxo/oxyl ligand is highly basic and can be readily protonated with a driving force of −19.2 kcal mol−1 to form a simple Co(III) hydroxide. Surprisingly, the transition state located for the formation of the unusual complex 3 was found to be relatively low in energy, leading to an activation energy of 18.1 kcal mol−1 for this step. Further examination of this transition state via the Mulliken spin and NO analyses shows significant radical character on the nitrate substrate itself, and pyramidalization of the nitrate group. Additionally, the radical character on the DIM ligand has disappeared, indicating that nitrate has undergone one-electron reduction by the redox-active DIM ligand, while Co has yet to participate in the electron transfer. Initial single-electron transfer to nitrate can induce homolysis of a nitrogen–oxygen bond, thereby releasing closed-shell fully-reduced nitrite and a Co(II) oxyl radical (3) (see Fig. S33†). The transition states obtained for the AF-T and Q states are close to each other in energy and ∼13–14 kcal mol−1 lower in energy than the AF-S and T states, this driving force likely resulting from their closer resemblance to the final ground state of 3.
Another variant of this mechanism (bidentate mechanism; see red pathway in Fig. 9) was found where the one-electron reduction of nitrate results in an intermediate before N–O cleavage has occurred (4). Intermediate 4 is characterized by a bidentate binding mode for nitrate, which necessitates folding the DIM ligand to allow the two nitrate oxygens to coordinate in a cis fashion. It is uphill by 9.3 kcal mol−1, possessing a low-energy “late” transition state with an activation energy of 10.7 kcal mol−1. Intermediate 4 can then undergo homolysis of the nitrogen–oxygen bond, resulting in 5 which has nitrite bound cis to a similar oxo/oxyl radical moiety as that described for 3. The barrier for this step is low at 11.6 kcal mol−1. However, as can be seen in the reaction coordinate diagram in Fig. 9, the additional energetic cost of forming 4 prior to nitrite formation will add into the overall activation energy, leading to a slightly larger barrier than going directly from 2 to 3. Nitrite can be readily released from 5 to form 3 which can re-enter the catalytic cycle after protonation.
While these mechanisms are computationally very promising, it is important to also consider mechanisms that avoid the formation of the Co(II) oxyl functionality. One way to accomplish this is by a direct protonation of 2, which will induce electron transfer from DIM to the substrate (now bound nitric acid) to form 6 (proton-assisted mechanism; see blue pathway in Fig. 9). In terms of electronic structure, this complex is also an AF-T and is similar to 2. This protonation is favorable by 6.9 kcal mol−1, after which 6 can break the nitrogen–oxygen bond, while simultaneously re-binding the hydroxyl ligand to form 7, which is downhill by 26.3 kcal mol−1. The calculated barrier for 6 going to 7 is exceptionally small; only 4.2 kcal mol−1. A low-barrier for this step conceptually makes sense, given how facile the similar cleavage in 4 to 5 is and the very large driving forces involved for formation of 7. Finally, complex 7 can also be directly formed by protonation of 5 (downhill by 34.9 kcal mol−1).
Of all the mechanisms examined, the proton-assisted pathway is unambiguously the lowest in energy assuming a source of protons is available (the calculations are performed in the standard state, pH = 0). The other two pathways are also viable at room temperature. The calculated pKa for 6 is 5.1, indicating that at higher pH 2 will be the majority species and forming 6 will be modestly uphill (2.6 kcal mol−1 at pH = 7 as opposed to −6.9 kcal mol−1 at standard conditions, pH = 0). The activation energy for the proton-assisted pathway (i.e., the free energy difference between 6–7‡ and 1) will thus range from 4.2 kcal mol−1 at pH 3.5 (energy difference between 6–7‡ and 6) to approximately 12.9 kcal mol−1 at pH 10.1 (free energy difference between 6–7‡ and 1). While this energetic penalty does not preclude the proton-assisted mechanism itself, it is not consistent with the pH-independence of the reaction observed experimentally. When the protonation is favorable (as in the standard state) the activation energy would be measured from 6 to the 6–7 transition state, and would not be proton-dependent. It is possible then, that the calculated pKa of 6 is too small, and that 2 becomes favorably protonated at all examined pH values. The simplest, and most probable explanation for the lack of pH-dependence is that nitrate binding, or the preparation of the active catalyst in general, is rate-determining, in which case a strong proton-dependence would not be expected. Given the small barriers calculated for the nitrate to nitrite reduction in each mechanism, it makes sense that these steps would not be rate-determining. Overall, the calculations themselves do not suggest a reason why the proton-assisted pathway would not occur, but nonetheless, they do indicate that nitrite formation can still occur via numerous different binding modes and protonation states.
While the initial DFT calculations identified reasonable mechanisms summarized in Fig. 9, they will need to be followed-up by more detailed studies exploring other mechanistic pathways that include explicit involvement of the solvent or the NH protons on DIM ligand. Future work will also focus on gaining a better understanding of the multistate reactivity in these systems. This will necessitate identification of the minimum energy crossing points and application of wavefunction-based methods (e.g., CASPT2) to obtain more accurate barriers and spin-state energetics.56,57
Summary and conclusions
A combined experimental and computational investigation reveal that two electron reduction of the Co(III) complexes [Co(DIM)X2]+ (X = Br−, NO3−) in aqueous solution leads to formation of a four-coordinate complex [Co(DIM)]+, in which both cobalt and the DIM ligand are reduced by one electron. This complex then enters the cycle for the electrocatalytic reduction of aqueous nitrate to ammonia, which occurs with high faradaic efficiency and over a wide pH range. In this context, it is notable that proton reduction is not competitive, even at relatively acidic pH.58–60The computational investigation highlights several critical features of this system, most notably the multiple roles played by the redox active DIM ligand in enhancing the efficacy of this catalyst. Firstly, the DIM ligand facilitates active catalyst formation by providing an additional site for electron storage, which avoids higher energy electronic states in which the Co ion is doubly reduced. Since Co(II) is expected to be more Lewis acidic and less nucleophilic than Co(I), this is also expected to favor the reduction of nitrate over protons. Secondly, the reduced DIM ligand is also able to transfer this electron directly to nitrate, which activates it for N–O bond homolysis and nitrite release. Thus, the two electron reduction of nitrate to nitrite occurs via two single electron transfers. Further mechanistic studies are underway to explore these and other features that impact formation of nitrite and its subsequent conversion to ammonia. Finally, the structural flexibility of the macrocycle facilitates N–O bond cleavage by allowing the substrate to access a cis-coordination mode on cobalt. While the current work does not yet provide an explanation for the increased selectivity and lack of side-product formation for [Co(DIM)X2]+ compared to [Co(cyclam)X2]+, it does provide a starting place for further investigation of mechanistic features of these (and other) cyclam-based ligands. More generally, the insights from these studies suggest strategies for the design of improved nitrate reduction catalysts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. X. and J. M. S. acknowledge funding from Indiana University and the NSF (CHE-1566258). We thank Ken Caulton for alerting us to ref. 38. D. C. A, H. Y. K., G. R. W. and E. J. acknowledge funding from North Carolina State University and the NSF (CHE-1359377), as well as the services of the High-Performance Computing center at NCSU. This work used the Extreme Science and Engineering Discovery Environment (XSEDE) Bridges at the Pittsburgh Supercomputing Center through allocation TG-CHE170031. XSEDE is supported by the NSF ACI-1548562.61Notes and references
- V. Smil, Enriching the Earth, MIT Press, Cambridge, MA, 2001 Search PubMed.
- J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636 CrossRef.
- R. Schlögl, Angew. Chem., Int. Ed., 2003, 42, 2004 CrossRef PubMed.
- I. Rafiqul, C. Weber, B. Lehmann and A. Voss, Energy, 2005, 30, 2487 CrossRef.
- P. Pfromm, J. Renewable Sustainable Energy, 2017, 9, 034702 CrossRef.
- S. Matassa, D. J. Batstone, T. Hülsen, J. Schnoor and W. Verstraete, Environ. Sci. Technol., 2015, 49, 5247 CrossRef PubMed.
- J. N. Galloway, J. D. Aber, J. W. Erisman, S. P. Seitzinger, R. W. Howarth, E. B. Cowling and B. J. Cosby, BioScience, 2003, 53, 341 CrossRef.
- D. Fowler, M. Coyle, U. Skiba, M. A. Sutton, J. N. Cape, S. Reis, L. J. Sheppard, A. Jenkins, B. Grizzetti, J. N. Galloway, P. Vitousek, A. Leach, A. F. Bouwman, K. Butterbach-Bahl, F. Dentener, D. Stevenson, M. Amann and M. Voss, Philos. Trans. R. Soc., B, 2013, 368, 1621 Search PubMed.
- M. Sebilo, B. Mayer, B. Nicolardot, G. Pinay and A. Mariotti, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18185 CrossRef PubMed.
- M. D. Smith, A. Oglend, A. J. Kirkpatrick, F. Asche, L. S. Bennear, J. K. Craig and J. M. Nance, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1512 CrossRef PubMed.
- R. Vaquer-Sunyer and C. M. Duarte, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15452 CrossRef PubMed.
- R. J. Diaz and R. Rosenberg, Science, 2008, 321, 926 CrossRef PubMed.
- L. Canter, Nitrate in Groundwater, Lewis Publishers, Boca Raton, 1997 Search PubMed.
- J. A. Camargo and Á. Alonso, Environ. Int., 2006, 32, 831 CrossRef PubMed.
- V. Rosca, M. Duca, M. T. de Groot and M. T. M. Koper, Chem. Rev., 2009, 109, 2209 CrossRef PubMed.
- M. Duca and M. T. M. Koper, Energy Environ. Sci., 2012, 5, 9726 Search PubMed.
- G. Sahara and O. Ishitani, Inorg. Chem., 2015, 54, 5096 CrossRef PubMed.
- H. Tian, ChemSusChem, 2015, 8, 3746 CrossRef PubMed.
- S. Sultana, P. Chandra Sahoo, S. Martha and K. Parida, RSC Adv., 2016, 6, 44170 RSC.
- X. Liu, S. Inagaki and J. Gong, Angew. Chem., Int. Ed., 2016, 55, 14924 CrossRef PubMed.
- R. Kuriki and K. Maeda, Phys. Chem. Chem. Phys., 2017, 19, 4938 RSC.
- H. Takeda, C. Cometto, O. Ishitani and M. Robert, ACS Catal., 2017, 7, 70 CrossRef.
- Saturated calomel electrode (SCE): +0.2412 V vs. NHE, see A. J. Bard and L. J. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2000 Search PubMed.
- Non-electrocatalytic nitrate reduction to NO, see C. L. Ford, Y. Park, E. M. Matson, Z. Gordon and A. R. Fout, Science, 2016, 354, 741 CrossRef PubMed.
- N. Chebotareva and T. Nyokong, J. Appl. Electrochem., 1997, 27, 975 CrossRef.
- B. Keita, E. Abdeljalil, L. Nadjo, R. Contant and R. Belgiche, Electrochem. Commun., 2001, 3, 56 CrossRef.
- Z. Zhang, Y. Qi, C. Qin, Y. Li, E. Wang, X. Wang, Z. Su and L. Xu, Inorg. Chem., 2007, 46, 8162 CrossRef PubMed.
- J. Shen, Y. Y. Birdja and M. T. M. Koper, Langmuir, 2015, 31, 8495 CrossRef PubMed.
- T. Yoshioka, K. Iwase, S. Nakanishi, K. Hashimoto and K. Kamiya, J. Phys. Chem. C, 2016, 120, 15729 Search PubMed.
- M. Delgado and J. D. Gilbertson, Chem. Commun., 2017, 53, 11249 RSC.
- A. J. Timmons and M. D. Symes, Chem. Soc. Rev., 2015, 44, 6708 RSC.
- L. Taniguchi, N. Nakashima and K. Yasukouchi, J. Chem. Soc., Chem. Commun., 1986, 1814 RSC.
- I. Taniguchi, N. Nakashima, K. Matsushita and K. Yasukouchi, J. Electroanal. Chem. Interfacial Electrochem., 1987, 224, 199 CrossRef.
- H. L. Li, W. C. Anderson, J. Q. Chambers and D. T. Hobbs, Inorg. Chem., 1989, 28, 863 CrossRef.
- L. Ma, B.-Y. Zhang, H.-L. Li and J. Q. Chambers, J. Electroanal. Chem., 1993, 362, 201 CrossRef.
- L. Ma and H. Li, Electroanalysis, 1995, 7, 756 CrossRef.
- E. Simon, E. Sablé, H. Handel and M. L'Her, Electrochim. Acta, 1999, 45, 855 CrossRef.
- Y. Xiang, D.-L. Zhou and J. F. Rusling, J. Electroanal. Chem., 1997, 424, 1 CrossRef.
- S. C. Jackels, K. Farmery, E. K. Barefield, N. J. Rose and D. H. Busch, Inorg. Chem., 1972, 11, 2893 CrossRef.
- This conclusion is based on the fact that in every instance (that is not hampered by ligand dissociation) the calculated electronic structures of any two-electron reduced Co–DIM complex considered in this study show ligand-based reduction. Given the consistency of this electronic structure feature there is no reason to assume it would be different for the two-electron reduction of [Co(DIM)Br2]+.
- H. L. Schläfer and G. Gliemann, Basic Principles of Ligand Field Theory, Wiley Interscience, New York, 1969 Search PubMed.
- For more details of conductivity values, please see Table S2.†.
- For pKa values of other reported Co(III) complexes, please see Table S1.†.
- Fast scan rates (>100 mV s−1) were applied for the study to avoid possible catalytic nitrate reduction.
- The energetic cost of ∼4 kcal mol−1 for ligand exchange in and of itself could suggest that water cannot substitute for bromide or nitrate, but given the expected error range of typical DFT calculations being 3–5 kcal mol−1 this value is not conclusive one way or the other. The more critical conclusion to draw is that for both complexes the first ligand exchange is not highly energetically uphill.
- When the pH of solution was below 3.5, proton reduction was observed instead of nitrate reduction.
- Q. Yu, A. Kandegedara, Y. Xu and D. B. Rorabacher, Anal. Biochem., 1997, 253, 50 CrossRef PubMed.
- M. W. Weatherburn, Anal. Chem., 1967, 39, 971 CrossRef.
- D. S. Frear and R. C. Burrell, Anal. Chem., 1955, 27, 1664 CrossRef.
- J. Li, R. Guttinger, R. More, F. Song, W. Wan and G. R. Patzke, Chem. Soc. Rev., 2017, 46, 6124 RSC.
- R. H. Crabtree, Chem. Rev., 2015, 115, 127 CrossRef PubMed.
- See ESI for detailed tests for catalyst homogeneity.†.
- C. Costentin and J. M. Savéant, ChemElectroChem, 2014, 1, 1226 CrossRef.
- E. S. Rountree, B. D. McCarthy, T. T. Eisenhart and J. L. Dempsey, Inorg. Chem., 2014, 53, 9983 CrossRef PubMed.
- See ESI for more details on the FOWA.†.
- D. C. Ashley and E. Jakubikova, Coord. Chem. Rev., 2017, 337, 97 CrossRef.
- J. Harvey, Coord. Chem. Rev., 2003, 238–239, 347 CrossRef.
- V. S. Thoi, Y. Sun, J. R. Long and C. J. Chang, Chem. Soc. Rev., 2013, 42, 2388 RSC.
- B. B. Beyene, S. B. Mane and C.-H. Hung, Chem. Commun., 2015, 51, 15067 RSC.
- J. W. Jurss, R. S. Khnayzer, J. A. Panetier, K. A. El Roz, E. M. Nichols, M. Head-Gordon, J. R. Long, F. N. Castellano and C. J. Chang, Chem. Sci., 2015, 6, 4954 RSC.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazelwood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkins-Diehr, Comput. Sci. Eng., 2014, 16, 62 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1823665 and 1823666. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc00721g |
| ‡ Details on computational methods; comparison of calculated structures with experimental crystal structures, methodology verification/benchmarking; additional discussion on the computational prediction of the active species formation; calculated square schemes for all electrochemical processes considered; reaction coordinate diagrams for all considered spin surfaces; schematic of how electron transfer is affected by different spin states; NOs of quintet 3, energetics of anion binding studies; raw calculated energies for all species considered (PDF). Cartesian coordinates of all optimized structures (xyz). |
| This journal is © The Royal Society of Chemistry 2018 |