Open Access Article
Open Access ArticleSelective hydrogenation of 1,3-butadiene catalyzed by a single Pd atom anchored on graphene: the importance of dynamics†
Yingxin
Feng
 a,
Linsen
Zhou
b,
Qiang
Wan
a,
Sen
Lin
a,
Linsen
Zhou
b,
Qiang
Wan
a,
Sen
Lin
 *ab and
Hua
Guo
*ab and
Hua
Guo
 *b
*b
aState Key Laboratory of Photocatalysis on Energy and Environment, College of Chemistry, Fuzhou University, Fuzhou 350002, China. E-mail: slin@fzu.edu.cn
bDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque, New Mexico 87131, USA. E-mail: hguo@unm.edu
First published on 14th June 2018
Abstract
The active-site structure, reaction mechanism, and product selectivity of the industrially important selective hydrogenation of 1,3-butadiene are investigated using first principles for an emerging single-atom Pd catalyst anchored on graphene. Density functional theory calculations suggest that the mono-π-adsorbed reactant undergoes sequential hydrogenation by Pd-activated H2. Importantly, the high selectivity towards 1-butene is attributed to the post-transition-state dynamics in the second hydrogenation step, which leads exclusively to the desorption of the product. This dynamical event prevails despite the existence of energetically preferred 1-butene adsorption on Pd, which would eventually lead to complete hydrogenation to butane and be thus inconsistent with experimental observations. This insight underscores the importance of dynamics in heterogeneous catalysis, which has so far been underappreciated.
Introduction
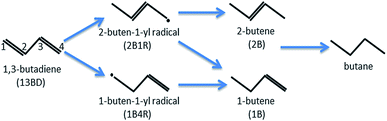
1,3-Butadiene (CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH
CH–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2) formed in petroleum cracking is a potent poison for polymerization catalysts in industrial alkene streams, and its removal is essential and commonly accomplished with catalytic hydrogenation.1 In the catalyzed hydrogenation of 1,3-butadiene, several products, including butenes and butane, can be produced with the classical Horiuti–Polanyi mechanism (see Scheme 1). Despite their high activity, the commonly used catalysts of supported precious transition metal (e.g., Pd or Pt) nanoparticles are not very selective.2–6 It is thus highly desirable to design active catalysts with high selectivity towards one or more specific products, preferably 1-butene (CH2
CH2) formed in petroleum cracking is a potent poison for polymerization catalysts in industrial alkene streams, and its removal is essential and commonly accomplished with catalytic hydrogenation.1 In the catalyzed hydrogenation of 1,3-butadiene, several products, including butenes and butane, can be produced with the classical Horiuti–Polanyi mechanism (see Scheme 1). Despite their high activity, the commonly used catalysts of supported precious transition metal (e.g., Pd or Pt) nanoparticles are not very selective.2–6 It is thus highly desirable to design active catalysts with high selectivity towards one or more specific products, preferably 1-butene (CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH2–CH3), which can be used as the pure alkene feedstock for subsequent polymerization reactions. This process underscores the importance of selectivity in heterogenous catalysis in general.
CH–CH2–CH3), which can be used as the pure alkene feedstock for subsequent polymerization reactions. This process underscores the importance of selectivity in heterogenous catalysis in general.
Single-atom catalysts (SACs) have recently emerged as a promising alternative to traditional catalysts for catalyzing various chemical transformations, because of their high atomic efficiency and unique reaction mechanisms.7–9 Highly active and selective SACs of the hydrogenation of 1,3-butadiene have been reported by several groups. Zhang et al.,10 for example, found that the hydrogenation of 1,3-butadiene over Au/ZrO2 catalysts has 100% selectivity towards butenes owing to a small number of isolated Au3+ ions on the ZrO2 surface. Sykes and coworkers showed that isolated Pt atoms on a Cu surface can also catalyze under mild conditions the butadiene hydrogenation reaction with high selectivity towards butenes.11 More recently, by using two-dimensional graphene as the support, atomically dispersed Pd has been reported by Yan et al.12 to exhibit near 100% butene selectivity in 1,3-butadiene hydrogenation with 95% conversion at 50 °C.
The observed selectivity in SAC-catalyzed butadiene hydrogenation can be rationalized partially by the fact that an atomically dispersed SAC site is incapable of the di-π-adsorption commonly seen on metal surfaces or nanoparticles,13–17 where the molecular plane is parallel to the metal surface. Rather, the atomic size of the SAC necessitates mono-π-adsorption and preferential hydrogenation of one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond at a time. Nevertheless, SAC catalytic mechanisms are often more complex than this simple geometric argument, particularly on the question of selectivity. Indeed, a sequential hydrogenation mechanism does not automatically lead to selectivity. The selective production of a butene has to stem from either thermodynamic or kinetic obstacles to its further hydrogenation.
C double bond at a time. Nevertheless, SAC catalytic mechanisms are often more complex than this simple geometric argument, particularly on the question of selectivity. Indeed, a sequential hydrogenation mechanism does not automatically lead to selectivity. The selective production of a butene has to stem from either thermodynamic or kinetic obstacles to its further hydrogenation.
To gain a deeper understanding of the selectivity, theoretical insights are very helpful. On the Pt(111) and Pd(111) surfaces, for example, density functional theory (DFT) calculations by Sautet and coworkers have revealed that the selectivity can be attributed to the difference in adsorption energy between 1,3-butadiene (stronger adsorption due to two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds) and butene (weaker adsorption due to one C
C double bonds) and butene (weaker adsorption due to one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond) as well as the different stabilization energies of key radical intermediates.14 However, such a mechanism is unlikely to operate on SACs because the adsorption energy of neither the reactant nor intermediate will be much different, given the fact each SAC can only bind to a single C
C double bond) as well as the different stabilization energies of key radical intermediates.14 However, such a mechanism is unlikely to operate on SACs because the adsorption energy of neither the reactant nor intermediate will be much different, given the fact each SAC can only bind to a single C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond.
C double bond.
Liu and coworkers recently investigated the conversion of 1,3-butadiene catalyzed by an Au SAC supported by a ZrO2 surface.18 Their DFT calculations revealed that the first hydrogenation step is with a OH group on the oxide surface followed by abstraction of H adsorbed on Au, while the subsequent hydrogenation toward butane was found to have a similar barrier height as the first hydrogenation step. Arguments against the total hydrogenation were offered, but no direct evidence was presented.18 While this insightful work sheds much light on the catalytic mechanism on metal SACs on oxide supports, neither would it be applicable for SACs on metals11 or on 2D materials,12 as OH groups are unlikely to be present in the latter two systems.
In this work, by combining static DFT calculations with ab initio molecular dynamics (AIMD)19 or direct dynamics20 simulations, the key steps of 1,3-butadiene hydrogenation over a graphene supported Pd SAC (Pd1/graphene) are examined. This system is unique as it offers a clean prototype for understanding the selective butadiene hydrogenation on a structurally well-defined SAC.12 Our DFT calculations pay particular attention to the active-site structure of the SAC and putative catalytic pathways, which are found to be consistent with existing experimental observations. Perhaps more interestingly, the origin of selectivity is revealed by AIMD simulations to be the post-transition-state dynamics in the second hydrogenation step, in which the 1-butene desorbs as the exothermic transfer of a hydrogen atom from Pd supplies sufficient kinetic energy to overcome the adsorption energy. This dynamical event prevails even when there exists a lower energy alternative for the binding of the remaining C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond of 1-butene with Pd, which would lead to the total hydrogenation to butane and thus be inconsistent with the experimental observation.
C double bond of 1-butene with Pd, which would lead to the total hydrogenation to butane and thus be inconsistent with the experimental observation.
The importance of dynamics in heterogeneous catalysis has recently attracted much attention. For the mandatory initial dissociative chemisorption, detailed experiments have shown that different forms of the reactant energy (vibration vs. translation) promote the dissociation with different efficacies.21–23 However, there has been no example on the influence of dynamics in product branching in surface chemistry. The dynamically driven selectivity demonstrated here is conceptually at odds with the conventional picture in which the potential energy surface (PES) dictates not only the mechanism and reactivity, but also product branching. Specifically in the so-called statistical paradigm,24 a reaction should follow the intrinsic reaction coordinate (IRC) on the PES, which defines the minimum energy path from reactants to the transition state and then to the various products. However, there is increasing experimental and theoretical evidence indicating that this energetically based picture may not be valid for many chemical reactions, in which the avoidance of the IRC after passing through the reaction transition state leads to “unexpected” products.25–31 The key factor in non-IRC reactions is the kinetic energy, which is not accounted for by the PES alone. In a full dynamic characterization of the reaction, as a result, the kinetic energy gained after passing through the transition state can lead trajectories to stray from the minimum energy path. In the system discussed here, the dynamically driven selectivity in the hydrogenation of 1,3-butadiene demonstrates that potential energy is not always the only determining factor in heterogeneous catalysis. Under such circumstances, the dynamics has to be explicitly considered.
Computational details
DFT
All spin-polarized density functional theory (DFT) calculations were carried out using the Vienna Ab initio Simulation Package (VASP)32,33 with the gradient-corrected Perdew–Burke–Ernzerhof (PBE) functional.34 The valence electrons were described with a plane-wave basis set with a cutoff energy of 400 eV, while the core electrons were approximated using the projector augmented-wave method.35 Total energies were corrected for dispersion interaction by employing Grimme's semi-empirical scheme36 and the test results without this van der Waals correction are provided in the Table S1.† An orthorhombic unit cell of graphene with a = 9.84 Å (four hexagons in the x direction), b = 12.78 Å (five hexagons in the y direction) and c = 30.0 Å is used. A 2 × 2 × 1 Monkhorst–Pack k-point grid37 were adopted for Brillouin zone integration and test for convergency. The geometries were optimized by the conjugate gradient algorithm until the maximum force on any ion was less than 0.03 eV Å−1, in which all the atoms in the catalyst and adsorbate were fully relaxed. The climbing image nudged elastic band (CI-NEB)38,39 approach was employed to determine the reaction paths and vibrational analyses were further performed to ensure the stationary point characteristics of the local minima and transition states.AIMD simulations
To follow post-transition-state dynamics, ab initio molecular dynamics (AIMD) simulations19 were carried out using VASP with the same set up as described above. A characteristic trajectory is first propagated by starting it at the transition state determined by the NEB calculation with zero atomic velocities. Further trajectories were computed with the same initial geometry at the transition state, but with initial velocities of the atoms assigned randomly and scaled to make the average kinetic energy of 300 K. We also employed microcanonical sampling for the initial conditions of the trajectories using normal modes at the transition state,40,41 which are obtained from diagonalizing the mass-weighted Hessian in normal mode analysis. The velocities of the surface atoms were sampled at 300 K. These trajectories were propagated with a microcanonical (NVE) ensemble using the leap-frog algorithm implemented in VASP, with a maximum propagation time of 2 ps and a time step of 0.5 fs. The total energy was well conserved within ∼20 meV for all trajectories.Results and discussion
Model of the Pd1/graphene SAC
How a Pd SAC forms on the graphene support is the first step toward a complete understanding of the catalytic mechanism of the selective hydrogenation of 1,3-butadiene. The model developed here is based on information from the experiment of Yan et al.,12 who reported the fabrication of the Pd–graphene system as well as X-ray photoemission spectroscopy (XPS), the scanning transmission electron microscopy (STEM), and extended X-ray absorption fine structure (EXAFS) measurements. These experimental data suggest that atomically dispersed Pd species are anchored on graphene with tetra-coordination with one C and three O atoms.Our model of the Pd1/graphene SAC thus consists of one Pd–C and three Pd–O bonds, as shown in Fig. 1, consistent with the observed first-shell peaks of the EXAFS spectrum.12 The oxygen species Oa, which bridges the Pd atom and graphene, corresponds to a phenolic oxygen created by oxidation of graphene.12 The Pd atom is further anchored on the graphene with Ca. To complete the tetra-coordination of Pd, two other oxygen species (Ob and Ob′) are included (Fig. 1a), which are presumably the residues after the removal of the hexafluoroacetylacetate ligands used in the atomic layer deposition of the Pd species.12 Furthermore, we found that an additional oxygen is needed to saturate two carbon atoms in the graphene defect site in order to avoid the formation of two additional Pd–C bonds. This C–O–C moiety is formed on the opposite side of the graphene and serves largely as a structural rather than catalytic motif. As shown in Table 1, the optimized geometry of the SAC yields bond lengths that are in good agreement with the experimental values of the Pd–C and Pd–O bond lengths in the first coordination shell.12 In addition, the presence of second shell carbon atoms in our model is also consistent with the weak peaks in EXAFS.12 The Bader charge analysis indicates that the charge of the Pd atom is +0.69e, consistent with the experimental observation that the isolated Pd atoms on the graphene surface are positively charged.12
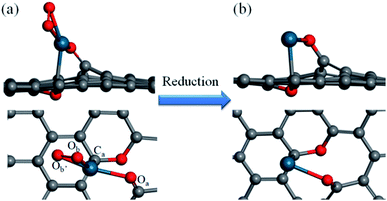 | ||
| Fig. 1 Side and top views of the Pd1/graphene SAC (a) before and (b) after reduction. Color scheme: C, gray; O, red; Pd, blue. | ||
| Bond | Theo. | Expt.12 |
|---|---|---|
| Pd–Oa | 2.09 | 2.05 |
| P–Ob | 2.05 | 2.07 |
| Pd–Ob′ | 2.00 | 2.07 |
| Pd–Ca | 2.25 | 2.00 |
The SAC structure discussed above is unfortunately not a very active catalyst based on our preliminary DFT calculations of the hydrogenation reaction (not shown here), presumably because of the chemical inertness of the tetra-coordinated Pd. It is noted however that in the experiment the catalyst was pretreated in 10% H2 in Ar at 150 °C, which could conceivably reduce the O moieties bonded to Pd. To explore this possibility, reactions (1)–(3) are examined theoretically:
| PdO2/graphene + H2 → Pd(OH)2/graphene | (1) |
| Pd(OH)2/graphene + H2 → PdOH/graphene + H2O | (2) |
| PdOH/graphene + H2 → Pd/graphene + H2O | (3) |
It was found from DFT calculations that reaction (1) has a large exothermicity of −3.28 eV, indicating that two Pd binding O moieties can be readily reduced to hydroxyl (OH) groups in the presence of H2 (Fig. S1 in ESI†). These two ligands can be further reduced by an additional H2 molecule to form two free H2O molecules in reactions (2) and (3). These two reactions are calculated to have moderate barriers, 0.98 and 0.63 eV, respectively (Fig. S2†). The final activated SAC is thus likely an unsaturated single Pd atom anchored on graphene (Fig. 1b).
The resulting Pd1/graphene SAC model is used below to investigate both the adsorption and catalysis. This SAC is reasonably stable, with a Pd binding energy of −1.87 eV which is calculated from Eb = EPd–support − Esupport − EPd where EPd–support is the energy of Pd-SAC, Esupport is the energy of the support by removing the Pd atom and EPd is the energy of the Pd atom. This is similar to the Pd adsorption energy (−1.75 eV) on CeO2(111).42 The Pd atom has a charge of +0.30e, suggesting a significant cationic character due to charge transfer to its two ligands.
Adsorption of pertinent species
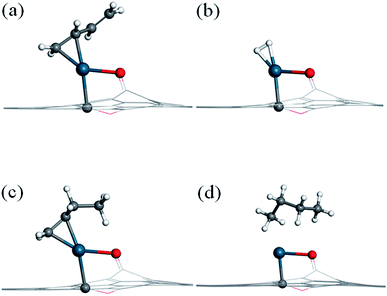
Before investigating the reaction mechanism, the adsorption behavior of H2, 1,3-butadiene (13BD), 1-butene (1B), and butane is studied (Fig. 2). The hydrogen molecule is found to adsorb on Pd with Pd–H distances of 1.73 and 1.74 Å, respectively, and with a binding energy of −0.78 eV. The bond length of H2 is about 0.87 Å, which is 0.12 Å longer than that in its isolated state. Therefore, the hydrogen can be considered activated by the Pd atom, but not dissociated.For 1,3-butadiene, we have used the trans-form in our calculations because it is the dominant isomer at room temperature. Since the SAC-catalyzed hydrogenation is sequential, furthermore, no fundamental difference is expected between the cis and trans isomers because the corresponding products (cis and trans-1-butene) are related by a (free) rotation around the middle single C–C bond. As expected, only one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond is capable to bind with the Pd atom, while another C
C double bond is capable to bind with the Pd atom, while another C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond is tilted from the graphene surface. The length of the adsorbed C
C double bond is tilted from the graphene surface. The length of the adsorbed C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond moiety is 1.41 Å, which is elongated by 0.07 Å relative to the isolated molecule, and the Pd–C bond distances are 2.13 and 2.17 Å, respectively. The binding energy is −1.66 eV, much larger than that of H2.
C double bond moiety is 1.41 Å, which is elongated by 0.07 Å relative to the isolated molecule, and the Pd–C bond distances are 2.13 and 2.17 Å, respectively. The binding energy is −1.66 eV, much larger than that of H2.
For 1-butene, the most stable adsorption configuration involves the remaining C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond attached to the Pd atom. Its adsorption energy (−1.72 eV) is quite similar to that for 1,3-butadiene. For butane, on the other hand, the molecule is found to interact weakly with the Pd atom with a relatively small binding energy of −0.56 eV. For all these adsorption states, the Pd atom keeps its bonds with the substrate carbon atom and the phenolic oxygen of the graphene support.
C double bond attached to the Pd atom. Its adsorption energy (−1.72 eV) is quite similar to that for 1,3-butadiene. For butane, on the other hand, the molecule is found to interact weakly with the Pd atom with a relatively small binding energy of −0.56 eV. For all these adsorption states, the Pd atom keeps its bonds with the substrate carbon atom and the phenolic oxygen of the graphene support.
Reaction mechanism of 1,3-butadiene hydrogenation
The hydrogenation reaction starts with the co-adsorption of H2 and 1,3-butadiene on the Pd SAC (IS1 in Fig. 3). In this co-adsorption state, the binding energies of H2 and 1,3-butadiene is −0.21 eV and −1.09 eV, respectively. For convenience of discussion, we label the four carbon atoms in 1,3-butadiene as 1, 2, 3, and 4. As indicated in Scheme 1, it is possible for one of the coadsorbed hydrogen atoms to attack either the terminal (C1) or interior (C2) carbon in the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 double bond adsorbed to Pd, resulting in 2-buten-1-yl radical (2B1R) and 1-buten-1-yl radical (1B4R), respectively. As shown in Fig. 3, our calculations indicate that the addition of H to C2 results in a significantly larger energy barrier of 1.89 eV with a reaction energy of 0.50 eV, while for the attack of H to C1 the energy barrier is much lower (1.33 eV) and the reaction is become thermoneutral. As a result, the latter is considered as the favored channel and the former is not pursued further. In the transition state (TS1) of the terminal attack pathway (IS1 → TS1 → IM1), the distance of the forming C1–H bond is 1.46 Å and the H–Pd bond length is 1.65 Å. After reaction, the intermediate (IM1 or 2B1R*) adsorbs at the Pd center with a mono-dentate configuration with a C–Pd distance of 2.09 Å.
C2 double bond adsorbed to Pd, resulting in 2-buten-1-yl radical (2B1R) and 1-buten-1-yl radical (1B4R), respectively. As shown in Fig. 3, our calculations indicate that the addition of H to C2 results in a significantly larger energy barrier of 1.89 eV with a reaction energy of 0.50 eV, while for the attack of H to C1 the energy barrier is much lower (1.33 eV) and the reaction is become thermoneutral. As a result, the latter is considered as the favored channel and the former is not pursued further. In the transition state (TS1) of the terminal attack pathway (IS1 → TS1 → IM1), the distance of the forming C1–H bond is 1.46 Å and the H–Pd bond length is 1.65 Å. After reaction, the intermediate (IM1 or 2B1R*) adsorbs at the Pd center with a mono-dentate configuration with a C–Pd distance of 2.09 Å.
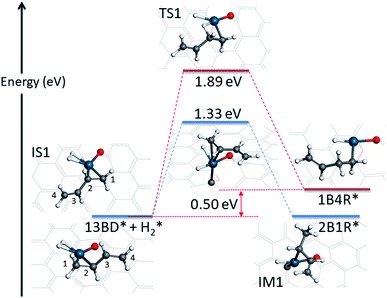 | ||
| Fig. 3 Energetics and structures of stationary points along the reaction pathway for the first hydrogenation step of 1,3-butadiene to form 1-butene on the Pd1/graphene SAC. IS: initial state; TS: transition state; IM: intermediate state; FS: final state. The same color scheme as in Fig. 2 is used. | ||
The first hydrogenation step is rate limiting in this SAC catalyzed reaction. Its barrier of 1.33 eV is higher than that of the Pd catalyzed hydrogenation reaction, which is 1.24 eV on Pd(111).14 This is not inconsistent with the smaller turnover frequency (0.35 s−1)12 on the SAC than that on supported Pd nanocrystals with particle sizes of about 4 nm (>6.5 s−1).43
The first hydrogenation step described above opens the Pd atom up for a further adsorption of H2, because of the conversion of the mono-π-adsorption of 13BD* to a mono-π-adsorption of 2B1R* accompanied by the loss of a Pd-bound H. This is quite plausible as the feed gas in the experiment contains a large amount of H2 (4.7%),12 and necessary for the formation of the final product. The adsorption of an additional H2 has a binding energy of −0.20 eV with the H–H bond length of 0.81 Å, signifying its relative stability. In Fig. 4, the energy profile of the second hydrogenation step is given starting with IS2. The attack of C2 of 2B1R* by the Pd-bound H leads to a small barrier of 0.35 eV. At the transition state (TS2), the H–Pd distance is 1.57 Å while the H–C2 distance is 1.59 Å.
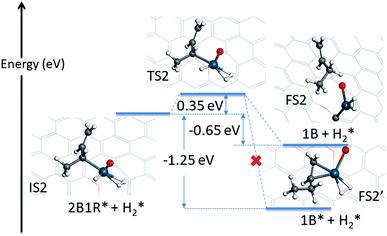 | ||
| Fig. 4 Energetics and geometries of stationary points along the reaction pathway for the second hydrogenation step of 1,3-butadiene to form 1-butene with a preadsorbed H2 on the Pd1/graphene SAC. The same color scheme as in Fig. 2 is used. | ||
The possible outcome of the second hydrogenation step presents an interesting situation. On one hand, the 1-butene product can stick to Pd, as shown in Fig. 4, with a strong mono-π-adsorption with the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 moiety (adsorption energy of −1.72 eV). In Fig. S3,† the minimum energy path connecting the transition state (TS2) and adsorbed 1-butene (1B*) is shown and it is clear that it involves significant reorientation of the molecule. This energetically favored state is expected to undergo further hydrogenation to butane, thus inconsistent with the experimental observation. On the other hand, the 1-butene product can desorb, leading to a product state with an energy of −0.65 eV, as shown in the same figure. If energy were the only determining factor, the former would dominate, but this would be inconsistent with the experimentally observed high selectivity toward 1-butene, as the subsequent hydrogenation of the C3
C4 moiety (adsorption energy of −1.72 eV). In Fig. S3,† the minimum energy path connecting the transition state (TS2) and adsorbed 1-butene (1B*) is shown and it is clear that it involves significant reorientation of the molecule. This energetically favored state is expected to undergo further hydrogenation to butane, thus inconsistent with the experimental observation. On the other hand, the 1-butene product can desorb, leading to a product state with an energy of −0.65 eV, as shown in the same figure. If energy were the only determining factor, the former would dominate, but this would be inconsistent with the experimentally observed high selectivity toward 1-butene, as the subsequent hydrogenation of the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 double bond would be readily catalyzed by the same Pd SAC.
C4 double bond would be readily catalyzed by the same Pd SAC.
Post-transition-state dynamics
By inspecting TS2 in Fig. 4, it is not difficult to see that the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 moiety is quite far from Pd and the incipient 1-butene could indeed desorb, rather than following the IRC towards adsorbed 1B* shown in Fig. S3.† To determine the preference of these two product states, we first performed an AIMD calculation starting from TS2 (Fig. 5a) with zero initial velocity for all atoms. The final (2 ps) snapshot of the trajectory is shown in Fig. 5b, where the center of mass of the 1-butene product has moved about 15 Å away from the Pd. The movies of this trajectory can be found in SI. To further confirm our finding, nine additional trajectories were initiated at the same TS2 geometry, but with randomly assigned initial velocities and 16 zero-point energy sampled trajectories of the hydrogenation reaction began with different geometries displaced along the normal modes orthogonal to the reaction coordinate. All trajectories lead to the desorption of 1-butene, with none to the lower-energy adsorption of 1-butene with the Pd SAC.
C4 moiety is quite far from Pd and the incipient 1-butene could indeed desorb, rather than following the IRC towards adsorbed 1B* shown in Fig. S3.† To determine the preference of these two product states, we first performed an AIMD calculation starting from TS2 (Fig. 5a) with zero initial velocity for all atoms. The final (2 ps) snapshot of the trajectory is shown in Fig. 5b, where the center of mass of the 1-butene product has moved about 15 Å away from the Pd. The movies of this trajectory can be found in SI. To further confirm our finding, nine additional trajectories were initiated at the same TS2 geometry, but with randomly assigned initial velocities and 16 zero-point energy sampled trajectories of the hydrogenation reaction began with different geometries displaced along the normal modes orthogonal to the reaction coordinate. All trajectories lead to the desorption of 1-butene, with none to the lower-energy adsorption of 1-butene with the Pd SAC.
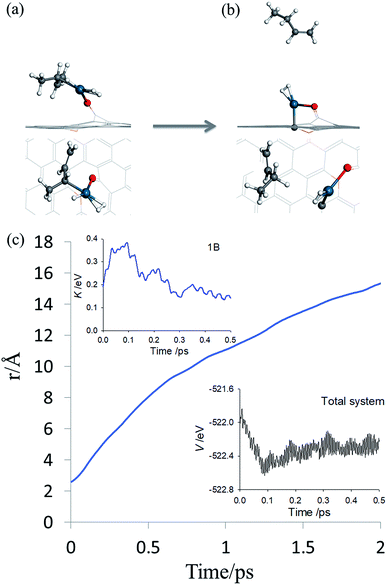 | ||
| Fig. 5 AIMD post-transition state simulation of product formation. (a and b) Initial and final snapshots of AIMD trajectory in both top and side views, respectively. The same color scheme as in Fig. 2 is used. (c) Time evolution of the distance between the center-of-mass of carbon atoms in 13BD and the Pd atom. The insets depict the potential energy of the entire system and kinetic energy of 1-butene, respectively. | ||
The desorption of 1-butene is apparently driven by the repulsion between the incipient 1-butene and Pd SAC following the hydrogenation. Recall that a saturated carbon is significantly farther from Pd (∼2.52 Å in the butane–Pd system) than that before hydrogenation (2.09 Å in IM1), so the hydrogenation places the incipient 1-butene in a repulsive part of the PES, which pushes it to desorption. This is reflected in the insets of Fig. 5c where the potential energy of the entire system and kinetic energy of 1-butene are plotted as a function of time. The post-transition-state repulsive interaction results in a rapid decrease of the potential energy of the system and concomitant increase of kinetic energy of 1-butene in the first 100 fs, some of which is subsequently used to overcome the adsorption potential during desorption. The kinetic energy forces the system to avoid the minimum energy path defined by the IRC, which eventually leads to the adsorption of 1-butene.
These AIMD calculations clearly demonstrated that the post-transition-state dynamics drives the system to the desorption of the desired product (namely the 1-butene), without accessing the energetically preferred state of adsorbed 1-butene, which can be further hydrogenated to butane. This non-IRC mechanism, which has recently been found to operate in many organic25–30 and enzymatic reactions,31 explains the experimentally observed high selectivity in this SAC-catalyzed reaction. Interestingly, this mechanism for selectivity is fundamentally different from that on Pt(111) and Pd(111), where the different adsorption energies of 1,3-butadiene and 1-butene in combination with different stabilization energies for key radical intermediates are responsible for the selective production of 1-butene.14 There, no dynamics is needed to rationalize the selectivity.
Conclusions
In this work, we address here two important issues in the industrially important selective hydrogenation of 1,3-butadiene catalyzed by a Pd SAC anchored on graphene. First, DFT calculations were used to elucidate the nature of the SAC active site and the catalytic mechanism. Our Pd SAC model is consistent with experimental structural information. Following the classical Horiuti–Polanyi mechanism, the hydrogenation of 1,3-butadiene to 1-butene is found to have two elemental steps corresponding to sequential hydrogen additions to the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 double bond of the Pd-adsorbed 1,3-butadiene by Pd activated H2. Perhaps more importantly, the dynamically driven 1-butene desorption after the second hydrogenation step avoids the re-adsorption of the product to Pd with its remaining double bound and thus its total hydrogenation. This theoretical insight is unprecedented in heterogeneous catalysis and underscores the importance of dynamics. This mechanism for selectivity may be operative in other SAC processes and it offers an effective designing principle for SAC catalyzed heterogenous chemical transformations.
C2 double bond of the Pd-adsorbed 1,3-butadiene by Pd activated H2. Perhaps more importantly, the dynamically driven 1-butene desorption after the second hydrogenation step avoids the re-adsorption of the product to Pd with its remaining double bound and thus its total hydrogenation. This theoretical insight is unprecedented in heterogeneous catalysis and underscores the importance of dynamics. This mechanism for selectivity may be operative in other SAC processes and it offers an effective designing principle for SAC catalyzed heterogenous chemical transformations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from National Natural Science Foundation of China (21673040 to S. L.), Natural Science Foundation of Fujian Province (2016J01052 to S. L.), Fuzhou University Qishan Scholarship Program (XRC-17055 to S. L.), and U.S. National Science Foundation (CHE-1462109 to H. G.). L. Z. acknowledges partial support from the Chinese Scholarship Council (201604890009).Notes and references
- M. L. Derrien, in Stud. Surf. Sci. Catal., ed. L. Cerveny, Elsevier, 1986, vol. 27, pp. 613–666 Search PubMed.
- T. Ouchaib, J. Massardier and A. Renouprez, J. Catal., 1989, 119, 517–520 CrossRef.
- A. Sarkany, Z. Zsoldos, G. Stefler, J. W. Hightower and L. Guczi, J. Catal., 1995, 157, 179–189 CrossRef.
- J. Goetz, M. A. Volpe, C. E. Gigola and R. Touroude, J. Catal., 2001, 199, 338–345 CrossRef.
- J. Silvestre-Albero, G. Rupprechter and H.-J. Freund, J. Catal., 2006, 240, 58–65 CrossRef.
- H. Yi, H. Du, Y. Hu, H. Yan, H.-L. Jiang and J. Lu, ACS Catal., 2015, 5, 2735–2739 CrossRef.
- M. Flytzani-Stephanopoulos and B. C. Gates, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 545–574 CrossRef PubMed.
- X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef PubMed.
- J. Liu, ACS Catal., 2017, 7, 34–59 CrossRef.
- X. Zhang, H. Shi and B. Q. Xu, Angew. Chem., Int. Ed., 2005, 44, 7132–7135 CrossRef PubMed.
- F. R. Lucci, J. Liu, M. D. Marcinkowski, M. Yang, L. F. Allard, M. Flytzani-Stephanopoulos and E. C. Sykes, Nat. Commun., 2015, 6, 8550 CrossRef PubMed.
- H. Yan, H. Cheng, H. Yi, Y. Lin, T. Yao, C. Wang, J. Li, S. Wei and J. Lu, J. Am. Chem. Soc., 2015, 137, 10484–10487 CrossRef PubMed.
- A. Valcárcel, A. Clotet, J. M. Ricart, F. Delbecq and P. Sautet, Surf. Sci., 2004, 549, 121–133 CrossRef.
- A. Valcárcel, A. Clotet, J. M. Ricart, F. Delbecq and P. Sautet, J. Phys. Chem. B, 2005, 109, 14175–14182 CrossRef PubMed.
- X.-F. Yang, A.-Q. Wang, Y.-L. Wang, T. Zhang and J. Li, J. Phys. Chem. C, 2010, 114, 3131–3139 CrossRef.
- B. Yang, R. Burch, C. Hardacre, P. Hu and P. Hughes, J. Phys. Chem. C, 2014, 118, 1560–1567 CrossRef.
- C. Hu, J. Sun, D. Kang, Q. Zhu and Y. Yang, Catal. Sci. Technol., 2017, 7, 2717–2728 RSC.
- Z. P. Liu, C. M. Wang and K. N. Fan, Angew. Chem., Int. Ed., 2006, 45, 6865–6868 CrossRef PubMed.
- D. Marx and J. Hutter, in Modern Methods and Algorithms of Quantum Chemistry, ed. J. Grotendorst, Cambridge University Press, Cambridge, 2009 Search PubMed.
- S. Pratihar, X. Ma, Z. Homayoon, G. L. Barnes and W. L. Hase, J. Am. Chem. Soc., 2017, 139, 3570–3590 CrossRef PubMed.
- R. D. Beck, P. Maroni, D. C. Papageorgopoulos, T. T. Dang, M. P. Schmid and T. R. Rizzo, Science, 2003, 302, 98–100 CrossRef PubMed.
- D. R. Killelea, V. L. Campbell, N. S. Shuman and A. L. Utz, Science, 2008, 319, 790–793 CrossRef PubMed.
- P. M. Hundt, B. Jiang, M. van Reijzen, H. Guo and R. D. Beck, Science, 2014, 344, 504–507 CrossRef PubMed.
- T. Baer and W. L. Hase, Unimolecular Reaction Dynamics, Theory and Experiments, Oxford University Press, New York, 1996 Search PubMed.
- L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875–878 CrossRef PubMed.
- S. C. Ammal, H. Yamataka, M. Aida and M. Dupuis, Science, 2003, 299, 1555–1557 CrossRef PubMed.
- D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, Science, 2004, 306, 1158–1161 CrossRef PubMed.
- J. G. López, G. Vayner, U. Lourderaj, S. V. Addepalli, S. Kato, W. A. deJong, T. L. Windus and W. L. Hase, J. Am. Chem. Soc., 2007, 129, 9976–9985 CrossRef PubMed.
- J. Rehbein and B. K. Carpenter, Phys. Chem. Chem. Phys., 2011, 13, 20906–20922 RSC.
- K. Black, P. Liu, L. Xu, C. Doubleday and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12860–12865 CrossRef PubMed.
- Z. Yang, S. Yang, P. Yu, Y. Li, C. Doubleday, J. Park, A. Patel, B.-s. Jeon, W. K. Russell, H.-w. Liu, D. H. Russell and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E848–E855 CrossRef PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef.
- S. Chapman and D. L. Bunker, J. Chem. Phys., 1975, 62, 2890–2899 CrossRef.
- W. L. Hase and D. G. Buckowski, Chem. Phys. Lett., 1980, 74, 284–287 CrossRef.
- Z. Yang, Z. Lu, G. Luo and K. Hermansson, Phys. Lett. A, 2007, 369, 132–139 CrossRef.
- G. Garcia Cervantes, F. J. Cadete Santos Aires and J. C. Bertolini, J. Catal., 2003, 214, 26–32 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00776d |
| This journal is © The Royal Society of Chemistry 2018 |