Long distance ion–water interactions in aqueous sulfate nanodrops persist to ambient temperatures in the upper atmosphere

Abstract

The effect of temperature on the patterning of water molecules located remotely from a single SO₄²⁻ ion in aqueous nanodrops was investigated for nanodrops containing between 30 and 55 water molecules using instrument temperatures between 135 and 360 K. Magic number clusters with 24, 36 and 39 water molecules persist at all temperatures. Infrared photodissociation spectroscopy between 3000 and 3800 cm⁻¹ was used to measure the appearance of water molecules that have a free O–H stretch at the nanodroplet surface and to infer information about the hydrogen bonding network of water in the nanodroplet. These data suggest that the hydrogen bonding network of water in nanodrops with 45 water molecules is highly ordered at 135 K and gradually becomes more amorphous with increasing temperature. An SO₄²⁻ dianion clearly affects the hydrogen bonding network of water to at least ∼0.71 nm at 135 K and ∼0.60 nm at 340 K, consistent with an entropic drive for reorientation of water molecules at the surface of warmer nanodrops. These distances represent remote interactions into at least a second solvation shell even with elevated instrumental temperatures. The results herein provide new insight into the extent to which ions can structurally perturb water molecules even at temperatures relevant to Earth's atmosphere, where remote interactions may assist in nucleation and propagation of nascent aerosols.

---

1 Introduction

The chemistry and physics of ion-containing aqueous nanodrops are vital to understanding the behavior of atmospheric aerosols.^1,2 Aerosols impact global radiative forcing,^3,4 act as cloud condensation nuclei to limit the rate of droplet coalescence and suppress rainfall,^5,6 and, in high concentrations, can lead to haze pollution, which negatively impacts human health and agricultural sustainability.^7,8 Sources of atmospheric aerosols are both natural and anthropogenic, ranging from oceanic waves and wind erosion to the use of coal and other fossil fuels.⁹ Stratospheric aerosol modification strategies are being considered to mitigate the increase in global temperatures via seeding ice clouds to increase the reflection of solar radiation and furthermore diminishing the presence of homogeneously formed cirrus clouds, which contribute negatively to climate warming.^10–12 Aerosol formation in the lower stratosphere can occur through ion-induced nucleation, in which embryonic nanometer-sized clusters act to expedite the rate of aerosol growth.^13,14 An appreciation of the fundamental interactions originating from ions in small aqueous nanodrops is therefore essential for accurately modeling and investigating the chemistry of atmospheric aerosols.

A property of fundamental interest concerning ion–water interactions is the length to which a water molecule can “see” an ion, i.e., the distance ions structurally or dynamically perturb the hydrogen-bonding network of water molecules. Although a previous report suggests that ions act only locally to directly coordinated water molecules,¹⁵ several opposing results have demonstrated that interactions persist into extended hydration shells.^16–28 Small-angle X-ray scattering experiments indicate an increased water molecule density with respect to bulk water surrounding SO₄²⁻ and PO₄³⁻ extending to ∼2.9 and ∼3.6 Å, respectively.²⁹ More recently, long-distance perturbations as a result of ion–water interactions were reported using terahertz spectroscopy, which showed that tri- and tetraanionic hexacyanoferrates, Fe(CN)₆³⁻ and Fe(CN)₆⁴⁻, affect water molecule dynamics beyond the inner coordination shell.²⁸ An intrinsic complication with solution-phase studies of ion–water interactions is the presence of counterions, which can themselves affect the hydrogen bonding network of water molecules, form ion pairs, and otherwise shield the electrostatic interactions with water. Furthermore, the high ionic concentrations typically required for adequate signal lead to close ion–ion proximities with potentially overlapping solvation shells and ion pairing. To overcome these issues, aqueous droplet studies have emerged as a useful means to investigate the physical and chemical properties of ions while excluding influence from cosolutes in order to provide information about effects of an individual ion on the hydrogen bonding network of water molecules in the effective limit of infinite dilution.

Ion-containing aqueous nanodrops of X^z−(H₂O)_n can be readily formed via nanoelectrospray ionization of aqueous solutions. The structures of nanodrops containing SO₄²⁻ have been extensively studied between n = 3 and 24.^30–33 For instance, photoelectron spectroscopy of SO₄²⁻(H₂O)_n has shown that formation of water–water hydrogen bonds are favored over ion–water bonding after n > 4 due to sufficient shielding of the negative charges.³⁴ Comparison of infrared photodissociation (IRPD) spectroscopy to computational structures for n = 6 has revealed formation of cyclic water rings.³³ Similarly, IRPD measurements for the structure of n = 12, which has an enhanced abundance in the mass spectrum with respect to the neighboring hydration sizes, suggest either a completion of the inner coordination shell,³¹ or a highly symmetrical structure with three water molecules in a second solvation shell.³² In the latter investigation, the lowest-energy structures for the n = 11 and n = 13 clusters are described by either removal or addition of a single water molecule from the structural motif present in the especially stable n = 12 cluster.

Long-distance anion–water interactions in aqueous nanodrops can be measured as a function of size by investigating the structural orientation of surface water molecules, which preferentially orient with their dipoles facing inward as a result of interactions with the solvated anion.^24–27 Previous measurements of nanodrops containing SO₄²⁻ show that the structure of the hydrogen bonding network is perturbed up to ∼0.7 nm.²⁵ Further studies on the multivalent hexacyanoferrates Fe(CN)₆³⁻ and Fe(CN)₆⁴⁻ reveal ion–water interactions persisting to ∼0.8 and ∼1.0 nm, respectively.^26,27 These experiments were performed with the instrument cooled to 133 K in order to slow the dissociation of nanodrops due to rapid water molecule evaporation from the trapped clusters. However, relevant atmospheric temperatures are ∼180 K for mesospheric and ∼220 K for stratospheric aerosols. Therefore, a structural investigation of aqueous nanodrops as a function of temperature could provide information regarding their structures and stabilities as well as the extent of ion–water interactions within nanodrops that more closely resemble nascent atmospheric aerosols.

Herein, we investigate the temperature dependence of ion–water interactions in aqueous sulfate nanodrops, SO₄²⁻(H₂O)_n, between n = 30 and 55. Mass spectral measurements reveal specific cluster sizes, n, with enhanced abundances attributed to unique hydrogen-bonding structures that remain with temperatures elevated above ambient conditions. Remarkably, structural ion–water interactions between the solvated SO₄²⁻ and water molecules residing at the droplet surface persist up to 340 K in n = 30, which suggests that these long range interactions are prevalent at ambient atmospheric conditions. These experiments are the first temperature-dependent studies of extensively hydrated anions and provide new insight into fundamental intermolecular properties that exist at relevant atmospheric temperatures.

2 Experimental methods

2.1 Mass spectra

All experimental data were acquired using a home-built 7.0 T Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometer that has been modified from an instrument described in detail elsewhere to incorporate a 7.0 T magnet.³⁵ Briefly, hydrated ions are formed via nanoelectrospray ionization (nESI) of 5 mM aqueous solutions of copper sulfate (Fischer Chemical, Fair Lawn, NJ) using Milli-Q purified water (Millipore, Billerica, MA). Solutions are loaded into borosilicate capillaries (Sutter Instrument, Novato, CA) with tips pulled to an inner diameter of ∼1 μm. The hydrated ions are formed by applying ∼700 V (relative to the entrance capillary of the mass spectrometer) to a platinum wire that is inserted into the solution. The emitter tip is positioned ∼1 mm from the heated (∼80 °C) metal entrance capillary of the mass spectrometer.

Ions are guided via a set of electrostatic lenses through five stages of differential pumping toward the ion cell, which is surrounded by a copper jacket.³⁶ The jacket is temperature-regulated to within ±3 K using a solenoid controlled with home-built regulation software to time pulses of liquid nitrogen for cooling, or with a resistive blanket wrapped around the vacuum chamber containing the cell for heating. The copper jacket is thermalized to the set temperature for at least ∼8 h prior to data acquisition. A pulse of dry nitrogen gas is introduced during ion accumulation to bring the cell region to ∼2 × 10⁻⁶ Torr, which assists in both the trapping and thermalization of ions. After ∼6 s, the cell pressure returns to ∼5 × 10⁻⁹ Torr. Precursor ions are isolated using a stored waveform inverse Fourier transform excitation and can thereafter be activated by IRPD prior to detection to measure photon energy dependent dissociation kinetics for acquiring infrared spectra. A weighted average ensemble method, in which three consecutive cluster sizes are isolated, is implemented to improve the signal-to-noise ratios of these measurements.³⁷ This technique uses the average dissociation kinetics of the precursor ensemble instead of the dissociation rate of a single nanodrop size. To clearly specify an ensemble distribution versus a single nanodrop size, the notation n_e is used to represent an n ± 1 ensemble, i.e., n_e = 45 ≡ n = 44–46.

2.2 Infrared spectroscopy

IRPD spectra between 3000 and 3800 cm⁻¹ are measured using infrared photons from a tunable OPO/OPA system (LaserVision, Bellevue, WA) pumped by the 1064 nm fundamental of a Nd:YAG laser (Continuum Surelight I-10, Santa Clara, CA) operating at a 10 Hz repetition rate. Ions are irradiated between 0.25 and 1.0 s (between 2 and 10 pulses) to achieve substantial, but not complete, dissociation of the precursor distribution. A first-order dissociation rate constant is determined from the weighted average of products with respect to the initial precursor distribution using the ensemble method.³⁷ IRPD rate constants are corrected for dissociation due to the absorption of blackbody photons originating from the instrument walls by subtracting the blackbody infrared dissociation (BIRD) rate constant, which is measured separately in the absence of infrared radiation. IRPD rate constants are also corrected for frequency dependent variations in laser power.

3 Results and discussion

3.1 Magic number clusters

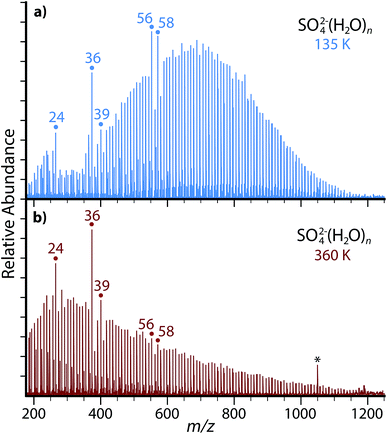
nESI of a 5 mM aqueous copper sulfate solution produces ion-containing aqueous nanodrops over a broad size range (Fig. 1). Cluster distributions can be shifted to larger or smaller values of hydration size, n, by adjusting the entrance capillary temperature and potentials applied to source optics. Increasing the temperature of the copper jacket surrounding the ion cell from 135 K (Fig. 1a) to 360 K (Fig. 1b) results in a shift of the most abundant peaks to a lower value of m/z, but the range of cluster sizes trapped is comparable for both temperatures. Both SO₄²⁻(H₂O)_n and HSO₄⁻(H₂O)_n are produced by nESI and at 135 K and 360 K, the largest clusters observed are n ≃ 125 for SO₄²⁻(H₂O)_n and n ≃ 35 for HSO₄⁻(H₂O)_n. The smallest clusters detected are limited by the excitation waveform conditions used in these experiments. Thermodynamic stabilities for small clusters of SO₄²⁻(H₂O)_n and HSO₄⁻(H₂O)_n have been extensively investigated previously.^38–44

Fig. 1 Nanoelectrospray mass spectra acquired from 5 mM aqueous copper sulfate with the copper jacket temperature (a) cooled to 135 K or (b) elevated to 360 K. Magic number clusters of SO₄²⁻(H₂O)_n with n = 24, 36 and 39 are prominent for both temperatures. Frequency noise is labeled with an asterisk (*).

The relative abundances of SO₄²⁻(H₂O)_n with n = 24, 36, 39, 56, 58 at low temperature (Fig. 1a) are anomalously high relative to the neighboring hydration states. At higher temperature (Fig. 1b), the n = 24, 36 and 39 clusters remain more prominent in abundance, but the n = 56 and 58 clusters much less so. Enhanced abundances, commonly referred to as magic number clusters (MNCs), originate from either a higher stability of the nanodroplet at that size or an inherent instability of the neighboring n + 1 cluster. MNCs have been previously observed with a diverse range of hydrated species, including the hydrated electron,^45,46 hydrated proton,^47,48 monatomic ions,^49,50 small organic ions,^51–54 transition metal complexes^26,27 and peptides.^55–57 Previous photodissociation experiments and theory have revealed the presence of pentagonal dodecahedral clathrate structures leading to enhanced stability in n = 20 hydrates of H₃O⁺, NH₄⁺, Cs⁺, Rb⁺, and K⁺.^{47,48,50–52} Similar cage-like structural motifs may be responsible for the enhanced abundance of the observed SO₄²⁻(H₂O)_n MNC nanodrops. There are also alternating MNCs between n = 49 and 58 for (H₂O)_n⁻,^45,46 H⁺(H₂O)_n,⁵⁸ protonated amines,^53,57 and halides,⁴⁹ which alternatively suggests that SO₄²⁻(H₂O)_n clusters at n = 56 and 58 may originate from the inclusion of SO₄²⁻ into similar structural motifs without significantly disrupting the enhanced structure of the hydrogen bonding network. The continued presence of MNCs with n = 24, 36 and 39 at high temperature in these experiments suggests that these stable configurations may be relevant to nascent aerosols at ambient atmospheric temperatures.

3.2 Temperature dependence of bonded O–H stretches

To investigate the hydrogen bonding network and water molecule orientations as a function of temperature, IRPD spectra were acquired for SO₄²⁻(H₂O)_n with n_e = 45 and with the copper jacket at a fixed temperature between 135 and 215 K (Fig. 2). The broad feature spanning ∼3000–3650 cm⁻¹ is characteristic of absorptions from hydrogen-bonded O–H stretches. This region can be further subdivided based on the local colligative physical state of water molecules, which depends on both the number of hydrogen bonds involved and the O–H–O angles for hydrogen bonding.⁵⁹ In the bulk phase, water molecules that accept and donate two hydrogen bonds (AADD: acceptor–acceptor–donor–donor) in a near-optimal, i.e. O–H||O–O, four-coordinate tetrahedral conformation, absorb low energy photons near ∼3300 cm⁻¹ and can be referred to as highly-ordered oscillators.^60,61 Amorphous hydrogen bonding oscillators, in which either four-coordinate water molecules adopt less-optimal distorted tetrahedral structures, or the water molecules are three-coordinate (ADD: acceptor–donor–donor), are blue-shifted and absorb photons near ∼3450 cm⁻¹. The relative ratios of these two regions have been explored as a function of droplet size for both neutral water and ion-containing nanodrops up to n = 550 in order to explore the onset of crystallinity.^23,62 Although small nanodrops with n = 30–55 do not have a discrete phase, these absorptive regions observed in bulk water can be used to describe changes in the composite structure of the hydrogen bonding network as a function of hydration.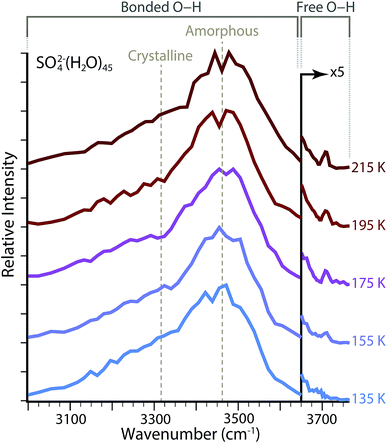

Fig. 2 Full O–H stretching region for IRPD of SO₄²⁻(H₂O)_n with n_e = 45 and copper jacket temperatures thermalized between 135 and 215 K.

Temperature dependence of the amorphous to highly-ordered hydrogen bonding ratio for SO₄²⁻(H₂O)_n with n_e = 45 was determined by fitting the bonded O–H region with two Gaussian lineshapes for absorptions centered at ∼3470 cm⁻¹ and ∼3320 cm⁻¹, respectively. Fitting parameters for these lineshapes are provided in Table 1. There is no systematic change in the width of these two absorptive regions over the temperature range investigated. There is a minor blue shift by Δv = 7 cm⁻¹ from 3470 cm⁻¹ to 3477 cm⁻¹ for the center frequency of amorphous hydrogen bonding across the temperatures measured, whereas the center of the highly-ordered water absorption center blue shifts from 3323 cm⁻¹ to 3325 cm⁻¹, a difference of only Δv = 2 cm⁻¹. The largest systematic change is the ratio of relative abundances for these two peaks. Using the integrated areas of the Gaussian lineshapes, the hydrogen bonding network composition for n_e = 45 is ∼40% amorphous at 135 K and becomes less ordered as the copper jacket temperature is elevated, which results in an increase of the amorphous contribution to ∼46% at 215 K. Because the intensity of absorptive bands can depend nonlinearly on single photon absorption cross sections using IRPD,⁶³ these integrated bands may provide a more qualitative than quantitative measure of structural change with increasing temperature. However, the increase in the ratio for amorphous to highly-ordered bands indicates that the nanodrop structures have less-optimal O–H–O hydrogen-bonding angles and a decrease in water molecule coordination.

Table 1 Gaussian fitting parameters for IRPD spectra of SO₄²⁻(H₂O)_n with n_e = 45. Parameters for amorphous and highly-ordered oscillators are given with subscripts am and ho, respectively, for f(x) = a exp[−((x − b)/c)²]. The ±% for 2σ standard error for least squares fitting is provided as a relative percentage in parentheses following the parameter, (%)

	a am	b am	c am	a ho	b ho	c ho	% am
135 K	0.0787 (10)	3470 (0.1)	96.23 (7.5)	0.0570 (8.0)	3323 (0.5)	199.6 (6.3)	40.0
155 K	0.0987 (6.3)	3472 (0.1)	89.73 (5.6)	0.0571 (6.6)	3327 (0.4)	206.1 (5.1)	42.6
175 K	0.0823 (2.9)	3476 (0.1)	92.15 (3.5)	0.0467 (4.1)	3324 (0.4)	220.1 (4.6)	42.5
195 K	0.0977 (9.3)	3468 (0.1)	97.13 (7.3)	0.0425 (13)	3325 (0.8)	204.9 (9.2)	47.9
215 K	0.0794 (10)	3477 (0.1)	99.50 (8.2)	0.0436 (11)	3325 (0.8)	210.7 (8.2)	46.2

---

3.3 Temperature dependence of long-distance interactions

Information about the extent of ion–water interactions between the solvated SO₄²⁻ and surface water molecules as a function of temperature can be determined from IRPD spectra of SO₄²⁻(H₂O)_n. Dangling or “free” O–H stretches at the surface of the water droplet that do not participate in hydrogen bonding (A: acceptor, AD: acceptor–donor, or AAD: acceptor–acceptor–donor) occur between ∼3650 and 3800 cm⁻¹. Water molecules in the first coordination shell orient with their hydrogen atoms facing inward toward SO₄²⁻.^32,33 This is due to both the Coulombic interaction between the anion and the partial positive charge of the hydrogen atoms and to hydrogen-bonding between water and the anion. These interior water molecules donate both hydrogen atoms for hydrogen bonding to either the anion or to other water molecules (DD, ADD, or AADD). With increasing n and the formation of subsequent solvation shells, the distance between the anion and surface water molecules lengthens and the magnitude of interactions resulting in patterning the orientation of water molecules at the surface diminishes. This decreasing impetus for water molecules to orient inward is eventually overcome by both the entropic drive to incorporate free O–H water molecules and the enthalpic drive to optimize hydrogen bonding at the surface as occurs in neutral and cationic clusters as well as the bulk air–water interface. Therefore, the onset of spectroscopic features at ∼3700 cm⁻¹ measured as a function of n provides an effective distance to which the anion can strongly orient water molecules at the droplet surface.

In the IRPD spectra of SO₄²⁻(H₂O)_n with n_e = 45 and T = 135 K (Fig. 2), all of the spectral intensity between 3650 and 3800 cm⁻¹ is attributable to the shoulder of the hydrogen-bonding feature centered at 3470 cm⁻¹, consistent with previous size-dependent experiments of SO₄²⁻ at low temperature.²⁵ A distinct band at ∼3707 cm⁻¹ emerges at 155 K and gradually increases in intensity with temperature, indicating that there are an increasing number of free O–H oscillators at the surface. Therefore, although the surface of n_e = 45 is composed entirely of inward doubly donating water molecules at 135 K, these nanodrops begin to incorporate free O–H water molecules at 155 K, where the free O–H reorientation becomes competitive with long distance ion–water interactions between SO₄²⁻ and the surface. It is important to note that the onset of the free O–H is not equivalent to a complete loss of interaction between the anion and surface, but rather the onset for the loss of strong structural orientation at the surface.

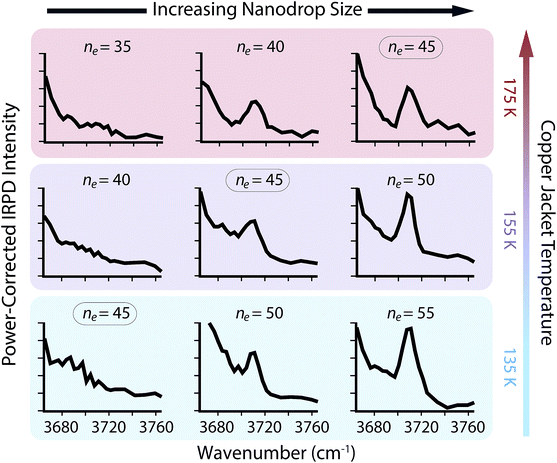
The appearance of free O–H oscillators in SO₄²⁻(H₂O)_n clusters with n_e between 35 and 55 and copper jacket temperatures between 135 and 175 K was measured (Fig. 3). The free O–H ADD stretch at ∼3707 cm⁻¹ that is not observed for n_e = 45 at 135 K appears at n_e = 50, and the intensity of this peak is higher for n_e = 55. The ion–water distance between the solvated anion and surface water molecules, which can be calculated from the density of water with the assumption that clusters are spherical,† is approximately 0.71 nm for n_e = 50. Therefore, the strong structural influences from SO₄²⁻ extend to ∼0.71 nm when the copper jacket is at 135 K. When the copper jacket temperature is increased to 155 K, the onset of the free O–H occurs with n_e = 45 (∼0.69 nm) and therefore, the increased temperature has slightly diminished the distal extent to which SO₄²⁻ can strongly orient water molecules. Similarly, the free O–H band emerges at n_e = 40 (∼0.66 nm) with the copper jacket at 175 K. This corresponds to a decrease of the orientation extent by ∼0.03 nm for each 20 K increase for this size range.

Fig. 3 Dependence of the nanodrop free O–H band appearance with respect to copper jacket temperature as a function of cluster size between n_e = 30 and 55. Within a given cluster size (see n_e = 45 above), increasing the temperature results in a greater abundance of the free O–H band, whereas within a static temperature, increased cluster size results in larger free O–H absorbance. The appearance of this peak is due to decreased Coulombic interactions and reorientation of hydrogen-bonding interactions to accommodate water molecules with a free O–H stretch.

There is no free O–H peak in the IRPD spectrum of n_e = 35 until the copper jacket is at 295 K (Fig. 4b). Although the free O–H emergence for clusters between n_e = 40 and 50 occurs within a small temperature range (ΔT ≃ 40 K), the strong ion–water interactions in the n_e = 35 cluster structure the surface until 295 K, or ΔT ≃ 120 K with respect to the free O–H emergence in n_e = 40. There are MNCs in the precursor distribution of both n_e = 35 and 40 at n = 36 and 39, respectively. Therefore, the large temperature offset is not attributable to an anomalous stability in just one of these precursors. Instead, the increased temperature required for surface reorientation is due to the smaller ion–surface distance that requires higher internal energies to overcome the strong Coulombic and hydrogen-bonding interactions. Remarkably, there is no free O–H band for n_e = 30 until the ion cell is heated to 340 K (Fig. 4c). The approximate droplet radii for n_e = 30 and 35 are ∼0.60 nm and ∼0.63 nm, respectively. The inner coordination shell for SO₄²⁻ consists of n ≃ 14 water molecules.³⁰ Thus, the ion–water interactions reported here are each representative of long-range interactions into at least a second solvation shell.

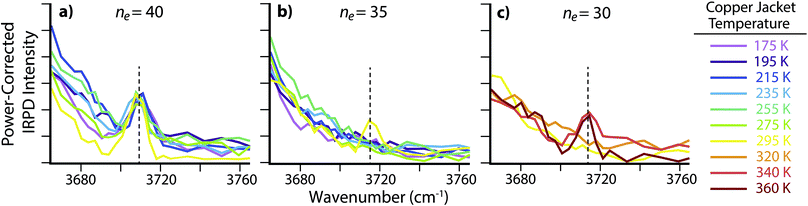Fig. 4 IRPD spectra of the free O–H region for SO₄²⁻(H₂O)_n with (a) n_e = 40, (b) n_e = 35 and (c) n_e = 30 with copper jacket temperatures between 175 and 360 K.

There are no MNCs in the n_e = 30 ensemble distribution and as a result, the long-distance structural interactions at elevated temperatures observed here are not a consequence of atypical stabilities. Instead, the structural interactions present in these nanodrops are analogous to ion–water interactions in aqueous solutions at ∼0.60 nm, or roughly a second solvation shell from the anion. These results provide evidence for remote structuring of water molecules beyond the inner coordination shell by dianionic species at ambient temperatures. This is consistent with a recent terahertz investigation of tri- and tetraanionic hexacyanoferrates in ambient temperature aqueous solutions that were found to dynamically perturb a minimum of ∼19 and ∼25 water molecules, respectively.²⁸ Under the low-pressure conditions used in these experiments, water molecules can rapidly evaporate and lead to significant cooling of the nanodrops.⁶⁴ As a result, the actual “effective” temperatures of these nanodrops are expected to be cooler than the temperatures reported here for the copper jacket. The calculation of quantitative values for these effective temperatures requires extensive modeling to account for energy transfer via water evaporation or the absorption and emission of blackbody photons.^36,65–70 Although a detailed investigation into the effective temperatures of nanodrops is underway, preliminary results suggest that SO₄²⁻(H₂O)_n clusters with n_e = 30 trapped in an ion cell at 340 K have an effective temperature of ∼180 ± 6 K (ΔT ≃ 160 K). Under these experimental conditions, more than 99% of the ions have an internal energy above the threshold dissociation energy for water molecule loss. The steady state distribution of ion internal energies is much narrower than that of a Boltzmann distribution at 180 K, but the maximum values in the two distributions are centered at the same energy. This effective droplet temperature is comparable to temperatures in the upper atmosphere, where the unique stability of MNCs and strong ion–water interactions beyond the inner coordination shell may aid in nucleation and propagation of nascent atmospheric aerosols.

4 Conclusions

IRPD spectroscopy in the hydrogen bonding region between 3000 and 3800 cm⁻¹ was used to investigate the temperature dependence of ion–water interactions in aqueous SO₄²⁻(H₂O)_n with instrumental temperatures between 135 and 360 K. In this spectral region, absorption of photons at ∼3700 cm⁻¹ is indicative of “free” O–H water molecules at the surface of the droplet that orient one O–H group outward and away from the droplet interior. The appearance of this free O–H band was measured as a function of both temperature and cluster size to determine the onset of diminished structural ion–water interactions at remote distances from the dianion. For a given cluster size, an increase in temperature results in a greater population of free O–H water molecules at the surface as a result of the entropic and enthalpic drives for surface reorientation that are able to overcome the strong Coulombic and hydrogen-bonding interactions with increased internal energies. At smaller cluster size, higher temperatures are required to reorient water molecules as a result of decreased ion–surface distances, where greater Coulombic interactions exist between the solvated ion and surface water molecules. These results are consistent with an increase in the less optimal hydrogen bonding observed in the bonded O–H region of the spectra with increasing nanodrop size. Water molecules beyond the first solvation shell must reorient in order for their dipoles to point outward and away from the solvated anion to accommodate water molecules with a free O–H stretch at the nanodrop surface. In contrast to solution-phase experiments, which generally require high concentrations and consequentially limit the amount of unperturbed bulk water due to counterions, the long distance interactions observed here using anion-containing aqueous nanodrops provide the first unambiguous evidence for remote ion–water interactions by a singular anion at temperatures relevant to Earth's atmosphere. These findings provide new insight into fundamental ion–water interactions that may contribute to favorable nucleation and propagation of nascent aerosols in the upper atmosphere. These same techniques can be used to investigate the temperature dependence of larger anion-containing nanodrops as well as the hydration of clustered anionic cores.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by the National Science Foundation under CHE-1609866 and the Graduate Research Fellowship Program under Grant No. DGE 1752814, as well as the American Chemical Society Division of Analytical Chemistry and Society for Analytical Chemists of Pittsburgh (MJD). The authors would like to acknowledge financial support from the Ford Foundation (CNS), through its pre-doctoral fellowship program, and the National Academies of Sciences, Engineering, and Medicine, the administrative agency for the Ford fellowship program. The authors are grateful for financial support from CalSolv.

References

1. V. F. McNeill, Annu. Rev. Chem. Biomol. Eng., 2017, 8, 427–444.
2. Atmospheric Aerosols: Characterization, Chemistry, Modeling, and Climate, ed. K. T. Valsaraj and R. R. Kommalapati, American Chemical Society, 2009, vol. 1005.
3. R. J. Charlson, S. E. Schwartz, J. M. Hales, R. D. Cess, J. A. Coakley, J. E. Hansen and D. J. Hofmann, Science, 1992, 255, 423–430.
4. P. Stier, J. H. Seinfeld, S. Kinne and O. Boucher, Atmos. Chem. Phys., 2007, 7, 5237–5261.
5. Q. Zhang, J. Quan, X. Tie, M. Huang and X. Ma, Atmos. Environ., 2011, 45, 665–672.
6. M. O. Andreae, D. Rosenfeld, P. Artaxo, A. A. Costa, G. P. Frank, K. M. Longo and M. A. F. Silva-Dias, Science, 2004, 303, 1337–1342.
7. X. Han, Q. Guo, C. Liu, P. Fu, H. Strauss, J. Yang, J. Hu, L. Wei, H. Ren, M. Peters, R. Wei and L. Tian, Sci. Rep., 2016, 6, 29958.
8. X. Tie, R. J. Huang, W. Dai, J. Cao, X. Long, X. Su, S. Zhao, Q. Wang and G. Li, Sci. Rep., 2016, 6, 29612.
9. M. O. Andreae and P. J. Crutzen, Science, 1997, 276, 1052–1058.
10. P. J. Crutzen, Clim. Change, 2006, 77, 211–219.
11. U. Niemeier and S. Tilmes, Science, 2017, 357, 246–248.
12. U. Lohmann and B. Gasparini, Science, 2017, 357, 248–249.
13. R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011.
14. S.-H. Lee, J. M. Reeves, J. C. Wilson, D. E. Hunton, A. A. Viggiano, T. M. Miller, J. O. Ballenthin and L. R. Lait, Science, 2003, 301, 1886–1889.
15. A. W. Omta, M. F. Kropman, S. Woutersen and H. J. Bakker, Science, 2003, 301, 347–349.
16. R. Mancinelli, A. Botti, F. Bruni, M. A. Ricci and A. K. Soper, Phys. Chem. Chem. Phys., 2007, 9, 2959–2967.
17. M. A. Vovk, M. S. Pavlova, V. I. Chizhik and A. A. Vorontsova, Russ. J. Phys. Chem. A, 2011, 85, 1597–1602.
18. W. W. Rudolph and G. Irmer, Appl. Spectrosc., 2007, 61, 1312–1327.
19. J. Stangret and T. Gampe, J. Phys. Chem. A, 2002, 106, 5393–5402.
20. R. Buchner, Pure Appl. Chem., 2008, 80, 1239–1252.
21. A. Eiberweiser, A. Nazet, G. Hefter and R. Buchner, J. Phys. Chem. B, 2015, 119, 5270–5281.
22. F. Böhm, V. Sharma, G. Schwaab and M. Havenith, Phys. Chem. Chem. Phys., 2015, 17, 19582–19591.
23. R. J. Cooper, M. J. DiTucci, T. M. Chang and E. R. Williams, J. Am. Chem. Soc., 2016, 138, 96–99.
24. J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 10228–10236.
25. J. T. O'Brien, J. S. Prell, M. F. Bush and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 8248–8249.
26. M. J. DiTucci, S. Heiles and E. R. Williams, J. Am. Chem. Soc., 2015, 137, 1650–1657.
27. M. J. DiTucci and E. R. Williams, Chem. Sci., 2017, 8, 1391–1399.
28. M. J. DiTucci, F. Böhm, G. Schwaab, E. R. Williams and M. Havenith, Phys. Chem. Chem. Phys., 2017, 19, 7297–7306.
29. C. Chen, C. Huang, I. Waluyo, T. Weiss, L. Pettersson and A. Nilsson, Phys. Chem. Chem. Phys., 2015, 17, 8427–8430.
30. F. Thaunay, C. Clavaguéra and G. Ohanessian, Phys. Chem. Chem. Phys., 2015, 17, 25935–25945.
31. J. Zhou, G. Ssantambrogio, M. Brümmer, D. T. Moore, L. Wöste, G. Meijer, D. M. Neumark and K. R. Asmis, J. Chem. Phys., 2006, 125, 111102.
32. F. Thaunay, A. A. Hassan, R. J. Cooper, E. R. Williams, C. Clavaguéra and G. Ohanessian, Int. J. Mass Spectrom., 2017, 418, 15–23.
33. M. F. Bush, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 2220–2221.
34. X. B. Wang, J. B. Nicholas and L. S. Wang, J. Chem. Phys., 2000, 113, 10837–10840.
35. M. F. Bush, J. T. O'Brien, J. S. Prell, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 1612–1622.
36. R. L. Wong, K. Paech and E. R. Williams, Int. J. Mass Spectrom., 2004, 232, 59–66.
37. J. S. Prell, J. T. O'Brien and E. R. Williams, J. Am. Soc. Mass Spectrom., 2010, 21, 800–809.
38. N. Mardirossian, D. S. Lambrecht, L. McCaslin, S. S. Xantheas and M. Head-Gordon, J. Chem. Theory Comput., 2013, 9, 1368–1380.
39. D. S. Lambrecht, L. McCaslin, S. S. Xantheas, E. Epifanovsky and M. Head-Gordon, Mol. Phys., 2012, 19, 2513–2521.
40. L. C. Smeeton, J. D. Farrell, M. T. Oakley, D. J. Wales and R. L. Johnston, J. Chem. Theory Comput., 2015, 11, 2377–2384.
41. R. L. Wong and E. R. Williams, J. Phys. Chem. A, 2003, 107, 10976–10983.
42. A. Whitehead, R. Barrios and J. Simons, J. Chem. Phys., 2002, 116, 2848–2851.
43. Y. Xin, X. B. Wang and L. S. Wang, J. Phys. Chem. A, 2002, 106, 7607–7616.
44. B. Gao and Z. Liu, J. Chem. Phys., 2005, 123, 224302.
45. L. Ma, K. Majer, F. Chirot and B. v. Issendorff, J. Chem. Phys., 2009, 131, 144303.
46. M. Knapp, O. Echt, D. Kreisle and E. Recknagel, J. Phys. Chem., 1987, 91, 2601–2607.
47. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Science, 2004, 304, 1134–1137.
48. J. A. Fournier, C. T. Wolke, C. J. Johnson, M. A. Johnson, N. Heine, S. Gewinner, W. Schöllkopf, T. K. Esser, M. R. Fagiani, H. Knorke and K. R. Asmis, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18132–18137.
49. S. Chakrabarty and E. R. Williams, Phys. Chem. Chem. Phys., 2016, 18, 25483–25490.
50. R. J. Cooper, T. M. Chang and E. R. Williams, J. Phys. Chem. A, 2013, 117, 6571–6579.
51. E. G. Diken, N. I. Hammer, M. A. Johnson, R. A. Christie and K. D. Jordan, J. Chem. Phys., 2005, 123, 164309.
52. T. M. Chang, R. J. Cooper and E. R. Williams, J. Am. Chem. Soc., 2013, 135, 14821–14830.
53. S.-W. Lee, H. Cox, W. A. Goddard and J. L. Beauchamp, J. Am. Chem. Soc., 2000, 122, 9201–9205.
54. K. Sekimoto and M. Takayama, J. Mass Spectrom., 2011, 46, 50–60.
55. S. E. Rodrigez-Cruz, J. S. Klassen and E. R. Williams, J. Am. Soc. Mass Spectrom., 1999, 10, 958–968.
56. S. E. Rodriguez-Cruz, J. S. Klassen and E. R. Williams, J. Am. Soc. Mass Spectrom., 1997, 8, 565–568.
57. S.-W. Lee, P. Freivogel, T. Schindler and J. L. Beauchamp, J. Am. Chem. Soc., 1998, 120, 11758–11765.
58. T. Schindler, C. Berg, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys. Lett., 1996, 250, 301–308.
59. V. Buch and J. P. Devlin, J. Chem. Phys., 1999, 110, 3437–3443.
60. J. B. Brubach, A. Mermet, A. Filabozzi, A. Gerschel and P. Roy, J. Chem. Phys., 2005, 122, 184509.
61. G. D'Arrigo, G. Maisano, F. Mallamace, P. Migliardo and F. Wanderlingh, J. Chem. Phys., 1981, 75, 4264.
62. C. C. Pradzynski, R. M. Forck, T. Zeuch, P. Slaviček and U. Buck, Science, 2012, 337, 1529–1532.
63. J. S. Prell, T. C. Correra, T. M. Chang, J. A. Biles and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 14733–14735.
64. R. C. Dunbar, Mass Spectrom. Rev., 2004, 23, 127–158.
65. W. D. Price, P. D. Schnier and E. R. Williams, J. Phys. Chem. B, 1997, 101, 664–673.
66. R. A. Jockush and E. R. Williams, J. Phys. Chem. A, 1998, 102, 4543–4550.
67. E. F. Strittmatter, P. D. Schnier, J. S. Klassen and E. R. Williams, J. Am. Soc. Mass Spectrom., 1999, 10, 1095–1104.
68. W. D. Price and E. R. Williams, J. Phys. Chem. A, 1997, 101, 8844–8852.
69. P. D. Schnier, W. D. Price, E. F. Strittmatter and E. R. Williams, J. Am. Soc. Mass Spectrom., 1997, 8, 771–780.
70. R. C. Dunbar, T. B. McMahon, D. Thölmann, D. S. Tonner, D. R. Salahub and D. Wei, J. Am. Chem. Soc., 1995, 117, 12819–12825.

---

Footnote

† This approximation uses the density of water at room temperature and does not consider any specific ion or structural effects. However, these approximations provide distances similar to those calculated using molecular mechanics simulations for specific hydrated ions.²⁷

---