Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nontrigonal constraint enhances 1,2-addition reactivity of phosphazenes†
Yi-Chun
Lin‡
,
James C.
Gilhula‡
and
Alexander T.
Radosevich
 *
*
Department of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: radosevich@mit.edu
First published on 6th April 2018
Abstract
The syntheses and 1,2-addition reactivities of nontrigonal phosphazenes supported by trianionic tricoordinating chelates of the type L3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ndipp (3: L3 = N[CHC(tBu)O]23−; 4: L3 = N(o-NMeC6H4)23−; dipp = 2,6-diisopropylphenyl) are reported. These compounds are characterized by multinuclear NMR and single-crystal X-ray diffraction experiments. Distorted phosphazenes 3 and 4 are shown to add B–H, B–O, and Si–H bonds across the formal P
Ndipp (3: L3 = N[CHC(tBu)O]23−; 4: L3 = N(o-NMeC6H4)23−; dipp = 2,6-diisopropylphenyl) are reported. These compounds are characterized by multinuclear NMR and single-crystal X-ray diffraction experiments. Distorted phosphazenes 3 and 4 are shown to add B–H, B–O, and Si–H bonds across the formal P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond, and their reactivities are contrasted with acyclic analogues. Derivatives of phosphazene 3 bearing sterically unencumbered N-substitutents readily dimerize to form the corresponding cyclodiphosphazanes; compounds with sterically demanding N-substituents are interconvertible between their monomeric and dimeric forms. The enhanced electrophilicity of the phosphorus center in nontrigonal phosphazenes 3 and 4 is rationalized by DFT calculations. Gas phase fluoride ion affinities are computed to be markedly higher for distorted phosphazenes, while proton affinities are largely unaffected by geometric distortion. These results are interpreted to suggest that distortion from pseudotetrahedral geometry results in stabilization of the P-based LUMO, while HOMO energies are essentially unchanged.
N double bond, and their reactivities are contrasted with acyclic analogues. Derivatives of phosphazene 3 bearing sterically unencumbered N-substitutents readily dimerize to form the corresponding cyclodiphosphazanes; compounds with sterically demanding N-substituents are interconvertible between their monomeric and dimeric forms. The enhanced electrophilicity of the phosphorus center in nontrigonal phosphazenes 3 and 4 is rationalized by DFT calculations. Gas phase fluoride ion affinities are computed to be markedly higher for distorted phosphazenes, while proton affinities are largely unaffected by geometric distortion. These results are interpreted to suggest that distortion from pseudotetrahedral geometry results in stabilization of the P-based LUMO, while HOMO energies are essentially unchanged.
1. Introduction
Phosphazenes, σ4,λ5-phosphorus compounds of the form R3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR′, comprise a broad class of functionally diverse main group inorganic molecules.1 The properties and reactivities of phosphazenes can be modulated over a wide range depending on substitution at the two heteroatom positions. In many circumstances, the P
NR′, comprise a broad class of functionally diverse main group inorganic molecules.1 The properties and reactivities of phosphazenes can be modulated over a wide range depending on substitution at the two heteroatom positions. In many circumstances, the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit proves quite inert; indeed, the robustness of the P
N unit proves quite inert; indeed, the robustness of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N moiety forms the basis for the many remarkable applications of polyphosphazene inorganic/organic hybrid materials.2
N moiety forms the basis for the many remarkable applications of polyphosphazene inorganic/organic hybrid materials.2
As might be expected on the basis of the differing electronegativities of phosphorus and nitrogen, however, the polarization of the formal P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond (i.e., contributing Lewis structures R3P
N double bond (i.e., contributing Lewis structures R3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR′ ↔ R3P+–N−R′) also gives rise to numerous applications for phosphazenes as nitrogen-based electron pair donors. For instance, phosphazenes are known to be strong donor ligands for transition metals.3 Phosphazenes have found synthetic use as strong, non-ionic organic superbases; the tetrameric triaminophosphazene superbase t-Bu-P4 displays exceptionally high Brønsted–Lowry basicity and has been investigated for a variety of base-mediated transformations.4
NR′ ↔ R3P+–N−R′) also gives rise to numerous applications for phosphazenes as nitrogen-based electron pair donors. For instance, phosphazenes are known to be strong donor ligands for transition metals.3 Phosphazenes have found synthetic use as strong, non-ionic organic superbases; the tetrameric triaminophosphazene superbase t-Bu-P4 displays exceptionally high Brønsted–Lowry basicity and has been investigated for a variety of base-mediated transformations.4
Apart from this nitrogen-based reactivity, phosphazenes also have been employed in a number of transformations that leverage the vicinal ambiphilic character of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. Chief among this class of reactions are metathetical transformations stemming from formal (2 + 2) addition/elimination of unsaturated organic compounds at the phosphazene P
N unit. Chief among this class of reactions are metathetical transformations stemming from formal (2 + 2) addition/elimination of unsaturated organic compounds at the phosphazene P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N moiety, of which the aza-Wittig5 and related imine metathesis6 reaction are representative. An increasingly important use of phosphazenes comes in the Staudinger ligation reaction, which has become an important tool in bioconjugation chemistry.7
N moiety, of which the aza-Wittig5 and related imine metathesis6 reaction are representative. An increasingly important use of phosphazenes comes in the Staudinger ligation reaction, which has become an important tool in bioconjugation chemistry.7
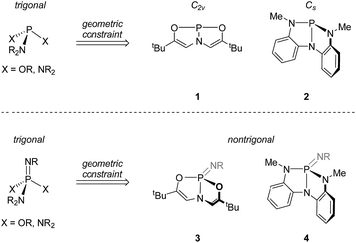
Recently, we have been investigating the connection between equilibrium ground-state structure and reactivity in a class of nontrigonal phosphabicyclic compounds. We have documented that the distorted molecular geometries for these tricoordinate phosphorus compounds have a significant impact on both their electronic structure and reactivity. For instance, we have reported that Arduengo's T-shaped phosphorus compound81 (Fig. 1 top) supports transfer hydrogenation catalysis9 and N–H oxidative addition reactivity.10
In addition, we reported the synthesis of Cs-symmetric phosphorus compound 2 (Fig. 1, top) and its ability to undergo E–H bond activation reactivity (E = –OR, –NHR, –BR2) at phosphorus through a ligand-cooperative mechanism.11,12
Based on this precedent, we wished to ascertain the extent to which the distinctive reactivity traits of nontrigonal phosphorus compounds 1 and 2 might range beyond the tricoordinate state to support interesting chemical properties of their distorted σ4,λ5-phosphazene derivatives. In this study, we report a combined theoretical and experimental treatment of phosphazenes based on supporting structures 1 and 2 which validate the hypothesis that imposition of a geometric constraint at positions ancillary to the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit enhances vicinal ditopic ambiphilicity of these phosphazenes. We also show that 1,2-reactivity of the P
N unit enhances vicinal ditopic ambiphilicity of these phosphazenes. We also show that 1,2-reactivity of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit leads to facile addition of σ-bonded B–H, B–O, and Si–H reagents across the P
N unit leads to facile addition of σ-bonded B–H, B–O, and Si–H reagents across the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N moiety. In total, the results establish a rational framework for the design of bespoke phosphazenes with novel properties and reactivities that expand the functional role of this important class of main group compounds.
N moiety. In total, the results establish a rational framework for the design of bespoke phosphazenes with novel properties and reactivities that expand the functional role of this important class of main group compounds.
2. Results and discussion
2.1. Computational model of the phosphazene distortion coordinate
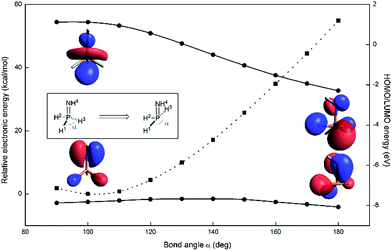
A computational appraisal of the consequence of molecular distortion on phosphazene frontier electronic structure illustrates the theoretical framework underlying our experimental study. With the parent phosphazene H3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH (Fig. 2, inset) as a minimalistic model system, orbital and overall electronic energies were computed as a function of internal bond angle ∠H1–P–H3 (α) in the range 90° < α < 180° at the M06-2X/def2-TZVP level of theory13,14 as implemented in the ORCA 4.0.0 software package.15,16 For each structure scanned, the dihedral angle ∠H2–P–N–H4 was relaxed to minimize energy associated with rotation about the P
NH (Fig. 2, inset) as a minimalistic model system, orbital and overall electronic energies were computed as a function of internal bond angle ∠H1–P–H3 (α) in the range 90° < α < 180° at the M06-2X/def2-TZVP level of theory13,14 as implemented in the ORCA 4.0.0 software package.15,16 For each structure scanned, the dihedral angle ∠H2–P–N–H4 was relaxed to minimize energy associated with rotation about the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N formal double bond; bond lengths were held constant at values obtained from the equilibrium geometry of H3P
N formal double bond; bond lengths were held constant at values obtained from the equilibrium geometry of H3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH (dP–H = 1.44 Å, dP–N = 1.61 Å, dN–H = 1.02 Å); these parameters are in good agreement with those found in previous computational studies of H3P
NH (dP–H = 1.44 Å, dP–N = 1.61 Å, dN–H = 1.02 Å); these parameters are in good agreement with those found in previous computational studies of H3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH.17
NH.17
Deviations from the equilibrium geometry (α = 97.9°) predictably lead to increases in overall energy (Fig. 2, dotted line). Notwithstanding this fact, the energy of the highest occupied orbital (εHOMO) remains more or less constant across the scanned coordinate. Visual inspection of the relevant orbitals provides for a qualitative interpretation of this observation; highest occupied molecular orbitals are found to be mostly nitrogen-based, corresponding largely to the N lone pair (nN) with minor contributions from the ancillary phosphorus substituents.
By contrast, the energy of the lowest unoccupied orbital (εLUMO) decreases as the bond angle α increases, ultimately resulting in stabilization of more than 3 eV as LUMO takes on increasing s-orbital character in the distortion to seesaw geometry (α = 180°). This electronic picture suggests that the nontrigonal distortion of phosphazenes should retain the Lewis basicity of the N position but dramatically increase the Lewis acidity of the P position. We posit that the juxtaposition of donor and acceptor character at adjacent atoms should lead to an increase in 1,2-ambiphilic reactivity of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit, in analogy to well-established chemistry of early transition metal imido (M
N unit, in analogy to well-established chemistry of early transition metal imido (M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR) complexes.18 We sought to confirm these theoretical predictions experimentally with a suite of phosphazene compounds.
NR) complexes.18 We sought to confirm these theoretical predictions experimentally with a suite of phosphazene compounds.
2.2. Phosphazene synthesis and characterization
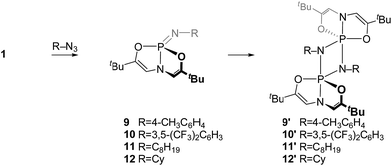
Similarly, compound 4 was prepared by the reaction of 2 with 1 equiv. of 2,6-diisopropylphenyl azide (C6D6, RT, 12 h) and subsequent recrystallization from a solution of pentane and dichloromethane. The 31P{1H} NMR spectrum of this compound showed a resonance at δ 14.5 ppm, consistent with typical values for tetraazaphosphazenes. The spectroscopic equivalence of both ligand N-methyl substituents in the 1H NMR spectrum suggest time-averaged Cs or higher symmetry, as with compound 3.
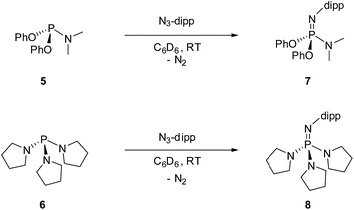
For the purpose of comparison, acyclic phosphazene analogues 7 and 8 were likewise synthesized from the corresponding phosphorus compounds 5 and 6 (Scheme 2).
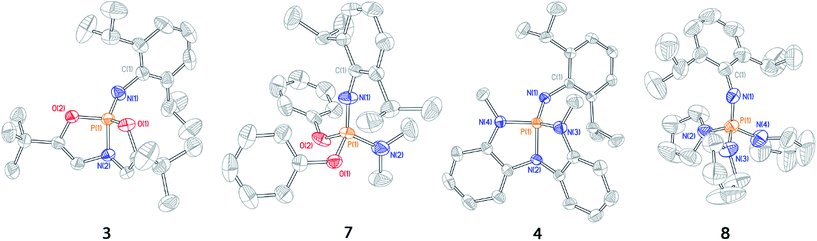 | ||
| Fig. 3 Thermal ellipsoid plots of phosphazenes 3, 7, 4, and 8 rendered at 50% probability level. Hydrogen atoms omitted for clarity. | ||
| Metric | 3 | 7 | 4 | 8 |
|---|---|---|---|---|
| a See ESI for full crystallographic details. Bond angles most relevant to nontrigonal distortion in bold. | ||||
| d(P1–N1) | 1.5069(14) | 1.4810(17) | 1.5309(11) | 1.525(3) |
| d(P1–N2) | 1.6903(13) | 1.613(2) | 1.7095(10) | 1.644(3) |
| d(P1–O1) | 1.6044(12) | 1.6044(15) | ||
| d(P1–O2) | 1.5962(11) | 1.5985(15) | ||
| d(P1–N3) | 1.6723(12) | 1.639(3) | ||
| d(P1–N4) | 1.6591(11) | 1.632(3) | ||
| ∠O1–P1–O2 | 112.62(6) | 96.70(8) | ||
| ∠O1–P1–N1 | 115.30(7) | 120.04(9) | ||
| ∠O1–P1–N2 | 96.68(7) | 101.79(9) | ||
| ∠O2–P1–N1 | 109.40(7) | 112.35(9) | ||
| ∠O2–P1–N2 | 96.19(6) | 107.06(11) | ||
| ∠N1–P1–N2 | 124.96(7) | 116.46(11) | 129.22(6) | 117.32(15) |
| ∠N1–P1–N3 | 114.72(6) | 104.41(16) | ||
| ∠N1–P1–N4 | 107.24(6) | 108.23(14) | ||
| ∠N2–P1–N3 | 92.35(5) | 104.41(16) | ||
| ∠N2–P1–N4 | 92.84(5) | 102.58(15) | ||
| ∠N3–P1–N4 | 119.73(6) | 108.45(16) | ||
| ∠P1–N1–C1 | 135.72(10) | 153.82(15) | 137.19(10) | 137.3(2) |
The solid state structure of 3 displays substantial opening of the O1–P1–O2 bond angle relative to the acyclic phosphazene 7; the bond angle in 3 (112.62(6)°) is 16° wider than that of 7 (96.70(8)°). The increase in O1–P1–O2 bond angle in 3 is complemented by a moderate (ca. 5–10°) decrease in internal bond angles O1–P1–O2. Additionally, the N1–P1–N2 angle likewise increases in 3 (124.96(7)°) relative to 7 (116.46(11)°) in order to restrict unfavorable steric interactions between the N-dipp substituent and the ligand backbone. Thus, the solid state structure of phosphazene 3 corresponds to a deviation from idealized pseudo-tetrahedral geometry along the distortion coordinate illustrated in Fig. 2.
Similarly, N,N,N-phosphabicyclic phosphazene 4 has an expanded N3–P1–N4 bond angle of 4 (119.73(6)°), 14° greater than the average angle in 8 (105.15(15)°). Furthermore, the N2–P1–N3 and N3–P1–N4 endocyclic angles were generally smaller relative to 8. As with constrained phosphazene 3, there was also an expansion of the N1–P1–N2 bond angle in 4 (129.22(6)°) versus8 (109.99(15)°, average of 3 angles), constituting a difference of 19°; this difference is greater than that of the 3/7 pair and is likely a result of increased steric congestion imposed by the N-methylanilides of 4.
These solid state structures confirm our hypothesis that imposing geometric constraints via a bicyclic ligand framework results in a nontrigonal geometry along the distortion coordinate toward see-saw molecular structures.
CF2O + [R3P(F)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR′]− → CF3O− + R3P NR′]− → CF3O− + R3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR′ ΔHrxn = FIA NR′ ΔHrxn = FIA | (1) |
[R3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(H)R′]+ → H+ + R3P N(H)R′]+ → H+ + R3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR′ ΔHrxn = PA NR′ ΔHrxn = PA | (2) |
Fluoride ion affinities for constrained phosphazenes 3 and 4 are significantly greater (>20 kcal mol−1 difference in each case) than their unconstrained analogues 7 and 8. This result conforms with qualitative predictions from the model system H3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH (vide supra, Section 2.1.); upon distortion from pseudo-tetrahedral geometry, the phosphorus-based LUMOs decrease in energy, allowing for stronger interactions of exogenous anions like F− with nontrigonal 3 and 4 than with trigonal compounds 7 and 8.
NH (vide supra, Section 2.1.); upon distortion from pseudo-tetrahedral geometry, the phosphorus-based LUMOs decrease in energy, allowing for stronger interactions of exogenous anions like F− with nontrigonal 3 and 4 than with trigonal compounds 7 and 8.
Differences in proton affinities, on the other hand, are much smaller in magnitude. For instance, the computed PAs for compounds 3 and 7 are 238 kcal mol−1 and 239 kcal mol−1, respectively. For compounds 4 and 8, the PAs are 246 kcal mol−1 and 258 kcal mol−1, respectively. Given the magnitude of the calculated proton affinities, the difference in calculated PAs for 3/7 and 4/8 does not exceed 6% overall. This outcome is in accord with the interpretation from calculations in Section 2.1. in which molecular distortion would not be expected to affect significantly the N-based HOMOs responsible for Lewis basicity.
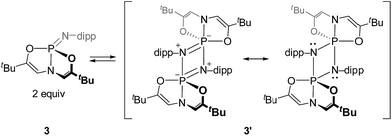
2.3. Monomer–dimer speciation of nontrigonal phosphazenes
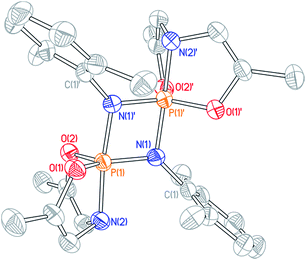
Cyclophosphazane 3′ is found to crystallize in the centrosymmetric monoclinic space group C2/c, with one phosphazene monomer fragment in the asymmetric unit and the dimer generated by symmetry. The structural data indicate local trigonal bipyramidal geometry about each phosphorus center, where the formerly imino nitrogen atoms occupy one equatorial and one apical site (Fig. 4). The most distinctive feature of this stereochemical arrangement is the dissymmetric P–N bond distances within a planar diamond-like P2N2 core. As might be expected on the basis of the Rundle–Pimentel model of bonding in pentacoordinate p-block compounds,24 the axial P–N bond is significantly longer (dP–N = 1.783(3) Å) than the equatorial P–N bonds (dP–N = 1.665(3) Å). Both bond distances are elongated as compared to monomeric 3 (dP–N = 1.5069(14) Å). In short, the structural metrics are consistent with a superposition of the Lewis structures for 3′, displayed in Scheme 3.
Dissolution of a single-crystalline sample of 3′ in C6D6 at ambient temperature resulted in repopulation of the mixture containing both dimer 3′ and monomer 3 as judged by 1H and 31P NMR spectroscopy. Consequently, we conclude that the formal 2 + 2 dimerization of 3 to 3′ is reversible, as illustrated in Scheme 3. Notwithstanding the apparent dynamic nature of the monomer–dimer equilibrium, the appearance of two distinct resonances for 3 and 3′ in the 31P NMR spectra is most consistent with a slow interconversion relative to the NMR timescale.
In contrast to the deformed O,N,O-phosphazene 3, dimerization of the constrained N,N,N-phosphazene 4 was not observed under any conditions.25 We posit that in this case the steric crowding by N–Me substituents of the bicyclic ligand framework and imino N-substituent prohibits close approach of a second phosphazene as would be necessary for dimer formation. Additionally, the phosphorus center of 4 is less Lewis acidic than that of 3 (as revealed by FIA analysis above), so it is possible that decreased electrophilicity at P precludes sufficient driving force for phosphazene dimerization.
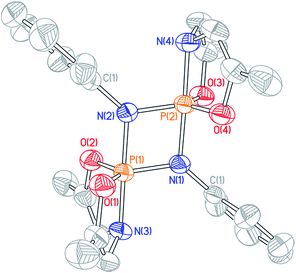
The 31P NMR resonances of cyclodiphosphazanes 9′–12′ appear at noticeably lower field compared to 3′, suggesting a geometric distinction between the very bulky 2,6-diisopropyl-substituted cyclodiphosphazane and less sterically demanding congeners. Single crystals of dimeric N-p-tolyl derivative 9′ were obtained by slow evaporation of a benzene solution, and the structure was interrogated by X-ray diffraction (Fig. 5). Globally, compound 9′ adopts the same planar 1,3-diaza-2,4-diphosphetidine P2N2 diamond core structure as 3′. There are, however, notable metrical differences; the axial P–N (dP–N = 1.744(3) Å) and equatorial P–N (dP–N = 1.635(3) Å) bond lengths for N-p-tolyl cyclodiphosphazane 9′ are approximately 0.04 Å shorter than for N-dipp cyclodiphosphazane 3′. We infer that the reduced steric congestion about the P2N2 core for 9′ permits tighter association of the monomer subunits in a head-to-tail fashion that is manifest in the 31P isotropic chemical shielding differences. Congruent with this assessment, attempts to access monomeric phosphazenes 9–12 by heating of benzene solutions of 9′–12′ were unsuccessful; formal (2 + 2) dimerization appears to be prohibitively downhill in enthalpy and, therefore, irreversible for these less sterically congested cyclodiphosphazanes.
Formal [2 + 2]-cyclodimerization of phosphazene P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N units is well-precedented in the literature, specifically for phosphazenes bearing strongly electron-withdrawing P-substituents or where relief of ring strain provides a driving force.26 That geometrically constrained O,N,O-phosphazenes (9′–12′) readily dimerize is thus a qualitative indication of the marked Lewis acidity of these phosphorus centers as compared to their acyclic congeners. Furthermore, the sum of the observations concerning the monomer–dimer speciation of distorted phosphazenes 3/3’ evidences a propensity for 1,2-ambiphilic reactivity of the P
N units is well-precedented in the literature, specifically for phosphazenes bearing strongly electron-withdrawing P-substituents or where relief of ring strain provides a driving force.26 That geometrically constrained O,N,O-phosphazenes (9′–12′) readily dimerize is thus a qualitative indication of the marked Lewis acidity of these phosphorus centers as compared to their acyclic congeners. Furthermore, the sum of the observations concerning the monomer–dimer speciation of distorted phosphazenes 3/3’ evidences a propensity for 1,2-ambiphilic reactivity of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit, suggesting that intermolecular 1,2-additions of exogenous reagents might be feasible.
N unit, suggesting that intermolecular 1,2-additions of exogenous reagents might be feasible.
2.4. 1,2 addition reactivity of nontrigonal phosphazenes
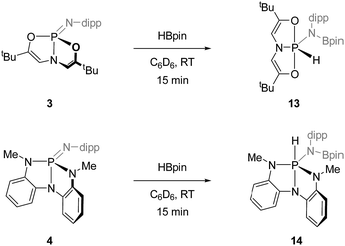
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit in deformed phosphazenes 3 and 4, we elected to attempt the 1,2-addition of σ-bonded E–H small molecules. To this end, treatment of O,N,O-phosphazene 3 with 1 equiv. of pinacolborane (HBpin) in C6D6 at room temperature resulted in rapid consumption of the starting materials and formation of a single new compound with a 31P NMR resonance at δ −43.7 ppm presenting as a doublet of triplets (J = 837, 33 Hz). The magnitude of the larger coupling constant is indicative of a direct P–H linkage; existence of a P–H moiety was confirmed in 1H NMR spectra by the appearance of a doublet centered at δ 9.37 ppm with complementary coupling (1JP–H = 837 Hz). Although attempts to obtain a solid state structure of 13 from X-ray diffraction analysis were unsuccessful, these spectroscopic signatures are consistent with formation of hydrido amido phosphorane 13 in which the O,N,O-chelate spans two apical and one equatorial position about a phosphorus-centered trigonal bipyramid, and the hydride and borylamide substituents reside in the equatorial plane. Further support for this assignment comes by way of analogy to previous results from our group. We reported previously that hydrido amido phosphoranes related to 13 are accessible via intermolecular N–H oxidative addition to 3.10 More specifically, the addition of 2,6-diisopropylaniline to 3 gave a crystallographically characterized oxidative addition product (i.e. the des-boryl congener of 13) that exhibits spectroscopic features (31P δ −51.4 ppm; 1JP–H = 841 Hz) in close agreement with those obtained for 13. In short, the combined data lend strong evidence to the structural assignment of the B–H addition product 13.
N unit in deformed phosphazenes 3 and 4, we elected to attempt the 1,2-addition of σ-bonded E–H small molecules. To this end, treatment of O,N,O-phosphazene 3 with 1 equiv. of pinacolborane (HBpin) in C6D6 at room temperature resulted in rapid consumption of the starting materials and formation of a single new compound with a 31P NMR resonance at δ −43.7 ppm presenting as a doublet of triplets (J = 837, 33 Hz). The magnitude of the larger coupling constant is indicative of a direct P–H linkage; existence of a P–H moiety was confirmed in 1H NMR spectra by the appearance of a doublet centered at δ 9.37 ppm with complementary coupling (1JP–H = 837 Hz). Although attempts to obtain a solid state structure of 13 from X-ray diffraction analysis were unsuccessful, these spectroscopic signatures are consistent with formation of hydrido amido phosphorane 13 in which the O,N,O-chelate spans two apical and one equatorial position about a phosphorus-centered trigonal bipyramid, and the hydride and borylamide substituents reside in the equatorial plane. Further support for this assignment comes by way of analogy to previous results from our group. We reported previously that hydrido amido phosphoranes related to 13 are accessible via intermolecular N–H oxidative addition to 3.10 More specifically, the addition of 2,6-diisopropylaniline to 3 gave a crystallographically characterized oxidative addition product (i.e. the des-boryl congener of 13) that exhibits spectroscopic features (31P δ −51.4 ppm; 1JP–H = 841 Hz) in close agreement with those obtained for 13. In short, the combined data lend strong evidence to the structural assignment of the B–H addition product 13.
Likewise, treating N,N,N-phosphazene 4 with 1 equiv. of pinacolborane in C6D6 at ambient temperature quickly consumed starting materials to yield a species 14 with a doublet 31P NMR signal at δ −37.6 ppm (doublet, 1JP–H = 579 Hz). Complementary coupling was observed in the 1H NMR spectrum with a doublet resonance at δ 6.36 ppm. As with the reaction of 3 and HBpin, these spectral data are characteristic of pentacoordinated hydrido amido phosphorane featuring a direct P–H bond. By analogy to previous results on the intermolecular N–H oxidative addition of 2,6-diisopropylaniline to 4,11 we posit the assignment of 14 as in Scheme 5 with a folded non-meridional N,N,N-ligand, equatorial N-dipp substituent, and an axial hydride.
By contrast to 3 and 4, acyclic O,N,O- and N,N,N-phosphazenes 7 and 8 were unreactive with respect to pinacolborane under identical reaction conditions. Additionally, none of the dimeric cyclodiphosphazanes 9′–12′ were found to undergo reaction with HBpin. We conclude, therefore, that the ability of the phosphazenes 3 and 4 to undergo 1,2-addition of H–Bpin is dependent on the distorted structure enforced by the trianionic heteroatom supporting structures, and that access to the monomeric form of the phosphazene is critical for intermolecular addition.
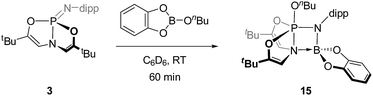
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. Addition of 1 equiv. of n-butoxy catecholborane to a C6D6 solution of 3 at room temperature (Scheme 6) resulted in consumption of 3 with concomitant generation of a new 31P NMR singlet resonance at δ −31.4 ppm indicative of pentacoordinated phosphorus species 15; scalar coupling could not be resolved. The corresponding 1H NMR spectrum featured a resonance at δ 5.33 ppm (doublet, 3JP–H = 17 Hz), which can be attributed to coupling between the phosphorus center and the vinylic protons of the O,N,O-ligand. The magnitude of this coupling is smaller than would be expected for σ5-phosphorus compounds with a planar, meridional O,N,O-chelate. This result suggests that antiperiplanarity between P and H has been lost; that is, the dihedral angle between the phosphorus and vinylic hydrogen atoms has decreased from 180° in accordance with the Karplus equation for 3J scalar coupling,27 implying that the O,N,O-framework adopts a folded geometry.
N unit. Addition of 1 equiv. of n-butoxy catecholborane to a C6D6 solution of 3 at room temperature (Scheme 6) resulted in consumption of 3 with concomitant generation of a new 31P NMR singlet resonance at δ −31.4 ppm indicative of pentacoordinated phosphorus species 15; scalar coupling could not be resolved. The corresponding 1H NMR spectrum featured a resonance at δ 5.33 ppm (doublet, 3JP–H = 17 Hz), which can be attributed to coupling between the phosphorus center and the vinylic protons of the O,N,O-ligand. The magnitude of this coupling is smaller than would be expected for σ5-phosphorus compounds with a planar, meridional O,N,O-chelate. This result suggests that antiperiplanarity between P and H has been lost; that is, the dihedral angle between the phosphorus and vinylic hydrogen atoms has decreased from 180° in accordance with the Karplus equation for 3J scalar coupling,27 implying that the O,N,O-framework adopts a folded geometry.
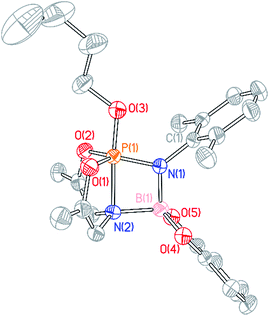
A single crystal suitable for X-ray diffraction was grown from benzene solution, and the solid state structure corroborates the above conclusion regarding O,N,O-folding (Fig. 6). A distinguishing feature of compound 15 is the unexpectedly short distance between the ligand amido N atom and the N-dipp-bound boron (dN2–B1 = 1.637(3) Å), consistent with the presence of a dative interaction N2 → B1 in 15; pyramidalization of the boron atom evident in the solid state structure further evidences this conclusion. By consequence of this interaction, compound 15 may be viewed as a trigonal bipyramidal phosphorus compound supported by a tetracoordinating boroazaphosphatrane ligand, where the fifth apical binding site of the trigonal bipyramid is occupied by the n-butoxy substituent. Indeed, the apical bond distance dP1–N2 is quite long (1.9392(19) Å), conforming to precedent from cationic phosphatranes28 (cf. dP–N = 1.986(5) Å for [HP(OCH2CH2)3N][BF4];29adP–N = 1.967(8) Å for [HP(MeNCH2CH2)3N][BF4]29b). Additionally, the apical P1–N2 bond in 15 is substantially longer than the equatorial P1–N1 bond (1.6195(18) Å), comprising a difference of more than 0.3 Å. As a consequence, the trans apical P1–O3 bond is found to be quite short (1.5906(16) Å); in fact, the apical P–O bond is shorter than the equatorial P–O bonds (1.6242(16) Å and 1.6252(16) Å). This observation runs counter to typical trigonal bipyramidal geometries, where the 3-center, 4-electron apical bonds are usually longer than the 2-center, 2-electron equatorial bonds. These unusual structural features of the B–O adduct of phosphazene 3 likely arise from molecular constraint imposed by the O,N,O-ligand and by the Lewis acidic boron atom.
Unlike phosphazene 3, N,N,N-ligated phosphazene 4 did not react with n-butoxy catecholborane, perhaps again due to increased steric congestion about the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. Likewise, acyclic analogues 7 and 8 were unreactive to B–O bonds.
N unit. Likewise, acyclic analogues 7 and 8 were unreactive to B–O bonds.
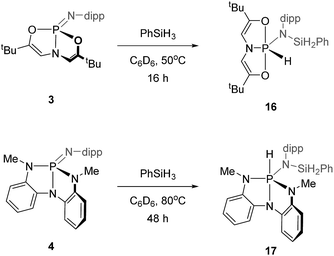
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond of 3 to give a hydrido phosphorane with a N-silyl substituent.
N bond of 3 to give a hydrido phosphorane with a N-silyl substituent.
N,N,N-Phosphazene 4 also reacted with phenylsilane, but at a slower rate than 3. The conversion of 4 and phenylsilane to hydrido phosphorane 17 was completed after 48 h of heating at 80 °C in C6D6. The resulting 31P NMR spectrum showed one signal centered at δ −29.1 ppm (d, 1JP–H = 535 Hz); the magnitude of the scalar coupling constant is characteristic of a P–H bond, consistent with the structure of the σ5-phosphorus Si–H addition product 17. By analogy to other N,N,N-ligated compounds synthesized earlier, we expect the trianionic chelate to adopt a folded structure, as in Scheme 7.
Acyclic phosphazenes 7 and 8 were found to be unreactive to Si–H addition. The fact that compounds of this type are robust to silane addition has been exploited by Fontaine, who has shown that phosphazenes similar to 8 can be used as Lewis base-catalysts for catalysed hydrosilylation of CO2.30
The 1,2-addition of hydrosilane across the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit of a phosphazene has often been invoked, albeit usually in tandem with subsequent elimination from P(V) and without direct observation of the elementary step. Kawashima has studied the intramolecular addition of a Si–H bond to a functionalized phosphazene.31 Phosphine-catalyzed variants of the Staudinger reduction of azides are believed to rely on the addition of hydrosilane to phosphazene intermediates to close the catalytic cycle.32 Relatedly, Denton has demonstrated that a phosphine-catalyzed Staudinger amidation reaction relies on the in situ reduction of a phosphazene, presumably initiated by 1,2-addition of hydrosilane.33 In each of these chemistries the silane reduction step likely proceeds via 1,2-addition via a trigonal bipyramidal hydrido amido phosphorane intermediate, but despite the prevalence of the 1,2-addition proposal, there do not exist discrete, well-characterized analogues of this key step. Our current results represent a rare well-defined addition reaction giving rise to stable pentacoordinate adducts that substantiate the notion of 1,2-addition of hydrosilanes to phosphazenes.
N unit of a phosphazene has often been invoked, albeit usually in tandem with subsequent elimination from P(V) and without direct observation of the elementary step. Kawashima has studied the intramolecular addition of a Si–H bond to a functionalized phosphazene.31 Phosphine-catalyzed variants of the Staudinger reduction of azides are believed to rely on the addition of hydrosilane to phosphazene intermediates to close the catalytic cycle.32 Relatedly, Denton has demonstrated that a phosphine-catalyzed Staudinger amidation reaction relies on the in situ reduction of a phosphazene, presumably initiated by 1,2-addition of hydrosilane.33 In each of these chemistries the silane reduction step likely proceeds via 1,2-addition via a trigonal bipyramidal hydrido amido phosphorane intermediate, but despite the prevalence of the 1,2-addition proposal, there do not exist discrete, well-characterized analogues of this key step. Our current results represent a rare well-defined addition reaction giving rise to stable pentacoordinate adducts that substantiate the notion of 1,2-addition of hydrosilanes to phosphazenes.
3. Conclusions
Constrained phosphabicyclic phosphazenes supported by trianionic scaffolding O,N,O- and N,N,N-ligands exhibit increased cyclodimerization and 1,2-addition reactions of B–H, B–O, and Si–H σ bonds as compared to acyclic congeners. The results of the combined experimental and theoretical studies above support the conclusion that nontrigonal distortion of phosphazenes leads to an enhancement of the 1,2-ambiphilic reactivity of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. In view of the multivarious roles of phosphazenes, the ability to master electronic structure and reactivity as a function of a modifiable parameter contributes to the discovery of novel applications. In conjunction with established approaches to synthetic tuning through substituent effects, the current results establish a rational geometry-based framework for modulating the reactivity of this important class of main group compounds, which may be leveraged in the design of functionally novel entities.
N unit. In view of the multivarious roles of phosphazenes, the ability to master electronic structure and reactivity as a function of a modifiable parameter contributes to the discovery of novel applications. In conjunction with established approaches to synthetic tuning through substituent effects, the current results establish a rational geometry-based framework for modulating the reactivity of this important class of main group compounds, which may be leveraged in the design of functionally novel entities.
4. Experimental section
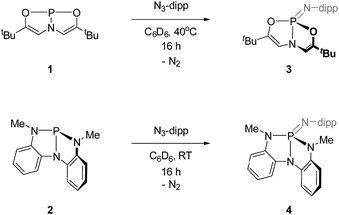
Full experimental details are available in the online ESI.†4.1. Synthesis of 3
A solution of 1 (100 mg, 0.42 mmol) with 2,6-diisopropylphenyl azide (85 mg, 0.42 mmol) in C6D6 (1 mL) was stirred at 40 °C for 16 h. All volatiles were removed in vacuo, and the resulting residue was triturated with pentane. The crude product was obtained after filtration, and pure 3 was isolated as a white solid by recrystallization from a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dichloromethane/pentane solution (131 mg, 75% yield). 1H NMR (C6D6, 400 MHz): δ 7.23–7.21 (m, 2H), 7.12–7.07 (m, 1H), 7.07 (d, 1H, J = 7.7 Hz), 5.49 (d, 2H, J = 28.8 Hz), 3.83 (hept, 1H, J = 6.9 Hz), 1.40 (d, 12H, J = 6.8 Hz), 0.91 (s, 18H) ppm. 13C NMR (C6D6, 126 MHz): δ 154.19, 141.29 (d, J = 8.7 Hz), 123.03, 121.98, 112.43 (d, J = 10.1 Hz), 32.64 (d, J = 8.6 Hz), 29.35, 26.89, 23.75 ppm. 31P NMR (C6D6, 162 MHz): δ 7.21 (t, J = 28.8 Hz) ppm. MS (ESI) calc'd for C24H37N2O2P (M+) 416.2593, found 416.2596.
1 dichloromethane/pentane solution (131 mg, 75% yield). 1H NMR (C6D6, 400 MHz): δ 7.23–7.21 (m, 2H), 7.12–7.07 (m, 1H), 7.07 (d, 1H, J = 7.7 Hz), 5.49 (d, 2H, J = 28.8 Hz), 3.83 (hept, 1H, J = 6.9 Hz), 1.40 (d, 12H, J = 6.8 Hz), 0.91 (s, 18H) ppm. 13C NMR (C6D6, 126 MHz): δ 154.19, 141.29 (d, J = 8.7 Hz), 123.03, 121.98, 112.43 (d, J = 10.1 Hz), 32.64 (d, J = 8.6 Hz), 29.35, 26.89, 23.75 ppm. 31P NMR (C6D6, 162 MHz): δ 7.21 (t, J = 28.8 Hz) ppm. MS (ESI) calc'd for C24H37N2O2P (M+) 416.2593, found 416.2596.
4.2. Synthesis of 4
A solution of 2 (100 mg, 0.39 mmol) with 2,6-diisopropylphenyl azide (80 mg, 0.39 mmol) in C6D6 (1 mL) was stirred under ambient temperature for 12 h. The solvent was removed in vacuo, and the resulting solid product was recrystallized from a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dichloromethane/pentane solution (121 mg, 72% yield). 1H NMR (C6D6, 400 MHz): δ 7.26 (d, J = 7.7 Hz, 2H), 7.16 (d, J = 7.4 Hz, 2H), 7.09–7.02 (m, 1H), 6.98–6.85 (m, 3H), 6.77 (d, J = 7.6 Hz, 3H), 6.23 (d, J = 7.7 Hz, 2H), 3.65 (hept, J = 6.9 Hz, 2H), 2.73 (d, J = 9.2 Hz, 6H), 1.22 (d, J = 6.9 Hz, 12H) ppm. 13C NMR (C6D6, 125 MHz): δ 141.38, 141.00 (d, J = 11.7 Hz), 138.09 (d, J = 17.6 Hz), 134.58 (d, J = 13.0 Hz), 124.56, 123.26, 121.34, 120.14, 116.34 (d, J = 10.2 Hz), 108.66 (d, J = 10.0 Hz), 29.29 (d, J = 18.9 Hz), 23.75 ppm. 31P NMR (C6D6, 162 MHz): δ 14.54 ppm. MS (ESI) calc'd for C26H31N4P (M+) 430.2286, found 430.2290.
1 dichloromethane/pentane solution (121 mg, 72% yield). 1H NMR (C6D6, 400 MHz): δ 7.26 (d, J = 7.7 Hz, 2H), 7.16 (d, J = 7.4 Hz, 2H), 7.09–7.02 (m, 1H), 6.98–6.85 (m, 3H), 6.77 (d, J = 7.6 Hz, 3H), 6.23 (d, J = 7.7 Hz, 2H), 3.65 (hept, J = 6.9 Hz, 2H), 2.73 (d, J = 9.2 Hz, 6H), 1.22 (d, J = 6.9 Hz, 12H) ppm. 13C NMR (C6D6, 125 MHz): δ 141.38, 141.00 (d, J = 11.7 Hz), 138.09 (d, J = 17.6 Hz), 134.58 (d, J = 13.0 Hz), 124.56, 123.26, 121.34, 120.14, 116.34 (d, J = 10.2 Hz), 108.66 (d, J = 10.0 Hz), 29.29 (d, J = 18.9 Hz), 23.75 ppm. 31P NMR (C6D6, 162 MHz): δ 14.54 ppm. MS (ESI) calc'd for C26H31N4P (M+) 430.2286, found 430.2290.
4.3. Representative B–H addition
A solution of 3 (30 mg, 0.07 mmol) and HBpin (9 mg, 0.07 mmol) in C6D6 (0.3 mL) was stirred at ambient temperature for 15 min. The solvent was removed in vacuo to afford the crude product (37 mg, 95% crude yield). 1H NMR (C6D6, 500 MHz): δ 9.38 (d, 1H, J = 837.7 Hz), 7.27–7.25 (m, 1H), 7.08–7.04 (m, 2H), 5.49 (d, 2H, J = 33.2 Hz), 3.62–3.56 (m, 2H), 1.53 (d, 6H, J = 6.6 Hz, 1.45) (d, 6H, J = 6.6 Hz, 6H), 1.19 (s, 12H), 1.15 (s, 18H) ppm. 13C NMR (C6D6, 126 MHz): δ 150.73 (d, J = 6.4 Hz), 147.14, 126.64, 124.52 (d, J = 4.4 Hz), 124.02, 123.42, 100.51 (d, J = 18.8 Hz), 82.52, 31.69, 28.25, 27.51, 24.66, 23.62, 23.26 ppm. 31P NMR (C6D6, 203 MHz): δ −43.02 (dt, J = 837.0, 31.5 Hz) ppm. MS (ESI) calc'd for C30H49BN2O4P (M–H+) 543.3518, found 543.3523.4.4. Representative Si–H addition
A solution of 4 (50 mg, 0.12 mmol) and phenylsilane (13 mg, 0.12 mmol) in C6D6 (0.3 mL) was stirred at 80 °C for 48 h. All volatiles were removed in vacuo to afford 20 as a yellow oil (62 mg, 99% crude yield). 1H NMR (C6D6, 500 MHz): δ 7.32 (d, J = 7.1 Hz, 2H), 7.14–6.99 (m, 7H), 6.95 (t, J = 7.2 Hz, 3H), 6.87 (t, J = 7.7 Hz, 2H), 6.73 (t, J = 7.8 Hz, 2H), 6.37 (d, J = 7.5 Hz, 2H), 5.75 (d, J = 534.0 Hz, 1H), 5.05 (d, J = 5.8 Hz, 2H), 3.45–3.33 (m, 2H), 2.49 (d, J = 15.9 Hz, 6H), 1.15 (d, J = 6.8 Hz, 6H), 1.06 (d, J = 6.7 Hz, 6H) ppm. 13C NMR (C6D6, 126 MHz): δ 148.30 (d, J = 5.8 Hz), 137.93, 135.77 (d, J = 10.4 Hz), 134.65 (d, J = 14.5 Hz), 134.25, 133.46, 129.01, 127.16 (d, J = 3.6 Hz), 123.90 (d, J = 4.0 Hz), 121.42, 119.38, 113.89 (d, J = 10.8 Hz), 108.72 (d, J = 7.6 Hz), 29.69 (d, J = 15.5 Hz), 27.61, 26.24, 23.84 ppm. 31P NMR (C6D6, 203 MHz): δ −28.54 (dt, J = 534.5, 17.2 Hz) ppm. MS (ESI) calc'd for C32H40N4PSi (M + H+) 539.2760, found 539.2763.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding support from NSF (CHE-1724505) for structural and computational studies, NIH NIGMS (GM114547) for reactivity studies, and MIT. We thank Hemant Yennawar (The Pennsylvania State University) for the collection of crystallographic data, and Greg Cleveland and Hye Won Moon for assistance in processing crystal structure data.References
- A. W. Johnson, Ylides and Imines of Phosphorus, Wiley-Interscience, New York, 1993 Search PubMed.
- H. R. Allcock, Chemistry and Applications of Polyphosphazenes, John Wiley & Sons, Hoboken, USA, 2003 Search PubMed.
- (a) M. Witt and H. W. Roesky, Chem. Rev., 1994, 94, 1163–1181 CrossRef CAS; (b) V. Chandrasekhar and S. Nagendran, Chem. Soc. Rev., 2001, 30, 193–203 RSC; (c) J. García-Álvarez, S. E. García-Garrido and V. Cadierno, J. Organomet. Chem., 2014, 751, 792–808 CrossRef.
- (a) R. Schwesinger, Chimia, 1985, 39, 269–272 CAS; (b) R. Schwesinger and H. Schlemper, Angew. Chem., Int. Ed., 1987, 26, 1167–1169 CrossRef; (c) R. Schwesinger, J. Willaredt, H. Schlemper, M. Keller, D. Schmitt and H. Fritz, Chem. Ber., 1994, 127, 2435–2454 CrossRef CAS; (d) Y. Kondo, Phosphazene: Preparation, Reaction and Catalytic Role, in Superbases for Organic Synthesis: Guanidines, Amidines, Phosphazenes, and Related Organocatalysts, ed. T. Ishikawa, John Wiley & Sons, Chicester, United Kingdom, 2009 Search PubMed.
- F. Palacios, C. Alonso, D. Aparicio, G. Rubiales and J. M. de los Santos, Tetrahedron, 2007, 63, 523–575 CrossRef CAS.
- (a) S. A. Bell, T. Y. Meyer and S. J. Geib, J. Am. Chem. Soc., 2002, 124, 10698–10705 CrossRef CAS PubMed; (b) M. C. Burland and T. Y. Meyer, Inorg. Chem., 2003, 42, 3438–3444 CrossRef CAS PubMed.
- (a) E. Saxon and C. R. Bertozzi, Science, 2000, 287, 2007–2010 CrossRef CAS PubMed; (b) E. Saxon, J. I. Armstrong and C. R. Bertozzi, Org. Lett., 2000, 2, 2141–2143 CrossRef CAS PubMed; (c) B. L. Nilsson, L. L. Kiessling and R. T. Raines, Org. Lett, 2000, 2, 1939–1941 CrossRef CAS PubMed.
- A. J. Arduengo III, C. A. Stewart, F. Davidson, D. A. Dixon, J. Y. Becker, S. A. Culley and M. B. Mizen, J. Am. Chem. Soc., 1987, 109, 627–647 CrossRef.
- N. L. Dunn, M. Ha and A. T. Radosevich, J. Am. Chem. Soc., 2012, 134, 11330–11333 CrossRef CAS PubMed.
- S. M. McCarthy, Y.-C. Lin, D. Devarajan, J. W. Chang, H. P. Yennawar, R. M. Rioux, D. H. Ess and A. T. Radosevich, J. Am. Chem. Soc., 2014, 136, 4640–4650 CrossRef CAS PubMed.
- W. Zhao, S. M. McCarthy, T.-Y. Lai, H. P. Yennawar and A. T. Radosevich, J. Am. Chem. Soc., 2014, 136, 17634–17644 CrossRef CAS PubMed.
- Y.-C. Lin, E. Hatzakis, S. M. McCarthy, K. D. Reichl, T.-Y. Lai, H. P. Yennawar and A. T. Radosevich, J. Am. Chem. Soc., 2017, 139, 6008–6016 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, e1327, DOI:10.1002/wcms.1327.
- (a) A. W. Johnson, in Ylides and Imines of Phosphorus, John Wiley & Sons, New York, USA, 1993. ch. 13, Iminophosphranes and Related Compounds Search PubMed; (b) D. Gonbeau, G. Pfister-Guillouzo, M. Mazieres and M. Sanchez, Can. J. Chem., 1985, 63, 3242–3248 CrossRef CAS; (c) M. T. Nguyen and A. F. Hegarty, J. Chem. Soc., Perkin Trans. 2, 1987, 47–54 RSC; (d) P. Molina, M. Alajarin, C. L. Leonardo, R. M. Claramunt, C. Foces-Foces, F. H. Cano, J. Catalan, J. L. G. de Paz and J. J. Elguero, J. Am. Chem. Soc., 1989, 111, 355–363 CrossRef CAS; (e) P. V. Sudhakar and K. J. Lammertsma, J. Am. Chem. Soc., 1991, 113, 1899–1906 CrossRef CAS.
- (a) W. A. Nugent and J. M. Mayer, Metal-Ligand Multiple Bonds: The Chemistry of Transition Metal Complexes Containing Oxo, Nitrido, Imido, Alkylidene, or Alkylidyne Ligands, Wiley-Interscience, New York, 1988 Search PubMed; (b) P. T. Wolczanski, Organometallics, 2018, 37, 505–516 CrossRef CAS.
- (a) Y. G. Gololobov, I. N. Zhmurova and L. F. Kasukhin, Tetrahedron, 1981, 37, 437–472 CrossRef CAS; (b) Y. G. Gololobov and L. F. Kasukhin, Tetrahedron, 1992, 48, 1353–1406 CrossRef CAS.
- V. P. Kukhar and V. A. Gilyarov, Pure Appl. Chem., 1980, 52, 891–904 CrossRef CAS.
- A. J. Arduengo III and C. A. Stewart, Chem. Rev., 1994, 94, 1215–1237 CrossRef.
- The pyrrolidine rings of 8 are found to be disordered, but the interior P, N, and C atoms were not.
- K. O. Christe, D. A. Dixon, D. McLemore, W. W. Wilson, J. A. Sheehy and J. A. Boatz, J. Fluorine Chem., 2000, 101, 151–153 CrossRef CAS.
- (a) R. E. Rundle, J. Am. Chem. Soc., 1947, 69, 1327–1331 CrossRef CAS; (b) R. E. Rundle, J. Chem. Phys., 1949, 17, 671–675 CrossRef CAS; (c) G. C. Pimentel, J. Chem. Phys., 1951, 19, 446–448 CrossRef CAS.
- We also prepared analogues of 4 with N-octyl and N-cyclohexyl substituents. Although we did not isolate these compounds, their crude 31P NMR data were consistent with exclusive monomer formation.
- (a) J. Boeske, E. Niecke, M. Nieger, E. Ocando, J. P. Majoral and G. Bertrand, Inorg. Chem., 1989, 28, 499–504 CrossRef CAS; (b) J. Boeske, E. Ocando-Mavarez, E. Niecke, J. P. Majoral and G. Bertrand, J. Am. Chem. Soc., 1987, 109, 2822–2823 CrossRef CAS; (c) B. A. Arbuzov, É. N. Dianova and E. Y. Zabotina, Russ. Chem. Bull., 1981, 30, 2192–2194 CrossRef; (d) Y. G. Shermolovich, A. V. Solov’ev, E. A. Danchenko and L. N. Markovskii, Zh. Obshch. Khim., 1983, 53, 2150 CAS; (e) A. P. Marchenko, V. V. Miroshnichenko, V. A. Kovenya, A. M. Pinchuk, A. N. Chernega, M. Y. Antipin and Y. T. Struchkov, Zh. Obshch. Khim., 1988, 58, 1758 CAS; (f) V. D. Romanenko, A. V. Ruban, S. V. Iksanova and L. N. Markovskii, Zh. Obshch. Khim., 1984, 54, 313–325 CAS; (g) A. Schmidpeter, H. Tautz and F. Schreiber, Z. Anorg. Allg. Chem., 1981, 475, 211–231 CrossRef CAS; (h) R. Francke and G.-V. Röschenthaler, Z. Anorg. Allg. Chem., 1989, 572, 135–139 CrossRef CAS.
- L. D. Quin, M. J. Gallagher, G. T. Cunkle and D. B. Chesnut, J. Am. Chem. Soc., 1980, 102, 3136–3413 CrossRef CAS.
- For a review of main group atranes, see: J. G. Verkade, Coord. Chem. Rev., 1994, 137, 233–295 CrossRef CAS.
- (a) J. C. Clardy, D. S. Milbrath, J. P. Springer and J. G. Verkade, J. Am. Chem. Soc., 1976, 98, 623–624 CrossRef CAS; (b) C. Lensink, S. K. Xi, L. M. Daniels and J. G. Verkade, J. Am. Chem. Soc., 1989, 111, 3478–3479 CrossRef CAS.
- M.-A. Courtemanche, M.-A. Légaré, É. Rochette and F.-G. Fontaine, Chem. Commun., 2015, 51, 6858–6861 RSC.
- N. Kano, K. Yanaizumi, X. Meng, N. Havare and T. Kawashima, Chem. Commun., 2013, 49, 10373–10375 RSC.
- H. A. van Kalkeren, J. J. Bruins, F. P. J. T. Rutjes and F. L. van Delft, Adv. Synth. Catal., 2012, 354, 1417–1421 CrossRef CAS.
- K. G. Andrews and R. M. Denton, Chem. Commun., 2017, 53, 7982–7985 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1821116–1821122. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc00929e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |