Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
79/81Br nuclear quadrupole resonance spectroscopic characterization of halogen bonds in supramolecular assemblies†
P.
Cerreia Vioglio‡
 a,
P. M. J.
Szell
a,
P. M. J.
Szell
 b,
M. R.
Chierotti
b,
M. R.
Chierotti
 a,
R.
Gobetto
a,
R.
Gobetto
 a and
D. L.
Bryce
a and
D. L.
Bryce
 *b
*b
aDepartment of Chemistry and NIS Centre, University of Torino, Via Pietro Giuria 7, 10125 Torino, Italy
bDepartment of Chemistry and Biomolecular Sciences & Centre for Catalysis Research and Innovation, University of Ottawa, 10 Marie Curie Private, Ottawa, Ontario K1N 6N5, Canada. E-mail: dbryce@uottawa.ca; Fax: +1-613-562-5170; Tel: +1-613-562-5800 ext. 2018
First published on 30th April 2018
Abstract
Despite the applicability of solid-state NMR to study the halogen bond, the direct NMR detection of 79/81Br covalently bonded to carbon remains impractical due to extremely large spectral widths, even at ultra-high magnetic fields. In contrast, nuclear quadrupole resonance (NQR) offers comparatively sharp resonances. Here, we demonstrate the abilities of 79/81Br NQR to characterize the electronic changes in the C–Br⋯N halogen bonding motifs found in supramolecular assemblies constructed from 1,4-dibromotetrafluorobenzene and nitrogen-containing heterocycles. An increase in the bromine quadrupolar coupling constant is observed, which correlates linearly with the halogen bond distance (dBr⋯N). Notably, 79/81Br NQR is able to distinguish between two symmetry-independent halogen bonds in the same crystal structure. This approach offers a rapid and reliable indication for the occurrence of a halogen bond, with experimental times limited only by the observation of 79/81Br NQR resonances.
Introduction
The halogen bond (XB) consists of a non-covalent interaction between the area of lower electron density1 associated with a covalently bonded halogen atom, named the σ-hole,2,3 and a Lewis base. It is conveniently schematized as R–X⋯Y, where X is the halogen bond donor (strength: I > Br > Cl ≫ F),4 R is a group covalently bonded to X, and Y represents the electron-rich nucleophilic region of the halogen bond acceptor.5 With unique physicochemical properties such as directionality,6,7 strength,8,9 tunability,10,11 hydrophobicity,12 and selectivity,13,14 the halogen bond has become an important tool in modern supramolecular chemistry.15,16 Many promising applications are evident in medicinal chemistry,17–19 catalysis,20 and conductive materials,21 to name a few, and full literature reviews covering key advances in the field are available.22,23Solid-state nuclear magnetic resonance (SSNMR) is a powerful tool to assess the occurrence of the halogen bond,24 to reliably determine phase purity,25 and to quantitatively relate local structural changes to geometrical features of the interaction.26,27 A key advantage of using SSNMR to characterize the halogen bond is the ability to non-destructively analyze samples in their powdered form, offering information on the chemical shift, quadrupolar coupling, dipolar coupling, and J-coupling.25,27–32 Notably, SSNMR experiments on 13C, 15N, 31P, or 77Se have been used at natural isotopic abundance to evaluate geometrical features of the halogen bond.33–35 Direct observation of the halogen bond donor has been limited to the study of 35Cl (nuclear electric quadrupole moment Q(35Cl) = −81.65(80) mb)36 covalently bonded to carbon,31 due to the broad spectral widths associated with the heavier halogens. This broadening arises as a consequence of the greater quadrupole moments of 79/81Br (Q(79Br) = 313(3) mb), 81Br (Q(81Br) = 262(3) mb), and especially 127I (Q(127I) = −696(12) mb),36 resulting in impractically broad solid-state NMR spectra. As the great majority of halogen-bonded compounds exhibit a halogen covalently bonded to a carbon atom,23 there have been various efforts towards the analysis of the 13C resonances for studying the halogen bond donor. However, 13C SSNMR spectroscopy of carbon covalently bonded to a quadrupolar halogen can be challenging due to the line shape distortion caused by residual dipolar coupling to the quadrupolar nucleus.26,27
As noted, 79/81Br and 127I both remain inaccessible by SSNMR when they are covalently bonded to carbon. Conversely, nuclear quadrupole resonance (NQR) offers advantages over SSNMR to directly characterize the XB; it enables the direct detection of the XB donor site and does not require an external magnetic field. For an exposition of the relative advantages and disadvantages of SSNMR and NQR, readers are referred to a recent Concepts article.37 The NQR frequencies for spin-3/2 nuclides, such as 79Br and 81Br, are a product of the quadrupolar coupling constant (CQ) and the asymmetry parameter (η), given by eqn (1):
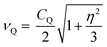 | (1) |
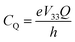 | (2) |
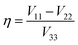 | (3) |
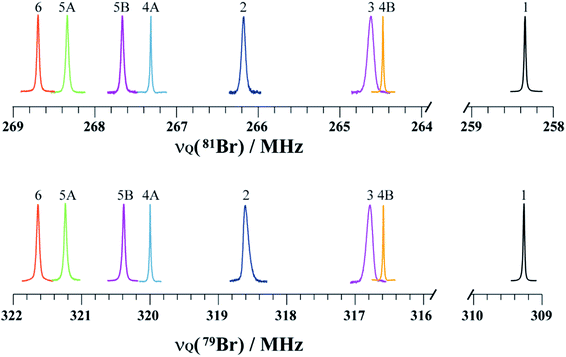
NQR has long played a role in characterizing charge-transfer complexes, but sparse information exists on the “halogen bond” as defined above.39–42 Consequently, the newest class of iconic halogen bond donors has not been thoroughly studied by NQR due in part to the fact that NMR has largely overtaken the field. Furthermore, clear and general relationships between the NQR frequencies and particular geometrical features have not yet been identified. Here, we report a systematic study of a series of prototypical C–Br⋯N XB motifs exhibiting different XB lengths and strengths (see Fig. 1) by 79Br and 81Br NQR spectroscopy. The geometrical features of the halogen bonds in each supramolecular assembly are summarized in Table 1. As the EFG at 79Br and 81Br are identical, the difference in the measured quadrupolar coupling constants for both isotopes is due to their different quadrupole moments (Q). Therefore, the 79Br and 81Br NQR frequencies should be related by a factor of ∼1.19 [Q(79Br)/Q(81Br)], providing a built-in verification of the experimental results.
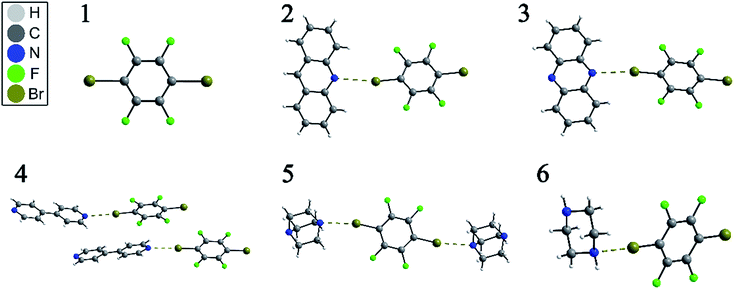 | ||
| Fig. 1 Depiction of the X-ray crystal structures of p-dibromotetrafluorobenzene (1) and its cocrystals (2–6), showing the C–Br⋯N halogen bond by dashed brown lines. | ||
| Entry | Compound | CSD ref. 43 | R XB | θ C–Br⋯N (°) | d Br⋯N (Å) | Note |
|---|---|---|---|---|---|---|
| a The normalized distance parameter RXB has been calculated as the ratio between the halogen bond length (dBr⋯N) and the sum of the van der Waals radii of Br and N. b The X-ray crystal structure shows disorder on the position of the nitrogen, resulting in two possible halogen bond geometries; the reported values herein are the averages over the two disordered halogen bond sites. | ||||||
| 1 | p-Dibromotetrafluorobenzene | ZZZAVJ ref. 44 | — | — | — | |
| 2 | (Acridine)(1) | 712![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047 ref. 45 047 ref. 45 |
0.891b | 172.13b | 3.031b | |
| 3 | (Phenazine)(1) | 712![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 ref. 45 045 ref. 45 |
0.878 | 172.59 | 2.985 | |
| 4 | (4,4′-Bipyridine)(1) | 199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 297 ref. 46 297 ref. 46 |
0.846 | 177.21 | 2.878 | Site 4A |
| 0.876 | 176.40 | 2.979 | Site 4B | |||
| 5 | (1,4-Diazabicyclo[2.2.2]octane)(1) | 649![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676 ref. 47 676 ref. 47 |
0.851 | 167.69 | 2.894 | Site 5A |
| 0.856 | 169.57 | 2.910 | Site 5B | |||
| 6 | (Piperazine)(1) | 649![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 ref. 47 675 ref. 47 |
0.847 | 177.72 | 2.881 | |
Results and discussion
The structures of pure p-dibromotetrafluorobenzene (p-DBrTFB) and a series of cocrystals featuring C–Br⋯N halogen bonds are shown in Fig. 1. The NQR experiments, consisting of one-dimensional spectra and nutation data, are presented in Fig. 2 and 3, respectively. The data obtained from the 81Br and 79Br NQR experiments are summarized in Tables 2 and 3, respectively.| Compounds | ν Q exp. (MHz) | ν Q calc.a (MHz) | η exp.b | η calc. | C Q exp. (MHz) | C Q calc. (MHz) | FWHM (kHz) |
|---|---|---|---|---|---|---|---|
| a The calculated νQ frequencies were obtained using eqn (1) and the corresponding calculated η and CQ values. b Measured from the 81Br nutation NQR spectra. | |||||||
| 1 | 258.34 ± 0.02 | 264.8 | 0.13 ± 0.04 | 0.114 | 515.23 ± 1.79 | 528.4 | 23 |
| 2 | 266.22 ± 0.04 | 268.9 | 0.15 ± 0.07 | 0.117 | 530.45 ± 3.72 | 536.6 | 66 |
| 3 | 264.64 ± 0.04 | 266.9 | 0.12 ± 0.09 | 0.109 | 528.01 ± 3.81 | 532.8 | 84 |
| 4A | 267.32 ± 0.01 | 270.4 | 0.10 ± 0.08 | 0.117 | 533.75 ± 2.85 | 539.5 | 17 |
| 4B | 264.47 ± 0.01 | 269.5 | 0.14 ± 0.06 | 0.125 | 527.22 ± 2.95 | 537.7 | 15 |
| 5A | 267.66 ± 0.04 | 268.7 | 0.15 ± 0.05 | 0.120 | 533.32 ± 2.67 | 536.2 | 30 |
| 5B | 268.33 ± 0.04 | 268.8 | 0.14 ± 0.06 | 0.119 | 535.02 ± 3.00 | 536.3 | 40 |
| 6 | 268.69 ± 0.02 | 269.2 | 0.16 ± 0.06 | 0.116 | 535.10 ± 3.43 | 537.1 | 26 |
| Compounds | ν Q exp. (MHz) | ν Q calc.a (MHz) | η exp.b | η calc. | C Q exp. (MHz) | C Q calc. (MHz) | FWHM (kHz) |
|---|---|---|---|---|---|---|---|
| a The calculated νQ frequencies were obtained using eqn (1) and the corresponding calculated values of η and CQ. b Measured from the 81Br nutation NQR spectra. | |||||||
| 1 | 309.32 ± 0.02 | 316.9 | 0.13 ± 0.04 | 0.114 | 616.92 ± 2.14 | 632.4 | 22 |
| 2 | 318.61 ± 0.05 | 321.9 | 0.15 ± 0.07 | 0.117 | 634.84 ± 4.45 | 642.3 | 95 |
| 3 | 316.81 ± 0.04 | 319.5 | 0.12 ± 0.09 | 0.109 | 632.25 ± 4.55 | 637.7 | 98 |
| 4A | 320.00 ± 0.02 | 323.6 | 0.10 ± 0.08 | 0.117 | 638.94 ± 3.41 | 645.8 | 17 |
| 4B | 316.59 ± 0.02 | 322.6 | 0.14 ± 0.06 | 0.125 | 631.12 ± 3.54 | 643.5 | 16 |
| 5A | 320.45 ± 0.03 | 321.7 | 0.15 ± 0.05 | 0.120 | 638.52 ± 3.19 | 641.8 | 43 |
| 5B | 321.24 ± 0.04 | 321.7 | 0.14 ± 0.06 | 0.119 | 640.39 ± 3.59 | 641.9 | 45 |
| 6 | 321.65 ± 0.02 | 322.2 | 0.16 ± 0.06 | 0.116 | 640.57 ± 4.10 | 642.9 | 29 |
The search for the NQR resonances over the amplifier frequency range was the only time-determining step: once the resonance has been found, an excellent signal-to-noise ratio is achieved in about one minute on approximately 200 mg of sample. The signal frequency is characteristic of the local electronic environment at the bromine nucleus; hence, it provides direct information on the halogen bond. To the best of our knowledge, only a handful of data has been published in the literature regarding the characterization of the halogen bond by 81Br NQR.48 As shown in Fig. 2, the 79Br and 81Br NQR frequencies shift towards a higher frequency upon the formation of a halogen bond. As a general trend for the compounds studied herein, the shorter the halogen bond, the greater the shift (vide infra). This is consistent with previous 81Br NQR results on Br⋯N adducts.48
Notably, both 79Br and 81Br NQR provide clear differentiation between the two crystallographically inequivalent Br sites in compounds 4 and 5 (sites A and B), with the site assignments aided by DFT calculations. Importantly, in previous work on the C–Br⋯N motif, neither 15N SSNMR of the halogen bond acceptor nor 13C SSNMR of the halogen bond donor were able to discriminate two crystallographic sites.26 Additionally, due to the large quadrupole moments of 79Br and 81Br, the NQR frequencies are very sensitive to subtle changes in the crystallographic environment. For instance, a 3.41 ± 0.03 MHz difference is observed between the 79Br NQR frequencies of sites 4A and 4B, with a difference of 0.101 Å in dBr⋯N. In addition, comparing the two bromine sites in the X-ray crystal structure of 5 reveals a subtle difference of 0.016 Å in the dBr⋯N between site 5A and 5B, while the value of θC–Br⋯N differs by merely 1.88°. Despite these very small geometrical differences, a clear and unambiguous difference of 0.79 ± 0.05 MHz is measured between the two 79Br NQR frequencies. In contrast, a 13C SSNMR analysis of these halogen-bonded compounds did not resolve the two crystallographically independent 13C sites due to residual dipolar coupling to both bromine isotopes (see ESI†).
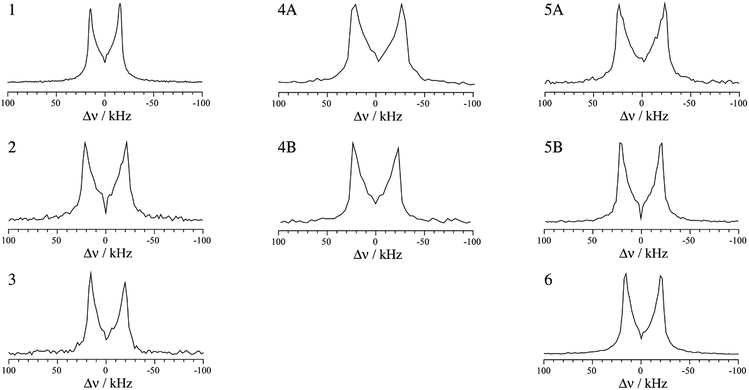
For spin-3/2 nuclides such as 79/81Br, the pure one-dimensional NQR spectrum yields a single frequency which is related to the product of CQ and η (see eqn (1)). In order to extract the individual EFG tensor components, several experimental methods have been proposed, such as Zeeman-perturbed NQR,49 nutation NQR,50,51 and level-crossing double resonance.52 Among these techniques, nutation NQR does not require a complex experimental setup, allowing for the determination of the quadrupolar asymmetry parameter in a straightforward manner. Implemented as a two-dimensional experiment, nutation NQR involves recording series of spectra where the pulse lengths are increased between each one-dimensional spectrum. This experiment allows for the observation of the orientation dependence of the quadrupolar interaction relative to the radiofrequency field. The result allows the measurement of η, which can then be used to determine the value of CQ.50
The highest intensity one-dimensional slices from the two-dimensional experimental 81Br nutation NQR spectra are shown in Fig. 3. Although a stronger RF field may improve the spectral line shapes, our home-built probe is limited to lower power levels. However, using the equation and method proposed for a spin-3/2 nucleus by Harbison,50,51 the experimental NQR line shapes have provided η values in agreement with the DFT calculated results (Tables 2 and 3). Confirmation bias was accounted for by measuring the maximum and minimum separation of the spectral singularities, thereby providing error limits on η.
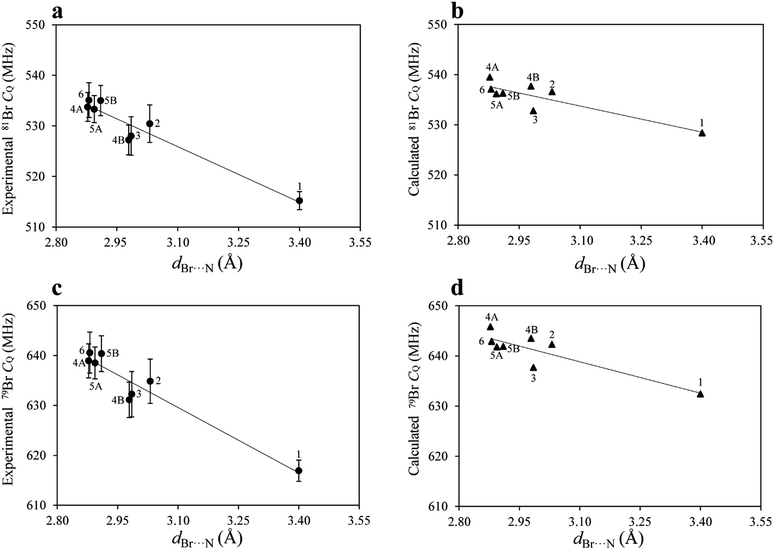
After measuring η by 81Br nutation NQR, the values of CQ for both isotopes were calculated using eqn (1), as both isotopes share the same η value. The CQ values obtained for 79Br and 81Br are related by a ratio of 1.19, further confirming the experimental results. The DFT results are in good agreement with the experimental results, both in terms of η and CQ. Although the experimental and calculated CQ data are close, the DFT results are systematically larger. While dispersion corrections were used in the calculations, the calculated CQ values were not as strongly correlated to the halogen bond geometry as were the experimental data (Fig. 4). For instance, the experimental CQ(79Br) values show an average increase of about 18 MHz upon halogen bond formation, whereas the calculated results suggest an average increase of only 10 MHz.
Upon plotting both the experimental and calculated CQ data as a function of the corresponding Br⋯N halogen bond distances, shown in Fig. 4, good linear correlations are observed. The origin of this effect can be mainly attributed to the interaction between the lone pair electrons from the nitrogen and the bromine atoms, which has historically been referred to as charge transfer. The increase in CQ observed for 79Br and 81Br upon halogen bonding is in agreement with the results for chlorine, obtained from previous 35Cl SSNMR experiments.31 In the case of the bromine halogen bond, CQ increases by 15 to 18 MHz, whereas in the case of chlorine halogen bonds, CQ increases by 0.3 to 1.2 MHz.
The 79Br and 81Br NQR observables are remarkably sensitive to the halogen bonding environment, to such an extent that they provide better evidence for the occurrence of a halogen bond compared to the 13C and 15N SSNMR chemical shift of the carbon covalently bonded to iodine, or the nitrogen on the halogen bond acceptor. To the best of our knowledge, this is the first time that such a large effect has been observed for bromine atoms involved in halogen bonding.
Conclusions
We have presented the first modern 79/81Br NQR study of halogen bonds, performed on a series of cocrystals based on 1,4-dibromotetrafluorobenzene and the C–Br⋯N motif. Through a combination of pure NQR and nutation NQR, we have measured both the quadrupolar coupling constant (CQ) and the asymmetry parameter (η). We demonstrate that this approach is sensitive to small changes in the halogen bond geometry, with the CQ in good correlation with the XB length. The sensitivity of the CQ values to the halogen bond geometry proved to be superior to 13C and 15N chemical shifts obtained by solid-state NMR, even allowing for the discrimination of several crystallographically inequivalent halogen bonds.Although the time-determining factor of this technique was the search for the NQR resonances, the reported correlation can be used in future work to narrow the frequency range to be scanned. As NQR is performed in the absence of an applied magnetic field and does not require sophisticated equipment, it can be readily implemented as a tool to characterize the bromine halogen bond, in excellent complementarity with solid-state NMR and diffraction methods.
Experimental
The starting materials were purchased from Sigma Aldrich and used without further purification. Solvents were purchased from Fisher Scientific and used as received. The synthesis of the cocrystal of 1,4-dibromotetrafluorobenzene (1, p-DBrTFB) with acridine (acd) to give 2 ((p-DBrTFB)(acd)), or phenazine (phz) to give 3 ((p-DBrTFB)(phz)), was performed as reported by Jones and collaborators.45 The synthesis of the cocrystal of 1 with 4,4′-bipyridine (bipy) to give 4 ((p-DBrTFB)(bipy)) was performed as reported by De Santis et al.46 The synthesis of the cocrystal of 1 with either 1,4-diazabicyclo[2.2.2]octane (dabco) to give 5 ((p-DBrTFB)(dabco)) or piperazine (pip) to give 6 ((p-DBrTFB)(pip)), was performed as reported by Cinčić et al.47 Powder X-ray diffraction and 13C CPMAS SSNMR were carried out to ensure phase purity (see the ESI†).Pulsed 79/81Br NQR experiments were performed in the absence of an applied magnetic field using a Bruker Avance III 400 NMR spectrometer. A home-built probe was used, which consisted of a tuning capacitor, a matching capacitor, and a solenoid. All samples were ground and packed in 4 mm o.d. glass tubes prior to being placed inside the probe's RF coil for NQR analysis. Each spectrum was acquired using a Hahn–Echo pulse sequence (π/2–τ–π–τ–acquire), with a 3 μs π/2 pulse and 6 μs π pulse. A total of 256 or 1024 transients were acquired depending on the signal intensity, with a recycle delay of 0.5 s. In order to search for the NQR frequencies, the applied RF was incremented in steps of 150 kHz. The experimental spectra were fit using QUEST.53 Nutation NQR spectra were recorded as per ref. 50. DC correction was applied to each nutation spectrum.
Density functional theory (DFT) calculations were performed using the Amsterdam Density Functional (ADF) software54 with the metaGGA TPSS55 functional and the TZ2P basis set implemented in ADF. Dispersion forces were accounted for using Grimme3 BJDAMP.56 Scalar and spin–orbit relativistic effects were accounted for using ZORA57 as implemented in the ADF software.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr Glenn Facey and Dr Eric Ye are thanked for technical support. P. C. V. thanks the Istituto Nazionale della Previdenza Sociale (INPS) for a scholarship. P. M. J. S. and D. L. B. thank the Natural Sciences and Engineering Research Council of Canada for scholarship and research funding, respectively.Notes and references
- P. Politzer and J. S. Murray, Crystals, 2017, 7, 212 CrossRef.
- P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and T. Clark, in Halogen Bonding I: Impact on Materials Chemistry and Life Sciences, ed. P. Metrangolo and G. Resnati, Springer-Verlag Berlin, Berlin, 2015, vol. 358, pp. 19–42 Search PubMed.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CrossRef CAS.
- A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef CAS PubMed.
- T. J. Mooibroek and P. Gamez, CrystEngComm, 2013, 15, 4565–4570 RSC.
- P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127 CrossRef CAS PubMed.
- K. Raatikainen and K. Rissanen, CrystEngComm, 2011, 13, 6972–6977 RSC.
- K. E. Riley, J. S. Murray, J. Fanfrlik, J. Řezáč, R. J. Solá, M. C. Concha, F. M. Ramos and P. Politzer, J. Mol. Model., 2011, 17, 3309–3318 CrossRef CAS PubMed.
- C. B. Aakeröy, M. Baldrighi, J. Desper, P. Metrangolo and G. Resnati, Chem.–Eur. J., 2013, 19, 16240–16247 CrossRef PubMed.
- A. Priimagi, G. Cavallo, P. Metrangolo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686–2695 CrossRef CAS PubMed.
- P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395 CrossRef CAS PubMed.
- G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati, M. Sansotera and G. Terraneo, Chem. Soc. Rev., 2010, 39, 3772–3783 RSC.
- C. B. Aakeröy and C. L. Spartz, in Halogen Bonding I: Impact on Materials Chemistry and Life Sciences, ed. P. Metrangolo and G. Resnati, Springer-Verlag Berlin, Berlin, 2015, vol. 358, pp. 155–182 Search PubMed.
- G. Berger, J. Soubhye and F. Meyer, Polym. Chem., 2015, 6, 3559–3580 RSC.
- R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363–1388 CrossRef CAS PubMed.
- M. Baldrighi, G. Cavallo, M. R. Chierotti, R. Gobetto, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Mol. Pharmaceutics, 2013, 10, 1760–1772 CrossRef CAS PubMed.
- M. Baldrighi, D. Bartesaghi, G. Cavallo, M. R. Chierotti, R. Gobetto, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, CrystEngComm, 2014, 16, 5897–5904 RSC.
- D. Bulfield and S. M. Huber, Chem.–Eur. J., 2016, 22, 14434–14450 CrossRef CAS PubMed.
- H. M. Yamamoto, Y. Kosaka, R. Maeda, J. Yamaura, A. Nakao, T. Nakamura and R. Kato, ACS Nano, 2008, 2, 143–155 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- D. L. Bryce and J. Viger-Gravel, in Halogen Bonding I: Impact on Materials Chemistry and Life Sciences, ed. P. Metrangolo and G. Resnati, Springer-Verlag Berlin, Berlin, 2015, vol. 358, pp. 183–203 Search PubMed.
- C. M. Widdifield, G. Cavallo, G. A. Facey, T. Pilati, J. Lin, P. Metrangolo, G. Resnati and D. L. Bryce, Chem.–Eur. J., 2013, 19, 11949–11962 CrossRef CAS PubMed.
- P. Cerreia Vioglio, L. Catalano, V. Vasylyeva, C. Nervi, M. R. Chierotti, G. Resnati, R. Gobetto and P. Metrangolo, Chem.–Eur. J., 2016, 22, 16819–16828 CrossRef CAS PubMed.
- J. Viger-Gravel, S. Leclerc, I. Korobkov and D. L. Bryce, CrystEngComm, 2013, 15, 3168–3177 RSC.
- J. Viger-Gravel, S. Leclerc, I. Korobkov and D. L. Bryce, J. Am. Chem. Soc., 2014, 136, 6929–6942 CrossRef CAS PubMed.
- M. Weingarth, N. Raouafi, B. Jouvelet, L. Duma, G. Bodenhausen, K. Boujlel, B. Schöllhorn and P. Tekely, Chem. Commun., 2008, 5981–5983 RSC.
- Y. Xu, J. Viger-Gravel, I. Korobkov and D. L. Bryce, J. Phys. Chem. C, 2015, 119, 27104–27117 CAS.
- P. M. J. Szell and D. L. Bryce, J. Phys. Chem. C, 2016, 120, 11121–11130 CAS.
- R. J. Attrell, C. M. Widdifield, I. Korobkov and D. L. Bryce, Cryst. Growth Des., 2012, 12, 1641–1653 CAS.
- P. Cerreia Vioglio, M. R. Chierotti and R. Gobetto, CrystEngComm, 2016, 18, 9173–9184 RSC.
- J. Viger-Gravel, I. Korobkov and D. L. Bryce, Cryst. Growth Des., 2011, 11, 4984–4995 CAS.
- J. Viger-Gravel, J. E. Meyer, I. Korobkov and D. L. Bryce, CrystEngComm, 2014, 16, 7285–7297 RSC.
- P. Pyykkö, Mol. Phys., 2008, 106, 1965–1974 CrossRef.
- P. M. J. Szell and D. L. Bryce, Concepts Magn. Reson., Part A, 2016, 45A, e21412 CrossRef.
- G. S. Harbison, in Characterization of Materials, John Wiley & Sons, Inc., 2012, pp. 1214–1232 Search PubMed.
- G. K. Semin, T. A. Babushkina, S. P. Khrlakyan, E. Y. Pervova, V. V. Shokina and I. L. Knunyants, Theor. Exp. Chem., 1971, 4, 179–181 CrossRef.
- G. Bowmaker and S. Hacobian, Aust. J. Chem., 1968, 21, 551–564 CrossRef.
- G. Bowmaker and S. Hacobian, Aust. J. Chem., 1969, 22, 2047–2059 CrossRef CAS.
- G. A. Bowmaker, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1964–1969 RSC.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- G. S. Pawley, G. A. Mackenzie and O. W. Dietrich, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1977, A33, 142–145 CrossRef CAS.
- D. Cinčić, T. Friščić and W. Jones, Chem. Mater., 2008, 20, 6623–6626 CrossRef.
- A. De Santis, A. Forni, R. Liantonio, P. Metrangolo, T. Pilati and G. Resnati, Chem.–Eur. J., 2003, 9, 3974–3983 CrossRef CAS PubMed.
- D. Cinčić, T. Friščić and W. Jones, Chem.–Eur. J., 2008, 14, 747–753 CrossRef PubMed.
- Y. M. Udachin, N. N. Artamonova, A. F. Volkov, A. S. Lebedeva and E. N. Gur'yanova, J. Appl. Spectrosc., 1978, 29, 812–816 CrossRef.
- R. Ramachandran and E. Oldfield, J. Chem. Phys., 1984, 80, 674–677 CrossRef CAS.
- G. S. Harbison, A. Slokenbergs and T. M. Barbara, J. Chem. Phys., 1989, 90, 5292–5298 CrossRef CAS.
- G. S. Harbison and A. Slokenbergs, Z. Naturforsch. A, 1990, 45, 575–580 CrossRef CAS.
- R. Blinc and J. Seliger, Z. Naturforsch. A, 1992, 47, 333–341 CAS.
- F. A. Perras, C. M. Widdifield and D. L. Bryce, Solid State Nucl. Magn. Reson., 2012, 45–46, 36–44 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: 13C SSNMR spectra, powder X-ray diffractograms. See DOI: 10.1039/c8sc01094c |
| ‡ Present address: Aix-Marseille Université, CNRS, ICR (UMR 7273), 13397 Marseille cedex 20 (France). |
| This journal is © The Royal Society of Chemistry 2018 |