Open Access Article
Open Access ArticleA DFT-based mechanistic proposal for the light-driven insertion of dioxygen into Pt(II)–C bonds†
Victor M.
Fernández-Alvarez
a,
Sarah K. Y.
Ho
b,
George J. P.
Britovsek
 b and
Feliu
Maseras
b and
Feliu
Maseras
 *ac
*ac
aInstitute of Chemical Research of Catalonia, The Barcelona Institute for Science and Technology, Avgda. Països Catalans, 16, Tarragona 43007, Catalonia, Spain. E-mail: fmaseras@iciq.es; Fax: +34 977 920231; Tel: +34 977 920202
bDepartment of Chemistry, Imperial College London, Exhibition Road, South Kensington, London SW7 2AY, UK
cDepartament de Química, Universitat Autònoma de Barcelona, 08193 Bellaterra, Catalonia, Spain
First published on 4th May 2018
Abstract
The photocatalyzed insertion of dioxygen into the Pt(II)–methyl bond in terpyridine platinum complexes has been shown to proceed efficiently, but its mechanism remains a challenge. In particular, there are serious counter-intuitive differences in the reactivity of structurally similar complexes. M06 calculations in solvent with a valence double-ζ basis set supplemented by polarization and diffusion shells (benchmarked against ωB97x-D calculations with a larger basis set) are able to provide a satisfactory mechanistic answer. The proposed mechanism starts with the absorption of a photon by the metal complex, which then evolves into a triplet state that reacts with the triplet dioxygen fragment. A variety of possible reaction paths have been identified, some leading to the methylperoxo product and others reverting to the reactants, and the validity of some of these paths has been confirmed by additional experiments. The balance between the barriers towards productive and unproductive paths reproduces the diverging experimental behavior of similar complexes and provides a general mechanistic picture for these processes.
1 Introduction
Functionalization of the metal–carbon bond is one of the main steps in the catalytic alkane activation process. Yet despite the extensive work on C–H activation reactions,1–3 the subsequent functionalization of alkyl ligands into useful products remains a challenge. Therefore, significant effort has been put in recent years to employ readily available agents that can insert into the M–C bond and release the functionalized product.4–6 In the case of alkane oxidation reactions involving organometallic Pt(II) and Pd(II) complexes, a range of oxidants have been reported, such as Cl2,7 PhICl2,8 PhI(OAc)2,8 (PhIAr)(BF4),9 PhI(CCSiMe3)(OTf),6 RSSR,10 and (C6H4CMe2O)ICF3.11 In this regard, the ideal scenario is to use environmentally benign oxidants such as H2O2 or O2. Evidently, one of the most desirable agents for this task is atmospheric dioxygen, due to its abundance and availability. However, triplet ground state oxygen is generally difficult to trap, as it is relatively unreactive due to the fact that bond formation between ground state dioxygen and organic substrates is spin-forbidden. This restriction imposes the need for a singlet–triplet crossing on the reaction coordinate, which reduces the efficiency of the process.12Recently, Britovsek et al.13–15 and Goldberg et al.16–18 reported that platinum methyl complexes can insert dioxygen to give the methylperoxo product. One of the remarkable aspects of the reaction reported by Britovsek was the strong dependence of the insertion on the substituents in the 6 and 6′ positions of the terpyridine ligand (Fig. 1). Whereas the diamino-substituted complex readily inserted dioxygen, replacing one or both groups with hydrogen made the system unreactive towards insertion. However, if the substituents are methyl groups, O2 insertion does take place under reaction conditions. This reactivity is rather counter-intuitive since, unlike in the diamino-substituted case in which hydrogen bond interactions might facilitate oxygen coordination, the methyl groups represent a hindering factor towards the approach of dioxygen. It is for this reason challenging to find a reaction mechanism able to explain why substituents that constitute fundamentally different interactions can both insert dioxygen while the rather innocuous dihydrogen-substituted complex remains unreactive.
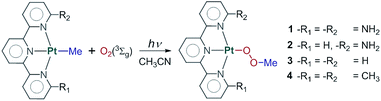 | ||
| Fig. 1 General reaction scheme of the O2 insertion. Reaction occurs for systems 1 and 4. Reaction does not occur for systems 2 and 3. | ||
To address this challenge we carried out a computational study of the reaction mechanism at the DFT level. Calculations are well established as a valuable tool to determine mechanisms in homogeneous catalysis, often in conjunction with experiments.19–22 Although DFT calculations have been used to describe the photoexcitation process,23,24 they have been seldom applied to light-driven reactions, with only few examples available.25–32 In this work we report a detailed study on the reaction of the 6,6′-diaminoterpyridine Pt(II)methyl complex (1), which is later extended to three other complexes with diverse experimental behaviors.
2 Results and discussion
2.1 Photoexcitation
The photochemical behavior of square planar Pt(II) and Pd(II) complexes with highly delocalized pyridine-type ligands has been previously studied in detail by computational and experimental methods, evidencing the existence of long-lived triplet states as a product of metal-to-ligand charge transfer (MLCT) excitations.33–36 Because of this, we focused our study on the photophysical part of the mechanism in the excitation itself from the ground state singlet to an excited state singlet. We did not study the inter-system crossing from this excited singlet state to the long-lived triplet state that is responsible for the reactivity that follows. The theoretical characterization of this inter-system crossing would be very computationally demanding and would add little to the discussion.The electronic distribution of the ground state singlet A is the expected one for a square-planar d8 Pt(II) complex 1, with four d orbitals doubly occupied in the metal. The TD-DFT calculations at the M06 level on this complex showed the existence of a strong band with a maximum absorption at 404 nm (oscillator strength f = 0.1343) and an even stronger one at 364 nm (f = 0.2789), in good agreement with the experimental spectrum of this complex (Fig. S5 in the ESI†).14 Both bands correspond to metal-to-ligand charge transfer (MLCT) transitions, specifically from a metal d orbital to a π* orbital in the disubstituted terpyridine ligand, as shown in Fig. 2. No charge transfer absorption bands were found between dioxygen and the complex when placed together forming an adduct, ruling out the existence of a donor–acceptor complex.25
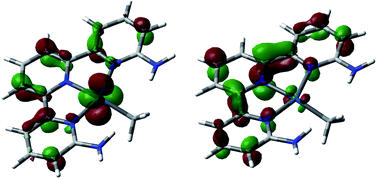 | ||
| Fig. 2 Leading orbitals involved in the key absorption bands in complex A. HOMO−3 (left) and LUMO (right). | ||
The evolution from this transient excited singlet to the long-lived triplet state 3A involves a significant electronic rearrangement. 3A contains most of the spin density on the Pt center and a very small amount on the π system of the terpyridine, in line with previous observations regarding fast interconversions between MCLT and d–d excited states in terpyridine platinum complexes.23,37 Examination of the orbitals of this intermediate points to a high-spin Pt(II) system. The analysis of the electronic structure is complicated by the fact that one of the semi-occupied orbitals is σ-antibonding with respect to the ligands, which results in spin delocalization towards both terpyridine and methyl.
Fig. 3 shows the optimized structure for both the ground state singlet A and the triplet state 3A resulting form the excitation. There is steric repulsion between the methyl ligand and the ortho substituents of the terpyridine ligand, in this case amine groups. This steric repulsion forces the methyl ligand slightly out of the plane even in the ground state A (N–Pt–Me angle, 167.2°). This distortion is significantly increased in the triplet state (N–Pt–Me angle, 117.7°), which also lengthens the Pt–Me bond from 2.08 to 2.12 Å. The increased distortion is associated with the electronic changes when moving from singlet to triplet. The singlet state contains a closed shell d8 platinum center, with an empty d orbital in the molecular plane, and thus a square planar arrangement is electronically favored. The triplet state 3A has a significant amount of spin density, 1.31, located in the platinum center, which therefore is no longer favoring the square planar geometry. The fact that the methyl ligand is entirely outside the molecular plane in 3A leaves a vacant site on the Pt centre for dioxygen to coordinate. 3A has an energy of 40.8 kcal mol−1 (1.77 eV) above A, and is thus only accessible through photoexcitation.
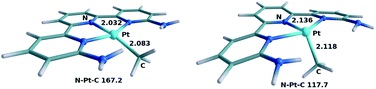 | ||
| Fig. 3 Optimized geometries of intermediates A (left) and 3A (right). Selected distances in Å and angles in degrees. | ||
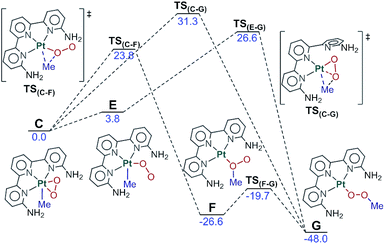
The rest of the manuscript will deal with the evolution of this triplet intermediate 3A. The different possibilities will be discussed in detail in separate sections, but the overall picture can be seen in Fig. 4. Complex 3A reacts with dioxygen to produce intermediate C, which can in turn evolve into product G through two different paths, or revert to the reactants through intermediate 3C.
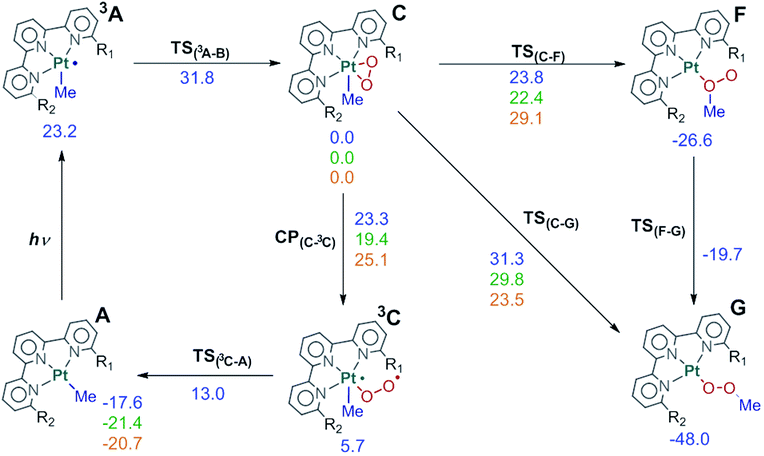 | ||
Fig. 4 Full reaction scheme for complex 1 (R1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) R2 R2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH2, blue) and key points for complex 2 (R1 NH2, blue) and key points for complex 2 (R1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) H, R2 H, R2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH2, green) and 4 (R1 NH2, green) and 4 (R1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) R2 R2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3, orange). Energies relative to C in kcal mol−1. CH3, orange). Energies relative to C in kcal mol−1. | ||
2.2 Reaction with O2
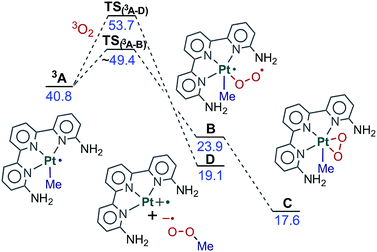
An effective strategy to incorporate dioxygen into a system is to convert it to the singlet form via excited state quenching.38,39 In this process, the photosensitizer absorbs light and reaches an excited state that can then transfer energy to ground state triplet dioxygen. There is evidence of Pt(II) complexes generating singlet oxygen and inserting it into the coordination sphere.40 The generation of singlet oxygen O2(1Δg) under photochemical conditions requires the excited state of the activator to be at least 22.7 kcal mol−1 above the ground state to allow sufficient energy transfer to generate O2(1Δg). This is a necessary condition for singlet oxygen generation,27,41 but we will discuss here a more detailed view of the process.Complex 3A, resulting from the photoexcitation, can react with dioxygen in two major ways, as shown in Fig. 5. In both of them, the overall spin of the sum of the interacting fragments is zero, as the metallic fragment can be seen as bringing two α electrons and the dioxygen bringing two β electrons. The first reaction path leads to intermediate C through intermediate B. In this path, one of the unpaired electrons on dioxygen couples with one unpaired electron at the metal center, resulting in open-shell singlet (OSS) intermediate B. In B one unpaired electron remains in the terminal oxygen and another one in the 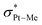 molecular orbital. This intermediate is 23.9 kcal mol−1 above the ground state reactants. Coordination of O2 to 3A is barrierless in the potential energy surface, but we could estimate an entropic barrier of ca. 8 kcal mol−1 for this step (TS(3A–B), see the ESI† for details). B has an O–O distance of 1.30 Å, which indicates a superoxo ligand.42 The formal oxidation state at the platinum centre is thus Pt(III). A related Pd(III) superoxo dimethyl complex with a dipyridine ligand was proposed by Mirica and could be trapped by the addition of a radical scavenger and then observed by EPR.43B evolves into closed-shell intermediate C in which dioxygen displaces the methyl group to the apical position. C is 17.6 kcal mol−1 above the reactants, and has lower energy than free singlet oxygen (22.7 kcal mol−1), and thus is an energetically favored intermediate. In C dioxygen is coordinated as a side-on peroxyde ligand with an O–O distance of 1.42 Å which is between the superoxo and peroxo distances (1.33 and 1.49 Å, respectively).42 The metal centre in C is formally in a Pt(IV) oxidation state. The formation of this peroxo complex C from Pt(II) complex Avia intermediate B resembles very closely the computational work on the binding of O2 to Pd(0) complexes reported by Landis and Stahl.12,44
molecular orbital. This intermediate is 23.9 kcal mol−1 above the ground state reactants. Coordination of O2 to 3A is barrierless in the potential energy surface, but we could estimate an entropic barrier of ca. 8 kcal mol−1 for this step (TS(3A–B), see the ESI† for details). B has an O–O distance of 1.30 Å, which indicates a superoxo ligand.42 The formal oxidation state at the platinum centre is thus Pt(III). A related Pd(III) superoxo dimethyl complex with a dipyridine ligand was proposed by Mirica and could be trapped by the addition of a radical scavenger and then observed by EPR.43B evolves into closed-shell intermediate C in which dioxygen displaces the methyl group to the apical position. C is 17.6 kcal mol−1 above the reactants, and has lower energy than free singlet oxygen (22.7 kcal mol−1), and thus is an energetically favored intermediate. In C dioxygen is coordinated as a side-on peroxyde ligand with an O–O distance of 1.42 Å which is between the superoxo and peroxo distances (1.33 and 1.49 Å, respectively).42 The metal centre in C is formally in a Pt(IV) oxidation state. The formation of this peroxo complex C from Pt(II) complex Avia intermediate B resembles very closely the computational work on the binding of O2 to Pd(0) complexes reported by Landis and Stahl.12,44
 | ||
| Fig. 5 Free energy profile for the reaction between 3A and O2. Energies relative to reactants in kcal mol−1. | ||
An alternative reaction path starts with the direct interaction of dioxygen with the methyl ligand and leads to intermediate D. This path involves a single electron transfer (SET) in which the Pt–Me bond undergoes homolytic dissociation. We were able to locate the transition state for this single electron transfer process, TS(3A–D),45 which is 53.7 kcal mol−1 above the reactants. The resulting fragments are a tricoordinated Pt(II) complex with a vacant site and methylperoxo radical (D, 19.1 kcal mol−1). Both fragments could combine without a significant barrier to yield the product directly. In any case, this alternative pathway is not feasible because it is not competitive. The direct attack on the metal discussed above is favored, as the barrier is ca. 5 kcal mol−1 lower. As a result, C is formed rather than D and the reaction proceeds from there. For the sake of simplicity, C will be considered as the origin of energies for the species discussed in what follows, as all thermal pathways described below involve this intermediate.
These results favour a monometallic pathway, in contrast to previous suggestions that photoexcitation and oxygen quenching take place through a bimetallic mechanism involving two complex molecules in the form of a dimer.13 Our calculations show that once 3A is formed, coordination of dioxygen takes place without the need for a second complex. We confirmed this conclusion through calculations on the bimolecular mechanism reported in the ESI.†
2.3 Evolution of the product
We have been able to characterize the three paths depicted in Fig. 6 for the evolution from the Pt(IV) intermediate C to the methylperoxo product G. The common feature of the three mechanisms is the migration of the methyl ligand from Pt to the η2-O2 unit and later rearrangement to the product conformation. In the first path, the methyl group is transferred to the nearest oxygen through TS(C–F) (23.8 kcal mol−1 above) to form intermediate F (at −26.6 kcal mol−1) in which both the methyl and the platinum are attached to the same oxygen. This intermediate quickly rearranges to form the methylperoxo product G through a low-barrier transition state, akin to the conversion of oxywater to hydrogen peroxide.46In the second mechanism, the side-on peroxo ligand rearranges to an end-on configuration in which the terminal oxygen is closer to the methyl group (E, 3.8 kcal mol−1), from which the methyl ligand migrates directly to the terminal oxygen (TS(E–G), 26.6 kcal mol−1) to yield the product. The third path involves dissociation of one “arm” of terpyridine from the metal and connects C directly to G through transition state TS(C–G) (31.3 kcal mol−1). Data in Fig. 6 indicate conclusively that for system 1, the first path through TS(C–F) is clearly favored, with a barrier of 2.8 kcal mol−1 below that of the closer alternative through TS(E–G). The other two paths are nevertheless included here because they become relevant for other complexes that will be discussed below.
2.4 Back to the reactants
The fact that the reaction takes place in the excited state and involves high energy species and transition states implies the possible competition with the unproductive deactivation processes that restore the initial ground state. We have computed the two paths depicted in Fig. 7 for this evolution from C to A plus O2. The first of these paths goes through intermediate 3C. This intermediate contains an end-on dioxygen ligand, is in a triplet state, and places one unpaired electron on platinum and another on the terminal oxygen. 3C has a similar electron distribution to B, described above, but differs in the electronic state, as 3C is a triplet and B was an open-shell singlet, with the same number of alpha and beta electrons. 3C has an energy of 5.7 kcal mol−1 above C and is reached through a minimum energy crossing point (MECP), CP(C–3C), 23.3 kcal mol−1 above C. Intermediate 3C can easily release O2(3Σg) through transition state TS(3C–A) (13.0 kcal mol−1) and restore the ground state reactant A.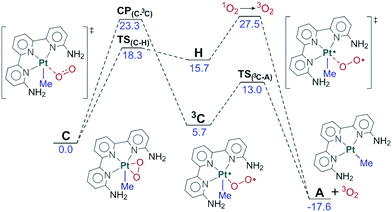 | ||
| Fig. 7 Free energy profile for the reversion from C to the reactants. Energies relative to C in kcal mol−1. | ||
An alternative path for reversion to the reactants goes through intermediate H. This intermediate is an adduct between singlet oxygen and the reactant A, with an energy of 15.7 kcal mol−1, which is reached through transition state TS(C–H), with an energy of 18.3 kcal mol−1. This step is mostly an intramolecular transfer of an electron pair from the dianionic peroxide ligand to the Pt(IV) center in C. Relaxation from H to the reactants requires the transition from singlet oxygen to triplet oxygen. We estimated the rate for this process from experimental data on radiative and non-radiative decay of singlet oxygen relaxation. Specifically, we used the experimental data of the singlet oxygen relaxation constant in acetonitrile (kAcCN = 1.5 × 104 s−1) to determine an energy barrier for this transformation of restoring ground state oxygen.47 Direct application of the Eyring equation led to an “activation energy” of 11.8 kcal mol−1 above H, which is included in the figure. The competition between the two processes of reversion to the reactants clearly favors the first one, through intermediate 3C with a barrier 4.2 kcal mol−1 lower.
2.5 Overall mechanism for system 1
The key features of the reaction mechanism for system 1, including all the significant pathways discussed above, are included in Fig. 4. The photochemical step leads to intermediate C, which is a singlet, with platinum in oxidation state IV and a formally dianionic peroxide ligand in the coordination sphere. C can evolve through three different paths, two leading to products, and one reverting to reactants. Of these three paths, the two with the lowest barriers lead to the reactants through CP(C–3C), with a barrier of 23.3 kcal mol−1, and to the products through TS(C–F), with a barrier of 23.8 kcal mol−1. The alternative path must be discarded for this system because it has a significantly higher barrier: 31.3 kcal mol−1 to reach the products through TS(C–G).The two lowest energy paths are highly competitive. The difference of 0.5 kcal mol−1 means that 31% of the photoexcited systems should evolve into products, with the other 69% returning to the reactants. This results in a net observation of product formation, in agreement with experiments. Even if two-thirds of the photoexcitations are non-productive, this would represent only a minor reduction in the reaction rate, as the deactivated reactants can be photoexcited again.
2.6 Photophysical properties of complexes 2, 3 and 4
Based on the mechanistic model built for 1 we studied the factors that affect the different reactivities of similar complexes which differ only in the substituents at the 6,6′ positions of the terpyridine ligand. The alternative ligands and their corresponding complexes are 6-amino terpyridine (2), unsubstituted terpyridine (3), and 6,6′-dimethyl terpyridine (4). Let us recall that systems 2 and 3 do not react, but system 4 does react with oxygen.As with 1, we began by studying the photophysical behavior of these complexes through TD-DFT calculations. The structures for complexes 3 and 4 before and after the excitation are shown in Fig. 8. The structures corresponding to compound 2 are not shown because of their similarity to those of compound 1. The values for the Pt–N, Pt–C and N–Pt–C parameters are 2.028 and 2.074 Å, and 173.4° for 2-A, and 2.019 and 2.095 Å, and 126.5° for 2-3A. The qualitative nature of the photophysical process is similar: the main structural modification associated with the conversion from the ground state A to the triplet state 3A is the displacement of the methyl group out of the ligand plane. This displacement is well characterized by the N–Pt–C angles shown in Fig. 3 and 8, which are provided in Table 1. It is remarkable that the two compounds which are active, 1 and 4, have the largest distortions in the triplet state. This hints at a possible correlation of this distortion with the reactivity towards dioxygen, but other differences need to be considered as well.
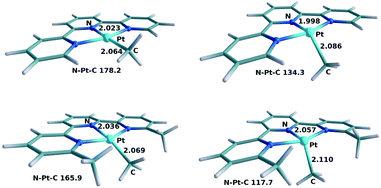 | ||
| Fig. 8 Optimized geometries of 3-A (top left), 3-3A (top right), 4-A (bottom left) and 4-3A (bottom right). Selected distances in Å and angles in degrees. | ||
| System | N–Pt–C | System | N–Pt–C |
|---|---|---|---|
| 1-A | 167.2 | 1-3A | 117.7 |
| 2-A | 173.4 | 2-3A | 126.5 |
| 3-A | 178.2 | 3-3A | 134.3 |
| 4-A | 165.9 | 4-3A | 117.7 |
The vertical spectrum of 2 showed a single MLCT band with a strong maximum absorption at 357 nm (f = 0.2245). 3 showed only a weak π–π* band at 358 nm (f = 0.0227) and a very strong MLCT band at 316 nm (f = 0.3996). The spectrum of 4 presented a somewhat weak MLCT band at 347 nm (f = 0.0506) and a stronger one at 330 nm (f = 0.3604). Let us recall for comparison that 1 absorbed at 404 nm (f = 0.1343) and 364 nm (f = 0.2789). These results are mostly in agreement with experimentally reported data for these species.13,14 The overall picture is that the maximum MLCT absorption for all these complexes is near the frontier between visible light and ultraviolet, which is often considered to be around 380 nm. There are however significant quantitative differences between them. The highest wavelength efficient absorptions are at 404 nm, 357 nm, 316 nm and 347 nm, respectively, which is in qualitative agreement with the experimental absorption spectra reported in the ESI (Fig. S5†). Calculations and experiments thus predict that complex 3 absorbs at a significantly lower wavelength. Complex 3 should not form the long-lived triplet intermediate under sunlight conditions, which correlates with its lack of reactivity under these reaction conditions. The reason why complex 3 does not absorb can be found in the structure of the ground state for this compound shown in Fig. 8. The complex is much closer to the ideal square planar geometry, with a N–Pt–C angle of 178.2°, because of the small steric repulsions between the methyl ligand and the ortho substituents at the terpyridine ligands, in this case hydrogen atoms. This planarity has the important consequence of stabilizing the non-bonding occupied d orbitals in the d8 platinum center. These orbitals are the origin of the photoexcitation (see Fig. 2), and their stabilization necessarily increases the photoexcitation energy.
2.7 Behavior after photoexcitation of complexes 2 and 4
Both complexes 2 and 4 absorb in the required range, but only 4 inserts dioxygen. We recomputed the key points in Fig. 4 for both 2 and 4. The qualitative aspects of the diagram are mostly unchanged. Both 2 and 4 form the reactive triplet state C which can then either evolve into products or revert to the reactants through the paths discussed above. There are however significant quantitative differences in the barriers for the different pathways, and they are summarized in Table 2.In the case of complex 2, our calculations show that the energy difference between TS(C–F) and CP(C–3C) increases by 2.5 kcal mol−1 compared to 1. The reversion to the reactants is now favored by 3.0 kcal mol−1, which corresponds to an efficiency of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
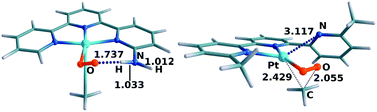
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99. 99% of the photoexcitations are thus unproductive. The reaction would certainly take place given sufficient time, but with a much lower reaction rate. The result is thus compatible with the experimental observation that this system does not react. Inspection of Fig. 4 indicates that the difference between systems 1 and 2 is in the energies of the CP(C–3C) crossing-point, as those of the TS(C–F) set are very similar. The difference is likely related to the hydrogen bonds formed by the NH2 substituents. The arrangement of the two oxygens in both C and TS(C–F) is rather symmetrical, close to the Me–Pt–O plane, which favors the formation of two hydrogen bonds, one with each NH2 group. In contrast, in 2-CP(C–3C), the dioxygen is significantly bent towards one side, an optimal arrangement for a single hydrogen bond, as shown in the left-hand side of Fig. 9. CP(C–3C) is thus favored in system 2 with only one NH2 group. As CP(C–3C) leads to reversion to the reactants, this system is significantly less reactive.
99. 99% of the photoexcitations are thus unproductive. The reaction would certainly take place given sufficient time, but with a much lower reaction rate. The result is thus compatible with the experimental observation that this system does not react. Inspection of Fig. 4 indicates that the difference between systems 1 and 2 is in the energies of the CP(C–3C) crossing-point, as those of the TS(C–F) set are very similar. The difference is likely related to the hydrogen bonds formed by the NH2 substituents. The arrangement of the two oxygens in both C and TS(C–F) is rather symmetrical, close to the Me–Pt–O plane, which favors the formation of two hydrogen bonds, one with each NH2 group. In contrast, in 2-CP(C–3C), the dioxygen is significantly bent towards one side, an optimal arrangement for a single hydrogen bond, as shown in the left-hand side of Fig. 9. CP(C–3C) is thus favored in system 2 with only one NH2 group. As CP(C–3C) leads to reversion to the reactants, this system is significantly less reactive.
The case of complex 4 presents some differences. In this case, the evolution of products through TS(C–F) (29.1 kcal mol−1) is clearly disfavored with respect to reversion to the reactants through CP(C–3C) (25.1 kcal mol−1). This is likely associated with the presence of the methyl substituents, which bring steric pressure without any option for hydrogen bonds. The weaker coordinating labile behaviour of the 6-methyl substituted pyridine ligand donors compared to a non-substituted pyridine donor due to steric reasons has been commented on previously,48 and this is well documented, and was also encountered during synthesis of the palladium(II) analogue of complex 4. Preparation of this complex from ligand L, [PdClMe(cod)] and AgSbF6 in acetone resulted initially in a bis(acetone) complex, [PdCl(L)(acetone)2]+, with non-coordinating 6-methyl pyridine moieties (see the ESI†). Conversion to the palladium analogue of complex 4, where the 6-methylpyridine moieties are coordinated, was achieved only after prolonged heating in acetone or in acetonitrile. The subsequent reaction of this palladium methyl analogue with oxygen resulted in the formation of a rather unstable methylperoxo complex, probably due to the lack of any stabilising hydrogen bonding interactions. The key result here is that the increased steric repulsion brings into the picture TS(C–G), which proceeds through partial decoordination of the terpyridine ligand. In this case, TS(C–G), with a free energy of 23.5 kcal mol−1, is the most favored channel out of C, thus explaining the efficiency of this system. The structure for TS(C–G) in system 4 is shown in the right-hand side of Fig. 9, where the release of steric pressure resulting from the cleavage of one Pt–N bond (distance of 3.117 Å) is apparent.
Our calculations thus reproduce the experimental behavior. Moreover, the four systems studied happen to share the same general picture presented in Fig. 4, but present significant differences due to the quantitative changes associated with different processes. System 3 does not react because it is unable to absorb in the visible or near UV light range. System 2 does not react because the deactivation pathway through CP(C–3C) is favored in the presence of a single hydrogen bond with substituents in the ligand. System 1 does react because a pair of hydrogen bonds is sufficient to make the forward reaction through transition state TS(C–F) efficient. System 4 does react despite the lack of hydrogen bonds because of the steric release associated with partial decoordination of one arm of the ligand through transition state TS(C–G).
3 Computational details
Calculations reported in the text were performed using the M06 functional49 with continuum solvent contributions (acetonitrile ε = 35.688) from the Polarizable Continuum Model (PCM) as implemented in Gaussian09,50 Revision B.01. The basis set was LANL2DZ with an extra polarization function for Pt and 6-31+G(d) for light atoms (BS1).51–53 Additional calculations (reported in the ESI†) were carried out with the ωB97x-D functional54 and the 6-31++G(d) basis set for light atoms and the LANL2TZ(f) basis set for Pt (BS2).55–58 The benchmarking showed only minor changes in the results. All geometry optimizations were performed without symmetry constraints. Frequency calculations were carried out to determine whether stationary points were minima or saddle points. Connectivity between the transition states and the minima was confirmed through optimization from the corresponding transition states. All energies reported in the manuscript are Gibbs energies in kcal mol−1. Free energy corrections used a temperature of 298 K and a pressure of 1 atm. A dataset collection of the computational results is available in the ioChem-BD repository,59 and can be accesed viahttp://dx.doi.org/10.19061/iochem-bd-1-77.4 Conclusions
We have characterized the mechanism for the light-driven insertion of dioxygen into the Pt(II)–Me bond of [Pt(terpyridine)Me]+ complexes using ground state DFT and TD-DFT methods. Four different complexes have been analyzed, differing in the substituents at the 6,6′ positions of the terpyridine ligand, and the experimental behavior has been reproduced in the four cases. The following requirements have been identified for an efficient process: (i) photon absorption in the appropriate range, requiring the presence of either π-donating (such as NH2) or σ-donating (such as Me) substituents in the terpyridine ligand, and (ii) the presence of either two hydrogen-bonding groups (such as NH2) or two groups with mild steric effects (such as Me). When none of these requirements is met, with only hydrogen substituents, or only one hydrogen bonding group, the dioxygen insertion does not proceed. Our results confirm the specificity of the systems that can undertake this reaction, as a subtle balance must be reached between diverse effects. These results also point to the promising role of computational chemistry in the screening of reaction candidates for this and other related photoinduced processes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful for financial support from the CERCA Programme (Generalitat de Catalunya) and MINECO (project CTQ2017-87792-R and Severo Ochoa Excellence Accreditation 2014-2018 SEV-2013-0319). The authors also thank COST Action CARISMA CM1205 for support. V. M. F.-A. is grateful to MINECO for a FPI fellowship (ref BES-2012-057655).Notes and references
- R. H. Crabtree, J. Chem. Soc., Dalton Trans., 2001, 2437–2450 RSC.
- S. S. Stahl, J. A. Labinger and J. E. Bercaw, Angew. Chem., 1998, 110, 2298–2311 CrossRef.
- M. Lersch and M. Tilset, Chem. Rev., 2005, 105, 2471–2526 CrossRef PubMed.
- S. R. Neufeldt and M. S. Sanford, Acc. Chem. Res., 2012, 45, 936–946 CrossRef PubMed.
- L. Boisvert and K. I. Goldberg, Acc. Chem. Res., 2012, 45, 899–910 CrossRef PubMed.
- T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147–1169 CrossRef PubMed.
- G. Bandoli, P. A. Caputo, F. P. Intini, M. F. Sivo and G. Natile, J. Am. Chem. Soc., 1997, 119, 10370–10376 CrossRef.
- D. C. Powers and T. Ritter, Nat. Chem., 2009, 1, 302–309 CrossRef PubMed.
- N. R. Deprez and M. S. Sanford, J. Am. Chem. Soc., 2009, 131, 11234–11241 CrossRef PubMed.
- K. J. Bonnington, M. C. Jennings and R. J. Puddephatt, Organometallics, 2008, 27, 6521–6530 CrossRef.
- Y. Ye, N. D. Ball, J. W. Kampf and M. S. Sanford, J. Am. Chem. Soc., 2010, 132, 14682–14687 CrossRef PubMed.
- C. R. Landis, C. M. Morales and S. S. Stahl, J. Am. Chem. Soc., 2004, 126, 16302–16303 CrossRef PubMed.
- A. R. Petersen, R. A. Taylor, I. Vicente-Hernández, P. R. Mallender, H. Olley, A. J. P. White and G. J. P. Britovsek, J. Am. Chem. Soc., 2014, 136, 14089–14099 CrossRef PubMed.
- R. Taylor, D. Law, G. Sunley, A. White and G. Britovsek, Angew. Chem., Int. Ed., 2009, 48, 5900–5903 CrossRef PubMed.
- A. R. Petersen, A. J. P. White and G. J. P. Britovsek, Dalton Trans., 2016, 45, 14520–14523 RSC.
- L. Boisvert, M. C. Denney, S. K. Hanson and K. I. Goldberg, J. Am. Chem. Soc., 2009, 131, 15802–15814 CrossRef PubMed.
- K. A. Grice and K. I. Goldberg, Organometallics, 2009, 28, 953–955 CrossRef.
- M. L. Scheuermann and K. I. Goldberg, Chem.–Eur. J., 2014, 20, 14556–14568 CrossRef PubMed.
- W. M. C. Sameera and F. Maseras, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 375–385 CrossRef.
- S. Fantacci and F. D. Angelis, Coord. Chem. Rev., 2011, 255, 2704–2726 CrossRef.
- J. Ma, T. Su, M.-D. Li, W. Du, J. Huang, X. Guan and D. L. Phillips, J. Am. Chem. Soc., 2012, 134, 14858–14868 CrossRef PubMed.
- B. Matt, X. Xiang, A. L. Kaledin, N. Han, J. Moussa, H. Amouri, S. Alves, C. L. Hill, T. Lian, D. G. Musaev, G. Izzet and A. Proust, Chem. Sci., 2013, 4, 1737–1745 RSC.
- C. Gourlaouen and C. Daniel, Dalton Trans., 2014, 43, 17806–17819 RSC.
- C. Gourlaouen and C. Daniel, Coord. Chem. Rev., 2017, 344, 131–149 CrossRef.
- V. M. Fernández-Alvarez, M. Nappi, P. Melchiorre and F. Maseras, Org. Lett., 2015, 17, 2676–2679 CrossRef PubMed.
- M. Kayanuma, T. Stoll, C. Daniel, F. Odobel, J. Fortage, A. Deronzier and M.-N. Collomb, Phys. Chem. Chem. Phys., 2015, 17, 10497–10509 RSC.
- L.-H. Liu, D. Wu, S.-H. Xia and G. Cui, J. Comput. Chem., 2016, 37, 2212–2219 CrossRef PubMed.
- L. Dell'Amico, V. M. Fernández-Alvarez, F. Maseras and P. Melchiorre, Angew. Chem., Int. Ed., 2017, 56, 3304–3308 CrossRef PubMed.
- N. Münster, N. A. Parker, L. van Dijk, R. S. Paton and M. D. Smith, Angew. Chem., Int. Ed., 2017, 56, 9468–9472 CrossRef PubMed.
- C. Yang, W. Zhang, Y.-H. Li, X.-S. Xue, X. Li and J.-P. Cheng, J. Org. Chem., 2017, 82, 9321–9327 CrossRef PubMed.
- V. M. Fernandez-Alvarez and F. Maseras, Org. Biomol. Chem., 2017, 15, 8641–8647 Search PubMed.
- S. Chen, X. Huang, E. Meggers and K. N. Houk, J. Am. Chem. Soc., 2017, 139, 17902–17907 CrossRef PubMed.
- M. R. R. Prabhath, J. Romanova, R. J. Curry, S. R. P. Silva and P. D. Jarowski, Angew. Chem., Int. Ed., 2015, 54, 7949–7953 CrossRef PubMed.
- W. H. Lam, E. S.-H. Lam and V. W.-W. Yam, J. Am. Chem. Soc., 2013, 135, 15135–15143 CrossRef PubMed.
- X.-H. Li, L.-Z. Wu, L.-P. Zhang, C.-H. Tung and C.-M. Che, Chem. Commun., 2001, 2280–2281 RSC.
- J. A. G. Williams, in Photochemistry and Photophysics of Coordination Compounds: Platinum, ed. V. Balzani and S. Campagna, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 205–268 Search PubMed.
- Q.-Z. Yang, L.-Z. Wu, Z.-X. Wu, L.-P. Zhang and C.-H. Tung, Inorg. Chem., 2002, 41, 5653–5655 CrossRef PubMed.
- M. Selke and C. S. Foote, J. Am. Chem. Soc., 1993, 115, 1166–1167 CrossRef.
- D. Zhang, L.-Z. Wu, Q.-Z. Yang, X.-H. Li, L.-P. Zhang and C.-H. Tung, Org. Lett., 2003, 5, 3221–3224 CrossRef PubMed.
- J. M. Praetorius, D. P. Allen, R. Wang, J. D. Webb, F. Grein, P. Kennepohl and C. M. Crudden, J. Am. Chem. Soc., 2008, 130, 3724–3725 CrossRef PubMed.
- M. C. DeRosa and R. J. Crutchley, Coord. Chem. Rev., 2002, 233, 351–371 CrossRef.
- P. L. Holland, Dalton Trans., 2010, 39, 5415–5425 RSC.
- J. R. Khusnutdinova, N. P. Rath and L. M. Mirica, J. Am. Chem. Soc., 2012, 134, 2414–2422 CrossRef PubMed.
- B. Popp, J. Wendlandt, C. Landis and S. Stahl, Angew. Chem., Int. Ed., 2007, 46, 601–604 CrossRef PubMed.
- I. Funes-Ardoiz, P. Garrido-Barros, A. Llobet and F. Maseras, ACS Catal., 2017, 7, 1712–1719 CrossRef.
- H. H. Huang, Y. Xie and H. F. Schaefer, J. Phys. Chem., 1996, 100, 6076–6080 CrossRef.
- F. Wilkinson, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1995, 24, 663–677 CrossRef.
- K. Chen and L. Que, J. Am. Chem. Soc., 2001, 123, 6327–6337 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, 2009 Search PubMed.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef.
- M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, J. Chem. Inf. Model., 2015, 55, 95–103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc01161c |
| This journal is © The Royal Society of Chemistry 2018 |