Open Access Article
Open Access ArticleModulating the oxygen reduction activity of heteroatom-doped carbon catalysts via the triple effect: charge, spin density and ligand effect†
Na
Yang
,
Li
Li
*,
Jing
Li
,
Wei
Ding
and
Zidong
Wei
 *
*
The State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing Key Laboratory of Chemical Process for Clean Energy and Resource Utilization, School of Chemistry and Chemical Engineering, Chongqing University, Shazhengjie 174, Chongqing 400044, China. E-mail: liliracial@cqu.edu.cn; zdwei@cqu.edu.cn; Tel: +86 2365678945
First published on 31st May 2018
Abstract
To enhance the intrinsic activity of and increase the number of active sites in heteroatom-doped graphene (doped-G), it is necessary to recognize the origin of its catalytic activity, and to search for a universal definition and description of the different active sites. Herein, we report an evaluation of a series of heteroatom-doped graphene materials as oxygen reduction reaction (ORR) catalysts with the aid of density functional theory (DFT) calculations. The results of the DFT calculations indicate that the intrinsic catalytic activity and the ORR mechanism depend on the triple effect, that is, the charge, the spin density and the coordinate state (ligand effect) of the carbon sites. The contribution of the above effects towards increasing the binding energies of *OOH or *OH has the following order: negative charge effect < positive charge effect < low spin effect < ligand effect < high spin effect. For nonmetallic single-heteroatom-doped-G, the triple effect separately activates the carbon sites around the doped atom. On each single carbon active site, only the end-on adsorption of *OOH is preferred, leading to the ORR following the associative mechanism, which has an intrinsic limitation in its overpotential of 0.44 V. However, for metal-doped-G and dual-heteroatom-doped-G, the triple effect can activate double carbon sites, and lead to the ORR following the dissociative mechanism, which breaks through the activity limitation of the associative mechanism, and further enhances the catalytic activity for the ORR. With comprehensive theoretical calculation, we conclude that it is possible for the heteroatom-doped-G, if well-modulated via the triple effect, to exceed Pt-based materials in catalysis of the ORR.
1. Introduction
Graphene, a two-dimensional monolayer structure of sp2-hybridized carbon, has been widely investigated in the area of electrochemistry owing to its extraordinary electrical conductivity, high specific surface area and excellent mechanical properties.1–3 One of the most extensively studied applications of graphene is as a catalyst for the oxygen reduction reaction (ORR) occurring at the cathode of fuel cells and metal–air batteries. To improve the ORR performance of graphene-based materials, tremendous efforts have been undertaken. Experimental and theoretical studies revealed that doping a graphene matrix with heteroatoms (e.g., N, B, O, P, S, Cl, Se, Br, and I) could cause electron modulation that could tune its catalytic activity. Heteroatom-doped graphene (doped-G) has been recognized as a promising alternative to the state-of-the-art precious Pt catalysts.4–10 Nevertheless, doped-G always suffers from some problems, such as poor stability, limited activity and a low active site density. Accordingly, these problems hinder doped-G from being used in commercial applications.Although the catalytic activity of doped-G for the ORR has been abundantly investigated, the essential decisive factor for doped-G for the ORR is not yet clear. Dai et al. proposed that the high activity of nitrogen-doped carbon (N-G) catalysts may be attributed to the larger electronegativity of N (3.04) with respect to C (2.55), thus creating a positive charge density on the adjacent C atoms.11 Obviously, this explanation is not applicable for the carbon materials doped with the less electronegative atoms such as P (2.19) and B (2.04), which also show pronounced catalytic activities.12,13 Additionally, when S or Se, whose electronegativity (S: 2.58, Se: 2.55) is quite close to that of C, is used as the dopant species, the charge transfer between S/Se and C is almost negligible. Thus a new explanation for the enhanced ORR activity was proposed, that is, that the charge density and spin density may play some important role in the catalysis of the ORR for S-doped carbon materials.14 Recently, Xia’s team15,16 found that the ORR activity of p-orbital-element-doped-G can be assessed via the electronegativity and electron affinity of the dopant, by which they proposed a design principle for enhancing the ORR activity of p-orbital-element-doped-G.
Obviously, the above explanations for heteroatom-doped-G catalyzing the ORR are only suitable for specific types of heteroatom-doped-G. The intrinsic role of the carbon active sites in catalysis of the ORR is still unclear. In fact, besides the dopants, the defects/edges of the graphene and the distances from the carbon atom to the dopants or defects/edges also participate in changing the electronic structure of the active sites, and naturally their influence on the catalytic activity of doped-G cannot be ignored any longer. To enhance the intrinsic activity of and increase the number of active sites in doped-G, it is necessary to recognize the origin of the catalytic activity, and to search for a universal definition of and descriptor for the different types of doped-G in the catalysis of the ORR.
In this report, on the basis of density functional theory (DFT) calculations, an underlying universal mechanism of the ORR catalyzed by doped-G, called the “triple effect”, is proposed, in which the doped atoms can be either B or P atoms with low electronegativity, N or F atoms with high electronegativity, or S or Se atoms with similar electronegativity to a C atom. The “triple effect”, integrating the effects of charge, spin density, and the coordination state of carbon atoms in doped-G, is used to evaluate and predict the intrinsic activity of the carbon sites. Our systematic calculations demonstrate that the “triple effect” is not only suitable for explaining the activity of nonmetallic single-heteroatom-doped-G (N, F, P, B, S and Se-G), but is also applicable for explaining the activity of metal-doped-G and dual-heteroatom-doped-G. The “triple effect” might offer a universal description for the different active sites of doped-G, and can be used to guide further improvement of the catalytic activity of this type of material.
2. Methods
2.1 The thermodynamics of the ORR
The 4e− overall reaction scheme of O2 reducing to OH− in an alkaline environment is O2 + 2H2O + 4e− → 4OH−, which includes two possible reaction pathways (the associative and dissociative mechanisms).Associative:
| * + O2(g) + H2O(l) + e− → *OOH + OH− | (1) |
| *OOH + e− → *O + OH− | (2) |
| *O + H2O(l) + e− → *OH + OH− | (3) |
| *OH + e− → * + OH− | (4) |
Dissociative:
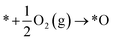 | (5) |
| *O + H2O(l) + e− → *OH + OH− | (6) |
| *OH + e− → OH− | (7) |
Adsorption free energy values for various oxygenated species (ΔG*OOH, ΔG*O and ΔG*OH) are calculated as the reaction free energy (* represents surface sites):
| ΔG1 = ΔG*OOH − 4.92 eV − ΔGH+(pH) + eU | (8) |
| ΔG2 = ΔG*O − ΔG*OOH − ΔGH+(pH) + eU | (9) |
| ΔG3 = ΔG*OH − ΔG*O − ΔGH+(pH) + eU | (10) |
| ΔG4 = −ΔG*OH − ΔGH+(pH) + eU | (11) |
| ΔG5 = ΔG*O − 2.46 eV | (12) |
| ΔG6 = ΔG*OH − ΔG*O − ΔGH+(pH) + eU | (13) |
| ΔG7 = −ΔG*OH − ΔGH+(pH) + eU | (14) |
The Gibbs free energies of eqn (8)–(14) (ΔG) are related to the adsorption energies of the various intermediate species. The adsorption free energy changes of these intermediate species are determined using ΔG = ΔE + ΔZPE − TΔS, where ΔE can be calculated relative to H2O and H2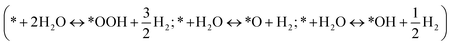 , ΔZPE and TΔS are the zero point energy difference and the entropy change between the absorbed state and the free state, i.e., the gas phase (listed in Table S1†), respectively, and T is the temperature (298 K in this work). e is the elementary charge and U is the potential difference between the electrode and the normal hydrogen electrode (NHE). The free energy change of H+ is derived according to ΔGH+(pH) = −kBT
, ΔZPE and TΔS are the zero point energy difference and the entropy change between the absorbed state and the free state, i.e., the gas phase (listed in Table S1†), respectively, and T is the temperature (298 K in this work). e is the elementary charge and U is the potential difference between the electrode and the normal hydrogen electrode (NHE). The free energy change of H+ is derived according to ΔGH+(pH) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10) × pH (kB is Boltzmann’s constant, and pH = 13). Because the high-spin ground state of an oxygen molecule is difficult to describe in DFT calculations, the free energy of O2(g) is derived as GO2(g) = 2GH2O(l) − 2GH2(g) + 4.92 eV. Additionally, the activation energy barrier (ΔEb) is defined as the difference between the energy of the transition structures (ETS) and the initial structures (EIS), ΔEb = ETS − EIS.
ln(10) × pH (kB is Boltzmann’s constant, and pH = 13). Because the high-spin ground state of an oxygen molecule is difficult to describe in DFT calculations, the free energy of O2(g) is derived as GO2(g) = 2GH2O(l) − 2GH2(g) + 4.92 eV. Additionally, the activation energy barrier (ΔEb) is defined as the difference between the energy of the transition structures (ETS) and the initial structures (EIS), ΔEb = ETS − EIS.
2.2 Model construction
Based on our previous research,17 we found that C atoms possessing a high negative charge could also be active sites for the ORR. Owing to boron and phosphorus having higher electron-donating abilities (the electronegativity of B and P: 2.04 and 2.19) than those of nitrogen and fluorine (the electronegativity of N and F: 3.04 and 3.98), the boron- and phosphorus-doped-G (B-G and P-G) with different doped structures were built as the first type of models, as shown in Fig. 1a. Simultaneously, the nitrogen- and fluorine-doped-G (N-G and F-G),11,15 as opposite models, i.e., the secondary type of models, are displayed in Fig. 1a. Different from B, P, N and F atoms, S and Se almost have the same electronegativity as C (S: 2.58, Se: 2.55, and C: 2.55). Therefore, sulfur and selenium doped-G (S-G and Se-G),16 as the third type of models, were also considered and are presented in Fig. 1a. Moreover, along the arrows shown in Fig. 1a, the edge effect of graphene becomes more and more profound. Therefore, six types of nonmetallic heteroatom, i.e., B, P, N, F, S and Se, together with the edge effect, could induce 18 different doping configurations in graphene slabs with different electronic properties and around 50 possible active sites, which may be heteroatoms themselves or adjacent carbon atoms. According to whether or not P binds to O, the P-doped models in Fig. 1a were labeled nPCm-G, or nOPCm-G, where the symbol n (a1, a2, a3, b1, b2, b3,…) represents the substitutional site of the nonmetal atom, and the m denotes the number of carbon atoms binding to the P atom. Analogously, the B-, N- and F-doped-G (nBCm-G, nOBCm-G, nNCm-G, and nFCm-G) were also labeled with the same description as P-G. Incidentally, we used G to denote a pristine graphene framework. One of the most important but sometimes ignored structures, zigzag graphene, usually introduces spin density by itself without dopant participation (Fig. S2a†). To exclude the spin density introduced by the zigzag graphene structure, for P-, B-, N-, S- and Se-doped-G, we only considered armchair graphene frameworks (Fig. S2b†). Because F only bonds to one carbon atom, it does not introduce spin density, thus, both the zigzag and armchair structures of F-G were considered.2.3 Computational details
Our computational simulations were performed using the Vienna ab initio simulation package (VASP) with the projector augmented wave pseudo-potentials (PAW) to describe the interaction between atomic cores and valence electrons with density functional theory (DFT). The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) was used to implement the DFT calculations. The transition state (TS) searches were carried out using the climbing-image nudged elastic band method (CI-NEB).18 The models of the graphene sheets were built in this study in the armchair configuration (12.6 Å × 8.5 Å) with the periodic boundary conditions (Fig. S1†). The reasonable vacuum layers were set around 12 and 18 Å in the x- and z-directions, respectively, to avoid interaction between the planes, and two edges were saturated with hydrogen in the x-direction. A cutoff energy of 400 eV was provided and a 1 × 3 × 1 Monkhorst Pack k-point sampling was chosen for well converged energy values. Geometry optimizations were pursued until the force on each atom fell below the convergence criterion of 0.02 eV Å−1 and the energies were converged within 10−5 eV. Moreover, all calculations were spin polarized.3. Results and discussion
3.1 The thermodynamics of the ORR
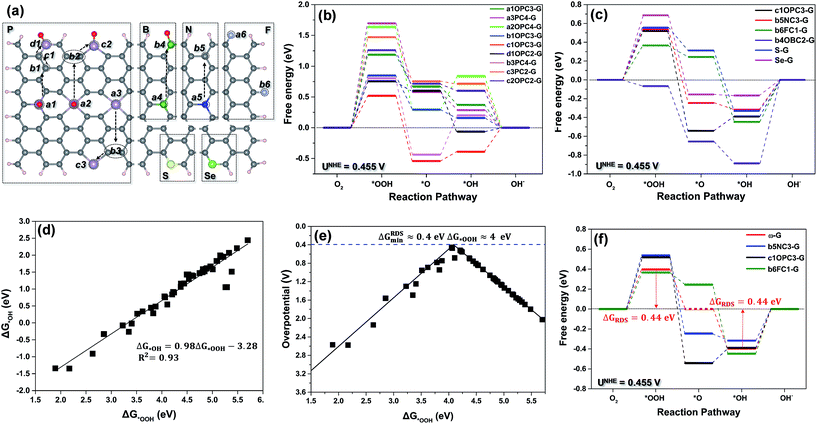
Due to the too-weak adsorption of O2 and *OOH on pristine graphene and nonmetallic single-heteroatom-doped-G, such as B-G and N-G, the ORR always proceeds via the associative mechanism rather than the dissociative mechanism on these surfaces. The latter on these surfaces needs the ORR to overcome an energy barrier as great as 1.2 eV.19–21 Therefore, in our calculation, we calculated the catalytic activity of nonmetallic single-heteroatom-doped-G using the associative pathway of the ORR (eqn (1)–(4)). To rationally search for the best ORR carbon active sites among all the investigated model surfaces (Fig. 1a), the free energy and overpotential of the ORR associative mechanism on all possible carbon and dopant atoms in the doped-G were calculated. The elementary reaction step with maximal free energy change is defined as the potential-determining step (PDS), which usually possesses maximal overpotential, and hence, can possibly be the rate-determining step (RDS) in a catalytic reaction.22 As an example, Fig. 1b shows the free energy diagram of the carbon sites with the best activity on various P-G materials. Fig. 1c shows the free energy diagram of the carbon sites with the best performance among all the investigated carbon sites for each dopant model, and the free energy diagram of the dopant sites is shown in Fig. S3.† As shown in Fig. lb and c, the majority of the carbon active sites have weak interactions with the ORR intermediates, and the formation of *OOH (eqn (1)) possesses the greatest free energy change value among the four reaction steps. This indicates that the *OOH formation is the RDS (ΔGRDS = ΔG1) for most of the carbon active sites. On the carbon sites of b6FC1-G and b4OBC2-G, the desorption of *OH (eqn (4)) becomes the RDS (ΔGRDS = ΔG4) due to the strong binding of the intermediates. A similar phenomenon is also shown in Fig. S3,† where the dopants with weak binding of the intermediates, such as S, Se, B (a4BC3-G) and P (a2OPC4-G), hinder the formation of *OOH, and the dopants with strong binding including those on a3BC3-G, c3PC2-G, b3PC4-G and a3PC4-G can be considered to be poisoned by *OH. Among all the discussed models, c1OPC3-G, b5NC3-G, and b6FC1-G exhibit the lowest values of ΔGRDS. Accordingly, the overpotential of the ORR (ηORR) under the conditions of ΔGRDS = 0 at the equilibrium potential (UNHE = 0.455 V vs. NHE at pH = 13)20 can be calculated, and this shows that c1OPC3-G, b5NC3-G and b6FC1-G exhibit the smallest ηORR (0.52, 0.54 and 0.46 V, respectively), suggesting that they are the best ORR catalysts from the theoretical viewpoint.Generally, a site that binds *OOH strongly is also expected to bind *OH strongly, as each adsorbate binds to the surface via the oxygen atom.23–27 As shown in Fig. 1d, the adsorption free energies of *OH (ΔG*OH) are linearly related to those of *OOH (ΔG*OOH) by
| ΔG*OH = 0.98ΔG*OOH − 3.28 | (15) |
| ΔG1 = ΔG*OOH − 4.92 eV − ΔGH+(pH) + eU = 1.02ΔG*OH − 1.57 eV − ΔGH+(pH) + eU | (16) |
| ΔG4 = −0.98ΔG*OOH + 3.28 − ΔGH+(pH) + eU= −ΔG*OH − ΔGH+(pH) + eU | (17) |
Eqn (16) and (17) determine the relationship between ΔG1 and ΔG4, and demonstrate that the first proton transfer, ΔG1, to the oxygen forming *OOH is the RDS for the weakly binding active sites. In ΔG4, the proton transfer to the *OH forming water is the RDS for the strongly binding active sites. Obviously, a perfect catalyst with the smallest free energy change should have a ΔG1 and ΔG4 of the same height (ΔG1 = ΔG4) at the equilibrium potential. Otherwise, the step with the bigger ΔG will be the RDS, and then the whole reaction will be sluggish. When ΔG1 = ΔG4, ΔG*OOH and ΔG*OH on single-heteroatom-doped-G are 4.14 and 0.78 eV, respectively. At the equilibrium potential (UNHE = 0.455 V), the smallest value of ΔG1 or ΔG4 is 0.44 eV. Accordingly, the minimum ηORR on a perfect single-heteroatom-doped-G catalyst will be at least 0.44 V. This suggests that the ORR on single-heteroatom-doped-G has an intrinsic limitation under the control of the associative mechanism.
As shown in Fig. 1e, the volcano relationship between the overpotential of the ORR and ΔG*OOH is highly consistent with the Sabatier principle. The top of the volcano also suggests that there is an intrinsic limitation for the ORR proceeding via the associative mechanism.28 On the left hand side of the volcano, the binding energies of *OOH or *OH on active sites are too strong, while on the right hand side, they are too weak. The value of ΔG*OOH at the peak of the volcano is the value that a perfect single-heteroatom-doped-G catalyst should have. Thus ΔG*OOH or ΔG*OH can be used as a descriptor to indicate the ORR catalytic activity of the doped-G. Fig. 1e also shows that the optimum binding free energy of *OOH (ΔG*OOH) is about 4 eV, and the lowest limitation of ηORR is about 0.4 V. This is consistent with the result derived from eqn (16) and (17). Consequently, an ideal free energy diagram of a perfect ω-doped-G (ω-G, where ω is an ideal nonmetallic element) for the ORR proceeding via the associative mechanism is speculated, and is represented by a red line in Fig. 1f, in which the minimum ΔGRDS (ΔG1 and ΔG4) is 0.44 eV. Unfortunately, only three types of single-heteroatom-doped-G (b6FC1-G, c1OPC3-G and b5NC3-G) among the 18 discussed single-heteroatom-doped-G catalysts are close to the ω-G. The minimum ΔGRDS (0.44 eV) of ω-G is close to that of noble metal catalysts (≈0.45 eV on Pt for the ORR),25 indicating that ω-G can be as good as Pt for the ORR.
3.2 Triple effect – catalytic activity origin
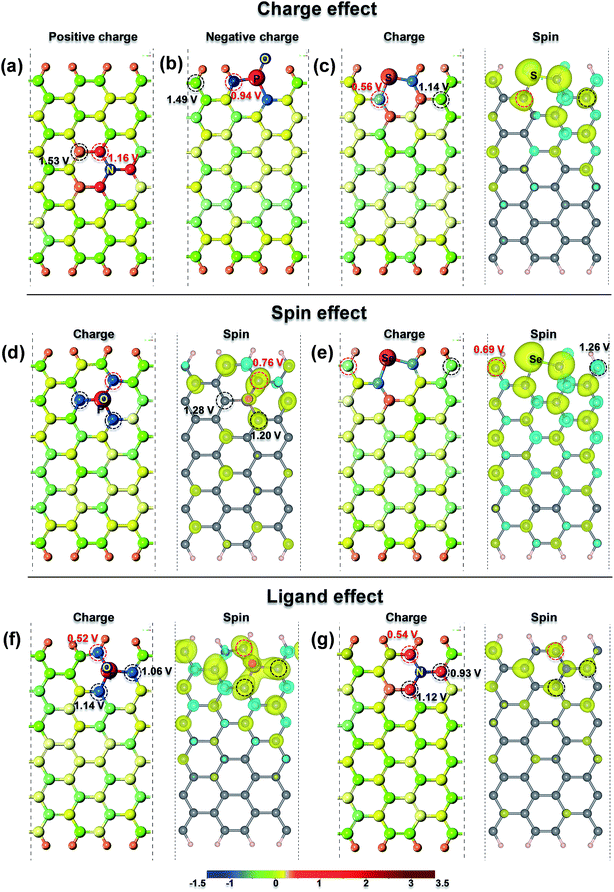
Setting up an essential descriptor for the ORR active sites on doped-G is critical for rationally designing the best ω-G catalyst. Previous studies9,14,29,30 disclosed that most of the active sites are attributed to the redistribution of surface charge and induced spin via the incorporation of heteroatoms into the carbon matrix. Moreover, appropriately increasing the edges or defects can lead to more unsaturated carbon atoms, which can enhance the catalytic activity of doped-G for the ORR.30–32 Therefore, by taking the carbon active sites of all the above doped-G frameworks as objects, we analyzed the contribution of the Bader charge, spin density distribution and edges to the catalytic activity of single-heteroatom-doped-G. Fig. 2 shows the role of the above factors in influencing the catalytic activity of several typical single-heteroatom-doped-G structures. Additionally, the ηORR, Bader charge and spin density of the carbon sites on all the studied single-heteroatom-doped-G structures are listed in Fig. S4.†Fig. 2a–c displays the charge effect on the catalytic activity of the carbon sites on the several investigated single-heteroatom-doped-G, and reveal that the carbon sites with positive or negative charge can be the active sites for the ORR. As shown in Fig. 2a, the carbon site (in a red circle) on a5NC3-G with more positive charge (0.225, in Fig. S4l†) exhibits superior ORR catalytic activity (ηORR = 1.16 V) compared to that of the carbon site (in a black circle) with less positive charge (0.106, in Fig. S4l,†ηORR = 1.53 V). A similar phenomenon also exists in d1OPC2-G as shown in Fig. 2b, in which the carbon site (in a red circle) possessing much more abundant negative charge (−0.924, Fig. S4d†) can also enhance the ORR performance (ηORR = 0.94 V). Meanwhile, in a similar position (in a black circle), the carbon site without obvious negative charge (−0.098, Fig. S4d†) has poor catalytic activity for the ORR (ηORR = 1.49 V). In the case of doped-G with magnetization, such as S-G, as shown in Fig. 2c, if the carbon sites in S-G have a similar spin density, the carbon site with more negative charge (−0.261, Fig. S4n†) has the higher catalytic activity for the ORR (ηORR = 0.56 V) than that with less negative charge (−0.019, Fig. S4n,†ηORR = 1.14 V). Thus, the charge effect plays an important role in enhancing the catalytic activity of doped-G.
It should be pointed out that the spin effect on the carbon sites also has a critical effect on the catalytic activity of the ORR as shown in Fig. 2d and e. Fig. 2d suggests that the ηORR of the carbon sites on b1OPC3-G for the ORR decreases (1.28 V > 1.20 V > 0.76 V) with increasing atomic spin density (μ, 0 < 0.011 < 0.021, Fig. S4b†), when the charge and coordination state of these carbon active sites remain similar. In addition, Fig. 2e further reveals that a carbon active site in Se-G with a positive spin density (μ = 0.016, ηORR = 0.69 V) is more favorable for the ORR than one with a negative spin density (μ = −0.009, ηORR = 1.26 V).
If the values of the Bader charge and spin density of the studied carbon sites are similar, as illustrated in Fig. 2f and g, the ηORR on these carbon sites decreases with a decrease in distance from the center to the edge of doped-G. Also, it is worth pointing out that the carbon atoms at the edge have very small ηORR values (0.52 V and 0.54 V) due to their unsaturated coordination. We define this phenomenon as the “ligand effect”. Experimentally, it has been proven that the atoms at the graphene edge demonstrate a much higher catalytic activity than those inside the graphene plane.30
Therefore, the ORR catalytic activity of the carbon sites on doped-G can be jointly determined using the charge effect, the spin effect and the ligand effect. Here, we describe this comprehensive factor as the “triple effect”.
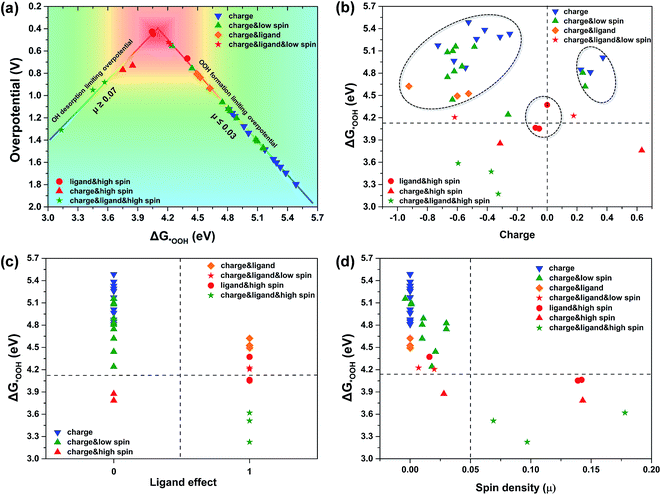
To gain further insight into the particular role of the above mentioned effects in enhancing catalytic activity, in Fig. 3 we have calculated the ηORR on all the possible carbon sites involving the above three effects, and deciphered the contribution of each special effect. As shown in Fig. 3a, in the case of joint participation of the charge, spin and ligand effects, there are two lines with two different slopes located in the two ranges of ΔG*OOH, the weak binding strength and strong binding strength of *OOH, respectively (Fig. 3a). These two lines form a volcano with the top at a value of 4.14 eV for ΔG*OOH.
As shown in Fig. 3a, the majority of the carbon active sites with weak binding energies of *OOH or *OH are located on the right side of the volcano, where the atomic spin densities on the carbon sites are less than or equal to 0.03 (μ ≤ 0.03). This suggests that the *OOH formation is the RDS for the ORR. In the case where only the charge effect is applied to the carbon sites (blue triangles), they exhibit poor catalytic performance for the ORR (with the highest ηORR). In the case of the charge effect together with a low atomic spin density, the binding strength of *OOH on the carbon sites (green triangles) becomes stronger, and the ηORR decreases as the binding strength of *OOH increases (and the value of ΔG*OOH decreases). In the case of the charge effect together with the ligand effect (yellow diamonds), an obvious reinforcement is observed on the carbon sites for catalyzing the ORR. Likewise, the association between the spin effect and ligand effect could also obviously improve the ORR catalytic activity of the carbon sites (red dots). Undoubtedly, the combination of the charge, spin and ligand effects (the triple effect) on the carbon sites (red pentagrams) can enhance catalytic activity more significantly. The red square area around the top of the volcano is close to the optimum value of ηORR (0.44 V).
In addition, a minority of carbon active sites with strong binding energies of *OOH or *OH are situated on the left side of the volcano, where the spin densities on the carbon sites are greater than or equal to 0.07 (μ ≥ 0.07). In this range, the triple effect on the carbon sites pushes the ΔG*OOH of the carbon sites to climb over the volcano peak and arrive at the left side. Then the RDS changes to the desorption of the oxygen containing species, that is, the *OH desorption becomes the RDS. Accordingly, the too-strong binding strength induced by the triple effect makes the ηORR increase and forces catalytic activity to move out of the optimum area.
The detailed partition of the triple effect at all the carbon sites according to the relationship between ΔG*OOH and the special effect is shown in Fig. 3b–d. Fig. 3b shows that the carbon sites with positive charge have stronger binding to *OOH than those with negative charge. As the charge effect combines with the spin and ligand effects, the binding strength of *OOH can be further enhanced, and can even become so strong as to cross the optimum value of ΔG*OOH. More importantly, Fig. 3b shows that even though the carbon sites are not heavily charged, that is, they are around zero charge, with the aid of high spin and the ligand effect, the carbon sites can also be modulated to reach the best catalytic activity. This result gives us the following inspiration that one can obtain a better ORR catalyst via tuning S- and Se-doped graphene with an enhanced ligand effect. Fig. 3c shows that the ΔG*OOH of the carbon sites with unsaturated coordination (ligand effect 1) exhibits higher binding of *OOH than that of the carbon sites with saturated coordination (ligand effect 0). In addition, Fig. 3c also shows that it is difficult to obtain a better catalytic site via just the charge effect without participation of the ligand effect (blue triangles). However, this situation can be improved with participation of either the low spin effect (green triangles) or high spin effect (red triangles). In Fig. 3d, the spin density divides the carbon sites into two parts. The carbon sites with a low atomic spin density (μ ≤ 0.03) are concentrated in the upper left area and have a weak binding energy of *OOH, while the carbon sites with a high atomic spin density (μ ≥ 0.07) are located in the lower right area and show a strong binding of *OOH. This suggests that the spin effect can tune the *OOH binding in a wide range (from the weak to the strong) compared with other effects. According to our calculations, zigzag graphene and dopants on the edge of the doped graphene are more likely to induce discontinuous high spin density on the carbon sites. It is particularly important to modulate the catalytic activity of the carbon sites, especially the inner carbon sites of doped graphene. Thus, we can conclude that the contributions of the above effects towards enhancing the binding energy of *OOH increase in the order of negative charge effect < positive charge effect < low spin effect < ligand effect < high spin effect.
Overall, most of the carbon sites in our calculated doped-G models have too weak an interaction with the intermediates. Only a few of the carbon sites show a strong interaction with *OOH. Therefore, for most of the carbon sites of doped-G, introducing the triple effect is an important strategy for enhancing the binding strength of the intermediates, and consequently improving the catalytic activity for the ORR. In particular, increasing the atomic spin density and the charge of the carbon sites can effectively enhance the catalytic activity of the inner carbon sites. By combining the ligand effects of the carbon sites (which usually take place around the edges/defects of doped-G), the triple effect can effectively enhance the catalytic activity as a whole. Notably, a single carbon active site with the triple effect and discontinuous spin density on the carbon sites merely benefits the end-on adsorption of *OOH, which means the ORR still follows the associative mechanism rather than the dissociative mechanism. Thus, generating double carbon active sites with the triple effect and introducing continuous spin density for the carbon sites might benefit the bridge adsorption of *OOH, and then force the ORR to follow the dissociative mechanism, breaking through the activity limitation of the associative mechanism.
3.3 Principle for catalyst design
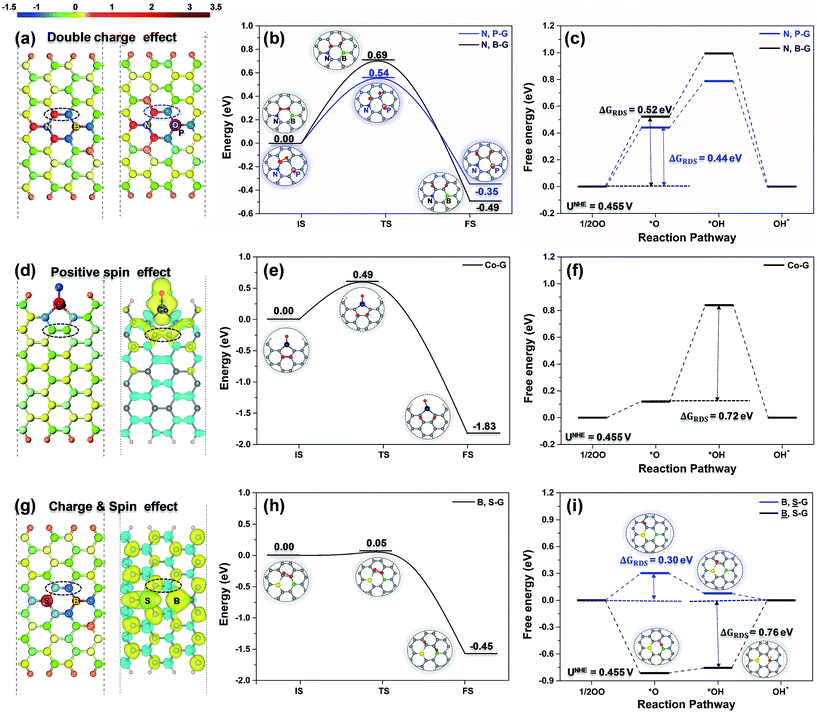
Based on our understanding of the triple effect, we tried to set up a principle to improve the catalytic activity of doped-G for the ORR. It is well known that the carbon atoms at the edge of doped-G generally show higher catalytic activity than that shown by the inner carbon atoms. Therefore, to enhance the intrinsic activity of doped-G, improving the catalytic activity of inner carbon sites is more important than increasing the activity of edge carbon sites. As there is no ligand effect on the inner carbon atoms of doped-G, in the following discussion, only the charge effect, spin effect and spin & charge effects are considered.As shown in Fig. 4a, incorporating N and P or N and B (the electronegativity of N, P and B are 3.04, 2.19 and 2.04, respectively) heteroatoms into the carbon sheet surface constructs well-defined and tunable double carbon active sites (circled with black and blue dotted lines, respectively), which simultaneously inherit positive and negative charges. On the double carbon sites, the O2 dissociation in N, P-G and N, B-G (Fig. 4b) is an exothermic reaction and has energy barriers of 0.54 and 0.69 eV, respectively, while the associative mechanism on these carbon active sites in N, B-G has energy barriers of 1.12 and 1.19 eV (Fig. S5†) when the carbon atom is bonded to the N or B atom, respectively. This means that the ORR is likely to follow the dissociative pathway (eqn (5)–(7)) at the working temperature, because the energy barrier of the O2 dissociation is lower than 0.75 eV (a magnitude regarded as surmountable for the reaction occurring at room temperature),33 and is even close to that of a Pt surface (0.51 eV).25,34 The Gibbs free energy diagram of the ORR dissociative pathway on the double carbon sites of N, P-G and N, B-G (shown in Fig. 4c) demonstrates that the largest free energy change (0.52 and 0.44 eV, respectively) happens in the step of O2 dissociation (eqn (5)), which is therefore the RDS (ΔGRDS = ΔG5) of the overall reaction at equilibrium potential.
Transition metallic heteroatoms can induce continuous spin density in the graphene. In Fig. 4d, the two contiguous carbon atoms circled with a black dotted line on Co-G possess a continuous spin density of 0.03 and have a slight charge of −0.01. The double carbon sites on Co-G are prone to proceeding via the ORR dissociative pathway in the same way as those on N, B-G or N, P-G, and show an even lower energy barrier to O2 dissociation (0.49 eV, Fig. 4e) than those on N, B-G or N, P-G. The Gibbs free energy diagram (Fig. 4f) shows that the RDS of the ORR becomes the protonation of *O (eqn (6)), and that the value of ΔG6 is 0.72 eV. This means that the double carbon sites with a continuous spin density benefit the dissociation of O2 and have a strong interaction with the intermediates.
In the case of S, B-G (Fig. 4g), the charge effect and spin effect simultaneously play a role in tuning the electronic configuration of the neighboring carbon atoms (circled with a black dotted line). As expected, the double carbon sites in B, S-G show a much lower energy barrier to O2 dissociation (0.05 eV as shown in Fig. 4h) than those tuned only via the charge effect or only the spin effect. As shown in Fig. 4i, the RDS of the ORR on the carbon atom bonded to the B atom (marked as ![[B with combining low line]](https://www.rsc.org/images/entities/char_0042_0332.gif) , S-G) is the desorption of *OH with a free energy change of 0.76 eV due to the too-strong interaction of B with the intermediates, while on the carbon atom bonded to the S atom (marked as B,
, S-G) is the desorption of *OH with a free energy change of 0.76 eV due to the too-strong interaction of B with the intermediates, while on the carbon atom bonded to the S atom (marked as B, ![[S with combining low line]](https://www.rsc.org/images/entities/char_0053_0332.gif) -G), the RDS of the ORR is the dissociation of O2 with a free energy barrier of 0.30 eV. This once again demonstrates that the double carbon sites that combine the charge and spin effects can improve the ORR catalytic activity more significantly than a single carbon site with the same effects.
-G), the RDS of the ORR is the dissociation of O2 with a free energy barrier of 0.30 eV. This once again demonstrates that the double carbon sites that combine the charge and spin effects can improve the ORR catalytic activity more significantly than a single carbon site with the same effects.
Therefore, by carefully controlling the type of dopant, it is possible to synchronously introduce two or even three effects into the carbon frameworks. On metal-doped-G and dual-heteroatom-doped-G, the triple effect induces the ORR mainly via the dissociative mechanism rather than the associative mechanism. Thus, metal-doped-G and dual- or multi-heteroatom-doped-G have great potential to become better catalysts (which should have a flat potential energy landscape at the equilibrium potential) by well modulating the triple effect.
4. Conclusions
Through linking the activities of various doped-G models with DFT calculations on the reaction energies on the active sites of the models, the catalytic processes involved in the ORR on doped-G have been thoroughly investigated. Following the investigation of an extensive range of the surface carbon atoms’ properties, we have shed light on the underlying origin of the activity of the carbon active sites for the ORR triple effect, which includes the charge, the spin density and the ligand effect. The contribution of the above effects towards enhancing the binding energies of *OOH or *OH increases in the order of negative charge effect < positive charge effect < low spin effect < ligand effect < high spin effect. This means that the spin effect can tune the *OOH binding in a wide range, and the charge effect and the spin effect might be particularly important in modulating the catalytic activity of the inner carbon sites on doped-G. The ligand effect, which only happens at the edge of the graphene sheet, has a profound influence on the neighboring carbon atoms. This means it is important to open a large number of pores on doped-G to generate the edges. These findings lead to a two-step experimentally achievable strategy concerning the intrinsic electronic structure (charge and magnetism) and the extrinsic physical character (defects) of graphene-based materials to modulate the triple effect of the carbon sites, and to promote the apparent activities that reach the levels of those of the metal-based catalysts that are used as benchmarks.Conflicts of interest
There is no conflict of interest.Acknowledgements
This research work was financially sponsored by the National Natural Science Foundation of China (Grant No. 21436003, 21576032 and 91535205), and the National Key Research and Development Plan of China (No. 2016YFB0101202).Notes and references
- J. J. Duan, S. Chen, M. Jaroniec and S. Z. Qiao, ACS Catal., 2015, 5, 5207–5234 CrossRef.
- J. Y. Cheon, J. H. Kim, J. H. Kim, K. C. Goddeti, J. Y. Park and S. H. Joo, J. Am. Chem. Soc., 2014, 136, 8875–8878 CrossRef PubMed.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086 RSC.
- W. Ding, Z. Wei, S. Chen, X. Qi, T. Yang, J. Hu, D. Wang, L. J. Wan, S. F. Alvi and L. Li, Angew. Chem., Int. Ed., 2013, 52, 11755–11759 CrossRef PubMed.
- X. Wang, G. Sun, P. Routh, D. H. Kim, W. Huang and P. Chen, Chem. Soc. Rev., 2014, 43, 7067–7098 RSC.
- D. Yan, Y. Li, H. Jia, C. Ru, L. Dai and S. Wang, Adv. Mater., 2017, 29, 1606459 CrossRef PubMed.
- C. Tang and Q. Zhang, Adv. Mater., 2017, 29, 1604103 CrossRef PubMed.
- C. Tang, M.-M. Titirici and Q. Zhang, J. Energy Chem., 2017, 26, 1077–1093 CrossRef.
- I. Y. Jeon, S. Zhang, L. P. Zhang, H. J. Choi, J. M. Seo, Z. H. Xia, L. M. Dai and J. B. Baek, Adv. Mater., 2013, 25, 6138–6145 CrossRef PubMed.
- D. S. Yang, D. Bhattacharjya, S. Inamdar, J. Park and J. S. Yu, J. Am. Chem. Soc., 2012, 134, 16127–16130 CrossRef PubMed.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef PubMed.
- X. Zhang, Z. Lu, Z. Fu, Y. Tang, D. Ma and Z. Yang, J. Power Sources, 2015, 276, 222–229 CrossRef.
- G. Fazio, L. Ferrighi and C. Di Valentin, J. Catal., 2014, 318, 203–210 CrossRef.
- L. P. Zhang, J. B. Niu, M. T. Li and Z. H. Xia, J. Phys. Chem. C, 2014, 118, 3545–3553 Search PubMed.
- Z. Zhao, M. Li, L. Zhang, L. Dai and Z. Xia, Adv. Mater., 2015, 27, 6834–6840 CrossRef PubMed.
- Z. H. Zhao and Z. H. Xia, ACS Catal., 2016, 6, 1553–1558 CrossRef.
- N. Yang, X. Zheng, L. Li, J. Li and Z. Wei, J. Phys. Chem. C, 2017, 121, 19321–19328 Search PubMed.
- Y. Dong, P. Zhang, Y. Kou, Z. Yang, Y. Li and X. Sun, Catal. Lett., 2015, 145, 1541–1548 CrossRef.
- H. J. Yan, B. Xu, S. Q. Shi and C. Y. Ouyang, J. Appl. Phys., 2012, 112, 104316 CrossRef.
- I. Sakellis, J. Appl. Phys., 2012, 112, 034302 CrossRef.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, J. Am. Chem. Soc., 2014, 136, 4394–4403 CrossRef PubMed.
- W. Liang, J. Chen, Y. Liu and S. Chen, ACS Catal., 2014, 4, 4170–4177 CrossRef.
- M. Bajdich, M. Garcia-Mota, A. Vojvodic, J. K. Norskov and A. T. Bell, J. Am. Chem. Soc., 2013, 135, 13521–13530 CrossRef PubMed.
- J. Greeley, I. E. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Norskov, Nat. Chem., 2009, 1, 552–556 CrossRef PubMed.
- J. K. Norskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef.
- M. García-Mota, M. Bajdich, V. Viswanathan, A. Vojvodic, A. T. Bell and J. K. Nørskov, J. Phys. Chem. C, 2012, 116, 21077–21082 Search PubMed.
- I. E. L. Stephens, A. S. Bondarenko, U. Grønbjerg, J. Rossmeisl and I. Chorkendorff, Energy Environ. Sci., 2012, 5, 6744 Search PubMed.
- L. P. Zhang and Z. H. Xia, J. Phys. Chem. C, 2011, 115, 11170–11176 Search PubMed.
- J. Liang, Y. Jiao, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2012, 51, 11496–11500 CrossRef PubMed.
- I. S. Amiinu, J. Zhang, Z. Kou, X. Liu, O. K. Asare, H. Zhou, K. Cheng, H. Zhang, L. Mai, M. Pan and S. Mu, ACS Appl. Mater. Interfaces, 2016, 8, 29408–29418 Search PubMed.
- G. L. Chai, Z. Hou, D. J. Shu, T. Ikeda and K. Terakura, J. Am. Chem. Soc., 2014, 136, 13629–13640 CrossRef PubMed.
- H. F. Wang and Z. P. Liu, J. Am. Chem. Soc., 2008, 130, 10996–11004 CrossRef PubMed.
- Y. Sha, T. H. Yu, B. V. Merinov and W. A. Goddard, ACS Catal., 2014, 4, 1189–1197 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc01801d |
| This journal is © The Royal Society of Chemistry 2018 |