Modular O₂ electroreduction activity in triphenylene-based metal–organic frameworks

Abstract

Triphenylene ligands hexasubstituted with amino or phenol groups afford two phases of electrically conductive layered two-dimensional metal–organic frameworks upon reaction with various metals. Regardless of the identity of the metal or chelating atom, π-stacking within the MOF layers is essential to achieve high electrical conductivity, redox activity, and catalytic activity.

---

Control over the architectural and electronic properties of heterogeneous catalysts poses a major obstacle in the targeted design of active, stable, and economically sustainable materials for producing fuels.¹ Metal–organic frameworks (MOFs) are compelling choices for electrocatalytic applications as their high surface area and tunable porosity and ligand structure affords densely packed active sites and tailor-made microenvironments for controllable reaction conditions within the pores. Despite the high potential for MOF-based electrocatalysts, synthesis of these materials often involves chelation of hard metal ions to hard N or O atoms in redox-inactive ligands. Typical compositions thus offer no low energy charge transport pathways or charge carriers, rendering these materials electrically insulating.² Excitingly, the emergence of intrinsically conducting or semiconducting metal–organic species^2–9 has made accessible the use of such materials as tunable, high surface area electrocatalysts for energy conversion reactions such as H₂ evolution,^10,11 O₂ evolution,^11,12 CO₂ reduction,⁸ O₂ reduction,^13,14 and others.¹⁵ The high level of atomic definition in these materials offers an opportunity to gain insight into the operative catalytic mechanisms and establish structure–function behavior. In particular, mechanistic studies of Ni₃(HITP)₂ (HITP = 2,3,6,7,10,11-hexaiminotriphenylene) revealed that the O₂ reduction reaction (ORR) proceeds on a ligand-based active site, and suggested that the metal identity and electron delocalization throughout the framework could have important implications for the electronic structure which in turn should govern electrocatalytic activity.¹⁶ Herein, we probe the role of the metal identity, chelating atom, and π-stacking in a suite of triphenylene-based conductive MOFs in influencing the ORR activity and mechanism, with the goal of identifying the key players in this class for MOFs for dictating electrocatalytic behavior.

To this end, we synthesized several analogues featuring a hexa-substituted triphenylene core. As shown in Fig. 1, chelation of a divalent first-row transition metal with either the hexaamino or hexahydroxytriphenylene (HHTP) ligand in the presence of base and air affords one of two phases. The three analogues of the hexagonal crystal system, Ni₃(HITP)₂, Cu₃(HITP)₂, and Cu₃(HHTP)₂ (referred to as the hexagonal MOFs), feature a 2D honeycomb lattice stacked in a slipped parallel configuration along the c axis (Fig. 1a and c).^3,4,7 The two analogues of the trigonal crystal system, Co₃(HHTP)₂ and Ni₃(HHTP)₂ (referred to as the trigonal MOFs), feature alternating layers of the honeycomb lattice and trinuclear M₃(HHTP)(H₂O)₁₂ clusters that are rotated 60° with respect to the honeycomb lattice (Fig. 1b and d).⁷ Isolation of the hexagonal MOFs as well as the trigonal MOFs was confirmed with powder X-ray diffraction (Fig. 1c and d).

Fig. 1 (a) Hexagonal and (b) trigonal phases of the triphenylene MOFs, and corresponding powder X-ray diffraction patterns ((c) and (d) for hexagonal and trigonal diffraction patterns, respectively). M = Co, Ni, or Cu; X = NH or O. H atoms are omitted for clarity.

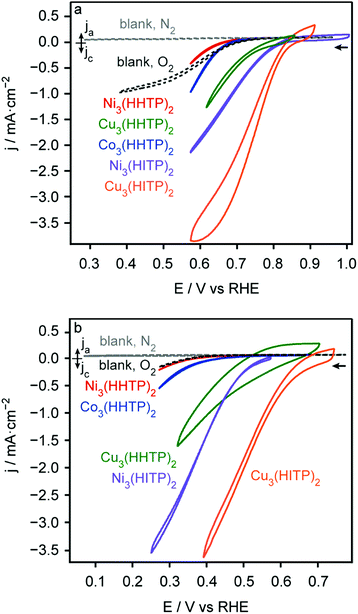
The ORR activity of the MOF powders deposited on glassy carbon electrodes was probed in pH 13 and 8. The reductive current shown in Fig. 2 is observed for all analogues only under O₂, confirming that the current indeed stems from O₂ reduction (Fig. S1†). The cyclic voltammograms under O₂ atmosphere shown in Fig. 2 reveal that the hexagonal MOF Cu₃(HITP)₂ exhibits the highest initial ORR activity in both pH environments. However, the instability of this analogue to O₂ under experimental conditions resulted in a rapid loss of activity after the first CV cycle (Fig. S2†). This instability prevented collection of reliable data for ORR with Cu₃(HITP)₂, as the catalyst activity continuously declined during prolonged data collection. The other hexagonal MOFs, Ni₃(HITP)₂ and Cu₃(HHTP)₂, reduce O₂ with lower overpotential and higher current density than the trigonal MOFs. Although the trigonal MOFs Co₃(HHTP)₂ and Ni₃(HHTP)₂ seem to contribute no catalytic activity beyond the glassy carbon background current, depositing these analogues on the more inert indium tin oxide showed nominal ORR activity (Fig. S3†). This substrate-independent activity confirmed that kinetic data collected for these analogues on glassy carbon rotating disk electrodes represents the ORR kinetics of the MOFs rather than simply the blank electrodes. Potentiostatic reduction of O₂ over 8 hours in pH 13 revealed that the HHTP-based MOFs deactivate more quickly in base than does Ni₃(HITP)₂ (Table S1†). This is likely due to thermodynamic differences arising from better energetic and/or spatial overlap between the HITP ligand and Ni orbitals than the HHTP ligand and metal orbitals. The resulting longer metal–ligand bond distances in the HHTP MOFs could enable more facile decomposition of these analogues compared to that which features Ni–N coordination.^7,17–19

Fig. 2 Cyclic voltammograms of O₂ electroreduction with the triphenylene MOFs in (a) pH 13 and (b) pH 8 electrolyte. “Blank” indicates the background current from the unmodified glassy carbon electrode cycled under O₂ and N₂ atmosphere.

To determine the product distribution of ORR with the triphenylene MOFs and how this may change as a function of increasing driving force, potentiostatic rotating ring disk electrode (RRDE) studies were conducted over the ORR potential window (Fig. S4†). Dividing the anodic current passed at the Pt ring from back-oxidizing the 2e⁻ reduction product by the total cathodic current passed at the MOF-modified disk from both the 2e⁻ and 4e⁻ reduction products (hydrogen peroxide and water, respectively) gives the potential-dependent faradaic efficiency plots shown in Fig. S5.† Unsurprisingly,²⁰ all MOFs exhibit potential-dependent faradaic efficiency, with the 4e⁻ reduction product favored when more than ∼300 mV of overpotential is applied, with the 2e⁻ reduction product favored at lower overpotentials.

The kinetic rate laws for ORR with the hexagonal and trigonal MOFs were obtained by probing the order in [O₂], [H⁺], and electrons. Activation-controlled Tafel plots (Fig. 3) generated by Koutecky–Levich data collected in pH 8 and 13 (Fig. S6†) reveal slopes of 110–170 mV dec⁻¹ (Table 1). A slope of 118 mV dec⁻¹ is indicative of rate-limiting electron transfer,²¹ which we believe to be relevant for all analogues here. One notable exception is the Tafel data collected for Co₃(HHTP)₂ in pH 13, which features a Tafel slope of 81 mV dec⁻¹. This slope could indicate that in pH 13, ORR with Co₃(HHTP)₂ does not proceed with rate-limiting electron transfer, but rather perhaps with rate-limiting O₂ chemisorption.²² This pH-dependent electrokinetic behavior is consistent with the behavior Co-macrocycles active for ORR catalysis.²³ The Tafel data not only gives insight into whether rate-limiting electron transfer is relevant, but also provides relative rate constants as a means to directly compare catalytic activity (Table S2†). The placement of the Tafel slopes from Ni₃(HITP)₂ in the lower right quadrant of the Tafel plot (Fig. 3, dashed triangle) reflects the fast electrokinetics of this analogue at both pH 8 and 13, i.e. Ni₃(HITP)₂ passes a high cathodic current density (log(j)) with low overpotential (η).^21,22

Fig. 3 Tafel plots from ORR with the triphenylene MOFs at pH 13 (circles) and 8 (triangles). η represents the ORR overpotential and j represents the current density at a given overpotential. Orange dashed section indicates best catalyst performance (high current density passed with low overpotential).

Table 1 Tafel slopes corresponding to the Tafel plots in Fig. 3

MOF	pH	Tafel slope (V dec^−1)
Ni3(HITP)2	8	0.124
Cu3(HHTP)2	8	0.170
Ni3(HHTP)2	8	0.120
Co3(HHTP)2	8	0.120
Ni3(HITP)2	13	0.128
Cu3(HHTP)2	13	0.110
Ni3(HHTP)2	13	0.110
Co3(HHTP)2	13	0.081

---

Potentiostatic data collected with varying overpotential and varying concentrations of O₂ in the electrolyte shows that for all analogues, more cathodic current (I) can be passed with increasing [O₂] in pH 8 (Fig. S7†). This linear increase in log(I) versus log([O₂]) with slopes of ∼1 (Table S3†) over the ORR potential window indicates that all analogues follow first-order kinetics in [O₂]. Experimental and computational data previously reported for ORR with Ni₃(HITP)₂ suggested rate-limiting O₂ binding concomitant with e⁻ transfer to Ni₃(HITP)₂ to form the superoxide adduct was likely.^13,16 The similar [O₂] order and Tafel data of the triphenylene MOF analogues (with the exception of ORR with Co₃(HHTP)₂ in pH 13) supports the assertion that all other triphenylene MOFs reported here also exhibit rate-limiting electron transfer–O₂ binding to the catalyst during ORR.

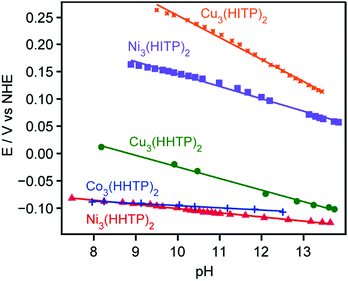
Given that the Tafel data from all analogues points to ORR proceeding with rate-limiting electron transfer, and considering the protonated nature of the ORR products, we investigated the possibility of proton-coupled electron transfer (PCET) occurring in our systems. Galvanostatic data from each analogue was collected under O₂ while titrating the electrolyte from pH 13.5 to pH 8 (Fig. 4). As shown in Table 2, all hexagonal MOFs exhibit a non-zero dependence of the ORR overpotential with [H⁺], whereas the trigonal MOFs feature δE/δpH slopes of nearly zero. The independence of ORR overpotential on [H⁺] during ORR with the trigonal MOFs suggests that no electron transfer during ORR with those analogues is proton-coupled.²⁴ In contrast, all hexagonal MOFs exhibit a non-zero order in [H⁺]. As seen with Ni₃(HITP)₂,¹⁶ the δE/δpH slopes for all hexagonal MOFs‡ are ∼20 mV dec⁻¹, revealing a fractional [H⁺] dependence that rules out rate-limiting PCET.²⁴

Fig. 4 Dependence of ORR onset potential on pH for the triphenylene MOFs. Purple squares, orange X symbols, blue cross symbols, red triangles, and green circles correspond to Ni₃(HITP)₂, Cu₃(HITP)₂, Co₃(HHTP)₂, Ni₃(HHTP)₂, and Cu₃(HHTP)₂ respectively.

Table 2 Slopes corresponding to the ORR [H⁺] order data in Fig. 4

MOF	Phase	δE/δpH (V dec^−1)
Ni3(HITP)2	Hexagonal	0.022
Cu3(HITP)2	Hexagonal	0.039
Cu3(HHTP)2	Hexagonal	0.020
Ni3(HHTP)2	Trigonal	0.007
Co3(HHTP)2	Trigonal	0.004

---

To explore the relationship between electron transfer and available proton concentration, cyclic voltammetry was run on the various MOFs under an inert atmosphere in varying pH environments. As previously observed with Ni₃(HITP)₂,¹⁶ the hexagonal analogues Cu₃(HHTP)₂ and Cu₃(HITP)₂ undergo oxidation events that exhibit Nernstian pH dependence, i.e. are proton-coupled (Fig. S8 and S9†).²⁴ As with Ni₃(HITP)₂, the fractional [H⁺] order observed in ORR with the hexagonal analogues likely stems from PCET in the MOF-hydroperoxide adduct. If the rate of this second, proton-coupled electron transfer to O₂ is only marginally faster than the rate-limiting first electron transfer to O₂, some fractional [H⁺] may experimentally manifest. Fractional order in [H⁺] during ORR has also been observed in ORR with nitrogen-doped graphitic carbon²⁵ and precious metal catalysts.^26,27

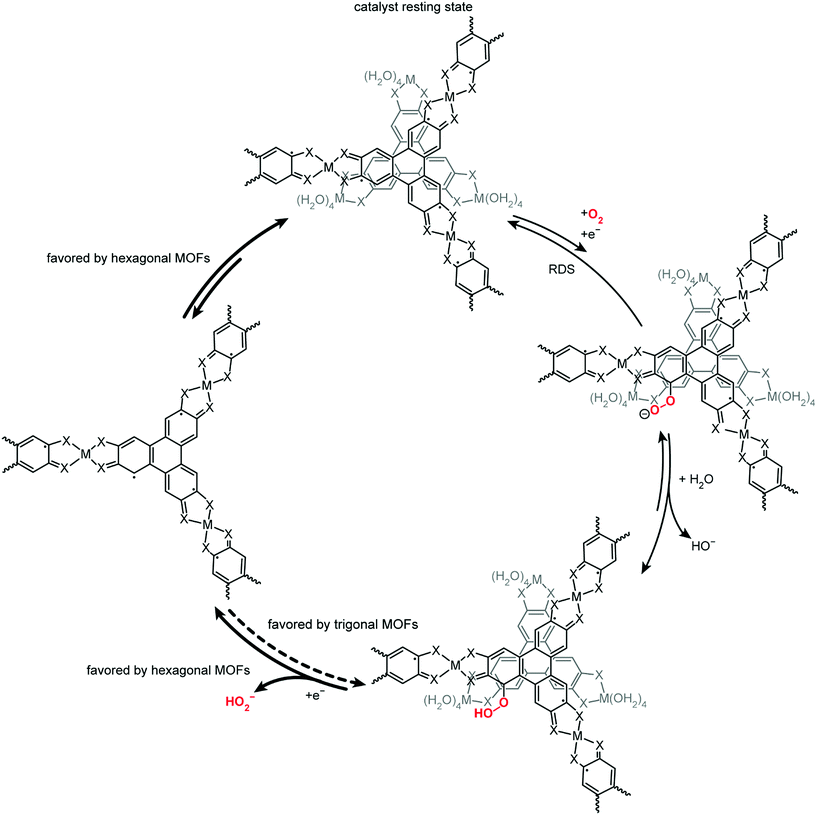
Considering that the non-zero ORR order in [H⁺] with the hexagonal MOFs is attributed to PCET in these redox-active analogues, the independence of ORR potential on pH observed in the trigonal MOFs is consistent with the lack of any faradaic events observed in the cyclic voltammograms of these analogues (Fig. S10†). This observation highlights that although both the hexagonal and trigonal MOFs feature a honeycomb lattice that could enable electron delocalization in the ab plane, the disruption of the π-stacking in the c direction of the trigonal MOFs greatly alters the electrochemical properties of this phase. These phase-dependent differences in electrochemical properties are further underscored by the electrical conductivity (σ) and electroactive surface area (ESA) values (Table 3). The catalytically active hexagonal MOFs exhibit conductivity values upwards of 60 S cm⁻¹, whereas the conductivity values of the trigonal MOFs are up to five orders of magnitude lower. Similarly, deriving the ESAs from double layer capacitance measurements²⁸ reveals an order of magnitude higher ESAs in the hexagonal MOFs than in the trigonal MOFs. Lower electrical conductivity and lower electroactive surface area values in the trigonal MOFs may indicate that the inferior catalytic activity is a result of slower electron transfer kinetics and a lower density of electroactive catalytic sites. The redox inactivity of the trigonal MOFs also points to unfavorable electron transfer, and is consistent with the low activity for ORR. The experimental data indicates that concomitant electron transfer and O₂ binding to the trigonal MOFs is still relevant. However, in order to obtain the O₂ reduction products and achieve catalyst turnover, at least one more electron must be transferred to the bound hydroperoxide, and the reduced product can then dissociate from the catalyst. If the second electron transfer to O₂ is expected to occur by PCET from the MOF, but the MOF is redox-inactive in the ORR potential window (as seen in the trigonal analogues), significantly more driving force will be needed to reduce the hydroperoxide and achieve product formation and catalyst turnover (Scheme 1).³⁰ This greater necessary driving force is evident in the ORR cyclic voltammograms and Tafel data from the trigonal phases; much higher overpotential is required to achieve reductive current with the trigonal MOFs in the presence of O₂ relative to the hexagonal MOFs. As such, the trigonal analogues never achieve the current density observed with the redox-active, hexagonal MOFs. Conversely, the high electrical conductivity and redox activity in the hexagonal MOFs enables facile electron transfer to O₂ and subsequent catalyst turnover, which contributes the high ORR activity observed in this phase.

Table 3 Electrical conductivity (σ) and electroactive surface area (ESA) values for the triphenylene MOFs

MOF	σ (S cm^−1)	ESA (F m^−2)
a Single crystal data. b This work. c An ESA value for Cu3(HITP)2 could not be obtained due to its instability during prolonged measurements.
Ni3(HITP)2	6 × 10^1 (ref. 3 and 29)	7.7 × 10^−7^b
Cu3(HITP)2	2 × 10^−1 (ref. 4)	N/A^c
Cu3(HHTP)2	2 × 10^−1 (ref. 7)^a	1.6 × 10^−6^b
Ni3(HHTP)2	6 × 10^−3^b	1.0 × 10^−7^b
Co3(HHTP)2	2 × 10^−3^b	1.0 × 10^−7^b

---

Scheme 1 Proposed mechanisms for 2e⁻ ORR with the hexagonal and trigonal MOFs. The black complex represents a fragment from the honeycomb lattice present in both phases. The gray complex indicates the M₃(HHTP)(H₂O)₁₂ cluster present in the trigonal MOFs. The bold solid versus dashed arrows indicate where the two mechanisms are thought to diverge, due to the redox inactivity of the trinuclear MOFs that hinders reduction of the hydroperoxide adduct.

These results demonstrate that materials made from identical ligands and bearing structural similarities exhibit vastly different electron transfer properties under electrochemical bias. This leads to distinct electrocatalytic responses in the oxygen reduction reaction, with the nearly eclipsed hexagonal phases exhibiting excellent activity that contrast with the virtual inactivity of the trigonal phases containing molecular species. We attribute the lack of catalytic activity in the latter to the high overpotential required for oxidizing a purported hydroperoxide intermediate. Knowledge of how the physical structures of conductive MOFs influence the electronic properties provides a foundation for predicting the broader utility of each analogue, and tailoring the phases to unique applications such as faradaic and capacitive energy storage, chemiresistive sensing, and electrochemical catalysis of other transformations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the MIT Energy Initiative Seed Fund Grant No. 015728-00168. E. M. M. gratefully acknowledges the National Science Foundation for a Graduate Research Fellowship under Grant No. 1122374. We thank Ms A. Stubbs for assistance with the [O₂] order data collection.

Notes and references

1. Heterogeneous Catalysis for Today's Challenges, ed. B. Trewyn, Royal Society of Chemistry, Cambridge, 2015.
2. L. Sun, M. G. Campbell and M. Dincă, Angew. Chem., Int. Ed., 2016, 55, 3566–3579.
3. D. Sheberla, L. Sun, M. A. Blood-Forsythe, S. Er, C. R. Wade, C. K. Brozek, A. Aspuru-Guzik and M. Dincă, J. Am. Chem. Soc., 2014, 136, 8859–8862.
4. M. G. Campbell, D. Sheberla, S. F. Liu, T. M. Swager and M. Dincă, Angew. Chem., Int. Ed., 2015, 54, 4349–4352.
5. M. G. Campbell, S. F. Liu, T. M. Swager and M. Dincă, J. Am. Chem. Soc., 2015, 137, 13780–13783.
6. J. Dou, L. Sun, Y. Ge, W. Li, C. H. Hendon, J. Li, S. Gul, J. Yano, E. A. Stach and M. Dincă, J. Am. Chem. Soc., 2017, 139, 13608–13611.
7. M. Hmadeh, Z. Lu, Z. Liu, F. Gándara, H. Furukawa, S. Wan, V. Augustyn, R. Chang, L. Liao, F. Zhou, E. Perre, V. Ozolins, K. Suenaga, X. Duan, B. Dunn, Y. Yamamto, O. Terasaki and O. M. Yaghi, Chem. Mater., 2012, 24, 3511–3513.
8. S. Lin, C. S. Diercks, Y.-B. Zhang, N. Kornienko, E. M. Nichols, Y. Zhao, A. R. Paris, D. Kim, P. Yang, O. M. Yaghi and C. J. Chang, Science, 2015, 349, 1208–1213.
9. A. J. Clough, J. M. Skelton, C. A. Downes, A. A. de la Rosa, J. W. Yoo, A. Walsh, B. C. Melot and S. C. Marinescu, J. Am. Chem. Soc., 2017, 139, 10863–10867.
10. A. J. Clough, J. W. Yoo, M. H. Mecklenburg and S. C. Marinescu, J. Am. Chem. Soc., 2015, 137, 118–121.
11. C. A. Downes and S. C. Marinescu, ChemSusChem, 2017, 10, 4374–4392.
12. H. Jia, Y. Yao, J. Zhao, Y. Gao, Z. Luo and P. Du, J. Mater. Chem. A, 2018, 6, 1188–1195.
13. E. M. Miner, T. Fukushima, D. Sheberla, L. Sun, Y. Surendranath and M. Dincă, Nat. Commun., 2016, 7, 10942–10949.
14. X.-H. Liu, W.-L. Hu, W.-J. Jiang, Y.-W. Yang, S. Niu, B. Sun, J. Wu and J.-S. Hu, ACS Appl. Mater. Interfaces, 2017, 9, 28473–28477.
15. P.-Q. Liao, J.-Q. Shen and J.-P. Zhang, Coord. Chem. Rev., 2017 DOI:10.1016/j.ccr.2017.09.001.
16. E. M. Miner, S. Gul, N. D. Ricke, E. Pastor, J. Yano, V. K. Yachandra, T. Van Voorhis and M. Dincă, ACS Catal., 2017, 7, 7726–7731.
17. C. Brückner, D. L. Caulder and K. N. Raymond, Inorg. Chem., 1998, 37, 6759–6764.
18. G. S. Hall and R. H. Soderberg, Inorg. Chem., 1968, 7, 2300–2303.
19. D. S. Liaw, S. M. Peng, S. S. Chern and S. C. Sheu, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 402–404.
20. G. Passard, A. M. Ullman, C. N. Brodsky and D. G. Nocera, J. Am. Chem. Soc., 2016, 138, 2925–2928.
21. E. Gileadi, Electrode Kinetics for Chemists, Chemical Engineers, and Materials Scientists, Wiley, John & Sons, Incorporated, New York, NY, 1993.
22. C. Song and J. Zhang, in PEM Fuel Cell Electrocatalysts and Catalyst Layers, ed. J. Zhang, Springer, London, 2008, pp. 89–134.
23. J. H. Zagal, M. J. Aguirre and M. A. Páez, J. Electroanal. Chem., 1997, 437, 45–52.
24. D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Chem. Rev., 2012, 112, 4016–4093.
25. Q. Li, B. W. Noffke, Y. Wang, B. Menezes, D. G. Peters, K. Raghavachari and L. Li, J. Am. Chem. Soc., 2014, 136, 3358–3361.
26. D. B. Sepa, M. V. Vojnovic, L. M. Vracar and A. Damjanovic, Electrochim. Acta, 1987, 32, 129–134.
27. N. Ramaswamy and S. Mukerjee, J. Phys. Chem. C, 2011, 115, 18015–18026.
28. L. Wang, Y. Wu, R. Cao, L. Ren, M. Chen, X. Feng, J. Zhou and B. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 16736–16743.
29. L. Sun, B. Liao, D. Sheberla, D. Kraemer, J. Zhou, E. A. Stach, D. Zakharov, V. Stavila, A. A. Talin, Y. Ge, M. D. Allendorf, G. Chen, F. Léonard and M. Dincă, Joule, 2017, 1, 168–177.
30. C. Costentin and J.-M. Savéant, ACS Catal., 2017, 7, 4876–4880.

---

Footnotes

† Electronic supplementary information (ESI) available: Materials and methods. CVs of the MOFs under N₂. CVs of Cu₃(HITP)₂ deactivating. CVs of the trigonal MOFs on ITO. % current retained during potentiostatic ORR. RRDE data. Faradaic efficiencies. Koutecky–Levich data. ORR exchange current densities. ORR [O₂] order data. pH-dependent redox activity of the hexagonal MOFs. Redox inactivity of the trigonal MOFs. See DOI: 10.1039/c8sc02049c

‡ Although the δE/δpH slope reflecting the ORR order in [H⁺] with Cu₃(HITP)₂ is reported here as 0.039 V dec⁻¹, this may be quantitatively inaccurate due to the instability of this analogue to O₂ under experimental conditions. This data was included to reflect that ORR with Cu₃(HITP)₂, as with the other hexagonal analogues, exhibits a non-zero order in [H⁺].

---