Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Can percolation theory explain the gelation behavior of diblock copolymer worms?†
Joseph R.
Lovett
a,
Matthew J.
Derry
 a,
Pengcheng
Yang
a,
Fiona L.
Hatton
a,
Pengcheng
Yang
a,
Fiona L.
Hatton
 a,
Nicholas J.
Warren
b,
Patrick W.
Fowler
a and
Steven P.
Armes
a,
Nicholas J.
Warren
b,
Patrick W.
Fowler
a and
Steven P.
Armes
 *a
*a
aDepartment of Chemistry, The University of Sheffield, Dainton Building, Brook Hill, Sheffield, South Yorkshire S3 7HF, UK. E-mail: s.p.armes@sheffield.ac.uk
bSchool of Chemical and Process Engineering, University of Leeds, Leeds, West Yorkshire LS2 9JT, UK
First published on 2nd August 2018
Abstract
It is well known that polymerization-induced self-assembly (PISA) offers an efficient synthetic route for the production of highly anisotropic diblock copolymer worms. When prepared in aqueous media, such worms form thermoresponsive free-standing hydrogels that are (i) readily sterilizable, (ii) can act as a 3D matrix for the culture of normal mammalian cells and (iii) can induce stasis in human stem cell colonies. Herein we critically examine the gelation behavior of two types of diblock copolymer worms in terms of recent advances in percolation theory for rigid rods, which explicitly account for the effect of rod length polydispersity. More specifically, we use small-angle X-ray scattering (SAXS) to determine the weight-average worm contour length, Lw, and the mean worm cross-sectional radius, R. This approach enables a direct comparison to be made between the theoretical critical worm volume fraction, ϕc, required for gelation and the experimental values indicated by rheological measurements and tube inversion experiments. Given that these diblock copolymer worms are relatively flexible rather than truly rod-like, reasonably good agreement between these two parameters is observed, particularly for shorter, relatively stiff worms. For longer, more flexible worms a proportionality constant of approximately two is required to reconcile theory with experimental values for ϕc. These findings are expected to have important implications for the aqueous gelation behavior exhibited by various other anisotropic nanoparticles, such as cellulose nanocrystals and semicrystalline block copolymer rods, and also fibril-forming small molecule (e.g. dipeptide) gelators.
Introduction
It is well known that certain surfactants (or binary mixtures thereof) can form highly anisotropic worms in aqueous solution.1–4 These systems have potential applications as thickeners,5,6 in drag reduction,7 and for enhanced oil recovery.4,8 The ‘living’ nature of these self-healing systems has been demonstrated and sophisticated techniques such as contrast variation neutron scattering have been utilized to characterize their structure.9,10 Surfactant worms typically exhibit mean contour lengths of the order of 1–10 μm. The concept of worm entanglements as a physical mechanism for gelation has been suggested on the basis of a combination of rheological and theoretical studies.10–12Diblock copolymer worm gels have been recognized for almost two decades.13 Over the last five years or so, the development of polymerization-induced self-assembly (PISA) has enabled the rational, reproducible synthesis of a wide range of diblock copolymer worm gels directly in water, polar solvents (e.g. ethanol) or non-polar solvents (e.g. n-alkanes).14–22 In particular, diblock copolymer worms prepared via dispersion polymerization often exhibit thermoresponsive gelation, undergoing a reversible worm-to-sphere morphological transition either on heating in ethanol or n-alkanes18,23,24 or on cooling in aqueous solution.20,25 In each case, this morphological transition appears to be the result of surface plasticization of the core-forming block, which leads to a subtle change in the packing parameter for the diblock copolymer chains.26,27 Typically, the mean worm width is well-defined, is of the order of a few tens of nm and is dictated by the mean degree of polymerization (DP) of the core-forming block. In contrast, the mean worm length is rather ill-defined and is typically of the order of hundreds of nm. Compared to the dimensions reported for surfactant worms, diblock copolymer worms appear to be too short to account for the observed formation of free-standing gels via a worm entanglement mechanism.
Percolation theory has been used for many years to account for the substantial differences in conductivity thresholds observed for many types of conductive particles dispersed in electrically insulating matrices.28–35 Typically, spheres exhibit a percolation threshold volume fraction of around 0.16,29,30 whereas highly anisotropic rods (e.g. polyaniline needles or carbon nanotubes) form fully-connected conductive networks at significantly lower volume fractions, sometimes below 0.01.31–35 Recently, percolation theory has been extended to include polydisperse rods exhibiting a wide range of rod lengths,36,37 which is often the case encountered experimentally. More specifically, for cylindrical rods with a high aspect ratio (i.e. length/width ratio), Chatterjee36 has used mean field theory to show that the critical volume fraction for the percolation threshold, ϕc, can be estimated using eqn (1):
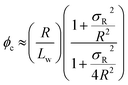 | (1) |
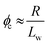 | (2) |
We postulated that the percolation threshold required for the formation of an extended 3D network of inter-connected electrically conductive rods randomly dispersed in an insulating matrix to produce macroscopic electrical conductivity38,39 should be equivalent to that required for formation of a macroscopic physical gel by a colloidal dispersion of rods. Herein, we evaluate to what extent eqn (2) provides a useful description of the gelation behavior observed for two examples of diblock copolymer worms.36,37 For this approach to be valid, gelation should occur as a result of multiple inter-worm contacts (see Scheme 1), which would provide an alternative gelation mechanism to the inter-worm entanglements model previously (and correctly) invoked for surfactant worms. The two diblock copolymer systems studied herein were chosen because they represent relatively long, highly flexible worms25 and relatively short, stiff worms, respectively.40 Thus they represent two limiting copolymer morphologies for which contrasting experimental data might be anticipated.
Results and discussion
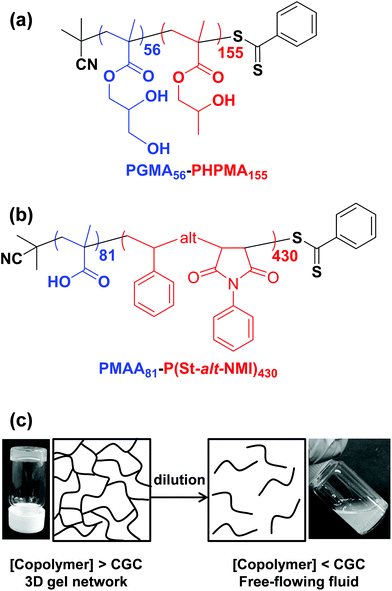
Initially, we sought literature data for colloidal dispersions of rigid rods to support our hypothesis. Recently, Nordenström et al. reported an interesting study of the aqueous gelation behavior of various cellulosic nanorods of varying dimensions and surface charge.41 More specifically, a series of six cellulose nanorods were prepared with varying length/diameter ratios (or aspect ratios) and their (de)gelation behavior was characterized using dynamic light scattering (DLS). The critical volume fraction for gelation was shown to be inversely proportional to the aspect ratio. Furthermore, it was postulated that gelation was simply a result of multiple contacts with neighboring nanorods, which arrests their translational diffusion in solution. However, no specific link was made to the recent mathematical advances developed to describe the percolation behavior of polydisperse rods.36,37 Of the six types of cellulose nanorods reported by Nordenström et al.,41 the most relevant to the present study of neutral worms is that with the lowest surface charge, which had a mean length of 520 nm (determined by DLS) and a mean radius of 3.35 nm (measured by AFM studies). Using eqn (2), we calculate the theoretical percolation volume fraction, ϕc, for such cellulosic nanorods to be 0.0064, which is in reasonably good agreement with the experimental ϕc of 0.0073 reported by Nordenström and co-workers.41 Thus our hypothesis of physical equivalence between the respective critical percolation thresholds required for solid-state electrical conductivity and physical gelation appears to have some merit.The poly(glycerol monomethacrylate)56–poly(2-hydroxypropyl methacrylate)155 [PGMA56–PHPMA155] and poly(methacrylic acid)81–poly(styrene-alt-N-phenylmaleimide)430 [PMAA81–P(St-alt-NMI)430] worm gels evaluated in this study were prepared using PISA as described by Blanazs et al.22 and Yang and co-workers40 respectively (see Scheme 1 for the relevant chemical structures). More specifically, the highly flexible PGMA56–PHPMA155 worms were synthesized via reversible addition–fragmentation chain transfer (RAFT) aqueous dispersion polymerization of 2-hydroxypropyl methacrylate (HPMA), and are clearly highly anisotropic as judged by transmission electron microscopy (TEM, see Fig. 1a). In contrast, the relatively short, stiff PMAA81–P(St-alt-NMI)430 worms were prepared by RAFT dispersion alternating copolymerization of styrene with N-phenylmaleimide using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol/1,4-dioxane mixture. These latter worms are much less anisotropic (see Fig. 1b). In both cases, the diblock copolymer chains possess relatively narrow molecular weight distributions as determined by gel permeation chromatography (GPC) and comparison to their respective macro-CTAs indicates high blocking efficiencies (see Fig. S1†). The mean aspect ratio (i.e. length/width ratio) for each type of worm can be determined using small-angle X-ray scattering (SAXS), as described below.42 TEM analysis confirms that the worm cross-sectional radius is well-defined in both cases. More specifically, the mean core radius, rc, for PGMA56–PHPMA155 and PMAA81–P(St-alt-NMI)430 is estimated to be 11.1 ± 1.3 and 19.2 ± 2.1 nm, respectively.
1 ethanol/1,4-dioxane mixture. These latter worms are much less anisotropic (see Fig. 1b). In both cases, the diblock copolymer chains possess relatively narrow molecular weight distributions as determined by gel permeation chromatography (GPC) and comparison to their respective macro-CTAs indicates high blocking efficiencies (see Fig. S1†). The mean aspect ratio (i.e. length/width ratio) for each type of worm can be determined using small-angle X-ray scattering (SAXS), as described below.42 TEM analysis confirms that the worm cross-sectional radius is well-defined in both cases. More specifically, the mean core radius, rc, for PGMA56–PHPMA155 and PMAA81–P(St-alt-NMI)430 is estimated to be 11.1 ± 1.3 and 19.2 ± 2.1 nm, respectively.
 | ||
| Fig. 1 TEM images obtained for dry dispersions of (a) PGMA56–PHPMA155 and (b) PMAA81–P(St-alt-NMI)430 diblock copolymer worms prepared by PISA. | ||
In contrast, the worm contour length, Lw, is clearly rather ill-defined. This is because such worms are formed via stochastic 1D fusion of multiple spheres during PISA.44 In principle, SAXS is a powerful technique for characterizing block copolymer nano-objects, not least because X-ray scattering is averaged over many millions of particles and hence much more statistically robust than TEM studies.45 Accordingly, SAXS patterns were recorded for the two worm dispersions at 1.0% w/w copolymer concentration, see Fig. 2. Both SAXS patterns exhibit a gradient of approximately −1 at low q, which is indicative of highly anisotropic rods (or worms). Fitting such patterns using an established worm model46 provides detailed and robust structural information, including the weight-average Lw and cross-sectional worm radius R. For example, SAXS indicates an Lw of approximately 1100 nm for PGMA56–PHPMA155 worms, with a corresponding core radius, rc, of 8.5 ± 0.9 nm (see Fig. 2a). However, the highly hydrated stabilizer chains also contribute to the overall effective worm dimensions. Given the mean DP of the PGMA56 chains, the thickness of this additional stabilizer layer is estimated to be 3.6 nm by SAXS analysis. Thus the effective worm cross-sectional radius, R, for these ‘hairy’ PGMA56–PHPMA155 worms is calculated to be 12.1 ± 0.9 nm (see ESI† for calculation details). In contrast, SAXS analysis of the PMAA81–P(St-alt-NMI)430 diblock copolymer worms suggests an Lw of approximately 296 nm (see Fig. 2b). These latter worms have an rc value of 20.0 ± 2.7 nm and a stabilizer thickness of 6.6 nm, giving an overall R value of 26.6 ± 3.0 nm. Hence the mean aspect ratios (or Lw/R values) for the PGMA56–PHPMA155 and PMAA81–P(St-alt-NMI)430 worms are 89 and 11, respectively. These strikingly different aspect ratios are useful in the context of the present study because they enable a more rigorous test of the percolation theory recently developed for polydisperse rods.36,37 Thus, according to eqn (2), the critical percolation volume fraction, ϕc, required to form a 3D gel network comprising PGMA56–PHPMA155 worms is expected to be significantly lower than that required for gelation when using the PMAA81–P(St-alt-NMI)430 worms.
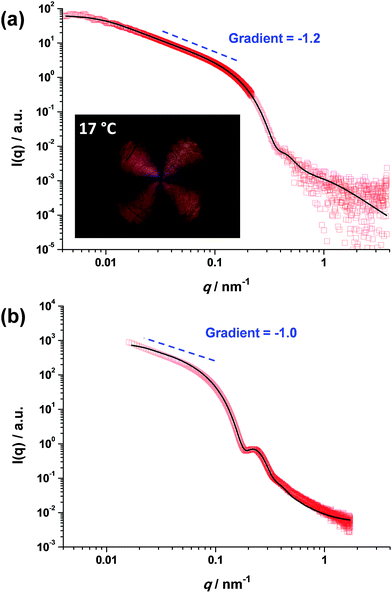 | ||
| Fig. 2 SAXS patterns recorded for 1.0% w/w dispersions of (a) PGMA56–PHPMA155 worms at 18 °C and (b) PMAA81–P(St-alt-NMI)430 worms at 20 °C. Inset in (a) shows a shear-induced polarized light image of the corresponding 5.0% w/w worm dispersion obtained at a maximum shear rate of 20 s−1. The Maltese cross observed is the distinctive signature for birefringence, indicating in situ worm alignment.43 | ||
It is well-known that semi-concentrated dispersions of such PGMA–PHPMA worm gels exhibit thermoresponsive behavior, with degelation occurring on cooling below the critical gelation temperature (CGT) as a result of a worm-to-sphere transition.20,25 When applying percolation theory to such thermosensitive systems, it is important to determine the characteristic temperature that corresponds to long, linear worms (as opposed to branched worms or worm clusters). This is readily achieved using shear-induced polarized light imaging (SIPLI), as recently reported by Mykhaylyk and co-workers.43 Briefly, an aqueous worm dispersion is subjected to applied shear using an opto-rheometer, which enables simultaneous interrogation of the sample using polarized light. The appearance of a distinctive Maltese cross motif indicates shear-induced alignment of the highly anisotropic worms. If such experiments are performed as a function of temperature, the temperature at which the brightest Maltese cross is observed corresponds to the formation of the most linear (i.e. longest) worms. Such measurements are shown in the inset of Fig. 2a and S2† and indicate an optimum temperature of 17 °C, which is very close to that at which the SAXS studies were performed (18 °C). It is noteworthy that the PMAA81–P(St-alt-NMI)430 diblock copolymer worms do not exhibit such thermoresponsive behavior, so the temperature at which SAXS analysis is conducted is not particularly important in this case.
Utilizing the structural information provided by SAXS in combination with eqn (2), the theoretical critical volume fraction (ϕc) required for the percolation threshold (and hence macroscopic gelation) is predicted to be 0.011 ± 0.001 and 0.090 ± 0.009 for the PGMA56–PHPMA155 and PMAA81–P(St-alt-NMI)430 worms, respectively. This approximate eight-fold difference simply reflects the substantial difference in aspect ratio for these two types of worms.
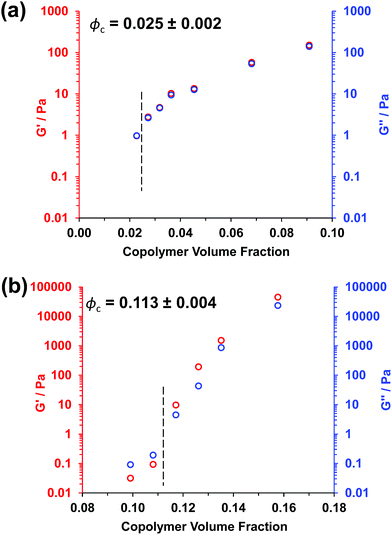
Experimental ϕc values can be estimated from tube inversion tests, which were performed at ambient temperature (17–18 °C) for varying copolymer volume fractions (see Fig. S3† and related calculations). These observations indicated ϕc values of approximately 0.025 ± 0.002 and 0.121 ± 0.004 for the PGMA56–PHPMA155 and PMAA81–P(St-alt-NMI)430 worms, respectively. Very similar ϕc values (0.025 ± 0.002 and 0.113 ± 0.004) were obtained from oscillatory rheology, see Fig. 3. In this case, degelation is indicated by the point of intersection of the storage modulus (G′) and the loss modulus (G′′) curves, and these latter experiments are considered more reliable.
In polymer physics, the worm-like chain model is used to describe the behavior of semi-flexible polymers.47 For such worm-like chains, the Kuhn length is equal to twice the persistence length, where the latter parameter quantifies the chain stiffness. In principle, the behavior of the long, flexible diblock copolymer worms described in our study is analogous to that of an individual polymer chain.48 The Kuhn lengths derived from SAXS studies of both types of worms are included in Table 1. The Kuhn length for the short, stiff worms is simply equal to the weight-average worm contour length (Lw). In contrast, the Kuhn length for the long, flexible worms is much lower than Lw, which implies significant flexibility.
| Anisotropic nanoparticle type | Weight-average worm length, Lw/nm | Worm cross-sectional radius, R/nm | Aspect ratio (Lw/R) | Kuhn length/nm | ϕ c, theorya | ϕ c, experimentb |
|---|---|---|---|---|---|---|
| a Calculated using eqn (2). b Determined by oscillatory rheology. | ||||||
| PGMA56–PHPMA155 worms | 1100 | 12.3 | 89 | 300 | 0.011 | 0.025 |
| PMAA81–P(St-alt-NMI)430 worms | 296 | 26.6 | 11 | 296 | 0.090 | 0.113 |
Clearly, there is some discrepancy between the theoretical and experimental ϕc values summarized in Table 1. However, percolation theory is derived assuming rigid rods, whereas the PGMA56–PHPMA155 worms clearly exhibit significant flexibility (see TEM images in Fig. 1). This necessarily reduces the effective weight-average worm length Lw, which in turn leads to a higher ϕc value. Given this important caveat, the fair agreement observed between the experimental and theoretical ϕc values supports our hypothesis that such worm gels form a 3D network simply via multiple contacts between neighbouring worms. In contrast, the PMAA81–P(St-alt-NMI)430 worms are much stiffer (the glass transition temperature for the core-forming P(St-alt-NMI)430 block is around 208 °C.40 Thus, better agreement between experimental and theoretical ϕc values is expected, and indeed observed.
From Table 1, the theoretical ϕc for stiff worms is approximately eight times greater than that for flexible worms. In contrast, the corresponding experimental ϕc ratio is approximately four. This suggests that eqn (2) can be rewritten as:
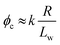 | (3) |
Conclusions
In summary, recent advances in percolation theory for polydisperse rods provide an improved understanding of the gelation behavior exhibited by diblock copolymer worms. Combined with experimental data, this suggests that a 3D gel network forms primarily via multiple contacts between neighbouring worms, rather than as a result of worm entanglements. In view of the growing number of studies utilizing worm-based hydrogels for various biomedical applications,25,49–58 this new physical insight is likely to be important for the design of next-generation diblock copolymer worm gels, as well as the growing literature on block copolymer rods.58–62 Indeed, it seems likely that our findings are also relevant to the growing literature on supramolecular gels composed of amphiphilic small molecules63–71 as well as hydrogels based on cellulose and silica nanorods.41,72–77Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. P. A. is the recipient of a five-year ERC Advanced Investigator grant (PISA 320372). EPSRC is thanked for a Platform grant (EP/J007846/1) and a Particle Technology Fellowship grant (EP/R003009/1). The Leverhulme Trust is thanked for post-doctoral funding of M. J. D. (RPG-2016-330).Notes and references
- M. E. Cates and S. J. Candau, J. Phys.: Condens. Matter, 1990, 2, 6869–6892 CrossRef.
- F. C. MacKintosh, S. A. Safran and P. A. Pincus, Europhys. Lett., 1990, 12, 697–702 CrossRef.
- G. Porte, J. Appell and Y. Poggi, J. Phys. Chem., 1980, 84, 3105–3110 CrossRef.
- Z. Chu, C. A. Dreiss and Y. Feng, Chem. Soc. Rev., 2013, 42, 7174–7203 RSC.
- T. S. Davies, A. M. Ketner and S. R. Raghavan, J. Am. Chem. Soc., 2006, 128, 6669–6675 CrossRef PubMed.
- B. Chase, W. Chmilowski, R. Marcinew, C. Mitchell, Y. Dang, K. Krauss, E. Nelson, T. Lantz, C. Parham and J. Plummer, Oilfield Rev., 1997, 9, 20–33 Search PubMed.
- J. L. Zakin, B. Lu and H.-W. Bewersdorff, Rev. Chem. Eng., 1998, 14, 253–320 Search PubMed.
- J. Yang, Curr. Opin. Colloid Interface Sci., 2002, 7, 276–281 CrossRef.
- N. A. Spenley, M. E. Cates and T. C. B. McLeish, Phys. Rev. Lett., 1993, 71, 939–942 CrossRef PubMed.
- C. A. Dreiss, Soft Matter, 2007, 3, 956–970 RSC.
- H. Rehage and H. Hoffmann, J. Phys. Chem., 1988, 92, 4712–4719 CrossRef.
- M. E. Cates, Macromolecules, 1987, 20, 2289–2296 CrossRef.
- Y.-Y. Won, H. T. Davis and F. S. Bates, Science, 1999, 283, 960–963 CrossRef PubMed.
- X. Zhang, S. Boissé, W. Zhang, P. Beaunier, F. D'Agosto, J. Rieger and B. Charleux, Macromolecules, 2011, 44, 4149–4158 CrossRef.
- Y. W. Pei and A. B. Lowe, Polym. Chem., 2014, 5, 2342–2351 RSC.
- Y. W. Pei, N. C. Dharsana, J. A. Van Hensbergen, R. P. Burford, P. J. Roth and A. B. Lowe, Soft Matter, 2014, 10, 5787–5796 RSC.
- M. Semsarilar, E. R. Jones, A. Blanazs and S. P. Armes, Adv. Mater., 2012, 24, 3378–3382 CrossRef PubMed.
- L. A. Fielding, J. A. Lane, M. J. Derry, O. O. Mykhaylyk and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 5790–5798 CrossRef PubMed.
- L. A. Fielding, M. J. Derry, V. Ladmiral, J. Rosselgong, A. M. Rodrigues, L. P. D. Ratcliffe, S. Sugihara and S. P. Armes, Chem. Sci., 2013, 4, 2081–2087 RSC.
- R. Verber, A. Blanazs and S. P. Armes, Soft Matter, 2012, 8, 9915–9922 RSC.
- S. Boisse, J. Rieger, K. Belal, A. Di-Cicco, P. Beaunier, M.-H. Li and B. Charleux, Chem. Commun., 2010, 46, 1950–1952 RSC.
- A. Blanazs, A. J. Ryan and S. P. Armes, Macromolecules, 2012, 45, 5099–5107 CrossRef.
- Y. Pei, O. R. Sugita, L. Thurairajah and A. B. Lowe, RSC Adv., 2015, 5, 17636–17646 RSC.
- Y. Pei, L. Thurairajah, O. R. Sugita and A. B. Lowe, Macromolecules, 2015, 48, 236–244 CrossRef.
- A. Blanazs, R. Verber, O. O. Mykhaylyk, A. J. Ryan, J. Z. Heath, C. W. I. Douglas and S. P. Armes, J. Am. Chem. Soc., 2012, 134, 9741–9748 CrossRef PubMed.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- A. Blanazs, S. P. Armes and A. J. Ryan, Macromol. Rapid Commun., 2009, 30, 267–277 CrossRef PubMed.
- F. Lux, J. Mater. Sci., 1993, 28, 285–301 CrossRef.
- S. Hotta, S. D. D. V. Rughooputh and A. J. Heeger, Synth. Met., 1987, 22, 79–87 CrossRef.
- B. D. Malhotra, S. Ghosh and R. Chandra, J. Appl. Polym. Sci., 1990, 40, 1049–1052 CrossRef.
- E. C. Cooper and B. Vincent, J. Phys. D: Appl. Phys., 1989, 22, 1580–1585 CrossRef.
- P. Banerjee and B. M. Mandal, Synth. Met., 1995, 74, 257–261 CrossRef.
- C. Y. Yang, Y. Cao, P. Smith and A. J. Heeger, Synth. Met., 1993, 53, 293–301 CrossRef.
- J. Sandler, M. S. P. Shaffer, T. Prasse, W. Bauhofer, K. Schulte and A. H. Windle, Polymer, 1999, 40, 5967–5971 CrossRef.
- J. K. W. Sandler, J. E. Kirk, I. A. Kinloch, M. S. P. Shaffer and A. H. Windle, Polymer, 2003, 44, 5893–5899 CrossRef.
- A. P. Chatterjee, J. Chem. Phys., 2010, 132, 224905 CrossRef PubMed.
- R. H. J. Otten and d. S. P. van, J. Chem. Phys., 2011, 134, 094902 CrossRef PubMed.
- T. Komori and K. Makishima, Text. Res. J., 1977, 47, 13–17 CrossRef.
- V. Kumar and A. Rawal, Polymer, 2016, 97, 295–299 CrossRef.
- P. Yang, L. P. D. Ratcliffe and S. P. Armes, Macromolecules, 2013, 46, 8545–8556 CrossRef.
- M. Nordenström, A. Fall, G. Nyström and L. Wågberg, Langmuir, 2017, 33, 9772–9780 CrossRef PubMed.
- Strictly speaking, SAXS reports the volume-average dimensions of nano-objects. Hence the volume-average worm length Lv is directly related to the weight-average worm length Lw by the worm density. Moreover, given that the worm cross-sectional radius R is narrowly distributed, the volume-average (and weight-average) radius lies close to the number-average value.
- O. O. Mykhaylyk, N. J. Warren, A. J. Parnell, G. Pfeifer and J. Laeuger, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 2151–2170 CrossRef.
- N. J. Warren and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 10174–10185 CrossRef PubMed.
- H. Schnablegger and Y. Singh, The SAXS Guide, Anton Paar GmbH, Austria, 2011 Search PubMed.
- J. S. Pedersen, J. Appl. Crystallogr., 2000, 33, 637–640 CrossRef.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1988 Search PubMed.
- W. J. Zhang, B. Charleux and P. Cassagnau, Soft Matter, 2013, 9, 2197–2205 RSC.
- K. A. Simon, N. J. Warren, B. Mosadegh, M. R. Mohammady, G. M. Whitesides and S. P. Armes, Biomacromolecules, 2015, 16, 3952–3958 CrossRef PubMed.
- I. Canton, N. J. Warren, A. Chahal, K. Amps, A. Wood, R. Weightman, E. Wang, H. Moore and S. P. Armes, ACS Cent. Sci., 2016, 2, 65–74 CrossRef PubMed.
- D. E. Mitchell, J. R. Lovett, S. P. Armes and M. I. Gibson, Angew. Chem., Int. Ed., 2016, 55, 2801–2804 CrossRef PubMed.
- Y. Li, N. Khuu, A. Gevorkian, S. Sarjinsky, H. Therien-Aubin, Y. Wang, S. Cho and E. Kumacheva, Angew. Chem., 2017, 56, 6083–6087 CrossRef PubMed.
- S. Cho, Y. Li, M. Seo and E. Kumacheva, Angew. Chem., Int. Ed., 2016, 55, 14014–14018 CrossRef PubMed.
- D. Velasco, M. Chau, H. Therien-Aubin, A. Kumachev, E. Tumarkin, Z. Jia, G. C. Walker, M. J. Monteiro and E. Kumacheva, Soft Matter, 2013, 9, 2380–2383 RSC.
- H. Thérien-Aubin, Y. Wang, K. Nothdurft, E. Prince, S. Cho and E. Kumacheva, Biomacromolecules, 2016, 17, 3244–3251 CrossRef PubMed.
- K. Younghoon, D. Paul, A. C. David and E. D. Dennis, Nanotechnology, 2005, 16, 484–491 CrossRef.
- P. Dalhaimer, F. S. Bates and D. E. Discher, Macromolecules, 2003, 36, 6873–6877 CrossRef.
- P. H. J. Kouwer, M. Koepf, V. A. A. Le Sage, M. Jaspers, A. M. van Buul, Z. H. Eksteen-Akeroyd, T. Woltinge, E. Schwartz, H. J. Kitto, R. Hoogenboom, S. J. Picken, R. J. M. Nolte, E. Mendes and A. E. Rowan, Nature, 2013, 493, 651–655 CrossRef PubMed.
- J. B. Gilroy, T. Gadt, G. R. Whittell, L. Chabanne, J. M. Mitchels, R. M. Richardson, M. A. Winnik and I. Manners, Nat. Chem., 2010, 2, 566–570 CrossRef PubMed.
- J. A. Massey, K. Temple, L. Cao, Y. Rharbi, J. Raez, M. A. Winnik and I. Manners, J. Am. Chem. Soc., 2000, 122, 11577–11584 CrossRef.
- S. K. Patra, R. Ahmed, G. R. Whittell, D. J. Lunn, E. L. Dunphy, M. A. Winnik and I. Manners, J. Am. Chem. Soc., 2011, 133, 8842–8845 CrossRef PubMed.
- P. A. Rupar, L. Chabanne, M. A. Winnik and I. Manners, Science, 2012, 337, 559–562 CrossRef PubMed.
- L. E. Buerkle and S. J. Rowan, Chem. Soc. Rev., 2012, 41, 6089–6102 RSC.
- D. J. Adams and P. D. Topham, Soft Matter, 2010, 6, 3707–3721 RSC.
- R. J. Wojtecki, M. A. Meador and S. J. Rowan, Nat. Mater., 2011, 10, 14–27 CrossRef PubMed.
- B. O. Okesola and D. K. Smith, Chem. Soc. Rev., 2016, 45, 4226–4251 RSC.
- A. R. Hirst, I. A. Coates, T. R. Boucheteau, J. F. Miravet, B. Escuder, V. Castelletto, I. W. Hamley and D. K. Smith, J. Am. Chem. Soc., 2008, 130, 9113–9121 CrossRef PubMed.
- A. R. Hirst, B. Escuder, J. F. Miravet and D. K. Smith, Angew. Chem., Int. Ed., 2008, 47, 8002–8018 CrossRef PubMed.
- M. Zelzer and R. V. Ulijn, Chem. Soc. Rev., 2010, 39, 3351–3357 RSC.
- S. Fleming and R. V. Ulijn, Chem. Soc. Rev., 2014, 43, 8150–8177 RSC.
- V. Jayawarna, M. Ali, T. A. Jowitt, A. F. Miller, A. Saiani, J. E. Gough and R. V. Ulijn, Adv. Mater., 2006, 18, 611–614 CrossRef.
- K. R. Peddireddy, I. Capron, T. Nicolai and L. Benyahia, Biomacromolecules, 2016, 17, 3298–3304 CrossRef PubMed.
- M. C. Li, Q. L. Wu, K. L. Song, S. Lee, Y. Qing and Y. Q. Wu, ACS Sustainable Chem. Eng., 2015, 3, 821–832 CrossRef.
- A. E. Way, L. Hsu, K. Shanmuganathan, C. Weder and S. J. Rowan, ACS Macro Lett., 2012, 1, 1001–1006 CrossRef.
- T. Saito, T. Uematsu, S. Kimura, T. Enomae and A. Isogai, Soft Matter, 2011, 7, 8804–8809 RSC.
- C. Zhou, Q. Wu, Y. Yue and Q. Zhang, J. Colloid Interface Sci., 2011, 353, 116–123 CrossRef PubMed.
- R. P. Murphy, K. Hong and N. J. Wagner, Langmuir, 2016, 32, 8424–8435 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental details including synthesis and characterisation of diblock copolymers; GPC chromatograms; SIPLI images; digital images of tube inversion test; calculations for effective worm density, worm cross-sectional radius and volume fraction. See DOI: 10.1039/c8sc02406e |
| This journal is © The Royal Society of Chemistry 2018 |