Open Access Article
Open Access ArticleCyclic tris-[5]helicenes with single and triple twisted Möbius topologies and Möbius aromaticity†
Guillaume
Naulet
a,
Ludmilla
Sturm
a,
Antoine
Robert
a,
Pierre
Dechambenoit
a,
Fynn
Röhricht
b,
Rainer
Herges
 *b,
Harald
Bock
a and
Fabien
Durola
*b,
Harald
Bock
a and
Fabien
Durola
 *a
*a
aCentre de Recherche Paul Pascal, CNRS, Université de Bordeaux, 115 av. Schweitzer, 33600 Pessac, France. E-mail: durola@crpp-bordeaux.cnrs.fr
bOtto-Diels-Institut für Organische Chemie, Christian-Albrechts-Universität Kiel, Kiel 24119, Germany. E-mail: rherges@oc.uni-kiel.de
First published on 16th November 2018
Abstract
A number of singly (180°) twisted, largely single-stranded and thus conformationally rather fragile, Möbius molecules have been synthesized within the last 15 years, which are aromatic with 4n electrons, thus violating the Hückel rule. Annulenes with significantly higher twist (e.g. 540°) that retain a full cyclic conjugation path have been elusive, mainly because of the high strain and loss of orbital overlap. Recently, a topological strategy was devised to project the “twist” into “writhe”, thus reducing the strain. However, orbital overlap was still severely reduced within the flexible building blocks. We now present a single and a triple twisted annulene with fully conjugated peripheries. They are unique in their pronounced band shape and conformational robustness as they are made up of three fully kata-condensed [5]helicene fragments. The triple twisted molecule exhibits a strong diatropic ring current in the outer periphery, even though the π system includes 4n electrons. The diatropic current is counterbalanced by a paratropic current in the σ system, resulting in no net manifestation of macrocyclic aromaticity. The key step of the synthesis of both Möbius compounds is a Perkin condensation of complementary bifunctional bismaleates leading to a flexible macrocycle containing alternating benzene and biphenyl fragments. Subsequent photocyclization yields a separable mixture of rigid diastereomeric tris-helicene macrocycles of the above topologies.
Introduction
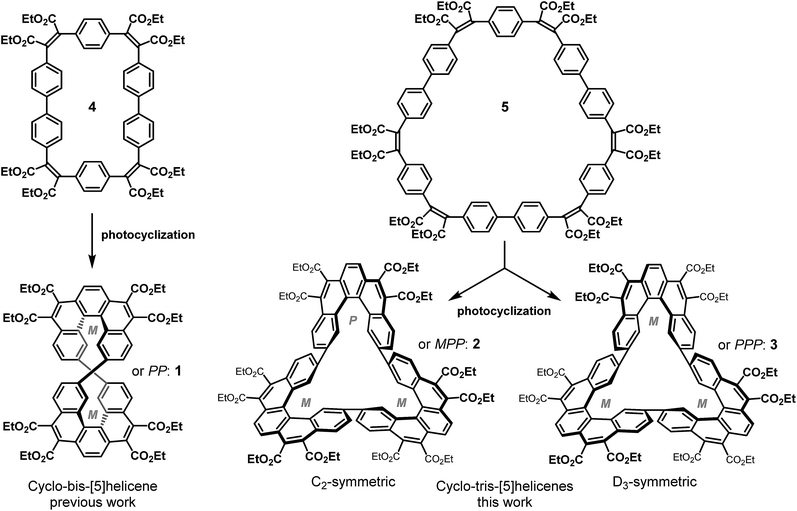
According to the Hückel rule, annulenes are aromatic with 4n + 2 electrons and antiaromatic with 4n electrons delocalized in a cyclic topology.1,2 Heilbronner in 1964 predicted that the Hückel rule should be reversed in Möbius annulenes.3 The latter structures can be envisioned by formally cutting a bond in a “normal” annulene, giving one end a 180° twist, and rejoining both ends. Möbius annulenes were predicted to be aromatic with 4n electrons and antiaromatic with 4n + 2 electrons. Heilbronner further pointed out that the severe strain induced by the twist should decrease at ring sizes >20. It took 40 years until the first Möbius annulene was synthesized, and Heilbronners electron count rules were experimentally confirmed.4–6 Within the last 15 years a number of 4n electron aromatic Möbius annulenes with a 180° twist were prepared. The majority of these systems are extended porphyrins.7 Heilbronner's electron count rules should also formally hold for higher twisted systems, or more precisely, for any annulene with an odd number of twists (n·180°, n = 1, 3, 5…). However, the severe strain induced by multiple twists is expected to prevent synthesis or at least should drastically reduce overlap between neighbouring p orbitals. We recently pointed out that there are strategies to overcome these problems.6,8,9 The decisive topological parameter determining aromaticity is not the number of twists Tw, but the linking number Lk.10 Hückel systems have an even linking number (Lk = 0, 2, 4…) and Möbius objects exibit an odd linking number (Lk = 1, 3, 5…). Tw and Lk are connected by Calugareanu's theorem: Lk = Tw + Wr (Wr = writhe).11 Besides the precise mathematical definition, Calugareanu's theorem can be demonstrated by an everyday life experiment. If a band e.g. a two-core power cord is twisted and both ends are joined, the band would wind around itself. Thus, the strain induced by the twists Tw is released, and projected into writhe Wr without changing the linking number Lk. Similar arguments hold for molecules. The topological transformation can be used as a strategy to reduce strain, while keeping the topological parameter Lk constant. We recently used this strategy to synthesize the first triply twisted Möbius annulene.8 Unfortunately, the building block diethynyl-binaphthalene is too flexible to provide a smooth distribution of dihedral angles along the periphery of the annulene and the conjugation was interrupted by torsional angles close to 90°. We now present the synthesis of a triple twisted annulene (540°) with small dihedral angles, and thus retaining full conjugation, and a diatropic ring current within the twisted π system in the periphery.In the last five years, we have developed an efficient and versatile synthetic approach for the formation of large carboxy-substituted polycyclic arenes. It relies on Perkin reactions that yield flexible diarylmaleate-type precursors, followed by catalyst- or light-induced cyclization reactions.12,13 This synthetic method has shown considerable potential for the construction of double helicenes14,15 as well for as the formation of large conjugated macrocycles.16,17 Recently, we have combined these two structural elements in a Perkin-assembled propeller-shaped macrocycle that incorporates two identical [5]helicene fragments.18 This dimeric cyclo-bis-[5]helicene 1 has been obtained as a racemic mixture of two enantiomers whose helicene fragments have identical helicity: PP or MM. The PM (meso) compound has not been observed, which is in line with the extreme distortion of its simulated structure.
This article presents the synthesis and study of trimeric homologs of macrocycle 1: the C2-symmetric cyclo-tris-[5]helicenes 2 (MPP and PMM configurations), and the D3-symmetric cyclo-tris-[5]helicenes 3 (PPP and MMM configurations) which are diastereomers and have been obtained as racemic mixtures (Scheme 1). In contrast to the dimeric case (the non-observed meso isomer of 1), three helicenes of different helicity can be cyclically linked without generating much distortion, thus both possible diastereomers are formed. In both of these two rigid conjugated macrocycles, the adjacent terminal benzene rings at the interhelicene bonds are essentially coplanar, leading to an overall Möbius band geometry of π electron systems of both macrocycles. The C2-symmetric isomer has the geometry of a simple (singly twisted) Möbius band, whereas the D3-symmetric isomer has the geometry of a triply twisted Möbius band.
Results and discussion
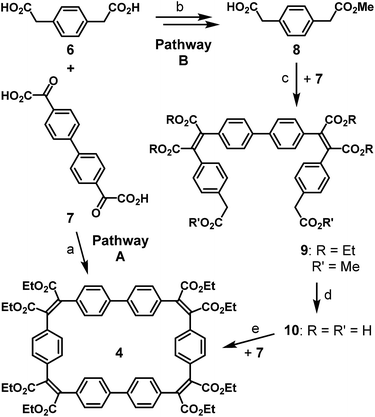
The Perkin condensation of bifunctional arylene–diglyoxylic acids with bifunctional arylene–diacetic acids leads with surprisingly good size-selectivities and yields to the 2 + 2 macrocyclic products, where four arylene moieties are connected by four maleic bridges. This approach has been used in the reported synthesis18 of the four-block flexible macrocycle 4 (Scheme 2, pathway A), with a moderate yield of 21%, precursor of the cyclic dimer of [5]helicene 1 (Scheme 1). Aiming at the formation of the trimeric counterparts 2 and 3 of the latter, the synthetic strategy based on the Perkin reaction involves one common macrocyclic intermediate 5 made of six building blocks: three 1,4-phenylenediacetic acid units 6 and three 4,4′-bis(phenylglyoxylic acid) units 7. The formation of a six-block macrocycle by Perkin reaction from bifunctional simple building blocks has been observed only once, as a minor side product of a four-block macrocycle composed exclusively of biphenyl units.18 A stepwise procedure is therefore necessary for the controlled synthesis of large six-block macrocycles by Perkin reaction. We focused on the combination of two complimentary linear bifunctional three-block intermediates (3 + 3 approach), which is more convergent than a 5 + 1 approach and synthetically simpler than a 4 + 2 approach due to the symmetry of the precursors.We have recently reported the synthesis of three-block linear intermediates, bearing two acetic acid functions at their extremities for the formation of long phenacenes.17 The same synthetic strategy has been applied to the diacetic and diglyoxylic building blocks 6 and 7 in the synthesis of the three-block diacetic precursor 10. 1,4-Phenylenediacetic acid 6 was first fully esterified in presence of methanol and SOCl2 to give dimethyl 1,4-phenylenediacetic ester,19 which was then partially saponified with one equivalent of potassium hydroxide. The resulting mixture of remaining diester, diacetate and monoacetate monoester compounds was separated by selective pH-dependant solid–liquid extractions to finally give pure mono-protected phenylene diacetic acid 8. The yield of this mono-deprotection reaction is satisfying (47%) as it can be carried out on a large scale (10 g) without complicated purification and 48% of the starting compound is recovered separately as diacid or diester. Mono-protected phenylene diacetic acid 8 reacted twice with diglyoxylic acid 7 by Perkin reaction to afford the three-block hexaester 9 in good yield (65%), and then full saponification by treatment with potassium hydroxide quantitatively formed the three-block diacetic acid precursor 10. To verify its reactivity in the formation of macrocycles, it has been combined with the diglyoxylic building block 7 (Scheme 2, pathway B) by Perkin reaction in high dilution conditions to form the four-block macrocycle 4 with an improved yield of 55%, compared to 21% when single building blocks 6 and 7 are mixed under the same reaction conditions (Scheme 2, pathway A).18
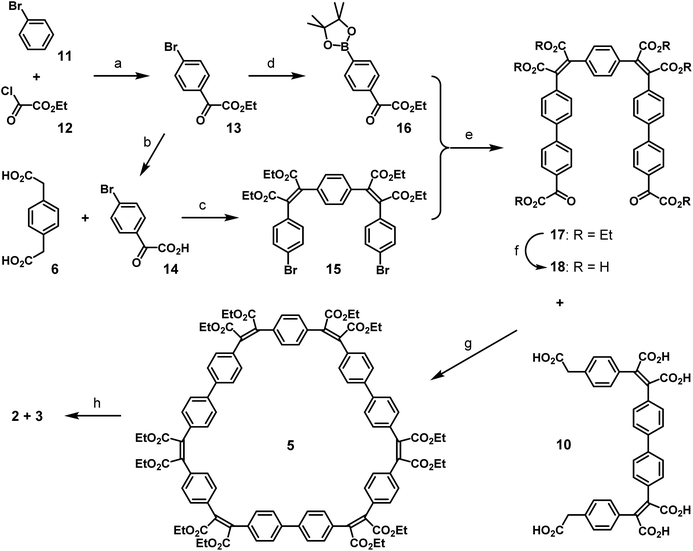
The mono-protection of arylene-diglyoxylic acids for the Perkin reaction not yet having been developed, a different synthetic approach was pursued for the complimentary three-block diglyoxylic precursor 18 (Scheme 3). In biphenyl-based species, the central sigma C–C bond can easily be formed by usual palladium-catalyzed coupling reactions between adequately functionalized aryl fragments. Thus bromobenzene 11 was first functionalized with one glyoxylic ester function by a Friedel–Crafts reaction with ethyl oxalyl chloride 12 as an electrophile in presence of AlCl3 following a recently reported procedure.20 The glyoxylic ester function of the resulting ester 13 was saponified efficiently by treatment with sodium hydrogen carbonate and the resulting para-brominated phenylglyoxylic acid 14 reacted then twice with 1,4-phenylenediacetic acid 6 in Perkin conditions to give the dibrominated bis-maleate precursor 15 with a very good yield (83%). In parallel, para-brominated phenylglyoxylic ester 13 was transformed into the corresponding boronic ester 16 by palladium-catalyzed substitution of the bromo-substituent in presence of bis(pinacolato)diboron. In spite of non-removable traces of pinacol in the latter, it was coupled twice to the dibrominated bis-maleate precursor 15 by a double Suzuki reaction with Pd(PPh3)4 as a catalyst. The resulting bis-maleate hexaester 17 was obtained with a modest yield (45%) for this usually efficient reaction, because of partial saponification of the product in basic conditions, even in the absence of water. Full saponification of the hexa-ester 17 quantitatively afforded the three-block diglyoxylic acid precursor 18.
The two three-block diacetic 10 and diglyoxylic 18 precursors were then coupled together by double Perkin reaction to form the six-block flexible conjugated macrocycle 5. High dilution conditions were not used, because of the low solubility of compound 18, but the cyclic product 5 was obtained with a very satisfying macrocyclization yield of 28%, after a difficult purification process. Irradiation of a 0.07 mM solution of 5 in ethyl acetate in the presence of iodine and oxygen for two days with pyrex-filtered light from a medium pressure mercury lamp afforded a mixture of the two cyclo-tris-[5]helicenes 2 and 3 with an average yield of 40%. 1H-NMR analysis of this mixture revealed that these two rigid macrocycles are present in near-equal proportions. In spite of their structural differences, compounds 2 and 3 could not be separated by chromatography, but recrystallization of this mixture in a large amount of ethanol surprisingly afforded crystals of pure racemic C2-symmetric cyclo-tris-[5]helicene 2, and further purification of the remaining product in the mother liquor gave pure racemic D3-symmetric cyclo-tris-[5]helicene 3, in 18% yield each. Racemic crystals suitable for X-ray structure determination (Fig. 1) where obtained by slow diffusion of methanol into a chloroform solution in the case of 2, and by slow diffusion of cyclohexane into a toluene solution in the case of 3.
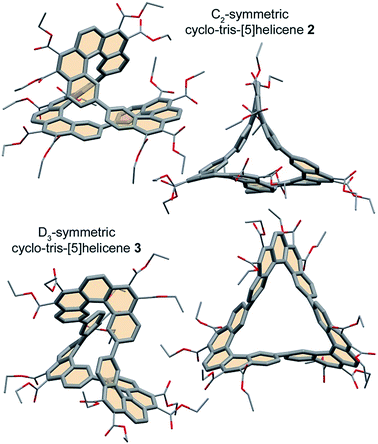 | ||
| Fig. 1 Crystal structures of cyclo-tris-[5]helicenes 2 and 3 (PMM and MMM represented respectively). | ||
Whereas the dimeric homolog 1 did not show any evidence of coplanarity and thus of conjugation between the two helicenes, the crystal structures of the trimers show that the two linked benzene rings of adjacent helicenes are almost coplanar. In these conditions, the conjugated π electron systems of these rigid macrocycles have persistent shapes of cyclic twisted ribbons.
A first evidence of the conjugation between the three helicenes composing the cyclo-tris-[5]helicenes 2 and 3 has been obtained from their optical absorption. The cyclo-bis-[5]helicene 1 was expected not to exhibit any conjugation between its two parts due to a lack of coplanarity at the junctions between helicenes. This was confirmed by the absorption spectra, where this cyclic dimer of ester-substituted [5]helicenes behaved approximately like two independent ester-substituted [5]helicenes21 (Fig. 2). In contrast, trimeric cyclo-tris-[5]helicenes 2 and 3 show a significantly modified absorption profile compared to the single [5]helicene.
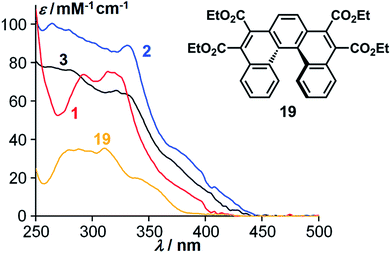 | ||
| Fig. 2 Absorption spectra of a single [5]helicene tetraester 19 (yellow) and of the corresponding cyclic dimer 1 (red) and trimers 2 (blue) and 3 (black). | ||
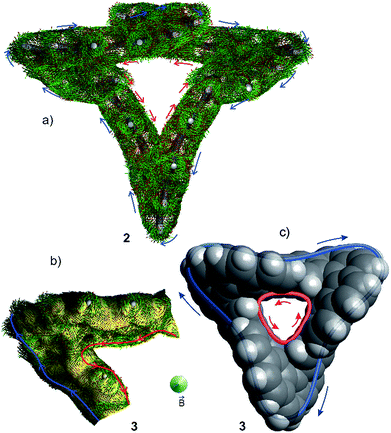
For a closer inspection of the topology of 2 and 3, we used our program ANEWWRITHM22 and determined the topological parameters Lk, Tw and Wr. Since both annulenes are not single stranded, there are different conjugation pathways that can be defined within the cyclic π system. We distinguish between the inner cyclic pathway with 24 π electrons (red line) and the outer pathway with 48 π electrons (blue line, Fig. 3). Thus, both conjugation pathways exhibit 4n π electrons. In Fig. 3cyclo-tris-[5]helicenes are represented as topologically stretched 2D projections (2′ and 3′), as well as with their native 3D geometry (2 and 3). The stretched representation is easier to conceive, and it reveals that 2 is singly twisted and 3 is triply twisted. Cyclo-helicene 2 is composed of two helicene units of like helicity, and one unit with opposite helicity. In terms of the stretched representation, the opposite twists cancel, and a singly twisted Möbius ribbon results. The helicities of the three helicene units in 3 are equal, and the twists add up to a triply twisted Möbius band. Note that the term “twist” has different meanings in the general English language and in topology. In the following we use the topological twist (as defined in the Calugeanou theorem: Lk = Tw + Wr) in combination with the symbol Tw. The topologically stretched geometries would be highly strained, and exhibit reduced overlap between neighbouring p orbitals. In the native geometry large part of the twist Tw is projected into writhe Wr by folding into a 3D geometry (Fig. 3). This topological transformation is obviously more efficient in 3 than in 2. Surprisingly, the triply twisted 3 is 5.8 kcal mol−1 more stable than its singly twisted isomer 2. However, if dispersion is included (D3 method, see ESI†) the relative energies are reverse. Obviously, singly twisted 2 is more densely packed which leads to stabilization by an increased intramolecular dispersion interaction. The inner (red) and outer (blue) conjugation pathways in both cyclo-tris-[5]helicenes 2 and 3 exhibit odd linking numbers Lk (Möbius topology) however, they have different linking numbers Lk in the same molecule (Fig. 3).
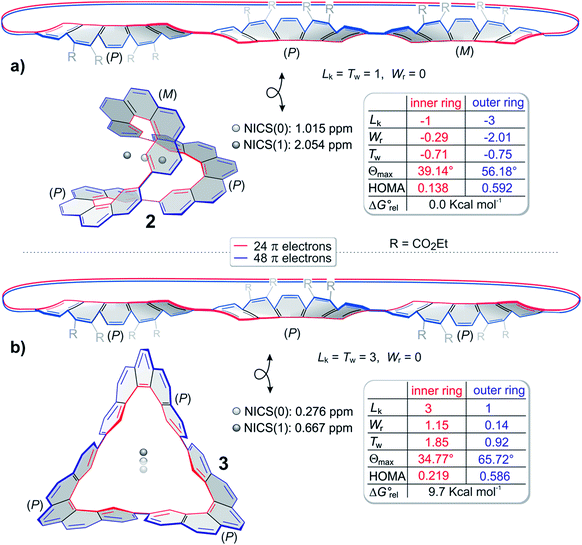 | ||
| Fig. 3 Topologies and aromaticity parameters of cyclo-tris-[5]helicenes 2 and 3. Geometries are optimized at the B3LYP/6-31G* level of density functional theory. The ester substituents are omitted for clarity. The topological parameters Lk, Wr and Tw are calculated with the program ANEWWRITHM.22 The looped double headed arrows define that both objects are topologically equivalent (homeomorphic). (a) top and (b) top: cyclo-tris-helicene 2 and 3 in topological stretched, writhe-free (Wr = 0) representations. In these forms the linking numbers Lk equal the twists Tw. (a) bottom and (b) bottom: 3D structures of 2 and 3. In these “relaxed” structures a considerable part of the twist Tw is projected into writhe Wr. The topological parameters are given for the inner (red) and the outer conjugation path (blue). θmax is the largest dihedral angle between neighboring carbon atoms, and thus is a measure of the conjugation. Note that enantiomers have the same topological parameters, albeit with opposite algebraic sign, and inner and outer periphery exhibit different linking numbers Lk. Erel are the relative energies of 2 and 3 at the B3LYP/6-31G* level of DFT. NICS values are calculated at the B3LYP/6-31G* level of DFT using the GIAO method.23 NICS(0) was calculated at the center of gravity of molecules 2 and 3. NICS(1) was calculated in a distance of 1 Å on an axis dissecting the center of gravity. In structure 3 the axis is identical to the C2 axis, and in 2 the axis is orthogonal to the largest enclosed area obtained by all conceivable 2D projections (relative orientation of the molecule and the magnetic field leading to the largest ring current). HOMA values were calculated for the inner and outer periphery according to the published method.24 | ||
Since the conjugation pathways in 2 and 3 include 4n electrons, and exhibit odd linking numbers Lk, they should be Möbius aromatic. ACID (anisotropy of the induced current density)25–27 calculations reveal that the situation is more complicated. Similar to the paragon of aromatic compounds benzene, Möbius compound 3 exhibits a diatropic ring current in the outer π system, and a paratropic current in the inner σ system.26,28 In 3 these currents cancel, and almost no net ring current results (Fig. 4).29 In benzene the paratropic current is located within the ring plane, and there are two maximum diatropic ring currents approximately 1 Å above and underneath the ring plane (along the two paths with the highest π electron density).30,31 In the triply twisted Möbius molecule 3, however, the current follows a path mainly restricted to outer part of the molecule, changing the side of the π system three times.32 As a consequence of the inner paratropic ring current in the σ system, the six inner protons (8.88 ppm) are deshielded by 0.58 ppm as compared to the corresponding two protons in the [5]helicene building block 19. The diatropic ring current in the outer periphery (blue) does not induce a strong shift of the remaining 18 protons, because they are not located in the range of the induced magnetic field. Similar arguments hold for the singly twisted Möbius compound 2. There is a diatropic ring current in the periphery and a paratropic current in the σ system in the inner conjugation path (Fig. 3). NICS values23 calculated for Möbius structures 2 and 3 are close to zero (Fig. 3) and corroborate the fact that diatropic and paratropic ring currents almost cancel. Also in agreement with our ACID analysis are the bond length analyses of 2 and 3 using the HOMA method.24 For both Möbius compounds, the HOMA values are considerably larger in the periphery (diatropic, aromatic) than in the inner conjugation path (paratropic, antiaromatic) (see Fig. 3a and b). The C–C bonds connecting the [5]helicene units in 2 and 3 exhibit a bond length of 1.48–1.49 Å which is considerably longer than the bond length in the prototypic aromatic molecule benzene (∼1.40 Å). Upon distortion of D6h benzene towards a D3h 1,3,5-hexatriene structure with alternating C–C bond lengths of 1.553 Å and 1.337 Å, benzene retains 72% of its diatropic ring current.33 We conclude that a corresponding bond length elongation by 0.01 Å in 2 and 3 does not significantly reduce the ring currents.
Conclusions
Highly twisted annulenes have been considered as very challenging targets because of the severe strain and weak π overlap induced by the twist. In contrast to this intuitive conclusion, we prove that even a triple twisted Möbius annulene with a 540° twist in its π system, is easily accessible by standard chemical synthesis. Within the inner and the outer conjugation path of the triply twisted system, no torsional angle between neighbouring p orbitals is larger than 35° and 66°. So, conjugation is still efficient. All conjugation pathways include 4n electrons and an odd linking number Lk. Hence, they should be Möbius aromatic. A detailed ring current analysis reveals that a paratropic current is induced in the inner σ system, and a diatropic current in the outer π periphery, which almost cancel. The surprisingly low strain and considerable π overlap is due to a topological transformation of twist into writhe by folding of the Möbius ring into a 3D structure, a process which is similar to the supercoiling of DNA.34 Annulenes with chiral π systems are interesting from another point of view. Theoretical calculations predict that upon irradiation with a strong laser pulse (even in the absence of a magnetic field), ring currents should be induced which are orders of magnitude larger than the currents induced in a superconducting NMR magnet.35,36 Moreover, peculiar nonlinear optical37 and two photon absorption properties38 have been predicted for Möbius annulenes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding by the Agence Nationale de la Recherche (13-JS07-0009-01) and the German Research Foundation (SFB677) are gratefully acknowledged.Notes and references
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef.
- E. Hückel, Z. Phys., 1932, 76, 628–648 CrossRef.
- E. Heilbronner and E. Hückel, Tetrahedron Lett., 1964, 29, 1923–1928 CrossRef.
- D. Ajami, O. Oeckler, A. Simon and R. Herges, Nature, 2003, 426, 819–821 CrossRef CAS PubMed.
- D. Ajami, K. Hess, F. Köhler, C. Näther, O. Oeckler, A. Simon, C. Yamamoto, Y. Okamoto and R. Herges, Chem.–Eur. J., 2006, 12, 5434–5445 CrossRef CAS PubMed.
- R. Herges, Chem. Rev., 2006, 106, 4820–4842 CrossRef CAS PubMed.
- T. Tanaka and A. Osuka, Chem. Rev., 2017, 117, 2584–2640 CrossRef CAS PubMed.
- G. R. Schaller, F. Topić, K. Rissanen, Y. Okamoto, J. Shen and R. Herges, Nat. Chem., 2014, 6, 608–613 CrossRef CAS PubMed.
- S. M. Rappaport and H. S. Rzepa, J. Am. Chem. Soc., 2007, 130, 7613–7619 CrossRef PubMed.
- P. W. Fowler and H. S. Rzepa, Phys. Chem. Chem. Phys., 2006, 8, 1775–1777 RSC.
- G. Calugareanu, Czech. Math. J., 1961, 11, 588–625 Search PubMed.
- P. Sarkar, F. Durola and H. Bock, Chem. Commun., 2013, 49, 7552–7554 RSC.
- T. S. Moreira, M. Ferreira, A. Dall'armellina, R. Cristiano, H. Gallardo, E. A. Hillard, H. Bock and F. Durola, Eur. J. Org. Chem., 2017, 4548–4551 CrossRef CAS.
- H. Bock, S. Huet, P. Dechambenoit, E. A. Hillard and F. Durola, Eur. J. Org. Chem., 2015, 1033–1039 CrossRef CAS.
- M. Ferreira, G. Naulet, H. Gallardo, P. Dechambenoit, H. Bock and F. Durola, Angew. Chem., Int. Ed., 2017, 56, 3379–3382 CrossRef CAS PubMed.
- A. Robert, P. Dechambenoit, H. Bock and F. Durola, Can. J. Chem., 2017, 95, 450–453 CrossRef CAS.
- G. Naulet, A. Robert, P. Dechambenoit, H. Bock and F. Durola, Eur. J. Org. Chem., 2018, 619–626 CrossRef CAS.
- A. Robert, P. Dechambenoit, E. A. Hillard, H. Bock and F. Durola, Chem. Commun., 2017, 53, 11540–11543 RSC.
- M. Neeb, C. Hohn, F. R. Ehrmann, A. Härtsch, A. Heine, F. Diederich and G. Klebe, Bioorg. Med. Chem., 2016, 24, 4900–4910 CrossRef.
- M. Sasikumar, D. Bharath, G. S. Kumar, N. R. Chereddy, S. Chithiravel, K. Krishnamoorthy, B. Shanigaram, K. Bhanuprakash and V. J. Rao, Synth. Met., 2016, 220, 236–246 CrossRef CAS.
- M. G. Belarmino Cabral, D. Pereira de Oliveira Santos, R. Cristiano, H. Gallardo, A. Bentaleb, E. A. Hillard, F. Durola and H. Bock, ChemPlusChem, 2017, 82, 342–346 CrossRef CAS.
- F. Köhler, Dissertation, University of Kiel, 2008 CrossRef CASThe algorithm is based is based on a method developed by K. Klenin and J. Langowski, Biopolymers, 2000, 54, 307–317 CrossRef CAS.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1420 CrossRef CAS.
- R. Herges and D. Geuenich, J. Phys. Chem. A, 2001, 105, 3214–3220 CrossRef CAS.
- D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772 CrossRef CAS PubMed.
- R. Herges, Magnetic Properties of aromatic compounds and aromatic transition states, in The Chemical Bond : Chemical Bonding Across the Periodic Table, ed. G. Frenking and S. Shaik, Wiley-VCH-Verlag, 2014 Search PubMed.
- E. Steiner and P. W. Fowler, Int. J. Quantum Chem., 1995, 60, 609–616 CrossRef.
- A partial cancelling of the paratropic and diatropic ring current is also observed in benzene, explaining the rather small downfield shift of the protons in benzene as compared to hexatriene: S. Pelloni, A. Ligabue and P. Lazzaretti, Org. Lett., 2004, 6, 4451–4454 CrossRef CAS PubMed.
- J. S. Waugh and R. W. Fessenden, J. Am. Chem. Soc., 1957, 79, 846–849 CrossRef CAS.
- C. E. Johnson and F. A. Bovey, J. Chem. Phys., 1958, 29, 1012–1014 CrossRef CAS.
- Note that the ring currents don't exhibit a topology because they are not bands with two edges.
- D. E. Bean and P. W. Fowler, J. Phys. Chem. A, 2011, 115, 13649–13656 CrossRef CAS PubMed.
- O. M. J. Lilley, Biochem. Soc. Trans., 1986, 14, 489–493 CrossRef.
- I. Barth, J. Manz, Y. Shigeta and K. Yagi, J. Am. Chem. Soc., 2006, 128, 7043–7049 CrossRef CAS PubMed.
- H. Mineo and Y. Fujimura, J. Phys. Chem. Lett., 2017, 8, 2019–2025 CrossRef CAS PubMed.
- Z. S. Yoon, J. H. Kwon, M.-C. Yoon, M. K. Koh, S. B. Noh, J. L. Sessler, J. T. Lee, D. Seidel, A. Aguilar, S. Shimizu, M. Suzuki, A. Osuka and D. Kim, J. Am. Chem. Soc., 2006, 128, 14128–14134 CrossRef CAS PubMed.
- V. Kundi, M. M. Alam and P. P. Thankachan, Phys. Chem. Chem. Phys., 2015, 17, 6827–6833 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures, NMR spectra, 2D NMR spectra, single crystal X-ray diffraction, ACID plots, orbital plots, cartesian coordinates of B3LYP/6-31G* optimized structures. CCDC 1826373 and 1826374. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc02877j |
| This journal is © The Royal Society of Chemistry 2018 |