Surprising solvent-induced structural rearrangements in large [N⋯I⁺⋯N] halogen-bonded supramolecular capsules: an ion mobility-mass spectrometry study

Abstract

Coordinative halogen bonds have recently gained interest for the assembly of supramolecular capsules. Ion mobility-mass spectrometry and theoretical calculations now reveal the well-defined gas-phase structures of dimeric and hexameric [N⋯I⁺⋯N] halogen-bonded capsules with counterions located inside their cavities as guests. The solution reactivity of the large hexameric capsule shows the intriguing solvent-dependent equilibrium between the hexamer and an unprecedented pentameric [N⋯I⁺⋯N] halogen-bonded capsule, when the solvent is changed from chloroform to dichloromethane. The intrinsic flexibility of the cavitands enables this novel structure to adopt a pseudo-trigonal bipyramidal geometry with nine [N⋯I⁺⋯N] bonds along the edges and two pyridine binding sites uncomplexed.

---

Introduction

Supramolecular capsules have attracted continuous attention since Rebek introduced his famous hydrogen-bonded “tennis ball” in 1993.¹ A plethora of examples have been described in the literature, which feature a broad range of different binding motifs such as hydrogen bonding,² metal coordination,³ ion-pair interactions,⁴ or more recently, halogen bonding.^5–8 Among these interactions, the strength and directionality of the halogen bond (XB) renders it exceptionally promising for the development of novel, structurally well-defined supramolecular complexes.⁹

The halogen bond is a noncovalent interaction between a polarized halogen atom and a Lewis base.¹⁰ Positively charged iodonium ions are a special case of XB donor, as they can bind two Lewis bases in a three-center-four-electron bond.^11,12 Since these two Lewis bases can be identical, building block synthesis for larger supramolecular assemblies is more easily achieved, as no attention needs to be paid to complementary couples of matching XB donors and acceptors. This renders iodonium ions excellent synthons for the self-assembly of novel supramolecular capsules.^6,7,13

The structural analysis of large supramolecular capsules,¹⁴ as well as the investigation of their dynamic rearrangements in condensed phase are challenging.^15,16 Self-assembly and self-sorting processes can be very fast, produce transient intermediates, or numerous products of low abundance. Standard condensed phase techniques, such as NMR, often struggle to provide information on the composition of these mixtures due to substantial signal superposition or fast dynamic processes averaging the signal positions. Moreover, the ability to target individual complexes in the mixture to conduct a detailed structural analysis is limited. However, these analytical shortcomings can be readily overcome by complementary gas-phase techniques.¹⁷

Electrospray ionization (ESI) is a soft ionization method capable of transferring even large noncovalent complexes from solution into the gas phase with minimal to no fragmentation.¹⁸ The transfer of ions into the gas phase interrupts the operation of underlying solution equilibria, thereby enabling their separation and subsequent analysis. Mass spectrometry (MS) offers a range of gas-phase experiments to investigate the structure and reactivity of a mass-selected ion of interest.¹⁹ Moreover, traditional MS experiments can be augmented with orthogonal separation techniques such as ion mobility spectrometry (IMS), which adds another dimension by separating analytes beyond their mass-to-charge (m/z) ratio. In a drift tube IMS (DT-IMS) experiment, ions are guided by a weak electric field through a drift tube filled with an inert buffer gas typically at pressures of a few millibars. During their migration, more extended ions are decelerated by a larger number of collisions with the buffer gas than compact ions of the same m/z and, as a result, leave the IMS cell after longer drift times. Consequently, the combination of IMS and MS to ion mobility-mass spectrometry (IM-MS) accomplishes ion separation not only based on their m/z, but also differences in charge, size, and shape.²⁰ The drift time of an ion can be further converted to a collision cross section (CCS), which represents an intrinsic molecular property independent from instrumental parameters.^21,22 Comparison of CCS values to reference experimental or theoretical values can provide quite detailed insight into the molecular structure. Hence, the characterization of supramolecular complexes in solution can largely benefit from gas-phase techniques such as MS and IMS.²³

Theoretical modelling of large supramolecular complexes presents challenges due to their size and delicate balance of various forces governing their stability. Grimme et al. presented quantum chemical calculations on a neutral halogen-bonded, heterodimeric capsule using semi-empirical methods tailored for the treatment of such systems.²⁴ Alternatively, composite methods, in which a more advanced quantum-mechanical treatment of the XB can be combined with a lower level of theory for the remaining framework of the capsules,²⁵ offer a feasible solution to study larger complexes.

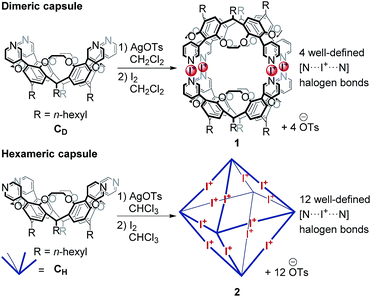
Recently, we reported the synthesis and characterization of dimeric and hexameric halogen-bonded capsules self-assembling from the different pyridyl-substituted resorcin[4]arene cavitands C_D and C_H and positively charged iodonium ions through coordinative [N⋯I⁺⋯N] halogen bonds (Scheme 1).^6,7 Their syntheses follow a two-step protocol. First, the cavitands are reacted with silver(I) p-toluenesulfonate to yield the Ag(I)-containing capsules. Then, a reaction with molecular iodine leads to an [N⋯Ag⁺⋯N] → [N⋯I⁺⋯N] exchange reaction. The halogen-bonded capsules were characterized by NMR and diffusion ordered spectroscopy (DOSY), together with preliminary MS experiments.

Scheme 1 Assembly of dimeric and hexameric halogen-bonded capsules 1 and 2.

Here, we focus on a detailed structural analysis of dimeric and hexameric halogen-bonded capsules 1 and 2 in the gas phase (Scheme 1). Collision cross sections derived from DT-IM-MS measurements in helium buffer gas (^DTCCS_He) were compared with theoretical values obtained from structures optimized with composite density-functional theory (DFT) and semi-empirical calculations. The calculations confirm formation of highly regular complexes and provide insights into their anion-guest binding behaviour. We furthermore observe a selective, solvent-dependent rearrangement of the hexamer into new pentameric halogen-bonded capsules 3 upon a rather subtle change of the solvent from chloroform to dichloromethane. The capsules are thus responsive to a chemical stimulus. The novel structure has been identified to exhibit an unusual pseudo-trigonal bipyramidal geometry with nine [N⋯I⁺⋯N] bonds along the edges and two pyridines uncomplexed.

Material and methods

Sample preparation

For the assembly of the [N⋯I⁺⋯N] halogen-bonded dimeric capsule 1, the hexameric capsule 2, and the pentameric capsule 3 (1 mM), a solution of the corresponding cavitand C_D (for 1, 1 eq.) or C_H (for 2 and 3, 1 eq.) was first mixed with AgOTs (2.0 eq.), stirred for 1 h and subsequently treated with I₂ (2.5 eq.), stirred for 20 min and centrifuged to remove precipitated AgI from the mixture. Dimeric and pentameric capsules (1, 3) were assembled and investigated using dichloromethane as the reaction and electrospray solvent; for the hexameric capsule 2, chloroform was used instead.^6,7

Electrospray ionization mass spectrometry

Positive-mode electrospray ionization quadrupole-time-of-flight high resolution mass spectrometric (ESI-Q-TOF-HRMS) experiments were performed with a Synapt G2-S HDMS (Waters Co., Milford, MA, USA) instrument. The following settings were used: flow rate 5–10 μL min⁻¹, capillary voltage 3.3 kV, sample cone voltage 40 V, source offset 80 V, source temperature 90 °C, desolvation temperature 250 °C, nebulizer gas 6 bar, desolvation gas flow 500 L h⁻¹. For collision-induced dissociation (CID), N₂ was used as the collision gas. Fragmentation experiments were conducted in the trap cell of the Synapt G2-S HDMS instrument with collision energies of 2–25 V. Data acquisition and processing was carried out using MassLynx™ (version 4.1).

Drift tube ion mobility-mass spectrometry

Measurements to obtain experimental collision cross sections (^DTCCS_He) have been conducted on an in-house-constructed DT-IM-MS instrument (iMob), which is described in detail elsewhere.²⁶ Briefly, ions are generated using a nano-electrospray ionization (nESI) source and subsequently pulsed into an ion mobility cell in which they travel under the influence of a weak electric field (10–15 V cm⁻¹) through helium buffer gas (∼5 mbar). After ion separation in the ion mobility cell, the ions of interest are m/z-selected using a quadrupole mass filter and their arrival time distributions (ATDs) are recorded by measuring their time-dependent ion current. ATDs have been recorded at six different drift voltages (950–1200 V) and were fitted by Gaussian functions. The center of each Gaussian corresponds to the drift time of a single species and is further converted into a ^DTCCS_He using the Mason–Schamp equation.^21,22

Theoretical calculations

The size of the capsules under consideration prohibits full treatment at the density-functional theory level. To decrease the computational effort while maintaining the quantum mechanical description of the halogen bond, the multilayered ONIOM method was used as implemented in the Gaussian09 rev.D01 code.²⁷ The DFT level of theory has been applied to the iodonium ions, the pyridine groups and the tosylate counterions (see Fig. 2), while the cavitand scaffold was described with the semi-empirical AM1 method.²⁸

To choose a suitable exchange-correlation density functional, we first evaluated the performance of commonly used methods on the [pyridine⋯I⁺⋯pyridine] model system. The structure has been optimized at the MP2 level of theory with a def2-TZVP basis set and the binding energy has been calculated. Next, the binding energy of various functionals in def2-type²⁹ basis sets were computed (see ESI, Table S1‡) and compared with MP2/def2-QZVPP single-point energies. Among the tested methods, the PBE0 ³⁰ hybrid exchange-correlation functional in a small def2-SVP basis set yields a small absolute error of 8.8 kJ mol⁻¹ which promises a good balance between accuracy and tractability of calculations. Moreover, the comparison of geometric parameters of the [pyridine⋯I⁺ pyridine] model system optimized at the PBE0/def2-SVP level of theory with the corresponding MP2-optimized complex resulted only in very minor geometrical differences. Hereafter, we will refer to the ONIOM(PBE0/def2-SVP:AM1) method used in this work simply as DFT/AM1.

The theoretical collision cross sections ™CCS_He were calculated using a trajectory method, as implemented in the Mobcal program.³¹ We used a uniform charge model for all atoms and adopted silicon parameters for the iodonium ions.

All calculated structures were optimized with the n-hexyl sidechains in a fully extended zigzag conformation. The CCS values derived from such arbitrary structures are likely to be overestimated by some constant increment per cavitand associated with the flexibility of the side chains. Therefore, we introduced a correction which was estimated as follows: a short molecular dynamics simulation was performed for a dimeric capsule for which the halogen-bonds were constrained to equilibrium bond lengths and angles, as derived from the [pyridine⋯I⁺⋯pyridine] model.³² Next, we extracted 30 random snapshots which featured n-hexyl chains in diverse orientations. The n-hexyl dihedral angles were translated to a pre-optimized capsule and the structure was again reoptimized at the DFT/AM1 level of theory. The geometry-optimized structures, which span several kJ mol⁻¹ energy range, exhibit CCS values between 560 and 590 Ų (see ESI, Fig. S9‡) with a mean of approximately 575 Ų, significantly below the 610 Ų calculated for a dimer with fully extended side chains. To account for this inherent flexibility of the n-hexyl chains, we corrected all reported ™CCS_He values by an increment of (610–575 Ų)/2 cavitands ≈ 20 Ų per cavitand.

Results and discussion

Structural analysis of halogen-bonded dimeric and hexameric capsules in the gas phase

Dimeric capsule. A dichloromethane solution of dimeric [N⋯I⁺⋯N] halogen-bonded capsule 1 was electrosprayed and the ions were transferred into a DT-IM-MS instrument. The ATDs of the capsule-derived ions all feature a single narrow and Gaussian-shaped peak. The two most prominent peaks in the mass spectrum correspond to intact capsules in two different charge states with one and two tosylates ([2·C_D + 4I + OTs]³⁺ and [2·C_D + 4I + 2·OTs]²⁺). Both ions exhibit virtually identical ^DTCCS_He values of 558 and 557 Ų, respectively (Fig. 1). This clearly indicates the tosylate anions to be located inside the capsule's cavity, as a clear size difference between the +2 and +3 charge states would be expected if one or both counterions would bind to the outer periphery.

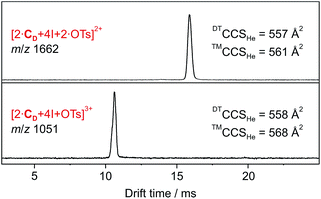Fig. 1 DT-IM-MS ATDs of ions derived from dimeric halogen-bonded capsule 1. Experimental ^DTCCS_He and theoretical ™CCS_He values are given.

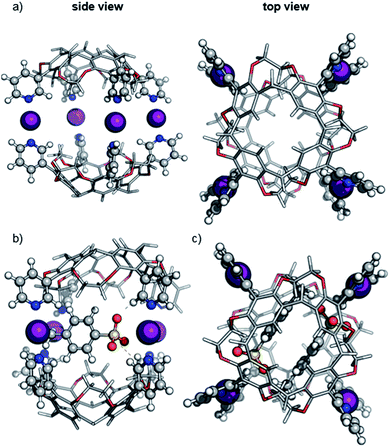
The optimized structure of the empty dimeric halogen-bonded capsule (Fig. 2a) reveals a slight helical twist of the two cavitands against each other to allow the formation of four linear [N⋯I⁺⋯N] bonds with an equilibrium N⋯I⁺ distance of 2.28 Å. The twist between two capsules is significantly smaller than that observed in the previously reported crystal structure for the silver-coordinated precursor capsule.⁶ The smaller twist can be attributed to the linearity of the halogen bonds with N–I–N angles close to 180 degrees, whereas the [N⋯Ag⁺⋯N] motif adopts an angle of 150–160 degrees.^6,12

Fig. 2 Geometry-optimized structures of dimeric halogen-bonded capsule 1 (a) in the absence of tosylate counterions ([2·C_D + 4I]⁴⁺; side and top view); (b) with one tosylate inside the cavity ([2·C_D + 4I + OTs]³⁺), [C_aryl–H⋯O⁻] interactions are marked with dotted lines; (c) with two tosylates inside the cavity ([2·C_D + 4I + 2OTs]²⁺). PBE0/def2-SVP was used for I⁺, pyridines and tosylates (ball-and-stick representation); AM1 for the cavitand scaffold (stick representation). For clarity, the n-hexyl chains are omitted in the images.

For calculations of capsular complexes with one tosylate counterion, several different starting structures were considered, which included positions of the anion inside and outside of the cavity (see ESI, Fig. S10‡). A tosylate ion inside the cavity has been found to be more stable, however, the energy preference is small (<4 kJ mol⁻¹). In the optimized geometry, the tosylate anion does not interact with any iodonium ion directly, but rather with the cavitand through [C_aryl–H⋯O⁻] interactions (Fig. 2b).³³ The insertion of the second tosylate ion into the cavity leads to a cooperative stabilization of 35 kJ mol⁻¹ – more than any other position around the capsule. Their antiparallel arrangement does not only reduce charge repulsion, but forms stabilizing van der Waals interactions between the two aromatic rings of the tosylates (Fig. 2c).

The predicted ™CCS_He values (corrected by 20 Ų per cavitand; see above and ESI, Fig. S8‡) are 568 and 561 Å for the ions carrying one and two tosylate ions, respectively and agree well with experimental data (Fig. 1). We conclude that both anions bind cooperatively inside the cavity. The virtually identical collision cross sections suggest that already the first anion occupies the cavity.

Hexameric capsules. DT-IM-MS experiments were also performed on the hexameric halogen-bonded capsule 2 in its +6 and +7 charge states ([6·C_H + 12I + 6·OTs]⁶⁺ and [6·C_H + 12I + 5·OTs]⁷⁺). Both ATDs feature a prominent, narrow peak, which indicates the presence of a well-defined structure in the gas phase. Their corresponding ^DTCCS_He values of 1517 and 1499 Ų are again very similar to each other, suggesting that an additional counterion does not have a significant influence on the overall shape (Fig. 3). The DFT/AM1-optimized structure of the hexameric capsule is an octahedron held together by twelve linear [N⋯I⁺⋯N] bonds along the edges with N⋯I⁺ distances of 2.29 Å (Fig. 4a). Tosylate ions can attach to this capsule in several accessible locations: in the proximity of the halogen bond as observed inside the dimer or above the upper rim of the cavitand, located in between two pyridine units and stabilized by [C_aryl–H⋯O⁻] interactions (Fig. 4b, inset). The calculations predict that the latter binding mode, above the upper rim and inside a pocket of the cavitand, is more favourable by 31 kJ mol⁻¹.

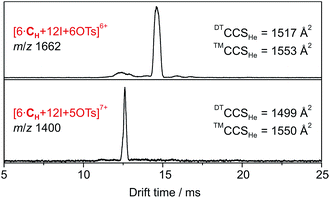Fig. 3 DT-IM-MS ATDs of ions derived from hexameric halogen-bonded capsule 2. Experimental ^DTCCS_He and theoretical ™CCS_He values are given.

Fig. 4 Geometry-optimized structure of the hexameric halogen-bonded capsule 2 (a) in the absence of tosylate ions ([6·C_H + 12I]¹²⁺) and (b) with six tosylate anions ([6·C_H + 12I + 6·OTs]⁶⁺). The n-hexyl chains are omitted for clarity. Inset: binding situation of a tosylate counterion.

Accordingly, six spatially distributed binding pockets at such positions provide binding sites for six tosylates (Fig. 4b). The calculated ™CCS_He for the [6·C_H + 12I + 6·OTs]⁶⁺ and [6·C_H + 12I + 5·OTs]⁷⁺ ions of 1550 and 1553 Ų are in good agreement with the experiment thus indicating that the hexameric capsule retains an intact octahedral geometry upon transfer into the gas phase with linear [N⋯I⁺···N] halogen bonds along all edges (Fig. 3). An anion-binding mode with tosylates bridging two adjacent pyridine rings of the same cavitand by multiple [C_aryl–H⋯O⁻] interactions is proposed. It also appears to be well-suited in terms of size and shape complementarity of this host–guest complex.

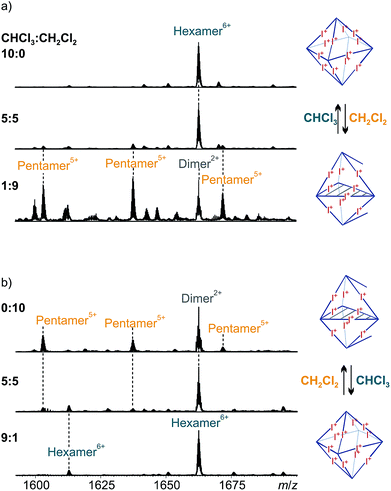
Solvent-dependent formation of pentameric capsules

Structure elucidation. Upon successively exchanging chloroform as the solvent by dichloromethane, a solvent-dependent transition of the hexameric capsule 2 into a novel pentameric complex (3, Scheme 2) was observed. To investigate the effect in more detail, we first conducted the assembly of cavitand C_H with silver(I) p-toluenesulfonate in dichloromethane, which clearly gave the silver-coordinated hexameric capsule 4 (ESI, Fig. S4‡). The [N⋯Ag⁺⋯N] → [N⋯I⁺⋯N] exchange reaction in dichloromethane results in a ¹H NMR spectrum significantly different from that of the highly symmetrical, octahedral capsule 2 (ESI, Fig. S3‡). A rather complex NMR spectrum with several sets of rather broad signals at positions comparable to the NMR spectrum of the hexamer is obtained for 3. This suggests the formation of an assembly of lower symmetry and/or the formation of a mixture of different assemblies. A straightforward signal assignment is, however, impossible.

Scheme 2 Selective formation of halogen-bonded pentameric capsule 3 using CH₂Cl₂ as the solvent.

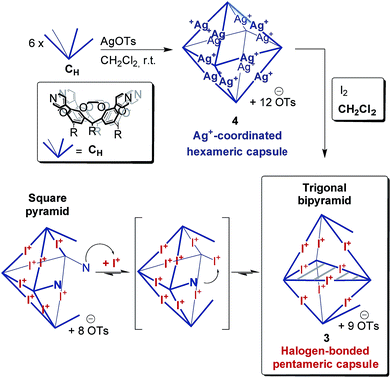
The corresponding ESI mass spectrum (90 μM in CH₂Cl₂) clearly shows the selective formation of a halogen-bonded pentamer 3 (Fig. 5). The almost exclusive appearance of pentameric species, instead of a non-specific distribution of oligomers, strongly suggests stable and well-defined structures to form. The signals can be assigned to charge states 6+ to 3+ and the most abundant signal of each charge state belongs to a complex with a formal [5·C_H + 9I]⁹⁺ core to which a varying number of anions is attached. The most dominant peak at m/z 1602 belongs to the complex [5·C_H + 9I + 4·OTs]⁵⁺. The observed exact mass and experimental isotope pattern agree with those simulated based on natural abundances. The mass spectrum furthermore exhibits ions which correspond to singly and doubly protonated species for each charge state accompanying the [5·C_H + 9I + x·OTs]^(9−x)+ peaks, e.g. [5·C_H + 9I + H + 5·OTs]⁵⁺ and [5·C_H + 9I + 2H + 6·OTs]⁵⁺ ions at m/z 1637 and 1671. Considering possible pentameric assemblies which would maintain linear [N⋯I⁺⋯N] halogen bonds quickly makes clear that the formation of a complex which has all pyridine binding sites coordinated is impossible. Two possible candidates that maintain structural specificity, a bowl-shaped square pyramid and a pseudo-trigonal bipyramid, are possible (Scheme 2). In order to accommodate the geometrical constrains, both structures must feature uncomplexed pyridines, i.e. two for the pseudo-trigonal bipyramid and four for the square pyramid. Similarly, earlier studies by Aakeröy et al. demonstrated the formation of a heterodimeric halogen-bonded capsule in the solid state, in which one of four possible XBs is sacrificed in a fraction of the complexes due to steric congestion.⁸

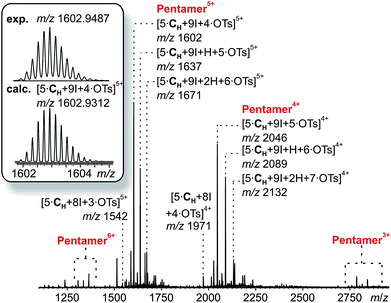Fig. 5 ESI-Q-TOF-HRMS spectrum of pentameric halogen-bonded capsule 3 (90 μM in CH₂Cl₂) with experimental and calculated isotopic pattern (inset).

The two most prominent peaks for [5·C_H + 9I + x·OTs]^(9−x)+ ions contain five and four tosylate counterions (x = 4, 5). This agrees with the trends observed for dimeric and hexameric [N⋯I⁺⋯N] capsules: each cavitand monomer offers one tosylate binding site within the capsule cavity. Upon ionization, the additional outer counterions are easily stripped off. In addition, the elimination of one of the inner tosylates can occur, but is energetically somewhat more demanding. This observation thus supports the assumption that the pentamer is a closed capsule and consequently speaks in favour of the bipyramidal structure. The 5 : 9 cavitand-to-iodonium stoichiometry observed in the prominent peaks of the mass spectrum is also in good agreement with the bipyramidal structure of the pentamer, as the square pyramid only requires eight [N⋯I⁺⋯N] halogen bonds, while the bipyramid bears nine. Capsule-derived complexes with singly coordinated I⁺ have not been observed, neither in this nor in our previous study.⁶ Consequently, the [N⋯I⁺⋯N] bond is likely much more stable than the hypothetical [N⋯I⁺] group. Furthermore, the observed single and double – but not triple or quadruple – protonation indicates the presence of two free pyridines as in the bipyramid rather than the four of the square pyramid. All these findings thus agree that the structure of the pentamer is that of a bipyramid that bears two non-coordinated pyridines. Nevertheless, low-abundant signals corresponding to ions with a formal [5·C_H + 8I]⁸⁺ core, which appear at m/z 1542 and 1971, may indicate that the square pyramidal complex is present in solution at low concentrations. Therefore, the pseudo-trigonal bipyramidal pentameric [5·C_H + 9I]⁹⁺ and the square pyramidal [5·C_H + 8I]⁸⁺ complexes may exist in an equilibrium with each other. This equilibrium, however, is strongly shifted towards the pseudo-trigonal bipyramidal complex as this structure helps maximizing the number of halogen bonds within the pentamer (Scheme 2).

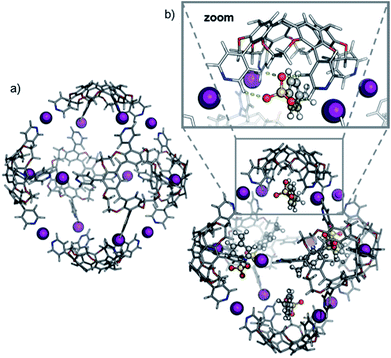
Theory confirms the individual cavitands to be sufficiently flexible to form a stable pseudo-trigonal bipyramidal pentameric capsule. Three cavitands in equatorial positions participate with all four pyridine groups in linear [N⋯I⁺⋯N] bonds (Fig. 6a). These cavitands are capped axially by the other two which bind in a somewhat distorted conformation. The two apical cavitands form only three [N⋯I⁺⋯N] bonds each and the fourth pyridine moiety remains unbound. In principle, two different configurational isomers of this pentameric capsule are possible: the two unbound pyridines can adopt an eclipsed or a gauche position relative to each other. This accounts for the complex ¹H NMR of capsule 3; multiple sets of signals likely originate from a mixture of two different complexes that both have lower symmetry than the hexamer. Alike the hexameric capsule, tosylate ions can bind inside the cavity of the pentameric capsule above the upper rim of the cavitands stabilized by [C_aryl–H⋯O⁻] interactions (Fig. 6b). In contrast to the hexameric capsules, the binding sites are not equivalent anymore; the tosylates prefer to populate the more remote apical cavitands first, and then bind to more crowded equatorial cavitands.

Fig. 6 Calculated structures of the pentameric halogen-bonded capsule 3 with pseudo-trigonal bipyramidal arrangement (a) in the absence of tosylate ions ([5·C_H + 9I]⁹⁺) and (b) with four tosylate anions ([5·C_H + 9I + 4·OTs]⁵⁺). For clarity, the n-hexyl side chains are omitted. Cavitands in axial positions, unbound pyridines and tosylates are highlighted.

The ATD obtained for the [5·C_H + 9I + 4·OTs]⁵⁺ ion in a DT-IM-MS experiment shows a single narrow peak which is consistent with the presence of a well-defined species in the gas phase (Fig. 7). The difference in size and shape of the two possible configurational isomers of capsule 3 is apparently not sufficient to differentiate the species in the ATD. The measured ^DTCCS_He for capsule 3 of 1286 Ų is approximately 20% smaller than that of the hexameric capsule 2. The optimized structure of the pseudo-trigonal bipyramidal pentamer capsule, with four tosylates occupying the cavity, yielded a calculated ™CCS_He value of 1279 Ų which is in excellent agreement with the experimental value.

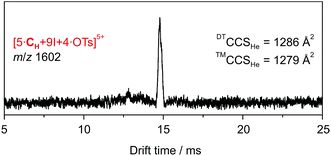Fig. 7 DT-IM-MS ATDs of ions derived from pentameric halogen-bonded capsule 3. Experimental ^DTCCS_He and theoretical ™CCS_He values are given.

These results confirm the discovery of a new type of large, well-behaved supramolecular complex based on [N⋯I⁺⋯N] halogen bonds. This is the first example of a resorcinarene-based pentameric supramolecular capsule. The selective formation of pentameric capsules illustrates the possible interplay of preorganized, but inherently flexible cavitands and directional halogen bonds being modulated by a third factor – solvent effects. Solvent-induced transformations in discrete supramolecular assemblies have been described for numerous other systems and are most likely to arise from changes between protic/aprotic and polar/apolar solvents.¹⁶ However, examples which feature the change between two very similar solvents, as in our case chloroform and dichloromethane, are extremely rare which makes this finding especially intriguing.²⁴

Self-assembly most often leads to the smallest possible, not too highly strained assembly in which all binding sites are coordinatively saturated. This is the best compromise between entropic (particle number) and enthalpic effects (avoiding strain and unsaturated binding sites). It is thus surprising that a solvent effect can be large enough to energetically overcome the energetic penalty associated with two pyridine binding sites remaining unsaturated. However, when considering all effects that come into play here, the hexamer → pentamer rearrangement appears reasonable: (i) Dichloromethane has a significantly higher polarity than chloroform as expressed in their dielectric constants ε of 8.93 and 4.81, respectively, and thus provides better solvation to the free pyridines. (ii) More pentamers can form from the same number of building blocks, increasing particle number and thus entropy. (iii) The formation of mixtures of isomers also contributes to a favourable entropy of the pentamer. (iv) Space filling³⁴ of the voids between the encapsulated tosylates inside the capsules with solvent molecules likely contributes differently for the hexamer (larger voids) and the pentamer (smaller voids). Chloroform and dichloromethane differ in size and might therefore template the assembly of one complex or the other by providing a more optimal filling of this particular cavity.³⁵ All these (and maybe more) effects help balancing the energetic penalty arising from leaving two binding sites open. We therefore propose an equilibrium between the hexameric and the pentameric capsules which is susceptible to the small shift in energetics associated with the solvent change.

Solvent-dependent switching. To account for this hypothesis, a switching experiment was performed (see ESI, Scheme S1, Fig. S1, S2 and S5‡). A 1 mM sample solution of hexameric halogen-bonded capsule 2 in chloroform was diluted using different ratios of chloroform to dichloromethane, resulting in a constant sample concentration of 0.1 mM, but different solvent ratios. These samples were analyzed by ESI-MS two minutes after dilution. The mass spectrum of the sample in pure chloroform reveals the presence of the intact octahedral hexameric capsule in form of a prominent peak at m/z 1662 ([6·C_H + 12I + 6·OTs]⁶⁺, Fig. 8a, top). Upon increase of the dichloromethane fraction to 50%, signals corresponding to pentameric complexes appear in the spectrum at m/z 1602, 1637 and 1672 (Fig. 8a, center). When the ratio of chloroform to dichloromethane is at 1 : 9, the hexameric capsule vanishes and the pentamer prevails (Fig. 8a, bottom). Note that the remaining peak at m/z 1662 belongs to a dimeric ion which is likely an ionization artifact.

Fig. 8 ESI-Q-TOF-HRMS spectra of titration experiments to investigate the solvent-dependent transitions (a) from the hexameric to the pentameric halogen-bonded capsule (from top to bottom: CHCl₃/CH₂Cl₂ 1 : 0 → 1 : 1 → 1 : 9) and (b) from the pentameric halogen-bonded capsule to the hexameric halogen-bonded capsule (from top to bottom: CHCl₃/CH₂Cl₂ 0 : 1 → 1 : 1 → 9 : 1). Isobaric hexamers and dimers can be distinguished by isotope pattern analysis.

The experiment can be carried out in the opposite direction as well. Starting from a clear solution (1 mM) of pentameric halogen-bonded capsule 3 in dichloromethane, dilution of the sample to 0.1 mM in a 1 : 1 mixture of chloroform and dichloromethane leads to a mixture of pentameric and hexameric complexes in a very similar ratio as observed in the first experiment (Fig. 8b, center). An increase of the amount of chloroform to 90% of the spray solvent gives exclusively hexameric complexes (Fig. 8b, bottom). These switching experiments indeed demonstrate the solvent-dependent equilibrium between the two capsules 2 and 3.

A CID tandem MS experiment provides evidence that the hexamer–pentamer transition is solely taking place in solution. No gas-phase rearrangement leading preferentially from hexameric to pentameric complexes was observed (see ESI, Fig. S6 and S7‡).

These results emphasize the certainly unexpected solvent effects and clearly demonstrate the halogen-bonded hexameric capsule to be a stimuli-responsive assembly, which reacts to changes in its environment by substantial structural rearrangements.

Conclusions

The first study on the solution reactivity of large [N⋯I⁺⋯N] halogen-bonded capsules revealed a solvent-dependent rearrangement of the known hexameric capsule into a novel pentameric [N⋯I⁺⋯N] halogen-bonded capsule. While condensed phase methods could not provide detailed insight, the combination of ESI-MS, DT-IM-MS and theoretical calculations enabled us to elucidate the structure of this new [N⋯I⁺⋯N] halogen-bonded capsule. The complex possesses an unusual pseudo-trigonal bipyramidal geometry with nine [N⋯I⁺⋯N] bonds along the edges and two of the five incorporated cavitands partially uncomplexed. We demonstrate that this fascinating and rather unexpected equilibrium between the hexameric and the pentameric complex originates solely from a subtle change of solvent from chloroform to dichloromethane. This stimuli-responsive rearrangement is rationalized by a combination of microsolvation, space-filling, and different entropic contributions.

Moreover, we provide first evidence for the anion guest-binding in the different [N⋯I⁺⋯N] halogen-bonded capsules by a combination of experimental and theoretical gas-phase methods. Each cavitand incorporated into the dimeric, pentameric and hexameric complexes is capable of binding one tosylate ion within the capsule's cavity, resulting in the binding of up to two, five and six anions, in 1, 3, and 2 respectively. Two different binding modes depending on the size of the complex were predicted by DFT-level calculations. Especially the binding in the less sterically crowded pentamers and hexamers is interesting. It shows the tosylate ions without interaction with the [N⋯I⁺⋯N] moieties, but rather between the two pyridine units and above the upper rim of the cavitand stabilized by [C_aryl–H⋯O⁻] interactions. This agrees well with studies on similar, yet significantly less complex systems investigated by Erdélyi and coworkers.¹² Furthermore, this is also in marked contrast to the anion binding of the silver-coordinated, dimeric precursor capsule, for which X-ray crystal structure analysis showed the anions to be located outside the cavity and in direct interaction with the silver cations.⁶

In conclusion, the large [N⋯I⁺⋯N] halogen-bonded capsules feature [C_aryl–H⋯O⁻] interactions and halogen bonds as orthogonal noncovalent interactions which determine the assembly of the host and the guest binding. This underlines the potential for their application for the hierarchical self-assembly of supramolecular architectures in solution.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has been supported by the Deutsche Forschungsgemeinschaft (CRC 765).

References

1. R. Wyler, J. de Mendoza and J. Rebek, Angew. Chem., Int. Ed. Engl., 1993, 32, 1699–1701.
2. J. Rebek, T. Heinz and D. M. Rudkevich, Nature, 1998, 394, 764–766.
3. M. Fujita, S. Nagao and K. Ogura, J. Am. Chem. Soc., 1995, 117, 1649–1650.
4. G. V. Oshovsky, D. N. Reinhoudt and W. Verboom, J. Am. Chem. Soc., 2006, 128, 5270–5278.
5. (a) O. Dumele, B. Schreib, U. Warzok, N. Trapp, C. A. Schalley and F. Diederich, Angew. Chem., Int. Ed., 2017, 56, 1152–1157; (b) O. Dumele, N. Trapp and F. Diederich, Angew. Chem., Int. Ed., 2015, 54, 12339–12344.
6. L. Turunen, U. Warzok, R. Puttreddy, N. K. Beyeh, C. A. Schalley and K. Rissanen, Angew. Chem., Int. Ed., 2016, 55, 14033–14036.
7. L. Turunen, U. Warzok, C. A. Schalley and K. Rissanen, Chem, 2017, 3, 861–869.
8. C. B. Aakeröy, A. Rajbanshi, P. Metrangolo, G. Resnati, M. F. Parisi, J. Desper and T. Pilati, CrystEngComm, 2012, 14, 6366–6368.
9. L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195.
10. (a) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601; (b) M. Erdélyi, Chem. Soc. Rev., 2012, 41, 3547–3557.
11. (a) A.-C. C. Carlsson, M. Uhrbom, A. Karim, U. Brath, J. Gräfenstein and M. Erdélyi, CrystEngComm, 2013, 15, 3087–3092; (b) A.-C. C. Carlsson, J. Gräfenstein, A. Budnjo, J. L. Laurila, J. Bergquist, A. Karim, R. Kleinmaier, U. Brath and M. Erdélyi, J. Am. Chem. Soc., 2012, 134, 5706–5715; (c) S. B. Hakkert and M. Erdélyi, J. Phys. Org. Chem., 2015, 28, 226–233; (d) A.-C. C. Carlsson, K. Mehmeti, M. Uhrbom, A. Karim, M. Bedin, R. Puttreddy, R. Kleinmaier, A. A. Neverov, B. Nekoueishahraki, J. Gräfenstein, K. Rissanen and M. Erdélyi, J. Am. Chem. Soc., 2016, 138, 9853–9863.
12. M. Bedin, A. Karim, M. Reitti, A.-C. C. Carlsson, F. Topić, M. Cetina, F. Pan, V. Havel, F. Al-Ameri, V. Sindelar, K. Rissanen, J. Gräfenstein and M. Erdélyi, Chem. Sci., 2015, 6, 3746–3756.
13. L. Turunen, A. Peuronen, S. Forsblom, E. Kalenius, M. Lahtinen and K. Rissanen, Chem.–Eur. J., 2017, 23, 11714–11718.
14. (a) D. Beaudoin, F. Rominger and M. Mastalerz, Angew. Chem., Int. Ed., 2016, 55, 15599–15603; (b) L. R. MacGillivray and J. L. Atwood, Nature, 1997, 389, 469–472; (c) T. Gerkensmeier, W. Iwanek, C. Agena, R. Fröhlich, S. Kotila, C. Näther and J. Mattay, Eur. J. Org. Chem., 1999, 2257–2262; (d) R. M. McKinlay, G. W. V. Cave and J. L. Atwood, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 5944–5948; (e) T. Schröder, R. Brodbeck, M. C. Letzel, A. Mix, B. Schnatwinkel, M. Tonigold, D. Volkmer and J. Mattay, Tetrahedron Lett., 2008, 49, 5939–5942; (f) O. Ugono, J. P. Moran and K. T. Holman, Chem. Commun., 2008, 1404–1406.
15. R. Custelcean, Chem. Soc. Rev., 2014, 43, 1813–1824.
16. W. Wang, Y.-X. Wang and H.-B. Yang, Chem. Soc. Rev., 2016, 45, 2656–2693.
17. (a) S. Sato, Y. Ishido and M. Fujita, J. Am. Chem. Soc., 2009, 131, 6064–6065; (b) S. P. Black, D. M. Wood, F. B. Schwarz, T. K. Ronson, J. J. Holstein, A. R. Stefankiewicz, C. A. Schalley, J. K. M. Sanders and J. R. Nitschke, Chem. Sci., 2016, 7, 2614–2620; (c) N. K. Beyeh, M. Kogej, A. Ahman, K. Rissanen and C. A. Schalley, Angew. Chem., Int. Ed., 2006, 45, 5214–5218; (d) W. Hoffmann, K. Folmert, J. Moschner, X. Huang, H. von Berlepsch, B. Koksch, M. T. Bowers, G. von Helden and K. Pagel, J. Am. Chem. Soc., 2018, 140, 244–249.
18. (a) D. Fujita, Y. Ueda, S. Sato, H. Yokoyama, N. Mizuno, T. Kumasaka and M. Fujita, Chem, 2016, 1, 91–101; (b) B. Baytekin, H. T. Baytekin and C. A. Schalley, Org. Biomol. Chem., 2006, 4, 2825–2841; (c) Analytical methods in supramolecular chemistry, ed. C. A. Schalley, Wiley-VCH, Weinheim, 2012.
19. (a) L. Cera and C. A. Schalley, Chem. Soc. Rev., 2014, 43, 1800–1812; (b) Z. Qi, T. Heinrich, S. Moorthy and C. A. Schalley, Chem. Soc. Rev., 2015, 44, 515–531.
20. F. Lanucara, S. W. Holman, C. J. Gray and C. E. Eyers, Nat. Chem., 2014, 6, 281–294.
21. C. Uetrecht, R. J. Rose, E. van Duijn, K. Lorenzen and A. J. R. Heck, Chem. Soc. Rev., 2010, 39, 1633–1655.
22. E. S. Baker, B. H. Clowers, F. Li, K. Tang, A. V. Tolmachev, D. C. Prior, M. E. Belov and R. D. Smith, J. Am. Soc. Mass Spectrom., 2007, 18, 1176–1187.
23. (a) P. Bonakdarzadeh, F. Topić, E. Kalenius, S. Bhowmik, S. Sato, M. Groessl, R. Knochenmuss and K. Rissanen, Inorg. Chem., 2015, 54, 6055–6061; (b) O. Jurček, P. Bonakdarzadeh, E. Kalenius, J. M. Linnanto, M. Groessl, R. Knochenmuss, J. A. Ihalainen and K. Rissanen, Angew. Chem., Int. Ed., 2015, 54, 15462–15467; (c) A. Kiesilä, L. Kivijärvi, N. K. Beyeh, J. O. Moilanen, M. Groessl, T. Rothe, S. Götz, F. Topić, K. Rissanen, A. Lützen and E. Kalenius, Angew. Chem., Int. Ed., 2017, 56, 10942–10946; (d) M. Petryk, A. Troć, B. Gierczyk, W. Danikiewicz and M. Kwit, Chem.–Eur. J., 2015, 21, 10318–10321; (e) J. Ujma, M. de Cecco, O. Chepelin, H. Levene, C. Moffat, S. J. Pike, P. J. Lusby and P. E. Barran, Chem. Commun., 2012, 48, 4423–4425; (f) C. Wang, X.-Q. Hao, M. Wang, C. Guo, B. Xu, E. N. Tan, Y.-Y. Zhang, Y. Yu, Z.-Y. Li, H.-B. Yang, M.-P. Song and X. Li, Chem. Sci., 2014, 5, 1221–1226; (g) M. Wang, C. Wang, X.-Q. Hao, X. Li, T. J. Vaughn, Y.-Y. Zhang, Y. Yu, Z.-Y. Li, M.-P. Song, H.-B. Yang and X. Li, J. Am. Chem. Soc., 2014, 136, 10499–10507.
24. R. Sure and S. Grimme, Chem. Commun., 2016, 52, 9893–9896.
25. (a) T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815–826; (b) L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796; (c) R. Wieczorek and J. J. Dannenberg, J. Am. Chem. Soc., 2003, 125, 8124–8129.
26. (a) S. Warnke, C. Baldauf, M. T. Bowers, K. Pagel and G. von Helden, J. Am. Chem. Soc., 2014, 136, 10308–10314; (b) P. R. Kemper, N. F. Dupuis and M. T. Bowers, Int. J. Mass Spectrom., 2009, 287, 46–57.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Rana-singhe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. To-masi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision rev.D01, Gaussian, Inc., Wallingford CT, 2016.
28. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909.
29. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
30. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
31. M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082–16086.
32. Maestro Schrödinger Release 2017-4, Maestro, Schröding-er, LLC, New York, NY, 2017.
33. S. S. Zhu, H. Staats, K. Brandhorst, J. Grunenberg, F. Gruppi, E. Dalcanale, A. Lützen, K. Rissanen and C. A. Schalley, Angew. Chem., Int. Ed., 2008, 47, 788–792.
34. S. Mecozzi and J. J. Rebek, Chem.–Eur. J., 1998, 4, 1016–1022.
35. B. Kilbas, S. Mirtschin, R. Scopelliti and K. Severin, Chem. Sci., 2012, 3, 701–704.

---

Footnotes

† Dedicated to Prof. Helmut Schwarz on the occasion of his 75th birthday.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03040e

§ Currently at Hunter College, The City University of New York.

¶ Currently at Department of Chemistry – BMC, Uppsala University.

---