Open Access Article
Open Access ArticleDynamics of the excited-state hydrogen transfer in a (dG)·(dC) homopolymer: intrinsic photostability of DNA†
Antonio
Francés-Monerris
 *a,
Hugo
Gattuso
*a,
Hugo
Gattuso
 b,
Daniel
Roca-Sanjuán
b,
Daniel
Roca-Sanjuán
 c,
Iñaki
Tuñón
c,
Iñaki
Tuñón
 d,
Marco
Marazzi
d,
Marco
Marazzi
 e,
Elise
Dumont
e,
Elise
Dumont
 f and
Antonio
Monari
f and
Antonio
Monari
 *a
*a
aUniversité de Lorraine, CNRS, LPCT, Nancy F-54000, France. E-mail: Antonio.Francés@univ-lorraine.fr; Antonio.Frances@univ-lorraine.fr
bTheoretical Physical Chemistry, Research Unit Molecular Systems (UR MOLSYS), University of Liège, 4000 Liège, Belgium
cInstituto de Ciencia Molecular, Universitat de València, Apartado 22085, ES-46071 Paterna, Spain
dDepartamento de Química Física, Universitat de València, 46100 Burjassot, Spain
eDepartamento de Química, Centro de Investigación en Síntesis Química (CISQ), Universidad de La Rioja, 26006 Logroño, Spain
fUniv. Lyon, ENS de Lyon, CNRS UMR 5182, Université Claude Bernard Lyon 1, Laboratoire de Chimie, F69342, Lyon, France
First published on 18th September 2018
Abstract
The intrinsic photostability of nucleic acids is intimately related to evolution of life, while its understanding at the molecular and electronic levels remains a challenge for modern science. Among the different decay pathways proposed in the last two decades, the excited-state hydrogen transfer between guanine–cytosine base pairs has been identified as an efficient non-reactive channel to dissipate the excess of energy provided by light absorption. The present work studies the dynamics of such phenomena taking place in a (dG)·(dC) B-DNA homopolymer in water solution using state-of-the-art molecular modelling and simulation methods. A dynamic effect that boosts the photostability of the inter-strand hydrogen atom transfers, inherent to the Watson–Crick base pairing, is unveiled and ascribed to the energy released during the proton transfer step. Our results also reveal a novel mechanism of DNA decay named four proton transfer (FPT), in which two protons of two adjacent G–C base pairs are transferred to form a biradical zwitterionic intermediate. Decay of the latter intermediate to the ground state triggers the transfer of the protons back to the guanine molecules recovering the Watson–Crick structure of the tetramer. This FPT process is activated by the close interaction of a nearby Na+ counterion with the oxygen atoms of the guanine nucleobases and hence represents a photostable channel operative in natural nucleic acids.
Introduction
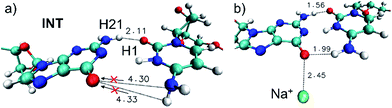
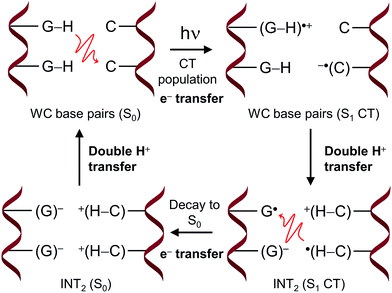
The comprehension of the intricate photochemical events triggered by UV-light absorption taking place in nucleic acids is crucial to understand life on Earth as we know it.1 It is recognized that the specific chemical structures of nucleic acids, in particular DNA components, have great capability to dissipate the excess of energy in a non-reactive way and hence ultimately avoid the production and accumulation of photoinduced lesions.2–5 The excited-state hydrogen transfer (ESHT) process6 between Watson–Crick (WC) base pairs,4,5 especially guanine–cytosine (G–C) couples (see Scheme 1),7–15 was identified in a series of independent ultrafast time-resolved infrared (IR) spectroscopy studies.16–20 Major evidence for the occurrence of the ESHT process was provided by the IR fingerprint of the G[–H] radical, a key intermediate in this mechanism (see the INT structure in Scheme 1).16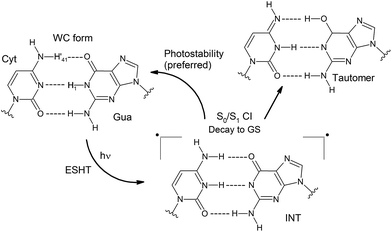 | ||
| Scheme 1 Photostablility and tautomerization mechanisms involved in the ESHT mechanism.10,11 | ||
Two decay components at the picosecond scale are registered for G–C base pairs embedded in different environments. The fast one is ascribed to the G[–H] radical decay and therefore to the ESHT process. On the other hand, the slow component of several tens of picoseconds has been recently ascribed to a different mechanism named proton-coupled electron transfer (PCET), which involves the interplay of two adjacent G–C base pairs.17,18,21 In this case, an intra-strand G → C electron transfer drives the subsequent inter-strand G → C proton transfer, producing a distonic radical ion base pair. This feature is obviously not possible in a single G–C base pair, and the slow component is absent in this system.16 Moreover, it has also been suggested that the PCET mechanism should be less relevant in non-alternating DNA sequences, i.e. when the same nucleobases are repeatedly stacked in the same strand, given the equal oxidation/reduction potentials of the intra-strand monomers.17 This hypothesis is supported by the larger amplitudes registered for the fast components (ascribed to the ESHT processes) with respect to the slow components (associated with PCET mechanisms) in non-alternating vs. alternating sequences.17,18
ESHT channels can split into branches recovering the correct WC pairing or cause base tautomerization which ultimately may lead to a mismatch in replication or transduction (see Scheme 1).10,12,16 Even though these two possibilities should be operative, the G–C base pairing displays a clear preference for photostability. Only 10% of tautomerization has been reported for G–C base pairs dissolved in chloroform,16 whereas in GC/GC miniduplexes and duplexes, the tautomer species has not been detected.17–19
However, despite these pieces of evidence, the specific reasons explaining the preferred photostability of G–C base pairs over the phototautomerization have been so far much less analysed. For this reason, we have performed a quantum mechanics (QM)/molecular mechanics (MM) study of a 14 base-pair (dG)·(dC) homopolymer in the B-DNA form (see Fig. 1). This computational protocol allows the study of relevant fragments with accurate QM procedures, whereas the rest of the system is treated with much faster MM methods, allowing the description of large systems. As previously mentioned, the non-alternating sequence has been chosen to favour ESHT processes instead of PCET events.17,18,22,23
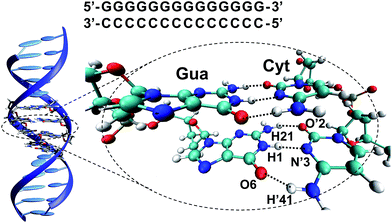 | ||
| Fig. 1 (GG/CC)QM partition of the (dG)·(dC) homopolymer system and atom numbering10,24 of a G–C base pair in the WC arrangement. | ||
Our study reveals an intrinsic mechanism displayed by the G–C base pair that hampers its tautomerization after light absorption, in particular during the excited-state vibrational relaxation toward the conical intersection (CI) region. Furthermore, we also show that the presence of a cation (Na+) in close surroundings can activate new DNA decay mechanisms. In particular, cations are able to trigger two proton transfers of two adjacent non-alternating G–C base pairs in a process that we call four proton transfer (FPT). To the best of our knowledge, this is a totally new feature of DNA photochemistry and is also a very nice example of the subtle balance and coupling at play in the photochemistry of complex environments such as DNA. The pivotal role of cations in opening new photochemical pathways also opens the question of the stability of DNA in a coiled, nucleosomal, environment due to the high density of positively charged amino acids in close contact with nucleic acids.
Methods and computational details
We performed classical molecular dynamics (MD) simulations over a 14 base-pair (dG)·(dC) homopolymer in the B-DNA form (see Fig. 1) using the AMBER16 software package.25 The DNA potential was represented via the amber parm99 force field including bsc1 corrections for DNA,26 while the water solvent was represented with the TIP3P force field.27 After equilibration and thermalization, a 100 ns production run was performed in the constant pressure and temperature (NPT) ensemble at 300 K and 1 atm. Full details of the MD protocol can be found in the ESI.†The optical properties of the DNA homopolymer were subsequently investigated in the Franck–Condon region by extracting 11 independent snapshots representative of the B-DNA conformational space (see Fig. S1†), taken every 10 ns from the MD simulation. Excited-state energies as well as other properties were obtained by employing two different QM methods. The first one is the time-dependent density functional theory (TD-DFT) method using the long-range corrected hybrid CAM-B3LYP functional as implemented in the GAUSSIAN 09 software package.28 The choice of the CAMB3LYP functional to compute the excited states is based on its proven good description of charge-transfer (CT) states29 of organic molecules,30–32 in particular, photoinduced processes in DNA and related systems.33–41 The second QM method is the ab initio complete-active-space second-order perturbation theory (CASPT2) as implemented in the MOLCAS 8 software package.42 For TD-DFT calculations, a tetramer involving two base pairs was treated at the quantum level while the molecular environment was taken into account via hybrid quantum mechanical/molecular mechanical (QM/MM) methods at the electrostatic embedding level including the force field point charges of the nearby residues, solvent, and ions. The QM/MM calculations performed will be hereafter denoted as CAMB3LYP/MM and CASPT2/MM, respectively. Further details on the active space definition and on the strategy adopted to reduce the computational overload of the CASPT2/MM calculations are reported in the ESI.†
Subsequently, adiabatic QM/MM dynamics were performed for the selected snapshots on the S0 and S1 potential energy surfaces at the DFT and TD-DFT levels of theory, respectively, using the AMBER/GAUSSIAN interface.43 Different QM partitions of increased complexity were considered: one, two, and four consecutive base pairs have been included in the QM partition [hereafter, (G–C)QM, (GG/CC)QM, and (GGGG/CCCC)QM partitioning, respectively (see Table S1†)]. To estimate the mechanisms giving rise to hydrogen transfer phenomena, snapshots were extracted from the S1 trajectories, and ground- and excited-state energies were subsequently recomputed with the same TD-CAMB3LYP/MM method using the TERACHEM44–46 and GAUSSIAN 09 software packages. Moreover, certain snapshots from the (G–C)QM and (GGGG/CCCC)QM trajectories were recomputed at the CASPT2/MM level to provide further benchmarking of the former method. In particular, the S0 → S1 energy gap was used to identify CI regions able to funnel the excited state return to the ground state. Even though TD-DFT/MM interfaces including surface-hopping algorithms do exist,47,48 the present work focused mainly on the excited state evolution of the system, thus reducing the computational cost while keeping a reliable description of the important features. The reader can refer to the ESI† for details on the active space used as well as the full computational details.
Results
Excited states in the Franck–Condon region
The vertical absorptions of the (dG)·(dC) homopolymer have been computed using the highly accurate CASPT2/MM method. We focused on the description of the S1 state since it constitutes the starting point for the following QM/MM simulations. The results are presented in Table S5.† For 2 out of 11 arrangements (g and i), the interstrand CT state represents the lowest-energy excited state, lying below the experimental absorption band of a (dG)·(dC) homopolymer (composed of ca. 1200 base pairs) at ∼255 nm (∼4.86 eV).49 It is reasonable to conclude that those particular situations in which the G → C states lie below the absorption peak are indeed frequent and hence deserve particular attention.In the rest of the studied DNA snapshots, the lowest-lying excited state corresponds to bright states localised in a single guanine or cytosine nucleobase and/or delocalised over π-stacked bases as Frenkel exciton states.3,4,50 Previous ab initio studies on the G–C base pair10,51 and the G/CC trimer11 at the S0 minimum are consistent with the present results. A detailed analysis is presented in the ESI.† The present CASPT2/MM results, in conjunction with the accumulated experimental16–20 and theoretical8,10–12,15,21 evidence about ESHT processes in DNA, encourage an in-depth study of the dynamics of the inter-strand CT states, which ultimately drive the hydrogen transfer processes.
In order to reduce the computational overload, we have chosen the much faster TD-CAMB3LYP/MM method to carry out the dynamic calculations. The TD-CAMB3LYP/MM method is capable of reproducing the relevant regions of the S1 surface of the G–C system in the gas phase, as can be seen from the comparison of Fig. S3† (TD-CAMB3LYP) and Fig. 6 (CASPT2) of ref. 10. As a matter of fact, at the TD-CAMB3LYP/MM level of theory, 6 out of 11 snapshots show the G → C CT state as the first singlet excited state (S1). Since here we are specifically interested in the H-transfer process, this feature can be used to facilitate the population of the G → C CT states and therefore increase the accumulation of statistical data on the ESHT events, making the dynamical study affordable.
The nature of the first excited state depends on the nuclear coordinates of the initial conditions, and it is not necessarily the brightest one. Starting the dynamics at the S1 state is an approximation of the real DNA excitation since light absorption will populate the energetically accessible bright state, mainly localized in the nucleobases,3,4,50,52 whereas the CT states are essentially dark. For this reason, even if one can expect a relatively rapid vibrational relaxation and internal conversion allowing for the population of the dark S1 state,16 the timescales presented in this work should not be considered as quantitative since the one-to-one mapping between theory and experiments is not fully achieved in the present work. Even though the G → C CT states are stabilized by the TD-DFT method, the computational protocol employed fully captures the intrinsic dynamical features of the proton transfer processes studied in this work, extensively documented by previous experimental16–20 and theoretical8,10–12,15,21 studies.
(G–C)QM dynamics
The ESHT process (see Scheme 1) consists in two sequential steps, namely an electron transfer from guanine to cytosine (G → C CT state) followed by a proton transfer triggered by the charge separation induced by the CT state.10,11 For the sake of clarity, the term ‘H atom transfer’ will be used throughout the present manuscript to refer to the asynchronous electron–proton transfer. Table 1 shows the time lapses between excitation (t = 0 fs) and the first evidence of an H atom transfer (either H1 or H21, see Fig. 1). Six out of eleven trajectories transfer an H atom (preferentially H1) before 100 fs, whereas four of them are required to stay for more than 200 fs on the S1 surface before triggering the process. In trajectories a, c, g, h, i, and j, the proton motion drives the immediate decay to the ground state, as shown by the time needed to reach the first intersection point also summarized in Table 1. On the other hand, trajectories b, d, e, and f do not immediately reach intersection areas even though the H transfer has already taken place.| Initial conditions | Time when the first H atom is transferred (dist. < 1.1 Å) | Time before reaching an intersection point (ΔE < 0.5 eV) | H atom transfer that mediates the decay |
|---|---|---|---|
| a | 285 (H21) | 288 | H21 |
| b | 20 (H1) | 386 | H1 |
| c | 99 (H1) | 112 | H1 |
| d | 113 (H1) | 216 | H1 |
| e | 235 (H1) | 280 | H1 & H21 |
| f | 26 (H1) | 226 | H1 |
| g | 15 (H21 & H1) | 30 | H1 |
| h | 288 (H21) | 288 | H21 |
| i | 296 (H1) | 300 | H1 |
| j | 50 (H1) | 64 | H1 |
| k | 39 (H1) | 40 | H1 |
| Total sum of structures | 1478 | 2241 | |
| Average time | 133 | 273 |
The results shown in Table 1 suggest that, in certain situations, the G–C base pair can actually remain in the excited state after H atom transfer, i.e. close to the INT structure (see Scheme 1), significantly increasing the INT species lifetime (runs b, d, and f). Experiments on G–C base pairs dissolved in chloroform quantified the INT lifetime as ∼2.9 ps.16 It is reasonable to think that the energy released during the H atom transfer will have an impact on the G–C geometry altering its canonical structure. Indeed, we have observed that in some trajectories, for example the run b (see Fig. S7†), the amino group of cytosine undergoes marked out-of-plane distortions. This phenomenon can be associated with the O6–H′41 hydrogen bond dissociation caused by the excess of kinetic energy provided by the H atom transfer relaxation (see Table 2).
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) O6–H′41 distances (Å) and H′41–N′4–C′4–N′3 dihedral angles (°) of the 11 (G–C)QM trajectories with the associated standard deviation (σ) values. Details on the trajectories can be found in the ESI (Fig. S6–S16)
) O6–H′41 distances (Å) and H′41–N′4–C′4–N′3 dihedral angles (°) of the 11 (G–C)QM trajectories with the associated standard deviation (σ) values. Details on the trajectories can be found in the ESI (Fig. S6–S16)
| Types of data | Average run time (fs) | # of structures |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
σ |
|---|---|---|---|---|
| a All initial conditions were run on the S0 surface for the same time lapse needed by each trajectory to reach the first intersection point on the S1 surface (see text and Table 1). | ||||
| O6–H′41 distances | ||||
| S0 dynamics | 273a | 2241a | 1.85 | 0.16 |
| S1 before any H atom transfer | 133 | 1478 | 1.88 | 0.16 |
| S1 before reaching an intersection point | 273 | 2241 | 2.05 | 0.49 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| H′41–N′4–C′4–N′3 dihedral angles | ||||
| S0 dynamics | 273a | 2241a | −1.27 | 10.26 |
| S1 before any H atom transfer | 133 | 1478 | −2.05 | 12.42 |
| S1 before reaching an intersection point | 273 | 2241 | 1.83 | 27.03 |
In order to quantify this effect, the O6–H′41 distances and the H′41–N′4–C′4–N′3 dihedral angles corresponding to the (G–C)QM trajectories at both S0 and S1 states until the system reaches an intersection point (see Fig. S6–S16†) have been statistically analysed. The results are summarized in Table 2. In the ground state, the average value (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) of the O6–H′41 distances is 1.85 ± 0.16 Å. The small standard deviation (σ) denotes a strong interaction between O6 and H′41. Propagating the system on the S1 surface before any H atom transfer has little effect on this distance. In contrast, the O6–H′41 average distance unambiguously increases from 1.85 to 2.05 Å, while the associated standard deviation reaches 0.49 Å, after the occurrence of the H atom transfers. Hence, it can be concluded that the H transfer is coupled with an increase of the distance between the nucleobases locally distorting the DNA structure.
) of the O6–H′41 distances is 1.85 ± 0.16 Å. The small standard deviation (σ) denotes a strong interaction between O6 and H′41. Propagating the system on the S1 surface before any H atom transfer has little effect on this distance. In contrast, the O6–H′41 average distance unambiguously increases from 1.85 to 2.05 Å, while the associated standard deviation reaches 0.49 Å, after the occurrence of the H atom transfers. Hence, it can be concluded that the H transfer is coupled with an increase of the distance between the nucleobases locally distorting the DNA structure.
Furthermore, the enhanced out-of-plane distortions of the –NH2 group of cytosine were evaluated by measuring the H′41–N′4–C′4–N′3 dihedral angles of both the ground and excited-state dynamics and comparing the corresponding results. The average values at the ground state are very close to 0° with standard deviations close to 10° (see Table 2). The distribution of these values is significantly wider after the H atom transfer, having a standard deviation of 27.03°. Thus, our results clearly indicate that a marked rotation of the amino group of cytosine follows the H atom transfer in the excited state before the system can decay to the ground state.
Groenhof et al.12 observed in their surface-hopping simulations that the trajectories encountered the CI seam more than once, undergoing a series of recrosses (four times, in average) between the ground and excited states. The overall consequence is the extension of the G–C excited-state lifetime after the first CI point is reached.12 Taking into account this phenomenon, the statistical results summarized in Table 2 must be considered as lower bounds of the real values. For this reason, structures more distorted and more distant from the canonical WC base pair than those observed in this work are expected in reality, in which the rotation of the –NH2 group of cytosine will likely be even more pronounced.
Since the H′41 atom can be involved in the formation of a G–C tautomer when it is transferred to the guanine nucleobase in the ground state,9–12 this dynamic effect will contribute to the intrinsic photostability of DNA hampering the tautomeric channel and favoring instead the H1 transfer back to guanine (see Fig. 2a).
The present findings allow interpreting the lack of tautomerization reported in time-resolved IR spectroscopy measurements of photoexcited DNA.17–20 It shall be noted that some tautomerization has been observed for G–C base pairs dissolved in chloroform,16 whereas in DNA duplexes only the WC arrangement is recovered. Since the former system is less constrained than the DNA double strands, we suggest that the dynamic effect presented in this work is also responsible for the preferred photostability displayed by the G–C base pair in chloroform.16 We thus ascribe the differences observed in the tautomerization yield to the sensitivity of the CI seam to the environment. Further evidence of this environment dependence is provided by the lifetimes of the INT species embedded in different systems. While the lifetime is ∼2.9 ps in a G–C base pair dissolved in chloroform,16 slower decays of ∼5 ps were recorded for GC/GC miniduplexes (tetramers)17 and of 7–7.6 ps for d(GC)·d(GC) duplexes,18–20 where the solvent is much less accessible and the G–C couple remains in the more hydrophobic DNA core. Therefore, there are no reasons to think that the out-of-plane distortions of the cytosine –NH2 group do not take place in the less-constrained G–C base pair dissolved in chloroform.
The lifetimes recorded experimentally at the few-picosecond scale do not contradict our present simulations for a number of reasons: (i) the large 0.5 eV threshold is used to consider a structure as part of the CI seam and (ii) the diabatic S1/S0 crossings/recrossings are not taken into account in the present work.
The majority of QM/MM simulations gave rise to H transfers at the central hydrogen bond H1–N1 (see Table 2), whereas three trajectories underwent H transfer at the H21–O′2 bond in agreement with what was predicted by the static calculations reported in a previous study.10 In fact, the N1–H1 and H21–O′2 distances of all (G–C)QM trajectories displayed in Fig. S6–S16† suggest that both H1 and H21 atoms play an important role in the evolution of the G–C system in the excited state, finding many situations in which both H atoms are partially or completely transferred simultaneously.
It is worth mentioning that two trajectories, namely runs d and g, had a Na+ counterion in the vicinity of the G–C base pair, in particular, interacting with the O6 atom of guanine (see Fig. S9 and S12,† respectively). However, only the G–C base pair of trajectory g seems to significantly show the effects of the positive charge on the surroundings (see Fig. 2b), probably due to the shorter Na+–O6 distances as compared to the ones of the run d. The effect of the nearby positive charge consists in triggering the transfer of both H1 and H21 atoms simultaneously accompanied by a marked energy degeneracy between the excited and ground states in all the snapshots. The enhancement of the capability to transfer H atoms could be explained by the interaction of the positive charge (Na+) with guanine, whose electronic density has been decreased due to the electron accumulation caused by the G → C CT nature of the excited state. The presence of a nearby positive charge can indeed increase the global polarity of the CT state favoring the proton transfer to cytosine. Thus, from our results emerge the possible role played by cations, or generally positive charges, in influencing DNA photochemistry.
(GG/CC)QM and (GGGG/CCCC)QM dynamics
In addition to the previous dynamics, we also run simulations using a (GG/CC)QM partitioning scheme, therefore enabling possible intra-strand delocalisation of the excitations (Frenkel excitons). The results, shown in Table 3 and Fig. S20–S22,† are in reasonable agreement with the (G–C)QM trajectories. Unsurprisingly, the weakening of the hydrogen bonding between guanine and cytosine in the excited state previously described for a single G–C base pair is operative when considering two stacked G-C systems, in view of the O6–H′41 distances and H′41–N′4–C′4–N′3 dihedral angles shown in Fig. S23 and S24,† respectively.| Run | Approx. time when the first H atom is transferred (fs) | Photochemical decay |
|---|---|---|
| (GG/CC) QM partition | ||
| a | 54 | ESHT |
| b | 32 | H21–O′2 transfer |
| c | 26 | ESHT |
| d | 113 | ESHT |
| e | 80 | ESHT |
| f | 83 | ESHT |
| g | 54 | FPT |
| h | 484 | ESHT |
| i | 38 | ESHT |
| j | 50 | ESHT |
| k | 104 | ESHT |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| (GGGG/CCCC) QM partition | ||
| g | 55 | FPT |
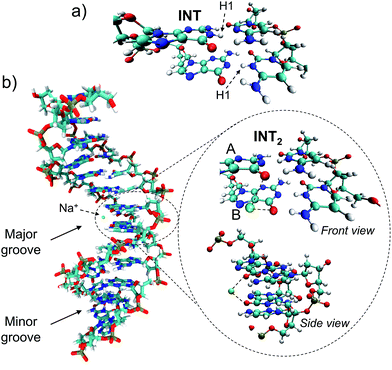
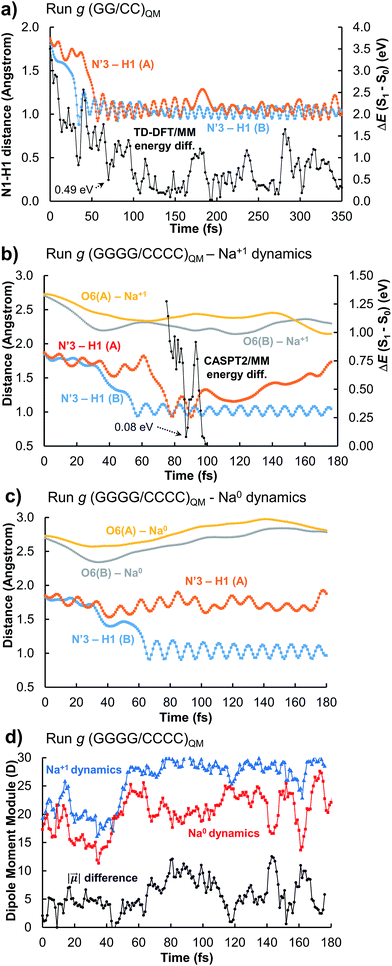
Trajectory g, however, led to an unexpected outcome consisting in the formation of two intermediate species in the adjacent G–C base pairs A and B. This phenomenon determines the generation of the so-called INT2 structure (see Fig. 3), leading to a FPT event. The motion of the two protons is coupled, resulting in a simultaneous multiple proton transfer. Fig. 4a displays the N1–H1 distances of both adjacent G–C base pairs A and B corresponding to the trajectory g of the (GG/CC)QM system. It can be seen that the system reaches the intersection seam at 70 fs, where both H atoms of adjacent G–C pairs are completely transferred to the corresponding cytosine molecules.
To better validate these results, the trajectory g was re-run increasing the QM partition up to four G–C base pairs, i.e. (GGGG/CCCC)QM partition (see Table S1 and Video in the ESI†). This increase of the QM subsystem allows the inclusion of polarization effects and improves the description of the excited states. The double H atom transfer is also observed, although the H atom of the G–C pair B returns to the guanine moiety after ∼120 fs. The S1 and S0 energies of the snapshots displaying a clear INT2 structure were computed at the CASPT2/MM level, describing with the ab initio method only the two G–C pairs of interest and treating the rest as point electrostatic charges. The results are reported in Fig. 4b which clearly confirm the FPT transfer mechanism as an operative channel to deactivate the DNA excited states, complementary to the ESHT (see Table 3). Note that a larger set of trajectories should be run in order to statistically quantify the relative occurrence of the ESHT and FPT processes; thus the present work should be considered only as a proof of principle for the coexistence of both processes. The (GGGG/CCCC)QM snapshot at t = 87 fs, corresponding to the CI point of Fig. 4b, was selected to compute the hop in the ground state, where the trajectory was restarted. The dynamics show the multiple proton transfer back to the guanine molecules, recovering the initial WC base pairing and completing the FPT event (see Fig. S25†).
In order to evaluate the possible influence of the environment on the S1/S0 energy gap, the snapshot at t = 87 fs was computed in vacuo, i.e. in the absence of the electrostatic charges of the environment, using the CASPT2 method. The resulting energy difference is 0.01 eV whereas with the CASPT2/MM protocol it is 0.08 eV (Fig. 4b). At the TD-CAMB3LYP/MM level, the system reaches the intersection at t = 106 fs, where the energy difference is 0.25 eV and the N3′–H1(A) and N3′–H1(B) distances are 1.22 and 0.96 Å, respectively (see Fig. S5†). The inherent CI character of the INT2 structure, independent from the QM method and the presence or absence of the full DNA environment, unveils a novel decay mechanism involving H transfers in two adjacent G–C base pairs that further supports the natural photostability of DNA.
The role of possible jumps to higher excited states (S2), not considered in this work, has also been evaluated and shown in the ESI.† This possibility arises from the excess of kinetic energy provided by the relaxation from the FC region. Tables S8 and S9† compile the energy differences between the S1 and S2 states of the run g (Fig. 4b), whereas Fig. S26 and S27† show the nature of the excited wave functions for some relevant snapshots. Taking into account that S2 is unlikely to be populated prior to the proton transfer, the relatively similar nature of the lowest-lying G → C CT states, the absence of alternative minima or additional features between the FC and CT/S0 structures,12 and the experimental evidence of proton transfer,16–20 it can be safely concluded that while hops to S2 should be possible in certain situations, these non-adiabatic effects will not change the outcome of the dynamics reported in the present work.
The driving force of the photoinduced FPT could be ascribed to the presence of Na+ ions in the vicinity of the G–C base pair placed in the major groove (Fig. 3b). The presence of a nearby positive charge can actually induce perturbation in the polarity of the delocalized CT states along the DNA strand, favouring the motion of the protons of the two adjacent G–C base pairs. This hypothesis has been checked by changing the charge of the nearby sodium atom from +1 to 0 and repeating the (GGGG/CCCC)QM dynamics using the same initial coordinates and velocities as the trajectory shown in Fig. 4b; the results of the ‘Na0 dynamics’ are displayed in Fig. 4c. It can be readily seen that the FPT transfer does not take place since only one H1 atom (base pair B) is completely transferred. Obviously, the ‘Na0 dynamics’ should be considered as a computational artificial model; however, it is useful to understand the specific impact of the nearby positive charge on the DNA excited-state dynamics. Fig. 4d shows the dipole moment modules |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | of the QM subsystem corresponding to both the ‘Na1+ dynamics’ (Fig. 4b) and the ‘Na0 dynamics’ (Fig. 4c). The time series describing both trajectories are almost parallel, although the latter has significantly lower values due to the neutral charge of the sodium atom and its less pronounced electrostatic influence. Important differences, larger than 5 D, are noted from 60 to 120 fs, which correspond to the time lapse in which the second proton transfer takes place in the ‘Na1+ simulation’(Fig. 4b).
| of the QM subsystem corresponding to both the ‘Na1+ dynamics’ (Fig. 4b) and the ‘Na0 dynamics’ (Fig. 4c). The time series describing both trajectories are almost parallel, although the latter has significantly lower values due to the neutral charge of the sodium atom and its less pronounced electrostatic influence. Important differences, larger than 5 D, are noted from 60 to 120 fs, which correspond to the time lapse in which the second proton transfer takes place in the ‘Na1+ simulation’(Fig. 4b).
The proposed FPT transfer mechanism is displayed in Fig. 5. In contrast to the intermediate (INT) structure ascribed to the ESHT process,9–12 INT2 has a biradical zwitterionic nature in the excited state, in which a net negative charge is delocalised over a guanine nucleobase. The molecular charges compiled in Tables S6 and S7† support this evidence. Note that even though the charge separation can be localized either in the same or different G–C pairs (see molecular charges of S1 and S2 states in Table S6†), the charge separation between adjacent G–C base pairs drove the FPT mechanism observed in the present work. Therefore, it can be suggested that the nearby Na+ could stabilize the negative charge of guanine displayed in the INT2 structure. The radiationless decay from S1 to S0 implies an electron back-transfer to the guanine base. The negative charge over the two stacked G/G nucleobases drives the overall return of the two protons back to the corresponding guanine moieties.
Discussion and conclusions
This work reports the excited-state dynamic simulation of a (dG)·(dC) B-DNA homopolymer in water solution using QM/MM computational methods. An intrinsic feature of the G–C base pairs that prevents the formation of tautomeric structures is unveiled on the basis of the comparative study of the O6–H′41 distances and the H′41–N–C–N1 dihedral angles both in the excited and ground states. The phenomenon is ascribed to the energy released during the proton transfer in the excited state. In addition, the influence of the nearby cations on the DNA excited-state decay has been assessed for the first time. A novel mechanism of DNA deactivation (FPT process) leading to the recovery of the Watson–Crick pairing is presented, in which two protons of two adjacent G–C base pairs are transferred forth and back from the guanine to the corresponding cytosine moieties. This photoresponse mechanism is triggered by the polarization of the CT state caused by a nearby Na+ atom, occurring via an intermediate structure (INT2), which possesses biradical zwitterionic character in the excited state. Future experimental studies capable of detecting this likely elusive species are strongly encouraged.Hence, our results suggest that cations in solution could enhance proton transfer processes taking place during the excited-state decay of DNA structures. This is important since positive charges are needed to neutralize the negative charges of DNA and therefore are ubiquitous around DNA under biological conditions. In particular, the intracellular concentration of K+, Na+, and Mg2+ under physiological conditions ranges from 1 to 100 mM.53 The DNA–cation interactions have been extensively documented in the last few decades.54–56 In particular, direct contact of Na+ atoms with the O6 position of guanine in helical RNA has been recently reported.57 Lavery et al. used microsecond MD to show that K+ ions exhibit a density peak in the radial distribution function within the grooves (ca. 2.5 Å).58 Furthermore, Pasi et al.59 reported K+ occupancies up to ∼0.3 in the major groove of a (dG)·(dC) homopolymer. While these values were not considered to be particularly high, they prove the occurrence of ion–DNA interactions in the major groove of the homopolymer in agreement with our shorter MD simulations. However, it shall be remarked that the specific DNA sequence modulates the cation availability.59 Since more ion–DNA interactions were documented for other sequences containing adjacent GC base pairs like GGGA, the FPT mechanism could be even more favoured in other DNA sequences not considered in this work.
The radial distribution function g(r) of the Na+ atoms with respect to the O6 atoms of the guanine molecules of G–C base pairs A and B (see Fig. 3) of the present MD simulation (100 ns) is displayed in Fig. 6, showing reasonable agreement with the much longer simulations performed by Lavery et al.,58 also pointing to the accumulation of sodium ions in the vicinity of the DNA double strand.53,59
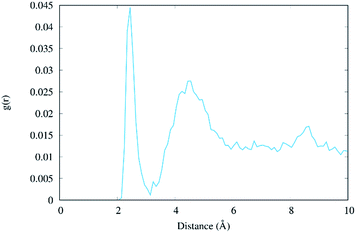 | ||
| Fig. 6 Radial distribution function g(r) of the distance between Na+ ions and the O6 atoms of the two central guanine molecules (residues #7 and #8, see Table S1†). | ||
Surprisingly, we found that the intermediate formed in the photo-induced processes under the close interaction of Na+ favours photostability, unveiling another factor that may have played a role in the natural chemical selection of nucleic acids over the past millions of years. It is, however, currently unclear if other photochemical processes operating under the influence of nearby charged species may lead to any kind of DNA photodamage. Hence our studies, while unequivocally confirm the extremely complicated mechanisms operating in DNA photochemistry, in particular, the coupling between different decay pathways and the crucial role of the environment in their specific modulation, also shed light on entirely new channels strongly enhancing photostability. This aspect is indeed even more relevant taking into account that the DNA photostability should be considered as the result of the competition between different deactivation channels that open upon light absorption.1 The crucial role played by cations implies us to reconsider the role of the environment – that it should be taken into account not only as a spectator but also as an active player in the excited state evolution of DNA. A particularly intriguing related hypothesis could be related to the role played by the highly positively charged nucleosomal environment necessary to maintain the supercoiled structure of DNA. Indeed, one could speculate that in addition to its structural role, the positive charge of this specific environment could also act as a protective agent against the production of photolesions. To confirm this hypothesis we plan to extend our study to DNA in the presence of compacting proteins, such as bacterial histone-like units or human histones.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. F. M. is grateful to the French ANR and ‘Région Grand Est’ government for the financial support. D. R.-S. acknowledges the “Ramón y Cajal” grant (Ref. RYC-2015-19234) by the Spanish MINECO. A. F.-M. and D. R.-S. thank the Spanish MINECO for the financial support (CTQ2017-87054-C2-2-P project and Unidad de Excelencia María de Maeztu MDM-2015-0538). M. M. is grateful to the Universidad de La Rioja (UR) for a postdoctoral grant.References
- A. A. Beckstead, Y. Zhang, M. S. de Vries and B. Kohler, Phys. Chem. Chem. Phys., 2016, 18, 24228–24238 RSC.
- L. Serrano-Andrés and M. Merchán, J. Photochem. Photobiol., C, 2009, 10, 21–32 CrossRef.
- A. Giussani, J. Segarra-Martí, D. Roca-Sanjuán and M. Merchán, Top. Curr. Chem., 2015, 355, 57–97 CrossRef PubMed.
- R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593 CrossRef PubMed.
- C. E. Crespo-Hernandez, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019 CrossRef PubMed.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939–6960 CrossRef PubMed.
- A. Abo-Riziq, L. Grace, E. Nir, M. Kabelac, P. Hobza and M. S. de Vries, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 20–23 CrossRef PubMed.
- A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2004, 6, 2763–2771 RSC.
- A. L. Sobolewski, W. Domcke and C. Hattig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906 CrossRef PubMed.
- V. Sauri, J. P. Gobbo, J. J. Serrano-Pérez, M. Lundberg, P. B. Coto, L. Serrano-Andrés, A. C. Borin, R. Lindh, M. Merchán and D. Roca-Sanjuán, J. Chem. Theory Comput., 2013, 9, 481–496 CrossRef PubMed.
- A. Francés-Monerris, J. Segarra-Martí, M. Merchán and D. Roca-Sanjuán, Theor. Chem. Acc., 2016, 135, 31 Search PubMed.
- G. Groenhof, L. V. Schaefer, M. Boggio-Pasqua, M. Goette, H. Grubmueller and M. A. Robb, J. Am. Chem. Soc., 2007, 129, 6812–6819 CrossRef PubMed.
- A. N. Alexandrova, J. C. Tully and G. Granucci, J. Phys. Chem. B, 2010, 114, 12116–12128 CrossRef PubMed.
- P. R. L. Markwick and N. L. Doltsinis, J. Chem. Phys., 2007, 126, 175102 CrossRef PubMed.
- S. Yamazaki and T. Taketsugu, Phys. Chem. Chem. Phys., 2012, 14, 8866–8877 RSC.
- K. Röttger, H. J. B. Marroux, M. P. Grubb, P. M. Coulter, H. Bohnke, A. S. Henderson, M. C. Galan, F. Temps, A. J. Orr-Ewing and G. M. Roberts, Angew. Chem., Int. Ed., 2015, 54, 14719–14722 CrossRef PubMed.
- Y. Zhang, X.-B. Li, A. M. Fleming, J. Dood, A. A. Beckstead, A. M. Orendt, C. J. Burrows and B. Kohler, J. Am. Chem. Soc., 2016, 138, 7395–7401 CrossRef PubMed.
- Y. Zhang, K. de La Harpe, A. A. Beckstead, R. Improta and B. Kohler, J. Am. Chem. Soc., 2015, 137, 7059–7062 CrossRef PubMed.
- D. B. Bucher, A. Schlueter, T. Carell and W. Zinth, Angew. Chem., Int. Ed., 2014, 53, 11366–11369 CrossRef PubMed.
- G. W. Doorley, D. A. McGovern, M. W. George, M. Towrie, A. W. Parker, J. M. Kelly and S. J. Quinn, Angew. Chem., Int. Ed., 2009, 48, 123–127 CrossRef PubMed.
- L. Martínez-Fernández and R. Improta, Faraday Discuss., 2018, 207, 199–216 RSC.
- C. Ko and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2013, 4, 2540–2545 CrossRef.
- A. W. Lange and J. M. Herbert, J. Am. Chem. Soc., 2009, 131, 3913–3922 CrossRef PubMed.
- M. K. Shukla and J. Leszczynski, J. Phys. Chem. A, 2002, 106, 4709–4717 CrossRef.
- D. A. Case, R. M. Betz, D. S. Cerutti, I. T. E. Cheatham, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER 2016, Univ. California, San Francisco Search PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2016, 13, 55–58 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martín, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, 2010, Gaussian Inc., Wallingford CT Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- M. M. Alam, R. Misra and K. Ruud, Phys. Chem. Chem. Phys., 2017, 19, 29461–29471 RSC.
- L. E. R. Buckley, B. J. Coe, D. Rusanova, V. D. Joshi, S. Sánchez, M. Jirásek, J. Vávra, D. Khobragade, L. Severa, I. Císařová, D. Šaman, R. Pohl, K. Clays, G. Depotter, B. S. Brunschwig and F. Teplý, J. Phys. Chem. A, 2017, 121, 5842–5855 CrossRef PubMed.
- C. Ma, Y. Yang, C. Li and Y. Liu, Theor. Chem. Acc., 2016, 135, 229 Search PubMed.
- L. Martínez-Fernández, A. J. Pepino, J. Segarra-Martí, J. Jovaisaite, I. Vaya, A. Nenov, D. Markovitsi, T. Gustavsson, A. Banyasz, M. Garavelli and R. Improta, J. Am. Chem. Soc., 2017, 139, 7780–7791 CrossRef PubMed.
- F. Santoro, V. Barone and R. Improta, J. Am. Chem. Soc., 2009, 131, 15232–15245 CrossRef PubMed.
- J. M. Olsen, K. Aidas, K. V. Mikkelsen and J. Kongsted, J. Chem. Theory Comput., 2010, 6, 249–256 CrossRef PubMed.
- L. Biemann, S. A. Kovalenko, K. Kleinermanns, R. Mahrwald, M. Markert and R. Improta, J. Am. Chem. Soc., 2011, 133, 19664–19667 CrossRef PubMed.
- F. Santoro, V. Barone, A. Lami and R. Improta, Phys. Chem. Chem. Phys., 2010, 12, 4934–4948 RSC.
- L. Martínez-Fernández, A. J. Pepino, J. Segarra-Martí, A. Banyasz, M. Garavelli and R. Improta, J. Chem. Theory Comput., 2016, 12, 4430–4439 CrossRef PubMed.
- M. Pola, M. A. Kochman, A. Picchiotti, V. I. Prokhorenko, R. J. D. Miller and M. Thorwart, J. Theor. Comput. Chem., 2017, 16, 1750028 CrossRef.
- Y.-J. Ai, F. Zhang, G.-L. Cui, Y. Luo and W.-H. Fang, J. Chem. Phys., 2010, 133, 64302 CrossRef PubMed.
- M. S. Nørby, C. Steinmann, J. M. H. Olsen, H. Li and J. Kongsted, J. Chem. Theory Comput., 2016, 12, 5050–5057 CrossRef PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2015, 37, 506–541 CrossRef PubMed.
- A. W. Götz, M. A. Clark and R. C. Walker, J. Comput. Chem., 2014, 35, 95–108 CrossRef PubMed.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2008, 4, 222–231 CrossRef PubMed.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2009, 5, 1004–1015 CrossRef PubMed.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef PubMed.
- S. Mai, H. Gattuso, M. Fumanal, A. Muñoz-Losa, A. Monari, C. Daniel and L. González, Phys. Chem. Chem. Phys., 2017, 19, 27240–27250 RSC.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 26–33 Search PubMed.
- I. Vaya, P. Changenet-Barret, T. Gustavsson, D. Zikich, A. B. Kotlyar and D. Markovitsi, Photochem. Photobiol. Sci., 2010, 9, 1193–1195 RSC.
- J. J. Nogueira, F. Plasser and L. González, Chem. Sci., 2017, 8, 5682–5691 RSC.
- H. Sun, S. Zhang, C. Zhong and Z. Sun, J. Comput. Chem., 2016, 37, 684–693 CrossRef PubMed.
- M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458 CrossRef PubMed.
- I. Turel and J. Kljun, Curr. Top. Med. Chem., 2011, 11, 2661–2687 CrossRef PubMed.
- M. Egli, Chem. Biol., 2002, 9, 277–286 CrossRef PubMed.
- N. V. Hud and M. Polak, Curr. Opin. Struct. Biol., 2001, 11, 293–301 CrossRef PubMed.
- C. F. Anderson, M. T. Record and P. A. Hart, Biophys. Chem., 1978, 7, 301–316 CrossRef PubMed.
- N. M. Fischer, M. D. Polêto, J. Steuer and D. van der Spoel, Nucleic Acids Res., 2018, 46, 4872–4882 CrossRef PubMed.
- R. Lavery, J. H. Maddocks, M. Pasi and K. Zakrzewska, Nucleic Acids Res., 2014, 42, 8138–8149 CrossRef PubMed.
- M. Pasi, J. H. Maddocks and R. Lavery, Nucleic Acids Res., 2015, 43, 2412–2423 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details; energy differences for the (G–C)QM runs; N1–H1 and O6–H′41 distances, and H′41–N′4–C′4–N′3 dihedral angles; molecular charges of the FPT mechanism. Video representing the FPT transfer. See DOI: 10.1039/c8sc03252a |
| This journal is © The Royal Society of Chemistry 2018 |