Open Access Article
Open Access ArticleA quantitative connection of experimental and simulated folding landscapes by vibrational spectroscopy†
Caitlin M.
Davis‡
ab,
Laura
Zanetti-Polzi‡
c,
Martin
Gruebele
 ad,
Andrea
Amadei
ad,
Andrea
Amadei
 e,
R. Brian
Dyer
e,
R. Brian
Dyer
 *b and
Isabella
Daidone
*b and
Isabella
Daidone
 *c
*c
aDepartment of Chemistry and Department of Physics, University of Illinois at Urbana-Champaign, IL 61801, USA
bDepartment of Chemistry, Emory University, Atlanta, GA 30322, USA. E-mail: briandyer@emory.edu
cDepartment of Physical and Chemical Sciences, University of L'Aquila, 67010 L'Aquila, Italy. E-mail: Isabella.daidone@univaq.it
dCenter for Biophysics and Quantitative Biology, University of Illinois at Urbana-Champaign, IL 61801, USA
eDepartment of Chemical and Technological Sciences, University of Rome “Tor Vergata”, 00133 Rome, Italy
First published on 3rd October 2018
Abstract
For small molecule reaction kinetics, computed reaction coordinates often mimic experimentally measured observables quite accurately. Although nowadays simulated and measured biomolecule kinetics can be compared on the same time scale, a gap between computed and experimental observables remains. Here we directly compared temperature-jump experiments and molecular dynamics simulations of protein folding dynamics using the same observable: the time-dependent infrared spectrum. We first measured the stability and folding kinetics of the fastest-folding β-protein, the GTT35 WW domain, using its structurally specific infrared spectrum. The relaxation dynamics of the peptide backbone, β-sheets, turn, and random coil were measured independently by probing the amide I′ region at different frequencies. Next, the amide I′ spectra along folding/unfolding molecular dynamics trajectories were simulated by accurate mixed quantum/classical calculations. The simulated time dependence and spectral amplitudes at the exact experimental probe frequencies provided relaxation and folding rates in agreement with experimental observations. The calculations validated by experiment yield direct structural evidence for a rate-limiting reaction step where an intermediate state with either the first or second hairpin is formed. We show how folding switches from a more homogeneous (apparent two-state) process at high temperature to a more heterogeneous process at low temperature, where different parts of the WW domain fold at different rates.
Introduction
Our understanding of how protein dynamics regulate folding and function has made great strides thanks to parallel developments in experiment, theory, and computation. Protein folding simulations have extended to the millisecond timescale, providing extensive sampling of fast folding proteins and atomistic-level structural prediction of folding mechanisms.1,2 Meanwhile, sub-millisecond ensemble or single-molecule experiments often report on a single parameter, for example fluorescence lifetime of tryptophan residues or Förster resonance energy transfer (FRET) efficiency.3 Yet the connection between experimental and computational observables remains limited: while the computed solvent-accessible surface area of tryptophan4 or interatomic distances5,6 can serve as proxies for fluorescence or FRET, they are just rough approximations of real fluorescence spectra and quenching. Furthermore, multiple experimental probes are necessary to even begin to capture the full complexity of the protein folding energy landscape.3,5,7–10Infrared spectroscopy (IR) offers a label-free multiple-probe approach for monitoring protein structure and dynamics.11 The amide I′ mode of the peptide backbone is sensitive to secondary structure; characteristic infrared bands can be assigned to solvated and buried α-helices, β-sheets, turns and random coil structures. Time-resolved infrared spectroscopy of these bands has been successfully employed to identify complexities in the folding landscape that are hidden to single-probe experiments. Differences in the folding order and times of β-sheets and turns in β-proteins have been identified,7–9,12,13 the order of helix packing in α-helical proteins14 has been identified, and secondary structure formation has been distinguished from formation of the local tryptophan environment.7,10
Calculations that accurately reconstruct the time-resolved experimental IR spectra could solve the conundrum of not comparing the exact same computed and measured observables. However, most computational IR approaches15–19 suffer from insufficient configurational sampling due to the computational expense of modeling many interconverting structures over a wide range of time scales. Our approach addresses these challenges using a mixed quantum mechanics/molecular dynamics (QM/MD) computational methodology based on the Perturbed Matrix Method (PMM), called MD-PMM.20 Differently from other hybrid methods, MD-PMM makes use of classical MD simulations to provide configurational sampling of the whole system. This enables statistically relevant sampling of the quantum-center and environment configurations, which is required for accurate IR spectra calculations of proteins. This method has been calibrated recently with static IR spectra of amyloids,21 unfolded protein states,22,23 and equilibrium protein folding,24,25 as well as by calculating reduction potentials26,27 and electron transfer processes28,29 in proteins.
Here we directly compare measurements and quantitative modeling of the time-resolved amide I′ IR spectrum of one of the most widely studied fast-folding β-proteins, the WW domain. The WW domain family consists of an antiparallel and highly twisted three-stranded β-sheet structure with a small hydrophobic core and two conserved tryptophan residues.30–32 WW domains have been the focus of extensive computational and experimental studies because of their fast folding rates and simple structure.7,8,12,24,33–45 Most models predict folding through an intermediate where predominantly the first hairpin is formed.7,12,34,36,41,42 Recently, a multi-path model has emerged where folding can proceed in a concerted fashion, or via intermediate states that have either the first or second hairpin formed.24,39,46 These different pathways are difficult to unravel with a single observable such as tryptophan fluorescence.
We directly compare measured and calculated time-resolved IR spectra at multiple frequencies for the fast-folding WW domain, GTT35 (Fig. 1). GTT35 relaxes in approximately 4 μs in response to a laser-induced temperature jump (T-jump).40 T-jump experiments probed by time-resolved IR spectroscopy independently monitored β-sheets, turns, and random coil by looking at different wavelengths of the amide I′ IR spectrum. Three kinetics time scales, corresponding to at least four states were revealed. Above 55 °C the time scales converge and there is little difference in the observed kinetics at different frequencies. Below 55 °C, the dynamics of the turn are faster than the β-sheets, consistent with a zipping folding mechanism.
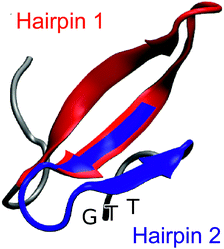 | ||
| Fig. 1 Representative snapshot of the folded structure extracted from the folding/unfolding MD simulation40 of GTT35, a fast-folding variant of FiP35 WW domain. The residues belonging to hairpin 1 (residue 8–22) are highlighted in red and the residues belonging to hairpin 2 (residues 19–30) are highlighted in blue. The position of the GTT mutation in hairpin 2 of the parent FiP35 WW domain is labeled. | ||
To structurally characterize the kinetic folding intermediates, we computed the time-dependent amide I′ IR signal of the backbone for four independent folding/unfolding MD simulations of GTT35 previously performed on the ANTON supercomputer.40,47 Three kinetic states are identified (fully folded, unfolded, and intermediate with either one of the hairpins formed) and the time evolution of the probability of each state is used to develop a three-state kinetic model. The time-resolved frequency-dependent IR signal is calculated at the same frequencies as the experiments at high temperature. There is excellent agreement between the slow phase of the experiments and the calculated IR signals. Furthermore, these calculations reveal that the IR signal is consistent with folding through intermediates where either hairpin 1 or hairpin 2 is formed first. Such an atomistic level interpretation of the experimental results was possible due to the quantitative comparison between the same computed and experimental observable. This demonstrates how high-fidelity computation of actual experimental observables can provide a deep understanding of the dynamics of complex molecules, and at the same time validate the mechanisms found in simulations.
Results and discussion
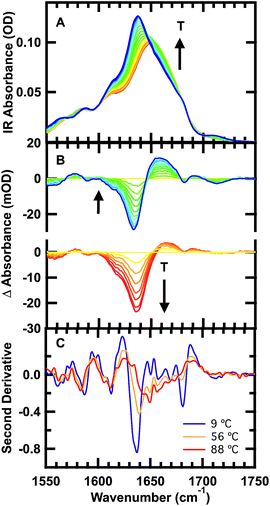
Temperature-dependent FTIR spectra
The FTIR spectra of GTT35 provide evidence for non-two-state folding behavior: pre-melting of the β-sheets prior to the main transition. The thermal unfolding of GTT35 was studied over the range from 9 to 88 °C in 5 °C intervals using FTIR spectroscopy monitored in the amide I′ region (Fig. 2A), the amide I region of peptides in D2O. The amide I′ absorbance arises from C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations of the polypeptide backbone carbonyls and is an established indicator of secondary structure.48–50 This relatively broad band contains contributions from the entire polypeptide backbone, which in the case of GTT35 includes β-sheet, β-turn, and random coil structure. Although signals due to amino acid side chains may overlap with the amide I mode, there are many more amide I vibrations and the extinction coefficient of the amide I mode is an order of magnitude larger than that of the amino acid side chains in the amide I region.11 Interstrand coupling between hydrogen bonds in the β-sheets will further enhance vibrations in the amide I mode. Therefore, the side chain resonances do not strongly influence the IR spectra and were not included in the calculations.
O stretching vibrations of the polypeptide backbone carbonyls and is an established indicator of secondary structure.48–50 This relatively broad band contains contributions from the entire polypeptide backbone, which in the case of GTT35 includes β-sheet, β-turn, and random coil structure. Although signals due to amino acid side chains may overlap with the amide I mode, there are many more amide I vibrations and the extinction coefficient of the amide I mode is an order of magnitude larger than that of the amino acid side chains in the amide I region.11 Interstrand coupling between hydrogen bonds in the β-sheets will further enhance vibrations in the amide I mode. Therefore, the side chain resonances do not strongly influence the IR spectra and were not included in the calculations.
The changes in structure with temperature are highlighted by the difference spectra (Fig. 2B). The difference spectra are generated using the spectrum at 56 °C as a reference. Negative peaks correspond to specific structures or interactions present at low temperature, and positive peaks correspond to new interactions at higher temperature. Both below and above the reference temperature, the spectra exhibit similar spectral changes associated with the loss of folded population as the temperature is raised.
Although structure is lost continuously with temperature, states that are structurally intermediate between the folded state and the heat-denatured state are clearly populated. The isosbestic point shifts from 1645 cm−1 to 1652 cm−1 in the IR spectrum (Fig. 2A), and there is no clear isosbestic point when the lowest temperature spectrum is used as the basis for generating the difference spectra (Fig. 2B and S1†).
The second derivative spectra at 9 °C, 56 °C, and 88 °C further demonstrate differences between folded, intermediate, and denatured structures (Fig. 2C). At 9 °C there are three major peaks in the amide I′ region centered at 1613 cm−1, 1637 cm−1, and 1681 cm−1. These peaks have previously been observed in other WW domains.7,8,51 The peak at ≈1611 cm−1 has been assigned to an amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group in the turn of β-hairpins, typically involved in multiple hydrogen bonds with side chain or backbone donors.52,53 IR bands at 1634 and 1681 cm−1 are well-established indicators of antiparallel β-sheets.54 The peak at 1634 cm−1 arises from out-of-phase and the peak at 1681 cm−1 from in-phase carbonyl vibrations in the sheet. Interstrand coupling between multiple or longer β-sheets increases the intensity and decreases the frequency of the lower frequency peak.54
O group in the turn of β-hairpins, typically involved in multiple hydrogen bonds with side chain or backbone donors.52,53 IR bands at 1634 and 1681 cm−1 are well-established indicators of antiparallel β-sheets.54 The peak at 1634 cm−1 arises from out-of-phase and the peak at 1681 cm−1 from in-phase carbonyl vibrations in the sheet. Interstrand coupling between multiple or longer β-sheets increases the intensity and decreases the frequency of the lower frequency peak.54
The same three peaks observed at 9 °C are also observed in the intermediate temperature spectrum at 56 °C: 1612, 1640 and 1680 cm−1. The shift of the band at 1634 cm−1 to 1640 cm−1 is indicative of melting of the β-sheets in the intermediate state. A peak at 1713 cm−1 present in the low temperature melt (56-T) is absent in the high temperature melt (T-56). This vibrational mode was also observed in FiP35, the parent of GTT35, and was assigned to hydrogen bonding between the carbonyl of the protonated aspartic acid side chain and the hydroxyl of the serine in the first turn.8 Hence, there are distinct structural rearrangements in both the turn and β-sheets of the WW domain at intermediate temperature.
Finally, at the highest temperature tested, 88 °C, there is a peak at 1612 and a broad peak centered at 1660 cm−1. The broad peak at 1660 cm−1 is characteristic of disordered polypeptides, as GTT35 mostly unfolds at high temperature.55–57 That the 1612 cm−1 peak is unchanged at 88 °C suggests that the WW domain is not completely unfolded yet.
A similar pattern of non-two-state folding emerges from singular value decomposition (SVD) of the spectra, with addition of a clearly identifiable cold-denatured state (see ESI, Fig. S2 and S3†). While a cold-denatured state of GTT35 has not been previously reported, such a state was previously postulated to exist.37 The SVD analysis, together with the IR difference spectra (Fig. 2B) and a global fitting of the thermal melts (Fig. S4†), supports the population of at least two thermodynamic states below the main thermal transition, one of which could be a folding intermediate, and the other cold denatured.
Temperature-jump relaxation kinetics
The relaxation kinetics of GTT35 WW domain following a laser-induced temperature jump were probed using time-resolved infrared spectroscopy (Fig. 3). Structure-specific measurements were made using the amide I′ frequency for the turns (1613 cm−1), residues involved in interstrand coupling of the sheets (1637 and 1681 cm−1), and disordered polypeptide (1660 cm−1). The fits of the data in Fig. 3 are reported in Table 1. The complete relaxation kinetics for each frequency is reported in the ESI (Tables S1–S4†). The magnitude of the jump was kept constant while varying the final temperature. Similar to FiP35 and other WW domains,7,8,12 at low temperatures the relaxation kinetics in the amide I′ region are best fit by a triple exponential (eqn (1), see Experimental). Multiple exponentials are observed due to overlap between the bands. It is also likely that the spectral response is coupled, so that formation of one structure affects others.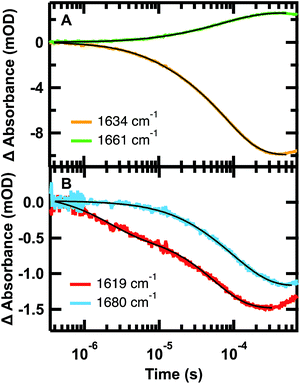 | ||
| Fig. 3 Representative IR T-jump relaxation kinetics of 2.0 mM GTT35 in 20 mM potassium phosphate buffer pD 7.0 monitored in the amide I′ spectral region at 1619, 1634, 1660, and 1680 cm−1 following a T-jump from 30–45 °C. A triple exponential fit is overlaid on the 1634 cm−1 kinetic trace, a double exponential fit is overlaid on the 1661 and 1619 cm−1 kinetic traces, and a single exponential fit is overlaid on the 1680 cm−1 kinetic trace (eqn (1)). | ||
| Wavelength | τ 1 (μs) | τ 2 (μs) | τ 3 (μs) |
|---|---|---|---|
| 1619 cm−1 | — | 1.9 ± 0.6 | 54.0 ± 0.7 |
| 1634 cm−1 | 1.8 ± 0.3 | 12.5 ± 0.4 | 83.2 ± 0.3 |
| 1661 cm−1 | — | 15.1 ± 0.7 | 84 ± 1 |
| 1680 cm−1 | — | — | 90.0 ± 0.7 |
As anticipated, there is good agreement between the kinetics of the slow phase (τ3) measured at 1634 and 1680 cm−1, which are both probes of the β-sheets. The intermediate (τ2) and slow (τ3) kinetics measured at 1634 cm−1 and 1660 cm−1 also agree, but with opposite signal change (Fig. 3A). This is consistent with the main absorbance changes arising from loss of β-sheet and the gain of disordered polypeptide at higher temperature. In general, the dynamics measured at 1634, 1661, and 1680 cm−1 matched across all temperatures tested (Tables S2–S4†). The fastest phase (τ1) was not resolved at any temperature at 1680 cm−1, either because of the overall smaller absorbance, or because the fast phase observed at 1634 cm−1 is a result of overlap with the faster forming turn at 1619 cm−1. Supporting the latter hypothesis, the dynamics measured at the turn, 1619 cm−1 (Fig. 3B, Tables 1 and S1†), was faster than that measured at the other frequencies. This suggests that like other WW domains7,8,12 the turn(s) of GTT35 forms prior to the β-sheets of the WW domain. In this model, the intermediate phase is assigned to formation of one of the β-hairpins and the final phase is folding of the second β-hairpin.
Arrhenius plots of the observed kinetics (Fig. S5†) highlight additional complexity in the folding of GTT35. For all frequencies probed, >80% of the absorbance change occurs in the slowest phase (Fig. 3, Tables S1–S4†), so the slowest phase is assigned primarily to the global folding transition. If the WW domain were to follow a simple two-state transition, an Arrhenius plot of the natural log of the measured rate constants versus 1/T for temperatures below the melting temperature would be linear and identical at all probe frequencies, assuming no heat capacity change upon folding.
Our key experimental result here is that an Arrhenius plot of the slowest phase below the global Tm of ≈78 °C shows two distinct regions (Fig. 4). Above 55 °C, all frequencies probed have the same slope within measurement uncertainty, consistent with an apparent two-state behavior. At 55 °C and below (not far from the intermediate transition temperature of 52 °C in the SVD model of Fig. S3 and S4†), the Arrhenius plot shows differences in the apparent barrier to folding depending on the spectral region being probed: 1619, 1634, 1680, or 1661 cm−1. (The barriers are apparent because the Arrhenius analysis does not account for the temperature dependence of the viscosity of the solution.)
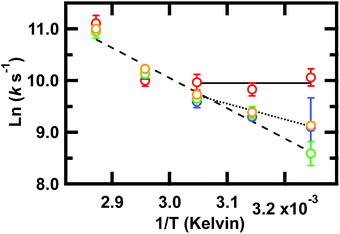 | ||
Fig. 4 Arrhenius plot of the slowest relaxation kinetics of GTT35 in the folding branch (below Tm). The values of T used for the (1/T) axis are the final temperatures reached during the jump; jumps were collected with final temperatures between 35 and 75 °C. k is the value obtained from a fit (eqn (1)) of the T-jump transient probed by infrared at the 1619 cm−1 (turn,  ), 1634 cm−1 (β-sheets, ), 1634 cm−1 (β-sheets,  ), 1661 cm−1 (disordered polypeptide, ), 1661 cm−1 (disordered polypeptide,  ), or 1680 cm−1 (β-sheets, ), or 1680 cm−1 (β-sheets,  ). Error bars are standard deviation of the fit. Lines are a result of fitting individual frequencies 1619 and 1634 cm−1 below 55 °C and 1661 cm−1 across all temperatures. ). Error bars are standard deviation of the fit. Lines are a result of fitting individual frequencies 1619 and 1634 cm−1 below 55 °C and 1661 cm−1 across all temperatures. | ||
The turn (1619 cm−1) exhibits faster relaxation rates and an apparent activation energy near zero. The barrier for turn formation must be negligible and mostly entropic, a consequence of the search to find stabilizing contacts and the correct alignment of the turn. Activation energies near zero as the temperature is lowered are commonly found in ultrafast folders like GTT35,9 indicating that a particular structure can fold ‘downhill’ under optimal temperature conditions.
The β-sheets (1634 and 1680 cm−1) have slower relaxation rates and a small but non-zero activation energy. The apparent enthalpic barrier to β-sheet formation is likely due to the rearrangement of the hydrophobic interactions in the core of the WW domain. This assignment is supported by past combined fluorescence and infrared T-jump studies of β-peptides that show fluorescence measurements, which are sensitive to hydrophobic packing of the tryptophan sidechains, occur on the same timescale as IR measurements of the β-sheets.7,9
Finally, the disordered region (1661 cm−1) has a slope that extrapolates from the high temperature slope, indicating that it is associated with a larger barrier, likely the main barrier for the protein's unfolding reaction.
Taken together, these results imply that fast rearrangement of the turn provides a template for subsequent β-sheet extension and packing of the hydrophobic core, similar to the zipper mechanism of β-hairpin formation.58
Above 55 °C, the observed activation energy is the same regardless of probed frequency. Since both the turn and β-sheet experience the same apparent activation energy, we conclude that this is the apparent global two-state transition that follows initial rapid structure formation.
MD-PMM calculations of time-dependent IR signal
Infrared spectra are highly structure-sensitive. To better understand the structural origin of the multi-exponential behavior of GTT35, we investigated its folding kinetics along four independent molecular dynamics trajectories previously performed on the supercomputer ANTON with a total simulation time of ≈600 μs at 122 °C (ESI†). In order to directly compare with experimental results, the MD-PMM methodology was used to calculate the time-dependent intensity of the IR signal (see Methods section).Firstly, a full kinetic model for the folding process was obtained by analyzing the time-evolution of the probability of four conformational states identified in the trajectories: the folded state (F), the state in which the first hairpin formed (H1F), the state in which the second hairpin is formed (H2F), and the unfolded state (U) (additional information in the ESI, Fig. S6†). These states were defined based on previous experimental8 and computational24 studies of the FiP35 WW domain.
To follow the folding process, we selected twenty-four 13 μs-long subtrajectories with starting points having spectral intensities representative of either the folded or the unfolded state in a suitable proportion to simulate a folding jump (i.e. from a lower to a higher population of the folded state). 70% of the trajectories (17 out of 24) were selected with starting points with a spectral intensity representative of U. 30% of the trajectories (7 out of 24) were selected with starting points with a spectral intensity representative of F (additional information in the ESI, Fig. S7†). The equilibrium folded population at the end of the simulated jump is 67% (Fig. 5A).
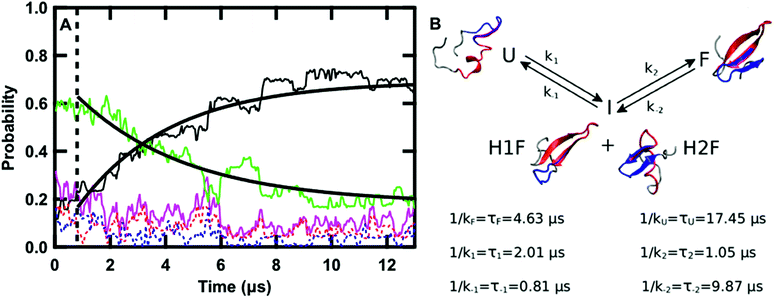 | ||
| Fig. 5 (A) Time evolution of the probability of the F state (black), H1F state (red), H2F state (blue), U state (green), intermediate state (I, magenta, P(I) = P(H1F) + P(H2F)) averaged over the twenty-four 13 μs sub-trajectories at 122 °C. The curves obtained by fitting the F and U probabilities with eqn (11) and (12), respectively, are overlaid on the data. The dashed line highlights the region of the graph at times lower than 0.8 μs. (B) Schematic representation of the kinetics of the folding process: folding from U to F occurs via the I state with the kinetic constants reported in the scheme together with the values of the corresponding lifetimes. A representative structure of GTT in each of the four states is reported. In each structure, the residues belonging to hairpin 1 (8–22) are highlighted in red and the ones belonging to hairpin 2 (19–30) are highlighted in blue. | ||
The time evolution of the probabilities of the four conformational states was binned into 40 ns intervals along each sub-trajectory, and subsequently averaged across the 24 sub-trajectories. Fig. 5A shows that there are three kinetically relevant states: the F state, the U state, and an intermediate state (I) comprised of both H1F and H2F. H1F and H2F are combined into a single I state because of their similar behavior. The I state can be approximated as a stationary state in the folding process. After an initial phase corresponding to 0.8 μs (Fig. 5A), the probability of the I state builds up to a low steady-state value (≈12% on average) and there is no net flux from I to F or U. During the initial 0.8 μs phase, the U state concentration is approximately constant and there is an exchange between I and F. Once the stationary state is established, an increase in F corresponds to a decrease in U. Close inspection of the 24 sub-trajectories also reveals that folding always proceeds via the I state, either through H1F (70%) or H2F (30%).
Keeping I stationary, the change in probability of F and U with time can be fit by eqn (11) and (12) (see Experimental). This yields a relaxation time of τ = 3.66 μs, a folding time τF = 4.63 μs and an unfolding time τU = 17.45 μs. This agrees well with previous fluorescence T-jump experiments that reported a relaxation time τ = 3.7 μs for GTT35 and a folding time (assuming a two-state model) of τF = 5.7 μs following a jump from 80 to 90 °C.40 The computed relaxation time also agrees well with our infrared T-jump experiments to 90 °C (Fig. 6) that show relaxation times of ≈5 μs. From the stationary model, it is possible to calculate the rate constants of the U ⇔ I and I ⇔ F processes (see ESI†). The lifetimes associated to the calculated constants are reported in Fig. 5B.
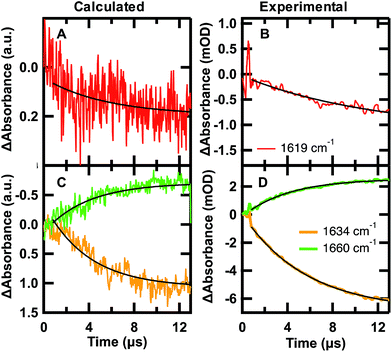 | ||
Fig. 6 Calculated folding (A and C) and experimental unfolding (B and D) time-dependent amide I′ IR signal probed at 1619 (red), 1634 (orange), and 1680 cm−1 (green). (A and C) Each calculated point in time of the kinetic trace corresponds to the intensity at the specific frequency averaged over the 24 sub-trajectories at 122 °C °C sampled from initial U states and F states in a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. (B and D) IR T-jump relaxation kinetics of 2.0 mM GTT35 in 20 mM potassium phosphate buffer pD 7.0 following a jump from 75 to 90 °C. A single exponential is overlaid on the calculated and experimental kinetic traces between 0.8 and 13 μs (eqn (1)). 3 ratio. (B and D) IR T-jump relaxation kinetics of 2.0 mM GTT35 in 20 mM potassium phosphate buffer pD 7.0 following a jump from 75 to 90 °C. A single exponential is overlaid on the calculated and experimental kinetic traces between 0.8 and 13 μs (eqn (1)). | ||
The time-dependent IR signal at specific IR frequencies of interest calculated by the MD-PMM method can be directly compared to time-resolved IR experiments because the computed and experimental observables are matched. First, the 24 sub-trajectories were divided into segments of 40 ns, and the average amide I′ spectrum for each 40 ns segment was calculated by the MD-PMM approach (see Experimental). Then transients were generated at specific frequencies corresponding to each secondary structure element: turn (≈1619 cm−1), β-sheet (≈1634 cm−1), and disordered (≈1660 cm−1). Finally, the time evolution of the intensity (ΔAbsorbance) was averaged across the 24 sub-trajectories, corresponding to an equilibration from 30% F to 67% F.
The calculated and experimental transients at 1619, 1634, and 1661 cm−1 are compared in Fig. 6. The decreased signal/noise ratio at 1619 cm−1 is due to the reduced signal, which is less than half the intensity of the other frequencies. The calculated transients at 122 °C are compared to experimental measurements following a T-jump to 90 °C. It is well known that classical force fields used in MD simulations overestimate protein stability by ca. 30–40 °C,59 so we are comparing corresponding states in Fig. 6. The calculation monitors a folding jump (starting at 30% F and ending at 67% F), while the experiment monitors an unfolding jump, so we inverted the sign of ΔAbsorbance in Fig. 6. Sufficiently small jumps (here: 15 °C) to the same final temperature should exhibit the same relaxation times irrespective of initial conditions.60
The calculated relaxation times (Table 2) and relative intensities (Fig. 6) can be compared to the experimental transients at 90 °C. Calculated transients were fit by a single exponential starting at t = 0.8 μs, following establishment of the stationary state. The good agreement between the calculated relaxation times at 1634 and 1661 cm−1 (3.9, 3.8 μs) and the one obtained by fitting the time evolution of the probabilities (3.7 μs) validates the three-state model used to describe the folding kinetics of GTT35. In addition, such an agreement also confirms that the change in IR absorbance along time is mainly due to the conformational changes associated with the folding process. Most importantly, the relative intensities (Fig. 6) and frequency-dependent lifetimes obtained from the fit of the calculated transients are similar to the corresponding slowest experimental ones (τ3, 5.4 and 4.9 μs in Table 2).
| Wavelength | Calculated τ (μs) | Experimental τ1 (μs) | Experimental τ3 (μs) |
|---|---|---|---|
| 1619 cm−1 | 5.5 ± 0.7 | — | 7.3 ± 0.2 |
| 1634 cm−1 | 3.9 ± 0.5 | 0.45 ± 0.06 | 5.4 ± 0.5 |
| 1661 cm−1 | 3.8 ± 0.7 | — | 4.90 ± 0.04 |
The faster experimental phases occur within the time necessary to establish the stationary state identified in the simulated data (0.8 μs in Fig. 6). These phases (τ1 and τ2) are most consistently resolved in the data collected at 1634 cm−1 at 45 °C (1.8 and 12 μs in Table 1), but still seen at higher temperature (0.45 μs in Table 2). Because they make up only ≈20% of the total signal, the lower signals in the experiment and reduced sampling in the calculations preclude a fully quantitative comparison. In this and past experimental studies of WW domains the fast sub-microsecond time is assigned to turn formation and the intermediate microsecond phase is assigned to formation of an intermediate with one hairpin formed.7,8,12,39 These assignments are consistent with establishment of the stationary state identified in the simulations, which also occurs in hundreds of nanoseconds and involves relaxation within the unfolded state46 and fast turn-structuring processes.
At the high temperatures where simulation and experiment can be compared, a three-state model, with a stationary kinetic intermediate, is compatible with the time-dependent IR signals. IR T-jump measurements have been able to identify WW domain folding via the H1F intermediate using either unique aspartic acid or hydrogen bond interactions in the first turn.8,12 Identification of the H2F intermediate is more difficult, because, according to previously computed spectra, it has a partially formed three-stranded core that would have a nearly identical spectra to the fully folded state.24 Kinetic experiments should be able to distinguish this state, because the intensity of the peak associated with H2F would increase as the protein folds. However, this is challenging because the total population of the H2F intermediate is only ≈4% (30% of the total population of the intermediate state) and overlaps with many bands. One possibility would be to use 13C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 18O isotopic substitutions to shift interactions in the second turn to a lower less congested spectral region.61 Vibrational coupling between labeled cross-strand amides in the second hairpin would enhance and shift the 13C
18O isotopic substitutions to shift interactions in the second turn to a lower less congested spectral region.61 Vibrational coupling between labeled cross-strand amides in the second hairpin would enhance and shift the 13C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 18O labeled bands, which could be used to confirm the H2F intermediate.62
18O labeled bands, which could be used to confirm the H2F intermediate.62
While evidence for an intermediate state was observed by both T-jumps and P-jumps of FiP35 WW domain detected by tryptophan fluorescence,39 we now have direct structural information from equilibrium and time-resolved infrared measurements to support a folding model through at least one hairpin intermediate. It is worth noting that while fast pressure jumps detected by fluorescence showed evidence for ‘slow’ (10–20 μs) formation of H1F/H2F states in FiP35 WW domain, T-jumps showed a faster phase interpreted as incipient downhill folding.39 Our structural analysis based on IR spectroscopy is more nuanced, showing two distinct folding mechanisms at low and high temperatures.
Conclusions
We have directly compared well-matched experimental and simulated time-dependent IR observables of the fastest folding WW domain, GTT35. IR experiments reveal a new thermodynamic intermediate and two kinetic intermediates that were not directly assigned by previous fluorescence studies. Time-resolved measurements of the turn and β-sheets show that the folding mechanism at lower temperatures is a combination of activated and downhill folding, and as the temperature increases the rates converge towards an apparent two-state behavior. The MD-PMM calculations provide atomic resolution of the second kinetic intermediate, and show that GTT35 folds through at least two pathways where either one of the two hairpins is fully formed in the intermediate state. In conclusion, time-dependent IR calculations along molecular dynamics simulations reproduce the time dependence of the IR signal and the relative amplitude changes at each frequency. The reproduction of experimental observables from molecular dynamics simulations provides an atomic level of detail that is not accessible by experiments, while validating the mechanisms observed in simulations. Since it is now possible to simulate and measure biomolecule kinetics on the same timescale, methods that quantitatively compare computed and experimental observables provide the highest possible resolution of the dynamics of complex molecules.Experimental
Protein synthesis and purification
GTT35 WW domain, sequence GSKLPPGWEKRMSRDGRVYYFNHITGTTQFERPSG, was synthesized via standard 9-fluorenylmethyloxycarbonyl (Fmoc) based solid-phase chemistry on a Liberty1 microwave peptide-synthesizer (CEM, Matthews, NC). Fmoc-PAL-PS resin (Applied Biosystems, Foster City, CA) was used to form a peptide amide. The peptide was purified by reverse-phase chromatography (C18 column) using a water/acetonitrile gradient with 0.1% trifluoroacetic acid (TFA) as the counter ion. TFA interferes in the amide-I′ IR region at 1672 cm−1, so the peptide was dissolved in 2 mM HCl and lyophilized to allow exchange of the TFA counter-ion for HCl.63 The identity of the peptide was confirmed by matrix-assisted laser desorption time-of-flight mass spectrometry. The peptide was lyophilized and dissolved in D2O to allow deuterium–hydrogen exchange of the amide protons. The peptide was lyophilized a second time and resuspended in D2O buffer with 20 mM potassium phosphate buffer at pD* 7.0 (pD* refers to uncorrected pH meter reading). Circular dichroism confirmed the secondary structure of the WW domain (ESI, Fig. S8†). Sample concentrations between 0.5–2.0 mM were prepared for IR measurements.FTIR spectroscopy
The equilibrium melting behavior was monitored on a Varian Excalibur 3100 FTIR spectrometer (Varian Inc., Palo Alto, CA) using a temperature-controlled IR cell. The IR cell consists of two CaF2 windows separated by a 100 μm Teflon spacer split into two compartments, a sample and a reference. The reference is comprised of a solution of 20 mM potassium phosphate buffer at pD* 7.0 in D2O, the same conditions as the sample solution but without protein. Using this design, reference data can be collected under nearly identical conditions as the sample data. The same cells are used for equilibrium FTIR and T-jump experiments. No aggregation was observed in the infrared at reported concentrations. All spectra shown at a specific temperature are obtained from the ratio of the single beam spectra of sample solution with protein to the reference buffer solution without protein. The temperature-dependent difference spectra were then generated by subtracting the spectrum at the lowest temperature from the spectra at higher temperatures. The second derivative spectra were computed in IGOR PRO (WaveMetrics, Lake Oswego, OR) after smoothing the data with a sixth order binomial algorithm to remove any residual water vapor.Time-resolved temperature jump (T-jump) relaxation measurements
The principle of T-jump and the IR T-jump apparatus has been described previously.55 Pulsed laser excitation is used to rapidly perturb the folding equilibrium on a timescale faster than the molecular dynamics of interest. Time-resolved infrared spectroscopy is then used to probe the reaction. A Q-switched GCR-4 Nd:YAG laser (Spectra Physics, Mountain View, CA) fundamental at 1064 nm is Raman shifted (one stokes shift in 200 psi H2 gas) to produce a 10 ns pulse at 2 μm. The magnitude of the T-jump is calculated using the change in reference absorbance with temperature (ESI, Fig. S9 and S10†). Absorbance changes at the reference frequency are due only to changes in D2O absorbance, which is used as an internal thermometer.55 IR T-jump experiments were conducted at multiple concentrations between 0.5 and 2.0 mM of GTT35.The change in signal induced by the T-jump is probed in real time by a continuous laser with a frequency in the amide I′ band of the IR. Jumps were performed slightly off the peak centers to maximize the transient absorbance signal. The mid IR probe beam is generated by a continuous wave quantum cascade laser (Daylight Solutions Inc., San Diego, CA) with a tunable output range of 1570–1730 cm−1. The transient transmission of the probe beam through the sample is measured using a fast, 100 MHz, photovoltaic MCT IR detector/preamplifier (Kolmar Technologies, Newburyport, MA). Transient signals are digitized and signal averaged (100 shots) using a Tektronics digitizer (7612D, Beaverton, OR). Instrument control and data collection are controlled using a LabView (National Instruments, Austin, TX) computer program.
Analysis of kinetic data
GTT35 relaxation kinetics must be deconvolved from the observed kinetics. Accurate deconvolution is possible as the instrument response is determined from the reference measurement under the exact conditions of the sample measurements. In order to minimize detector artifacts, the reference is scaled prior to subtraction from the sample. The decay function is a multi-exponential decay with the formula: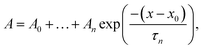 | (1) |
The data were fit over the interval from 380 ns to an order of magnitude outside the slowest exponential. The data analysis was performed in IGOR PRO.
IR spectra calculation with the MD-PMM approach
The method used to reconstruct amide I′ infrared spectra has been previously described.64,65 Briefly, similar to other mixed quantum-classical procedures,66–68 a portion of the system to be treated at the electronic level is pre-defined (the quantum center QC). The rest of the system (i.e. the environment) is described at a classical atomistic level and exerts an electrostatic effect on the QC electronic states, typically obtained by the environment atomistic charge distribution at each frame of the MD simulation and evaluated in QC center of mass. The phase space sampling of the whole system (the QC and the environment) is provided by fully classical MD simulations and thus the MD-PMM approach can be applied to a very large set of molecular configurations, providing the dynamic coupling of electronic properties with classical degrees of freedom. The statistically relevant sampling of the system configurations is the main strength of the MD-PMM approach, as it ensures accurate calculation of the spectra of complex systems.For the calculation of amide I′ IR spectra, the trans-N-methylacetamide (NMA) moiety is chosen as the QC for each peptide backbone unit. The mass-weighted Hessian eigenvectors of the isolated trans-NMA molecule, calculated quantum chemically, provide the gas-phase vibrational modes of each peptide backbone unit, including the amide I′ frequency and eigenvector. Along such an eigenvector, a set of atomic configurations of the trans-NMA model were generated, and, for each of these structures, an orthonormal set of unperturbed (gas-phase) electronic Hamiltonian eigenfunctions were initially evaluated (see Unperturbed Quantum Chemical Calculations section in the ESI†). For each MD frame and for each IR chromophore (i.e. each of the N backbone peptide units), the electrostatic perturbation of the environment is included and the perturbed electronic ground state energy is calculated as a function of the mode coordinate. This perturbed energy curve is modeled by a Morse potential, yielding the vibrational frequency of the perturbed mode. The perturbing environment at each MD frame is defined as the side chain of the considered peptide group, the N-1 residues, and the solvent. Changes in secondary structure and/or hydrogen bonding networks provide different perturbing environments to the peptide backbone unit, making the perturbed energy curve sensitive to the instantaneous conformation of the environment. Local solvation effects also affect the spectral lineshape upon folding/unfolding.64
Mode coupling effects, due to interacting vibration centers (i.e. excitonic effects), at each MD frame are included by constructing the excitonic coupling matrix describing the coupling among the quantum center modes by means of the transition dipole coupling (TDC) approximation. With this approach only mode coupling effects due to interacting fundamental excitations are considered, while the couplings involving overtones, which typically provide higher order effects on the spectral lineshape, are neglected. Diagonalization of the excitonic coupling matrix provides the instantaneous vibrational eigenstates and eigenvalues (now including vibrational mode coupling), and yields the perturbed vibrational frequencies and corresponding transition dipoles of the whole peptide. The perturbed excitation frequencies and the corresponding transition dipoles are used to reconstruct the complete vibrational spectrum. The distribution of perturbed frequencies and transition dipoles obtained over all of the MD frames are binned in frequency space to generate the vibrational spectrum. Thus, the band width and line shape of the calculated spectra are obtained from the distribution of the perturbed frequencies as calculated via the MD-PMM approach at each MD frame and for each peptide group, avoiding the use of any empirical or adjustable parameter.
Kinetic model
The kinetic model uses three states: the folded state (F), the unfolded state (U) and the intermediate state (I), which corresponds to either one of the hairpins formed. The differential rate laws for the reaction scheme can be written:| ṖF = k2PI − k−2PF, | (2) |
| ṖI = k1PU − (k−1 + k2)PI + k−2PF, | (3) |
| ṖU = −k1PU + k−1PI, | (4) |
| ṖI = k1PU − (k−1 + k2)PI + k−2PF ≅ 0, | (5) |
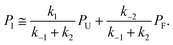 | (6) |
This can be used to redefine ṖF and ṖU:
| ṖF ≅ kFPU − kUPF. | (7) |
| ṖU ≅ −kFPU + kUPF. | (8) |
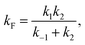 | (9) |
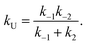 | (10) |
Considering the region where I has reached a steady state (t ≥ 0.8 μs), we fix the probability of I to its mean value, PI ≅ ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) I and solve for the integrated rate laws:
I and solve for the integrated rate laws:
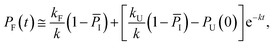 | (11) |
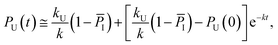 | (12) |
The other rate constants characterizing the kinetic model can be obtained as reported in the ESI.†
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Institutes of Health (NIH R01 GM093318 to MG and NIH R01 GM53640 to RBD). CMD was supported by a postdoctoral fellowship provided by the PFC: Center for the Physics of Living Cells funded by NSF PHY 1430124. LZP, ID, and AA acknowledge the CINECA award IscrC CSC under the ISCRA initiative for the availability of high-performance computing resources and support. The authors are grateful to the D. E. Shaw Research group for making trajectories available. ID and LZP acknowledge funding from the FORTISSIMO project FP7-2013-NMP-ICT-FOF.Notes and references
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, Science, 2011, 334, 517–520 CrossRef CAS PubMed.
- C. D. Snow, H. Nguyen, V. S. Pande and M. Gruebele, Nature, 2002, 420, 102–106 CrossRef CAS PubMed.
- M. B. Prigozhin and M. Gruebele, Phys. Chem. Chem. Phys., 2013, 15, 3372–3388 RSC.
- U. Samanta, R. P. Bahadur and P. Chakrabarti, Protein Eng., Des. Sel., 2002, 15, 659–667 CrossRef CAS.
- M. B. Prigozhin, S.-H. Chao, S. Sukenik, T. V. Pogorelov and M. Gruebele, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7966–7971 CrossRef CAS PubMed.
- T. Cellmer, M. Buscaglia, E. R. Henry, J. Hofrichter and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6103–6108 CrossRef CAS PubMed.
- C. M. Davis and R. B. Dyer, Biochemistry, 2014, 53, 5476–5484 CrossRef CAS PubMed.
- C. M. Davis and R. B. Dyer, J. Am. Chem. Soc., 2016, 138, 1456–1464 CrossRef CAS PubMed.
- C. M. Davis, S. Xiao, D. P. Raleigh and R. B. Dyer, J. Am. Chem. Soc., 2012, 134, 14476–14482 CrossRef CAS PubMed.
- H. Ma and M. Gruebele, Proc. Natl. Acad. Sci., 2005, 102, 2283–2287 CrossRef CAS PubMed.
- A. Barth and C. Zscherp, Q. Rev. Biophys., 2002, 35, 369–430 CrossRef CAS PubMed.
- C. M. Davis and R. B. Dyer, J. Am. Chem. Soc., 2013, 135, 19260–19267 CrossRef CAS PubMed.
- D. M. Vu, S. H. Brewer and R. B. Dyer, Biochemistry, 2012, 51, 9104–9111 CrossRef CAS PubMed.
- C. M. Davis, A. K. Cooper and R. B. Dyer, Biochemistry, 2015, 54, 1758–1766 CrossRef CAS PubMed.
- J. Jeon, S. Yang, J. H. O. Choi and M. Cho, Acc. Chem. Res., 2009, 42, 1280–1289 CrossRef CAS PubMed.
- N. A. Besley and K. A. Metcalf, J. Chem. Phys., 2007, 126, 035101 CrossRef PubMed.
- M. Reppert and A. Tokmakoff, Annu. Rev. Phys. Chem., 2016, 67, 359–386 CrossRef CAS PubMed.
- J.-H. Choi, H. Lee, K.-K. Lee, S. Hahn and M. Cho, J. Chem. Phys., 2007, 126, 45102 CrossRef PubMed.
- F. S. Husseini, D. Robinson, N. T. Hunt, A. W. Parker and J. D. Hirst, J. Comput. Chem., 2017, 38, 1362–1375 CrossRef CAS PubMed.
- M. Aschi, R. Spezia, A. Di Nola and A. Amadei, Chem. Phys. Lett., 2001, 344, 374–380 CrossRef CAS.
- L. Zanetti Polzi, A. Amadei, M. Aschi and I. Daidone, J. Am. Chem. Soc., 2011, 133, 11414–11417 CrossRef CAS PubMed.
- L. Zanetti Polzi, I. Daidone, M. Anselmi, G. Carchini, A. Di Nola and A. Amadei, J. Phys. Chem. B, 2011, 115, 11872–11878 CrossRef CAS PubMed.
- L. Zanetti Polzi, I. Daidone and A. Amadei, J. Phys. Chem. B, 2012, 116, 3353–3360 CrossRef CAS PubMed.
- L. Zanetti-Polzi, C. M. Davis, M. Gruebele, R. B. Dyer, A. Amadei and I. Daidone, FEBS Lett., 2017, 591, 3265–3275 CrossRef CAS PubMed.
- I. Daidone, L. Thukral, J. C. Smith and A. Amadei, J. Phys. Chem. B, 2015, 119, 4849–4856 CrossRef CAS PubMed.
- L. Zanetti-Polzi, I. Daidone, C. A. Bortolotti and S. Corni, J. Am. Chem. Soc., 2014, 136, 12929–12937 CrossRef CAS PubMed.
- L. Paltrinieri, G. Di Rocco, G. Battistuzzi, M. Borsari, M. Sola, A. Ranieri, L. Zanetti-Polzi, I. Daidone and C. A. Bortolotti, J. Biol. Inorg Chem., 2017, 22, 615–623 CrossRef CAS PubMed.
- A. Amadei, I. Daidone and M. Aschi, Phys. Chem. Chem. Phys., 2012, 14, 1360–1370 RSC.
- L. Zanetti-Polzi, M. Aschi, A. Amadei and I. Daidone, J. Phys. Chem. Lett., 2017, 8, 3321–3327 CrossRef CAS PubMed.
- M. J. Macias, M. Hyvönen, E. Baraldi, J. Schultz, M. Sudol, M. Saraste and H. Oschkinat, Nature, 1996, 382, 646–649 CrossRef CAS PubMed.
- M. J. Macias, V. Gervais, C. Civera and H. Oschkinat, Nat. Struct. Biol., 2000, 7, 375–379 CrossRef CAS PubMed.
- M. A. Verdecia, M. E. Bowman, K. P. Lu, T. Hunter and J. P. Noel, Nat. Struct. Biol., 2000, 7, 639–643 CrossRef CAS PubMed.
- F. Noe, C. Schutte, E. Vanden-Eijnden, L. Reich and T. R. Weikl, Proc. Natl. Acad. Sci., 2009, 106, 19011–19016 CrossRef CAS PubMed.
- H. Nguyen, M. Jager, A. Moretto, M. Gruebele and J. W. Kelly, Proc. Natl. Acad. Sci., 2003, 100, 3948–3953 CrossRef CAS PubMed.
- N. Ferguson, J. Berriman, M. Petrovich, T. D. Sharpe, J. T. Finch and A. R. Fersht, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 9814–9819 CrossRef CAS PubMed.
- M. Petrovich, A. L. Jonsson, N. Ferguson, V. Daggett and A. R. Fersht, J. Mol. Biol., 2006, 360, 865–881 CrossRef CAS PubMed.
- F. Liu, D. Du, A. A. Fuller, J. E. Davoren, P. Wipf, J. W. Kelly and M. Gruebele, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2369–2374 CrossRef CAS PubMed.
- C. M. Davis, M. J. Reddish and R. B. Dyer, Spectrochim. Acta, Part A, 2017, 178, 185–191 CrossRef CAS PubMed.
- A. J. Wirth, Y. Liu, M. B. Prigozhin, K. Schulten and M. Gruebele, J. Am. Chem. Soc., 2015, 137, 7152–7159 CrossRef CAS PubMed.
- S. Piana, K. Sarkar, K. Lindorff-Larsen, M. Guo, M. Gruebele and D. E. Shaw, J. Mol. Biol., 2011, 405, 43–48 CrossRef CAS PubMed.
- M. Jäger, H. Nguyen, J. C. Crane, J. W. Kelly and M. Gruebele, J. Mol. Biol., 2001, 311, 373–393 CrossRef PubMed.
- N. Ferguson, C. M. Johnson, M. Macias, H. Oschkinat and A. Fersht, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 13002–13007 CrossRef CAS PubMed.
- J. Karanicolas and C. L. Brooks, Proc. Natl. Acad. Sci., 2003, 100, 3954–3959 CrossRef CAS PubMed.
- J. Karanicolas and C. L. Brooks, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 3432–3437 CrossRef CAS PubMed.
- Y. Mu, L. Nordenskiöld and J. P. Tam, Biophys. J., 2006, 90, 3983–3992 CrossRef CAS PubMed.
- T. J. Lane, G. R. Bowman, K. Beauchamp, V. A. Voelz and V. S. Pande, J. Am. Chem. Soc., 2011, 133, 18413–18419 CrossRef CAS PubMed.
- D. E. Shaw, K. J. Bowers, E. Chow, M. P. Eastwood, D. J. Ierardi, J. L. Klepeis, J. S. Kuskin, R. H. Larson, K. Lindorff-Larsen, P. Maragakis, M. A. Moraes, R. O. Dror, S. Piana, Y. Shan, B. Towles, J. K. Salmon, J. P. Grossman, K. M. Mackenzie, J. A. Bank, C. Young, M. M. Deneroff and B. Batson, in Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis - SC '09, 2009 Search PubMed.
- W. J. Yang, P. R. Griffiths, D. M. Byler and H. Susi, Appl. Spectrosc., 1985, 39, 282–287 CrossRef CAS.
- J. L. Arrondo, F. J. Blanco, L. Serrano and F. M. Goni, FEBS Lett., 1996, 384, 35–37 CrossRef CAS PubMed.
- H. Susi and D. M. Byler, Methods Enzymol., 1986, 130, 290–311 CAS.
- T. Wang, Y. Xu, D. Du and F. Gai, Biopolymers, 2004, 75, 163–172 CrossRef CAS PubMed.
- J. Hilario, J. Kubelka and T. A. Keiderling, J. Am. Chem. Soc., 2003, 125, 7562–7574 CrossRef CAS PubMed.
- S. J. Maness, S. Franzen, A. C. Gibbs, T. P. Causgrove and R. B. Dyer, Biophys. J., 2003, 84, 3874–3882 CrossRef CAS PubMed.
- J. Kubelka and T. A. Keiderling, J. Am. Chem. Soc., 2001, 123, 12048–12058 CrossRef CAS PubMed.
- S. Williams, T. P. Causgrove, R. Gilmanshin, K. S. Fang, R. H. Callender, W. H. Woodruff and R. B. Dyer, Biochemistry, 1996, 35, 691–697 CrossRef CAS PubMed.
- J. H. Werner, R. B. Dyer, R. M. Fesinmeyer and N. H. Andersen, J. Phys. Chem. B, 2002, 106, 487–494 CrossRef CAS.
- R. B. Dyer, F. Gai, W. H. Woodruff, R. Gilmanshin and R. H. Callender, Acc. Chem. Res., 1998, 31, 709–716 CrossRef CAS.
- V. Munoz, E. R. Henry, J. Hofrichter and W. A. Eaton, Proc. Natl. Acad. Sci., 1998, 95, 5872–5879 CrossRef CAS.
- D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. a. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Science, 2010, 330, 341–346 CrossRef CAS PubMed.
- G. Schwarz, Rev. Mod. Phys., 1968, 40, 206–218 CrossRef CAS.
- J. Marecek, B. Ben Song, S. Brewery, J. Belyea, R. B. Dyer and D. P. Raleigh, Org. Lett., 2007, 9, 4935–4937 CrossRef CAS PubMed.
- R. Huang, V. Setnička, M. A. Etienne, J. Kim, J. Kubelka, R. P. Hammer and T. A. Keiderling, J. Am. Chem. Soc., 2007, 129, 13592–13603 CrossRef CAS PubMed.
- V. V. Andrushchenko, H. J. Vogel and E. J. Prenner, J. Pept. Sci., 2007, 13, 37–43 CrossRef CAS PubMed.
- I. Daidone, M. Aschi, L. Zanetti-Polzi, A. Di Nola and A. Amadei, Chem. Phys. Lett., 2010, 488, 213–218 CrossRef CAS.
- A. Amadei, I. Daidone, L. Zanetti-Polzi and M. Aschi, Theor. Chem. Acc., 2011, 129, 31–43 Search PubMed.
- M. J. Field, P. A. Bash and M. Karplus, J. Comput. Chem., 1990, 11, 700–733 CrossRef CAS.
- H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185 Search PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Temperature-dependent circular dichroism and FTIR, SVD analysis of the FTIR data, global fitting of thermal melts, Arrhenius plots of observed kinetics, expanded computational methods, the computational distribution of IR intensities, and complete tables of relaxation kinetics of 1619 cm−1, 1634 cm−1, 1661 cm−1 and 1680 cm−1. See DOI: 10.1039/c8sc03786h |
| ‡ C. M. Davis and L. Zanetti-Polzi contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |