Large electrocaloric response and energy storage study in environmentally friendly (1 − x)K0.5Na0.5NbO3–xLaNbO3 nanocrystalline ceramics
Raju
Kumar
 ,
Ashish
Kumar
and
Satyendra
Singh
,
Ashish
Kumar
and
Satyendra
Singh
 *
*
Special Centre for Nanoscience, Jawaharlal Nehru University, New Delhi-110067, India. E-mail: satyambd@gmail.com
First published on 11th September 2018
Abstract
An electrocaloric material with a negative and positive electrocaloric effect (ECE) is identified to be a high potential candidate for solid-state refrigeration technology due to a changing dipolar entropy under a varying electric field. We have experimentally observed large values of negative and positive electrocaloric (EC) response in environmentally friendly (1 − x)K0.5Na0.5NbO3–xLaNbO3 ceramics using Maxwell’s relationships. The maximum value of negative and positive ECE were found to be −0.88 K and 2.08 K at 50 kV cm−1 for x = 0.03. The material displays a high electrocaloric responsivity (−1.76 and 4.16 × 10−7 K m V−1 for negative and positive ECE, respectively), COP (4.16) and energy storage capacity (0.17 J cm−3) for x = 0.03. The large values of negative and positive ECE, high values of electrocaloric responsivity, COP and energy storage capacity make this compound a good candidate for electrocaloric refrigeration and high energy storage applications. The Olsen cycle is discussed to explain the process involved in using this material for electrocaloric refrigeration.
1 Introduction
About 20% of the world’s overall electricity is consumed in cooling and air-conditioning devices. Most of these devices are based on vapor-compression technology, which is not environmentally friendly as it produces greenhouse gases. In 2006, the European Union (EU) introduced regulation of fluorine based greenhouse gases, and later promoted solid-state refrigeration cooling technology. The traditional vapor-compression technology has been fully optimized for its highest efficiency and is not effective at the micro-scale due to its bulky size. Studies over the past few decades have focused on developing and intensifying research efforts for solid-state cooling technologies to replace freon-based refrigeration systems.Ferroelectric materials have attracted high interest in solid-state refrigeration technology and energy storage.1–5 They have been used in many applications such as optical electronic devices, piezoelectric energy harvesting, etc. The environmentally friendly caloric effect, shows an adiabatic temperature change (ΔT) and isothermal entropy change (ΔS) in polar materials under an external electric field known as the electrocaloric effect (ECE).6–8 A high ECE is required for electrocaloric refrigeration technology, which is suitable for small-scale cooling devices compact in size with a high efficiency, for sensors, medical equipment, etc. Electrocaloric refrigeration has advantages due to the ease of application, reducing the cost in comparison with other caloric effects e.g., elastocaloric, magnetocaloric.9
For a feasible electrocaloric refrigerator, high values of negative and positive adiabatic temperature change are needed especially, the coexistence of negative and positive ECE is a unique phenomenon which will undoubtedly lead to fruitful commercial devices from various fields e.g., temperature regulation, biological refrigeration, etc. since, the combination of both may increase it’s capacity for practical purposes.10,11 The higher ECE value is a figure of merit of high breakdown field; a large saturation polarization change caused by varying the temperature. At the paraelectric–ferroelectric phase transition of the electrocaloric material with no applied external electric field, the electric dipoles are disordered, which is associated with a large entropy.
On application of an external field, the dipoles realign as per the direction of the field, this ordering lowers the entropy associated with dipole alignment which is compensated by an increase in the EC material temperature, keeping the entropy constant of the system in a reversible adiabatic condition.3 The negative ECE can be observed near the phase transition in the inter-ferroelectric region induced due to the electric field to higher from lower symmetry phases, which occurs when the change of structural phase transition entropy is larger than the change of dipolar entropy.9 In general, materials showing positive and negative ECE are very rare but they have a large potential for versatile applications.
High ECE can be observed near the phase transition point which arises due to configurational disorder with this point.12 At this point (∂P/∂T)E is a maximum which is the key factor for ECE. The interaction among B-site atoms and oxygen in ABO3 leads to an explanation of the ECE, the larger ionic charge and the smaller radius of the atom is more preferable. These are factors in deciding on the correct material for high ΔT. Thin films have shown higher ΔT because of the higher breakdown field than bulk ceramics, which is effective for small scale devices, but have a low cooling capacity and electrocaloric coefficient. Bulk ceramics enjoy the advantages of higher cooling capacity, electrocaloric coefficient (ΔT/ΔE) suitable for large scale devices.3
Among bulk ceramics, lead-based ceramics have been reported with good ΔT, but their carcinogenic and environmentally harmful nature have prevented their application. Lead-free ferroelectric ceramics based on BaTiO3,13–16 (Na0.5Ba0.5)TiO3,17–19 (K0.5Na0.5)NbO3,20–22 and Ba0.65Sr0.35TiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23,24 are suitable candidates. Specifically, K0.5Na0.5NbO3 (KNN): a solid solution of NaNbO3 (AFE) and KNbO3 (FE) is a potential ferroelectric material with a high remanent polarization,25 the low coercive field. It has high electromechanical and piezoelectric responses with a larger dielectric constant.26–29 For enhancing ferroelectric and piezoelectric properties, doping of elements at the atomic site of the ABO3 structure is an effective technique that provides chemical stability by reducing local stress followed by oxygen valency concentration by equilibrating ionic charges. K0.5Na0.5NbO3 (KNN) is a good optical, piezoelectric material30,31 and it has simulated for exhibiting larger polarization change in the temperature which make it a promising candidate for larger ECE.25
23,24 are suitable candidates. Specifically, K0.5Na0.5NbO3 (KNN): a solid solution of NaNbO3 (AFE) and KNbO3 (FE) is a potential ferroelectric material with a high remanent polarization,25 the low coercive field. It has high electromechanical and piezoelectric responses with a larger dielectric constant.26–29 For enhancing ferroelectric and piezoelectric properties, doping of elements at the atomic site of the ABO3 structure is an effective technique that provides chemical stability by reducing local stress followed by oxygen valency concentration by equilibrating ionic charges. K0.5Na0.5NbO3 (KNN) is a good optical, piezoelectric material30,31 and it has simulated for exhibiting larger polarization change in the temperature which make it a promising candidate for larger ECE.25
In this work, we have experimentally explored the EC response in environmentally friendly (1−x)K0.5Na0.5NbO3–xLaNbO3 (KNN–xLN) ceramics using Maxwell’s relationships. The large values of negative and positive ECE, high values of electrocaloric responsivity, COP and energy storage were observed indicating its candidature for solid-state refrigeration and high energy storage applications.
2 Experimental procedure
KNN–xLN ceramics with x = 0.01, 0.03, and 0.05 were synthesized by a conventional solid-state fabrication method.8,21,32 Highly pure (≥99%) oxides and carbonates (K2CO3, Na2CO3, Nb2O5, La2O3) were used as initial precursors in stoichiometric ratios. All precursors were suitably mixed using an agate mortar and pestle for 8 h with periodic heating at 60 °C to avoid hygroscopic effects. The uniformly mixed dry powder was calcined at 1153 K for 4.5 h in a muffle furnace. The calcined powder was mixed with a few drops of polyvinyl alcohol (PVA) as a binder and shaped in the form of a disk of 10 mm diameter with a 1-mm thickness at 125 kN uniaxial pressure. The green pellet was sintered at an optimum temperature of 1373 K for 5 h, to make an electrical contact on the sintered pellet, silver paste was layered on both sides of the pellet and fired at 773 K for 30 min. The bulk density of the sintered pellets were calculated by Archimedes method and found to be 3.03, 3.13, and 3.60 g cm−3 for x = 0.01, 0.03, and 0.05 for KNN–xLN, respectively. A powder X-ray diffractometer (XRD, Rigaku mini Flex 600, Japan) was used to collect XRD data to study the phase purity and crystal structure. Field-emission scanning electron microscopy (FE-SEM, LYRA3-TESCAN) was used to observe the surface morphology. The temperature dependent dielectric permittivity and loss tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ data was recorded from 303 K to 755 K by an impedance analyzer (E4990A, Keysight Technologies) with a customized furnace and sample holder. The polarization-electric field (P–E) hysteresis loop measurement was performed over a large temperature range at 50 Hz by using a ferroelectric test system (Marine India).
δ data was recorded from 303 K to 755 K by an impedance analyzer (E4990A, Keysight Technologies) with a customized furnace and sample holder. The polarization-electric field (P–E) hysteresis loop measurement was performed over a large temperature range at 50 Hz by using a ferroelectric test system (Marine India).
3 Results and discussion
The room temperature X-ray diffraction (XRD) pattern of KNN–xLN sintered powder with x = 0.01, 0.03, and 0.05 is presented in Fig. 1a. A perovskite structure was observed for all the samples indicating a complete diffusion of LaNbO3 into the K0.5Na0.5NbO3 lattices. The XRD peaks can be indexed with ICDD PDF card no. 01-077-0038 and 00-051-1431. The doublet peak around 45° merges into a singlet progressively as the LaNbO3 percentage rises and tends to pseudo cubic from the orthorhombic structure for x = 0.05 as compared with KNN33 as clearly shown in Fig. 1b. With increasing x, the diffraction peaks lead towards the larger angle side which may be due to lattice contraction. For x = 0.03, the secondary peak of LaNb7O12 with much less intensity was observed. KNN has an ABO3 type perovskite structure. The A site is occupied with K+ (1.64 Å) and Na+ (1.39 Å) in KNN-based ceramics, whereas Nb5+ (0.64 Å) is acquired at the B site in the ABO3 perovskite structure. According to the crystal chemistry, La3+ (1.36 Å) has been introduced randomly at the A site. The nanocrystalline nature of ceramics can be validated by Scherrer’s equation, d = 0.9λ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,34 where λ is the wavelength taken to be 1.54 Å of CuKα radiation, d is the average crystallite size and β is the full width at half maximum (FWHM) value corrected with instrument broadening. The calculated average crystallite size obtained was about 27, 25, and 28 nm for KNN–xLN with x = 0.01, 0.03, and 0.05, respectively.
θ,34 where λ is the wavelength taken to be 1.54 Å of CuKα radiation, d is the average crystallite size and β is the full width at half maximum (FWHM) value corrected with instrument broadening. The calculated average crystallite size obtained was about 27, 25, and 28 nm for KNN–xLN with x = 0.01, 0.03, and 0.05, respectively.
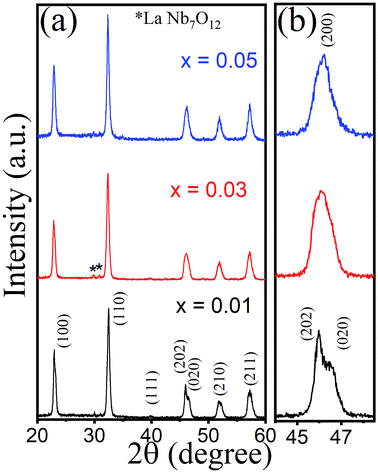 | ||
| Fig. 1 Room temperature XRD patterns (a) and the expanded view of XRD patterns (b) for KNN–xLN sintered powder with x = 0.01, 0.03, and 0.05. | ||
To investigate the effect of grain morphology on ECE by changing the doping concentration of LaNbO3, FE-SEM studies were performed on the surfaces of the sintered pellet, which is shown in Fig. 2 for KNN–xLN [x = 0.01 (a), 0.03 (b), 0.05 (c)] ceramics. The grains are cuboid, and compact, the size varying in the range of 50–150 nm for all the compositions. The grains appear to have diffused into each other due to the higher temperature sintering. The grain size has an impact on ECE as E ∝ G−a, where E, G, and a are breakdown field strength, grain size and a constant factor, respectively,35 implying that materials with a smaller grain size have a higher breakdown field strength which further produces a higher ECE. For x = 0.03, the smaller grain size produces a higher ECE as can be observed in Fig. 5.
 | ||
| Fig. 2 FE-SEM micrograph of KNN–xLN nanocrystalline ceramics [x = 0.01 (a), x = 0.03 (b), x = 0.05 (c)]. | ||
The temperature dependent real part of dielectric constant (ε′) and loss tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for KNN–xLN (x = 0.01, 0.03, and 0.05) at a fixed frequency of 1 kHz, are shown in Fig. 3. It is well known that KNN ceramics have two dielectric peaks, i.e., phase transitions around 463 K and 670 K corresponding to orthorhombic–tetragonal (TO–T) and tetragonal–cubic (TT–C) transitions, respectively.33 In KNN–xLN ceramics, these two phase transitions are observed at 457 K and 654 K for x = 0.01, 460 K and 664 K for x = 0.03 and 479 K and 676 K for x = 0.05, respectively, as shown in Fig. 3. The broad peak appears for x = 0.05 confirmed pseudo-cubic phases and it has a higher symmetry than the orthorhombic phase. As the LN concentration increases, the transition temperature is slightly shifted to the high temperature side and becomes broader. Local distortion of the crystal structure may be responsible for these changes.36 Among A site elements, La3+ have larger ions and smaller radii, which originates local electric fields with local charge imbalances due to local structure distortions. In the material, a large number of polar nanoregions (PNRs) have a pseudo cubic phase which is formed due to a hindrance of the protracted range dipole alignment that also stops the formation of ferroelectric order.37 In Fig. 3, as the LaNbO3 percentage increases the loss slightly increases and for x = 0.03, it is higher, but the value for all compositions is quite low. It can be seen that tan
δ for KNN–xLN (x = 0.01, 0.03, and 0.05) at a fixed frequency of 1 kHz, are shown in Fig. 3. It is well known that KNN ceramics have two dielectric peaks, i.e., phase transitions around 463 K and 670 K corresponding to orthorhombic–tetragonal (TO–T) and tetragonal–cubic (TT–C) transitions, respectively.33 In KNN–xLN ceramics, these two phase transitions are observed at 457 K and 654 K for x = 0.01, 460 K and 664 K for x = 0.03 and 479 K and 676 K for x = 0.05, respectively, as shown in Fig. 3. The broad peak appears for x = 0.05 confirmed pseudo-cubic phases and it has a higher symmetry than the orthorhombic phase. As the LN concentration increases, the transition temperature is slightly shifted to the high temperature side and becomes broader. Local distortion of the crystal structure may be responsible for these changes.36 Among A site elements, La3+ have larger ions and smaller radii, which originates local electric fields with local charge imbalances due to local structure distortions. In the material, a large number of polar nanoregions (PNRs) have a pseudo cubic phase which is formed due to a hindrance of the protracted range dipole alignment that also stops the formation of ferroelectric order.37 In Fig. 3, as the LaNbO3 percentage increases the loss slightly increases and for x = 0.03, it is higher, but the value for all compositions is quite low. It can be seen that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increases concurrently above 500 K and rapidly in the high temperature vicinity due to thermal activated conductivity in the material and can be explained as the conductivity loss, the volume fraction of the doping element.
δ increases concurrently above 500 K and rapidly in the high temperature vicinity due to thermal activated conductivity in the material and can be explained as the conductivity loss, the volume fraction of the doping element.
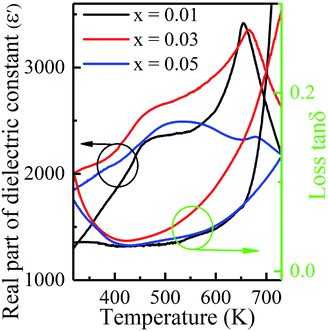 | ||
Fig. 3 Temperature dependencies of the real part of the dielectric constant (ε′) and loss tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ measured at 1 kHz for KNN–xLN ceramics with x = 0.01, 0.03, and 0.05. δ measured at 1 kHz for KNN–xLN ceramics with x = 0.01, 0.03, and 0.05. | ||
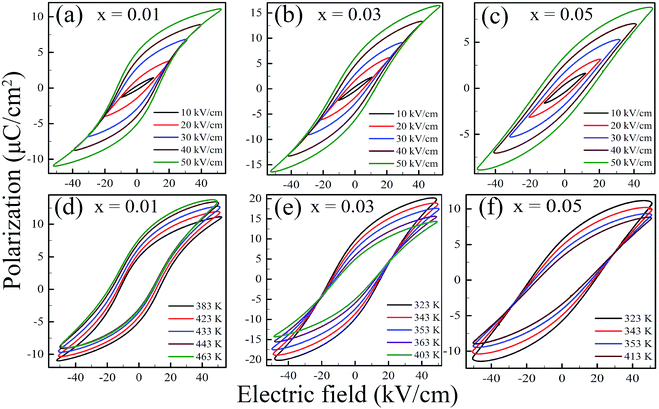
Fig. 4 shows the polarization–electric field (P–E) hysteresis loops of KNN–xLN (x = 0.01, 0.03, and 0.05) ceramics where a, b & c are P–E loops at a fixed temperature with a varying field, respectively while d, e & f are at a fixed field with a varying temperature, respectively for x = 0.01, 0.03, and 0.05. All the loops show ferroelectric behavior in the investigated operating temperature and also indicate the non-relaxor nature of the material.38 Since there is a lack of pinning defect dipoles, which makes P–E loops symmetric and due to increased space charge polarization, the P–E loop shape changes with composition variation. It can be observed the unsaturated loop at the lower field becomes saturated at the higher field, indicating a higher energy density state, and also the high dielectric constant of the material. For x = 0.01, maximum polarization (P) rises from 1.54 to 11.11 μC cm−2 whereas for x = 0.03, it increases from 2.42 to 16.52 μC cm−2 and in the case of x = 0.05, it is from 1.63 to 8.78 μC cm−2 for a field change of 10 to 50 kV cm−1. It can be observed for x = 0.01 and 0.05, the P–E loops are broader and shorter which is due to inducing depolarization fields and also defects in the domain switching reducing the field in the material, additionally the sharp phase transition is weakened and for x = 0.03, the P–E loops are narrow and have higher polarization values which is also represented by a high dielectric constant; a favorable condition for higher ECE.
Maxwell’s approach has been used for indirect measurement of ECE which is based on the adiabatic reversible process, a most acceptable method, i.e.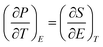 , The entropy change is39
, The entropy change is39
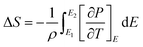 | (1) |
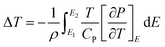 | (2) |
| Composition | ΔT (K) | E (kV cm−1) | Ref. |
|---|---|---|---|
| Na0.5Bi0.5TiO3 depoled | 0.14 | 20 | 40 |
| 0.9(K0.5Na0.5)NbO3–0.1Sr(Sc0.5Nb0.5)O3 | 0.28 | 25 | 8 |
| B0.91Ca0.09Zr0.14Ti0.86O3 | 0.3 | 20 | 41 |
| Ba(Zr0.2Ti0.8)O3 | 0.325 | 30 | 14 |
| 0.68Ba(Zr0.2Ti0.8)O3–0.32(Ba0.7Ca0.3)TiO3 | 0.33 | 20 | 42 |
| (Sr0.5Ba0.5)Nb2O6 | 0.35 | 100 | 43 |
| Na0.5Bi0.5TiO3 poled | 0.37 | 20 | 40 |
| Ba0.65Sr0.35TO3 | 0.42 | 20 | 44 |
| 0.9K0.5Na0.5NbO3–0.1SrTiO3 | - 0.85, 0.43 | 40 | 32 |
| Ba0.65Sr0.35TiO3 | 0.49 | 50 | 23 |
| 0.96(K0.48Na0.52)(Nb0.95Sb0.05)O3–0.04Bi(Na0.82K0.18)0.5ZrO3 | 0.51 | 40 | 20 |
| Ba0.94Sr0.06Ti0.9Sn0.1O3 | 0.55 | 20 | 45 |
| BaTi0.885Sn0.105O3 | 0.61 | 20 | 46 |
| Ba0.94Ca0.06Ti0.875Sn0.125O3 | 0.63 | 20 | 47 |
| Na1/2(Bi0.98Gd0.02)1/2TiO3 | 0.75 | 90 | 17 |
| BaZr0.2Ti0.8O3 | 1.1 | 21 | 48 |
| 0.94NBT–0.06BT | 1.5 | 50 | 49 |
| 0.75(Na0.5Bi0.5)TiO3–0.25(SrTiO3) | 1.64 | 50 | 19 |
| (Ba0.9Ca0.1)(Zr0.05Ti0.95)O3 | 1.64 | 70 | 50 |
| 0.99K0.5Na0.5NbO3–0.01LaNbO3 | 0.10, −0.99 | 50 | This work |
| 0.97K0.5Na0.5NbO3–0.03LaNbO3 | 2.08, −0.88 | 50 | This work |
| 0.95K0.5Na0.5NbO3–0.05LaNbO3 | 0.84, −0.47 | 50 | This work |
The ECE changes from positive to negative ECE with the rise in temperature at the point where the temperature change is null. At that point, (∂P/∂T)E tends to zero due to cancellation of both types of ECE. In general, for a ferroelectric application, the electric field reduces entropy by aligning the dipoles which leads to the positive ECE. In KNN materials, the effect of LN doping introduces the negative ECE. In such cases, induced polarization decreases with temperature below the phase transition temperature resulting in negative ECE in ferroelectrics.
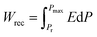 | (3) |
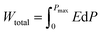 | (4) |
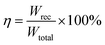 | (5) |
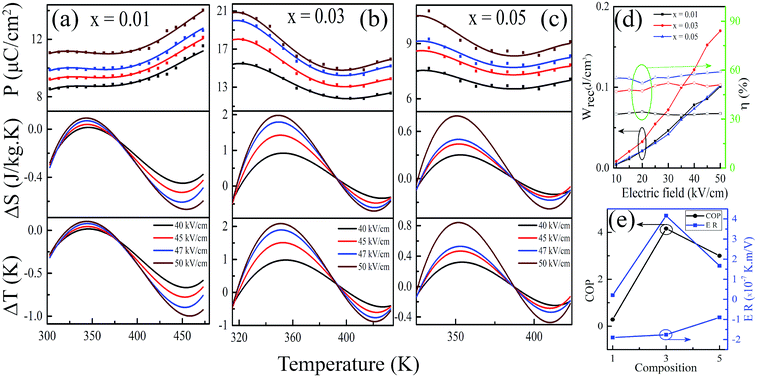
In the ferroelectric materials, the electrical energy storage properties are calculated from the P–E loops using eqn (3)–(5)33 and are presented in Fig. 5d which shows the variation of Wrec and η with the field in KNN–xLN ceramics for x = 0.01, 0.03, and 0.05. Here, Wrec is the recoverable energy, Wtotal is the total energy, η is the efficiency, E is applied electric field, Pr is the remanant polarization, Pmax is the maximum polarization. The calculated values of Wrec are found to be 0.10, 0.17 and 0.10 J cm−3, and efficiencies are 34, 50 and 59% for x = 0.01, 0.03, and 0.05, respectively. Amongst all, KNN–0.03LN has a greater potential for energy storage capacity which is higher than the other lead-free ceramics at this low field. A parameter for cooling performance i.e. the coefficient of performance (COP) can be calculated by |Q|/|Wtotal|,51 where Q is TΔS. The variation of maximum COP with composition is shown in Fig. 5e. The maximum COP is found to be 0.28, 4.16, and 3 for x = 0.01, 0.03, 0.05, respectively for KNN–xLN ceramics, which is higher than other ceramics e.g., Pb0.97La0.02(Zr0.87Sn0.08Ti0.07)O3 exhibit a COP of 2.9.52
Electrocaloric responsivity (ER) (ΔT/ΔE) is a quantity for estimating electrocaloric strength over an applied electric field.3,53 The calculated values of ER are found to be 0.21, −1.9 × 10−7 K m V−1 for x = 0.01; 4.16, −1.76 × 10−7 K m V−1 for x = 0.03 and 1.67, −0.9 × 10−7 K m V−1 for x = 0.05 of KNN–xLN, among which KNN–0.03LN is the more responsive material. The heat flow direction is expressed from the negative and positive sign and the magnitude is higher than many other lead-free ceramics; for (Ba0.95Ca0.05)(Zr0.1Ti0.9)O3 it is 2.4 × 10−7 K m V−1.15
A ferroelectric material whose P–E hysteresis loops shift with the operational temperature change can be employed in a cycle for thermal energy harvesting as reported by Olsen et al.54. Initially, it was studied for the case where polarization decreases with increments in temperature, but it can also be extended for the case where polarization increases with varying temperature or a combination of both. Fig. 6 exhibits the nature of the temperature dependent hysteresis loop for a ferroelectric material. The ferroelectric material can be used to produce electrical energy by controlling the temperature and applied electric field. For the case of decreasing polarization with increasing the temperature in Fig. 6a, the clockwise loop appears. The most suitable material will exhibit a large polarization change on changing the temperature and electric field, such a feature has been observed in the present material.
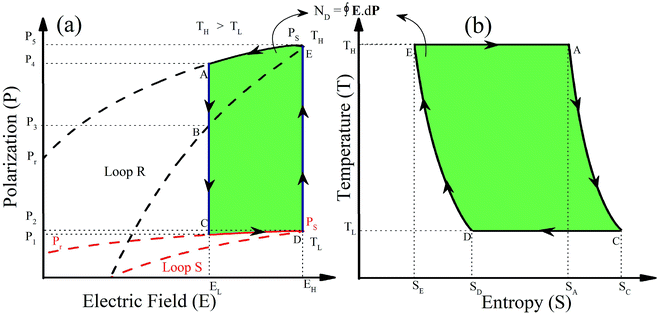 | ||
| Fig. 6 Polarization (isothermal) versus electric field (P–E) hysteresis loops (a), change in entropy (T–S) curves (A–C–D–E) using the Olsen cycle in operational temperatures TL and TH (b). | ||
We have observed a shift in P–E loops under varying fields and temperatures for KNN–xLN ceramics as can be seen in Fig. 4. The working cycle required is presented in Fig. 6 in order to explain this type of P–E loop behavior, we have considered two loops R and S, the 1st quadrant part is at a different temperature. The cycle A–B–C–D–E–A as shown in Fig. 6a has two isothermal (C–D and E–A) and two isoelectric (D–E and A–C) processes. In the C–D (isothermal) process, the ceramic is polarized from P1 to P2 using a unipolar EL to EH electric field at a lower temperature (TL), which is visible concurrently in the T–S curve in Fig. 6b reducing from SC to SD. In D–E (isoelectric heating), the temperature of the material rises to the TH high temperature, polarization rises from P2 to P5 and correspondingly SD to SE. The material depolarized at the temperature TH in the E–A step. Finally, by cooling ceramics at the lower field EL, the system gains its own initial state (TL, P1, SC). The area enclosed by the cycle (A–B–C–D–E–A) for a corresponding P–E curve is the electric energy density (ND). The T–S diagram provides data about the ceramic, which is suitable for refrigeration purposes. From a practical view point of using KNN–xLN (x = 0.01, 0.03, 0.05) in the Olsen cycle, the system should be able to achieve the oscillating heat currents and the external system absorb the electrical output.
4 Conclusions
We have studied the electrocaloric responses of (1−x)(K0.5Na0.5NbO3)–xLaNbO3 nanocrystalline ceramics with x = 0.01, 0.03, and 0.05. The rare properties of the coexistence of negative and positive temperatures have been observed with values of 2.08 K and −0.88 K for an applied field of 50 kV cm−1 for x = 0.03. The higher ER −1.76, 4.16 × 10−7 K m V−1 has been calculated with a high COP of 4.16, 0.17 J cm−3 recoverable energy and 50% efficiency. Thus, KNN–0.03LN has a great potential as a electrocaloric material in cooling technologies with a high capacity for energy storage applications providing an environmentally friendly lead-free solution.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Advanced Instrumentation Research Facility and School of Physical Sciences JNU, New Delhi for extending the instrumental research facilities. S. Singh acknowledges the partial financial support from DST (PURSE-II), UGC (Project #33, UPE-II), Govt. of India and SERB (EEQ/2016/000256). R. Kumar acknowledges the award of the junior research fellowship of UGC.References
- B. Neese, B. Chu, S.-G. Lu, Y. Wang, E. Furman and Q. Zhang, Science, 2008, 321, 821–823 CrossRef CAS PubMed.
- A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Science, 2006, 311, 1270–1271 CrossRef CAS PubMed.
- B. Lu, P. Li, Z. Tang, Y. Yao, X. Gao, W. Kleemann and S.-G. Lu, Sci. Rep., 2017, 7, 45335 CrossRef CAS PubMed.
- X. Moya, S. Kar-Narayan and N. D. Mathur, Nat. Mater., 2014, 13, 439–450 CrossRef CAS PubMed.
- J. Tušek, K. Engelbrecht, D. Eriksen, S. Dall’Olio, J. Tušek and N. Pryds, Nat. Energy, 2016, 1, 16134 CrossRef.
- S. Kar-Narayan, S. Crossley, X. Moya, V. Kovacova, J. Abergel, A. Bontempi, N. Baier, E. Defay and N. D. Mathur, Appl. Phys. Lett., 2013, 102, 032903 CrossRef.
- X. Moya, E. Stern-Taulats, S. Crossley, D. González-Alonso, S. Kar-Narayan, A. Planes, L. Mañosa and N. D. Mathur, Adv. Mater., 2013, 25, 1360–1365 CrossRef CAS PubMed.
- R. Kumar and S. Singh, J. Alloys Compd., 2017, 723, 589–594 CrossRef CAS.
- N. Novak, F. Weyland, S. Patel, H. Guo, X. Tan, J. Rödel and J. Koruza, Phys. Rev. B, 2018, 97, 094113 CrossRef.
- J. Chen, Z. Tang and S. Zhao, Phys. Status Solidi RRL, 2018, 12, 1700443 CrossRef.
- J. Li, S. Qin, Y. Bai, J. Li and L. Qiao, Appl. Phys. Lett., 2017, 111, 093901 CrossRef.
- I. Ponomareva and S. Lisenkov, Phys. Rev. Lett., 2012, 108, 167604 CrossRef CAS PubMed.
- Y. Bai, X. Han, K. Ding and L. Qiao, Energy Technol., 2017, 5, 703–707 CrossRef CAS.
- F. Weyland, T. Eisele, S. Steiner, T. Frömling, G. A. Rossetti Jr, J. Rödel and N. Novak, J. Eur. Ceram. Soc., 2018, 38, 551–556 CrossRef CAS.
- H. Kaddoussi, A. Lahmar, Y. Gagou, B. Manoun, J. N. Chotard, Z. Kutnjak, H. Khemakhem, B. Elouadi, M. E. Marssi, A. Lahmar, Y. Gagou, B. Manoun and J. N. Chotard, J. Alloys Compd., 2017, 713, 164–179 CrossRef CAS.
- K. S. Srikanth and R. Vaish, J. Eur. Ceram. Soc., 2017, 37, 3927–3933 CrossRef CAS.
- M. Zannen, A. Lahmar, Z. Kutnjak, J. Belhadi, H. Khemakhem and M. El Marssi, Solid State Sci., 2017, 66, 31–37 CrossRef CAS.
- Q. Li, J. Wang and H. Fan, Mater. Res. Bull., 2016, 74, 57–61 CrossRef CAS.
- W. P. Cao, W. L. Li, X. F. Dai, T. D. Zhang, J. Sheng, Y. F. Hou and W. D. Fei, J. Eur. Ceram. Soc., 2016, 36, 593–600 CrossRef CAS.
- X. X. Wang, J. Wu, B. Dkhil, B. Xu, G. Dong, G. Yang and X. Lou, Appl. Phys. Lett., 2017, 110, 063904 CrossRef.
- R. Kumar and S. Singh, Sci. Rep., 2018, 8, 3186 CrossRef PubMed.
- K. Xu, J. Li, X. Lv, J. Wu, X. Zhang, D. Xiao and J. Zhu, Adv. Mater., 2016, 28, 8519–8523 CrossRef CAS PubMed.
- P.-Z. Ge, X.-G. Tang, Q.-X. Liu, Y.-P. Jiang, W.-H. Li and J. Luo, J. Mater. Sci.: Mater. Electron., 2018, 29, 1075–1081 CrossRef CAS.
- X. Q. Liu, T. T. Chen, Y. J. Wu and X. M. Chen, J. Am. Ceram. Soc., 2013, 96, 1021–1023 CrossRef CAS.
- J. A. Barr and S. P. Beckman, Mater. Sci. Eng., B, 2015, 196, 40–43 CrossRef CAS.
- S. Priya and S. Nahm, Lead-Free Piezoelectrics, 2012 Search PubMed.
- X. Wang, J. Wu, D. Xiao, J. Zhu, X. Cheng, T. Zheng, B. Zhang, X. Lou and X. Wang, J. Am. Chem. Soc., 2014, 136, 2905–2910 CrossRef CAS PubMed.
- B. Wu, H. Wu, J. Wu, D. Xiao, J. Zhu and S. J. Pennycook, J. Am. Chem. Soc., 2016, 138, 15459–15464 CrossRef CAS PubMed.
- T. Zheng, J. Wu, D. Xiao and J. Zhu, Prog. Mater. Sci., 2018, 98, 552–624 CrossRef CAS.
- C. Long, T. Li, H. Fan, Y. Wu, L. Zhou, Y. Li, L. Xiao and Y. Li, J. Alloys Compd., 2016, 658, 839–847 CrossRef CAS.
- T. Zheng, H. Wu, Y. Yuan, X. Lv, Q. Li, T. Men, C. Zhao, D. Xiao, J. Wu and K. Wang, et al. , Energy Environ. Sci., 2017, 10, 528–537 RSC.
- A. Gupta, R. Kumar and S. Singh, Scr. Mater., 2018, 143, 5–9 CrossRef CAS.
- B. Qu, H. Du and Z. Yang, J. Mater. Chem. C, 2016, 4, 1795–1803 RSC.
- U. Holzwarth and N. Gibson, Nat. Nanotechnol., 2011, 6, 534 CrossRef CAS PubMed.
- M. Zhou, R. Liang, Z. Zhou, C. Xu, X. Nie, X. Chen and X. Dong, Mater. Res. Bull., 2018, 98, 166–172 CrossRef CAS.
- Z. Liu, H. Fan, S. Lei, X. Ren and C. Long, J. Eur. Ceram. Soc., 2017, 37, 115–122 CrossRef CAS.
- Z. Liu, H. Fan, Y. Zhao and G. Dong, J. Am. Ceram. Soc., 2016, 99, 146–151 CrossRef CAS.
- L. Jin, F. Li and S. Zhang, J. Am. Ceram. Soc., 2014, 97, 1–27 CrossRef CAS.
- F. Zhuo, Q. Li, H. Qiao, Q. Yan, Y. Zhang, X. Xi, X. Chu, X. Long and W. Cao, Appl. Phys. Lett., 2018, 112, 133901 CrossRef.
- E. Birks, M. Dunce, J. Peräntie, J. Hagberg and A. Sternberg, J. Appl. Phys., 2017, 121, 224102 CrossRef.
- Y. Bai, X. Han, X.-C. Zheng and L. Qiao, Sci. Rep., 2013, 3, 2895 CrossRef PubMed.
- M. Sanlialp, V. V. Shvartsman, M. Acosta and D. C. Lupascu, J. Am. Ceram. Soc., 2016, 99, 4022–4030 CrossRef CAS.
- T. Chen, S. Y. Wu, X. Q. Liu and X. M. Chen, J. Adv. Dielectr., 2017, 7, 1750012 CrossRef CAS.
- T. Zhang, W. Li, W. Cao, Y. Hou, Y. Yu and W. Fei, Appl. Phys. Lett., 2016, 108, 162902 CrossRef.
- S. Qi, G. Zhang, L. Duan, T. Zeng, J. Cao, J. C. Shuang Qia, G. Zhangb, L. Duana and Z. Tao, Mater. Res. Bull., 2017, 91, 31–35 CrossRef CAS.
- Z. Luo, D. Zhang, Y. Liu, D. Zhou, Y. Yao, C. Liu, B. Dkhil, X. Ren and X. Lou, Appl. Phys. Lett., 2014, 105, 102904 CrossRef.
- X. Wang, F. Tian, C. Zhao, J. Wu, Y. Liu, B. Dkhil, M. Zhang, Z. Gao and X. Lou, Appl. Phys. Lett., 2015, 107, 252905 CrossRef.
- X.-S. Qian, H.-J. Ye, Y.-T. Zhang, H. Gu, X. Li, C. A. Randall and Q. M. Zhang, Adv. Funct. Mater., 2014, 24, 1300–1305 CrossRef CAS.
- W. P. Cao, W. L. Li, D. Xu, Y. F. Hou, W. Wang and W. D. Fei, Ceram. Int., 2014, 40, 9273–9278 CrossRef CAS.
- X. Nie, S. Yan, S. Guo, F. Cao, C. Yao, C. Mao, X. Dong and G. Wang, J. Am. Ceram. Soc., 2017, 100, 5202–5210 CrossRef CAS.
- T.-F. Zhang, X.-X. Huang, X.-G. Tang, Y.-P. Jiang, Q.-X. Liu, B. Lu and S.-G. Lu, Sci. Rep., 2018, 8, 396 CrossRef PubMed.
- X. Hao, Y. Zhao and Q. Zhang, J. Phys. Chem. C, 2015, 119, 18877–18885 CrossRef CAS.
- S. Lu, B. Rožič, Q. Zhang, Z. Kutnjak, X. Li, E. Furman, L. J. Gorny, M. Lin, B. Malič and M. Kosec, et al. , Appl. Phys. Lett., 2010, 97, 162904 CrossRef.
- R. B. Olsen and D. D. Brown, Ferroelectrics, 1982, 40, 17–27 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |