Open Access Article
Open Access ArticleReversible generation of coacervate droplets in an enzymatic network†
Karina K.
Nakashima
,
Jochem F.
Baaij
and
Evan
Spruijt
 *
*
Institute for Molecules and Materials, Radboud University, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands. E-mail: e.spruijt@science.ru.nl
First published on 4th December 2017
Abstract
Cells can control the assembly and disassembly of membraneless organelles by enzymatic processes, but similar control has not been achieved in vitro yet. Here we develop ATP-based coacervate droplets as artificial membraneless organelles that can be fully controlled by two cooperating enzymes. Droplets can be generated within a minute following the addition of phosphoenolpyruvate as a substrate, and they can be dissolved within tens of seconds by adding glucose as the second substrate. We show how the rates of droplet generation and dissolution can be tuned by varying the enzyme and substrate concentrations, and we support our findings with a kinetic model of the underlying enzymatic reaction network. As all steps of the coacervate droplet life cycle, including nucleation, coarsening, and dissolution, occur under the same reaction conditions, the cycle can be repeated multiple times. In addition, by carefully balancing the rates of both enzymatic reactions, our system can be programmed to either form or dissolve droplets at specified times, acting as a chemical timer.
Introduction
Cells are composed of collections of highly complex but tightly regulated reaction networks that are well organized both in space and in time. Spatial organization can be achieved through localization of molecules and reactions at surfaces and in compartments.1,2 Besides membrane-encapsulated organelles, cells are known to form different types of membraneless organelles with varying compositions.2–4 Examples include germ granules,5,6 processing bodies,7,8 stress granules9,10 and nucleoli.11–13 Increasing evidence indicates that most of these compartments can be classified as coacervates:14,15 they are liquid droplets that are enriched in macromolecules and are formed by a liquid–liquid phase separation.3,14–21 The liquid-like nature and absence of an encapsulating membrane give rise to a direct link with processes taking place in the cytoplasm or nucleoplasm,3 providing for functions such as sequestration, buffering and reaction rate modulation.2 Like in many synthetic model systems that exhibit liquid–liquid phase separation,20–22 the formation of these biomolecular condensates can be triggered by changes in for example concentration,23,24 temperature25 and ionic strength.6 However, in most cases the exact mechanisms by which the assembly and disassembly, size and total volume are controlled remain elusive.Such a level of control would be particularly important in the development of synthetic cells. Implementing complex reaction networks in a biomimetic compartment requires not only a detailed understanding of the reactions involved, but also control over their spatial organization. Generating artificial membraneless organelles is one of the most versatile ways to organize solution composition and reactivity.26 Like in natural cells, compartments must be formed in a dynamic and reversible way, when and where needed. Mann and co-workers have shown that peptide–nucleotide coacervate droplets are promising membrane-free model organelles that sequester a variety of organic and inorganic molecules and promote secondary structure formation in peptides.27 These coacervate droplets could easily be generated and dissolved by changing the solution pH. However, this method of control is not compatible with all types of biological reactions and can be difficult to program into reaction networks. Huck and co-workers showed that disassembly of similar coacervates based on peptides and RNA can be triggered directly by an enzymatic reaction.28 More recently, Keating and co-workers showed that an alternative composition allows enzymatic control over both formation and disassembly of coacervate droplets, by respective dephosphorylation and phosphorylation of the serine residues of the peptide.14 The extreme sensitivity of their system was reflected by the fact that the difference between condensed and dissolved coacervates was as small as a single phosphate group. However, the reaction conditions required for the two enzymatic reactions were not mutually compatible and switching from condensation to dissolution always involved addition and removal of cofactors.
Here we develop a system that allows full dynamic control over the formation and dissolution of liquid coacervate droplets, as model membraneless organelles. We use the well-known peptide–ATP coacervates as the basis for our dynamic coacervates. The formation and disassembly of coacervate droplets is governed by two enzyme-catalysed reactions that turn over ATP, and can ultimately be controlled by the concentration of their respective substrates (Fig. 1). The coacervate life cycle of nucleation, growth through coarsening, and dissolution takes place under the same reaction conditions and can be repeated multiple times. We show how the rate of formation and dissolution depends on the enzyme kinetics. Finally, as both reactions take place simultaneously, we can program the system to act as a chemical timer, condensing spontaneously into liquid droplets at a specified time after substrate addition. This shows that enzyme-controlled dynamic coacervates can serve as model organelles that allow both spatial and temporal control over composition in a chemical reaction network.
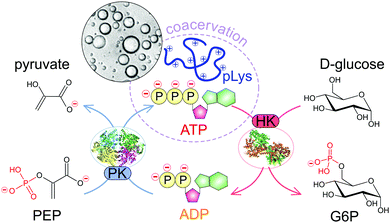 | ||
| Fig. 1 Schematic illustration of the enzymatic reaction network underlying dynamic and reversible formation and dissolution of ATP/pLys coacervate droplets. | ||
Experimental
Materials and methods
All chemicals were purchased from Sigma Aldrich and used as received unless otherwise stated. Poly-L-lysine hydrobromide (pLys, 15–30 kDa) was dissolved in Milli-Q water (18.2 MΩ cm) at a concentration of 50 mg mL−1 (0.28 M in monomer units). Adenosine triphosphate disodium salt (ATP) and adenosine diphosphate disodium salt (ADP) were freshly dissolved in water at a concentration of 100 mM and kept on ice throughout the experiments. Phosphoenolpyruvate monopotassium salt (PEP-K) solutions of 100 mM were prepared in 100 mM HEPES pH 7.4. A 0.5 M HEPES buffer was prepared from HEPES sodium salt, the pH was adjusted to 7.4 with 1 M HCl and the solution was filtered prior to use. D-Glucose, sodium chloride and magnesium chloride solutions were prepared in Milli-Q water.The pH of the all solutions was measured with a pH meter, whereas the pH of the coacervate dispersions was checked during dynamic measurements on a universal pH paper strip. Pyruvate kinase (PK) from rabbit muscle (EC 2.7.1.40, Sigma, type VII, 348 units mg−1) was freshly diluted in Milli-Q water prior to use to avoid the introduction of additional ions into the coacervate-forming solutions. Hexokinase (HK) from Saccharomyces cerevisiae was purchased as a lyophilized powder (EC 2.7.1.1, Fluka, mixture of isoforms, 41 units mg−1) and was dissolved in 10 mM HEPES pH 7.4 containing 50% (v/v) glycerol to make a concentrated stock. Dilutions were made in water prior to use. SYBR gold nucleic acid stain (Thermo Fischer, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× concentrate in DMSO) was used as a fluorescent dye for nucleotide-containing coacervates. The concentrated stock solution was diluted 100 times in buffer and added to the samples in a 1
000× concentrate in DMSO) was used as a fluorescent dye for nucleotide-containing coacervates. The concentrated stock solution was diluted 100 times in buffer and added to the samples in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio.
10 ratio.
Coacervate formation
Samples for turbidity measurements were prepared directly into 96-well plates (Greiner Bio-one, clear flat-bottom wells), by adding, respectively, HEPES, MgCl2, Milli-Q, hexokinase and/or pyruvate kinase (when applicable), pLys, ADP or ATP, and PEP and/or glucose (when applicable), to a total volume of 100 μL. Mixing was done by gentle pipetting (3×) before each measurement. Samples for the microscopy experiments were prepared in microcentrifuge tubes. After addition of the substrate, a 10 μL aliquot was immediately taken for imaging on a glass slide.Turbidimetry
Turbidity measurements were performed in triplicate using a Berthold Tristar(2) LB 942 microplate reader. Temperature was kept at 27 ± 1 °C. The absorbance was measured at 520 nm, where none of the mixture components absorbed significantly, and turbidity is reported as (100 − %T) with %T being the fraction of transmitted light at this wavelength. The absorbance of a well filled with the same volume of water was used as a blank. Samples were shaken for 0.5 s before every readout.Titrations
The critical salt concentration of ADP and ATP-coacervates with pLys was determined by mixing pLys (5 mM monomer concentration) and ADP or ATP in 50 mM HEPES pH 7.4 with 5 mM MgCl2 and increasing concentrations of NaCl, and measuring turbidity as a function of the concentration of added NaCl (triplicate). To evaluate the influence of PEP-K, some titrations were conducted in the presence of the substrate (5–15 mM), but in absence of any enzyme. The critical point was determined by extrapolating the first order derivative at the inflection point to zero turbidity. The inflection point was usually located in the region just before the turbidity stabilised at a minimum value (single-phase solution). Note that this critical salt concentration does not take into account ions from other sources than the added NaCl, and the actual critical ionic strength may therefore be higher.Optical and fluorescence microscopy
Images were recorded on an Olympus UIS2 microscope, equipped with a motorized stage (Prior, Optiscan II). Fluorescent images were recorded with an EMCCD camera (Andor, iXon), using illumination from a mercury lamp, an excitation filter of 482/18 nm (Semrock BrightLine) and an emission filter of 525/45 nm (Semrock BrightLine). Images were analyzed and prepared for presentation in ImageJ.Results and discussion
Coacervates are phase-separated dense liquid droplets that can coalesce to form a coacervate macrophase.15,20 The phase separation can be described as a partial desolvation (condensation) process, as a result of either a change in solvent quality (simple coacervation) or the neutralisation of charged groups by oppositely charged species (complex coacervation).16–19 The stability of most complex coacervates is a strong function of the charge density and overall charge of the oppositely charged components and the salt concentration of the medium.20 Small ions have a destabilising effect on complex coacervates by competing for ion pair formation, and the concentration at which this competition leads to dissolution of droplets or macroscopic phases normally increases with increasing size and charge density of the charged species.19,20,29 In practice, this means for example that ADP forms weaker coacervates than ATP with the same polycationic partner.We sought to develop a system of reversible coacervates that could be controlled by a combination of enzyme-catalysed reactions. Cells continuously convert ADP to ATP and back using a variety of different enzymes. We chose two such enzymes, pyruvate kinase and hexokinase, that both function under conditions where ATP condenses into droplets with a polycation (poly-L-lysine), whereas ADP remains in solution. By tuning the ratios of the small-molecule substrates used by both enzymes one can have full control over the thermodynamic state of the system. Fig. 1 shows a schematic illustration of the reaction network underlying these reversible coacervates.
Phase diagrams of ADP and ATP coacervates
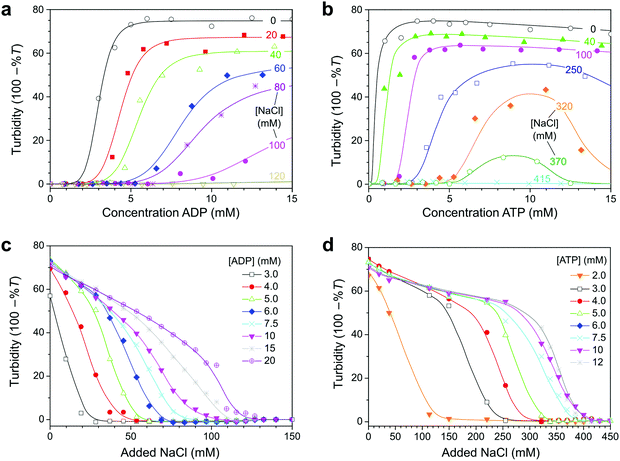
To determine the conditions under which the reaction network in Fig. 1 could give rise to reversible coacervate formation and dissolution, we first set out to determine phase diagrams of ADP/pLys and ATP/pLys coacervates, in the presence of magnesium, a critical cofactor for both enzymes. Fig. 2 shows turbidity-based titration curves of pLys (5 mM monomer units), as a function of ADP or ATP concentration, and as a function of salt concentration. Our results are in good agreement with previous reports on nucleotide/polyallylamine coacervates.30 The onset of turbidity was found at lower nucleotide concentrations for ATP than for ADP, whereas the subsequent response to the addition of nucleotides was steeper for ATP. Both effects can be explained by the higher charge density of ATP. Like the authors in ref. 30, we found that samples remained turbid up to nucleotide concentrations of 25 mM at low salt. Interestingly, we found that addition of NaCl shifted the onset of turbidity to higher nucleotide concentrations and led to a decreased response steepness. A decrease of the turbidity with increasing salt concentration results from a combination of a lower coacervate volume (fewer droplets),30 and a lower contrast between the coacervates and the surrounding solution.20The shift in the onset of turbidity results from an increased nucleotide solubility in the solution that coexists with the droplets. In most coacervates consisting of two polymeric species complexation remains centred around a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 overall charge ratio, while the intensity decreases with increasing salt.31 In the case of Mg–nucleotide/pLys coacervates without salt we found a maximal degree of coacervation near a 1
1 overall charge ratio, while the intensity decreases with increasing salt.31 In the case of Mg–nucleotide/pLys coacervates without salt we found a maximal degree of coacervation near a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 charge ratio, but with the addition of salt, the onset of coacervation was shifted beyond the point of charge compensation. For example, the onset of coacervation of Mg–ADP/pLys in 50 mM HEPES pH 7.4 and 80 mM NaCl was observed around 8 mM ADP (Fig. 2a), corresponding to an overall 5× excess of phosphate anions on ADP compared to amine cations on pLys (3× if Mg2+ is included in the complexation). It should be noted that this bears no direct implication for the charge ratio inside the coacervate droplets. Presumably, the unequal partitioning of nucleotides and pLys into the coacervate droplets still results in charge neutrality.27,30,32 The observed shift of the onset of coacervation simply reflects the strong asymmetry between the interacting species: pLys is a long polyelectrolyte, whereas nucleotides bear resemblance to small ions. As a consequence, the concentration of ADP (and ATP) in the solution that coexists with the coacervate is significant, whereas the pLys concentration in solution is low.27,32 The fact that the shift is more extreme for ADP than ATP suggests that ATP partitions more strongly into pLys coacervates.
1 charge ratio, but with the addition of salt, the onset of coacervation was shifted beyond the point of charge compensation. For example, the onset of coacervation of Mg–ADP/pLys in 50 mM HEPES pH 7.4 and 80 mM NaCl was observed around 8 mM ADP (Fig. 2a), corresponding to an overall 5× excess of phosphate anions on ADP compared to amine cations on pLys (3× if Mg2+ is included in the complexation). It should be noted that this bears no direct implication for the charge ratio inside the coacervate droplets. Presumably, the unequal partitioning of nucleotides and pLys into the coacervate droplets still results in charge neutrality.27,30,32 The observed shift of the onset of coacervation simply reflects the strong asymmetry between the interacting species: pLys is a long polyelectrolyte, whereas nucleotides bear resemblance to small ions. As a consequence, the concentration of ADP (and ATP) in the solution that coexists with the coacervate is significant, whereas the pLys concentration in solution is low.27,32 The fact that the shift is more extreme for ADP than ATP suggests that ATP partitions more strongly into pLys coacervates.
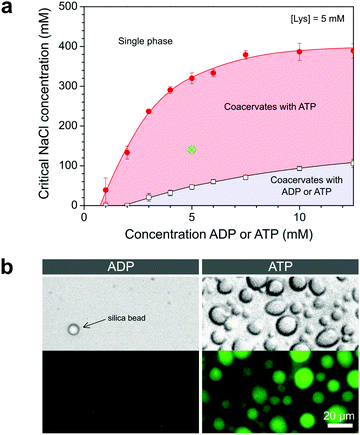
From plots of the turbidity as a function of added salt (Fig. 2c and d) we determined the critical salt concentration, the point at which coacervate droplets completely disappear. Fig. 3a shows the resulting phase diagram of both ADP and ATP coacervates. As expected, ATP-based coacervates have a significantly higher salt stability. It is interesting to note that under physiological conditions (100–200 mM ionic strength, 1–10 mM ATP, 0.5–10 mM Mg2+), ATP–pLys coacervates are expected to be stable, whereas ADP–pLys coacervates are not. Many enzymes could in principle be used under these conditions.
The operational window for the reversible coacervation in Fig. 1 is highlighted in Fig. 3a and was found to widen with increasing nucleotide concentration up to 5 mM, primarily because the ATP-based coacervates become more stable. Small amounts of charged enzymatic substrates, such as PEP-K, have no significant effect on the width of this window (Fig. S1, ESI†). To further illustrate the feasibility of the reaction network proposed in Fig. 1, we prepared mixtures of both nucleotides with pLys under identical conditions within the highlighted region of Fig. 3a. When observed under the microscope, the ATP-containing mixtures had clearly condensed into droplets, while the ADP-containing mixtures remained a homogeneous solution (Fig. 3b).
Enzyme-controlled formation and dissolution of coacervate droplets
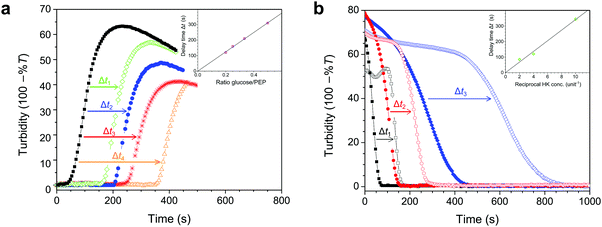
We established the conditions under which reversible switching of biomolecules from a condensed to a dissolved state is feasible. To realize this transition using enzymatic conversion, we prepared mixtures of nucleotides and pLys with the composition indicated in Fig. 3a, with varying amounts of hexokinase and D-glucose to dissolve coacervates, or pyruvate kinase and PEP to generate coacervates. Fig. 4a and b summarize our findings. Pyruvate kinase is able to use a stoichiometric amount of PEP to turn a homogeneous solution into a dispersion of droplet compartments of condensed ATP within one minute (Fig. 4a and Movie S1, ESI†), by converting ADP into ATP in the presence of pLys. The slowly decreasing turbidity after reaching a maximum is a result of coalescence and sedimentation of the formed droplets (Fig. S2, ESI†). Inversely, hexokinase can completely dissolve a dispersion of ATP droplets using glucose to convert ATP back into ADP within ten seconds (Fig. 4b and Movie S2, ESI†). The rate of droplet formation and dissolution can be controlled by varying the amount of enzyme, highlighting the fact that this transition is a direct result of enzyme-catalysed reactions.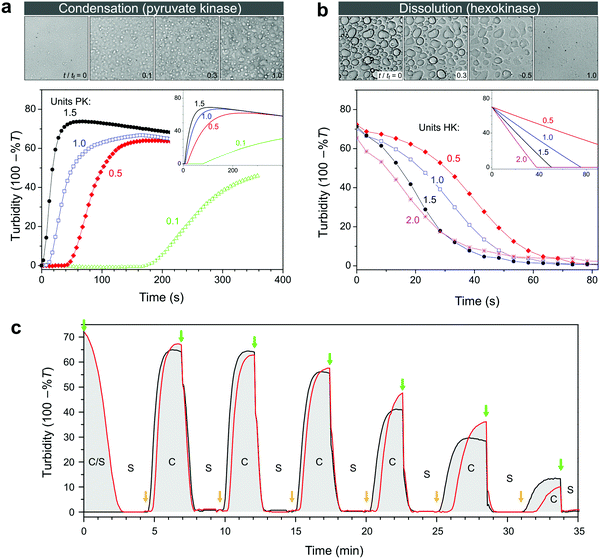 | ||
| Fig. 4 (a) Enzyme-catalysed condensation of ATP/pLys coacervate droplets by pyruvate kinase (PK) in the presence of 1 equivalent of PEP, and (b) dissolution catalysed by hexokinase (HK) in the presence of 2 equivalents of D-glucose. All mixtures contained 100 mM HEPES, 5 mM MgCl2, 30 mM NaCl, 5 mM pLys and 5 mM of the relevant nucleotide. The labels indicate the units of enzyme that were added to the mixtures, and the insets show the predicted changes in turbidity based on mass action kinetics in a single phase (see ESI† for details on the model and the kinetic parameters). The microscope images (200 μm × 200 μm) correspond to snapshots of the mixtures with 1 unit of enzyme, recorded in a separate experiment that was carried out in parallel under the microscope (see Movies S1 and S2, ESI† for the full time lapse of these experiments). The time labels indicate relative times with tf being the time to reach the final state of settled droplets or dissolved droplets. (c) Alternating additions of PEP and glucose show that condensation and dissolution are both reversible and that the system can be switched multiple times between a compartmentalized droplet state (C) and a single-phase, homogeneous solution (S). Concentrations are the same as in (a), apart from the enzymes: 1 unit of PK and 0.5 unit of HK were used. The red line corresponds to a system that started in the compartmentalized droplet state (ATP), while the black line corresponds to a system that started as a homogeneous solution (ADP). At t = 0, 1 equiv. of glucose was added to the ATP-containing system. Further additions were made simultaneously to both mixtures: 1 equiv. of PEP (at green arrows) and 0.9 equiv. of glucose (at orange arrows). | ||
To obtain better insight into the importance of the cooperating rates of binding, catalysis and inhibition for the formation of droplets we built a mathematical model of the enzyme-catalysed condensation and dissolution depicted in Fig. 1 (ESI†). For the sake of simplicity, we restricted all reactions to a single phase and assumed rapid partitioning of ATP into the droplets. As shown in the insets in Fig. 4a and b, simple mass-action kinetics underlying our model is sufficient to qualitatively capture the observed condensation and dissolution rates and the timescales of beginning and end of both processes. The delay of condensation in Fig. 4a for small amounts of pyruvate kinase results from a combination of product inhibition of the enzyme by ATP33 and the nonzero threshold ATP concentration required for droplet formation (Fig. 2b). By contrast, hexokinase is less strongly inhibited by ADP and the droplets started to dissolve directly after the addition of D-glucose. Although our model is able to qualitatively capture certain key aspects of the condensation and dissolution, it cannot predict droplet formation quantitatively for two main reasons. On the one hand, there is no clear way to convert ATP concentrations into turbidity, taking into account droplet sizes, nucleation, growth, coalescence and sedimentation. On the other hand, many enzymes have been found to partition into coacervate droplets, and retain their functionality to a certain degree.27,34,35 For hexokinase, a partitioning coefficient of 20 was found for salt-free ATP/pLys coacervates,27 but the partitioning coefficients and rate constants inside coacervates of almost all other components in Fig. 1 are still unknown.
A key advantage of our enzyme-catalysed coacervate system is the fact that both enzymes are functional under the same conditions. It is therefore possible to switch between condensation and dissolution by simple addition of substrates (PEP and D-glucose). Fig. 4c illustrates this reversibility: droplets could be generated and dissolved up to six times, and we were able to carry out identical transitions when starting from either ADP or ATP. After six cycles, the system loses its ability to condense into droplets, which is mainly caused by the accumulation of waste products, i.e., pyruvate and glucose-6-phosphate (G6P). After six cycles, the system contains a six-fold excess of pyruvate and G6P. Both small molecules exist as charged species under our reaction conditions and act to destabilize the coacervate droplets. However, the increased ionic strength alone can probably not explain the absence of ATP coacervates (Fig. 3a and Fig. S1, ESI†). The accumulated products also act to decrease the pyruvate kinase activity, as evidenced by the slopes of the condensation traces in Fig. 4c, by both pyruvate inhibition and inactivation as a result of phosphorylation and aggregation.33 Nevertheless, the level of enzymatic control over droplet generation shown in Fig. 4c has not been achieved before, and holds great promise for the development of dynamic artificial organelles. Removal of waste products via dialysis or by downstream enzymatic conversion can further improve the system's durability.
Temporal control over coacervate formation
In the reaction network underlying the observed condensation and dissolution of droplets, the two opposing pathways of ATP formation and consumption can operate simultaneously. Such a network can give rise to responses that are otherwise impossible with simple linear reactions. For example, by introducing an excess of hexokinase, but limiting the amount of glucose relative to PEP, one can control the time at which the mixture starts to condense into droplets and thus trigger the storage of ATP and other charged macromolecules. An excess of hexokinase results in faster ATP consumption than production by pyruvate kinase, preventing condensation. However, once all glucose has been consumed, ATP production by pyruvate kinase takes over and droplets are formed, as evidenced by an increase in turbidity. The amount of glucose, and indirectly the ratio of hexokinase and pyruvate kinase, set the time of droplet formation, as illustrated in Fig. 5a. By also varying the absolute amount of enzyme, the onset of condensation can be further tuned (Fig. S3, ESI†). On the other hand, if an excess of pyruvate kinase is present but the amount of PEP is limited, droplet dissolution can be programmed with a delay time that depends on the amount of PEP and pyruvate kinase (Fig. 5b).We emphasize that the behaviour shown in Fig. 5a and b, in which a mixture displays a shift in time while maintaining the same responsiveness, can only be realised in a network of cooperating reactions. The possibility to program this behaviour opens up a wide range of possibilities for use of this system as artificial organelles: it provides a natural way to control both spatial and temporal organization of biomolecules under physiological conditions.
Conclusions
We have shown that an enzymatic reaction network can be used to both generate and dissolve coacervate droplets in a reversible way. The onset and rate of condensation and dissolution can be controlled by varying the amount of enzyme and substrate. Using pyruvate kinase with PEP as substrate, ATP/pLys coacervates can be generated within a minute, whereas they can be dissolved again in tens of seconds using hexokinase with glucose as substrate. Because all reactions take place under the same conditions, the cycle of condensation and dissolution can be repeated multiple times, and, by combining both substrates, the onset of condensation and dissolution can be programmed to occur at predefined times. The performance of the system eventually decreases after twelve transitions, as a result of the accumulation of reaction waste products.The coacervate droplets formed in this way are natural storage compartments for nucleotides, charged biomolecules and organic compounds and the enzymatic network that governs their formation holds great promise in our attempt to build a synthetic cell: it allows control over both spatial and temporal organization of molecules, their interactions and reactions in complex systems. An important next step would be to include biorecognition motifs in the building blocks to give specificity to the partitioning of molecules into these condensates and further improve on the selective localization of chemically similar biomolecules.
Author contributions
K. K. N. and J. F. B. designed and carried out experiments and analysed data. E. S. conceived the project and analysed data. K. K. N. and E. S. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Netherlands Organization for Scientific Research (NWO) under project number 016.162.010.Notes and references
- S. Banjade and M. K. Rosen, eLife, 2014, 3, 04123 Search PubMed
.
- S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285 CrossRef CAS PubMed
.
- E. M. Courchaine, A. Lu and K. M. Neugebauer, EMBO J., 2016, 35, 1603 CrossRef CAS PubMed
.
- J. M. Shively, Annu. Rev. Microbiol., 1974, 28, 167 CrossRef CAS PubMed
.
- C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324, 1729 CrossRef CAS PubMed
.
- T. J. Nott, E. Petsalaki, P. Faber, D. Jervis, E. Fussner, A. Plochowietz, T. D. Craggs, D. P. Bazett-Jones, T. Pawson, J. D. Forman-Kay and A. J. Baldwin, Mol. Cell, 2015, 57, 936 CrossRef CAS PubMed
.
- U. Sheth and R. Parker, Science, 2003, 300, 5620 CrossRef PubMed
.
- C. J. Decker, D. Teixeira and R. Parker, J. Cell Biol., 2007, 179, 437 CrossRef CAS PubMed
.
- J. R. Buchan and R. Parker, Mol. Cell, 2009, 36, 932 CrossRef CAS PubMed
.
- J. R. Wheeler, T. Matheny, S. Jain, R. Abrisch and R. Parker, eLife, 2016, 5, 18413 Search PubMed
.
- C. P. Brangwynne, T. J. Mitchison and A. A. Hyman, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4334 CrossRef CAS PubMed
.
- M. Feric, N. Vaidya, T. S. Harmon, D. M. Mitrea, L. Zhu, T. M. Richardson, R. W. Kriwacki, R. V. Pappu and C. P. Brangwynne, Cell, 2016, 165, 1686 CrossRef CAS PubMed
.
- H. Falahati and E. Wieschaus, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1335 CrossRef CAS PubMed
.
- W. M. Aumiller Jr and C. D. Keating, Nat. Chem., 2016, 8, 129 Search PubMed
.
- Y. Jho, H. Y. Yoo, Y. Lin, S. Han and D. S. Hwang, Adv. Colloid Interface Sci., 2017, 239, 61 CrossRef CAS PubMed
.
- H. G. Bungenberg de Jong and H. R. Kruyt, Proc. K. Ned. Akad. Wet., 1929, 32, 849 Search PubMed
.
-
H. R. Kruyt, Colloid Science Vol. 2: Reversible Systems, Elsevier, 1949 Search PubMed
.
- I. Langmuir, J. Chem. Phys., 1938, 6, 873 CrossRef CAS
.
- J. Th., G. Overbeek and M. J. Voorn, J. Cell. Comp. Physiol., 1957, 49, 7 CrossRef
.
- E. Spruijt, A. H. Westphal, J. W. Borst, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 6476 CrossRef CAS
.
- J. van der Gucht, E. Spruijt, M. Lemmers and M. A. Cohen Stuart, J. Colloid Interface Sci., 2011, 361, 407 CrossRef CAS PubMed
.
- J. Fu, H. D. Fares and J. B. Schlenoff, Macromolecules, 2017, 50, 1066 CrossRef CAS
.
- S. C. Weber and C. P. Brangwynne, Curr. Biol., 2015, 25, 641 CrossRef CAS PubMed
.
- S. Saha, C. A. Weber, M. Nousch, O. Adame-Arana, C. Hoege, M. Y. Hein, E. Osborne-Nishimura, J. Mahamid, M. Jahnel, L. Jawerth, A. Pozniakovski, C. R. Eckmann, F. Jülicher and A. A. Hyman, Cell, 2016, 166, 1572 CrossRef CAS PubMed
.
- H. Jiang, S. Wang, Y. Huang, X. He, H. Cui, X. Zhu and Y. Zheng, Cell, 2015, 163, 108 CrossRef CAS PubMed
.
- W. M. Aumiller Jr and C. D. Keating, Adv. Colloid Interface Sci., 2017, 239, 75 CrossRef PubMed
.
- S. Koga, D. S. Williams, A. W. Perriman and S. Mann, Nat. Chem., 2011, 3, 720 CrossRef CAS PubMed
.
- S. N. Semenov, A. S. Y. Wong, R. M. van der Made, S. G. J. Postma, J. Groen, H. W. H. van Roekel, T. F. A. de Greef and W. T. S. Huck, Nat. Chem., 2015, 7, 160 CrossRef CAS PubMed
.
- E. Spruijt, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2013, 46, 1633 CrossRef CAS
.
- E. A. Frankel, P. C. Bevilacqua and C. D. Keating, Langmuir, 2016, 32, 2041 CrossRef CAS PubMed
.
- S. Lindhoud, R. de Vries, W. Norde and M. A. Cohen Stuart, Biomacromolecules, 2007, 8, 2219 CrossRef CAS PubMed
.
- J. Wang, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2012, 45, 8903 CrossRef CAS
.
- C. Wang, L. R. Chiarelli, P. Bianchi, D. J. Abraham, A. Galizzi, A. Mattevi, A. Zanella and G. Valentini, Blood, 2001, 98, 3113 CrossRef CAS PubMed
.
- S. Lindhoud and M. M. A. E. Claessens, Soft Matter, 2016, 12, 408 RSC
.
- E. Sokolova, E. Spruijt, M. M. K. Hansen, E. Dubuc, J. Groen, V. Chokkalingam, A. Piruska, H. A. Heus and W. T. S. Huck, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11692 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm01897e |
| This journal is © The Royal Society of Chemistry 2018 |