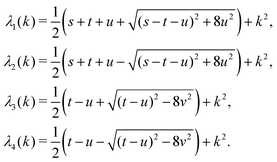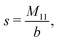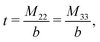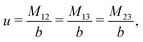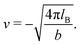DOI:
10.1039/C8SM00497H
(Paper)
Soft Matter, 2018,
14, 4126-4140
Electrolyte solutions at heterogeneously charged substrates
Received
9th March 2018
, Accepted 29th March 2018
First published on 25th April 2018
Abstract
The influence of a chemically or electrically heterogeneous distribution of interaction sites at a planar substrate on the number density of an adjacent fluid is studied by means of classical density functional theory (DFT). In the case of electrolyte solutions the effect of this heterogeneity is particularly long ranged, because the corresponding relevant length scale is set by the Debye length which is large compared to molecular sizes. The DFT used here takes the solvent particles explicitly into account and thus captures phenomena, inter alia, due to ion–solvent coupling. The present approach provides closed analytic expressions describing the influence of chemically and electrically nonuniform walls. The analysis of isolated δ-like interactions, isolated interaction patches, and hexagonal periodic distributions of interaction sites reveals a sensitive dependence of the fluid density profiles on the type of the interaction, as well as on the size and the lateral distribution of the interaction sites.
I. Introduction
Detailed knowledge of the structure of electrolyte solutions close to solid substrates is of great importance to numerous research areas and fields of application, ranging from electrochemistry1,2 and wetting phenomena3,4via coating5 and surface patterning6,7 to colloid science8,9 and microfluidics.10,11 The vast majority of models describing fluids in contact with substrates consider the latter as uniform with respect to the wall–fluid interaction. This approximation is commonly made partly due to a lack of experimental data on the actual local properties of the substrate under consideration and partly for the sake of simplicity. For fluids comprising only electrically neutral constituents and uncharged walls, assuming uniform substrates is typically an acceptable approximation because, in the absence of wetting transitions, heterogeneous substrate properties influence the fluid only on length scales of the order of the bulk correlation length,12 which, not too close to critical points, is of the order of a few molecular diameters. In contrast, nonuniformities of the surface charge density of charged substrates in contact with dilute electrolyte solutions influence the fluid on the scale of the Debye length, which is much larger than the size of the molecules. Furthermore, the charged sites of substrates, such as mineral surfaces and polyelectrolytes, are lateral distances apart which are typically comparable with the Debye length of the surrounding fluid medium.13–15 Hence, the assumption, that substrates in contact with electrolyte solutions carry a uniform surface charge density, is in general untenable.
In recent years considerable theoretical interest has emerged in the effective interaction between two heterogeneously charged walls (which typically are the surfaces of colloidal particles) mediated by an electrolyte solution.16–26 In contrast to uniform substrates, this effective interaction can lead to lateral forces, in addition to the common ones in normal direction. However, all the studies cited above model the solvent of the electrolyte solution as a structureless dielectric continuum. This approach precludes coupling effects due to a competition between the solvation and the electrostatic interaction, which are known to occur in bulk electrolyte solutions.27–29 In particular, in the presence of ion–solvent coupling and far away from critical points, correlations of the solvent number densities in a dilute electrolyte solution decay asymptotically on the scale of the Debye length. Consequently, under such conditions, nonuniformities of the nonelectrostatic solvent–wall interaction can influence the structure of an electrolyte solution close to a wall and hence the strength and range of the effective interaction between two parallel plates immersed in an electrolyte medium on a length scale much larger than the molecular size. This mechanism differs from the one studied in ref. 16, 20, 22 and 26, in which the walls are locally charged but overall charge neutral.
In the present analysis a first step is taken towards a description of the structure of electrolyte solutions close to chemically and electrically nonuniform walls in terms of all fluid components. The natural framework for obtaining the fluid structure in terms of number density profiles of solvent and ion species is classical density functional theory.30–32 Here, the most simple case of an electrolyte solution, composed of a single solvent species and a single univalent salt component, is considered far away from bulk or wetting phase transitions. Moreover, the spatial distribution of nonuniformities of the chemical and electrostatic wall–fluid interactions can be arbitrary but their strengths are assumed to be sufficiently weak such that a linear response of the number density deviations from the bulk values is justified. This setup allows for closed analytic expressions which are used to obtain a first overview of the influence of ion–solvent coupling on the structure of electrolyte solutions in contact with chemically or electrically nonuniform walls. This insight will guide future investigations of more general setups within more sophisticated models.
After introducing the formalism in Section II, selected cases of heterogeneous walls are discussed in Section III. Due to the linear relationship between the wall nonuniformities and the corresponding number density deviations from the bulk values, the latter are given by linear combinations of elementary response features, which are discussed first. Next, two main cases are studied: wall heterogeneities, which are laterally isotropic around a certain center and wall heterogeneities, which possess the symmetry of a two-dimensional lattice; the study of randomly distributed nonuniformities16,18–21 is left to future research. For both cases various length scale regimes are discussed, which are provided by the bulk correlation length of the pure solvent, the Debye length, and a characteristic length scale associated with the wall nonuniformities. Conclusions and a summary are given in Section IV.
II. Theoretical foundations
A. Setup
Here, the influence of a chemically and electrically nonuniform wall on the fluid density is studied. In spatial dimension d = 3 the system consists of an impenetrable planar wall for z < 0 and a fluid for z > 0, both parts being macroscopically large. In the following, the space occupied by the fluid is denoted by 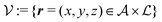 ; the positions r = (x, y, z) = (r‖,z) are uniquely decomposed into the lateral components
; the positions r = (x, y, z) = (r‖,z) are uniquely decomposed into the lateral components 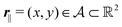 and the normal component
and the normal component 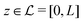 relative to the wall surface at z = 0. The size
relative to the wall surface at z = 0. The size 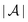 of the wall and the extent L of the system in normal direction are both assumed to be macroscopically large. The fluid is an electrolyte solution composed of an uncharged solvent (index “1”), univalent cations (index “2”), and univalent anions (index “3”). Two types of interactions between the fluid and the wall are considered: (i) electric monopoles at the wall surface (z = 0) and the fluid ions, giving rise to an electrostatic interaction, (ii) all other contributions, in particular those due to nearest-neighbor-like chemical bonds, referred to as nonelectrostatic interactions.
of the wall and the extent L of the system in normal direction are both assumed to be macroscopically large. The fluid is an electrolyte solution composed of an uncharged solvent (index “1”), univalent cations (index “2”), and univalent anions (index “3”). Two types of interactions between the fluid and the wall are considered: (i) electric monopoles at the wall surface (z = 0) and the fluid ions, giving rise to an electrostatic interaction, (ii) all other contributions, in particular those due to nearest-neighbor-like chemical bonds, referred to as nonelectrostatic interactions.
B. Density functional theory
We use density functional theory30–32 in order to determine the equilibrium number density profiles ϱ = (ϱ1, ϱ2, ϱ3) of the three fluid species. Since we focus on length scales larger than the sizes of the fluid particles and on weak wall–fluid interactions, the following dimensionless density functional within a Cahn–Hilliard-like square-gradient approximation33 is considered:| | 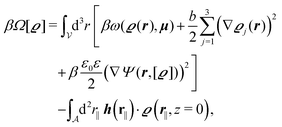 | (1) |
where β = 1/(kBT) is the inverse thermal energy, μ = (μ1, μ2, μ3) are the chemical potentials of the three species, b > 0 is a phenomenological parameter with dimension [b] = (length5), which can be inferred from microscopic models (see Section IIIA), ε0 ≈ 8.854 × 10−12 A s V−1 m−1 is the vacuum permittivity,37ε is the relative dielectric constant of the fluid, Ψ(r, [ϱ]) is the electrostatic potential at 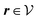 , and h(r‖) = (h1(r‖), h2(r‖), h3(r‖)) describes the strengths of the nonelectrostatic wall–fluid interactions at r = (r‖, 0) for the three species. Note that for the sake of simplicity, the coupling of number density gradients of different particle types is neglected in eqn (1) (see Section IIIA). In the present study the bulk state ϱb = (ϱ1,b, ϱ2,b, ϱ3,b) is considered to be thermodynamically far away from any phase transition so that the local contribution βω(ϱ) of the density functional in eqn (1) can be safely expanded around ϱb up to quadratic order in δϱ := ϱ − ϱb:
, and h(r‖) = (h1(r‖), h2(r‖), h3(r‖)) describes the strengths of the nonelectrostatic wall–fluid interactions at r = (r‖, 0) for the three species. Note that for the sake of simplicity, the coupling of number density gradients of different particle types is neglected in eqn (1) (see Section IIIA). In the present study the bulk state ϱb = (ϱ1,b, ϱ2,b, ϱ3,b) is considered to be thermodynamically far away from any phase transition so that the local contribution βω(ϱ) of the density functional in eqn (1) can be safely expanded around ϱb up to quadratic order in δϱ := ϱ − ϱb:| | 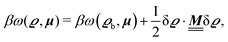 | (2) |
where the local part of the interactions between different types of particles is captured by the real-valued, symmetric, and positively definite 3 × 3-matrix 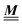 (see, cf., eqn (30)). Furthermore, ω(ϱb, μ) = −p specifies the grand potential density, evaluated for the equilibrium bulk densities ϱb, which equals minus the bulk pressure p; in the following its value is of no importance. For a given equation of state p(ϱb, T) the bulk densities ϱb = (ϱb,1, ϱb,2, ϱb,3) are free parameters of the model. Finally, the electrostatic potential Ψ(r, [ϱ]), which enters into eqn (1) on a mean-field level via the electric field energy density, fulfills the Poisson equation
(see, cf., eqn (30)). Furthermore, ω(ϱb, μ) = −p specifies the grand potential density, evaluated for the equilibrium bulk densities ϱb, which equals minus the bulk pressure p; in the following its value is of no importance. For a given equation of state p(ϱb, T) the bulk densities ϱb = (ϱb,1, ϱb,2, ϱb,3) are free parameters of the model. Finally, the electrostatic potential Ψ(r, [ϱ]), which enters into eqn (1) on a mean-field level via the electric field energy density, fulfills the Poisson equation| | | −ε0ε∇2Ψ(r, [ϱ]) = eZ·ϱ(r) | (3) |
for 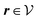 with the boundary conditions
with the boundary conditions| | 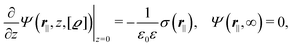 | (4) |
for 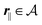 , where σ(r‖) is the surface charge density at the point r = (r‖, 0) on the wall surface (z = 0), and Z = (Z1, Z2, Z3) = (0, 1, −1) denotes the valences of the fluid species.
, where σ(r‖) is the surface charge density at the point r = (r‖, 0) on the wall surface (z = 0), and Z = (Z1, Z2, Z3) = (0, 1, −1) denotes the valences of the fluid species.
The Euler–Lagrange equations, corresponding to the minimum of the density functional specified in eqn (1)–(4), can be written as
| | 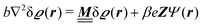 | (5) |
and
| | 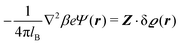 | (6) |
for
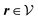
with the boundary conditions given by
eqn (4) and by
| | 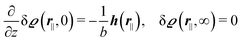 | (7) |
for
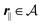
, where
lB =
βe2/(4π
ε0ε) is the Bjerrum length.
The linear nature of the Euler–Lagrange eqn (5) and (6) tells that the quadratic (Gaussian) approximation of the underlying density functional in eqn (1) and (2) corresponds to a linear response approach. It is widely assumed and in some cases it can be even quantified (see, e.g., the quantitative agreement between the full and the linearized Poisson–Boltzmann theory in the case that the surface charges are smaller than the saturation value8,34) that for sufficiently weak wall–fluid interactions linear response theory provides quantitatively reliable results.
C. Solution of the Euler–Lagrange equations
Instead of solving the Euler–Lagrange equations in eqn (5) and (6) as differential equations for the profiles δϱ and Ψ as functions of r = (r‖, z), it is convenient first to perform Fourier transformations with respect to the lateral coordinates r‖. The resulting transformed profiles| | 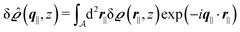 | (8) |
and 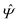 as functions of q‖ = (qx, qy) ∈
as functions of q‖ = (qx, qy) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2 and z ∈
2 and z ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) can be combined in the four-component quantity
can be combined in the four-component quantity 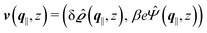 so that eqn (5) and (6) can be written as
so that eqn (5) and (6) can be written as| | 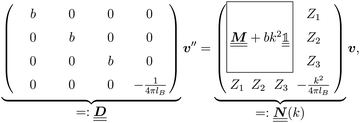 | (9) |
where 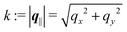 and v′′(q‖,z) is the second derivative of v(q‖, z) with respect to the coordinate z normal to the wall. Note that the components of v are quantities of different dimensions: [v1] = [v2] = [v3] = 1/length and [v4] = (length)2. This does not allow for the formation of a scalar product of two vectors of the type
and v′′(q‖,z) is the second derivative of v(q‖, z) with respect to the coordinate z normal to the wall. Note that the components of v are quantities of different dimensions: [v1] = [v2] = [v3] = 1/length and [v4] = (length)2. This does not allow for the formation of a scalar product of two vectors of the type 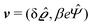 ; however, in the following scalar products will not occur. Writing
; however, in the following scalar products will not occur. Writing 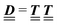 with
with 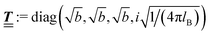 (i.e.,
(i.e., 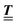 is a diagonal matrix with these entries), one obtains
is a diagonal matrix with these entries), one obtains| | 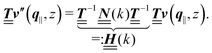 | (10) |
The 4 × 4-matrix 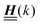 is independent of z and it is symmetric but not real-valued, because the bottom entry of
is independent of z and it is symmetric but not real-valued, because the bottom entry of 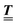 is imaginary.
is imaginary. 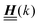 is not a normal matrix, i.e., it does not commute with its adjoint matrix
is not a normal matrix, i.e., it does not commute with its adjoint matrix 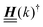 , and hence it does not possess an orthogonal basis composed of eigenvectors. However, the actual structures of the matrix
, and hence it does not possess an orthogonal basis composed of eigenvectors. However, the actual structures of the matrix 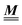 and of the vector Z used below guarantee the existence of a nonorthogonal basis {Λ1(k), …, Λ4(k)} of eigenvectors of the matrix
and of the vector Z used below guarantee the existence of a nonorthogonal basis {Λ1(k), …, Λ4(k)} of eigenvectors of the matrix 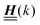 with respective positive (real-valued) eigenvalues λ1(k), …, λ4(k) ∈ (0,∞) (see Appendix A). Expanding the vector
with respective positive (real-valued) eigenvalues λ1(k), …, λ4(k) ∈ (0,∞) (see Appendix A). Expanding the vector 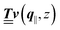 in this basis {Λ1(k),…,Λ4(k)},
in this basis {Λ1(k),…,Λ4(k)},| | 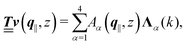 | (11) |
leads to eqn (10) in the form| | 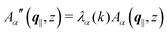 | (12) |
with the solution| | 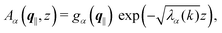 | (13) |
where the second boundary conditions in eqn (4) and (7) have been used. Therefore, the solution of eqn (10) can be expressed as| | 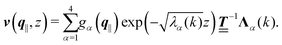 | (14) |
Finally, the first boundary conditions in eqn (4) and (7) can be expressed as| | 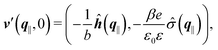 | (15) |
with| | 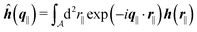 | (16) |
as the Fourier transform of h(r‖) with respect to the lateral coordinates r‖ and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖) as the Fourier transform of σ(r‖). Note that, as for v, the components of v′ are quantities of different dimensions: [v1′] = [v2′] = [v3′] = 1/(length)2 and [v4] = length. From eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) can be determined. Note that according to eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) and hence the profiles
(q‖) as the Fourier transform of σ(r‖). Note that, as for v, the components of v′ are quantities of different dimensions: [v1′] = [v2′] = [v3′] = 1/(length)2 and [v4] = length. From eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) can be determined. Note that according to eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) and hence the profiles 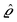 and
and ![[capital Psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b0.gif) depend linearly on the nonelectrostatic wall–fluid interactions ĥ(q‖) and the surface charge density
depend linearly on the nonelectrostatic wall–fluid interactions ĥ(q‖) and the surface charge density ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖). Such a linear response of the number density profiles inside the fluid to the wall properties requires weak wall–fluid interactions, which is assumed in the present study and which is consistent with the quadratic form of the density functional in eqn (1)–(4).
(q‖). Such a linear response of the number density profiles inside the fluid to the wall properties requires weak wall–fluid interactions, which is assumed in the present study and which is consistent with the quadratic form of the density functional in eqn (1)–(4).
III. Results and discussion
A. Choice of parameters
The present study discusses the influence of the wall–fluid interactions, represented by the nonelectrostatic wall–fluid interactions ĥ(q‖) and the surface charge density ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖), onto the number density profiles ϱ in the adjacent fluid. Applying density functional theory as described in Section II requires knowledge of the bulk number densities ϱb, the parameter b, and the coupling matrix
(q‖), onto the number density profiles ϱ in the adjacent fluid. Applying density functional theory as described in Section II requires knowledge of the bulk number densities ϱb, the parameter b, and the coupling matrix 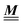 all of which are bulk quantities or characterize them.
all of which are bulk quantities or characterize them.
In the bulk local charge neutrality holds, i.e., Z·ϱb = 0. Hence the equilibrium bulk state is determined by the temperature T, the number density ϱ1,b of the solvent, and the bulk ionic strength I = ϱ2,b = ϱ3,b.
In order to obtain expressions for the parameter b and for the coupling matrix 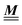 in terms of experimentally accessible quantities, in a first step the pure, ion-free solvent is considered, the particles of which interact only nonelectrostatically. Here this nonelectrostatic interaction between solvent particles at a distance r is modeled by a square-well pair potential U(r) as displayed in Fig. 1(a). At small distances r < σ a hard core repulsion prevents the overlap of two particles. At intermediate distances r ∈ (σ, σpot) two particles attract each other with an interaction energy −εpot, and at distances r > σpot the nonelectrostatic interaction vanishes. According to the scheme due to Barker and Henderson,35 the interaction potential U can be decomposed as U = Uhc + Upot into the hard core repulsion Uhc and the attractive well Upot (see Fig. 1(b)). The microscopic density functional Ωmic1[ϱ1] for the pure solvent (species 1) in the bulk can be approximated by the expression
in terms of experimentally accessible quantities, in a first step the pure, ion-free solvent is considered, the particles of which interact only nonelectrostatically. Here this nonelectrostatic interaction between solvent particles at a distance r is modeled by a square-well pair potential U(r) as displayed in Fig. 1(a). At small distances r < σ a hard core repulsion prevents the overlap of two particles. At intermediate distances r ∈ (σ, σpot) two particles attract each other with an interaction energy −εpot, and at distances r > σpot the nonelectrostatic interaction vanishes. According to the scheme due to Barker and Henderson,35 the interaction potential U can be decomposed as U = Uhc + Upot into the hard core repulsion Uhc and the attractive well Upot (see Fig. 1(b)). The microscopic density functional Ωmic1[ϱ1] for the pure solvent (species 1) in the bulk can be approximated by the expression
| | | βΩmic1[ϱ1] = βΩhc1[ϱ1] + βFex,pot[ϱ1]. | (17) |
The contribution
Ωmic1 (here within local density approximation (LDA)) is due to the reference system governed solely by the hard core interaction
Uhc:
| | 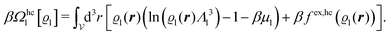 | (18) |
Here, contributions of external potentials are neglected, because they do not contribute to the bulk parameters
b and
. The second term on the rhs of
eqn (17) is (within random phase approximation (RPA)
30) the excess free energy functional due to the square-well attractive interaction
Upot:
| | 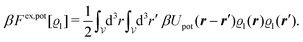 | (19) |
In
eqn (18)Λ1 is the thermal de Broglie wave length,
μ1 denotes the chemical potential of species 1, and
fex,hc(
ϱ1) is the excess free energy per volume of the reference system governed by the hard core interaction
Uhc.
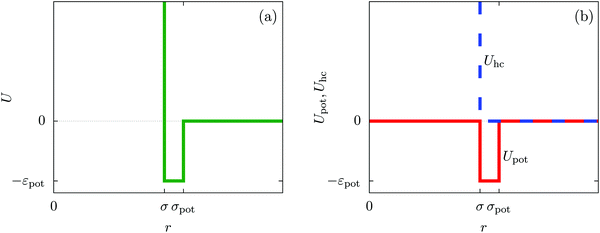 |
| | Fig. 1 The nonelectrostatic interaction between fluid particles is modeled by a square-well pair potential U(r) displayed in panel (a), where r denotes the distance between the centers of two spherical particles. For r < σ a hard core repulsion prevents the overlap of two particles. For r ∈ (σ, σpot) two particles attract each other with a constant interaction energy −εpot < 0. At distances r > σpot there is no nonelectrostatic interaction. Panel (b) sketches the decomposition U = Uhc + Upot of the nonelectrostatic interaction potential U according to the scheme due to Barker and Henderson into the hard core repulsion Uhc and the attractive well Upot, which is used in Section IIIA in order to obtain the parameters entering the Cahn–Hilliard square-gradient density functional in eqn (1). | |
Following Cahn and Hilliard,33eqn (19) can be approximated by a gradient expansion:
| | 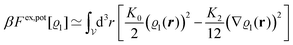 | (20) |
with the
m-th moment of the pair potential
Upot in units of
kBT,
| | 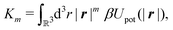 | (21) |
which, for the present form of
Upot, leads to
| | 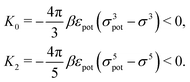 | (22) |
From
eqn (20) one obtains the gradient expansion of
βΩmic1[
ϱ1] in
eqn (17):
| | 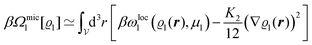 | (23) |
with the local contribution
| | 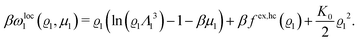 | (24) |
The comparison of
eqn (23) with
eqn (1) renders an expression for the parameter
b in terms of parameters of the interaction potential
U (see
Fig. 1):
| | 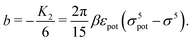 | (25) |
By expanding
βωloc1(
ϱ1,
μ1) up to quadratic order in the density deviation δ
ϱ1 =
ϱ1 −
ϱ1,b from the equilibrium bulk density
ϱ1,b, which is a solution of the Euler–Lagrange equation
| | 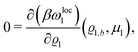 | (26) |
one obtains
| | 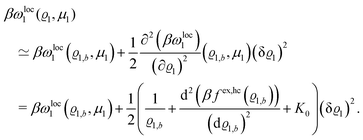 | (27) |
The comparison with
eqn (2) leads to the matrix element
| | 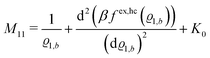 | (28) |
of the matrix
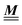
, where the first term on the rhs stems from the ideal gas contribution of the solvent particles. The argument
ϱ1,b of the second term, which is due to the hard core interaction
Uhc, is a measure of the packing fraction
η = π
ϱ1,bσ3/6.
The analogue of eqn (23) for the nonelectrostatic contribution of all three particle species is given by the first line of eqn (1) with the local contribution (compare eqn (24))
| | 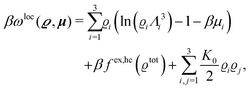 | (29) |
where
ϱtot =
ϱ1 +
ϱ2 +
ϱ3 denotes the total number density. Note that
eqn (29) assumes, that all interactions among the species are the same (see
eqn (21)). This implies that the last term in
eqn (29) takes the form
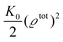
. By expanding
βωloc(
ϱ,
μ) up to quadratic order in the density deviations δ
ϱ =
ϱ −
ϱb from the equilibrium bulk densities
ϱb one finally finds (see the steps leading to
eqn (28))
| | 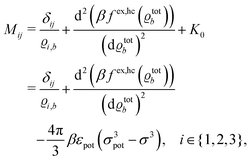 | (30) |
where
ϱtotb =
ϱ1,b +
ϱ2,b +
ϱ3,b =
ϱ1,b + 2
I denotes the total number density in the bulk. In the present study the hard core excess free energy per volume
fex,hc(
ϱb) is chosen as the one corresponding to the Carnahan–Starling equation of state:
35| | 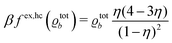 | (31) |
here with the packing fraction
η = π
ϱtotbσ3/6.
Accordingly, from eqn (24) one obtains the following equation of state of the pure solvent:
| | 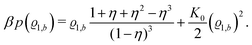 | (32) |
Its derivative with respect to the number density
ϱ1,b, using the relation ∂
p/∂
ϱ1,b = 1/(
κTϱ1,b) with the isothermal compressibility
κT, yields
| | 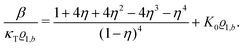 | (33) |
As an example we consider water at room temperature
T = 300 K and ambient pressure
p = 1 bar (which corresponds to the number density
ϱb,1 = 55.5 M ≈ 33.3 nm
−3 and the isothermal compressibility
κT = 4.5 × 10
−10 Pa
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37
37) with relative dielectric constant
ε = 80,
i.e., with Bjerrum length
lB = 0.7 nm, and with a univalent salt of ionic strength
I = 1 mM ≈ 6 × 10
−4 nm
−3. The strength of hydrogen bonds, which generate the dominant attractive interaction contribution, is of the order of
εpot ≈ 20 kJ mol
−1 ≈ 8
kBT.
36,37 Using these data, one obtains from
eqn (32) and (33) the bulk packing fraction
η ≈ 0.44 as well as
σ = 2.9 Å and
σpot = 3.4 Å. In the following the Debye length
| | 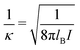 | (34) |
is used as length scale, which, for the present choice of parameters, is 1/
κ ≈ 10 nm.
In the case of a pure solvent (δϱ2 = δϱ3 = Ψ = 0), in the bulk the density two-point correlation function G(r1, r2) = Ḡ(r1 − r2) fulfills an equation similar to eqn (5):
Note that the similarity between
eqn (5) and (35) is due to the asymptotic proportionality between density deviations and two-point correlation functions (Yvon equation).
35 From
eqn (35), one can readily infer the relation
| | 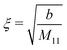 | (36) |
for the solvent bulk correlation length, which characterizes the exponential decay of
Ḡ(
r). For the present choice of parameters, one has
ξ ≈ 1.3 Å so that
κξ ≈ 0.013.
B. X-ray scattering
In the following subsections the Fourier transforms 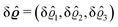 of the profiles of the density deviations as functions of the lateral wave vector q‖ and of the normal distance z from the wall are discussed in detail. However, from the experimental point of view, it is challenging to directly obtain the z-dependence of the density profiles. One of such direct methods is total internal reflection microscopy (TIRM)38 in the context of the structure of colloidal suspensions close to (optically transparent) substrates. In contrast, for molecular fluids, as the ones considered here, such direct methods are not available and one has to resort to, e.g., X-ray scattering techniques.39,40 As X-rays are predominantly scattered by the electrons of the fluid molecules one has to consider the electron number density
of the profiles of the density deviations as functions of the lateral wave vector q‖ and of the normal distance z from the wall are discussed in detail. However, from the experimental point of view, it is challenging to directly obtain the z-dependence of the density profiles. One of such direct methods is total internal reflection microscopy (TIRM)38 in the context of the structure of colloidal suspensions close to (optically transparent) substrates. In contrast, for molecular fluids, as the ones considered here, such direct methods are not available and one has to resort to, e.g., X-ray scattering techniques.39,40 As X-rays are predominantly scattered by the electrons of the fluid molecules one has to consider the electron number density| | 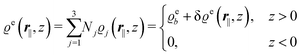 | (37) |
for  with the number Nj of electrons per molecule of particle species j ∈ {1, 2, 3}, the bulk electron density
with the number Nj of electrons per molecule of particle species j ∈ {1, 2, 3}, the bulk electron density 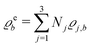 , and the deviation
, and the deviation 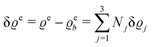 of the electron number density from its bulk value. The X-ray scattering signal for scattering vector q = (q‖,qz) is proportional to
of the electron number density from its bulk value. The X-ray scattering signal for scattering vector q = (q‖,qz) is proportional to 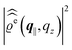 with the double Fourier transform
with the double Fourier transform 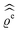 of the electron number density profile ϱe in both the lateral and the normal direction.35
of the electron number density profile ϱe in both the lateral and the normal direction.35
For common specular X-ray reflectivity measurements, i.e., for q‖ = 0, the normalized intensity reflected as function of the normal wave number qz is given by39,40
| | 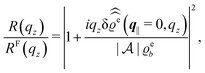 | (38) |
where
RF(
qz) denotes the Fresnel reflectivity of an ideal, step-like planar interface,
41 and where the notation
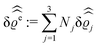
with
| | 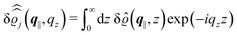 | (39) |
has been used. Moreover, off-specular diffuse X-ray scattering (
q‖ ≠ 0) at grazing incidence (GIXD, Im
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qz
qz ≠ 0) yields scattering intensities which are proportional to
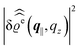
.
39 Hence, as the double Fourier transforms
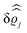
in
eqn (39) of the density deviation profiles δ
ϱj are of direct experimental relevance, they will be discussed in the following in parallel to the single Fourier transforms
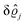
. Note that due to
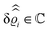
, in
Fig. 3 and 4 its absolute value is shown.
C. Basis vectors of boundary conditions
As mentioned above, the linear nature of the relationship between wall nonuniformities and the resulting number density deviations leads to the possibility of describing the latter in terms of linear combinations of elementary response patterns. These elementary response patterns correspond to four basis vectors, e.g., (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), and (0, 0, 0, 1), which span the four-dimensional space of boundary conditions v′(q‖,0) in eqn (15). Therefore, as a first step to study the influence of wall inhomogeneities onto the fluid, these four distinct boundary condition vectors v′(q‖, 0) are studied. The first one of these vectors is given by| | 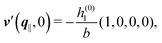 | (40) |
which requires (see eqn (15))| | 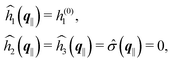 | (41) |
and which in real space corresponds to the boundary condition
| | | h2(r‖) = h3(r‖) = σ(r‖) = 0. | (42) |
This boundary condition corresponds to an attractive, δ-like interaction of the wall with the solvent located at the origin. Solving the Euler–Lagrange equations for this boundary condition, one finds the density distribution 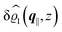 for the solvent and
for the solvent and 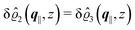 for the ions, as shown in Fig. 2(a) and (b), respectively. Since the boundary condition corresponds to a constant in Fourier space, the density distribution v(q‖, z) depends on k = |q‖| only. Actually, the solution v(q‖, z) for this system is proportional to the first column of the Green's function, which is a 4 × 4-matrix, of the differential operator corresponding to eqn (5) and (6).
for the ions, as shown in Fig. 2(a) and (b), respectively. Since the boundary condition corresponds to a constant in Fourier space, the density distribution v(q‖, z) depends on k = |q‖| only. Actually, the solution v(q‖, z) for this system is proportional to the first column of the Green's function, which is a 4 × 4-matrix, of the differential operator corresponding to eqn (5) and (6).
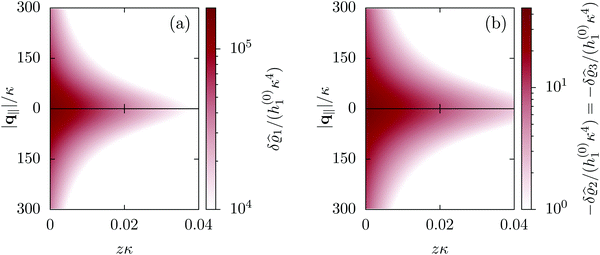 |
| | Fig. 2 Density distribution 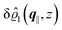 of the solvent (panel (a)) and of the ions of the solvent (panel (a)) and of the ions 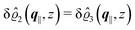 (panel (b)) as function of the distance z from the wall and of the absolute value of the lateral Fourier wave vector q‖ in units of the inverse Debye length κ (see eqn (34)). The plane z = 0 is given by the positions of the fluid particle centers when the surface-to-surface distance between the hard wall and the hard particles vanishes. The data correspond to the boundary condition (panel (b)) as function of the distance z from the wall and of the absolute value of the lateral Fourier wave vector q‖ in units of the inverse Debye length κ (see eqn (34)). The plane z = 0 is given by the positions of the fluid particle centers when the surface-to-surface distance between the hard wall and the hard particles vanishes. The data correspond to the boundary condition 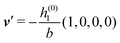 (see eqn (15) and (40)). The physical situation corresponding to this boundary condition is an attraction h1(r‖) = h(0)1δ(r‖) (see eqn (42)) of the solvent particles by the wall located at the origin of the wall. Concerning the remaining relevant parameters see Section IIIA. (see eqn (15) and (40)). The physical situation corresponding to this boundary condition is an attraction h1(r‖) = h(0)1δ(r‖) (see eqn (42)) of the solvent particles by the wall located at the origin of the wall. Concerning the remaining relevant parameters see Section IIIA. | |
Fig. 2 illustrates that for fixed |q‖| the density deviations from the bulk value increase for smaller normal distances from the wall and, for fixed z, also upon decreasing the absolute value of the lateral wave vector |q‖|. The behavior with respect to the normal distance from the wall can be anticipated, because the effect of the interaction between the wall and the fluid is expected to decrease with increasing distance from the wall. Moreover, also the behavior with respect to |q‖| is as expected, because a strong attraction at the origin leads to a radially decreasing density deviation, which in Fourier space corresponds to a maximum at the origin. In order to allow for a quantitative analysis of the behavior of the density deviations, Fig. 3 shows various cuts through the data of Fig. 2 along several lines.
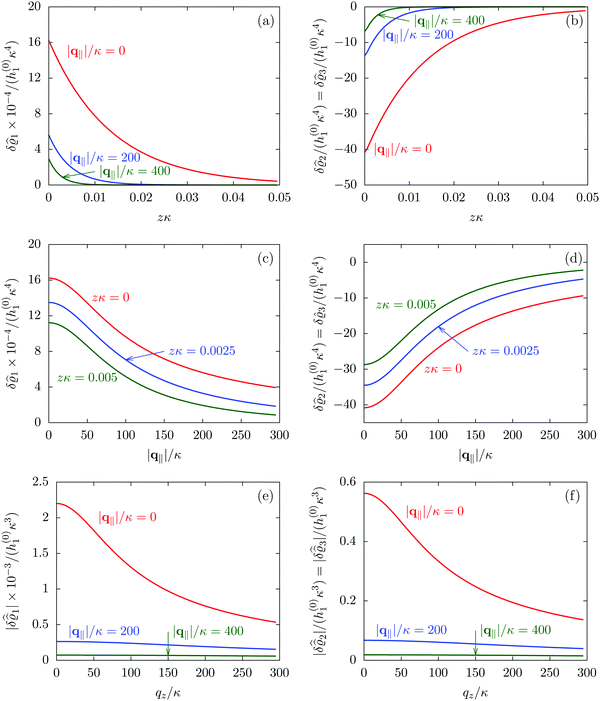 |
| | Fig. 3 Density profiles of the solvent (left column, panels (a), (c), and (e)) and of the ions (right column, panels (b), (d), and (f)) as functions of the normal distance z from the wall (top row, panels (a) and (b)), of the absolute value of the lateral wave vector |q‖| (middle row, panels (c) and (d)), and of the wave number qz in normal direction (bottom row, panels (e) and (f), with h(0)1κ3 being dimensionless) in corresponding units of the Debye length 1/κ and the inverse Debye length, respectively (see eqn (34)). Note that due to 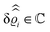 , in panels (e) and (f) the absolute values are shown. In each graph, there are three profiles shown corresponding to three values of the other relevant variable. Therefore the profiles correspond to cuts through Fig. 2(a) and (b) at various positions and in different directions. In this case the boundary condition is , in panels (e) and (f) the absolute values are shown. In each graph, there are three profiles shown corresponding to three values of the other relevant variable. Therefore the profiles correspond to cuts through Fig. 2(a) and (b) at various positions and in different directions. In this case the boundary condition is 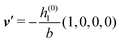 (see eqn (15) and (40)), corresponding to a δ-like nonelectrostatic attraction of the solvent particles at the origin of the wall (see Fig. 2 and eqn (42)). The graphs show, that the density deviations of the ions are proportional to the ones of the solvent, although different in sign. Since only the solvent particles are attracted by the wall, it is favorable for the system to increase their density close to the wall. However, due to the hard core nature of the particles and the equality of the interparticle attraction for all pairs of particles, the increase of solvent particles leads to an extrusion of ionic particles, leading to decreased ion densities at the wall. However, the density deviations of the ions are much weaker. For the remaining relevant parameters see Section IIIA. (see eqn (15) and (40)), corresponding to a δ-like nonelectrostatic attraction of the solvent particles at the origin of the wall (see Fig. 2 and eqn (42)). The graphs show, that the density deviations of the ions are proportional to the ones of the solvent, although different in sign. Since only the solvent particles are attracted by the wall, it is favorable for the system to increase their density close to the wall. However, due to the hard core nature of the particles and the equality of the interparticle attraction for all pairs of particles, the increase of solvent particles leads to an extrusion of ionic particles, leading to decreased ion densities at the wall. However, the density deviations of the ions are much weaker. For the remaining relevant parameters see Section IIIA. | |
Fig. 3(a), (c) and (e) show the density profiles for the solvent and Fig. 3(b), (d) and (f) the ones of the positive ions, which in this case are the same as the profiles for the negative ions. This equivalence is due to the nature of the boundary conditions in this special case, which in real space lead primarily to an increased solvent density close to the origin at the wall. The ions, however, react only indirectly via the solvent, with which both ion types interact in the same way. Since the solvent particles get attracted by the wall, it is favorable to increase their density close to the wall. Due to the hard core nature of the particles, the space occupied by the solvent particles is blocked for the ions. Since the solvent is attracted by the wall and the interparticle attraction is the same for all pairs of particles, this leads to an extrusion of the ions in favor of an increased number of solvent particles. Fig. 3(a) and (b) show the density deviations as function of the normal distance z from the wall for three values of |q‖|, i.e., Fig. 3(a) and (b) correspond to horizontal cuts through Fig. 2(a) and (b), respectively. For fixed |q‖|, as in Fig. 2(a) and (b), Fig. 3(a) and (b) clearly show an exponential decay of the density deviation for increasing distances from the wall. In contrast, Fig. 3(c) and (d) show vertical cuts through Fig. 2(a) and (b), i.e., density profiles as functions of the absolute value of the lateral wave number |q‖| for three normal distances z from the wall. The dependence of these profiles on the absolute value |q‖| of the lateral wave vector q‖ implies a laterally isotropic decay of the density deviations in real space. The third pair of graphs, Fig. 3(e) and (f), shows the Fourier transforms of the density profiles of Fig. 3(a) and (b), being additionally Fourier-transformed with respect to the normal direction z, which leads to the Fourier transforms 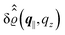 in terms of the lateral wave vector q‖ and the normal wave number qz, respectively. All curves in Fig. 3(c)–(f) exhibit a Lorentzian shape as functions of |q‖| and qz, respectively. These Lorentzian curves in Fourier space correspond to exponential decays in real space in lateral or normal direction. The curves in Fig. 3(c) and (d) show widths of half height which decrease with increasing normal distance z, i.e., the lateral decay length in real space increases with increasing distance from the wall. This implies that the density distribution broadens upon moving away from the source of the perturbation. The curves in Fig. 3(e) and (f) exhibit widths of half height which increase with the lateral wave number |q‖|, i.e., the normal decay length in real space decreases with increasing lateral wave number. Consequently, the range of influence of rapidly varying modes of wall heterogeneities onto the fluid is shorter than that of slowly varying modes. This relationship can also be inferred from Fig. 3(a) and (b). From the above discussions and from Fig. 3 one can conclude, that the response of all species to a simple attraction of nonelectrostatic type is the same up to a proportionality factor. This is confirmed by studying in addition the boundary conditions
in terms of the lateral wave vector q‖ and the normal wave number qz, respectively. All curves in Fig. 3(c)–(f) exhibit a Lorentzian shape as functions of |q‖| and qz, respectively. These Lorentzian curves in Fourier space correspond to exponential decays in real space in lateral or normal direction. The curves in Fig. 3(c) and (d) show widths of half height which decrease with increasing normal distance z, i.e., the lateral decay length in real space increases with increasing distance from the wall. This implies that the density distribution broadens upon moving away from the source of the perturbation. The curves in Fig. 3(e) and (f) exhibit widths of half height which increase with the lateral wave number |q‖|, i.e., the normal decay length in real space decreases with increasing lateral wave number. Consequently, the range of influence of rapidly varying modes of wall heterogeneities onto the fluid is shorter than that of slowly varying modes. This relationship can also be inferred from Fig. 3(a) and (b). From the above discussions and from Fig. 3 one can conclude, that the response of all species to a simple attraction of nonelectrostatic type is the same up to a proportionality factor. This is confirmed by studying in addition the boundary conditions 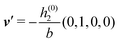 and
and 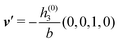 ; these results are not shown here.
; these results are not shown here.
After having discussed the effects of the boundary condition ĥ ≠ 0 viaFig. 2 and 3, the following second type of boundary condition is analyzed:
| | ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖) = σ(0), i.e., σ(r‖) = σ(0)δ(r‖), (q‖) = σ(0), i.e., σ(r‖) = σ(0)δ(r‖), | (43) |
leading to
| | 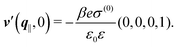 | (44) |
As before, the physical realization of this boundary condition is a δ-like interaction, with the only difference residing in the type of the basic interaction. Unlike in the previous case, here the interaction is of electrostatic character. Thus the situation corresponds to a δ-like negative charge distribution placed at the origin of the wall. Since the two ion types respond oppositely, the ion density profiles differ only in sign:
| | 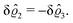 | (45) |
This implies that the total ion density deviations vanish
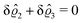
. Accordingly, also the density deviation for the solvent vanishes,
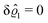
.
Fig. 4 shows the density profiles of the positive ions, which, up to the sign, are the same as the ones for the negative ions. As stated above, for this boundary condition, there is no need to discuss the behavior of the solvent particles.
The three panels in Fig. 4 are obtained similarly as the ones in Fig. 3. Fig. 4(a) shows the density profiles 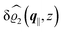 as functions of the normal distance z from the wall for three values of the lateral wave number |q‖|. Fig. 4(b) shows the same density profiles
as functions of the normal distance z from the wall for three values of the lateral wave number |q‖|. Fig. 4(b) shows the same density profiles 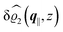 but as functions of |q‖| for three distances z from the wall. Fig. 4(c) displays the double Fourier transform
but as functions of |q‖| for three distances z from the wall. Fig. 4(c) displays the double Fourier transform 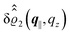 . Compared with the profiles in Fig. 3 for the previously discussed boundary conditions, all present profiles differ significantly from them. Fig. 4(a) reveals a much larger decay length in z-direction, i.e., normal to the wall. Also in Fourier space the decay in lateral direction occurs much more rapidly, i.e., on much longer length scales in real space than in the case of the nonelectrostatic wall–fluid interaction (cf.Fig. 3). This is also indicated by the much narrower peak in the double Fourier transform (see Fig. 4(c)). Furthermore, Fig. 4(a) shows a variation of the decay length in normal direction as function of |q‖|. In Fig. 4(b) one observes that the lateral wave numbers |q‖| at which the profiles
. Compared with the profiles in Fig. 3 for the previously discussed boundary conditions, all present profiles differ significantly from them. Fig. 4(a) reveals a much larger decay length in z-direction, i.e., normal to the wall. Also in Fourier space the decay in lateral direction occurs much more rapidly, i.e., on much longer length scales in real space than in the case of the nonelectrostatic wall–fluid interaction (cf.Fig. 3). This is also indicated by the much narrower peak in the double Fourier transform (see Fig. 4(c)). Furthermore, Fig. 4(a) shows a variation of the decay length in normal direction as function of |q‖|. In Fig. 4(b) one observes that the lateral wave numbers |q‖| at which the profiles 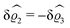 decay to half of the maximum values decrease upon increasing the distances z from the wall, from which one infers that the lateral decay length in real space increases upon increasing z. The decay with respect to |q‖| is much faster than in the previous case (compare Fig. 3(d)), indicating that in real space there is a slower decay in the lateral direction. Moreover, in Fig. 4(b) and (c) the functional form differs from the one shown in Fig. 2 and 3. These differences naturally occur due to the different form of the boundary condition. Since in the case of the boundary condition studied above (see Fig. 2 and 3) the relevant interaction is nonelectrostatic, the length scale dominating the decay is given by the corresponding short-ranged bulk correlation length ξ (see eqn (36)). In contrast, for the system shown in Fig. 4, due to the electrostatic nature of the corresponding interaction, the dominating length scale is the Debye length 1/κ (see eqn (34)), which is much larger than the correlation length ξ due to the nonelectrostatic interaction, giving rise to the much slower decay in Fig. 4(a) (on the scale of 1/κ) and the much faster decay in Fig. 4(b) and (c) (on the scale of κ).
decay to half of the maximum values decrease upon increasing the distances z from the wall, from which one infers that the lateral decay length in real space increases upon increasing z. The decay with respect to |q‖| is much faster than in the previous case (compare Fig. 3(d)), indicating that in real space there is a slower decay in the lateral direction. Moreover, in Fig. 4(b) and (c) the functional form differs from the one shown in Fig. 2 and 3. These differences naturally occur due to the different form of the boundary condition. Since in the case of the boundary condition studied above (see Fig. 2 and 3) the relevant interaction is nonelectrostatic, the length scale dominating the decay is given by the corresponding short-ranged bulk correlation length ξ (see eqn (36)). In contrast, for the system shown in Fig. 4, due to the electrostatic nature of the corresponding interaction, the dominating length scale is the Debye length 1/κ (see eqn (34)), which is much larger than the correlation length ξ due to the nonelectrostatic interaction, giving rise to the much slower decay in Fig. 4(a) (on the scale of 1/κ) and the much faster decay in Fig. 4(b) and (c) (on the scale of κ).
 |
| | Fig. 4 Density profiles of the ions as functions of the normal distance from the wall (a), of the absolute value of the lateral wave vector |q‖| (b), and of the wave number in normal direction (c). Note that due to  , in panel (c) the absolute value is shown. Each panel shows the profiles for three values of the other relevant variable. These profiles are cuts of the corresponding data (analogous to Fig. 2) along various directions. Here, the boundary condition is given by , in panel (c) the absolute value is shown. Each panel shows the profiles for three values of the other relevant variable. These profiles are cuts of the corresponding data (analogous to Fig. 2) along various directions. Here, the boundary condition is given by 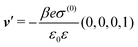 (see eqn (15) and (44)), which corresponds to a δ-like surface charge at the origin in real space (see eqn (43)). The profiles for the solvent are not shown, because the deviations linked to the two types of ions cancel out, (see eqn (15) and (44)), which corresponds to a δ-like surface charge at the origin in real space (see eqn (43)). The profiles for the solvent are not shown, because the deviations linked to the two types of ions cancel out, 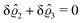 , leaving the density of the solvent unchanged as if there were no ions. In comparison with Fig. 3, the profiles in (a) decay much slower on the scale of the Debye length 1/κ (see eqn (34)) instead of on the scale of the much shorter bulk correlation length ξ (see Fig. 3(b) and eqn (36)) due to the nonelectrostatic interaction. Accordingly, the profiles in (b) and (c) decay on the scale of κ more rapidly than their counterparts in Fig. 3(d) and (f). For the remaining relevant parameters see Section IIIA. , leaving the density of the solvent unchanged as if there were no ions. In comparison with Fig. 3, the profiles in (a) decay much slower on the scale of the Debye length 1/κ (see eqn (34)) instead of on the scale of the much shorter bulk correlation length ξ (see Fig. 3(b) and eqn (36)) due to the nonelectrostatic interaction. Accordingly, the profiles in (b) and (c) decay on the scale of κ more rapidly than their counterparts in Fig. 3(d) and (f). For the remaining relevant parameters see Section IIIA. | |
D. Circular patch of interaction
Having discussed in Section IIIC actually point-like interactions between the wall and the fluid, as the next step we now study the influence of interaction patterns on the density deviations close to a wall upon broadening the spatial extent of the interaction area. To this end we analyze the influence of a two-dimensional circular interaction patch of radius R centered at the origin (see Fig. 5(a)).
 |
| | Fig. 5 Physical configurations studied in Section IIID (a) and in Section IIIE (b). In Section IIID, a two-dimensional circular patch of radius R centered at the origin is studied (a). The dots in panel (b) correspond to the positions of the centers of the Gaussian interaction sites for the model used in Section IIIE, which form a two-dimensional hexagonal lattice with lattice constant Δ. The variance of the Gauss distributions is Δ2peaks (eqn (52) and (53)). Our results are based on the choice Δ = 5Δpeaks (see, cf., Fig. 7). | |
Due to the radial symmetry, the spatial structures in Fourier space depend only on the absolute value |q‖| of the lateral wave vector q‖. Fig. 6 discusses four distinct configurations.
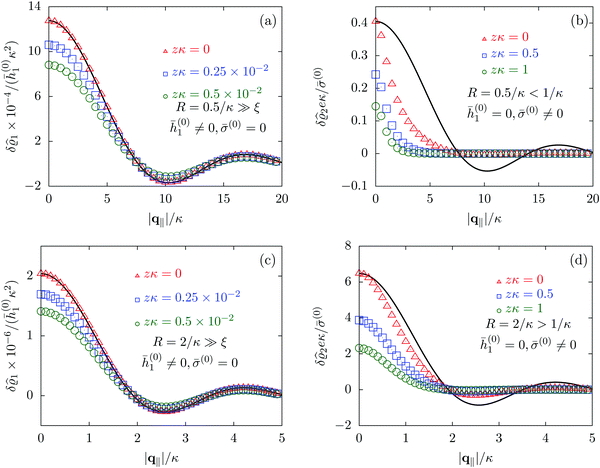 |
| | Fig. 6 Density profiles of the solvent (panels (a) and (c)) and of the ions (panels (b) and (d)) as functions of the absolute value |q‖| of the lateral wave vector for three normal distances z from the wall. The boundary condition corresponds to a circular interaction patch centered at the origin with radius R > 0. In the panels (a) and (b) the radius of the patch is R = 0.5/κ whereas in the panels (c) and (d) the radius is R = 2/κ, where 1/κ is the Debye length (see eqn (34)). All considered patch radii are much larger than the bulk correlation length, R ≫ ξ (see eqn (36)). In addition, there are different types of interaction. In panels (a) and (c) the interaction between the wall and the solvent particles is nonelectrostatic (h1(r‖) = ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) (0)1Θ(R − |r‖|), h2(r‖) = h3(r‖) = σ(r‖) = 0, see eqn (46) as well as Fig. 2 and 3), whereas in panels (b) and (d) the patch contains a constant surface charge and therefore interacts with the ions only (h(r‖) = 0, σ(r‖) = (0)1Θ(R − |r‖|), h2(r‖) = h3(r‖) = σ(r‖) = 0, see eqn (46) as well as Fig. 2 and 3), whereas in panels (b) and (d) the patch contains a constant surface charge and therefore interacts with the ions only (h(r‖) = 0, σ(r‖) = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (0)Θ(R − |r‖|), see eqn (49) and Fig. 4). Besides the profiles, all panels show also the lateral Fourier transform of the boundary condition (eqn (47) and (50)) displayed as a black solid line. In the case of the interaction of the wall with the solvent ((a) and (c)), the decay of the profiles as function of |q‖| is proportional to the lateral Fourier transform of the boundary condition, which implies, that the density deviations in real space closely follow the shape of the patch. However, in the case of a charged patch at the surface the density distribution of the ions reflects the competition between the length scale R of the radius of the patch and the Debye length 1/κ. In the case of small patches (R < 1/κ, panel (b)), the Debye length dominates and therefore dictates the decay as function of |q‖| without noticeable influence of the patch. In contrast, in the case of large patches (R > 1/κ, panel (d)), in which the radius of the patch is the dominating length scale, the shape of the profiles follows the Fourier transform of the charge distribution at the wall, i.e., the patch of radius R. For the remaining relevant parameters see Section IIIA. (0)Θ(R − |r‖|), see eqn (49) and Fig. 4). Besides the profiles, all panels show also the lateral Fourier transform of the boundary condition (eqn (47) and (50)) displayed as a black solid line. In the case of the interaction of the wall with the solvent ((a) and (c)), the decay of the profiles as function of |q‖| is proportional to the lateral Fourier transform of the boundary condition, which implies, that the density deviations in real space closely follow the shape of the patch. However, in the case of a charged patch at the surface the density distribution of the ions reflects the competition between the length scale R of the radius of the patch and the Debye length 1/κ. In the case of small patches (R < 1/κ, panel (b)), the Debye length dominates and therefore dictates the decay as function of |q‖| without noticeable influence of the patch. In contrast, in the case of large patches (R > 1/κ, panel (d)), in which the radius of the patch is the dominating length scale, the shape of the profiles follows the Fourier transform of the charge distribution at the wall, i.e., the patch of radius R. For the remaining relevant parameters see Section IIIA. | |
Alluding to the insights gained in the previous section, Fig. 6(a) and (c) correspond to a homogeneous circular patch of radius R, which interacts with the solvent only, similar to Fig. 2 and 3. This amounts to the boundary condition (see eqn (15))
| h1(r‖) = ℏ(0)1Θ(R − |r|), |
| | h2(r‖) = h3(r‖) = ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) (r‖) = 0 (r‖) = 0 | (46) |
leading to
| | 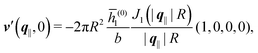 | (47) |
where the two-dimensional Fourier transform of the Heaviside function
Θ(
R − |
r|) is given by
| | 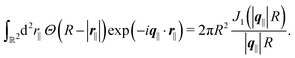 | (48) |
In contrast,
Fig. 6(b) and (d) refer to a charged circular patch of radius
R, similar to
Fig. 4:
| | h(r‖) = 0, σ(r‖) = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (0)Θ(R − |r‖|), (0)Θ(R − |r‖|), | (49) |
leading to the boundary condition
| | 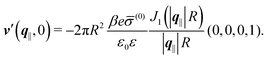 | (50) |
Fig. 6(a) and (b) correspond to the patch size
R = 0.5/
κ whereas
Fig. 6(c) and (d) correspond to
R = 2/
κ. In all four panels the black line is given by
AJ1(|
q‖|
R)/(|
q‖|
R) with
A chosen such that the first maximum of the data for
zκ = 0 is reproduced. In
Fig. 6(a) and (c) only the solvent density profiles are shown, because, due to linearity, Section IIIC indicates, that the ion profiles are proportional to the one of the solvent.
Fig. 6(a) and (c) clearly show, that the density deviations are proportional to the Fourier transform
v′(
q‖, 0) of the boundary condition (
eqn (47), solid black line). This implies that for increasing lateral distances from the center of the patch the decay of the profiles in real space is dominated by the length scale set by the radius
R of the patch. This trend holds for both patch sizes. However, as expected, the amplitudes of the density deviations increase for the larger patch size (note the different scales). In contrast, in
Fig. 6(b) and (d), where the density profiles of the positive ions are shown and where the profiles for the solvent are omitted for the same reasons as explained in Section IIIC, the profiles do not follow the Fourier transform of the boundary conditions (solid black line). This is particularly pronounced in
Fig. 6(b),
i.e., for the smaller patch size. In this case the decay as function of |
q‖| is faster than the Fourier transform of the boundary condition, which implies that the profiles decay on a length scale larger than that of the radius
R of the patch and also the shape of the decay differs from that of the expression
J1(|
q‖|
R)/(|
q‖|
R). This behavior can be understood in terms of two distinct dominating length scales. In
Fig. 6(b) and (d), where the effect of electrostatic interactions are shown, the dominating length scale is the Debye length 1/
κ in contrast to the much smaller correlation length
ξ (
ξ ≈ 1.3 × 10
−2κ−1) induced by the nonelectrostatic interactions characterizing
Fig. 6(a) and (c). Since in
Fig. 6(b) the radius
R of the patch is only half the Debye length 1/
κ, the dominating length scale is the Debye length 1/
κ, so that the density deviations decay in real space on a length scale which is larger than the patch radius
R. Also, since the profile in Fourier space is not proportional to the Fourier transform of the boundary condition, one can conclude that the shape of the patch has no significant influence on the decay behavior. The competition of the length scales
ξ, 1/
κ, and
R is also borne out in
Fig. 6(d), where the patch size
R is twice as large as the Debye length 1/
κ. This case is much more similar to the ones in
Fig. 6(a) and (c), because the dominating length scale is set by the radius
R, and consequently the profiles follow rather closely the shape (solid black line) dictated by the interaction patch. However, the influence of the smaller Debye length scale is still visible, which is the reason for the deviations from the Fourier transform of the boundary condition (solid black line). In conclusion, as already seen in Section IIIC, the largest length scale sets the decay behavior of the density deviations. In the present case of non-vanishing sizes of the interaction areas, the largest length scale dictates not only the range but also the shape of the density deviations.
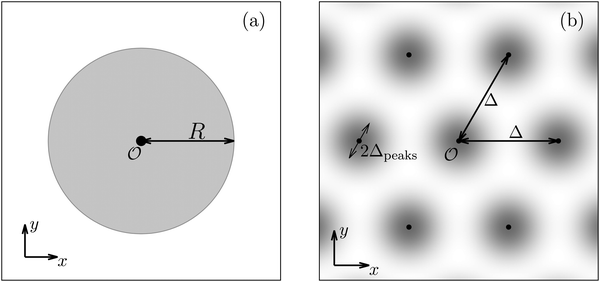
E. Periodic distribution of interaction sites
After having discussed the density profiles in the presence of spatially localized, single interaction sites in Sections IIIC and D, here we study the influence of interaction sites forming a regular hexagonal lattice:| | 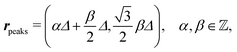 | (51) |
see Fig. 5(b); the distance between nearest neighbor sites is denoted as Δ.
Distinct from the previous examples in Sections IIIC and D, the interaction strength around the individual interaction sites rpeaks is taken to form a Gaussian distribution, providing either a nonelectrostatic or an electrostatic interaction with equal amplitudes for all interaction sites:
| | 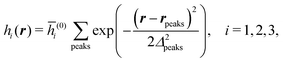 | (52) |
and
| | 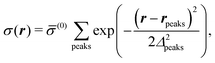 | (53) |
respectively, where
Δ2peaks is the variance of the Gaussian interaction. Lateral Fourier transformation leads to the corresponding boundary condition
v′ (see
eqn (15)) with
| | 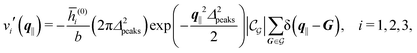 | (54) |
and
| | 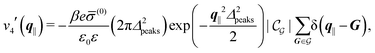 | (55) |
where
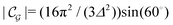
is the size of an elementary cell of the corresponding two-dimensional reciprocal lattice
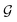
. Using this boundary condition, we have studied four different systems, as shown in
Fig. 7.
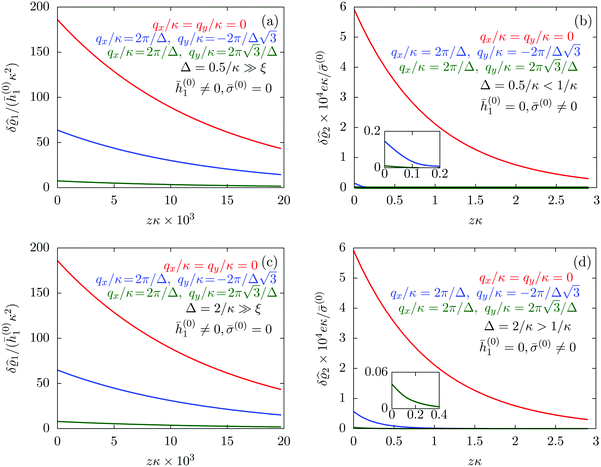 |
| | Fig. 7 Density profiles of the solvent (panels (a) and (c)) and of the ions (panels (b) and (d)) for three lateral wave vectors q‖ = (qx,qy) as functions of the normal distance z from the wall in units of the Debye length 1/κ. The boundary condition corresponds to a hexagonal lattice of interaction sites with a Gaussian charge distribution characterized by a standard deviation Δpeaks = Δ/5. The lattice constant is denoted as Δ (see Fig. 5). In panels (a) and (b) the lattice constant and the variance are Δ = 0.5/κ and Δpeaks = 0.1/κ, respectively, whereas in panels (c) and (d) the lattice constant and the variance are Δ = 2/κ and Δpeaks = 0.4/κ, respectively, with the Debye length 1/κ (see eqn (34)). Panels (a) and (c) correspond to systems with a nonelectrostatic interaction between the wall and the solvent particles (see eqn (56)), whereas panels (b) and (d) correspond to systems with electrostatic interaction sites between wall and ions (see eqn (57)). The insets in (b) and (d) show a magnified version of the respective profiles in the main plot. In all cases, the profiles decay exponentially upon increasing the normal distance z from the wall. However, the decay length differs significantly between the two aforementioned types of interactions. In the case of the nonelectrostatic interaction, the decay length is set by the bulk correlation length ξ (see eqn (36)) of the fluid, whereas in the case of the electrostatic interaction it is set by the much larger Debye length 1/κ. This difference in the decay lengths, both in lateral and in normal direction, which leads to a much faster lateral decay in the case of the electrostatic interactions, is also responsible for the decreasing amplitude of the ion profiles for increased wave vectors (panel (b) and (d)). Another significant difference between the two interaction types is the variation of the decay length as function of the lateral wave vectors. In panels (a) and (c) all profiles decay exponentially on the same decay length ξ, whereas in panels (b) and (d) the decay length depends significantly on the wave vectors. This effect follows from the dependence of the eigenvalues on |q‖| as discussed in eqn (A3), corresponding to a lateral decay proportional to 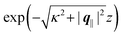 . In principle this occurs for both types of interactions. However only in the case of the electrostatic interactions it is relevant, which again is due to the difference between the dominating length scales. For the remaining relevant parameters see Section IIIA. . In principle this occurs for both types of interactions. However only in the case of the electrostatic interactions it is relevant, which again is due to the difference between the dominating length scales. For the remaining relevant parameters see Section IIIA. | |
The four panels are arranged as in Fig. 6, with the boundary conditions corresponding to an interaction between the wall and solvent only in Fig. 7(a) and (c),
| | 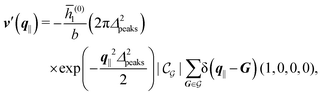 | (56) |
and in
Fig. 7(b) and (d) boundary conditions corresponding to an interaction between the wall and ions only,
i.e., due to a hexagonal lattice of interaction sites with Gaussian intrinsic charge distribution:
| | 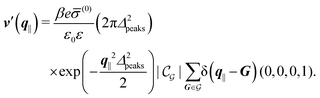 | (57) |
For the same reason as stated in the context of
Fig. 6, in the former case (
Fig. 7(a) and (c)) only the deviations of the solvent density and in the latter case (
Fig. 7(b) and (d)) only the deviations of the ion densities are shown.
Fig. 7(a) and (b) correspond to the lattice constant
Δ = 0.5/
κ whereas
Fig. 7(c) and (d) correspond to
Δ = 2/
κ. The variance
Δ2peaks of the peaks is taken as
Δpeaks =
Δ/5, so that
Δpeaks = 0.1/
κ in
Fig. 7(a) and (b) and
Δpeaks = 0.4/
κ in
Fig. 7(c) and (d).
Fig. 7(a) and (c) tell that, although different values for
q‖ change the amplitude of the profiles in all cases, the solvent profile decays exponentially, upon increasing the normal distance
z from the wall, on the scale of the bulk correlation length
ξ. This holds for both values of the lattice constant
Δ. However, the amplitude of the density deviations is slightly increased for the larger lattice constant
Δ, which is in line with the also increased variance
Δ2peaks of the interaction sites. In contrast to these findings,
Fig. 7(b) and (d) reveal a different picture. In these panels, one still finds an exponential decay of the profiles upon increasing the normal distance
z. However, the profiles decay on a much larger length scale than the ones in
Fig. 7(a) and (c). Moreover, not only the amplitude but also the decay length changes significantly for different values of
q‖. This was already encountered in
Fig. 4, where the decay length depends on the value of |
q‖|. This variation of the decay lengths can be inferred from
eqn (14), which shows that the eigenvalues and thus the decay length depends on
k = |
q‖|. The variation of the decay length can be expressed in terms of the Debye length 1/
κ, which determines the length scale in case of |
q‖| = 0. From
eqn (A3) one finds, that the decay as function of
z is proportional to
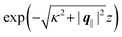
. The large differences in the amplitudes of the various profiles in
Fig. 7(b) and (d), as well as the pronounced increase of the decay length in comparison to
Fig. 7(a) and (c) can be understood in terms of the differences between the dominating length scale. Analogous to the previous sections, for the systems shown in
Fig. 7(a) and (c), the dominating length scale in lateral direction is the length scale set by the boundary conditions and the bulk correlation length
ξ, which characterizes the decay of the solvent density in normal direction. However, for the systems shown in
Fig. 7(b) and (d), the relevant inherent length scale of the fluid is the Debye length 1/
κ, which is significantly larger than the bulk correlation length
ξ and thus causes the increase in the length scale of the decay, both in lateral and in normal direction.
IV. Conclusions and summary
In the present analysis the influence of a chemically or electrostatically structured surface on an adjacent fluid has been studied and described in terms of the density profiles of the fluid components. The fluid, which comprises a single solvent species and a single univalent salt far away from bulk and wetting phase transitions, has been investigated within classical density functional theory.30–32 Within this model three examples of heterogeneous walls have been studied. First, single isolated interaction sites are discussed, which interact either nonelectrostatically (between the wall and solvent particles) or electrostatically (between the wall and ions) (see Sections IIIC and D). In the case of a δ-like nonelectrostatic interaction, the solvent density increases around the interaction site and decays exponentially on the length scale of the bulk correlation length ξ. The deviations of the ion number densities from their bulk values are proportional to that of the number density of the solvent (see Fig. 2 and 3). For a δ-like electrostatic interaction, within the present model, the solvent does not respond at all, because the deviations induced by the two ion types even out due to symmetries, whereas the density deviations of the ionic particles again decay exponentially. However, the length scale of the latter decay is significantly increased as compared to the former case, because the dominating scale in this case is the Debye length 1/κ ≫ ξ (see Fig. 4). The introduction of another length scale by studying interaction sites of non-vanishing extent (see Section IIID) shows, that the resulting density profiles strongly depend on the dominant length scale (see Fig. 6). If a bulk length scale (bulk correlation length ξ or Debye length 1/κ) dominates, the profiles resemble the ones for δ-like interactions. However, if a length scale set by a boundary condition at the wall dominates or is similar to the dominating length scale in the bulk, the decay of the density deviations increasingly reflects the boundary conditions. Finally, the examination of multiple interaction sites, arranged as a regular hexagonal lattice (see Fig. 5(b)), shows, that the size of the interaction sites and the distance between them influence the amplitude and thus the importance of density deviations for large values of the lateral wave number |q‖| (see Fig. 7).
In summary, the present study provides a flexible framework to determine the influence of various surface inhomogeneities on the density profiles of a fluid in contact with that substrate. The resulting profiles are found to be sensitive to the type of interaction as well as to the size and the distribution of the interaction sites.
This framework is considered as a starting point for extensions into various directions, aiming for the analysis of more sophisticated and realistic models. First, the model used here to describe the fluid is a very simple one, chosen to lay a foundation for further research and to introduce the approach as such. Concerning future work, more realistic descriptions of the fluid and more elaborate density functional descriptions could be used. For instance, the present restriction to low ionic strengths and equal particle sizes can be removed along the lines of ref. 42. Second, for the systems studied here, the fluid is thermodynamically far from any bulk or wetting phase transitions. This is solely done for the sake of simplicity. In future studies of more realistic systems, taking into account the occurrence of phase transitions and their influence on the systems is expected to be rewarding. Third, this study is restricted to linear response theory. Whereas this allows for a broad overview of structure formation in terms of superpositions of only a few elementary patterns, the occurrence of nonlinear structure formation phenomena requires approaches beyond linear response theory. Finally, studying the influence of disordered surface structures within the present framework appears to be very promising.
Conflicts of interest
There are no conflicts to declare.
Appendix A: eigenvectors and eigenvalues of 
According to the structure of the matrix  (eqn (2)), with entries given by eqn (30), and of the vector Z = (0, 1, −1), from eqn (9) and (10) one infers that the matrix
(eqn (2)), with entries given by eqn (30), and of the vector Z = (0, 1, −1), from eqn (9) and (10) one infers that the matrix 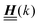 has the form
has the form| |  | (A1) |
with s, t, u, v ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) and k = |q‖|, s, t > 0. It can be readily verified that the four vectors
and k = |q‖|, s, t > 0. It can be readily verified that the four vectors| | 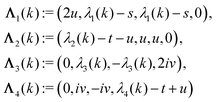 | (A2) |
with 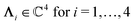 , form a nonorthogonal basis of eigenvectors of the matrix
, form a nonorthogonal basis of eigenvectors of the matrix 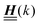 in eqn (A1) with the respective real eigenvalues
in eqn (A1) with the respective real eigenvalues| | 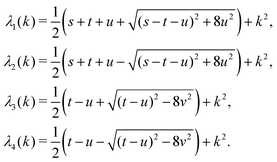 | (A3) |
The expressions for s, t, u, and v can be obtained from the bulk quantities mentioned in Section IIIA and take on the forms (see eqn (25) and (30))
| | 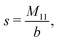 | (A4) |
| | 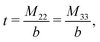 | (A5) |
| | 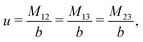 | (A6) |
| | 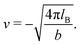 | (A7) |
Acknowledgements
Open Access funding provided by the Max Planck Society.
References
-
V. S. Bagotsky, Fundamentals of Electrochemistry, Wiley, Hoboken, 2006 Search PubMed.
-
W. Schmickler and E. Santos, Interfacial Electrochemistry, Springer, Berlin, 2010 Search PubMed.
-
S. Dietrich, Wetting phenomena, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1988, vol. 12, p. 1 Search PubMed.
-
M. Schick, Introduction to wetting phenomena, in Les Houches, Session XLVIII, 1988 – Liquides aux interfaces/liquids at interfaces, ed. J. Charvolin, J. F. Joanny and J. Zinn-Justin, North-Holland, Amsterdam, 1990, p. 415 Search PubMed.
-
Protective Coatings, ed. M. Wen and K. Dušek, Springer, Cham, 2017 Search PubMed.
-
N. Vogel, Surface Patterning with Colloidal Monolayers, Springer, Berlin, 2012 Search PubMed.
-
A. Y. C. Nee, Handbook of Manufacturing Engineering and Technology, Springer, London, 2015 Search PubMed.
-
W. Russel, D. Saville and W. Schowalter, Colloidal Dispersions, Cambridge University, Cambridge, 1989 Search PubMed.
-
R. J. Hunter, Foundations of Colloid Science, Oxford University, Oxford, 2001 Search PubMed.
-
Microfluidics, ed. B. Lin, Springer, Berlin, 2011 Search PubMed.
-
F. J. Galindo-Rosales, Complex Fluids and Rheometry in Microfluidics, in Complex Fluid-Flows in Microfluidics, ed. F. J. Galindo-Rosales, Springer, Cham, 2018, p. 1 Search PubMed.
- D. Andelman, On the Adsorption of Polymer Solutions on Random Surfaces: The Annealed Case, Macromolecules, 1991, 24, 6040 CrossRef CAS.
- W. Chen, S. Tan, T.-K. Ng, W. T. Ford and P. Tong, Long-ranged attraction between charged polystyrene spheres at aqueous interfaces, Phys. Rev. Lett., 2005, 95, 218301 CrossRef PubMed.
- W. Chen, S. Tan, S. Huang, T.-K. Ng, W. T. Ford and P. Tong, Measured long-ranged attractive interaction between charged polystyrene latex spheres at a water-air interface, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021406 CrossRef PubMed.
- W. Chen, S. Tan, Y. Zhou, T.-K. Ng, W. T. Ford and P. Tong, Attraction between weakly charged silica spheres at a water–air interface induced by surface-charge heterogeneity, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 041403 CrossRef PubMed.
- A. Naji, D. S. Dean, J. Sarabadani, R. R. Horgan and R. Podgornik, Fluctuation-induced interaction between randomly charged dielectrics, Phys. Rev. Lett., 2010, 104, 060601 CrossRef PubMed.
- D. Ben-Yaakov, D. Andelman and H. Diamant, Interaction between heterogeneously charged surfaces: surface patches and charge modulation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022402 CrossRef PubMed.
- A. Naji, M. Ghodrat, H. Komaie-Moghaddam and R. Podgornik, Asymmetric Coulomb fluids at randomly charged dielectric interfaces: anti-fragility, overcharging and charge inversion, J. Chem. Phys., 2014, 141, 174704 CrossRef PubMed.
- A. Bakhshandeh, A. P. dos Santos, A. Diehl and Y. Levin, Interaction between random heterogeneously charged surfaces in an electrolyte solution, J. Chem. Phys., 2015, 142, 194707 CrossRef PubMed.
- M. Ghodrat, A. Naji, H. Komale-Moghaddam and R. Podgornik, Ion-mediated interactions between net-neutral slabs: weak and strong disorder effects, J. Chem. Phys., 2015, 143, 234701 CrossRef PubMed.
- M. Ghodrat, A. Naji, H. Komaie-Moghaddama and R. Podgornik, Strong coupling electrostatics for randomly charged surfaces: antifragility and effective interactions, Soft Matter, 2015, 11, 3441 RSC.
- R. M. Adar and D. Andelman, Electrostatic attraction between overall neutral surfaces, Phys. Rev. E, 2016, 94, 022803 CrossRef PubMed.
-
R. M. Adar and D. Andelman, Osmotic pressure between arbitrarily charged surfaces: a revisited approach, 2017, arXiv:1709.02114.
- R. M. Adar, D. Andelman and H. Diamant, Electrostatics of patchy surfaces, Adv. Colloid Interface Sci., 2017, 247, 198 CrossRef CAS PubMed.
- S. Ghosal and J. D. Sherwood, Screened Coulomb interactions with non-uniform surface charge, Proc. – R. Soc. Edinburgh, Sect. A: Math., 2017, 473, 20160906 CrossRef.
- S. Zhou, Effective electrostatic interactions between two overall neutral surfaces with quenched charge heterogeneity over atomic length scale, J. Stat. Phys., 2017, 169, 1019 CrossRef.
- A. Onuki and H. Kitamura, Solvation effects in near-critical binary mixtures, J. Chem. Phys., 2004, 121, 3143 CrossRef CAS PubMed.
- M. Bier, A. Gambassi and S. Dietrich, Local theory for ions in binary liquid mixtures, J. Chem. Phys., 2012, 137, 034504 CrossRef PubMed.
- M. Bier and L. Harnau, The structure of fluids with impurities, Z. Phys. Chem., 2012, 226, 807 CrossRef CAS.
- R. Evans, The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids, Adv. Phys., 1979, 28, 143 CrossRef CAS.
-
R. Evans, Microscopic theories of simple fluids and their interfaces, in Les Houches, Session XLVIII, 1988—Liquides aux interfaces/Liquids at interfaces, ed. J. Charvolin, J. F. Joanny and J. Zinn-Justin, North-Holland, Amsterdam, 1990, p. 1 Search PubMed.
-
R. Evans, Density functionals in the theory of nonuniform fluids, in Fundamentals of inhomogeneous fluids, ed. D. Henderson, Marcel Dekker, New York, 1992, p. 85 Search PubMed.
- J. W. Cahn and J. E. Hilliard, Free energy of a nonuniform system. I. Interfacial free energy, J. Chem. Phys., 1958, 28, 258 CrossRef CAS.
- L. Bocquet, E. Trizac and M. Aubouy, Effective charge saturation in colloidal suspension, J. Chem. Phys., 2002, 117, 8138 CrossRef CAS.
-
H. P. Hansen and I. R. McDonald, Theory of simple liquids, Academic, San Diego, 2nd edn, 1986 Search PubMed.
- S. J. Suresh and V. M. Naik, Hydrogen bond thermodynamic properties of water from dielectric constant data, J. Chem. Phys., 2000, 113, 9727 CrossRef CAS.
-
D. R. Lide, Handbook of Chemistry and Physics, CRC, Boca Raton, 79th edn, 1998 Search PubMed.
- J. Y. Walz, Measuring particle interactions with total internal reflection microscopy, Curr. Opin. Colloid Interface Sci., 1997, 2, 600 CrossRef CAS.
- S. Dietrich and A. Haase, Scattering of X-rays and neutrons at interfaces, Phys. Rep., 1995, 260, 1 CrossRef CAS.
-
J. Als-Nielsen and D. McMorrow, Elements of modern X-ray physics, Wiley, New York, 2001 Search PubMed.
-
J. D. Jackson, Classical Electrodynamics, Wiley, Hoboken, 1999 Search PubMed.
- A. C. Maggs and R. Podgornik, General theory of asymmetric steric interactions in electrostatic double layers, Soft Matter, 2016, 12, 1219 RSC.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Markus
Bier
*ab,
Markus
Bier
 *ab and
S.
Dietrich
*ab and
S.
Dietrich
 ab
ab
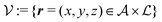 ; the positions r = (x, y, z) = (r‖,z) are uniquely decomposed into the lateral components
; the positions r = (x, y, z) = (r‖,z) are uniquely decomposed into the lateral components 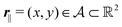 and the normal component
and the normal component 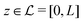 relative to the wall surface at z = 0. The size
relative to the wall surface at z = 0. The size 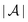 of the wall and the extent L of the system in normal direction are both assumed to be macroscopically large. The fluid is an electrolyte solution composed of an uncharged solvent (index “1”), univalent cations (index “2”), and univalent anions (index “3”). Two types of interactions between the fluid and the wall are considered: (i) electric monopoles at the wall surface (z = 0) and the fluid ions, giving rise to an electrostatic interaction, (ii) all other contributions, in particular those due to nearest-neighbor-like chemical bonds, referred to as nonelectrostatic interactions.
of the wall and the extent L of the system in normal direction are both assumed to be macroscopically large. The fluid is an electrolyte solution composed of an uncharged solvent (index “1”), univalent cations (index “2”), and univalent anions (index “3”). Two types of interactions between the fluid and the wall are considered: (i) electric monopoles at the wall surface (z = 0) and the fluid ions, giving rise to an electrostatic interaction, (ii) all other contributions, in particular those due to nearest-neighbor-like chemical bonds, referred to as nonelectrostatic interactions.
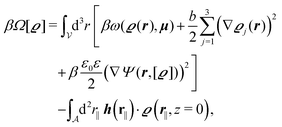
 , and h(r‖) = (h1(r‖), h2(r‖), h3(r‖)) describes the strengths of the nonelectrostatic wall–fluid interactions at r = (r‖, 0) for the three species. Note that for the sake of simplicity, the coupling of number density gradients of different particle types is neglected in eqn (1) (see Section IIIA). In the present study the bulk state ϱb = (ϱ1,b, ϱ2,b, ϱ3,b) is considered to be thermodynamically far away from any phase transition so that the local contribution βω(ϱ) of the density functional in eqn (1) can be safely expanded around ϱb up to quadratic order in δϱ := ϱ − ϱb:
, and h(r‖) = (h1(r‖), h2(r‖), h3(r‖)) describes the strengths of the nonelectrostatic wall–fluid interactions at r = (r‖, 0) for the three species. Note that for the sake of simplicity, the coupling of number density gradients of different particle types is neglected in eqn (1) (see Section IIIA). In the present study the bulk state ϱb = (ϱ1,b, ϱ2,b, ϱ3,b) is considered to be thermodynamically far away from any phase transition so that the local contribution βω(ϱ) of the density functional in eqn (1) can be safely expanded around ϱb up to quadratic order in δϱ := ϱ − ϱb: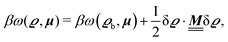
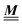 (see, cf., eqn (30)). Furthermore, ω(ϱb, μ) = −p specifies the grand potential density, evaluated for the equilibrium bulk densities ϱb, which equals minus the bulk pressure p; in the following its value is of no importance. For a given equation of state p(ϱb, T) the bulk densities ϱb = (ϱb,1, ϱb,2, ϱb,3) are free parameters of the model. Finally, the electrostatic potential Ψ(r, [ϱ]), which enters into eqn (1) on a mean-field level via the electric field energy density, fulfills the Poisson equation
(see, cf., eqn (30)). Furthermore, ω(ϱb, μ) = −p specifies the grand potential density, evaluated for the equilibrium bulk densities ϱb, which equals minus the bulk pressure p; in the following its value is of no importance. For a given equation of state p(ϱb, T) the bulk densities ϱb = (ϱb,1, ϱb,2, ϱb,3) are free parameters of the model. Finally, the electrostatic potential Ψ(r, [ϱ]), which enters into eqn (1) on a mean-field level via the electric field energy density, fulfills the Poisson equation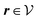 with the boundary conditions
with the boundary conditions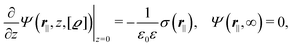
 , where σ(r‖) is the surface charge density at the point r = (r‖, 0) on the wall surface (z = 0), and Z = (Z1, Z2, Z3) = (0, 1, −1) denotes the valences of the fluid species.
, where σ(r‖) is the surface charge density at the point r = (r‖, 0) on the wall surface (z = 0), and Z = (Z1, Z2, Z3) = (0, 1, −1) denotes the valences of the fluid species.
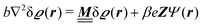
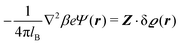
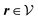 with the boundary conditions given by eqn (4) and by
with the boundary conditions given by eqn (4) and by
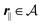 , where lB = βe2/(4πε0ε) is the Bjerrum length.
, where lB = βe2/(4πε0ε) is the Bjerrum length.
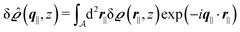
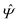 as functions of q‖ = (qx, qy) ∈
as functions of q‖ = (qx, qy) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2 and z ∈
2 and z ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) can be combined in the four-component quantity
can be combined in the four-component quantity 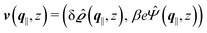 so that eqn (5) and (6) can be written as
so that eqn (5) and (6) can be written as
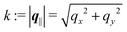 and v′′(q‖,z) is the second derivative of v(q‖, z) with respect to the coordinate z normal to the wall. Note that the components of v are quantities of different dimensions: [v1] = [v2] = [v3] = 1/length and [v4] = (length)2. This does not allow for the formation of a scalar product of two vectors of the type
and v′′(q‖,z) is the second derivative of v(q‖, z) with respect to the coordinate z normal to the wall. Note that the components of v are quantities of different dimensions: [v1] = [v2] = [v3] = 1/length and [v4] = (length)2. This does not allow for the formation of a scalar product of two vectors of the type 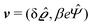 ; however, in the following scalar products will not occur. Writing
; however, in the following scalar products will not occur. Writing 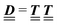 with
with 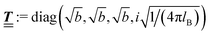 (i.e.,
(i.e., 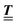 is a diagonal matrix with these entries), one obtains
is a diagonal matrix with these entries), one obtains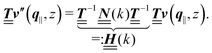
 is independent of z and it is symmetric but not real-valued, because the bottom entry of
is independent of z and it is symmetric but not real-valued, because the bottom entry of  is imaginary.
is imaginary. 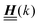 is not a normal matrix, i.e., it does not commute with its adjoint matrix
is not a normal matrix, i.e., it does not commute with its adjoint matrix 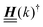 , and hence it does not possess an orthogonal basis composed of eigenvectors. However, the actual structures of the matrix
, and hence it does not possess an orthogonal basis composed of eigenvectors. However, the actual structures of the matrix 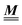 and of the vector Z used below guarantee the existence of a nonorthogonal basis {Λ1(k), …, Λ4(k)} of eigenvectors of the matrix
and of the vector Z used below guarantee the existence of a nonorthogonal basis {Λ1(k), …, Λ4(k)} of eigenvectors of the matrix 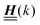 with respective positive (real-valued) eigenvalues λ1(k), …, λ4(k) ∈ (0,∞) (see Appendix A). Expanding the vector
with respective positive (real-valued) eigenvalues λ1(k), …, λ4(k) ∈ (0,∞) (see Appendix A). Expanding the vector 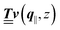 in this basis {Λ1(k),…,Λ4(k)},
in this basis {Λ1(k),…,Λ4(k)},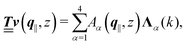
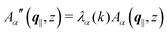
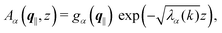
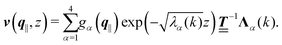
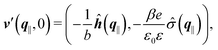
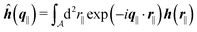
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖) as the Fourier transform of σ(r‖). Note that, as for v, the components of v′ are quantities of different dimensions: [v1′] = [v2′] = [v3′] = 1/(length)2 and [v4] = length. From eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) can be determined. Note that according to eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) and hence the profiles
(q‖) as the Fourier transform of σ(r‖). Note that, as for v, the components of v′ are quantities of different dimensions: [v1′] = [v2′] = [v3′] = 1/(length)2 and [v4] = length. From eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) can be determined. Note that according to eqn (14) and (15) the coefficients g1(q‖), …, g4(q‖) and hence the profiles  and
and ![[capital Psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b0.gif) depend linearly on the nonelectrostatic wall–fluid interactions ĥ(q‖) and the surface charge density
depend linearly on the nonelectrostatic wall–fluid interactions ĥ(q‖) and the surface charge density ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖). Such a linear response of the number density profiles inside the fluid to the wall properties requires weak wall–fluid interactions, which is assumed in the present study and which is consistent with the quadratic form of the density functional in eqn (1)–(4).
(q‖). Such a linear response of the number density profiles inside the fluid to the wall properties requires weak wall–fluid interactions, which is assumed in the present study and which is consistent with the quadratic form of the density functional in eqn (1)–(4).
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖), onto the number density profiles ϱ in the adjacent fluid. Applying density functional theory as described in Section II requires knowledge of the bulk number densities ϱb, the parameter b, and the coupling matrix
(q‖), onto the number density profiles ϱ in the adjacent fluid. Applying density functional theory as described in Section II requires knowledge of the bulk number densities ϱb, the parameter b, and the coupling matrix  all of which are bulk quantities or characterize them.
all of which are bulk quantities or characterize them.
 in terms of experimentally accessible quantities, in a first step the pure, ion-free solvent is considered, the particles of which interact only nonelectrostatically. Here this nonelectrostatic interaction between solvent particles at a distance r is modeled by a square-well pair potential U(r) as displayed in Fig. 1(a). At small distances r < σ a hard core repulsion prevents the overlap of two particles. At intermediate distances r ∈ (σ, σpot) two particles attract each other with an interaction energy −εpot, and at distances r > σpot the nonelectrostatic interaction vanishes. According to the scheme due to Barker and Henderson,35 the interaction potential U can be decomposed as U = Uhc + Upot into the hard core repulsion Uhc and the attractive well Upot (see Fig. 1(b)). The microscopic density functional Ωmic1[ϱ1] for the pure solvent (species 1) in the bulk can be approximated by the expression
in terms of experimentally accessible quantities, in a first step the pure, ion-free solvent is considered, the particles of which interact only nonelectrostatically. Here this nonelectrostatic interaction between solvent particles at a distance r is modeled by a square-well pair potential U(r) as displayed in Fig. 1(a). At small distances r < σ a hard core repulsion prevents the overlap of two particles. At intermediate distances r ∈ (σ, σpot) two particles attract each other with an interaction energy −εpot, and at distances r > σpot the nonelectrostatic interaction vanishes. According to the scheme due to Barker and Henderson,35 the interaction potential U can be decomposed as U = Uhc + Upot into the hard core repulsion Uhc and the attractive well Upot (see Fig. 1(b)). The microscopic density functional Ωmic1[ϱ1] for the pure solvent (species 1) in the bulk can be approximated by the expression
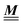 . The second term on the rhs of eqn (17) is (within random phase approximation (RPA)30) the excess free energy functional due to the square-well attractive interaction Upot:
. The second term on the rhs of eqn (17) is (within random phase approximation (RPA)30) the excess free energy functional due to the square-well attractive interaction Upot: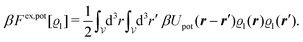

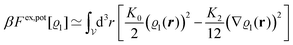
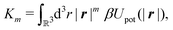
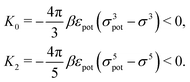
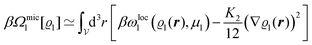
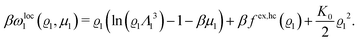
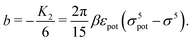
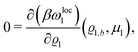
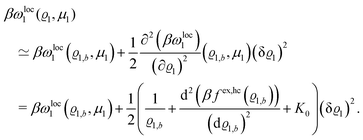
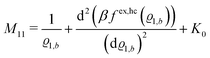
 , where the first term on the rhs stems from the ideal gas contribution of the solvent particles. The argument ϱ1,b of the second term, which is due to the hard core interaction Uhc, is a measure of the packing fraction η = πϱ1,bσ3/6.
, where the first term on the rhs stems from the ideal gas contribution of the solvent particles. The argument ϱ1,b of the second term, which is due to the hard core interaction Uhc, is a measure of the packing fraction η = πϱ1,bσ3/6.
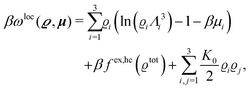
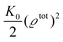 . By expanding βωloc(ϱ, μ) up to quadratic order in the density deviations δϱ = ϱ − ϱb from the equilibrium bulk densities ϱb one finally finds (see the steps leading to eqn (28))
. By expanding βωloc(ϱ, μ) up to quadratic order in the density deviations δϱ = ϱ − ϱb from the equilibrium bulk densities ϱb one finally finds (see the steps leading to eqn (28))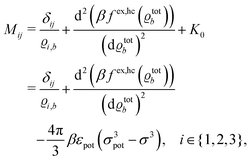
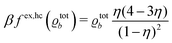
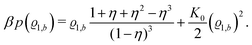
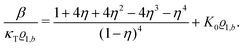
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37) with relative dielectric constant ε = 80, i.e., with Bjerrum length lB = 0.7 nm, and with a univalent salt of ionic strength I = 1 mM ≈ 6 × 10−4 nm−3. The strength of hydrogen bonds, which generate the dominant attractive interaction contribution, is of the order of εpot ≈ 20 kJ mol−1 ≈ 8kBT.36,37 Using these data, one obtains from eqn (32) and (33) the bulk packing fraction η ≈ 0.44 as well as σ = 2.9 Å and σpot = 3.4 Å. In the following the Debye length
37) with relative dielectric constant ε = 80, i.e., with Bjerrum length lB = 0.7 nm, and with a univalent salt of ionic strength I = 1 mM ≈ 6 × 10−4 nm−3. The strength of hydrogen bonds, which generate the dominant attractive interaction contribution, is of the order of εpot ≈ 20 kJ mol−1 ≈ 8kBT.36,37 Using these data, one obtains from eqn (32) and (33) the bulk packing fraction η ≈ 0.44 as well as σ = 2.9 Å and σpot = 3.4 Å. In the following the Debye length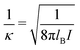
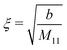
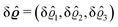 of the profiles of the density deviations as functions of the lateral wave vector q‖ and of the normal distance z from the wall are discussed in detail. However, from the experimental point of view, it is challenging to directly obtain the z-dependence of the density profiles. One of such direct methods is total internal reflection microscopy (TIRM)38 in the context of the structure of colloidal suspensions close to (optically transparent) substrates. In contrast, for molecular fluids, as the ones considered here, such direct methods are not available and one has to resort to, e.g., X-ray scattering techniques.39,40 As X-rays are predominantly scattered by the electrons of the fluid molecules one has to consider the electron number density
of the profiles of the density deviations as functions of the lateral wave vector q‖ and of the normal distance z from the wall are discussed in detail. However, from the experimental point of view, it is challenging to directly obtain the z-dependence of the density profiles. One of such direct methods is total internal reflection microscopy (TIRM)38 in the context of the structure of colloidal suspensions close to (optically transparent) substrates. In contrast, for molecular fluids, as the ones considered here, such direct methods are not available and one has to resort to, e.g., X-ray scattering techniques.39,40 As X-rays are predominantly scattered by the electrons of the fluid molecules one has to consider the electron number density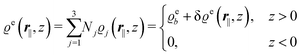
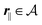 with the number Nj of electrons per molecule of particle species j ∈ {1, 2, 3}, the bulk electron density
with the number Nj of electrons per molecule of particle species j ∈ {1, 2, 3}, the bulk electron density 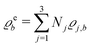 , and the deviation
, and the deviation 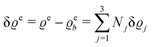 of the electron number density from its bulk value. The X-ray scattering signal for scattering vector q = (q‖,qz) is proportional to
of the electron number density from its bulk value. The X-ray scattering signal for scattering vector q = (q‖,qz) is proportional to 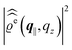 with the double Fourier transform
with the double Fourier transform 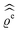 of the electron number density profile ϱe in both the lateral and the normal direction.35
of the electron number density profile ϱe in both the lateral and the normal direction.35
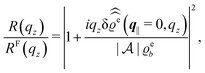
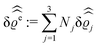 with
with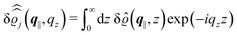
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qz ≠ 0) yields scattering intensities which are proportional to
qz ≠ 0) yields scattering intensities which are proportional to 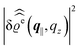 .39 Hence, as the double Fourier transforms
.39 Hence, as the double Fourier transforms 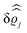 in eqn (39) of the density deviation profiles δϱj are of direct experimental relevance, they will be discussed in the following in parallel to the single Fourier transforms
in eqn (39) of the density deviation profiles δϱj are of direct experimental relevance, they will be discussed in the following in parallel to the single Fourier transforms 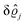 . Note that due to
. Note that due to 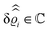 , in Fig. 3 and 4 its absolute value is shown.
, in Fig. 3 and 4 its absolute value is shown.
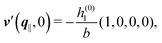
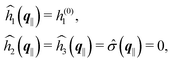
 for the solvent and
for the solvent and 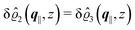 for the ions, as shown in Fig. 2(a) and (b), respectively. Since the boundary condition corresponds to a constant in Fourier space, the density distribution v(q‖, z) depends on k = |q‖| only. Actually, the solution v(q‖, z) for this system is proportional to the first column of the Green's function, which is a 4 × 4-matrix, of the differential operator corresponding to eqn (5) and (6).
for the ions, as shown in Fig. 2(a) and (b), respectively. Since the boundary condition corresponds to a constant in Fourier space, the density distribution v(q‖, z) depends on k = |q‖| only. Actually, the solution v(q‖, z) for this system is proportional to the first column of the Green's function, which is a 4 × 4-matrix, of the differential operator corresponding to eqn (5) and (6).

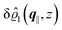 of the solvent (panel (a)) and of the ions
of the solvent (panel (a)) and of the ions 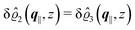 (panel (b)) as function of the distance z from the wall and of the absolute value of the lateral Fourier wave vector q‖ in units of the inverse Debye length κ (see eqn (34)). The plane z = 0 is given by the positions of the fluid particle centers when the surface-to-surface distance between the hard wall and the hard particles vanishes. The data correspond to the boundary condition
(panel (b)) as function of the distance z from the wall and of the absolute value of the lateral Fourier wave vector q‖ in units of the inverse Debye length κ (see eqn (34)). The plane z = 0 is given by the positions of the fluid particle centers when the surface-to-surface distance between the hard wall and the hard particles vanishes. The data correspond to the boundary condition 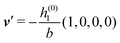 (see eqn (15) and (40)). The physical situation corresponding to this boundary condition is an attraction h1(r‖) = h(0)1δ(r‖) (see eqn (42)) of the solvent particles by the wall located at the origin of the wall. Concerning the remaining relevant parameters see Section IIIA.
(see eqn (15) and (40)). The physical situation corresponding to this boundary condition is an attraction h1(r‖) = h(0)1δ(r‖) (see eqn (42)) of the solvent particles by the wall located at the origin of the wall. Concerning the remaining relevant parameters see Section IIIA.
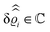 , in panels (e) and (f) the absolute values are shown. In each graph, there are three profiles shown corresponding to three values of the other relevant variable. Therefore the profiles correspond to cuts through Fig. 2(a) and (b) at various positions and in different directions. In this case the boundary condition is
, in panels (e) and (f) the absolute values are shown. In each graph, there are three profiles shown corresponding to three values of the other relevant variable. Therefore the profiles correspond to cuts through Fig. 2(a) and (b) at various positions and in different directions. In this case the boundary condition is 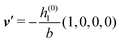 (see eqn (15) and (40)), corresponding to a δ-like nonelectrostatic attraction of the solvent particles at the origin of the wall (see Fig. 2 and eqn (42)). The graphs show, that the density deviations of the ions are proportional to the ones of the solvent, although different in sign. Since only the solvent particles are attracted by the wall, it is favorable for the system to increase their density close to the wall. However, due to the hard core nature of the particles and the equality of the interparticle attraction for all pairs of particles, the increase of solvent particles leads to an extrusion of ionic particles, leading to decreased ion densities at the wall. However, the density deviations of the ions are much weaker. For the remaining relevant parameters see Section IIIA.
(see eqn (15) and (40)), corresponding to a δ-like nonelectrostatic attraction of the solvent particles at the origin of the wall (see Fig. 2 and eqn (42)). The graphs show, that the density deviations of the ions are proportional to the ones of the solvent, although different in sign. Since only the solvent particles are attracted by the wall, it is favorable for the system to increase their density close to the wall. However, due to the hard core nature of the particles and the equality of the interparticle attraction for all pairs of particles, the increase of solvent particles leads to an extrusion of ionic particles, leading to decreased ion densities at the wall. However, the density deviations of the ions are much weaker. For the remaining relevant parameters see Section IIIA.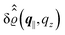 in terms of the lateral wave vector q‖ and the normal wave number qz, respectively. All curves in Fig. 3(c)–(f) exhibit a Lorentzian shape as functions of |q‖| and qz, respectively. These Lorentzian curves in Fourier space correspond to exponential decays in real space in lateral or normal direction. The curves in Fig. 3(c) and (d) show widths of half height which decrease with increasing normal distance z, i.e., the lateral decay length in real space increases with increasing distance from the wall. This implies that the density distribution broadens upon moving away from the source of the perturbation. The curves in Fig. 3(e) and (f) exhibit widths of half height which increase with the lateral wave number |q‖|, i.e., the normal decay length in real space decreases with increasing lateral wave number. Consequently, the range of influence of rapidly varying modes of wall heterogeneities onto the fluid is shorter than that of slowly varying modes. This relationship can also be inferred from Fig. 3(a) and (b). From the above discussions and from Fig. 3 one can conclude, that the response of all species to a simple attraction of nonelectrostatic type is the same up to a proportionality factor. This is confirmed by studying in addition the boundary conditions
in terms of the lateral wave vector q‖ and the normal wave number qz, respectively. All curves in Fig. 3(c)–(f) exhibit a Lorentzian shape as functions of |q‖| and qz, respectively. These Lorentzian curves in Fourier space correspond to exponential decays in real space in lateral or normal direction. The curves in Fig. 3(c) and (d) show widths of half height which decrease with increasing normal distance z, i.e., the lateral decay length in real space increases with increasing distance from the wall. This implies that the density distribution broadens upon moving away from the source of the perturbation. The curves in Fig. 3(e) and (f) exhibit widths of half height which increase with the lateral wave number |q‖|, i.e., the normal decay length in real space decreases with increasing lateral wave number. Consequently, the range of influence of rapidly varying modes of wall heterogeneities onto the fluid is shorter than that of slowly varying modes. This relationship can also be inferred from Fig. 3(a) and (b). From the above discussions and from Fig. 3 one can conclude, that the response of all species to a simple attraction of nonelectrostatic type is the same up to a proportionality factor. This is confirmed by studying in addition the boundary conditions 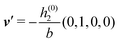 and
and 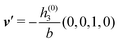 ; these results are not shown here.
; these results are not shown here.![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (q‖) = σ(0), i.e., σ(r‖) = σ(0)δ(r‖),
(q‖) = σ(0), i.e., σ(r‖) = σ(0)δ(r‖),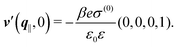
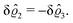
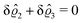 . Accordingly, also the density deviation for the solvent vanishes,
. Accordingly, also the density deviation for the solvent vanishes, 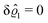 . Fig. 4 shows the density profiles of the positive ions, which, up to the sign, are the same as the ones for the negative ions. As stated above, for this boundary condition, there is no need to discuss the behavior of the solvent particles.
. Fig. 4 shows the density profiles of the positive ions, which, up to the sign, are the same as the ones for the negative ions. As stated above, for this boundary condition, there is no need to discuss the behavior of the solvent particles.
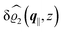 as functions of the normal distance z from the wall for three values of the lateral wave number |q‖|. Fig. 4(b) shows the same density profiles
as functions of the normal distance z from the wall for three values of the lateral wave number |q‖|. Fig. 4(b) shows the same density profiles 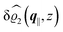 but as functions of |q‖| for three distances z from the wall. Fig. 4(c) displays the double Fourier transform
but as functions of |q‖| for three distances z from the wall. Fig. 4(c) displays the double Fourier transform 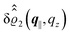 . Compared with the profiles in Fig. 3 for the previously discussed boundary conditions, all present profiles differ significantly from them. Fig. 4(a) reveals a much larger decay length in z-direction, i.e., normal to the wall. Also in Fourier space the decay in lateral direction occurs much more rapidly, i.e., on much longer length scales in real space than in the case of the nonelectrostatic wall–fluid interaction (cf.Fig. 3). This is also indicated by the much narrower peak in the double Fourier transform (see Fig. 4(c)). Furthermore, Fig. 4(a) shows a variation of the decay length in normal direction as function of |q‖|. In Fig. 4(b) one observes that the lateral wave numbers |q‖| at which the profiles
. Compared with the profiles in Fig. 3 for the previously discussed boundary conditions, all present profiles differ significantly from them. Fig. 4(a) reveals a much larger decay length in z-direction, i.e., normal to the wall. Also in Fourier space the decay in lateral direction occurs much more rapidly, i.e., on much longer length scales in real space than in the case of the nonelectrostatic wall–fluid interaction (cf.Fig. 3). This is also indicated by the much narrower peak in the double Fourier transform (see Fig. 4(c)). Furthermore, Fig. 4(a) shows a variation of the decay length in normal direction as function of |q‖|. In Fig. 4(b) one observes that the lateral wave numbers |q‖| at which the profiles 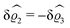 decay to half of the maximum values decrease upon increasing the distances z from the wall, from which one infers that the lateral decay length in real space increases upon increasing z. The decay with respect to |q‖| is much faster than in the previous case (compare Fig. 3(d)), indicating that in real space there is a slower decay in the lateral direction. Moreover, in Fig. 4(b) and (c) the functional form differs from the one shown in Fig. 2 and 3. These differences naturally occur due to the different form of the boundary condition. Since in the case of the boundary condition studied above (see Fig. 2 and 3) the relevant interaction is nonelectrostatic, the length scale dominating the decay is given by the corresponding short-ranged bulk correlation length ξ (see eqn (36)). In contrast, for the system shown in Fig. 4, due to the electrostatic nature of the corresponding interaction, the dominating length scale is the Debye length 1/κ (see eqn (34)), which is much larger than the correlation length ξ due to the nonelectrostatic interaction, giving rise to the much slower decay in Fig. 4(a) (on the scale of 1/κ) and the much faster decay in Fig. 4(b) and (c) (on the scale of κ).
decay to half of the maximum values decrease upon increasing the distances z from the wall, from which one infers that the lateral decay length in real space increases upon increasing z. The decay with respect to |q‖| is much faster than in the previous case (compare Fig. 3(d)), indicating that in real space there is a slower decay in the lateral direction. Moreover, in Fig. 4(b) and (c) the functional form differs from the one shown in Fig. 2 and 3. These differences naturally occur due to the different form of the boundary condition. Since in the case of the boundary condition studied above (see Fig. 2 and 3) the relevant interaction is nonelectrostatic, the length scale dominating the decay is given by the corresponding short-ranged bulk correlation length ξ (see eqn (36)). In contrast, for the system shown in Fig. 4, due to the electrostatic nature of the corresponding interaction, the dominating length scale is the Debye length 1/κ (see eqn (34)), which is much larger than the correlation length ξ due to the nonelectrostatic interaction, giving rise to the much slower decay in Fig. 4(a) (on the scale of 1/κ) and the much faster decay in Fig. 4(b) and (c) (on the scale of κ).
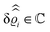 , in panel (c) the absolute value is shown. Each panel shows the profiles for three values of the other relevant variable. These profiles are cuts of the corresponding data (analogous to Fig. 2) along various directions. Here, the boundary condition is given by
, in panel (c) the absolute value is shown. Each panel shows the profiles for three values of the other relevant variable. These profiles are cuts of the corresponding data (analogous to Fig. 2) along various directions. Here, the boundary condition is given by 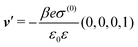 (see eqn (15) and (44)), which corresponds to a δ-like surface charge at the origin in real space (see eqn (43)). The profiles for the solvent are not shown, because the deviations linked to the two types of ions cancel out,
(see eqn (15) and (44)), which corresponds to a δ-like surface charge at the origin in real space (see eqn (43)). The profiles for the solvent are not shown, because the deviations linked to the two types of ions cancel out, 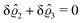 , leaving the density of the solvent unchanged as if there were no ions. In comparison with Fig. 3, the profiles in (a) decay much slower on the scale of the Debye length 1/κ (see eqn (34)) instead of on the scale of the much shorter bulk correlation length ξ (see Fig. 3(b) and eqn (36)) due to the nonelectrostatic interaction. Accordingly, the profiles in (b) and (c) decay on the scale of κ more rapidly than their counterparts in Fig. 3(d) and (f). For the remaining relevant parameters see Section IIIA.
, leaving the density of the solvent unchanged as if there were no ions. In comparison with Fig. 3, the profiles in (a) decay much slower on the scale of the Debye length 1/κ (see eqn (34)) instead of on the scale of the much shorter bulk correlation length ξ (see Fig. 3(b) and eqn (36)) due to the nonelectrostatic interaction. Accordingly, the profiles in (b) and (c) decay on the scale of κ more rapidly than their counterparts in Fig. 3(d) and (f). For the remaining relevant parameters see Section IIIA.

![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) (0)1Θ(R − |r‖|), h2(r‖) = h3(r‖) = σ(r‖) = 0, see eqn (46) as well as Fig. 2 and 3), whereas in panels (b) and (d) the patch contains a constant surface charge and therefore interacts with the ions only (h(r‖) = 0, σ(r‖) =
(0)1Θ(R − |r‖|), h2(r‖) = h3(r‖) = σ(r‖) = 0, see eqn (46) as well as Fig. 2 and 3), whereas in panels (b) and (d) the patch contains a constant surface charge and therefore interacts with the ions only (h(r‖) = 0, σ(r‖) = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (0)Θ(R − |r‖|), see eqn (49) and Fig. 4). Besides the profiles, all panels show also the lateral Fourier transform of the boundary condition (eqn (47) and (50)) displayed as a black solid line. In the case of the interaction of the wall with the solvent ((a) and (c)), the decay of the profiles as function of |q‖| is proportional to the lateral Fourier transform of the boundary condition, which implies, that the density deviations in real space closely follow the shape of the patch. However, in the case of a charged patch at the surface the density distribution of the ions reflects the competition between the length scale R of the radius of the patch and the Debye length 1/κ. In the case of small patches (R < 1/κ, panel (b)), the Debye length dominates and therefore dictates the decay as function of |q‖| without noticeable influence of the patch. In contrast, in the case of large patches (R > 1/κ, panel (d)), in which the radius of the patch is the dominating length scale, the shape of the profiles follows the Fourier transform of the charge distribution at the wall, i.e., the patch of radius R. For the remaining relevant parameters see Section IIIA.
(0)Θ(R − |r‖|), see eqn (49) and Fig. 4). Besides the profiles, all panels show also the lateral Fourier transform of the boundary condition (eqn (47) and (50)) displayed as a black solid line. In the case of the interaction of the wall with the solvent ((a) and (c)), the decay of the profiles as function of |q‖| is proportional to the lateral Fourier transform of the boundary condition, which implies, that the density deviations in real space closely follow the shape of the patch. However, in the case of a charged patch at the surface the density distribution of the ions reflects the competition between the length scale R of the radius of the patch and the Debye length 1/κ. In the case of small patches (R < 1/κ, panel (b)), the Debye length dominates and therefore dictates the decay as function of |q‖| without noticeable influence of the patch. In contrast, in the case of large patches (R > 1/κ, panel (d)), in which the radius of the patch is the dominating length scale, the shape of the profiles follows the Fourier transform of the charge distribution at the wall, i.e., the patch of radius R. For the remaining relevant parameters see Section IIIA.![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) (r‖) = 0
(r‖) = 0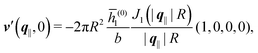
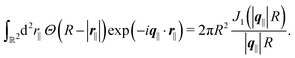
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (0)Θ(R − |r‖|),
(0)Θ(R − |r‖|),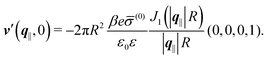
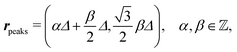
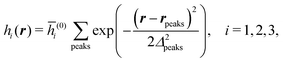
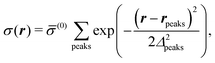
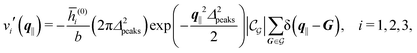
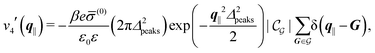
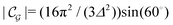 is the size of an elementary cell of the corresponding two-dimensional reciprocal lattice
is the size of an elementary cell of the corresponding two-dimensional reciprocal lattice 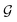 . Using this boundary condition, we have studied four different systems, as shown in Fig. 7.
. Using this boundary condition, we have studied four different systems, as shown in Fig. 7.

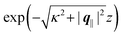 . In principle this occurs for both types of interactions. However only in the case of the electrostatic interactions it is relevant, which again is due to the difference between the dominating length scales. For the remaining relevant parameters see Section IIIA.
. In principle this occurs for both types of interactions. However only in the case of the electrostatic interactions it is relevant, which again is due to the difference between the dominating length scales. For the remaining relevant parameters see Section IIIA.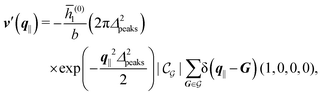
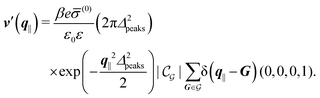
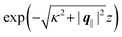 . The large differences in the amplitudes of the various profiles in Fig. 7(b) and (d), as well as the pronounced increase of the decay length in comparison to Fig. 7(a) and (c) can be understood in terms of the differences between the dominating length scale. Analogous to the previous sections, for the systems shown in Fig. 7(a) and (c), the dominating length scale in lateral direction is the length scale set by the boundary conditions and the bulk correlation length ξ, which characterizes the decay of the solvent density in normal direction. However, for the systems shown in Fig. 7(b) and (d), the relevant inherent length scale of the fluid is the Debye length 1/κ, which is significantly larger than the bulk correlation length ξ and thus causes the increase in the length scale of the decay, both in lateral and in normal direction.
. The large differences in the amplitudes of the various profiles in Fig. 7(b) and (d), as well as the pronounced increase of the decay length in comparison to Fig. 7(a) and (c) can be understood in terms of the differences between the dominating length scale. Analogous to the previous sections, for the systems shown in Fig. 7(a) and (c), the dominating length scale in lateral direction is the length scale set by the boundary conditions and the bulk correlation length ξ, which characterizes the decay of the solvent density in normal direction. However, for the systems shown in Fig. 7(b) and (d), the relevant inherent length scale of the fluid is the Debye length 1/κ, which is significantly larger than the bulk correlation length ξ and thus causes the increase in the length scale of the decay, both in lateral and in normal direction.
 (eqn (2)), with entries given by eqn (30), and of the vector Z = (0, 1, −1), from eqn (9) and (10) one infers that the matrix
(eqn (2)), with entries given by eqn (30), and of the vector Z = (0, 1, −1), from eqn (9) and (10) one infers that the matrix 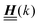 has the form
has the form
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) and k = |q‖|, s, t > 0. It can be readily verified that the four vectors
and k = |q‖|, s, t > 0. It can be readily verified that the four vectors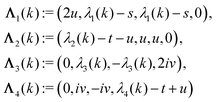
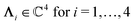 , form a nonorthogonal basis of eigenvectors of the matrix
, form a nonorthogonal basis of eigenvectors of the matrix  in eqn (A1) with the respective real eigenvalues
in eqn (A1) with the respective real eigenvalues