Open Access Article
Open Access ArticleNon-empirical calculation of X-ray magnetic circular dichroism in lanthanide compounds†
Harry
Ramanantoanina
 *,
Michał
Studniarek
,
Niéli
Daffé
*,
Michał
Studniarek
,
Niéli
Daffé
 and
Jan
Dreiser
and
Jan
Dreiser
 *
*
Paul Scherrer Institute, CH-5232, Villigen PSI, Switzerland. E-mail: harry.ra@hotmail.com; jan.dreiser@psi.ch
First published on 20th February 2019
Abstract
Affordable calculations of X-ray magnetic circular dichroism and X-ray linear dichroism spectra of lanthanide ions purely based on structural input are difficult to achieve. Here we report on the successful application of ligand-field density-functional theory to obtain an exquisite reproduction of experimental spectra. As a testbed we use TbPc2 single-molecule magnets on a flat substrate.
X-ray magnetic circular dichroism (XMCD) and X-ray linear dichroism (XLD) at the L2,3 edges of transition metals and at the M4,5 edges of lanthanides are increasingly employed for the study of an enormous variety of magnetic materials.1 XMCD probes the spin and orbital magnetic moments residing in the open d or f shell, respectively, by performing X-ray absorption spectroscopy (XAS) with the two circular polarizations of the X-rays.2 Its element specificity and ultrahigh sensitivity, owing to the very large absorption cross sections in the soft X-ray range, allow one to obtain insights, which are not possible or difficult to achieve with other techniques.
Despite the success of the XMCD method it is still a challenge to perform reliable calculations of the obtained X-ray absorption and XMCD/XLD spectra based on purely structural input. The most widespread approach, due to its simplicity and efficiency, is ligand-field multiplet theory (LFMT),3–7 which is extremely successful in reproducing the spectral shapes of lanthanide M4,5 spectra. However, these calculations heavily rely on empirical parameterization of the ligand-field Hamiltonian as well as on empirical adjustments of the Slater–Condon integrals and spin–orbit coupling constants with multiplication factors. The parameterization of the ligand-field potential is a problem in particular, since in the absence of any symmetry up to 15 + 28 independent parameters would be needed for a full description.8 While one-electron approaches using density-functional theory (DFT) calculations are interesting because of the strengths in structural modeling, these calculations are not designed to take into account the core-hole and valence electron interactions that are created during the X-ray absorption process.9 Hybrid approaches, in which ligand-field parameters of LFMT are obtained by electronic structure calculations, have been demonstrated for 3d transition metals XAS.7,10,11 The feasibility in the case of 4f lanthanides and 5f actinides application is possible but much effort is needed to establish a fully non-empirical model.12,13
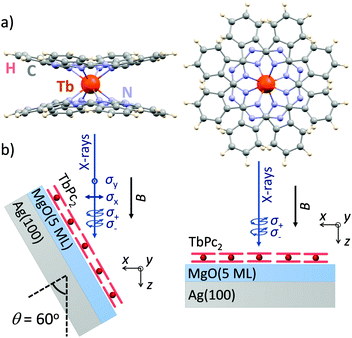
Here, we demonstrate that ligand-field density-functional theory (LFDFT)14–17 is able to reproduce in very detail the XMCD spectra as well as the corresponding XLD. As an example we employ the case of TbPc2 [bis(phthalo-cyaninato)terbium(III)] single-molecule magnets18 (Fig. 1a) adsorbed as a submonolayer on a flat and weakly interacting oxide surface.19 The method is particularly well suitable to treat the 4f shell magnetism because of the inner-shell nature and because of the rather low hybridization of 4f electrons, as compared to 3d transition metals, with the environment of the atom under consideration.
Details about the application of LFDFT to calculate unpolarized XAS can be found in ref. 13. Here we describe the extension of the method to obtain polarized X-ray spectra. Using DFT we set up an active subspace of Kohn–Sham orbitals that forms the basis of the fivefold 3d and sevenfold 4f orbitals of the trivalent lanthanide ions with the 3d104fn ground state and the 3d94fn+1 excited state configurations, respectively. This active subspace is defined with a fractional occupation of electrons, where the smearing of the electrons onto the manifolds of the 3d and 4f orbitals allows obtaining the electronic density that belongs to the totally symmetric representation under which the effective ligand-field Hamiltonian (eqn (1)) is operated.12–17
| Heff = H0 + HER + HSO + HLF + HZE, | (1) |
The interaction matrices for the configuration average energy correction (H0), electrostatic inter-electron repulsion (HER), spin–orbit coupling (HSO) and ligand-field splitting (HLF) are constructed.12–17 The input parameters include the energy gap (ΔEav), Slater–Condon integrals (Fk(4f,4f), with k = 2, 4 and 6; Fk(3d,4f), with k = 2 and 4; and Gk(3d,4f), with k = 1, 3 and 5), spin–orbit coupling constants (ζ3d and ζ4f) and ligand-field potential (a matrix with 12 × 12 elements), where in total 155 parameter values are non-empirically extracted from the DFT calculation.12–17 The eigendecomposition of the matrix elements of the effective Hamiltonian in eqn (1) yields the multiplet energies (E) and the multi-electronic eigenfunctions (ψ) that arise from the open-shell configurations 3d104fn and 3d94fn+1 of the trivalent lanthanide ions.
In the context of the magnetic dichroism experiment, i.e. in the presence of an external magnetic field (B), we add an extra term in eqn (1) that represents the electronic Zeeman interaction (HZE).20 This term is defined as follows:
| HZE = μB(gLL + geS)·B, | (2) |
We use the electric dipole approximation to model the X-ray absorption spectrum. The excitation energies and oscillator strengths of the intra-atomic 3d104fn + hν → 3d94fn+1 electron transitions are defined as follows:
| Eph = ΔEi,j = Ej − E(0)i, | (3) |
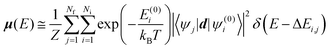 | (4) |
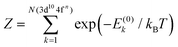 . The Boltzmann distribution in eqn (4) is taken over the manifold of the initial state configuration to account for finite temperature effects.
. The Boltzmann distribution in eqn (4) is taken over the manifold of the initial state configuration to account for finite temperature effects.
The electric dipole moment operator is split into three components that correspond to ex, ey and ez polarizations with e the vector of the oscillating electric field. The z term gives the absorption for the electric vector parallel to the magnetic axis, and the sum of the x and y terms gives the intensity for the oscillating electric field perpendicular to the magnetic axis. The XLD is defined as the difference in absorption of linearly polarized light, XLD = μy − μx, induced by the 4f ligand-field splitting and the resulting different orbital occupation. On the other hand, the magnetic circular dichroism is defined as the difference in absorption with respect to the left circular (μ−) and right circular (μ+) light 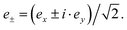 Hence, XMCD = [μ+ − μ−], and it is induced by the presence of a magnetic moment residing in the 4f shell.
Hence, XMCD = [μ+ − μ−], and it is induced by the presence of a magnetic moment residing in the 4f shell.
In order to make the calculated absorption spectra comparable to the experimental ones, they are convoluted with a Lorentzian function. The full width at half maximum (FWHM) was 1.0 eV and for simplicity only a single line width function was applied in the whole energy range to take into account both the core-hole lifetime and instrumental broadenings.
The DFT calculations were performed by means of the Amsterdam density functional (ADF) program package.21 Details about the computational procedure are given in the ESI,† Computational details section. We used the DFT relaxed structure of the isolated TbPc2 molecule as input geometry corresponding to the molecular gas phase. The DFT equilibrium geometry is in good agreement with the experimental structure22 (cf. ESI,† Fig. S1 and Table S1). The optimized Cartesian coordinates are given in the ESI,† Table S2. The calculated energy values of the Kohn–Sham orbitals of TbPc2 in the −6.125 eV to −4.425 eV energy range are listed in the ESI,† Table S3 together with the parentage of TbPc2 from Tb 3d and 4f atomic orbitals and the occupation scheme that was imposed in the DFT calculations. Seven Kohn–Sham Orbitals have nearly atomic-like Tb 4f character, with percentage characters larger than 90% (cf. ESI,† Table S3). These orbitals have been used as the active subspace that resolved the 4f ligand-field states of the Tb3+ ion. Based on this active subspace together with the Tb core 3d functions, the non-empirical parameters that are used as input of the effective ligand-field Hamiltonian in eqn (1) were obtained using the newly available LFDFT keyword in the ADF program package.21 Their tabulated values are listed in the ESI† (Tables S4–S7) for both ground state (3d104f8) and excited state (3d94f9) electron configurations of Tb3+ in the complex TbPc2. Note that the DFT calculations suggest the presence of hybridization or covalency of Tb 4f orbitals with ligand orbitals in the few percent range. The hybridization is expected to be slightly overestimated due to the self-interaction error in DFT.23 However, it does not affect the LF Hamiltonian, because the ligand contribution to the wave function is neglected.24
In order to validate the accuracy of the calculations we compare the simulated XAS, XMCD, and XLD spectra to the ones experimentally recorded on ca. 0.7 monolayers of TbPc2 molecules (Fig. 1a) deposited on a MgO thin film. We selected this system because the phthalocyanine–MgO hybridization is expected to be weak25 resulting in X-ray spectra of close-to-isolated (gas-phase-like, but spatially ordered) molecules, and because it is well known that the TbPc2 molecules are arranged in self-assembled islands with their planar ligands parallel to the surface plane.19 The molecules were sublimed from a Knudsen cell held at a temperature of 673 K onto the three monolayer thick film of MgO grown epitaxially on a Ag(100) crystal which has been cleaned previously by repeated Ar+ ion sputter annealing cycles.
The experimental spectra were recorded on samples prepared similar to ref. 19 at the X-Treme beamline of the Swiss Light Source.26 The XAS measurements were performed in normal (θ = 0°) and grazing (θ = 60°) incidence of the X-rays. We fix the frame of reference such that the z axis is along the X-ray propagation direction and at normal incidence the xy plane lies in the molecular plane, that is, in the plane of the phthalocyanine ligands (see Fig. 1b). All measurements were performed in total electron yield mode, and the magnetic field was always parallel to the beam propagation direction. A polynomial background was subtracted from the spectra.
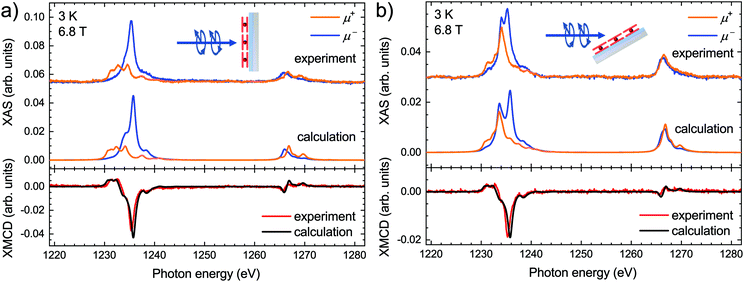
The calculated XAS and the corresponding XMCD along with the experimental spectra acquired on the submonolayer of TbPc2 molecules at both normal and grazing geometry are presented in Fig. 2. Note that the calculated spectra are obtained by means of LFDFT calculations using the DFT functional following the generalized gradient approximation formulation (see also the ESI,† Computational details section) and the optimized structure of TbPc2 is obtained with the same DFT functional (see also the ESI,† Table S2). The ESI,† Tables S8 and S9 list the multiplet energy levels and the ligand-field splitting of the Tb3+ ion in TbPc2 within the atomic ground state (3d104f8) and excited state (3d94f9) configurations as well as the oscillator strengths of the 3d104f8–3d94f9 electron transitions. The calculated spectra were normalized in order to have the same Tb M5 areas in the sum of the helicities as the experimental ones. Furthermore, the calculated spectra were shifted in photon energy by −3.1 eV to find the best match with the experiment. The comparison reveals that the simulated X-ray spectra are in excellent agreement with the experimental ones. The calculated differences between the simulated and experimental spectra, i.e., the residuals, are plotted in the ESI,† Fig. S2, indicating a larger splitting of the main features of the M5 edge in the calculations as already visible in Fig. 2. This is most likely due to a slight overestimation of the Slater–Condon parameters by LFDFT. Note that the inter-electron repulsion and spin–orbit coupling that induce the separation between the Tb M5 and M4 edges are obtained without any empirical correction in the present work. The strength of the XMCD signal is proportional to the Tb 4f magnetic moment projected onto the beam propagation vector.1 In this context the reduced XMCD amplitude at grazing incidence with respect to normal geometry is in line with the known strong out-of-plane easy-axis magnetic anisotropy of the TbPc2 molecules. Note that the XMCD spectra shown in Fig. 2 imply an excellent reproduction of the TbPc2 magnetic properties by our calculations.
The XLD reflects the angular distribution of the 4f holes, and it thus provides information on the molecular orientation on the surface. We acquired the experimental XLD at grazing incidence (see Fig. 1b) by recording the XAS spectra with linear vertical polarization ey probing 4f orbitals in the surface plane and linear horizontal polarization ex probing mostly out-of-plane 4f orbitals. The comparison of the calculated XLD spectra with the experimental ones is presented in Fig. 3. Both the shape and the amplitude of the calculated linearly polarized spectra excellently match the experimental data. The energy of the maximum of the Tb M5 edge depends on the linear polarization, that is, 1233.6 eV for the ex polarization and 1235.8 eV for ey, which indicates a preferential orientation of the TbPc2 molecules on the surface with the phthalocyanine ligand plane parallel to the surface, as shown by the STM studies19 and in comparison with previous work.27,28 The calculated spectra correctly reproduce these energetic positions of the main peak, albeit with a slightly larger splitting leading to weak satellite peaks at 1235.8 eV (1234.2 eV). The M4 edge is slightly overestimated in the calculations, which might result from imperfections in the background subtraction and/or from a stronger line broadening at the M4 edge, which was taken to be constant across the whole energy range for the sake of simplicity.
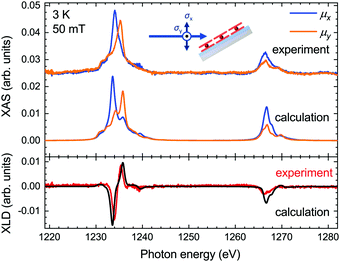 | ||
| Fig. 3 Comparison of the calculated and experimentally acquired X-ray absorption spectra (top panel) and X-ray linear dichroism (bottom panel) at the Tb M4,5 edges of TbPc2 at grazing geometry. | ||
In conclusion, we have developed a DFT-based theoretical model for the calculation of the X-ray magnetic circular dichroism and X-ray linear dichroism spectra of lanthanide compounds. By using a ligand-field Hamiltonian in association with the DFT calculations, we are able to model the XMCD and XLD at the Tb M4,5 edges of TbPc2, taking into consideration all the quantum physical interactions involved in the X-ray absorption process such as the inter-electronic repulsion, spin–orbit coupling and ligand-field splitting of the atomic multiplet energies. The calculations are in excellent agreement with the experimental spectra, providing deep insight into the microscopic origin of dichroism in optical spectra and a good understanding of the mechanism of 3d core-electron excitation in Tb3+ ions. We have also shown that the computational cost is economic and the methodology does not require sophisticated DFT functionals or basis functions.
Thus LFDFT, which works for the whole lanthanide series, is an excellent and efficient non-empirical method able to model spectral profiles with relevance in the study of existing and future applications of trivalent lanthanide ions. The performance of the LFDFT method is promising for the calculation of XMCD spectra of lanthanide centers in low-symmetry geometries, which can occur, e.g., in surface-adsorbed molecular magnets or atoms.
The authors thank Prof. Mario Ruben, Dr Svetlana Klyatskaya and Dr Yanhua Lan for providing the TbPc2 molecules. This project was supported by funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 701647. Furthermore, the authors acknowledge funding by Swissnuclear and by the Swiss National Science Foundation (grant no. 200021_165774/1).
Conflicts of interest
There are no conflicts to declare.Notes and references
- G. van der Laan and A. I. Figueroa, Coord. Chem. Rev., 2014, 277–278, 95–129 CrossRef CAS.
- J. Stöhr and H. C. Siegmann, Magnetism: From Fundamentals to Nanoscale Dynamics, Springer-Verlag, Berlin Heidelberg, 2006 Search PubMed.
- B. T. Thole, G. van der Laan and G. A. Sawatzky, Phys. Rev. Lett., 1985, 55, 2086–2088 CrossRef CAS PubMed.
- J. B. Goedkoop, B. T. Thole, G. van der Laan, G. A. Sawatzky, F. M. F. de Groot and J. C. Fuggle, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 2086–2093 CrossRef CAS.
- F. de Groot, Coord. Chem. Rev., 2005, 249, 31–63 CrossRef CAS.
- A. Uldry, F. Vernay and B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125133 CrossRef.
- M. W. Haverkort, M. Zwierzycki and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165113 CrossRef.
- H. Ramanantoanina, W. Urland, F. Cimpoesu and C. Daul, Phys. Chem. Chem. Phys., 2014, 16, 12282–12290 RSC.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- H. Ikeno, T. Mizoguchi and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155107 CrossRef.
- H. Ramanantoanina and C. Daul, Phys. Chem. Chem. Phys., 2017, 19, 20919–20929 RSC.
- H. Ramanantoanina, Phys. Chem. Chem. Phys., 2017, 19, 32481–32491 RSC.
- H. Ramanantoanina, J. Chem. Phys., 2018, 149, 054104 CrossRef PubMed.
- M. Atanasov, C. A. Daul and C. Rauzy, in Optical Spectra and Chemical Bonding in Inorganic Compounds: Special Volume dedicated to Professor Jørgensen I, ed. D. M. P. Mingos and T. Schönherr, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 97–125 Search PubMed.
- M. Atanasov, C. Rauzy, P. Baettig and C. Daul, Int. J. Quantum Chem., 2005, 102, 119–131 CrossRef CAS.
- H. Ramanantoanina, W. Urland, F. Cimpoesu and C. Daul, Phys. Chem. Chem. Phys., 2013, 15, 13902–13910 RSC.
- H. Ramanantoanina, M. Sahnoun, A. Barbiero, M. Ferbinteanu and F. Cimpoesu, Phys. Chem. Chem. Phys., 2015, 17, 18547–18557 RSC.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- C. Wäckerlin, F. Donati, A. Singha, R. Baltic, S. Rusponi, K. Diller, F. Patthey, M. Pivetta, Y. Lan, S. Klyatskaya, M. Ruben, H. Brune and J. Dreiser, Adv. Mater., 2016, 28, 5195–5199 CrossRef PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford Classic Texts in the Physical Sciences, 1970 Search PubMed.
- E. J. Baerends, et al., ADF2017, 2017, available at http://www.scm.com Search PubMed.
- K. Katoh, Y. Yoshida, M. Yamashita, H. Miyasaka, B. K. Breedlove, T. Kajiwara, S. Takaishi, N. Ishikawa, H. Isshiki, Y. F. Zhang, T. Komeda, M. Yamagishi and J. Takeya, J. Am. Chem. Soc., 2009, 131, 9967–9976 CrossRef CAS PubMed.
- I. Ciofini, C. Adamo and H. Chermette, Chem. Phys., 2005, 309, 67–76 CrossRef CAS.
- B. N. Figgis and M. A. Hitchman, Ligand field theory and its applications, Wiley-VCH, 2000 Search PubMed.
- M. Glaser, H. Peisert, H. Adler, M. Polek, J. Uihlein, P. Nagel, M. Merz, S. Schuppler and T. Chassé, J. Phys. Chem. C, 2015, 119, 27569–27579 CrossRef CAS.
- C. Piamonteze, U. Flechsig, S. Rusponi, J. Dreiser, J. Heidler, M. Schmidt, R. Wetter, M. Calvi, T. Schmidt, H. Pruchova, J. Krempasky, C. Quitmann, H. Brune and F. Nolting, J. Synchrotron Radiat., 2012, 19, 661–674 CrossRef CAS PubMed.
- S. Stepanow, J. Honolka, P. Gambardella, L. Vitali, N. Abdurakhmanova, T.-C. Tseng, S. Rauschenbach, S. L. Tait, V. Sessi, S. Klyatskaya, M. Ruben and K. Kern, J. Am. Chem. Soc., 2010, 132, 11900–11901 CrossRef CAS PubMed.
- L. Margheriti, D. Chiappe, M. Mannini, P. Car, P. Sainctavit, M.-A. Arrio, F. B. de Mongeot, J. C. Cezar, F. M. Piras, A. Magnani, E. Otero, A. Caneschi and R. Sessoli, Adv. Mater., 2010, 22, 5488–5493 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details; optimized DFT geometrical structure of TbPc2 and comparison with experimental structure; atomic cartesian coordinates; selected Kohn–Sham orbital energies and wavefunctions; calculated parameters and ligand-field matrix elements within the ground state and excited state configurations; calculated energy levels of the 7F6 ground state atomic multiplet of Tb3+ in TbPc2; selected energy levels of the excited state 3d94f9 configuration of Tb3+ in TbPc2; residual plots of the polarized X-ray spectra. See DOI: 10.1039/c8cc09321k |
| This journal is © The Royal Society of Chemistry 2019 |