Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvent reorganization triggers photo-induced solvated electron generation in phenol†
Isolde
Sandler
,
Juan J.
Nogueira‡
* and
Leticia
González
 *
*
Institute of Theoretical Chemistry, University of Vienna, Währinger Straße 17, 1090 Vienna, Austria. E-mail: JuanJose.NogueiraPerez@anu.edu.au; leticia.gonzalez@univie.ac.at
First published on 10th December 2018
Abstract
The analysis of the absorption spectrum and density of states of a cluster of phenol solvated with 15 water molecules indicates that the reorganization of the water molecules, facilitating the formation of solvated electrons, is a plausible mechanism in the photodissociation of phenol. Using quantitative wavefunction analysis, we demonstrate that while charge-transfer states involving electron transfer from phenol to water are mainly dark, a considerable number of them exists below the maximum of the ππ* absorption band and could be populated by internal conversion. These low-lying charge-transfer states do not show extended O–H distances, but are found for large electron–hole separations at which several water molecules can solvate and stabilize the transferred electron. Thus, charge-transfer states in solvated phenol can be stabilized by two factors: (i) elongation of the O–H bond, as was extensively discussed in the past, and (ii) reorganization of solvent molecules, as it is shown here.
1. Introduction
Phenol is a biologically relevant chromophore. It appears e.g. in tyrosin, a phenol derivative that plays a role in photosynthesis1 and in 5,6-dihydroxyindole, which is one of the building blocks of the photoprotective pigment eumelanine.2–4 As such, the photophysics of phenol has attracted considerable attention. However, and despite the large body of theoretical5–18 and experimental19–46 literature dealing with the photoinduced dynamics of phenol, a number of open questions, in particular regarding the photodissociation mechanism in aqueous solution, remain.Based on theoretical calculations,6–9 it has been proposed that after excitation to the bright first excited state of ππ* character, a conical intersection can be reached upon O–H elongation to finally populate a charge-transfer (CT) state of πσ* character with low oscillator strength. This state is dissociative with respect to the O–H bond, leading to the hydrogen atom and phenoxyl radical PhO˙ products. For gas-phase phenol, the second excited state in the Franck–Condon region corresponds to an electronic excitation to a Rydberg-type orbital that, upon elongation of the O–H bond, takes on O–H-antibonding σ* character. However, in aqueous solution this orbital is located in the solvent and, therefore, upon excitation of solvated phenol a concerted proton and electron transfer from phenol to the solvent has been postulated6 to take place.
Experimental studies in the gas phase,26–33 as well as in the apolar aprotic solvent cyclohexane,46 support the mechanism of photodissociation by an O–H elongation, without electron transfer to the solvent (as the latter do not exist or no polar protic solvent is available). In aqueous solution, evidence for a photodissociation mechanism different from gas-phase phenol was recently found by Oliver et al.47 using transient absorption spectroscopy. After excitation with 200 nm light, solvated electrons and phenoxyl radicals PhO˙ were observed within 200 fs. Additionally, a signal attributed to phenol radical cations PhOH+˙, decaying on a sub-picosecond time scale, was measured. The occurrence of this intermediate species suggests that the photodissociation of phenol in water does not occur in a concerted way, but rather that the electron is first transferred to the solvent, generating PhOH+˙, and then the proton follows sequentially in less than a picosecond, generating PhO˙. Based on previous theoretical work,6 one could speculate that these observations agree with a mechanism of direct population of the πσ* state with transfer of the electron to the solvent, followed by O–H bond dissociation in the dissociative πσ* state. In contrast, upon excitation of the bright ππ* state at 267 nm the signals of solvated electrons and phenoxyl radicals begin to rise after about 2 ns.47 In this case, no signal corresponding to the intermediate PhOH+˙ was observed, which the authors attributed to the short lifetime of this species.47 However, the absence of the signal may also indicate that the intermediate is not formed and that the proton and the electron are transferred to the solvent in a concerted way. Additional experiments on deuterated phenol (phenol-d1)47 at 267 nm revealed only a small kinetic isotope effect of 1.0 ± 0.4, thus indicating that proton transfer is not the rate-limiting step of the reaction in solution. However, this conclusion stands only if proton transfer is dominated by tunneling effects. Since for excitation at 267 nm no intermediate phenol radical cations PhOH+˙ were observed, it is not clear whether the transfer of proton and electron to the solvent is concerted, as suggested by previous theoretical calculations,6–9 or sequential, as observed after illumination at 200 nm.
Further evidence for a decoupled rather than concerted transfer of proton and electron to the solvent was found in the phenol-(NH3)5 cluster.36 While the near-infrared signal corresponding to Rydberg-type transitions of the transferred electron rose within 3 ps after excitation at 281 nm, the IR signal of the N–H vibrations indicating completed transfer of the hydrogen atom had a lifetime of 20 ps. These results show that first the electron is transferred to the solvent molecules and the proton follows shortly afterwards.
Recent photoelectron spectroscopy35 applied to phenol in water, using excitation at 235.5 nm, which corresponds to an energy just above the conical intersection between the ππ* and πσ* states, indicated the formation of solvated electrons after 150 fs. They were attributed to a direct excitation to the πσ* state leading to O–H dissociation by concerted proton-coupled electron transfer. However, these experiments could not rule out the occurrence of a mechanism involving a sequential transfer of proton and electron.
Actually, theoretical calculations by some of us predicted that sequential instead of concerted proton-coupled electron transfer operates in the phenol derivative 5,6-dihydroxyindole.48 After excitation to the bright ππ* state, the molecule relaxes to the minimum of this state. Then, the solvent molecules reorganize, facilitating the transfer of an electron to the solvent, generating a CT state. The proton transfer from one O–H moiety of the chromophore to the solvent occurs sequentially after the formation of the solvated electron. Thus, the reaction coordinate that drives electron transfer from the chromophore to the solvent is not the elongation of the O–H bond but solvent reorganization.
Motivated by these findings, the aim of the present paper is to investigate whether the mechanism of photodissociation by solvent reorganization, facilitating the formation of a solvated electron, as predicted for 5,6-dihydroxyindole, is also operative in phenol. If the reorganization of solvent molecules can lower the energy of the CT state without elongation of the O–H bond, one would expect that for some solvent configurations the CT state has a lower excitation energy than the bright ππ* state already in the Franck–Condon region. Therefore, after excitation to the ππ* state, the CT state could be easily populated by a conical intersection without O–H elongation. In order to investigate the existence of such low-lying CT states in the Franck–Condon region we report here the density of states (DOS) and the absorption spectrum of solvated phenol. In addition, we have characterized the involved electronic states by quantitative wavefunction analysis. We clearly show that some particular solvent configurations induce an energetic lowering of the CT state, supporting a sequential proton-coupled electron transfer mechanism in the excited-state dynamics of phenol.
2. Computational details
In order to describe a chromophore in solution, the introduction of vibrational sampling to sample the configurational space of both the chromophore and solvent is indispensable.49 For this purpose, a classical molecular dynamics (MD) simulation was evolved employing the AMBER 16 program50 on graphics processing units (GPUs).51–53 Phenol was solvated by a truncated octahedral box extended to a distance of 15 Å from any solute atom using the leap module of AmberTools14. The box was filled with 1223 TIP3P54 water molecules while phenol was described by the general AMBER force field (GAFF).55 A steepest descent minimization and a conjugate gradient minimization have been carried out for 500 steps each. After minimization, the system was heated to 300 K at constant volume and temperature (NVT), using a Langevin thermostat56 with a collision frequency of 5 ps−1, for 200 ps with a timestep of 1 fs. Once the system was at 300 K, an MD simulation at constant pressure and temperature (NPT) was performed for 5 ns with a timestep of 2 fs. The Berendsen barostat57 with a pressure relaxation time of 5 ps was used to keep the pressure at a value of 1 bar. The nonbonded interactions were truncated at 10 Å and the particle mesh Ewald method58–60 was employed for the calculation of the Coulomb interactions using a grid spacing of 0.911 Å in each direction for the charge grid, in which the reciprocal sums are computed by a fourth-order interpolation, and a direct sum tolerance of 10−5. During the heating and the NPT MD simulations the bonds involving hydrogen atoms were constrained employing the SHAKE61,62 algorithm. In order to allow for a more efficient sampling of relevant conformations where a water molecule forms a hydrogen bond with the acidic hydrogen atom of phenol, the water molecule closest to the acidic hydrogen atom of phenol was restrained during the heating and the 5 ns NPT MD trajectories employing a harmonic potential at an equilibrium distance between the acidic H atom of phenol and the O atom of water of 1.58 Å with a force constant of 50 kcal mol−1 Å−2. Since an analysis of an unconstrained MD simulation shows that there is a water molecule hydrogen-bonded to phenol more than 80% of the time, the introduction of the constraint does not significantly adulterate the simulation. We consider that a hydrogen bond is formed when the separation between the oxygen atoms of phenol and water is smaller than 3.0 Å and the angle formed by these two oxygen atoms and the acidic hydrogen of phenol is larger than 135°. Note that in the unbiased simulation different water molecules form hydrogen bonds with phenol, while in the biased simulation the same water molecule interacts with phenol along the whole simulation time.In order to calculate the absorption spectrum and DOS, 101 snapshots from the last 2 ns of the MD simulation were used where phenol is solvated by clusters containing a different number of water molecules. Specifically, three different clusters with 1, 5 and 15 water molecules were built. For the smallest cluster, only the water molecule forming a hydrogen bond with the acidic proton of phenol was selected along the 101 chosen snapshots, while the rest of solvent molecules were removed. For the larger cluster sizes, the four and fourteen water molecules closest to the hydrogen-bonded water molecule were selected, respectively. In each of the clusters, the excitation energies of the 6 lowest-lying electronic excited singlet states were computed describing the whole system quantum mechanically (QM) by the algebraic diagrammatic construction scheme for the polarization propagator to 2nd order (ADC(2))63 combined with the aug-cc-pVDZ basis set,64–67 as implemented in Turbomole.68–70
The absorption spectra were obtained by convolution of the excitation energies of the 101 snapshots with Gaussian functions of width of 0.2 eV and height proportional to the oscillator strength. Since the energetic region of the ππ* band is of interest to this study, only transitions with energies below 5.2 eV have been included in the absorption spectra and DOS. For comparability, the height of the spectra has been scaled to one. The same procedure was used to obtain the DOS but using Gaussian functions of height equal to unity. For comparison, also the absorption spectrum of phenol in the gas phase was computed following the same recipe. To this aim, the same snapshots were used and all the water molecules were removed.
Furthermore, in order to investigate whether bulk solvent effects, which are not properly described by the above cluster models, affect the excitation energies of phenol, two sets of QM/classical calculations including bulk-solvation effects were performed: one where the solvent is treated implicitly and another with explicit water molecules. In the implicit solvation calculation, we use the one-water-molecule cluster model described at the ADC(2)/aug-cc-pVDZ level of theory together with the conductor-like screening model71 (COSMO) as classical model for aqueous solvation. In the second set of calculations, bulk-solvent effects were included by a electrostatic-embedding quantum mechanics/molecular mechanics72–75 (QM/MM) scheme, where explicit TIP3P water molecules located in the MM region polarize the one-water-molecule cluster, which is defined as the QM region. The absorption spectra and DOS for both sets of QM/classical calculations were generated by using the same 101 snapshots and Gaussian convolution of excitation energies described above.
The excited states composing any of the so-obtained absorption spectra and DOS were characterized by analyzing the one-electron transition density with the TheoDORE package,76–81 using the Löwdin population analysis.82,83
The accuracy of ADC(2) was also investigated by calculating the absorption spectrum and DOS of phenol in the gas phase as well as with the 5 water molecule cluster model using the coupled cluster of 2nd order (CC2) method84 with the Turbomole program package68–70 and the aug-cc-pVDZ basis set.64–67 The results are shown in Fig. S1 and S2 of the ESI.† As both the gas-phase spectrum as well as the spectrum computed for the 5 water molecule cluster with CC2 are blue-shifted by 0.02 eV with respect to the ADC(2) spectra, and the convoluted spectra agree very well, all the results discussed below refer to ADC(2).
3 Results and discussion
We start by discussing the ability of the different cluster models in reproducing environmental effects. Fig. 1a shows the absorption spectra computed with phenol solvated by a different number of water molecules, as well as the experimental spectrum35 in gas phase and in aqueous solution. In order to evaluate the solvatochromic effects, also the computed gas-phase spectrum is included. To ease the discussion, the absorption peaks of the calculated bands are collected in Table 1, together with the experimental values (see also Tables S1 and S2, ESI†).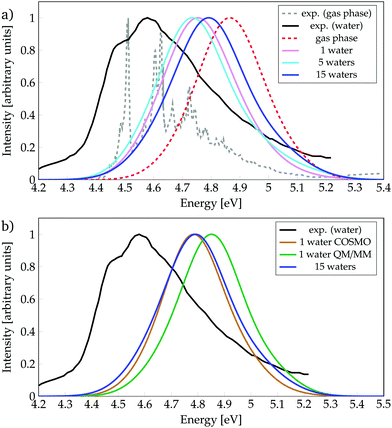 | ||
| Fig. 1 Absorption spectra calculated for phenol (a) solvated by a different number of water molecules, or (b) with different environment models, as indicated. Experimental data from ref. 35. | ||
| Environment | Cluster size | Excitation energy [eV] | |
|---|---|---|---|
| a Data from ref. 85. b Data from ref. 35. c Data from ref. 86. | |||
| Exp.a | Gas phase | 4.51, 4.63, 4.73 | |
| Exp.b | Gas phase | 4.51, 4.61, 4.63, 4.67, 4.73 | |
| Exp.b,c | Aqueous solution | 4.59, 4.49sh | |
| Calc. | Gas phase | 4.86 | |
| Calc. | 1 water | 4.75 | |
| Calc. | 5 waters | 4.74 | |
| Calc. | 15 waters | 4.79 | |
| Calc. | COSMO | 1 water | 4.78 |
| Calc. | QM/MM | 1 water | 4.85 |
The experimental spectrum in aqueous solution has a maximum at 4.59 eV35,86 while the one in the gas phase possesses few vibronic transitions35,85 around 4.6 eV (270 mm), indicating that the solvent barely affects the energy-range of the spectra. The calculated spectra show small shifts, depending on the model used, which are within the error of the method. Inclusion of just one water molecule leads to a red-shift of 0.11 eV compared to the calculated gas-phase spectrum, and a blue-shift of 0.16 eV compared to the experimental spectrum in aqueous solution. Thus, already the inclusion of a single water molecule reproduces reasonably well the experimental spectrum. Note, however, that the computed spectrum is not able to describe the shoulder seen experimentally at 4.49 eV, which is due to vibronic transitions that are not included in our calculations. An increase from one to five water molecules causes only a slight red-shift of 0.01 eV. Interestingly, further increasing the cluster size to 15 water molecules leads to a noticeable blue-shift of 0.05 eV, i.e., bringing the spectrum further from the experimental solvated one by 0.2 eV. This energy behaviour could be an indication that the energy of the bright ππ* state is not converged with respect to the number of water molecules treated explicitly. However, as the inclusion of more explicit water molecules at the quantum mechanical level of theory is intractable, we turn to hybrid QM/COSMO and QM/MM calculations in order to further simulate the effects of bulk solvation. The results obtained are collected in Fig. 1b.
In the QM/MM calculations, the QM region comprises phenol and the water molecule that is hydrogen-bonded to phenol – as we learnt from Fig. 1a that this water molecule induces an important red-shift in the spectrum and it is known23,87 that hydrogen bonding plays a relevant role in the excited-state dynamics of phenol. The QM/COSMO spectrum, peaking at 4.78 eV, agrees very well with the spectrum calculated with 15 water molecules, while the QM/MM spectrum with a maximum at 4.85 eV shows worse agreement with the experimental band. In order to understand the origin of these differences, it is useful to remember that the QM/COSMO scheme treats the electrostatic interactions between the QM and classical regions in a self-consistent manner, i.e., the chromophore and solvent are mutually polarized. In contrast, in the electrostatic-embedding QM/MM calculations the solvent is not polarized by the chromophore. Therefore, it is very likely that the erroneous blue-shift observed in the QM/MM spectrum is caused by the lack of polarizability in the electrostatic interactions.
In summary, from all the calculations, we observe that in terms of energetics the bulk solvent effects are better described by the QM/COSMO calculations than by the electrostatic-embedding QM/MM ones. Moreover, the agreement between the QM/COSMO spectrum and the spectrum calculated for 15 water molecules suggests that the energy of the ππ* state is already converged with this cluster size. Within this solvation model, there is a small bathochromic effect of 0.07 eV, which is reasonable for the employed level of theory, taking into account that experimentally there is basically no solvent effect on the absorption energy.
Accordingly, all further analyses of the spectra were done using the model of phenol microsolvated by a cluster of 15 water molecules. One reason why we do not employ the QM/COSMO model is that in order to investigate later whether solvated electrons can be formed at the Franck–Condon region or not, an explicit QM description of several water molecules able to solvate the electron is necessary.
In order to find the most suitable model for the description of solvent effects, we also attempted calculations using different cluster models up to 10 water molecules combined with a COSMO solvation model. The inspection of the σ* orbital involved in the CT state revealed that it is located at the surface of the water cluster, and the corresponding electron density is likely to extend beyond the cavity. As continuum models may fail88–90 when the electronic density goes outside, we refrained from using COSMO for the 15 water molecules cluster model.
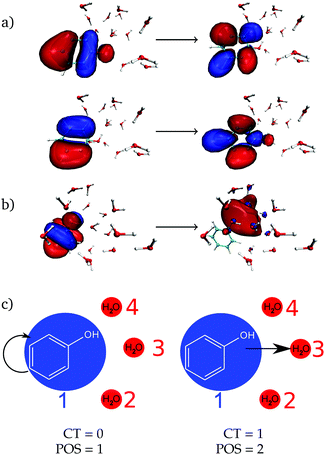
As a next step, the absorption spectrum and DOS of phenol solvated by 15 water molecules is decomposed into local and CT excitations. Local excitations in the energy range investigated here are ππ* transitions where both π orbitals are located in the phenol ring, see one example in Fig. 2a with the two pairs of natural transition orbitals contributing to it. Instead, CT excitations involve an electron transfer from a π orbital of phenol to a σ* orbital located in the solvent, as exemplified in Fig. 2b. In order to distinguish between the two different types of states, the one-electron transition density of each state composing the absorption band is analyzed by means of the TheoDORE wavefunction analysis package.76–81
For this analysis, the system is divided into fragments.91 Arbitrarily, we define phenol as one fragment and each water molecule as an additional fragment, i.e. we have 16 fragments. Two descriptors are used to classify the states. One is the CT number,78ΩCTAB
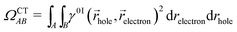 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) hole,
hole,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) electron) is the one-electron transition density matrix between the ground state and state I. The CT number gives the fraction of electron which is transferred from fragment A to fragment B. A pure CT transition corresponds to a CT number of 1, whereas a local excitation has a CT number of 0, as schematically illustrated in Fig. 2c. However, the CT number cannot unambiguously characterize different types of local excitations since any type of local excitation (located in phenol or in any water molecule) has a CT number close to zero. Thus, an additional descriptor is needed to distinguish between these two types of local states.
electron) is the one-electron transition density matrix between the ground state and state I. The CT number gives the fraction of electron which is transferred from fragment A to fragment B. A pure CT transition corresponds to a CT number of 1, whereas a local excitation has a CT number of 0, as schematically illustrated in Fig. 2c. However, the CT number cannot unambiguously characterize different types of local excitations since any type of local excitation (located in phenol or in any water molecule) has a CT number close to zero. Thus, an additional descriptor is needed to distinguish between these two types of local states.
The second descriptor, denominated POS value,77 provides the average position of the excitation in terms of the fragment number, i.e. the arithmetic mean of the position of the hole, POShole, and the position of the electron, POSelectron. The positions of the hole and of the electron can be calculated from the CT numbers and the norm of the exciton wavefunction Ωexc,81 which is the sum of the CT numbers over all fragments, as
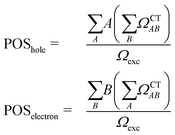 | (2) |
Then, the mean position of the excitation is
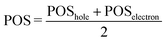 | (3) |
We label phenol (arbitrarily) as the fragment number 1 in our partition system while all the waters are numbered from 2 to 16, see Fig. 2c. Thus, a POS value close to 1 indicates that the excitation is located in phenol, i.e. both hole and electron are located within phenol orbitals. If, for example, for a given CT state the hole is located in phenol (fragment 1) and the electron is located in the water labeled as 3, then the POS value would be close to (1 + 3)/2 = 2.
Using the two descriptors, it is possible to define local ππ* states as those having small CT numbers – we arbitrarily fix the value as ≤0.5 – and a POS value around 1, say ≤1.2. The CT states are then those having a CT value >0.5, regardless of the POS value. Note that with this definition, contributions from CT among the waters themselves are not excluded. However, by comparing the CT numbers with those from an additional analysis where only two fragments, phenol and the whole collective of water molecules, were considered it is possible to discern the origin of the CT transitions (see below).
Following the definition of the 16 fragments, the spectrum and DOS could be decomposed in terms of local ππ* and CT states as shown in Fig. 3a and b, respectively. Panel a shows that the CT states are mainly dark, contributing only 5% to the spectrum. In addition, they are found at the blue end of the spectrum, mostly, at higher excitation energies than the maximum of the bright ππ* band. Therefore, population of CT states by direct excitation is unlikely. However, despite being dark, there is a significant number of CT states in the energy range of the absorption spectrum, as it can be best appreciated in the DOS (Fig. 3b): 36% are CT states. The number of CT states if only two fragments (i.e. phenol and all water molecules) are considered is 34%, indicating that the majority of CT states come from excitations from phenol to the water. Interestingly, a considerable number of these CT states exists at energies below the peak of the ππ* band. Indeed, the red tail observed in the DOS is virtually completely formed by CT states. These low-lying states can, in principle, be populated by internal conversion after excitation to the bright ππ* state. This is an important result for the photodetachment mechanism of phenol, as the existence of these CT states indicates that the elongation of the O–H bond of phenol is not required in order to have low-lying CT states. Indeed, this can be corroborated by the computation of the average O–H distance of the geometries corresponding to these CT states that are energetically below the absorption band maximum. The computed distance is 0.9739 ± 0.0004 Å, which is very similar to the average O–H distance of all the geometries of the MD ensemble of 0.9740 ± 0.0004 Å, confirming that geometries with low-lying CT states do not possess elongated O–H bonds.
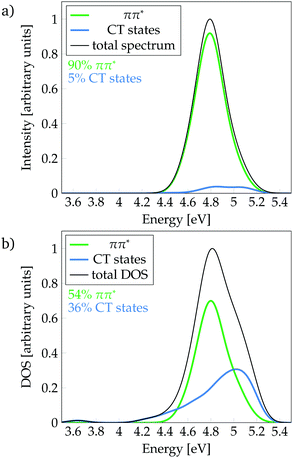 | ||
| Fig. 3 Decomposition of (a) absorption spectrum and (b) density of states (DOS) (b) into ππ* and charge-transfer (CT) states. | ||
The present results suggest that the formation of solvated electrons by electron transfer from phenol to solvent without being accompanied by proton transfer in a concerted mechanism seems plausible. Accordingly, the sequential mechanism observed for dihydroxyindole,48 where proton transfer occurs only once a solvated electron is formed, is also possible for solvated phenol.
Since the O–H elongation of phenol is not needed to lower the energy of CT states, it is very likely that such a lowering is caused by the arrangement of solvent molecules around the solvated electron. In order to test this hypothesis, we have attempted to optimize the crossing points between the ππ* and CT states at the SA3-CASSCF(6,7) level92,93 using the aug-cc-pvdz basis set. Geometry optimizations for the cluster of 15 water molecules are quite computationally demanding. Thus, the smaller cluster of 3 water molecules was employed. Despite the small number of water molecules present in the model, we were not able to identify any of the crossing points due to the bad convergence of the calculations as a consequence of the large number of low-frequency intermolecular normal modes.
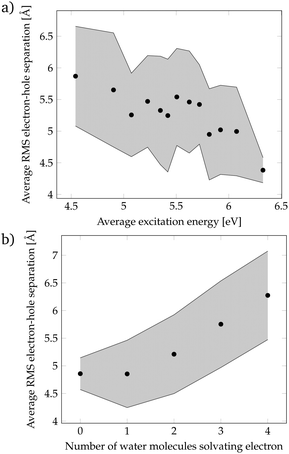
Since the localization of crossing points was unsuccessful, we came back to the more realistic cluster model composed by phenol and 15 water molecules, and we performed a geometric analysis to identify the features of the solvent orientation that lead to low-energy CT states. We have calculated the root-mean-square (RMS) electron–hole separation of all CT states of the DOS, and plotted it versus the excitation energy of the states, see Fig. 4a. The data points were sorted according to the excitation energy and for each consecutive 20 data points the average excitation energy and RMS electron–hole separation were calculated. The trend clearly shows that larger electron–hole separations are associated with lower excitation energies. In particular, excitation energies below the energy at the maximum of the absorption spectrum (4.8 eV) possess an electron–hole separation of 5.5–6.0 Å. This is a curious result since in order to form an exciton with a large electron–hole separation the attractive Coulomb electron–hole interactions have to be broken. Therefore, there should be another factor that compensates the Coulomb penalty to lower the excitation energy of the CT states. This factor could be the solvation energy of the solvated electron since a large electron–hole separation indicates that the electron is well separated from phenol and, therefore, a large number of water molecules can surround and stabilize the electron. To investigate this possibility, the number of water molecules solvating the electron was examined. We consider that a water molecule is solvating the electron when it contains more than 10% of the excited electron population. Fig. 4b shows that a larger electron–hole separation allows for more water molecules surrounding the electron corroborating, thus, our hypothesis. Specifically, for an electron–hole separation of 5.5–6.0 Å, which is the separation needed to have CT excitation energies lower than the energy at the maximum of the absorption band, 3 to 4 water molecules solvate the electron. This amount of water molecules provides a favorable solvation energy, which is able to compensate the unfavorable Coulomb penalty of having large exciton sizes.
Finally, it is worth to compare the experimental time scale of formation of solvated electrons after excitation to the ππ* state with our stationary computations. Solvated electrons and phenoxyl radicals were experimentally detected after 2 ns.47 Therefore, contrary to what happens upon excitation to the πσ* state, the photodetachment from phenol to water after excitation to the bright ππ* state is a slow process. As seen in Fig. 3b, a considerable number of CT states lie at the low-energy region of the DOS band. At first glance, one could conclude that the population of these low-energy CT states from the initially excited ππ* state might occur in an ultrafast manner (assuming a relatively strong coupling between both electronic states). However, the existence of low-energy CT states does not imply that for a particular phenol geometry and solvent arrangement the CT state is lower in energy than the bright ππ* state, which would be the ideal energetic scenario leading to ultrafast internal conversion from the ππ* state to the CT state, accompanied by formation of solvated electrons. Fig. 5 displays the probability distribution of the energy difference between the CT and ππ* states for the selected classical MD ensemble of geometries. As can be seen, for the vast majority of geometries the energy of the ππ* state is smaller than that of the CT state. In fact, the position of the maximum at 0.6 eV indicates that the two states are often energetically well separated. This means that after excitation to the ππ* state the CT state is likely not energetically accessible by internal conversion in an ultrafast manner. Population of the CT state will only happen after a strong red-shift of this state, which is induced by the diffusion of water molecules away from phenol such that the electron–hole separation increases, as shown in Fig. 4. The diffusion of solvent molecules required to induce solvated electron formation is a slow process – a fact, which agrees with the nanosecond time scale experimentally determined by Oliver et al.47 This speculative conclusion could be corroborated by running nonadiabatic dynamics simulations. However, the relatively large size of the system and the slowness of the process precludes performing such simulations with our current methods.
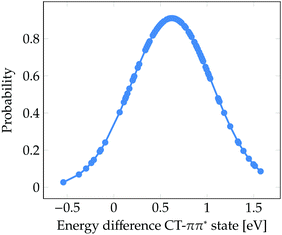 | ||
| Fig. 5 Probability distribution of the energy difference between the CT and ππ* states for the 101 snapshots from the classical MD simulation for which electronic excited states were computed. | ||
4 Conclusions
We show that the sequential proton-coupled electron transfer mechanism observed in dihydroxyindole48 is also possible in phenol. This conclusion is drawn from the characterization of the absorption spectrum and DOS of phenol solvated with 15 water molecules. Our analysis shows that the CT states, which correspond to the formation of the precursor of a solvated electron by electron transfer from phenol to the solvent without accompanying proton transfer, are considerably abundant at energies below the energy at the maximum of the absorbing ππ* band. Despite mostly dark, these low-lying CT states can be populated by internal conversion after excitation to the bright ππ* state. As the O–H distances of the geometries with low-lying CT states are not elongated compared to the ensemble, the main factor contributing to the lowering of the energy of CT states in phenol is not elongation of the O–H bond. Instead, the lower excitation energy of the CT state is associated with a large electron–hole separation of about 5.5–6.0 Å. While the larger exciton size results in a loss of attractive Coulomb interactions between hole and electron, it allows for a larger number of water molecules to surround and stabilize the electron, thereby reducing the energy of the CT state. We thus conclude that a sequential proton-coupled electron transfer mechanism is operative in phenol, complementing the well established photodissociation mechanism involving a stabilization of CT states by O–H elongation. Our results demonstrate that the reorganization of solvent molecules may drive photodissociation of phenol and suggest that the investigation of this mechanism in other phenol derivatives is worthwhile.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The University of Vienna is thanked for generous support. Part of the calculations were carried out at the Vienna Scientific Cluster.Notes and references
- B. A. Barry, Photochem. Photobiol., 1993, 57, 179–188 CrossRef CAS.
- G. Prota, Melanins and Melanogenesis, Academic Press, San Diego, CA, 1992 Search PubMed.
- P. Meredith and T. Sarna, Pigm. Cell Res., 2006, 19, 572–594 CrossRef CAS.
- M. d'Ischia, A. Napolitano, A. Pezzella, P. Meredith and T. Sarna, Angew. Chem., Int. Ed., 2009, 48, 3914–3921 CrossRef PubMed.
- G. Granucci, J. T. Hynes, P. Millié and T.-H. Tran-Thi, J. Am. Chem. Soc., 2000, 122, 12243–12253 CrossRef CAS.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275–9283 CrossRef CAS.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- Z. Lan, W. Domcke, V. Vallet, A. L. Sobolewski and S. Mahapatra, J. Chem. Phys., 2005, 122, 224315 CrossRef PubMed.
- O. P. J. Vieuxmaire, Z. Lan, A. L. Sobolewski and W. Domcke, J. Chem. Phys., 2008, 129, 224307 CrossRef.
- W. Domcke and A. L. Sobolewski, Science, 2003, 302, 1693–1694 CrossRef CAS.
- K. Daigoku, S.-I. Ishiuchi, M. Sakai, M. Fujii and K. Hashimoto, J. Chem. Phys., 2003, 119, 5149–5158 CrossRef CAS.
- R. N. Dixon, T. A. A. Oliver and M. N. R. Ashfold, J. Chem. Phys., 2011, 134, 194303 CrossRef PubMed.
- X. Xu, K. R. Yang and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 3612–3625 CrossRef CAS PubMed.
- S. G. Ramesh and W. Domcke, Faraday Discuss., 2013, 163, 73–94 RSC.
- X. Xu, J. Zheng, K. R. Yang and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 16378–16386 CrossRef CAS PubMed.
- K. R. Yang, X. Xu, J. Zheng and D. G. Truhlar, Chem. Sci., 2014, 5, 4661–4680 RSC.
- C. Xie, J. Ma, X. Zhu, D. R. Yarkony, D. Xie and H. Guo, J. Am. Chem. Soc., 2016, 138, 7828–7831 CrossRef CAS.
- W. Xie and W. Domcke, J. Chem. Phys., 2017, 147, 184114 CrossRef.
- D. Creed, Photochem. Photobiol., 1984, 39, 563–575 CrossRef CAS.
- W. R. Laws, J. B. A. Ross, H. R. Wyssbrod, J. M. Beechem, L. Brand and J. C. Sutherland, Biochemistry, 1986, 25, 599–607 CrossRef CAS.
- R. J. Lipert, G. Bermudez and S. D. Colson, J. Phys. Chem., 1988, 92, 3801–3805 CrossRef CAS.
- R. J. Lipert and S. D. Colson, J. Phys. Chem., 1989, 93, 135–139 CrossRef CAS.
- R. J. Lipert and S. D. Colson, J. Phys. Chem., 1990, 94, 2358–2361 CrossRef CAS.
- C. A. Hasselbacher, E. Waxman, L. T. Galati, P. B. Contino, J. B. A. Ross and W. R. Laws, J. Phys. Chem., 1991, 95, 2995–3005 CrossRef CAS.
- Z. Rappaport, The Chemistry of Phenols, Wiley, Chichester UK, 2003 Search PubMed.
- C.-M. Tseng, Y. T. Lee and C.-K. Ni, J. Chem. Phys., 2004, 121, 2459–2461 CrossRef CAS PubMed.
- M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640 CrossRef CAS PubMed.
- M. G. D. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 133318 CrossRef PubMed.
- C.-M. Tseng, Y. T. Lee, M.-F. Lin, C.-K. Ni, S.-Y. Liu, Y.-P. Lee, Z. F. Xu and M. C. Lin, J. Phys. Chem. A, 2007, 111, 9463–9470 CrossRef CAS PubMed.
- A. Iqbal, L.-J. Pegg and V. G. Stavros, J. Phys. Chem. A, 2008, 112, 9531–9534 CrossRef CAS PubMed.
- M. L. Hause, Y. Heidi Yoon, A. S. Case and F. F. Crim, J. Chem. Phys., 2008, 128, 104307 CrossRef PubMed.
- M. N. R. Ashfold, A. L. Devine, R. N. Dixon, G. A. King, M. G. D. Nix and T. A. A. Oliver, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12701–12706 CrossRef CAS PubMed.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352 CrossRef CAS.
- G. A. King, T. A. A. Oliver, M. G. D. Nix and M. N. R. Ashfold, J. Phys. Chem. A, 2009, 113, 7984–7993 CrossRef CAS PubMed.
- J. W. Riley, B. Wang, J. L. Woodhouse, M. Assmann, G. A. Worth and H. H. Fielding, J. Phys. Chem. Lett., 2018, 9, 678–682 CrossRef CAS PubMed.
- M. Miyazaki, R. Ohara, C. Dedonder, C. Jouvet and M. Fujii, Chem. – Eur. J., 2018, 24, 881–890 CrossRef CAS PubMed.
- G. A. Pino, A. N. Oldani, E. Marceca, M. Fujii, S.-I. Ishiuchi, M. Miyazaki, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2010, 133, 124313 CrossRef CAS PubMed.
- R. A. Livingstone, J. O. F. Thompson, M. Iljina, R. J. Donaldson, B. J. Sussman, M. J. Paterson and D. Townsend, J. Chem. Phys., 2012, 137, 184304 CrossRef PubMed.
- V. Poterya, L. Šištík, P. Slavíček and M. Fárník, Phys. Chem. Chem. Phys., 2012, 14, 8936–8944 RSC.
- G. Pino, G. Grégoire, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard and D. Solgadi, Phys. Chem. Chem. Phys., 2000, 2, 893–900 RSC.
- G. Grégoire, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard, A. Peremans and D. Solgadi, J. Phys. Chem. A, 2000, 104, 9087–9090 CrossRef.
- S.-I. Ishiuchi, M. Saeki, M. Sakai and M. Fujii, Chem. Phys. Lett., 2000, 322, 27–32 CrossRef CAS.
- A. Carrera, I. B. Nielsen, P. Çarçabal, C. Dedonder, M. Broquier, C. Jouvet, W. Domcke and A. L. Sobolewski, J. Chem. Phys., 2009, 130, 024302 CrossRef CAS PubMed.
- J. D. Rodríguez, M. G. González, L. Rubio-Lago and L. Bañares, Phys. Chem. Chem. Phys., 2014, 16, 3757–3762 RSC.
- M. Miyazaki, R. Ohara, K. Daigoku, K. Hashimoto, J. R. Woodward, C. Dedonder, C. Jouvet and M. Fujii, Angew. Chem., Int. Ed., 2015, 54, 15089–15093 CrossRef CAS PubMed.
- Y. Zhang, T. A. A. Oliver, M. N. R. Ashfold and S. E. Bradforth, Faraday Discuss., 2012, 157, 141–163 RSC.
- T. A. A. Oliver, Y. Zhang, A. Roy, M. N. R. Ashfold and S. E. Bradforth, J. Phys. Chem. Lett., 2015, 6, 4159–4164 CrossRef CAS PubMed.
- J. J. Nogueira, A. Corani, A. E. Nahhas, A. Pezzella, M. d'Ischia, L. González and V. Sundström, J. Phys. Chem. Lett., 2017, 8, 1004–1008 CrossRef CAS PubMed.
- J. J. Nogueira and L. González, Annu. Rev. Phys. Chem., 2018, 69, 473–497 CrossRef CAS PubMed.
- D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER 2016, University of California, San Francisco, 2016 Search PubMed.
- R. Salomon-Ferrer, A. W. Götz, D. Poole, S. L. Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- A. W. Götz, M. J. Williamson, D. Xu, D. Poole, S. L. Grand and R. C. Walker, J. Chem. Theory Comput., 2012, 8, 1542–1555 CrossRef PubMed.
- S. L. Grand, A. W. Götz and R. C. Walker, Comput. Phys. Commun., 2013, 184, 374–380 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628–3631 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera and M. L. Berkowitz, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- M. F. Crowley, T. A. Darden, T. E. Cheatham III and D. W. Deerfield II, J. Supercomput., 1997, 11, 255–278 CrossRef.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, WIREs Comput. Mol. Sci., 2014, 4, 91–100 CrossRef CAS.
- TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- A. Klamt, WIREs Comput. Mol. Sci., 2011, 1, 699–709 CrossRef CAS.
- R. A. Friesner and V. Guallar, Annu. Rev. Phys. Chem., 2005, 56, 389–427 CrossRef CAS PubMed.
- H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185–199 Search PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- E. Brunk and U. Rothlisberger, Chem. Rev., 2015, 115, 6217–6263 CrossRef CAS PubMed.
- F. Plasser, TheoDORE 1.5.1: a package for theoretical density, orbital relaxation, and exciton analysis; available from http://theodore-qc.sourceforge.net.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- F. Plasser, S. A. Bäppler, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024107 CrossRef PubMed.
- S. A. Bäppler, F. Plasser, M. Wormit and A. Dreuw, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 052521 CrossRef.
- S. A. Mewes, J.-M. Mewes, A. Dreuw and F. Plasser, Phys. Chem. Chem. Phys., 2016, 18, 2548–2563 RSC.
- P.-O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- P.-O. Löwdin, Adv. Quantum Chem., 1970, 5, 185–199 CrossRef.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- S. Karmakar, D. P. Mukhopadhyay and T. Chakraborty, J. Chem. Phys., 2015, 142, 184303 CrossRef PubMed.
- G. Nemethy and A. Ray, J. Phys. Chem., 1973, 77, 64–68 CrossRef CAS.
- R. Hermann, G. R. Mahalaxmi, T. Jochum, S. Naumov and O. Brede, J. Phys. Chem. A, 2002, 106, 2379–2389 CrossRef CAS.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 877–887 CrossRef CAS PubMed.
- S. Mai, F. Plasser, J. Dorn, M. Fumanal, C. Daniel and L. González, Coord. Chem. Rev., 2018, 361, 74–97 CrossRef CAS.
- P. E. M. Siegbahn, J. Chem. Phys., 1979, 70, 5391–5397 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06656f |
| ‡ Current address: Research School of Biology, Australian National University, Acton, ACT 2601, Australia. |
| This journal is © the Owner Societies 2019 |