Ab initio computation for solid-state 31P NMR of inorganic phosphates: revisiting X-ray structures†
Kartik
Pilar
 a,
Zeyu
Deng
a,
Zeyu
Deng
 b,
Molleigh B.
Preefer
b,
Molleigh B.
Preefer
 ac,
Joya A.
Cooley
ac,
Joya A.
Cooley
 a,
Raphaële
Clément
a,
Raphaële
Clément
 ad,
Ram
Seshadri
ad,
Ram
Seshadri
 acd and
Anthony K.
Cheetham
acd and
Anthony K.
Cheetham
 *ae
*ae
aMaterials Research Laboratory, University of California Santa Barbara, California 93106, USA
bDepartment of Materials Science and Metallurgy, University of Cambridge, 27 Charles Babbage Rd, CB3 0FS Cambridge, UK
cDepartment of Chemistry and Biochemistry, University of California Santa Barbara, California 93106, USA
dMaterials Department, University of California Santa Barbara, California 93106, USA
eDepartment of Materials Science and Engineering, National University of Singapore, Singapore 117575, Singapore. E-mail: akc30@cam.ac.uk
First published on 3rd May 2019
Abstract
The complete 31P NMR chemical shift tensors for 22 inorganic phosphates obtained from ab initio computation are found to correspond closely to experimentally obtained parameters. Further improvement was found when structures determined by diffraction were geometry optimized. Besides aiding in spectral assignment, the cases where correspondence is significantly improved upon geometry optimization point to the crystal structures requiring correction.
1 Introduction
Magnetic resonance spectroscopy is widely employed for probing the structure of materials. The strong dependence of the NMR chemical shift on the surrounding chemical environment provides a sensitive probe of local structure around atoms. However, a certain degree of difficulty arises in the interpretation of solid-state NMR spectra when there is more than one crystallographic site for the element of interest and those sites have the same multiplicity. In such cases the assignment of peaks to particular sites can be challenging.Several methods have been used for determining solid-state NMR peak assignments. Before the advent of high performance computing, Smith et al. reported a linear correlation between easily calculated oxygen bond-strength sums and 29Si isotropic chemical shifts in silicates.1 This method was later extended by Cheetham et al. to the 31P chemical shifts of 22 different inorganic phosphates: a recreation of the correlation they found is presented in Fig. 1(a).2
With growing access to high performance computing, more precise computational methods have become common for the assignment of solid-state NMR shifts. For example, correlation between chemical shifts and the computed Bader charges on atoms are sometimes found to be useful.3,4 In the context of this work, we have used standard computational routines5 to compute Bader charges on 31P atoms, and found that almost no correlation [data presented in Fig. 1(b)] is observed for the 31P chemical shifts on the set of phosphates investigated by Cheetham et al.2
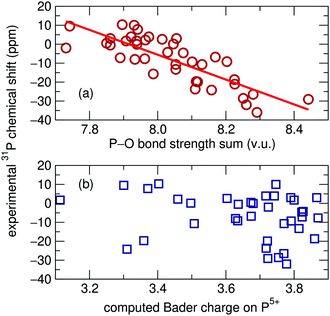 | ||
| Fig. 1 (a) Oxygen bond strength sums plotted against experimental isotropic 31P solid-state NMR chemical shifts recreated using data originally reported by Cheetham et al.2R2 = 0.666. (b) No relationship was found between chemical shift and Bader charge on the same set of phosphates. | ||
Cluster models employing gauge-including atomic orbitals have been used to predict chemical shifts.6,7 However, this type of cluster approximation can lead to issues in relation to cluster termination,8 as the cutoff at which interatomic interactions on the probed nucleus can be considered negligible is non-trivial.
In 2001, Mauri and Pickard developed the gauge-including projector augmented wave (GIPAW) formalism using periodic boundary conditions, thereby averting the issue of cluster termination.9,10 Their method included a linear transformation using projectors to reconstruct the all-electron density at the atomic core from the prescribed pseudopotential. The response of the electron density to an imposed magnetic field can be subsequently calculated. The core contribution to this magnetic shielding is independent from the surrounding chemical environment,11 so the core shielding contribution need only be calculated a single time, thereby saving significant computational resources over the all-electron approach.12 The GIPAW approach was first used for NMR spectral assignments by Profeta and coworkers in silicates13 and has since been applied to a wide range of organic and inorganic compounds, including sodium perovskites,14 organic solids,15,16 aluminum oxides,17 and phosphates.18–26
2 Computational methods
The present work utilizes the GIPAW methodology as a more precise method of computing 31P NMR chemical shift assignments for the set of inorganic phosphates previously reported by Cheetham et al.,2 with the aim of more precisely predicting NMR chemical shifts for the 22 phosphate phases, only two of which have been previously studied in this manner.20 All experimental data presented here has been taken from this previous work by Cheetham and coworkers.Three separate sets of calculations were completed using the GIPAW formalism to compute chemical shift tensors. The Vienna Ab initio Simulation Package (VASP) software was used to perform all calculations.27,28 The PBEsol generalized gradient approximation (GGA) functional was used to model electron correlation effects29 although calculations using the PBE functional (data presented in the ESI†) yield similar results. Previous GIPAW studies of NMR parameters have almost exclusively made use of the PBE functional; however, here we demonstrate minor improvement while using PBEsol. Dispersion forces were not taken into account. Automatically generated γ-centered k-point grids of varying sizes were used to sample the Brillouin zone based upon unit cell dimensions (ESI†). The first set of GIPAW computations was carried out on structures obtained directly from the Inorganic Crystal Structure Database (ICSD),30–51 using a plane-wave basis set cut-off energy of 800 eV. A second and third set of chemical shift calculations were also completed on DFT geometry optimized structures: one set in which atomic positions were allowed to relax but lattice parameters were kept rigid at the X-ray determined values and the other on structures which were fully relaxed. The plane-wave basis set cut-off energy was set to 500 eV for relaxations, although 800 eV was still used for subsequent chemical shift computations. DFT relaxations minimize structural energy and can lead to more precise atomic positions than can be obtained from X-ray diffraction, especially when referencing older crystallographic reports or when light elements are present in the compound,52 which is the case for most of the compounds being investigated in this work.
3 Results and discussion
Chemical shift tensors are second rank 3 × 3 matrices, which can be diagonalized and described in Herzfeld–Berger notation by three parameters: isotropic chemical shift, δiso, span, Ω, and skew, κ, defined as: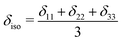 | (1) |
| Ω = δ11 − δ33 | (2) |
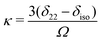 | (3) |
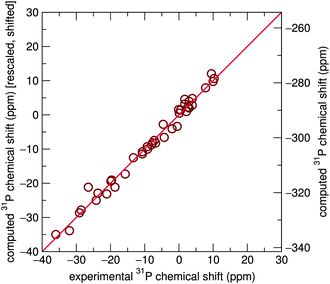
The scaling factors and reference shifts found using the PBE functional (see ESI†) are reasonable when compared to previously reported 31P GIPAW results for a set of aluminophosphates.26 However, as the scaling factor and reference shift seems to be partially dependent upon the GGA functional used, values obtained using the PBEsol functional differ from these previously reported results.
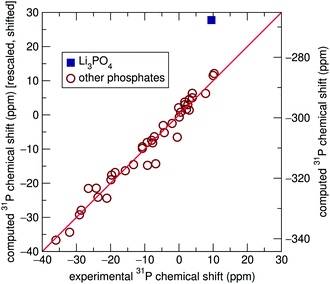
Significant improvement was observed when chemical shift tensors were computed for relaxed structures with rigid unit cell parameters taken from experiment, with an R2 value of 0.984, as shown in Fig. 3. This improved marginally to 0.987 when the lattice parameters were allowed to relax. It is obvious that although geometric relaxations alter the crystallographic structure of each compound only minimally, the computation of isotropic chemical shifts is highly sensitive to local environments surrounding the 31P sites, demonstrated most clearly by Li3PO4. By extension, this also demonstrates the sensitive nature of NMR to local environments, usually to a greater extent than X-ray diffraction experiments. This is likely to be particularly important in the case of hydrogen and lithium-containing systems, where the X-ray determinations of the light atoms will tend to be poor compared with the computed values. This is supported by previous literature which describes the importance of geometry optimization prior to chemical shift calculations.53–56
For complete relaxations, where unit cell parameters were free to optimize, most systems displayed parameters closely matching literature values.2 However, Ca(H2PO4)2 saw significant lattice parameter distortions upon relaxation. Table 1 includes lattice parameters from ICSD and fully relaxed structures for this compound, along with α-CaZn2(PO4)2 for reference. Fig. 4 shows the crystal structure of Ca(H2PO4)2 as reported by Dickens et al. and completely relaxed.32
| Compound | a/Å | b/Å | c/Å | α/° | β/° | γ/° |
|---|---|---|---|---|---|---|
| Ca(H2PO4)2 | 5.550 | 7.558 | 8.223 | 68.154 | 70.522 | 86.320 |
| 5.488 | 8.037 | 8.410 | 70.882 | 66.212 | 78.39 | |
| α-CaZn2(PO4)2 | 4.960 | 8.418 | 8.940 | 113.75 | 102.45 | 94.20 |
| 4.967 | 8.412 | 8.937 | 113.688 | 102.340 | 94.254 |
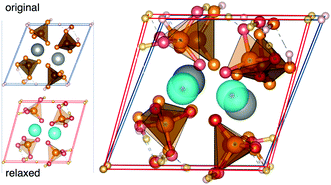 | ||
| Fig. 4 The crystal structure of Ca(H2PO4)2 as reported in ICSD32 and fully relaxed. | ||
To further support our results, we carried out powder XRD measurements on Ca(H2PO4)2, which was obtained by heating Ca(H2PO4)2·H2O (99% Strem Chemicals) in a vacuum oven at 200 °C for 3 days. Subsequent Rietveld refinements further confirmed the previously published lattice parameters. Based upon these results, we have given priority to the XRD determined lattice parameters and focus our attention on DFT relaxations with non-variant lattice parameters. We relaxed the Ca(H2PO4)2 structure again while taking into account dispersion interactions, however significant lattice parameter deviations were still observed. Previous work on aluminophosphates found that the inclusion of dispersion effects did not necessarily lead to a significantly stronger correlation between experimental and computed 31P chemical shifts, although in some cases it led to optimized geometries which more closely aligned with diffraction determined structures,26 which is not the case here.
Interestingly GIPAW chemical shift calculations on fully relaxed structures, including Ca(H2PO4)2, where the agreement between experiment and calculated lattice parameters is poor (Table 1), nevertheless exhibit strong correlations with experimentally determined NMR chemical shifts, more so than the originally reported structures (ESI†). This implies that computed nearest-neighbor ordering information can still be reliable even if the fit to the cell parameters is relatively poor, and it is these interactions which most strongly determine chemical shifts.
NMR line-widths of solids tend to be rather broad due to a combination of interactions, including dipole–dipole, chemical shift anisotropy (CSA), and quadrupolar interactions. However, these interactions, being orientationally dependent, can be at least partially averaged out through magic angle spinning (MAS), which narrows observed line-widths and enhances resolution, while also creating spinning sidebands in the observed spectrum. In solid-state NMR experiments, higher resolution spectra require fast MAS speeds which can eliminate visible spinning sidebands and isolate the NMR peak located at the isotropic chemical shift for a particular crystallographic site. This however leads to an inherent loss of information as the spinning sidebands contain valuable information on the CSA. It should be noted that high resolution solid-state NMR spectra can only be achieved with spin 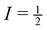 nuclei, such as 31P, or if Cq is small.
nuclei, such as 31P, or if Cq is small.
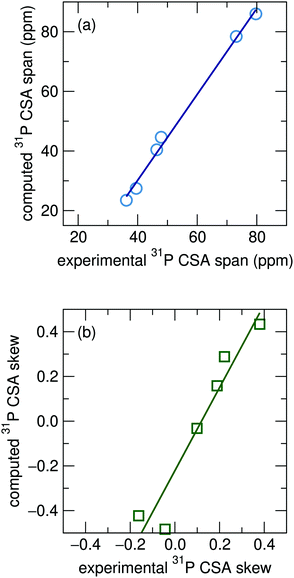
The experimentally determined CSA tensors for four of the 22 phosphate compounds, Mg3(PO4)2, α-CaZn2(PO4)2, α-Zn3(PO4)2, and β-Zn3(PO4)2, containing a total of six distinct phosphorous sites, have been previously reported through the analysis of sideband patterns.57 We compare these to the GIPAW computed CSA parameters of the relaxed structures with rigid cell parameters. Computations for the span and skew, shown in Fig. 5(a) and (b), show good agreement with experimentally determined values. This has the potential to be useful for spectral assignment for compounds which contain multiple crystallographic 31P sites with similar isotropic shifts when computed isotropic shifts for the sites fall within the bounds of uncertainty, as has previously been done for some aluminophosphate framework materials.58
4 Conclusions
As NMR has become widely used in the study of inorganic solids, the challenge of making spectral assignments becomes a non-trivial task. The GIPAW method allows for the calculation of the full second-rank chemical shift tensor for periodic systems. In all comparisons of GIPAW chemical shifts with experimental data (Fig. 2, 3 and 5), it can be seen that computed and experimentally derived CSA parameters, while displaying a linear relationship, require rescaling and shifting. This is in keeping with prior reports for isotropic chemical shifts;59–61 and it is clear that this phenomena extends to the CSA span and skew parameters as well. Importantly, this does not detract from the utility of the GIPAW method for NMR spectral assignment. The complete CSA tensor contains valuable and often underutilized information which can be used in NMR spectral analysis and in the developing field of NMR crystallography.While DFT structure optimizations can lead to errors in lattice parameter predictions, highly localized environments are well predicted via structural relaxation, as demonstrated by the improvement of the isotropic chemical shift predictions in the relaxed structures. This is especially surprising as DFT relaxations are done while neglecting thermal effects, effectively at 0 K. We have shown that GIPAW computations show clear improvement in the 31P isotropic chemical shifts calculated from relaxed structures rather than from XRD-determined structures, establishing that the calculated fractional coordinates of these older structures containing oxygen and other light atoms are more reliable than those reported experimentally. This effect could stem from the short nature of the P–O bond lengths inherent in phosphate systems, making the 31P chemical shifts less sensitive to thermal effects. On the other hand, the relaxation of the unit cell parameters, which are less accurate in DFT calculations, has only a minor effect on the calculated NMR shifts, at least for the phosphate systems studied here.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Ras al Khaimah Centre for Advanced Materials for supporting this research. Partial support from the National Science Foundation (NSF) Materials Research Science and Engineering Centers (MRSEC) program through DMR 1720256 (IRG-1) is acknowledged. This work made use of the computing infrastructure of the UC Santa Barbara Center for Scientific Computing, supported by NSF DMR 1720256 and NSF CNS 1725797. K. P. thanks Samuel Teicher for helpful discussions.References
- K. A. Smith, R. J. Kirkpatrick, E. Oldfield and D. M. Henderson, Am. Mineral., 1983, 68, 1206–1215 CAS.
- A. K. Cheetham, N. J. Clayden, C. M. Dobson and R. J. B. Jakeman, Chem. Commun., 1986, 195 RSC.
- A. R. Ferreira, E. Küçükbenli, A. A. Leitão and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235119 CrossRef.
- A. Knappschneider, C. Litterscheid, N. C. George, J. Brgoch, N. Wagner, J. Beck, J. A. Kurzman, R. Seshadri and B. Albert, Angew. Chem., Int. Ed., 2014, 53, 1684–1688 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, J. Chem. Phys., 2014, 141, 164121 CrossRef PubMed.
- S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, J. Chem. Theory Comput., 2015, 11, 5229–5241 CrossRef CAS PubMed.
- J. Weber and J. Schmedt auf der Günne, Phys. Chem. Chem. Phys., 2010, 12, 583–603 RSC.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–11 CrossRef.
- T. Gregor, F. Mauri and R. Car, J. Chem. Phys., 1999, 111, 1815–1822 CrossRef CAS.
- T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20 CrossRef CAS PubMed.
- M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548 CrossRef CAS PubMed.
- S. E. Ashbrook, L. Le Pollès, R. Gautier, C. J. Pickard and R. I. Walton, Phys. Chem. Chem. Phys., 2006, 8, 3423–3431 RSC.
- J. R. Yates, C. J. Pickard, M. C. Payne, R. Dupree, M. Profeta and F. Mauri, J. Phys. Chem. A, 2004, 108, 6032–6037 CrossRef CAS.
- L. Shao, J. R. Yates and J. J. Titman, J. Phys. Chem. A, 2007, 111, 13126–13132 CrossRef CAS PubMed.
- M. Choi, K. Matsunaga, F. Oba and I. Tanaka, J. Phys. Chem. C, 2009, 113, 3869–3873 CrossRef CAS.
- F. Vasconcelos, S. Cristol, J. F. Paul, L. Montagne, F. Mauri and L. Delevoye, Magn. Reson. Chem., 2010, 48, S142–S150 CrossRef CAS PubMed.
- F. Pourpoint, C. Gervais, L. Bonhomme-Coury, T. Azaïs, C. Coelho, F. Mauri, B. Alonso, F. Babonneau and C. Bonhomme, Appl. Magn. Reson., 2007, 32, 435–457 CrossRef CAS.
- F. Pourpoint, C. Gervais, L. Bonhomme-Coury, F. Mauri, B. Alonso and C. Bonhomme, C. R. Chim., 2008, 11, 398–406 CrossRef CAS.
- G. Girard, F. Vasconcelos, L. Montagne and L. Delevoye, Solid State Nucl. Magn. Reson., 2017, 84, 210–215 CrossRef CAS PubMed.
- C. Bonhomme, C. Gervais, C. Coelho, F. Pourpoint, T. Azaïs, L. Bonhomme-Coury, F. Babonneau, G. Jacob, M. Ferrari, D. Canet, J. R. Yates, C. J. Pickard, S. A. Joyce, F. Mauri and D. Massiot, Magn. Reson. Chem., 2010, 48, S86–S102 CrossRef CAS PubMed.
- D. M. Dawson and S. E. Ashbrook, J. Phys. Chem. C, 2014, 118, 23285–23296 CrossRef CAS.
- H. Chappell, M. Duer, N. Groom, C. Pickard and P. Bristowe, Phys. Chem. Chem. Phys., 2008, 10, 600–606 RSC.
- C. Gervais, C. Coelho, T. Azaïs, J. Maquet, G. Laurent, F. Pourpoint, C. Bonhomme, P. Florian, B. Alonso, G. Guerrero, P. H. Mutin and F. Mauri, J. Magn. Reson., 2007, 187, 131–140 CrossRef CAS PubMed.
- S. Sneddon, D. M. Dawson, C. J. Pickard and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2014, 16, 2660–2673 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- N. I. P. Ayu, E. Kartini, L. D. Prayogi, M. Faisal and Supardi, Ionics, 2016, 22, 1051–1057 CrossRef CAS.
- C. Calvo and P. K. L. Au, Can. J. Chem., 1969, 47, 3409–3416 CrossRef CAS.
- B. Dickens, E. Prince, L. W. Schroeder and W. E. Brown, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 2057–2070 CrossRef CAS.
- C. Calvo, Can. J. Chem., 1965, 43, 436–445 CrossRef CAS.
- K. Y. Leung and C. Calvo, Can. J. Chem., 1972, 50, 2519–2526 CrossRef CAS.
- R. J. B. Jakeman and A. K. Cheetham, J. Am. Chem. Soc., 1988, 110, 1140–1143 CrossRef CAS.
- M. T. Averbuch-Pouchot and A. Durif, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 151–152 CrossRef.
- J. S. Stephens and C. Calvo, Can. J. Chem., 1967, 45, 2303–2316 CAS.
- L. W. Schroeder, E. Prince and B. Dickens, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 9–12 CrossRef.
- N. A. Curry and D. W. Jones, J. Chem. Soc. A, 1971, 3725–3729 RSC.
- A. G. Nord, Mater. Res. Bull., 1977, 12, 563–568 CrossRef CAS.
- S. Boudin, A. Grandin, M. M. Borel, A. Leclaire and B. Raveau, Acta Crystallogr., 1993, 49, 2062–2064 Search PubMed.
- C. Calvo, Inorg. Chem., 1968, 7, 1345–1351 CrossRef CAS.
- A. G. Nord and P. Kierkegaard, Acta Chem. Scand., 1968, 22, 1466–1474 CrossRef CAS.
- B. E. Robertson and C. Calvo, J. Solid State Chem., 1970, 1, 120–133 CrossRef CAS.
- C. Calvo, Acta Crystallogr., 1967, 23, 289–295 CrossRef CAS.
- J. Alkemper, H. Paulus and H. Fueß, Z. Kristallogr., 1994, 209, 616 CAS.
- K. N. Ng and C. Calvo, Can. J. Chem., 1973, 51, 2613–2620 CrossRef.
- L. O. Hagman, I. Jansson and C. Magnéli, Acta Chem. Scand., 1968, 22, 1419–1429 CrossRef CAS.
- L.-O. Hagman and P. Kierkegaard, Acta Chem. Scand., 1968, 22, 1822–1832 CrossRef CAS.
- A. G. Nord and K. B. Lindberg, Acta Chem. Scand., Ser. A, 1975, 29, 1–6 CrossRef.
- B. P. Onac and H. S. Effenberger, Am. Mineral., 2007, 92, 1998–2001 CrossRef CAS.
- R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174–S186 CrossRef CAS PubMed.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS PubMed.
- F. Vasconcelos, S. Cristol, J.-F. Paul, G. Tricot, J.-P. Amoureux, L. Montagne, F. Mauri and L. Delevoye, Inorg. Chem., 2008, 47, 7327–7337 CrossRef CAS.
- S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204 RSC.
- G. Kieslich, A. C. Forse, S. Sun, K. T. Butler, S. Kumagai, Y. Wu, M. R. Warren, A. Walsh, C. P. Grey and A. K. Cheetham, Chem. Mater., 2016, 28, 312–317 CrossRef CAS.
- R. J. B. Jakeman, DPhil thesis, University of Oxford, 1986.
- D. M. Dawson, R. F. Moran, S. Sneddon and S. E. Ashbrook, Magn. Reson. Chem., 2018, 1–15 CAS.
- J. M. Griffin, J. R. Yates, A. J. Berry, S. Wimperis and S. E. Ashbrook, J. Am. Chem. Soc., 2010, 132, 15651–15660 CrossRef CAS PubMed.
- S. E. Ashbrook, D. M. Dawson and J. M. Griffin, in Local Structural Characterisation, ed. D. W. Bruce, D. O'Hare and I. Walton, Richard, John Wiley & Sons, Ltd, Chichester, UK, 2013, pp. 1–88 Search PubMed.
- A. Zheng, S. B. Liu and F. Deng, J. Phys. Chem. C, 2009, 113, 15018–15023 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01420a |
| This journal is © the Owner Societies 2019 |