Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The local electron attachment energy and the electrostatic potential as descriptors of surface–adsorbate interactions†
Joakim
Halldin Stenlid
 *ab,
Adam Johannes
Johansson
*ab,
Adam Johannes
Johansson
 c and
Tore
Brinck
c and
Tore
Brinck
 *a
*a
aApplied Physical Chemistry, Department of Chemistry, CBH, KTH Royal Institute of Technology, SE-100 44 Stockholm, Sweden. E-mail: tore@kth.se; joakim.halldin-stenlid@fysik.su.se
bDepartment of Physics, AlbaNova University Center, Stockholm University, SE-106 91 Stockholm, Sweden
cSwedish Nuclear Fuel and Waste Management Co (SKB), Evenemangsgatan 13, Box 3091, SE-169 03, Solna, Sweden
First published on 19th July 2019
Abstract
Two local reactivity descriptors computed by Kohn–Sham density functional theory (DFT) are used to predict and rationalize interactions of nucleophilic molecules (exemplified by CO and H2O) with transition metal (TM) and oxide surfaces. The descriptors are the electrostatic potential, VS(r), and the local electron attachment energy, ES(r), evaluated on surfaces defined by the 0.001 e Bohr−3 isodensity contour. These descriptors have previously shown excellent abilities to predict regioselectivity and rank molecular as well as nanoparticle reactivities and interaction affinities. In this study, we generalize the descriptors to fit into the framework of periodic DFT computations. We also demonstrate their capabilities to predict local surface propensity for interaction with Lewis bases. It is shown that ES(r) and VS(r) can rationalize the interaction behavior of TM oxides and of fcc TM surfaces, including low-index, stepped and kinked surfaces spanning a wide range of interaction sites with varied coordination environments. Broad future applicability in surface science is envisaged for the descriptors, including heterogeneous catalysis and electrochemistry.
Introduction
The ability to predict and rationalize the interactions and reactions of extended surfaces is of great interest in numerous research fields spanning from heterogeneous catalysis, electrochemistry and corrosion, to nanotoxicity, biocompatibility and biodegradability. In the present paper we discuss an alternative direction to assess surface reactivity as compared to those traditionally used in the materials science and surface chemistry communities. We will show that two local properties, the local electron attachment energy [E(r)] and the electrostatic potential [V(r)], can be used for characterization of site-resolved Lewis acidity of transition metal and oxide surfaces when evaluated on contours of constant electron density, i.e. isodensity surfaces. The predictions made by these properties are compared to experimental and computed adsorption energies of two nucleophilic probe molecules, i.e. the Lewis bases CO and H2O. Both E(r) and V(r) are obtained at the 0.001 a.u. isodensity surfaces, an approach which has been found useful for predictions and understanding of the interactive behavior of isolated molecules as well as transition metal and oxide nanoparticles.1–8Through the analysis of these properties, we have previously been able to rationalize e.g. the enhanced catalytic behavior of Au nanoparticles; undercoordinated sites (e.g. corner sites) are associated with a depletion of electron density (known as a σ-hole) and a corresponding local maximum in V(r).4 The σ-holes are more pronounced at the corner sites than at terrace sites; this explains the stronger interactions at corners, which are necessary for an increased catalytic activity compared to the inert, perfect surfaces of Au. We have found that the interactions at undercoordinated Au sites are similar in origin to those of e.g. hydrogen and halogen9 bonding. A similar behavior is also found for Ag and Cu nanoparticles.7 In light of these observations, we have introduced a new type of bonds, regium bonds,7 that take place between the σ-hole of a neutral Au, Ag or Cu site and a Lewis base, e.g. CO or H2O. Striving to explore similarities and differences within chemical interaction behavior over the periodic table, we will herein investigate if the above concepts are more generally applicable and can be used to also explain interaction tendencies of extended surface as well as of other metals and materials.
The use of DFT-based descriptors to characterize the reactive properties of surfaces is a common practice in the surface science community. An important example is the d-band model of Hammer and Nørskov,10 which have been successfully employed to rationalize trends in adsorption energies on transition metal substrates and thereby, in the extension, to predict e.g. catalytic activity of metals and alloys.11,12 Compared to the traditional descriptors, including the d-band model, both E(r) and V(r) have the advantage of being local in their nature. This means that they can not only be used to analyze the difference in reactivity/activity between different materials, but also the variation in reactivity over the same surface, i.e. the regioselectivity. In addition, we have found that the E(r) and V(r) are able to predict the local adsorption behavior for the interaction of Lewis bases with oxide surfaces; a process for which there are no generally applicable descriptor, including the d-band model and its extensions.13–15 In the following we will demonstrate that local minima in E(r), ES,min, and local maxima in V(r), VS,max, on isodensity contours indicate sites susceptible towards interaction with electron donating molecules. We will also show that the relative magnitude of ES,min and VS,max closely reflects trends in adsorption energies.
Theory
We shall begin by readopting the formulism of the descriptors to fit the solid-state framework. For a polyatomic non-periodic, isolated system (e.g. a gas phase molecule), V(r) at position r is rigorously defined by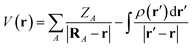 | (1) |
| Vper(r) = Vabs(r) + ΔV. | (2) |
| Vabs(r) = Vper(r) − Vpervac | (3) |
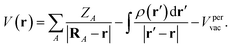 | (4) |
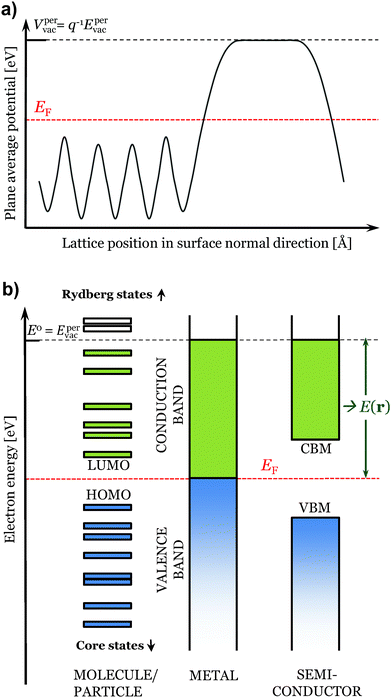 | ||
| Fig. 1 In (a) plane average electrostatic potential over a periodic slab. In (b) illustration of the considered states for the evaluation of E(r) of different types of compounds. | ||
Turning next to the E(r) property, we define it as (based on its definition for isolated systems2)
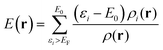 | (5) |
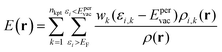 | (6) |
V(r) and E(r) are complementary properties to a certain degree; whereas the V(r) provides information on the electrostatic tendencies upon interaction, the E(r) property also contains components related to charge-transfer and polarization. E(r) can be partitioned into (shown here for the single k-point case):2,22
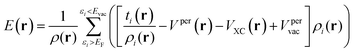 | (7) |
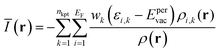 | (8) |
Methods
Surface models
To evaluate the descriptors, surface models where generated for different fcc metal substrates and for the transition metal oxides Cu2O and TiO2 in the anatase and rutile phases. The structures were based on crystal parameters from Xu et al.25 for the TiO2 structures, from Yu et al.26 for Cu2O and from Wellendorff et al.27 for the fcc metals. For TiO2 four-layer symmetric (1 × 1) unit cell slabs were used, separated by a 28 Å vacuum distance, with the outermost layer being allowed to relax. A range of surface facets were studied including the anatase (100), (001) and (101), as well as rutile(100), (110) and (101). For Cu2O, a six layer symmetric (1 × 1) unit cell slab model of the (111) facet was used with the outer two layers free to relax using a vacuum separation of 24 Å. The Cu2O(111) surface with 1/3ML OCUS (unsaturated oxygen) vacancies was modeled by a (√3 × √3)R30° unit cell. (1 × 1) unit cells were employed for the fcc metal (111) surfaces using symmetric slabs comprising 10 layers with the three top layers free to relax and vacuum separations of 36 Å. For copper we evaluated the low-index (100), (110) and (111) surfaces as well as the stepped (221) and chiral (643) surfaces. This was also compared to the cuboctahedral Cu147 nanoparticle. For the remaining fcc metals, Rh, Ni, Pt, Pd, Ir, Ag, and Au, only their (111) surfaces were included.For comparison of site-specific interactions with V(r) and E(r), and in the cases when experimental data was not available, CO adsorption energies where determined for the different structures using (2 × 2) unit cells for the low index surfaces. The adsorption energies were calculated by:
| ΔEad = [E*CO – (E* + ECO)] | (9) |
Computational details
All calculations were carried out with the Vienna ab initio simulation package (VASP).28 The PBE xc-functional was used throughout. For the oxides, on-site +U Hubbard corrections were included as proposed by Dudarev et al.29 The (U–j) parameters were taken from Xu et al.25 for the TiO2 structures and from Yu et al.26 for Cu2O. Grimme's D3 dispersion with Becke–Johnson damping was employed for the CO adsorption studies.30,31 During optimization the core states were represented by standard PBE-PAW potentials. Valence electrons were represented by plane-wave basis sets with an energy cut-off of 400 eV. 4 × 4 × 1 k-point Γ-centered meshes were used for the sampling of the k-space during the geometry optimizations employing the tetrahedron method with Blöchl corrections32 for the oxides and the first order Methfessel–Paxton smearing method33 for the metals. For the final energy evaluations and for the descriptor evaluations, 9 × 9 × 1 meshes were used for the oxides and 11 × 11 × 1 meshes for the metals. Hard PAW potentials and extended valences where used for the final energy and descriptor evaluations using a plane-wave cut-off of 800 eV. Molecular CO was treated by a single Γ-point. V(r) where generated in VASP (LOCPOT including only the ionic and Hartree potential contributions). E(r) was computed from the optimized wave function according to eqn (6) in the main article. Spin-polarization was considered for Ni(111). The VS(r) and ES(r) were visualized at the 0.001 a.u. (e Bohr−3) isodensity surface in VESTA.34VS,max and ES,min where evaluated at the same isodensity surface.Results & discussion
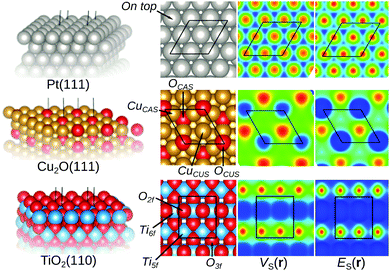
Now to the central question: how do the E(r) and V(r) properties outlined above correlate with the Lewis acidic behavior of extended surfaces? The first feature that we shall explore is the local character of the descriptors. To investigate this, the properties are first mapped on the 0.001 a.u. isodensity contours of Pt(111), Cu2O(111) and rutile TiO2(110) shown in Fig. 2. These surface structures are suitable tests for the descriptors since the behavior upon adsorption of molecular species onto theses surfaces is experimentally well characterized.On Pt(111) both the descriptors suggest that the sites on top of Pt atoms are the most susceptible to interactions with Lewis bases. This since ES,min and VS,max (also known as σ-holes9) appear and coincide on these sites, suggesting that the on top sites are the preferred sites based on both charge-transfer (i.e. low electron affinity as indicated by ES,min) and electrostatic (i.e. strongly positive potential as indicated by VS,max) arguments. Nucleophilic areas of low electrostatic potential are found at bridge and three-fold hollow sites in between atoms. Note again that ES(r) can only be used to characterize local Lewis acidity whereas VS(r) identifies both Lewis acidic (VS,max) and Lewis basic (VS,min) sites. The identified adsorption sites on Pt(111) agree well with the experimental findings that the Lewis basic CO adsorbs on top of Pt atoms.35–37 Standard DFT LDA or GGA calculations do, however, notoriously rank the CO affinities of on top and hollow site incorrectly – known as the CO-puzzle.38 Our results show that the on top site indeed is the preferred site with respect to electrostatics and the accepting of electron density from the sigma-orbital (HOMO) of CO. This in accordance with earlier studies, which attributed the preference for hollow sites to an incorrect leveling of the CO HOMO/LUMO energies compared to the band structure of Pt resulting in an overestimation of the back donation to the CO LUMO orbital at the hollow sites.39,40
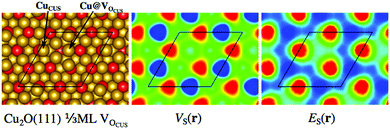
Fig. 2 also includes the examples of the stoichiometric and non-polar Cu2O(111) surface and the rutile TiO2(110) surfaces. For Cu2O(111), the ideal surface contains two possible Cu adsorption sites, the coordinatively unsaturated Cu (CuCUS) and coordinatively saturated Cu (CuCS) and two O sites (OCUS and OCS). Among these, the CuCUS site has been suggested as the favored site of interaction for Lewis bases,41 which has been confirmed by DFT calculations of e.g. CO, H2S, H2O and methanol adsorption.42–44 From the ES(r) map of the surface, we find that the CuCUS sites indeed correspond to local minima, while the CuCS sites are attributed lower Lewis acidity, i.e. lower electron affinity. The ES(r) indicates no tendency of O sites to be susceptible towards attack of Lewis bases. Hence, the predictions of the ES(r) are in line with the established knowledge. VS(r) outlines the same Lewis acidic surface characteristics as ES(r), but also ranks the OCUS as more Lewis basic (more negative potential) than OCS, again in agreement with the established picture.44,45Fig. 3 shows the same Cu2O surface but with 1/2 ML OCUS vacancies (VOCUS), a commonly observed surface reconstruction.46 This leaves behind a new type of undercoordinated Cu adsorption sites, Cu@VOCUS. Regardless, the most prominent ES,min and VS,max are still located at the same CuCUS site as on the unreconstructed surface suggesting these sites remain the most favorable adsorption sites. Again, this is in line with previous understanding of e.g. H2O and methanol interactions onto this surface.44,45 From the above, we note that our methods can be used for comparison to e.g. experimental STM (scanning tunneling microscopy) images, as well as in the initial assessment of reactive sites of complex nanostructured surfaces.
Concerning the rutile TiO2(110) surface, there are two possible Lewis acidic Ti sites, one six-fold (Ti6f) and on five-fold (Ti5f) coordinated. Similarly, there are two Lewis basic O sites, one three-fold (O3f) and one two-fold coordinated (O2f). ES(r) and VS(r) rank the Ti5f site as more Lewis acidic (i.e. stronger electron affinity and higher positive potential) than the Ti6f site, whereas the O2f is more Lewis basic than O3f, in line with experimental and previous DFT results for e.g. H2O, CO and methanol adsorption.47–50
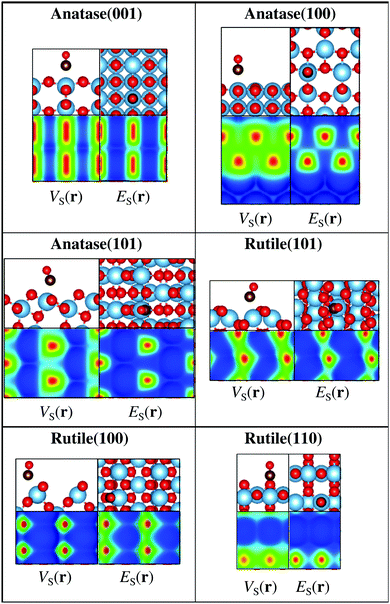
In addition to rutile(110), we have also investigated the ability of the descriptors to identify CO adsorption sites on other TiO2 surface facets including the rutile(101) and (100), as well as the anatase(100), (101), and (001) facets. TiO2 is e.g. an important photocatalyst material, and these facets constitute the most commonly observed surfaces.51–53Fig. 4 shows the above-mentioned TiO2 surfaces with CO adsorbed on the most favorable position and with the corresponding 0.001 a.u. ES(r) and VS(r) isocontour maps. Also for these surfaces it is found that the most extreme ES,min and VS,max correspond to the favored adsorption site.
From the above we conclude that E(r) and V(r) show promise as descriptors for the assessment of regioselectivity in surface Lewis acidity. However, the prevailing question is how well E(r) and V(r) can rank trends in adsorption energies for different substrates? Looking first at the series of Cu(111), (110) and (100) surface facets, Wang and Nakamura54 have determined their H2O affinities using GGA DFT as (110) > (100) > (111). The Cu on top ES,min (VS,max) for these surfaces are −8.35 eV (0.44 eV), −7.73 (0.34), and −6.53 (0.33) thus reproducing the trends in the adsorption energies. The corresponding surface maps are shown in Fig. 5C–E.
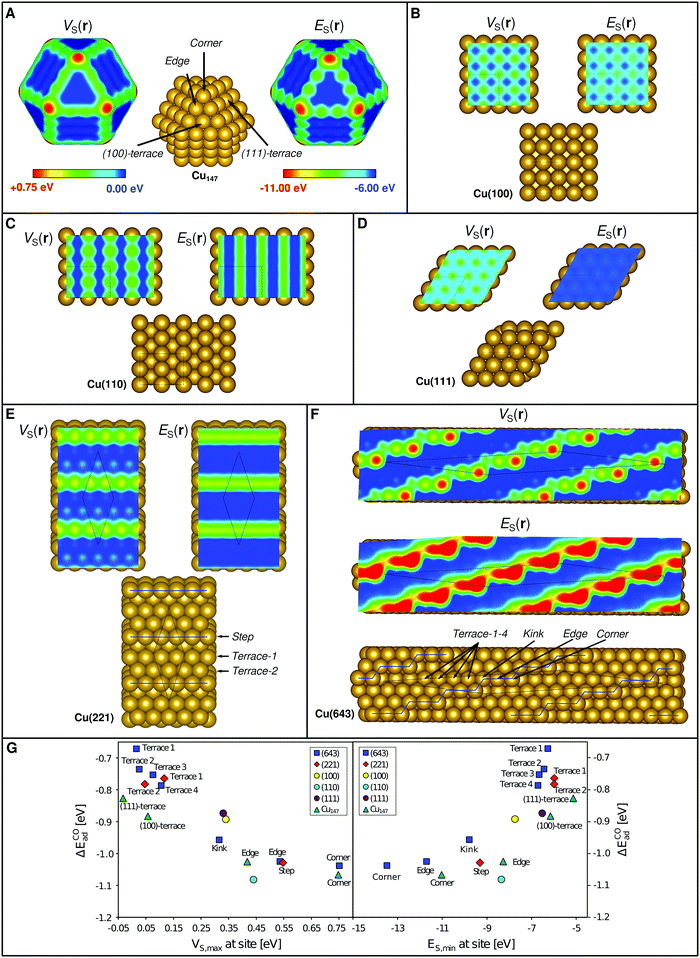 | ||
| Fig. 5 Structure, VS(r) and ES(r) at the 0.001 a.u. isodensity surface for (A) a copper cuboctahedral Cu147 nanoparticle, and in (B–F) for different crystallographic planes of Cu. All images show the VS(r) and ES(r) properties on the common color scales depicted in (A). Similar images with scales optimized to display different adsorption sites on each individual compound are shown in Fig. S1 of the ESI.† It can be noted that the more undercoordinated sites (corners > edges > kinks > facets) show larger positive electrostatic potential and higher electron affinity, which is found to correlate to a stronger Lewis acidity. In (G) CO interaction energies computed by DFT for the various sites of the different structures are compared to the local values of VS(r) and ES(r) (i.e. VS,max and ES,min). | ||
We have previously used the local variations of VS(r) to rationalize the enhanced catalytic activity of Au nanoparticles compared to its ideal crystalline surfaces.4 A similar analysis is here included for Cu using both VS(r) and ES(r), covering nanoparticles as well as ideal, stepped and kinked extended surfaces (Fig. 5). Analogous to Au, we find that Cu nanoparticles display VS,max (and ES,min) on top of the exposed atoms, with the most prominent VS,max and ES,min at corner sites, followed by edge and, lastly, terrace sites (Fig. 5B). Similarly, the extended surfaces have the VS,max and ES,min of largest magnitude (i.e. the most positive potential or strongest electron affinity) at corner sites followed by steps/edges, kinks (see definition in Fig. 5) and lastly terrace sites (Fig. 5C–G). Computed CO interaction energies follow the local descriptor values at the site of interaction. The correlations are strongest when comparing adsorption onto different sites for each substrate surface individually, but clear also when comparing adsorption onto all sites of all Cu substrates together (Fig. 5A). We note a tendency towards non-linear behavior going from the undercoordinated to the terrace sites. This could be seen as two different trends for the different classes of sites. We attribute this to a non-negligible effect of neighboring atoms, which could be captured by adding information from a larger coordination sphere to the interaction analysis.
One can also ask how sensitive the descriptors are to the choice of computational method? A test on Cu(100) using the BEEF-vdw55 DFT xc-functional instead of PBE corroborate the understanding from isolated systems2 that the V(r) property is rather insensitive to the functional while the absolute values of E(r) shifts depending on the choice of method. We find that VS,max at the on top site is 0.34 eV for both cases, whereas ES,min is −7.73 eV at the PBE level of theory and −7.45 eV using BEEF-vdw. The behavior of the descriptors using different functionals will be further evaluated in a follow-up study.
We next assess the experimental CO adsorption enthalpies of a series of fcc (111) transition metal substrates. The adsorption enthalpies are taken from a database of Wellendorff et al.27 and includes the Ir, Rh, Ni, Pt, Pd and Cu surfaces. CO adsorbs on top of all but the Pd and Ni surfaces, where the hollow sites are preferred.27 Using the ES,min value at the on top site from a 0.001 a.u. isodensity contour, we obtain an R2 of 0.82 compared to the experimental adsorption enthalpies (Fig. 6 top). For CO, we obtain a slightly improved trend (R2 of 0.89) when comparing to computed on top site adsorption energies at the PBE level§ and extending the series with Au and Ag. Fig. 6 bottom include data for computed H2O adsorption energies57 on fcc metals compared to ES,min showing a correlation with an R2 = 0.82. We note that the main outlier in all the series above is Pt.
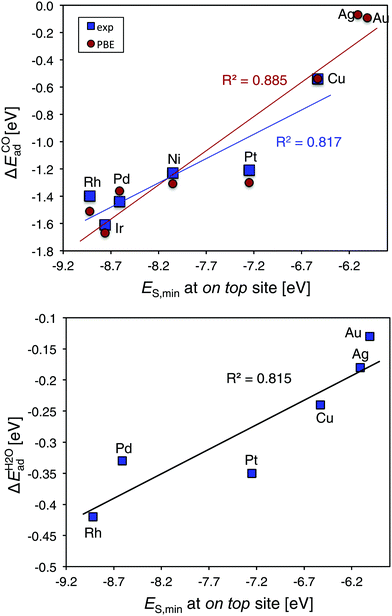 | ||
| Fig. 6 Top, correlation plots CO adsorption energies27 and computed ES,min§ at the metal on top site of fcc TM(111) surfaces, TM = Ir, Rh, Ni, Pt, Pd, Cu, Au, and Ag. Bottom, computed H2O adsorption energies from Michaelides et al.57versus ES,min. | ||
The corresponding correlation of VS,maxversus experimental data is poor R2 = 0.16. This suggests that the differences in CO affinity between the metal surfaces is determined by differences in charge-transfer capacity rather than electrostatics, which is in agreement with the success of the d-band model that downplays electrostatics in favor for orbital-band mixing.
Although the examples presented here represents a limited initial study, they demonstrate that the E(r) and V(r) descriptors can be used to predict and rationalize molecular interactions at both metal and oxide surfaces and have great potential for future applications. Results for other adsorbents including e.g. hydrogen atoms, hydrocarbons, water, ammonia and other nitrogen centered adsorbates will be presented in a follow-up study. For future directions, an interesting path is to further explore the Lewis basicity of metal and oxide surfaces. This could, as touched upon in the present study, be evaluated by the negative regions of V(r) in combination with the Lewis basicity analog to E(r), i.e. the Ī(r) of Sjoberg et al.23,24 This will be a focus of a future study.
Conclusion
In conclusion, we have shown that the local electron attachment energy E(r), as well as the electrostatic potential V(r), mapped on isodensity contours can reproduce the regional variations in Lewis acidity of metal and oxide surfaces. The relative magnitude at the site of interaction can, moreover, be used to correlate adsorption energy trends for CO and H2O onto fcc metal surfaces. A general applicability of the two properties for various types of surfaces and applications, e.g. in the fields of heterogeneous catalysis and electrochemistry, is envisioned. For instance, the approach shows great promise for the analysis of special sites/motifs on complex nanostructured material surfaces that may correspond to active sites for catalysis or sites that are susceptible to corrosion as well as seeding sites for electrochemical deposition. It is, moreover, likely that the descriptors can be used to screen for new, tailored materials of e.g. high catalytic activity, or for the comparison to experimental STM images as well as in the prediction of nanotoxicity by the differentiation of reactivity of nanoparticles. We furthermore recognize the applicability of our methods as a guiding tool for surface chemistry modeling, providing swift rationalization of the orientation and positioning of interacting molecules.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swedish Nuclear Fuel and Waste management company (SKB) and the School of Chemical Science and Engineering at KTH (via its excellence award to JHS). JHS acknowledge financial support from the Åforsk foundation, and TB support from the Swedish Research Council (VR). The calculations were performed at resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre in Linköping University NSC as well as at the PDC Centre for High Performance Computing (PDC-HPC).References
- J. S. Murray and P. Politzer, The electrostatic potential: an overview, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 153–163 CAS.
- T. Brinck, P. Carlqvist and J. H. Stenlid, Local Electron Attachment Energy and Its Use for Predicting Nucleophilic Reactions and Halogen Bonding, J. Phys. Chem. A, 2016, 120, 10023–10032 CrossRef CAS PubMed.
- J. H. Stenlid and T. Brinck, Nucleophilic Aromatic Substitution Reactions Described by the Local Electron Attachment Energy, J. Org. Chem., 2017, 82, 3072–3083 CrossRef CAS.
- J. H. Stenlid and T. Brinck, Extending the σ-Hole Concept to Metals: An Electrostatic Interpretation of the Effects of Nanostructure in Gold and Platinum Catalysis, J. Am. Chem. Soc., 2017, 139, 11012–11015 CrossRef CAS PubMed.
- J. H. Stenlid, A. J. Johansson and T. Brinck, σ-Holes on Transition Metal Nanoclusters and Their Influence on the Local Lewis Acidity, Crystals, 2017, 7, 222 CrossRef.
- J. H. Stenlid, A. J. Johansson and T. Brinck, Local Lewis Acidity of (TiO2)nn = 7–10 Nanoparticles Characterized by DFT-Based Descriptors: Tools for Catalyst Design, J. Phys. Chem. C, 2017, 121, 27483–27492 CrossRef CAS.
- J. H. Stenlid, A. J. Johansson and T. Brinck, σ-Holes and σ-lumps direct the Lewis basic and acidic interactions of noble metal nanoparticles: introducing regium bonds, Phys. Chem. Chem. Phys., 2018, 20, 2676–2692 RSC.
- T. Brinck and J. H. Stenlid, The Molecular Surface Property Approach: A Guide to Chemical Interactions in Chemistry, Medicine, and Material Science, Adv. Theory Simul., 2019, 2, 1800149 CrossRef.
- T. Clark, M. Hennemann, J. Murray and P. Politzer, Halogen bonding: the σ-hole, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- B. Hammer and J. K. Nørskov, Why gold is the noblest of all the metals, Nature, 1995, 376, 238–240 CrossRef CAS.
- T. Bligaard and J. K. Nørskov, in Chemical Bonding at Surfaces and Interfaces, ed. A. Nilsson, L. G. M. Pettersson and J. K. Nørskov, Elsevier, Amsterdam, 2008, pp. 255–321 Search PubMed.
- J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Energy Trends in Catalysis, in Fundamental Concepts in Heterogeneous Catalysis, John Wiley & Sons, Inc, Hoboken, 2014, pp. 85–96 Search PubMed.
- H. B. Tao, L. Fang, J. Chen, H. B. Yang, J. Gao, J. Miao, S. Chen and B. Liu, Identification of Surface Reactivity Descriptor for Transition Metal Oxides in Oxygen Evolution Reaction, J. Am. Chem. Soc., 2016, 138, 9978–9985 CrossRef CAS PubMed.
- F. Calle-Vallejo, N. G. Inoglu, H.-Y. Su, J. I. Martínez, I. C. Man, M. T. M. Koper, J. R. Kitchin and J. Rossmeisl, Number of outer electrons as descriptor for adsorption processes on transition metals and their oxides, Chem. Sci., 2013, 4, 1245–1249 RSC.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Density functional theory in surface chemistry and catalysis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- L. Kleinman, Comment on the average potential of a Wigner solid, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 7412–7414 CrossRef CAS.
- R. Ramprasad, P. von Allmen and L. R. C. Fonseca, Contributions to the work function: A density-functional study of adsorbates at graphene ribbon edges, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 6023–6027 CrossRef CAS.
- C. Campañá, B. Mussard and T. K. Woo, Electrostatic Potential Derived Atomic Charges for Periodic Systems Using a Modified Error Functional, J. Chem. Theory Comput., 2009, 5, 2866–2878 CrossRef.
- R. M. Feenstra and M. Widom, Low-energy electron reflectivity from graphene: First-principles computations and approximate models, Ultramicroscopy, 2013, 130, 101–108 CrossRef CAS PubMed.
- R. M. Feenstra, N. Srivastava, Q. Gao, M. Widom, B. Diaconescu, T. Ohta, G. L. Kellogg, J. T. Robinson and I. V. Vlassiouk, Low-energy electron reflectivity from graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041406 CrossRef.
- J. F. Janak, Proof that ∂E/∂ni = εi in density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 7165–7168 CrossRef CAS.
- F. A. Bulat, M. Levy and P. Politzer, Average Local Ionization Energies in the Hartree–Fock and Kohn–Sham Theories, J. Phys. Chem. A, 2009, 113, 1384–1389 CrossRef CAS PubMed.
- P. Sjoberg, J. S. Murray, T. Brinck and P. Politzer, Average local ionization energies on the molecular surfaces of aromatic systems as guides to chemical reactivity, Can. J. Chem., 1990, 68, 1440–1443 CrossRef CAS.
- P. Politzer, J. S. Murray and F. A. Bulat, Average local ionization energy: A review, J. Mol. Model., 2010, 16, 1731–1742 CrossRef CAS PubMed.
- Z. Xu, J. Rossmeisl and J. R. Kitchin, A Linear Response DFT+U Study of Trends in the Oxygen Evolution Activity of Transition Metal Rutile Dioxides, J. Phys. Chem. C, 2015, 119, 4827–4833 CrossRef CAS.
- K. Yu and E. A. Carter, Communication: Comparing ab initio methods of obtaining effective U parameters for closed-shell materials, J. Chem. Phys., 2014, 140, 121105 CrossRef PubMed.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, A benchmark database for adsorption bond energies to transition metal surfaces and comparison to selected DFT functionals, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- M. Methfessel, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. A. Stroscio and D. M. Eigler, Atomic and Molecular Manipulation with the Scanning Tunneling Microscope, Science, 1991, 254, 1319–1326 CrossRef CAS PubMed.
- G. S. Blackman, M.-L. Xu, D. F. Ogletree, M. A. Van Hove and G. A. Somorjai, Mix of molecular adsorption sites detected for disordered CO on Pt(111) by diffuse low-energy electron diffraction, Phys. Rev. Lett., 1988, 61, 2352–2355 CrossRef CAS PubMed.
- H. Steininger, S. Lehwald and H. Ibach, On the adsorption of CO on Pt(111), Surf. Sci., 1982, 123, 264–282 CrossRef CAS.
- P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, The CO/Pt(111) Puzzle, J. Phys. Chem. B, 2001, 105, 4018–4025 CrossRef CAS.
- A. Gil, A. Clotet, J. M. Ricart, G. Kresse, M. Garcıa-Hernández, N. Rösch and P. Sautet, Site preference of CO chemisorbed on Pt(111) from density functional calculations, Surf. Sci., 2003, 530, 71–87 CrossRef CAS.
- G. Kresse, Significance of single-electron energies for the description of CO on Pt(111), Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 073401 CrossRef.
- A. Önsten, J. Weissenrieder, D. Stoltz, S. Yu, M. Göthelid and U. O. Karlsson, Role of Defects in Surface Chemistry on Cu2O(111), J. Phys. Chem. C, 2013, 117, 19357–19364 CrossRef.
- W. An, A. E. Baber, F. Xu, M. Soldemo, J. Weissenrieder, D. Stacchiola and P. Liu, Mechanistic Study of CO Titration on CuxO/Cu(111) (x ≤ 2) Surfaces, ChemCatChem, 2014, 6, 2364–2372 CrossRef CAS.
- J. H. Stenlid, A. J. Johansson, C. Leygraf and T. Brinck, Computational Analysis of the Early Stage of Cuprous Oxide Sulphidation: A Top-Down Process, Corros. Eng. Sci. Technol., 2017, 52, 50–53 CrossRef CAS.
- Z. Besharat, J. H. Stenlid, M. Soldemo, K. Marks, A. Önsten, M. Johnson, H. Öström, J. Weissenrieder, T. Brinck and M. Göthelid, Dehydrogenation of methanol on Cu2O(100) and (111), J. Chem. Phys., 2017, 146, 244702 CrossRef.
- C. Riplinger and E. A. Carter, Cooperative Effects in Water Binding to Cuprous Oxide Surfaces, J. Phys. Chem. C, 2015, 119, 9311–9323 CrossRef CAS.
- A. Önsten, M. Göthelid and U. O. Karlsson, Atomic structure of Cu2O(111), Surf. Sci., 2009, 603, 257–264 CrossRef.
- C. T. Campbell and J. R. V. Sellers, Enthalpies and Entropies of Adsorption on Well-Defined Oxide Surfaces: Experimental Measurements, Chem. Rev., 2013, 113, 4106–4135 CrossRef CAS PubMed.
- Y. Zhao, Z. Wang, X. Cui, T. Huang, B. Wang, Y. Luo, J. Yang and J. Hou, What Are the Adsorption Sites for CO on the Reduced TiO2(110)-1 × 1 Surface?, J. Am. Chem. Soc., 2009, 131, 7958–7959 CrossRef CAS PubMed.
- B. Hammer, S. Wendt and F. Besenbacher, Water Adsorption on TiO2, Top. Catal., 2010, 53, 423–430 CrossRef CAS.
- K. Onda, B. Li, J. Zhao, K. D. Jordan, J. Yang and H. Petek, Wet Electrons at the H2O/TiO2(110) Surface, Science, 2005, 308, 1154–1158 CrossRef CAS PubMed.
- U. Diebold, The surface science of titanium dioxide, Surf. Sci. Rep., 2003, 48, 53–229 CrossRef CAS.
- P. Jones and J. A. Hockey, Infra-red studies of rutile surfaces. Part 2.—Hydroxylation, hydration and structure of rutile surfaces, Trans. Faraday Soc., 1971, 67, 2679–2685 RSC.
- A. Vittadini, A. Selloni, F. P. Rotzinger and M. Grätzel, Structure and Energetics of Water Adsorbed at TiO2 Anatase (101) and (001) Surfaces, Phys. Rev. Lett., 1998, 81, 2954–2957 CrossRef CAS.
- G.-C. Wang and J. Nakamura, Structure Sensitivity for Forward and Reverse Water-Gas Shift Reactions on Copper Surfaces: A DFT Study, J. Phys. Chem. Lett., 2010, 1, 3053–3057 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Density functionals for surface science: exchange-correlation model development with Bayesian error estimation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels, Energy Environ. Sci., 2010, 3, 1311–1315 RSC.
- A. Michaelides, V. A. Ranea, P. L. de Andres and D. A. King, General Model for Water Monomer Adsorption on Close-Packed Transition and Noble Metal Surfaces, Phys. Rev. Lett., 2003, 90, 216102 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03099a |
| ‡ We note that in future applications, for non-zero Kelvin interactions, a Fermi–Dirac smearing of the electron occupation might be necessary to accurately capture the interaction behavior, thus leading to fractional occupation and corresponding weighting of the valence states. |
| § The CO adsorption energy bias of the PBE functional with respect to experimental data has here been accounted for by adding the corrections suggested by Petersen et al.56 to the computed values (i.e. a constant energy shift). No D3 corrections were used for this series. |
| This journal is © the Owner Societies 2019 |