Open Access Article
Open Access ArticleUltrafast dynamics in polycyclic aromatic hydrocarbons: the key case of conical intersections at higher excited states and their role in the photophysics of phenanthrene monomer†
M.
Nazari
 a,
C. D.
Bösch
b,
A.
Rondi
a,
A.
Francés-Monerris
a,
C. D.
Bösch
b,
A.
Rondi
a,
A.
Francés-Monerris
 c,
M.
Marazzi
c,
M.
Marazzi
 cde,
E.
Lognon
cde,
E.
Lognon
 c,
M.
Gazzetto
a,
S. M.
Langenegger
b,
R.
Häner
c,
M.
Gazzetto
a,
S. M.
Langenegger
b,
R.
Häner
 b,
T.
Feurer
a,
A.
Monari
b,
T.
Feurer
a,
A.
Monari
 *c and
A.
Cannizzo
*c and
A.
Cannizzo
 *a
*a
aInstitute of Applied Physics, University of Bern, Switzerland. E-mail: andrea.cannizzo@iap.unibe.ch
bDepartment of Chemistry and Biochemistry, University of Bern, Switzerland
cUniversité de Lorraine & CNRS, LPCT UMR 7019, Nancy, France. E-mail: antonio.monari@univ-lorraine.fr
dDepartment of Analytical Chemistry, Physical Chemistry and Chemical Engineering, University of Alcalà, Spain
eChemical Research Institute ‘‘Andrés M. del Río’’ (IQAR), University of Alcalà, Spain
First published on 18th July 2019
Abstract
In this study we reveal the detailed photocycle of a phenanthrene monomer. Phenanthrene serves as a popular building block for supramolecular systems and as an archetypal molecule to study the photochemistry of polycyclic aromatic hydrocarbons. By means of femtosecond time-resolved UV-vis transient absorption spectroscopy and molecular modeling, we found that the first bright transition involves the second excited singlet state, which relaxes toward the lowest excited singlet state with a biphasic internal conversion through a conical intersection region: a fast coherent branching followed by an exceptionally slow (∼ps) incoherent internal conversion. We succeeded to pinpoint the complete relaxation pathways and to extract the relevant parameters, e.g., the branching ratio at the conical intersection and internal conversion rates.
Introduction
Investigating phenanthrene per se serves as a model system to study the photochemistry of polycyclic aromatic hydrocarbons (PAHs), whose ubiquitous presence as pollutants on Earth1 and proven carcinogenic activity have motivated the regulation of their emissions by authorities.2 Furthermore, the detection of various PAHs in extraterrestrial environments makes their study of paramount interest in astrochemistry.3,4 In the fields of supramolecular chemistry and molecular devices, phenanthrene has received significant attention as a building block and photoactive unit for efficient, multichromophoric structure based light harvesting systems.5–8 In these systems the photophysics of both the individual dyes and the aggregate systems must be precisely tuned and tailored to achieve not only the desired spectroscopic properties but also the formation of excited states, which allows for a fast and directional energy transfer (EnT) over several nm (>10 nm) with a high quantum yield.5,9–12 Recently, some of us have explored the photophysical properties of phenanthrene as a building block of light harvesting complexes in a variety of self-assembling polymeric and DNA-hosted structures.9,13–17 Such multichromophoric systems (MCS) show extraordinary optical properties, strong coupling among chromophores, high absorption cross section and unitary EnT quantum yield over more than several 10s of nm.9,13,16 The origin of such an efficient EnT is still unclear and, even more surprisingly, this unique behaviour is so far only observed when phenanthrene is incorporated into supramolecular structures.Despite the relative simplicity and the wide range of applications of phenanthrene and its aggregates, their photophysics and in particular the competing relaxation pathways have not been thoroughly characterized, neither experimentally nor theoretically. Accordingly, the motivation to carry out this study was twofold. On one hand we aimed at filling the knowledge gap in the photophysics of PAHs, using phenanthrene as an illustrative case study and on the other hand to unveil the unique photophysical features of phenanthrene responsible for the efficient EnT mechanism. The perspective is to build a new paradigm for the development of large and efficient MCS light harvesters in the visible range. Indeed, the present study is the first step to understand and characterize efficient EnT in DNA-hosted MCSs bearing phenanthrene building blocks as light harvesters.
Femtosecond (fs) time-resolved transient absorption (TA) spectroscopy18 is one of the methods of choice to study and characterize the population and energy migration dynamics following photoexcitation. The experimental results also serve as invaluable feedback for molecular modelling. Only such a synergic approach can identify and characterize the relevant relaxation channels. In the broader perspective of designing more efficient MCSs, unravelling the interplay between photoinduced electronic and nuclear dynamics inherent to the monomer itself is a prerequisite to identify those dynamics emerging as a consequence of the mutual coupling in the MCS structure.
Therefore, we investigated the excited state population dynamics in phenanthrene monomers with UV-Vis fs time-resolved TA spectroscopy and complemented the experiments with static and non-adiabatic molecular dynamics (NAMD) simulations. This combined study reveals that the phenanthrene photocycle cannot be described via a simple two-state model typical for other small π-conjugated organic dyes. Indeed, even though it is usually recognized that a two-state model is a too crude approximation to allow for the proper characterization of the photophysical phenomena, the precise identification of the complex excited state landscape of PAHs is usually overlooked. In particular, the excited state dynamics of phenanthrene is quite complex and we identified a population redistribution mediated first by a conical intersection (CI) region followed by a slow thermally activated adiabatic exchange with the lowest excited singlet state. The excellent quantitative agreement between simulation and the experimental results suggests phenanthrene as a benchmark system to study the photophysical and photochemical processes mediated by CIs amongst several excited states.
Results and discussion
In this contribution we focused on a carboxamide-substituted phenanthrene unit (see Fig. 1), as it is the main building block of the family of DNA-hosted MCSs reported in ref. 13 The influence of the linker, which was found to be relevant for the synthesis of the different MCSs, should be negligible on the photophysics of the monomer since the accessible photoexcited states and the subsequent relaxations are expected to be localized on the aromatic moiety only. This is also confirmed by the time-dependent density functional theory (TD-DFT) calculations reported herein. Hence, we believe that most of the results reported here are of general validity for any phenanthrene-linker composite.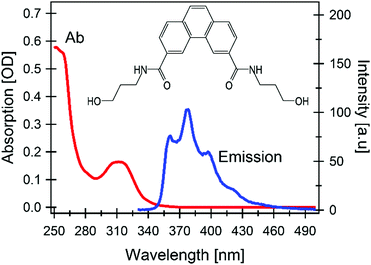 | ||
| Fig. 1 Steady state UV-Vis absorption and emission spectra (conditions: excitation at 320 nm, concentration 5 μM); (inset) chemical structure of aqueous carboxamide-substituted phenanthrene. | ||
Fig. 2A shows a representative selection of TA spectra of aqueous phenanthrene monomers in a buffer solution at pH 7 upon excitation at 320 nm. The fastest dynamic is dominated by a short-lived strong negative signal at shorter wavelengths (λ < 500 nm) which decays in 120 fs. The main features in the sub-picosecond domain are a signal rise within 400 fs, followed by a decay of the overall signal in 10s to 100s of ps. The negative signal drop at λ < 350 nm is assigned to a ground state bleach (GSB) of the steady state absorption, in particular of the ∼310 nm band (Fig. 1).
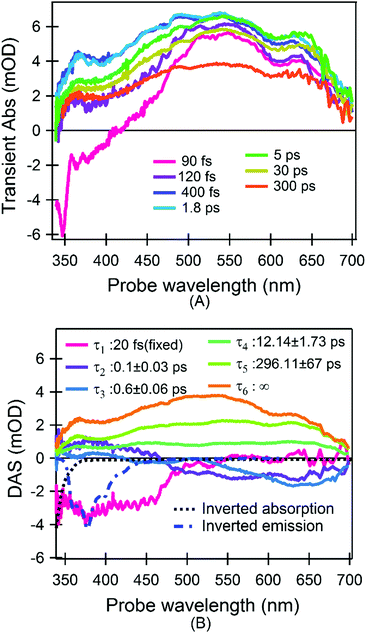 | ||
| Fig. 2 TA results. (A) A representative selection of spectra upon excitation at 320 nm; (B) time-spectrum decomposition analysis (see eqn (2)): DASs and the relative decay time constants are shown. Inverted steady state absorption and emission bands are also shown. For the sake of visualization the τ1 component is multiplied by 0.01 (see section “Data analysis of time-resolved spectra” in “Experimental and computational methods”). | ||
To better define the timescales and the corresponding spectral evolutions, we carried out a global analysis based on singular value decomposition,19 which decomposes the experimental data in a series of exponential decays with characteristic lifetimes (τk) and decay associated spectra (DASs). More details are found in the section “Experimental and computational methods”.
The 6 DASs reported in Fig. 2B confirm the previous qualitative model. In particular we find: a pulse limited component (τ1) describing a negative spectrum centered at 390 nm and ranging up to approximately 470 nm, which is not accompanied by any GSB recovery; a biphasic kinetics with two time constants of 100 fs (τ2) and 600 fs (τ3) describing the decay of excited state absorption (ESA) for wavelengths λ<500 nm and a signal rise for longer wavelengths; a decay of the entire signal with two time constants of 12 ps (τ4) and 296 ps (τ5) to a very long-lived (τ6) signal (infinity long-lived with respect to the measured delay interval). The sub-picosecond components are assigned to population dynamics rather than cooling according to the following arguments: (1) the τ1 component is characteristic of a stimulated emission since we observed a large negative signal in a spectral region where no GSB is expected; however it cannot be attributed to the steady state emission in Fig. 1. Indeed it is expected that the width and the shape of unrelaxed emission in fs timescales are still close to the relaxed one.20,21 On the contrary the comparison in Fig. 2B reveals that the pulse-limited signal has a shape distinctly different from the emission/absorption spectrum, i.e. it has a much broader width. As a further confirmation, emission and absorption spectra in Fig. 1 definitively break a mirror-like symmetry pointing to major conformational or electronic change occurring after excitation.20 (2) The τ2 and τ3 components describe two spectral features centred at 360 nm and 650 nm which are spectrally well separated and can be therefore assigned to two ESA bands. τ2 and τ3 are different and are accompanied by sizable changes of the total area. The sign of the DASs is in agreement with a simultaneous decay of an ESA (positive) signal, mainly centred in the blue, and a rise (negative signal) of the long-lived ESA. This assignment is suggestive of a photocycle where the bright excited state does not coincide with the lowest singlet excited state. Consequently, the fastest dynamics are internal conversions (IC) to a low-lying singlet state, as revealed by the steady state emission in the ns timescale. This assignment is also corroborated by hole-burning measurements on phenanthrene monomers in glasses at cryogenic temperatures and time-resolved photoelectron spectroscopy in molecular beams, which report two distinct time constants of 80 fs and 521 fs for the excited states’ decay.22,23 Also the 100 fs component is in agreement with the lifetime of the higher excited singlet states in other aromatic molecules and the suggested IC process via CI was reported in several systems.23–28
Thus, the experimental evidence definitively points to a photocycle (a tentative scheme is depicted in Fig. S1 in ESI†) where (1) the very first relaxation is an ultrafast, pulse-limited (i.e. <40 fs) process, very likely due to the departure from the Frank-Condon (FC) region; (2) the IC relaxation from the bright higher-lying excited singlet state to the lowest excited singlet state consists of a fast (100 fs) and a slow (600 fs) contribution; (3) the 4th and the 5th components describe a decay of the overall signal. We assign the former to a thermally activated non-radiative decay, while the latter is dominated by rotational diffusion.
Molecular modelling using TD-DFT calculations fully confirms the model derived from the experimental observations in as much as they predict two low-lying excited states, namely SA and SB,22,23 both of π,π* nature (Fig. S2 in ESI†) with the former state being dark and the latter one being bright (first column of Table 1). The calculations also predict only a negligible change in the dipole moment norm when going from the ground to the excited state, and consequently solvatochromism can be safely neglected (Fig. S3 in ESI†). Conversely, the sampling of the dynamically and vibrationally allowed conformations29 permits to recover small, but non-zero oscillator strength for the transition to SA (evidenced by the long-wavelength tail in Fig. S3 in ESI†) in agreement with the observed absorption and fluorescence spectra shown in Fig. 1.
| R FC | R S A | R S B | |
|---|---|---|---|
| E(SA) eV | 4.25 | 4.10 | 4.29 |
| (fSA) | (0.00) | (0.00) | (0.00) |
| E(SB) eV | 4.44 | 4.31 | 4.15 |
| (fSB) | (0.29) | (0.28) | (0.53) |
Geometry optimization for the two excited states reveals that their potential energy surfaces (PESs) cross (see Table 1), resulting in a state-inversion process. More importantly the adiabatic energy difference between the two states’ PES minima is quite small, justifying the development of an equilibrium. Hence, to allow for a more precise exploration of the energetic landscape, we calculated the PES over a generalized two-dimensional surface (see the related discussion in computational methods section) connecting the FC region with the two excited state minima (Fig. 3A). For the SB state we find a very steep PES in the FC region which links without any barrier to the CI area between the two states. The appearance of two quasi-degenerate minima for the SA and SB states is also confirmed, and more importantly, the two are separated by a very small barrier that is thermally accessible, hence further justifying the appearance of an equilibrium process even at sub-picosecond timescales.
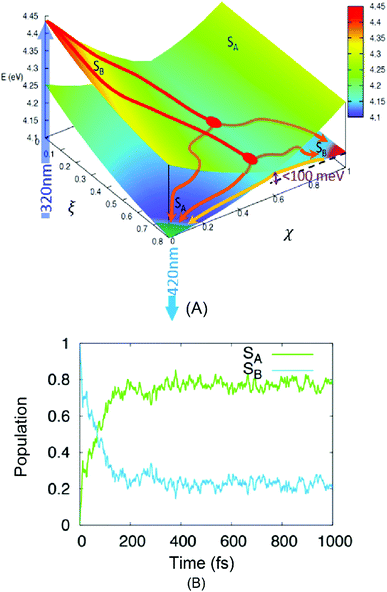 | ||
| Fig. 3 Results of TD-DFT calculations. (A) A low-dimensional representation of the phenanthrene monomer PES as a function of two generalized coordinates (eqn (S3) in ESI†) linking the FC region ((ξ,χ) = (0,0)) and the minima of the lower, dark excited state SA ((ξ,χ) = (1,0)) and the higher bright excited state SB ((ξ,χ) = (1,1)). Energy values from Table 1. An intersection region can be identified at χ = 0.6. The absorption and emission processes (the dark blue arrow at 320 nm and the light blue one at 420 nm, respectively) are also shown. Two possible relaxation paths are sketched for visual purposes. (B) The time-evolution of the population of the two lowest-lying singlet excited states of phenanthrene as obtained from the average of the NAMD trajectories, the dark line is obtained by fitting the population of the SA state to a biexponential model. | ||
The hypothesized relaxation pathway is also confirmed by analysing the evolution of the population of the excited state via NAMD simulations. Indeed, as reported in Fig. 3B one can observe that the population of the SA state reaches ∼80% at 1 ps. However, after a very fast and sharp increase in the population (t < 200 fs), also leading to an evident maximum in the SA population, a quasi-stationary plateau is achieved. The overall population evolution can be interpreted using a multi-step model that gives two distinct time regions: (1) a small impulsive offset (<5 fs) followed by a fast decay in ca. 150 fs, which accounts for ∼80% of the population transfer, and (2) a slow decay taking place in the hundreds of fs to ps regime. These results are in excellent agreement with the experimental measurements and describe the non-adiabatic population of the SA state via the CI region (1) and of the subsequent adiabatic equilibration (2). The evolution of the population in Fig. 3B allows us to estimate the branching ratio of the excited state populations upon passage through the CI to ∼80% and ∼20% towards SA and SB, respectively.
The presence of two distinct pathways is also confirmed by the analysis of the population flow between the states (data not shown). While in the first 200 fs the dynamics are dominated by a net flow from SB to SA, longer timescales show an almost equilibrated number of reciprocal hops between the two surfaces, indicative of an equilibrium between the quasi-degenerate states.
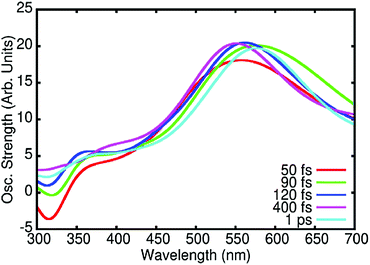
Finally, we also simulated the TA spectra at different times from the NAMD trajectories as reported in Fig. 4. Globally, our calculated spectra correctly reproduce the experimental results, in particular the fast disappearance of the stimulated emission band correlated with the appearance of the ESA band at about 550 nm due to the absorption from the SA state. It is also worth mentioning that Fig. 4 takes into account both ESA and stimulated emission but not GSB. Therefore, the negative simulated signal at λ < 350 nm is only due to the stimulated emission from SB. The stimulated emission from SA, which is centred at 420 nm is on the contrary masked by the much stronger positive ESA signals. Taking into account the lack of the negative contribution at λ < 350 nm due to GSB, the comparison with experimental data (Fig. 2A) and analysis (Fig. 2B) shows that these calculated spectra correctly reproduce the spectral features and temporal evolution of the experimental results, further confirming the soundness of the proposed photocycle.
The photocycle based on our data and simulations is reported in Fig. 5: after the initial population of the bright SB state, the system leaves the FC region in an ultrafast regime, evolving on the PES to the CI region. The absence of significant barriers results in a very rapid photochemical process, which is in accordance with the experimental observations. Once at the CI, the initial excited state population branches towards the SA and SB minima, followed by subsequent thermal equilibration. Hence, according to the experimental and computational results we assigned each DAS component (Fig. 2B) to the following processes: τ1 describes the cooling of the SB potential driven by ultrafast internal vibrational relaxation (IVR). The reported value for this signal is shorter than the measurements’ time resolution (standard deviation) and the real time constant could be a value from 10 to 40 fs; τ2 is ascribed to the arrival at the CI and the IC after branching toward SA; τ3 is assigned to the IC from the equilibrated (but still hot) SB to SA through the small barrier; τ4 refers to a decay of the entire signal without any spectral evolution on timescales typical of vibrational energy transfer to the solvent (cooling). A decrease in the population reveals the presence of non-radiative recombination channels from the hot state of SA; τ5 describes the decay in the amplitude of the entire signal with a value characteristic of rotational diffusion; and finally τ6 is associated with the long-lived population of the relaxed SA state which is responsible for the steady state emission (i.e. fluorescence). Following these assignments we renamed the τ1 to τ6 components as τFC, τIVR, τIC′, τIC′′, τVET, τRot, τFL (see Fig. 5), respectively.
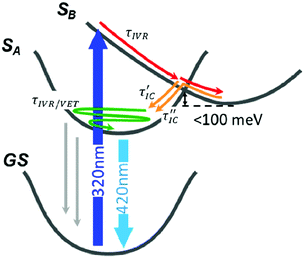 | ||
| Fig. 5 The photocycle of phenanthrene monomer derived from PES and population dynamics in Fig. 3. The different relaxation processes are shown and labelled according to the following notation: IVR, internal vibrational relaxation and redistribution; IC, internal conversion; VET, vibrational energy transfer (τRot, the rotational diffusion term is not shown). Thin grey arrows represent non radiative recombination channels acting only on hot, not thermalized SA. | ||
Experimental and computational methods
Synthesis and sample treatment
The phenanthrene monomer was synthesized according to the literature17 and dissolved in an aqueous buffer solution (10 mM sodium phosphate buffer pH 7.0, 100 mM NaCl). A concentration of ∼1 μM was used to reach an optical density of 0.1 to 0.3 at 320 nm, at the maximum of the phenanthrene lowest visible OA band, in a 200 μm optical path. To avoid sample accumulation and multiple excitations during TA measurements, the solution was flowed using a homemade 200 μm thick flow jet, pumped by a micro-gear pump (mzr-2505).Ultrafast transient absorption spectroscopy
The output of a 5 kHz Ti:Sapphire chirped pulse amplifier (Legend Elite by Coherent, fundamental wavelength at 800 nm, 0.5 mJ energy per pulse, 100 fs pulse duration) is used for pumping a commercial non-collinear optical parametric amplifier (Topas White by Light conversion) in order to produce visible pulses at 640 nm. UV pump pulses at 320 nm (∼2 to 3 nm FWHM), were generated by focusing the collimated 640 nm pulse into a β-BBO crystal (250 μm thickness) and then the frequency is doubled by choosing the right phase matching angle. Afterwards the residual visible radiation was filtered out by a UG11 filter and the excitation UV pulse was recollimated and subsequently focused to a ca. 60 μm diameter spot size (1/e2) with 200 nJ energy per pulse.The probe pulse was a broadband continuum covering from 320 nm to 720 nm, generated by focusing a small fraction of the Ti:Sapphire laser source into a 5 mm thick CaF2 crystal. To avoid thermal damage, the crystal was mounted on a motorized stage horizontally wobbling. The residual 800 nm beam was filtered out by a BG40 filter. Afterwards, the probe beam was split by a 50/50 beam-splitter and focused to two spots with ca. 30 μm diameter spot size on the sample. One of them was spatially overlapped with the pump beam and the other passed through an unexcited sample and was used as a reference (in the following probe and reference, respectively). The temporal overlap and delay time between the pump and the probe were computer controlled by a 30 cm motorized delay stage in the pump path. After the sample, both the probe and the reference beam were collected and collimated by a parabolic mirror and then are spectrally dispersed by a CaF2 prism on two 512 pixel complementary metal–oxide semiconductor (CMOS) sensors (S11105 series by Hamamatsu). The polarization of the pump with respect to the probe was parallel. A power dependence measurement was regularly carried out to ensure that experiments are conducted in a linear absorption regime.
The method used for broadband detection was a single-shot time-resolved spectroscopy scheme. In this scheme the TA signal was calculated from two consecutive probe spectra, the first (IU) without and the second (IP) with pump excitation. More details are presented in the ESI.†
Data analysis of time-resolved spectra
After correction for probe group velocity dispersion, data from −120 to 120 fs around time zero were neglected to avoid artefacts caused by pump–probe cross-phase modulation from the solvent. To analyse the data we adopted Singular Value Decomposition and Global Fit (SVD-GF) analysis19 of the TA data, TA(λ,t), to separate noise, Ξ(λ,t), from the spectral evolution of the system,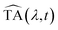 :
: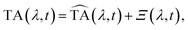 | (1) |
We decomposed the latter as an expansion of exponential decays with characteristic lifetimes (τk) and DASs:
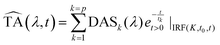 | (2) |
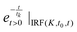 represents an exponential decay with a decay constant τk multiplied by the Heaviside step function u0(t) and convoluted with the instrument response function (IRF). The latter is assumed to be a Gaussian centred at t0 and with a full width at half maximum of K. For the measurements described here 6 exponential decay components (p = 6) were sufficient to describe all relevant (above noise) dynamics.
represents an exponential decay with a decay constant τk multiplied by the Heaviside step function u0(t) and convoluted with the instrument response function (IRF). The latter is assumed to be a Gaussian centred at t0 and with a full width at half maximum of K. For the measurements described here 6 exponential decay components (p = 6) were sufficient to describe all relevant (above noise) dynamics.
The presence of a pulse-limited contribution was necessary in order to obtain a satisfying fitting. To describe such a contribution we introduced the τ1 component which has indeed a time duration (20 fs) much smaller than the experimental time IRF (∼40 fs). In this case the preserved quantity in the fitting is the product of the amplitude and τ1. For this reason we can reduce the amplitude of the τ1 DAS, for the sake of visibility as shown in Fig. 2B, since the comparison of its amplitude with other DASs has no physical meaning.
Molecular modelling and simulation
The ground state equilibrium geometries of phenanthrene monomers were obtained at density functional theory (DFT) level, using the ωB97XD exchange, correlation functional and the 6-31G* basis set as implemented in the GAUSSIAN 09 software package.30 Absorption spectra at the FC region are obtained either as vertical transitions from the equilibrium geometry, only or taking into account the effects of thermal motions and vibrations by a sampling of the accessible conformational space via a Wigner distribution based on the harmonic vibrational frequencies, following a successful protocol widely used by some of the authors.31–36 The geometries of the first (SA, dark) and the second (SB, bright) excited states have been optimized using TD-DFT at the same level of theory as described above. In addition, the PESs have been explored by means of a bi-dimensional linear interpolation via two generalized coordinates linking the FC region (RFC) and the two excited states minima RSA and RSB, respectively as reported in eqn (3). For visualization purposes, weighting was chosen to have R(0,0) = RFC, R(1,0) = RSA and R(1,1) = RSB. This was done considering a weighted average of the three equilibrium geometries as the two generalized coordinates which take into account the electronic relaxation, ξ and χ, varying between 0 and 1. This method considers interpolation between the different structures and even though it could lead to an overestimation of the potential energy barriers, it ensures a connected path between the considered structures.| R(ξ,χ) = RFC(1 − ξ)(1 − χ) + RSAξ(1 − χ) + RSBχ | (3) |
The nature of the excited states has also been identified using Natural Transition Orbitals (NTOs). For the readers convenience we remind that NTOs, based on the singular value decomposition of the transition density matrix, represent the ideal orbital base to express an electronic transition. Thus, in most of the cases, each excited state can be represented as a transition from the occupied NTO, representing the area from which the electronic density is depleted, to the virtual NTO, representing the region to which the electronic density is accumulated. To validate the TD-DFT level of theory, the vertical excitation and the most relevant pathways along the PES have also been computed using the ab-initio, complete active space self-consistent field corrected by second order perturbation (CASPT2) method as implemented in the MOLCAS 8 software package (see ESI† for details).37
NAMD at the TD-DFT level of theory has been performed to study the excited state decay of phenanthrene and determine the CI branching ratio and the electronic relaxation timescales. 98 trajectories, all of them starting in the bright SB state (S2), have been run for 1 ps allowing excited state population exchanges via the surface hopping algorithm as implemented in SHARC 2.0.38,39 The initial conditions have been stochastically generated from a Wigner distribution around the Franck–Condon region, and the NAMD trajectories have been propagated in the diagonal formalism as implemented in the SHARC algorithm. The ADF modelling suite40–42 has been used for the calculation of the electronic energies, gradients and coupling. The benchmark of the level of theory used for the NAMD simulations, against the high-level multiconfigurational method is also presented in the ESI† fully validating our approach. The time-scales of all the relevant processes have been obtained by the analysis of the global, i.e. averaged over all the trajectories, evolution of the population of the SA and SB state. The time-resolved TA spectra have been calculated a posteriori on top of snapshots extracted from the NAMD at selected times using the TERACHEM software43,44 to obtain the oscillator strength values between the excited states giving access to stimulated emission and ESA signals. The corresponding vertical transitions have been convoluted with Gaussian functions following the same protocol as the one used for the simulation of the steady-state spectra. Note that excitation energies and the corresponding oscillator strengths have been calculated from the active states at a given time for each trajectory as obtained by the NAMD simulations. Further details can be found in the ESI.†
Conclusions
We carried out femtosecond transient absorption measurements on phenanthrene monomers with carboxamide substituents to reveal the photocycle of the monomer units. The combination of time-resolved spectroscopy and molecular modeling allows an original photophysical cycle to be proposed. The first ground state absorption band in phenanthrene is dominated by transition to the second excited singlet state, SB, which relaxes very quickly toward a CI with the darker SA state. Here the excited state population splits into two relaxation pathways, either giving rise to a non-adiabatic transition to SA (∼80%), or proceeding adiabatically towards the equilibrated SB minimum (∼20%). The fraction of the population reaching the SB equilibrium geometry rapidly equilibrates with the SA state because the former is higher in energy and separated from the latter by a relatively low and thermally accessible barrier. This photophysical mechanism shows the concurrence of different electronic states connected first by a CI and later via a thermal barrier, leading to different time constants of <40 fs (pulse limited), 100 fs and 600 fs. It can be safely concluded that the global dynamics is definitively more complex than a simple two level system, because of the change in the nature of the electronic states and time constants, and due to the simultaneous presence of non-adiabatic (i.e. CI mediated) and adiabatic (i.e. thermally mediated) transitions, which are strongly dependent on the topology of the excited state PES. In this case, the timescales of the different phenomena may be much more sensitive to environmental and configurational changes than the main optical features, as steady state optical absorption and emission bands. This novel knowledge on the major differences of phenanthrene photocycles with respect to a simpler two-level system photocycle, usually and silently assumed for small UV and Vis dyes, could be crucial to a proper comprehension of photochemistry of PAHs and MCSs based on them. For instance the presence of a ∼1 ps long-lived higher-lying excited state should question the validity of the Kasha's rule for phenanthrene based systems and PAHs in general.45 Indeed, phenanthrene can also be considered as a paradigmatic representative of the PAH family, that due to the rather extended π-conjugation pattern shows a high density of competing π−π* excited states, most notably giving raise to excited state CIs and to the instauration of rather complicated photophysical pathways, like the ones highlighted in the present study. As such, our results could also shed a novel and more general light on the interpretation of the photophysics of conjugated organic systems that should go beyond the simple and text-book interpretation of a S1 dominated relaxation channel taking into account the interplay with other low energy states that may become crucial.The insights gained by our combined study are not only fundamental to understand the photophysics of phenanthrene monomers, but may also be valuable in the design of efficient multichromophoric light harvesting systems. Indeed, the planar PAHs can provide strong inter-chromophoric coupling and hence a more directional and faster EnT. However to finely tune and control such processes a detailed knowledge of the evolution of the accessible excited states is necessary. In particular, higher excited states characterized by a ps lifetime can have a valuable impact on the global photo excited processes and can hence be exploited to achieve more efficient molecular devices.
Author contributions
M. Nazari, A. Rondi, M. Gazzetto, A. Cannizzo and T. Feurer implemented and performed the TA experiment and the data analysis. C. D. Bösch, S. M. Langenegger and R. Häner synthesized and characterized the sample by means of steady-state absorption measurement. All the computational study and molecular modeling were carried out by A. Francés-Monerris, M. Marazzi, E. Lognon and A. Monari. The scientific interpretation of the data, the final model and the manuscript were done through contributions from all the authors. All the authors have given their approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. Nazari, A. Rondi, M. Gazzetto, and A. Cannizzo gratefully acknowledge the financial support from the ERC Starting Grant 279599-FunctionalDyna and Swiss NSF through the NCCR MUST “Molecular Ultrafast Science and Technology”. The support from NCCR MUST is also acknowledged by T. Feurer. R. Häner gratefully acknowledges financial support by the SNSF (grant 200020_169030) and NCCR MUST. Molecular modeling and simulations have been performed on the LPCT local computing resources. M. Marazzi is grateful to Universidad de Alcalá for a postdoctoral fellowship. A. Francés-Monerris is grateful to the French ANR and the Spanish Government (CTQ2017-87054-C2-2-P) for the financial support.Notes and references
- K.-H. Kim, S. A. Jahan, E. Kabir and R. J. C. Brown, Environ. Int., 2013, 60, 71–80 CrossRef CAS PubMed.
- J. M. Delgado-Saborit, C. Stark and R. M. Harrison, Environ. Int., 2011, 37, 383–392 CrossRef CAS PubMed.
- C. Boersma, J. Bregman and L. J. Allamandola, Astrophys. J., 2018, 858, 65–84 CrossRef.
- K. I. Öberg, Chem. Rev., 2016, 116, 9631–9663 CrossRef PubMed.
- G. R. Fleming, G. S. Schlau-Cohen, K. Amarnath and J. Zaks, Faraday Discuss., 2012, 155, 27–41 RSC.
- A. C. Benniston and A. Harriman, Mater. Today, 2008, 11, 26–34 CrossRef CAS.
- D. M. Watkins and M. A. Fox, J. Am. Chem. Soc., 1994, 116, 6441–6442 CrossRef CAS.
- R. Huber, N. Amann and H.-A. Wagenknecht, J. Org. Chem., 2004, 69, 744–751 CrossRef CAS.
- C. B. Winiger, S. Li, G. R. Kumar, S. M. Langenegger and R. Häner, Angew. Chemie - Int. Ed., 2014, 53, 13609–13613 Search PubMed.
- G. Kodis, P. A. Liddell, L. De la Garza, P. C. Clausen, J. S. Lindsey, A. L. Moore, T. A. Moore and D. Gust, J. Phys. Chem. A, 2002, 106, 2036–2048 CrossRef CAS.
- E. Collini, Chem. Soc. Rev., 2013, 42, 4932–4947 RSC.
- S. S. Lampoura, C. Spitz, S. Dähne, J. Knoester and K. Duppen, J. Phys. Chem. B, 2002, 106, 3103–3111 CrossRef CAS.
- F. Garo and R. Häner, Angew. Chemie - Int. Ed., 2012, 51, 916–919 Search PubMed.
- M. Probst, S. M. Langenegger and R. Häner, Chem. Commun., 2014, 50, 159–161 RSC.
- M. Kownacki, S. M. Langenegger, S. X. Liu and R. Häner, Angew. Chem., Int. Ed., 2019, 58, 751–755 CrossRef CAS PubMed.
- C. D. Bösch, S. M. Langenegger and R. Häner, Angew. Chem., Int. Ed., 2016, 55, 9961–9964 CrossRef PubMed.
- S. M. Langenegger and R. Häner, Helv. Chim. Acta, 2002, 85, 3414–3421 CrossRef CAS.
- A. Cannizzo, Phys. Chem. Chem. Phys., 2012, 14, 11205–11223 RSC.
- A. Cannizzo, A. M. Blanco-rodríguez, A. El Nahhas, J. Šebera, S. Záliš, A. V. Jr and M. Chergui, J. Am. Chem. Soc., 2008, 3, 8967–8974 CrossRef PubMed.
- O. Braem, T. J. Penfold, A. Cannizzo and M. Chergui, Phys. Chem. Chem. Phys., 2012, 14, 3513–3519 RSC.
- O. Bräm, F. Messina, A. M. El-zohry, A. Cannizzo and M. Chergui, Chem. Phys., 2012, 393, 51–57 CrossRef.
- B. Dick and B. Nickel, Chem. Phys., 1986, 110, 131–134 CrossRef CAS.
- M. Schmitt, S. Lochbrunner, J. P. Shaffer, J. J. Larsen, M. Z. Zgierski and A. Stolow, J. Chem. Phys., 2001, 114, 1206–1213 CrossRef CAS.
- A. Sinicropi, E. Martin, M. Ryazantsev, J. Helbing, J. Briand, D. Sharma, J. Leonard, S. Haacke, A. Cannizzo, M. Chergui, V. Zanirato, S. Fusi, F. Santoro, R. Basosi, N. Ferre and M. Olivucci, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17642–17647 CrossRef CAS.
- J. Briand, O. Bräm, J. Réhault, J. Léonard, A. Cannizzo, M. Chergui, V. Zanirato, M. Olivucci, J. Helbing and S. Haacke, Phys. Chem. Chem. Phys., 2010, 12, 3178–3187 RSC.
- M. Vacher, J. Meisner, D. Mendive-Tapia, M. J. Bearpark and M. A. Robb, J. Phys. Chem. A, 2015, 119, 5165–5172 CrossRef CAS PubMed.
- G. Zgrablić, A. M. Novello and F. Parmigiani, J. Am. Chem. Soc., 2012, 134, 955–961 CrossRef PubMed.
- T. A. A. Oliver, N. H. C. Lewis and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10061–10066 CrossRef CAS PubMed.
- S. Mai, H. Gattuso, A. Monari and L. González, Front. Chem., 2018, 6, 495 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Incm, Wallingford CT, 2013 Search PubMed.
- A. Francés-Monerris, C. Hognon, M. A. Miranda, V. Lhiaubet-Vallet and A. Monari, Phys. Chem. Chem. Phys., 2018, 20, 25666–25675 RSC.
- A. Francés-Monerris, K. Magra, M. Darari, C. Cebrián, M. Beley, E. Domenichini, S. Haacke, M. Pastore, X. Assfeld, P. C. Gros and A. Monari, Inorg. Chem., 2018, 57, 10431–10441 CrossRef PubMed.
- H. T. Turan, Y. Eken, M. Marazzi, M. Pastore, V. Aviyente and A. Monari, J. Phys. Chem. C, 2016, 120, 17916–17926 CrossRef CAS.
- O. Sengul, M. Marazzi, A. Monari and S. Catak, J. Phys. Chem. C, 2018, 122, 16315–16324 CrossRef CAS.
- H. Gattuso, A. Monari and M. Marazzi, RSC Adv., 2017, 7, 10992–10999 RSC.
- H. Gattuso, M. Marazzi, F. Dehez and A. Monari, Phys. Chem. Chem. Phys., 2017, 19, 23187–23193 RSC.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- S. Mai, M. Richter, M. Heindl, M. F. S. J. Menger, A. Atkins, M. Ruckenbauer, F. Plasser, M. Oppel, P. Marquetand and L. González, http://sharc-md.org, 2018.
- S. Mai, P. Marquetand and L. González, WIREs Comput. Mol. Sci., 2018, 8, e1370 CrossRef PubMed.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, O. Baseggio, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerritger, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, S. M., M. Swart, D. Swerhone, G. te Velde, V. Tognetti, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2014, ADF2016, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2008, 4, 222–231 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 1004–1015 CrossRef CAS PubMed.
- A. P. Demchenko, V. I. Tomin and P. Chou, Chem. Rev., 2017, 117, 13353–13381 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (A) Calculation of TA signal in single-shot detection; (B) tentative photocycle derived from the analysis of the experimental data only; (C) TD-DFT calculations; (D) details on multiconfigurational calculations and calibration of the molecular models and the TD-DFT method; (E) non-adiabatic molecular dynamics simulations; supporting Fig. S1–S7; supporting Tables S1 and S2; supporting references. See DOI: 10.1039/c9cp03147b |
| This journal is © the Owner Societies 2019 |