Novel fluid–fluid interface domains in geologic media
Juliana B.
Araújo
 a and
Mark L.
Brusseau
*ab
a and
Mark L.
Brusseau
*ab
aSoil, Water, and Environmental Science Department, School of Earth and Environmental Sciences, The University of Arizona, Tucson, AZ 85721, USA. E-mail: Brusseau@email.arizona.edu
bHydrology and Atmospheric Sciences Department, School of Earth and Environmental Sciences, The University of Arizona, Tucson, AZ 85721, USA
First published on 13th December 2018
Abstract
Pore-scale fluid processes in geological media are critical for numerous applications in several fields. Continued improvement of high-resolution image acquisition and processing methods has provided a means to directly characterize pore-scale fluid processes for natural geomedia, and to test the representativeness of theoretical and computational models developed to simulate them. High-resolution synchrotron X-ray microtomography (XMT) combined with advanced 3-D image visualization was used to investigate the impact of larger-scale solid-surface heterogeneity on nonwetting–wetting (air–water) interfacial area for two natural geomedia (a sand and a soil). The studies revealed the presence of air–water interfaces associated with water residing within macroscopic features such as pits and crevices on the surfaces of the solids. The diameters of the features ranged from tens to 100's of μm for the sand, and the aggregate associated air–water interfacial area was estimated to represent ∼12% of the maximum capillary interfacial area. These features and respective fluid interfaces, which are not considered in standard conceptualizations of fluid distribution in geomedia, may have an impact on pore-scale physical and biogeochemical processes.
Environmental significanceThe pore-scale behavior of fluids in geological media is critical for numerous applications in an array of fields. Physical processes occurring at the pore scale dictate fundamental fluid behavior. A critical aspect of fluid configuration in unsaturated systems is the air–water interface. It influences interfacial retention of organic and inorganic contaminants, and mediates various mass-transfer processes. The study revealed the presence of air–water interfaces associated with water residing within macroscopic features on the surfaces of the solids. These features and respective fluid interfaces, are not considered in standard conceptualizations of fluid distribution in geomedia. Initial analysis suggests that the additional interfacial area may comprise an appreciable magnitude in comparison to capillary interfacial area. |
1. Introduction
Physical processes occurring at the pore scale dictate fundamental fluid behavior including fluid displacement and distribution. The pore-scale behavior of fluids in geological media is critical for numerous applications in an array of fields, including petroleum engineering, geoengineering, and hydrology. For example, multiphase-flow scenarios abound in energy applications, such as secondary/tertiary oil recovery and application of hydraulic fracturing to enhance oil and gas recovery. It is also central for geologic carbon sequestration via CO2 injection and storage, as well as radioactive waste storage in geologic formations. Multiphase flow controls soil-moisture distribution in vadose-zone systems, which in turn mediates plant and microbial activity (crop production, carbon/nutrient exchange), transport of pollutants, and land stability (e.g., landslides, land subsidence).The advent of advanced imaging methods such as high-resolution industrial and synchrotron XMT has provided a means to directly characterize 3-D porous-media systems at the pore scale. This has allowed investigation of immiscible-displacement processes, characterization of fluid–fluid interfaces, and examination of other relevant properties and processes.1–26 Concomitantly, significant effort over the past two decades has focused on integrating pore-scale characterization with pore-scale modeling, using XMT data for example to test the efficacy of theoretical and computational models.16,23,27–30
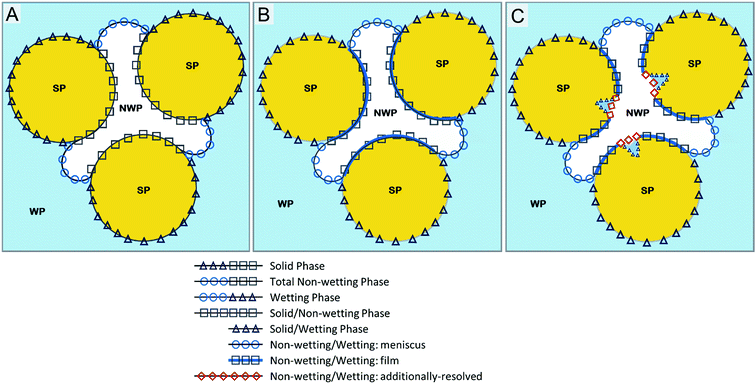
The initial focus of this work was on characterizing pore structure and fluid distribution for idealized systems. For example, a standard conceptualization used for theoretical and computational modeling is based on an ideal packing of smooth, spherical solids as illustrated in Fig. 1A. This approach reduces computational requirements while also simplifying theoretical considerations. These typical approaches employ simplifying assumptions for the representation of fluid–fluid interfaces. Many models are based on the assumption that fluid–fluid interface consists solely of capillary-associated interfacial area (terminal menisci, pendular-ring/wedge menisci), and that wetting-fluid films are nonexistent (Fig. 1A). Other models incorporate the presence of wetting films associated with smooth solid surfaces (Fig. 1B). While prior efforts based on these approaches have advanced our understanding of fluid behavior at the pore scale, continued advancement requires consideration of more representative geomedia. The continued development of newer-generation industrial XMT and particularly of synchrotron-based XMT has produced higher resolutions, in the range of 10 μm to 1 μm and lower, allowing for detailed examination of the many factors that influence fluid displacement and distribution in natural porous media.
One factor of interest is the impact of physical heterogeneities, often referred to as surface roughness, that are prevalent on the surfaces of the solid grains of most porous media. These heterogeneities encompass different sources and types of features that span a wide range of spatial scales. For example, nanometer-scale roughness has long been a focus of attention with respect to its impact on solid surface areas and relevant processes such as adsorption and surface-mediated reactions. The impacts of surface heterogeneities on the displacement and distribution of fluids in porous media have long been investigated.31–39 Much of this work has focused on smaller-scale surface features, often generated synthetically. Conversely, a study by Tokunaga et al.39 characterized the surfaces of gravel particles and demonstrated the presence of multiple scales of heterogeneities, with the largest features consisting of isolated pits with dimensions of several hundred μm. The potential impact of the water inferred to be residing within these features, based on indirect measurements, on hydraulic behavior and contaminant retention was discussed.
While the effects of surface roughness on pore-scale fluid behavior have been investigated in prior research, there has been minimal direct characterization of larger-scale (macroscopic) solid-surface features and their influence on the distribution of wetting fluid and the associated formation of fluid–fluid interfaces. This study employs high-resolution synchrotron XMT imaging in conjunction with advanced 3-D visualization tools to examine the air–water interface in natural geomedia, with a focus on interface associated specifically with surface heterogeneities that can be resolved by the micron-scale imaging resolution. This interface domain is not currently represented in standard conceptual models.
2. Materials and methods
The focus of this study is on characterizing the potential existence of novel air–water interfaces, and not on quantifying magnitudes of associated interfacial area. Therefore, the work employs only grey-scale, non-segmented image data. The absence of image segmentation significantly reduces the potential impact of segmentation-associated artifacts on image generation and interpretation. However, it also precludes the quantification of interfacial areas.2.1. Materials
A natural quartz sand and a sandy subsoil were used as representative natural geologic media. A model glass bead pack consisting of 1 mm borosilicate glass beads (Sigma-Aldrich) was used as a model reference porous medium for consistency with the standard conceptual model and prior imaging studies. Physical properties of the media are presented in Table 1. All properties were measured for this or prior studies conducted in our laboratory.| ρ p (g cm−3) | d 50 (mm) | U (d60/d10) | ρ b (g cm−3) | n g (—) | γ (°) | GSSAg (cm−1) | N2BETh (cm−1) | |
|---|---|---|---|---|---|---|---|---|
| a Particle density (ρp). b d 50 = mean particle diameter. c U a = uniformity coefficient, di is the percentage of grains smaller than a given sieve size. d Bulk density. e Gravimetric porosity. f Contact angle, measured with a Kruss model DSA10 sessile-drop contact angle system. g Geometric specific solid surface area based on smooth-sphere assumption, (=6(1 − n)/d50, where d50 is mean particle diameter). h N2-Brunauer, Emmet and Teller (NBET)40 surface area. This value represents the total external solid surface area available in the system and incorporates surface area associated with microscopic surface roughness. | ||||||||
| Glass beads | 2.21 | 1.00 | 1.0 | 1.52 | 0.42 | 22 | 31 ± 2 | 28 ± 2 |
| Sand | 2.64 | 0.35 | 1.1 | 1.8 | 0.36 | 39 | 113 ± 4 | 1333 ± 31 |
| Soil | 2.59 | 0.28 | 2.4 | 1.5 | 0.38 | n/a | 137 ± 5 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 5000 000 ± 5000 |
Both of the natural media have significant surface roughness, as illustrated by the orders of magnitude disparity between their respective geometric and NBET-measured solid surface areas (Table 1). Scanning electron micrographs (SEM) presented in Fig. 2 illustrate the presence of micrometer-scale surface features such as pits and crevices for the sand (Fig. 2A) and soil (Fig. 2B). In contrast to the two natural media, the glass beads have smooth surfaces devoid of roughness. This is illustrated by the similarity of geometric and NBET-measured solid surface areas (Table 1).
The wetting phase was doped with 12% potassium iodide (KI) (Fisher Scientific) to enhance image contrast between phases. Thin-walled polycarbonate columns (L = 3.2 cm, ID = 0.63 cm) were used for the experiments. The columns were packed with the selected porous media to obtain uniform bulk densities. A hydrophilic capillary membrane (15 μm pore diameter) was attached to the bottom of the column and a fine mesh was used at the top of the column to retain the porous media. A programmable electronic syringe pump (KD Scientific) with a 2.5 mL gas-tight syringe was connected to the bottom of the column. The columns were fully saturated with KI solution prior to imaging.
Once prepared, the columns were imaged as described below to determine baseline saturation conditions. After imaging of the saturated sample was completed, several drainage steps were induced by removing a small increment of solution from the column using a low flow rate. The column was then allowed to equilibrate between each drainage step for at least 15 minutes prior to imaging. The increment volume required was determined based on the pore volume of the column, and correlation to the soil-moisture characteristic curve. The displacement was monitored by weighing the column before and after each drainage step, and optimized for the allotted experimental time. This procedure was repeated multiple times until reaching residual saturation. Residual saturation was established when the weight of the column remained unchanged after a drainage step. The volume of water was measured for each image set after data acquisition, and the results showed that a constant water volume was attained by the last two image sets. The data presented in this study represent the end of a primary drainage cycle unless otherwise indicated.
2.2. Image acquisition
X-ray microtomography images were collected at the GeoSoilEnviroCARS (GSECARS) BM-13D beamline of the Advanced Photon Source at Argonne National Laboratory, Il. The images were collected from the vertical centers of the columns, to minimize the potential influence of column end effects. The imaged-domain volumes fulfill representative elementary volume requirements.1,4,15,41,42Sequential images of the columns were collected above and below the iodine absorption edge, at 33.269 and 33.069 keV, respectively. The above-the-edge image (A-image) was used to highlight the liquid phase, and the below-the-edge image (B-image) was used to distinguish the solid phase. The image data collection was conducted with a resolution of 7.4 μm (binned). Higher resolution (less than 2 μm) data were obtained at a single energy (26 keV) to further investigate the targeted features. These images required significantly greater collection time and thus could be collected only in limited quantities.
The images were reconstructed with GSECARS-developed software.43,44 The program consists of a set of IDL© (ITT, Visual Information Solutions) routines that were designed to view the CCD camera data, remove artifacts, correct for dark currents, and to perform a white field correction. Furthermore, it aligns the rotation axis based on alignment of the sonograms, removes ring artifacts, and filters noise. Finally, the program writes the reconstructed data as a single three-dimensional volume file, which can be exported into a series of individual slices or imported into a 3D viewer such as ImageJ.45 The resulting image consists of grayscale values ranging from 0 (black) to 255 (white) for 8 bit resolution for example, which corresponds to low and high X-ray attenuation, respectively. For the purposes of this work, this reconstructed greyscale image volume is referred to as the original greyscale. Further details regarding the microtomography capabilities are discussed in ref. 43 and 46. Facility details are available at the APS GSECARS webpage (http://cars9.uchicago.edu/software/tomography.html).
2.3. Image visualization
The original greyscale images were cropped with ImageJ. A circular cropping area was chosen such that it encompassed a large portion of the sample and removed the column wall, while maintaining an REV. The 3-D visualization was conducted using commercial software (AMIRA©, FEI visualization) designed for the analysis and visualization of tomography data, among other applications. Standard noise-reduction filters were applied to the cropped images within the program prior to visualization. Specifically, median smoothing and an intensity correction filter were applied uniformly to the entire domain. The application of these filters was optimized based on several subsample test sequences for each medium.2.4 Interfacial areas
The total surface area of air, the non-wetting phase, is used to determine total air–water interfacial area (Aia). This is based on the fact that the surfaces of the solids are water wetting, and therefore that thin water films are present that cannot be resolved by microtomography. The interfacial areas reported in this work represent the volume normalized specific interfacial area, wherein the areas are normalized by the volume of the imaged domain (with units of cm2 cm−3 or cm−1). Water saturation is computed from volumetric water content and total porosity obtained from phase volumes.Specific capillary interfacial area (Cia) refers to interfaces associated with the menisci of contacts between air and “bulk” water (partially filled capillaries, pendular rings, and wedges). It is calculated as one half of the difference between the combined sum of the water phase (aw) and air phase (aa) surface areas and the solid phase (as) surface area (0.5 × [aa + aw − as]).30,47 This calculation is based on a simple phase-balance analysis of surface areas and interfacial contacts in a three-phase (solid, wetting fluid, non-wetting fluid) porous medium. Water films are assumed to not exist for this conceptualization (Fig. 1A).
3. Results and discussion
Image data for a representative glass bead pack under primary drainage conditions are presented in Fig. 3. The spherical geometry of the glass beads and the accompanying ideal packing is clearly observed. The smooth nature of the solid surfaces, free of pits, crevices, and other such features, is also evident.The distribution of the wetting phase (water) is shown in a 2-D cross-sectional slice of the volume (Fig. 3B) and in a 3-D subsection (Fig. 3C). It is observed that water exists primarily as pendular rings and wedges in contact with the solids, as would be expected for a system at low water saturation. Wetting films present for these water-wetting solids (see Table 1 for contact angles) are not observed due to the resolution limitation of the imaging. The nonwetting–wetting fluid interface for the glass-bead system is visualized in Fig. 3D upon removal of the solids present in Fig. 3C. It is observed that the interfaces consist of menisci associated with the pendular rings and wedges. The observed distribution of fluid and interface is in agreement with conceptual model A (Fig. 1A).
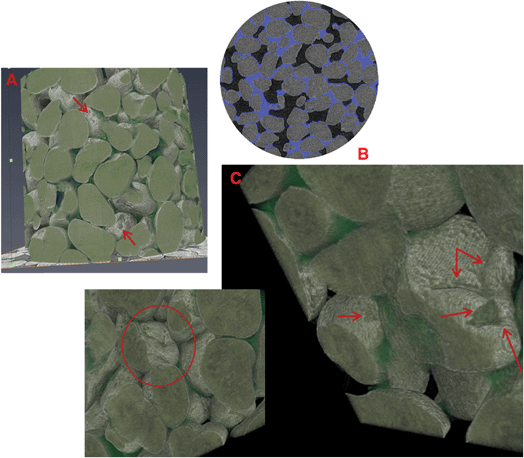
Fig. 4 shows a 3-D rendering of the natural sand under primary drainage conditions. The false-color map overlay (Fig. 4A) is used to visually accentuate the boundaries between the wetting fluid and solid grains. Features such as pits and crevices are observed on the surfaces of the solids, in contrast to the smooth glass beads. Comparison of the image data to scanning electron microscopy images (Fig. 2) indicates that the image acquisition and visualization methods preserved the original characteristics of the porous-medium solids. The ideal media, such as the glass beads shown in Fig. 3, often employed in pore-scale imaging or modeling do not represent these surface features.
The distribution of wetting fluid within the sand is presented for a 2-D slice in Fig. 4B and for a 3-D subsection in Fig. 4C. Additional imaging was conducted at a higher resolution for further evaluation of fluid distribution associated with the solid-surface features (see Fig. 5). Wetting fluid is observed to reside within some of the surface features (see for example Fig. 4C and 5). Nonwetting–wetting interface is created for such fluid when the local pore body domain is drained.
Fig. 6 shows a 3-D greyscale rendering of the soil at the midpoint of primary drainage. The blue false-color overlay is used to accentuate the boundaries between the wetting fluid and solid grains. Fig. 6C shows a ‘pit’ observed on the surface of a solid grain, with wetting fluid residing within as indicated by the red arrow. Fig. 6D shows 3-D magnification of this ‘pit’ on the surface of the solid grain.
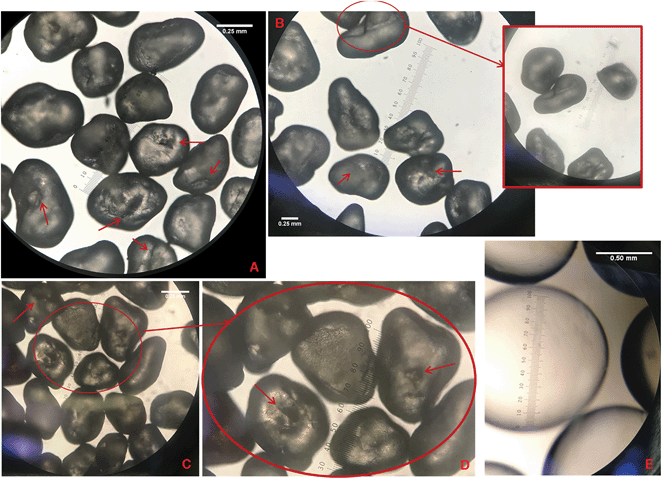
Fig. 7 and 8 show images of the sand and soil, respectively, obtained using a phase-contrast microscope. The red arrows indicate illustrative pits and crevices, as observed in the SEM and high-resolution synchrotron microtomographic images. Fig. 7B–D correspond to areas where larger features are observed. Similar features of varying sizes are also observed for the soil (Fig. 8), and they are comparable to those observed for the XMT images (Fig. 6). In contrast, Fig. 7E shows an image of a glass bead sample, where the beads are clearly smooth and spherical.
The macroscopic surface features observed for the grains are capable of retaining wetting fluid (Fig. 5 and 6) when the local pore body domain is drained. Thus, they can contribute to additional interfacial area not accounted for in the standard model. This additional interfacial domain is illustrated in Fig. 1C in a proposed updated conceptualization of fluid distribution in natural porous media. The water residing within these features create isolated menisci separate from menisci associated with the inter-granular pore space.
One question of interest is the overall contribution of the fluid–fluid interfaces associated with these features to the total interface inventory in the system. The size of each observable feature was measured for several individual sand grains present in Fig. 7A–D. Measurements of the size of each grain were also recorded for comparison. The mean average grain size (d50) of the selected sample is 0.42 mm, approximately 20% larger than the mean of 0.35 mm (Table 1) obtained using standard sieve analysis. The coefficient of uniformity is 1.4 and the GSSA is 92.1 cm−1. These values are comparable to those in Table 1 for the bulk sand, indicating that the subsample is representative of the bulk.
For the selected subsample, the diameters of the features ranged over a factor of four, with the smallest, more frequent features of approximately 0.036 mm (10th percentile) and larger features approximately 0.128 mm (85th percentile). The mean representative diameter of the surface features is 0.09 mm. A similar analysis conducted using the XMT images shown in Fig. 5 results in an average feature size of 0.1 mm, consistent with the prior analysis. Using these measurements, and assuming spherical geometries, the aggregate surface area of the features represents between approximately 1–3% of the total geometric solid surface area. The depth of the features range from a few micrometers to several tens of micrometers. The volume of water associated with these features is estimated to comprise a small fraction of the total water present, approximately 2%. This is consistent with the results reported by Tokunaga et al.39
Prior analysis of several XMT data sets collected for the sand produced a maximum capillary interfacial area of 18 cm−1 for a water saturation of 0.25.48 This is in contrast to a total Aia of 70 cm−1 at the same water saturation. Assuming that the aggregate area of the features is 2% of the total solid surface area results in an Aia for the features of ∼2 cm−1. This corresponds to approximately 12% of the maximum capillary interfacial area.
4. Conclusion
The high-resolution imaging and 3-D visualization conducted for this study revealed the presence of wetting-fluid bodies and attendant nonwetting–wetting fluid interface associated with macroscopic surface features on the surfaces of the solids. These isolated fluid bodies and menisci provide additional nonwetting–wetting interfacial area beyond that contributed by menisci associated with inter-granular pore space and films wetting solid surfaces. This fluid–fluid interfacial area is not accounted for in the standard conceptualizations used for modeling (Fig. 1A and B). This additional interfacial domain is illustrated in Fig. 1C in a proposed updated conceptualization of fluid distribution in porous media.The volume of water associated with the surface features was estimated to be a small percentage of total water volume. Because the media used herein are water-wetting, it is presumed that water films are solvating the surfaces of the solids. These films are likely connected to the water residing within the surface features. However, the films are generally not resolvable due to resolution limitations of the imaging. The overall impact of these features and associated water on hydraulic properties is anticipated to be relatively small, based on the results of prior investigations. However, the large-scale surface roughness may have an impact on local fluid-displacement processes and the associated distribution of fluids within a sample.
While the magnitude of air–water interface associated with the surface features was estimated to be a small fraction of total interfacial area, it could have an effect on biogeochemical processes relevant to contaminant transport and nutrient cycling. For example, altering the air–water interface can influence the disposition of microbial colonies (e.g., biofilms) on solid surfaces.18,19 Biofilms are dependent on a delicate balance of nutrients, and alterations to the air–water interface may affect the local microenvironment for the community. The water layers residing within the large surface features are generally thicker than the typical water films solvating solid surfaces, which could limit the nutrient access of microbes residing within that domain. Such impacts can alter the magnitude and rate of biogeochemical processes occurring within the microsites. The heterogeneity of the surfaces of natural media poses challenges to pore-scale imaging and modeling. Additional study is warranted to quantify the interfacial area contributed by these features, and their impact on pore-scale processes.
Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
The authors would like to thank Dr Mark Rivers (APS) for his assistance in conducting the imaging. Also, we thank Dr Hua Zhong and Asma El Ouni (UA Contaminant Transport Lab) for their assistance during image acquisition, as well as Marvin Landis and Chris Deer (Visualization Lab, UITS The University of Arizona) for their assistance with 3-D visualization software. Additional thanks to Dr Maier (The University of Arizona) for the use of the phase contrast microscope. Finally, we thank the reviewers for their constructive comments. The data presented in this study is available upon request. This research was supported by the NIEHS Superfund Research Program (Grant P42 ES 04940). This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. We acknowledge the support of GeoSoilEnviroCARS (Sector 13), which is supported by the National Science Foundation - Earth Sciences (EAR-1128799), and the Department of Energy, Geosciences (DE-FG02-94ER14466). The visualization resources were made available through the TRIF-SEOS grant initiative (AZ).References
- K. A. Culligan, D. Wildenschild, B. S. B. Christensen, W. G. Gray, M. L. Rivers and A. F. B. Tompson, Interfacial area measurements for unsaturated flow through a porous medium, Water Resour. Res., 2004, 40, W12413 CrossRef.
- R. I. Al-Raoush and C. S. Willson, Extraction of physically realistic pore network properties from three-dimensional synchrotron X-ray microtomography images of unconsolidated porous media systems, J. Hydrol., 2005, 300, 44–64 CrossRef CAS.
- G. Schnaar and M. L. Brusseau, Pore-scale characterization of organic immiscible-liquid morphology in natural porous media using synchrotron X-ray microtomography, Environ. Sci. Technol., 2005, 39, 8403–8410 CrossRef CAS PubMed.
- M. L. Brusseau, S. Peng, G. Schnaar and M. S. Costanza-Robinson, Relationships among air–water interfacial area, capillary pressure, and water saturation for a sandy porous medium, Water Resour. Res., 2006, 42, W03501 Search PubMed.
- K. A. Culligan, D. Wildenschild, B. S. B. Christensen, W. G. Gray and M. L. Rivers, Pore-scale characteristics of multiphase flow in porous media: A comparison of air–water and oil–water experiments, Adv. Water Resour., 2006, 29, 227–238 CrossRef CAS.
- M. Prodanovic, W. B. Lindquist and R. S. Seright, Porous structure and fluid partitioning in polyethylene cores from 3D X-ray microtomographic imaging, J. Colloid Interface Sci., 2006, 298, 282–297 CrossRef CAS PubMed.
- G. Schnaar and M. L. Brusseau, Characterizing pore-scale dissolution of organic immiscible liquid in natural porous media using synchrotron X-ray microtomography, Environ. Sci. Technol., 2006, 40, 6622–6629 CrossRef CAS PubMed.
- G. Schnaar and M. L. Brusseau, Characterizing pore-scale configuration of organic immiscible liquid in multiphase systems with synchrotron X-ray microtomography, Vadose Zone J., 2006, 5, 641–648 CrossRef CAS.
- M. L. Brusseau, S. Peng, G. Schnaar and A. Murao, Measuring air–water interfacial areas with X-ray microtomography and interfacial partitioning tracer tests, Environ. Sci. Technol., 2007, 41, 1956–1961 CrossRef CAS PubMed.
- M. Prodanovic, W. B. Lindquist and R. S. Seright, 3D image-based characterization of fluid displacement in a Berea core, Adv. Water Resour., 2007, 30, 214–226 CrossRef.
- M. L. Brusseau, H. Janousek, A. Murao and G. Schnaar, Synchrotron X-ray microtomography and interfacial partitioning tracer test measurements of NAPL–water interfacial areas, Water Resour. Res., 2008, 44, W01411 CrossRef PubMed.
- M. S. Costanza-Robinson, K. H. Harrold and R. M. Lieb-Lappen, X-ray microtomography determination of air–water interfacial area–water saturation relationships in sandy porous media, Environ. Sci. Technol., 2008, 42, 2949–2956 CrossRef CAS PubMed.
- M. L. Brusseau, M. Narter, S. Schnaar and J. Marble, Measurement and Estimation of Organic-Liquid/Water Interfacial Areas for Several Natural Porous Media, Environ. Sci. Technol., 2009, 43, 3619–3625 CrossRef CAS PubMed.
- A. E. Russo, M. Narter and M. L. Brusseau, Characterizing pore-scale dissolution of organic immiscible liquid in a poorly-sorted natural porous medium, Environ. Sci. Technol., 2009, 43, 5671–5678 CrossRef CAS PubMed.
- M. Narter and M. L. Brusseau, Comparison of interfacial partitioning tracer test and high-resolution microtomography measurements of fluid-fluid interfacial areas for an ideal porous medium, Water Resour. Res., 2010, 46, W08602 CrossRef PubMed.
- M. L. Porter, D. Wildenschild, G. Grant and J. I. Gerhard, Measurement and prediction of the relationship between capillary pressure, saturation, and interfacial area in a NAPL–water–glass bead system, Water Resour. Res., 2010, 46, W08512 CrossRef.
- C. J. Werth, C. Y. Zhang, M. L. Brusseau, M. Oostrom and T. Baumann, A review of non-invasive imaging methods and applications in contaminant hydrogeology research, J. Contam. Hydrol., 2010, 113, 1–24 CrossRef CAS PubMed.
- G. C. Iltis, R. T. Armstrong, D. P. Jansik, B. D. Wood and D. Wildenschild, Imaging biofilm architecture within porous media using synchrotron-based X-ray computed microtomography, Water Resour. Res., 2011, 47, W02601 CrossRef.
- R. T. Armstrong and D. Wildenschild, Investigating the pore-scale mechanisms of microbial enhanced oil recovery, J. Pet. Sci. Eng., 2012, 94–95, 155–164 CrossRef CAS.
- J. Ghosh and G. R. Tick, A pore scale investigation of crude oil distribution and removal from homogeneous porous media during surfactant-induced remediation, J. Contam. Hydrol., 2013, 155, 20–30 CrossRef CAS PubMed.
- M. Andrew, H. Menke, M. J. Blunt and B. Bijeljic, The Imaging of Dynamic Multiphase Fluid Flow Using Synchrotron-Based X-ray Microtomography at Reservoir Conditions, Transp. Porous Media, 2015, 110, 1–24 CrossRef CAS.
- K. C. Carroll, K. McDonald, J. Marble, A. E. Russo and M. L. Brusseau, The impact of transitions between two-fluid and three-fluid phases on fluid configuration and fluid–fluid interfacial area in porous media, Water Resour. Res., 2015, 51, 7189–7201 CrossRef PubMed.
- S. R. Tracy, K. R. Daly, C. J. Sturrock, N. M. J. Crout, S. J. Mooney and T. Roose, Three-dimensional quantification of soil hydraulic properties using X-ray Computed Tomography and image-based modeling, Water Resour. Res., 2015, 51, 1006–1022 CrossRef.
- K. McDonald, K. C. Carroll and M. L. Brusseau, Comparison of fluid–fluid interfacial areas measured with X-ray microtomography and interfacial partitioning tracer tests for the same samples, Water Resour. Res., 2016, 52, 5393–5399 CrossRef PubMed.
- Y. Lyu, M. L. Brusseau, A. El Ouni, J. B. Araujo and X. S. Su, The Gas-Absorption/Chemical-Reaction Method for Measuring Air–Water Interfacial Area in Natural Porous Media, Water Resour. Res., 2017, 53, 9519–9527 CrossRef PubMed.
- K. Singh, H. Menke, M. Andrew, Q. Lin, C. Rau, M. Blunt and B. Bijeljic, Dynamics of snap-off and pore-filling events during two-phase fluid flow in permeable media, Sci. Rep., 2017, 7, 5192 CrossRef PubMed.
- M. J. Blunt, Flow in porous media-pore-network models and multiphase flow, Curr. Opin. Colloid Interface Sci., 2001, 6, 197–207 CrossRef CAS.
- V. Joekar-Niasar, M. Prodanovic, D. Wildenschild and S. M. Hassanizadeh, Network model investigation of interfacial area, capillary pressure and saturation relationships in granular porous media, Water Resour. Res., 2010, 46, W06526 CrossRef.
- M. J. Blunt, B. Bijeljic, H. Dong, O. Gharbi, S. Iglauer, P. Mostaghimi, A. Paluszny and C. Pentland, Pore-scale imaging and modelling, Adv. Water Resour., 2013, 51, 197–216 CrossRef.
- E. Dalla, M. Hilpert and C. T. Miller, Computation of the interfacial area for two-fluid porous medium systems, J. Contam. Hydrol., 2002, 56, 25–48 CrossRef CAS PubMed.
- N. K. Adam and G. Jessop, Angles of contact and polarity of solid surfaces, J. Chem. Soc., Trans., 1925, 1863–1868 RSC.
- R. N. Wenzel, Resistance of solid surfaces to wetting by water, Ind. Eng. Chem., 1936, 28, 988–994 CrossRef CAS.
- A. B. D. Cassie and S. Baxter, Wettability of porous surfaces, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- J. R. Philip, Adsorption and capillary condensation on rough surfaces, J. Phys. Chem., 1978, 82, 1379–1385 CrossRef CAS.
- J. P. Oliver, C. Huh and S. G. Mason, An experimental study of some effects of solid surface roughness on wetting, Colloids Surf., 1980, 1(1), 79–104 CrossRef CAS.
- F. A. L. Dullien, C. Zarcone, I. F. Macdonald, A. Collins and R. D. E. Bochard, The Effects of Surface-Roughness on the Capillary-Pressure Curves and the Heights of Capillary Rise in Glass Bead Packs, J. Colloid Interface Sci., 1989, 127, 362–372 CrossRef.
- T. K. Tokunaga and J. Wan, Water film flow along fracture surfaces of porous rock, Water Resour. Res., 1997, 33, 1287–1295 CrossRef.
- W. J. Zheng, X. Yu and Y. Jin, Considering Surface Roughness Effects in a Triangular Pore Space Model for Unsaturated Hydraulic Conductivity, Vadose Zone J., 2015, 14, vzj2014.09.0121 Search PubMed.
- T. Tokunaga, K. Olson and J. Wan, Moisture Characteristics of Hanford Gravels – Bulk, Grain-Surface, and Intragranular Components, Vadose Zone J., 2003, 2, 322–329 CrossRef.
- S. Brunauer, P. H. Emmett and E. Teller, Adsorption of gases in multimolecular layers, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- M. R. Razavi, B. Muhunthan and O. Al Hattamleh, Representative elementary volume analysis of sands using X-ray computed tomography, Geotech. Test. J., 2007, 30, 212–219 Search PubMed.
- M. S. Costanza-Robinson, B. D. Estabrook and D. F. Fouhey, Representative elementary volume estimation for porosity, moisture saturation, and air–water interfacial areas in unsaturated porous media: Data quality implications, Water Resour. Res., 2011, 47, W07513 CrossRef.
- M. L. Rivers, D. T. Citron and Y. B. Wang, Recent developments in computed tomography at GSECARS, Developments in X-Ray Tomography VII, 2010, vol. 7804 Search PubMed.
- M. L. Rivers, High-speed tomography reconstruction on workstations using multi-threading, Proc. SPIE, 2012, 8506, 8506 CrossRef.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- M. L. Rivers, Y. B. Wang and T. Uchida, Microtomography at GeoSoilEnviroCARS, Proc. Soc. Photo-Opt. Instrum. Eng., 2004, 5535, 783–791 CrossRef.
- C. D. Montemagno and Y. Ma, in Characterization and measurement of the hydraulic properties of unsaturated porous media: proceedings of the International Workshop on Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media: Riverside, California, October 22–24, 1997, ed. M. T. van Genuchten, F. J. Leij and L. Wu, U.S. Salinity Laboratory, Agricultural Research Service Dept. of Environmental Sciences, University of California, Riverside, CA, 1999, vol. 1, pp. 121–132 Search PubMed.
- J. B. Araujo, Measuring Air–Water Interfacial Areas: Contributions of Capillary and Film Domains in Natural Porous Media, Ph.D. Dissertation, The University of Arizona, 2014.
| This journal is © The Royal Society of Chemistry 2019 |