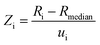Development and characterisation of new glycine certified reference materials for SI-traceable 13C/12C isotope amount ratio measurements
D.
Malinovsky
 *,
P. J. H.
Dunn
*,
P. J. H.
Dunn
 *,
G.
Holcombe
,
S.
Cowen
and
H.
Goenaga-Infante
*,
G.
Holcombe
,
S.
Cowen
and
H.
Goenaga-Infante
National Measurement Laboratory, LGC, Queens Road, Teddington, TW11 0LY, UK. E-mail: dmitriy.malinovskiy@lgcgroup.com; philip.dunn@lgcgroup.com
First published on 19th November 2018
Abstract
Variations in the stable isotopic composition of carbon are commonly expressed as δ(13C) values, and are used in diverse fields, including biology, environmental sciences, food and drug authentication and forensic applications. Progress in these fields requires accurate and comparable stable carbon isotope ratio measurements between laboratories and over time. Yet concerns about comparability of measurement results for stable carbon isotopes have been raised due to both replacement of one primary reference material by another and, more recently, due to the increase of δ(13C) values of the second primary reference material (LSVEC) when exposed to the atmosphere. Establishing traceability to the SI as a stable metrological reference system can be a sustainable solution in ensuring accuracy and metrological traceability of measurement results. To address the shortage of reference materials certified for carbon isotope ratios traceable to the SI, a new reference material LGC171-KT has been produced in this study. This consists of three glycine solutions with certified n(13C)/n(12C) isotope amount ratios of 0.010642, 0.010821 and 0.011227 with expanded uncertainties (k = 2) of 0.000030, 0.000030 and 0.000032, respectively, and indicative δ(13C)VPDB values of −42.22‰, −24.66‰ and +12.55‰ with expanded uncertainties (95% confidence) of 0.34‰, 0.24‰ and 0.22‰, respectively. A strategy for the development and characterisation steps has been described in detail and includes an improved approach for evaluating results of homogeneity testing. The n(13C)/n(12C) isotope amount ratio for the zero point of the VPDB scale was also re-determined and the current best estimate, based on all available results, was determined to be 0.011117 with expanded uncertainty of 0.000039 (k = 2.6).
Introduction
Isotope ratio measurements by mass spectrometry are subject to inherent measurement bias originating during both sample preparation and transmission of analyte ions in the mass spectrometer, resulting in measured isotope ratios that differ from their true values. This bias can be corrected for by using isotopic reference materials (RMs) and the principle of identical treatment (IT principle).1,2 RMs play key roles in calibration of isotope ratio mass spectrometers, the assignment of property values and the transfer of measurement accuracy among different laboratories over time.A long-standing problem associated with the latter function of isotopic RMs is the lack of comparability of results obtained in different laboratories over different periods of time. It stems from the fact that many RMs used in differential, or delta value, isotope ratio measurements lack a straightforward link to the International System of Units (SI). Traceability in these measurements is established to scale-defining artefacts which are recognised as International Standards and represent the end members of the traceability chain for the measurements. Once such an artefact becomes short in supply, another material is introduced as a replacement. Delta values of scale-defining International Standards are based on consensus and given without uncertainty.2 In practice, however, each replacement of an exhausted artefact by a new one is accompanied by an increase in the uncertainty of its assigned values.
Measurements of δ(13C) values are a good example of how problems with measurement comparability can escalate. The original primary isotopic reference material, PeeDee Belemnite (PDB) which was used to define the δ(13C) scale is no longer available and was found to be insufficiently homogeneous.2 Therefore the PDB scale was replaced by making NBS 19 calcite (a secondary RM on the PDB scale) the primary RM of the new Vienna PDB (VPDB) scale. Later, it was recommended to use LSVEC lithium carbonate as an additional primary material such that the VPDB scale was defined by two points, each with no associated uncertainty.3,4 Recently LSVEC has been discovered to increase in terms of δ(13C)VPDB value when containers of LSVEC are opened and exposed to laboratory air, and subsequently the Commission on Isotopic Abundances and Atomic Weights (CIAAW) of the International Union of Pure and Applied Chemistry (IUPAC) recommended that LSVEC no longer be used as a carbon isotopic RM.5 As a consequence, it becomes increasingly more difficult for practitioners to achieve comparability of measurement results, particularly as commercially available secondary reference material isotope delta values are often revised following changes to the reporting scale.
Establishing traceability to the SI as a stable metrological reference system can be a sustainable solution for ensuring comparability of measurement data. Although there have been attempts to establish a link between the VPDB scale and the SI by determining the R(13C/12C) value which corresponds to the δ(13C)VPDB scale zero point, the measurement models used in the earlier studies did not fully match current requirements on metrological traceability and the lack of agreement of the results made uncertainty of the average R(13C/12C) for the VPDB scale zero too large.6 Recent studies in our laboratory have shown that R(13C/12C) can be determined by both MC-ICPMS and continuous-flow IRMS with improved accuracy and uncertainty comparable to previous n(13C)/n(12C) ratio measurements by dual inlet IRMS.7,8
This work was based on calibration methods reported by our group elsewhere7,8 which have been applied here to certify new glycine reference materials for R(13C/12C) values which are traceable to the SI. The material set, LGC171-KT, consists of three glycine solutions which, in addition to R(13C/12C), have also been characterised in terms of δ(13C)VPDB values. The principal motivations behind the project were to support traceability and comparability of R(13C/12C) values while improving several aspects of the previously applied measurement methods. These improvements included the application of a better method to estimate the elemental impurities within isotopically enriched glycines; a thorough investigation of the molecular weights of the 12C- and 13C-enriched parent glycines; reduction of the measurement uncertainties associated to the indicative δ(13C)VPDB values as well as to the certified absolute carbon isotope ratios; use of an improved method to include the uncertainty arising from homogeneity assessment within certified R(13C/12C) values; and finally the production of a set of three reference materials affording the possibility of two point calibration with SI-traceable reference materials with an additional quality control material.
Experimental
Materials, reagents and glassware
Natural carbon isotope abundance, 13C-enriched and 13C-depleted glycines were obtained from Sigma Aldrich. The 13C-enriched glycine (glycine-13C2; CAS number 67836-0105, hereafter parent glycine A) was characterised by nominal abundances of 13C and 12C isotopes of 99% and 1%, respectively. The 13C-depleted glycine (glycine-12C2; product number 67836-0105, hereafter parent glycine B) was characterised by nominal abundances of 13C and 12C isotopes of 0.1% and 99.9%, respectively. High-purity deionised water (18 MΩ cm−1) was obtained from an ELGA water purification system (Veolia Water, Marlow, UK). Phosphoric acid BioUltra (≥85%) was acquired from Sigma Aldrich. Ultrapure nitric acid was purchased from Romil Ltd (Cambridge, UK). Pyrex borosilicate glass 2 L reagent bottles with polypropylene caps and pouring rings were acquired from Fisher Scientific UK Ltd. Borosilicate 40 mL amber glass vials with caps were obtained from Sigma Aldrich.Preparation procedure for the candidate RMs
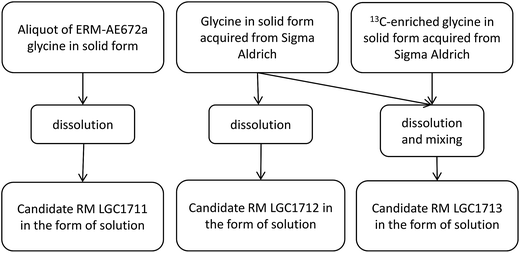
Three candidate reference material solutions of glycine in dilute phosphoric acid were prepared in separate 2 L Pyrex glass bottles. All glassware used during the preparation was pre-cleaned before use by soaking in 0.08 M H3PO4 for 2 days, followed by an abundant rinse with deionised water. Approximately 180 g of the corresponding source glycine were transferred into a 2 L Pyrex glass bottle under gravimetric control. Then 1.2 L of 0.08 M H3PO4 was added to the bottle by using a calibrated 200 mL glass flask. For LGC1711 the source glycine was an aliquot of ERM®-AE672a δ(13C)VPDB = −42.12 ± 0.42‰, (expanded uncertainty, k = 2), while for LGC1712 and LGC1713 the natural abundance source glycine was obtained from Sigma Aldrich (δ(13C)VPDB approximately equal to −25‰). For LGC1713 a small amount of doubly-labelled 13C2 glycine was also added to result in an isotopic composition of δ(13C)VPDB approximately equal to +12‰. The two glycines (natural abundance and 13C-labelled) were first dissolved in 0.08 M H3PO4 and then mixed as solutions under gravimetric control in amounts determined by mass balance to give the desired carbon isotopic composition. A schematic illustration of the preparation procedure is given in Fig. 1. Once prepared, each candidate RM solution was dispensed as 2 mL portions into amber glass ampoules. After flushing with argon, the ampoules were flame sealed and then stored at (18 ± 6) °C.Preparation of synthetic isotope mixtures
Parent glycines A and B were weighed and brought into solution by using 0.3 M ultrapure HNO3 and then mixed with each other in different proportions to produce synthetic isotope mixtures with different R(13C/12C) values, as shown in Fig. 2 and 3, for measurements by MC-ICPMS and IRMS, respectively. Synthetic isotope mixtures for confirmatory measurements by IRMS were prepared by mixing parent glycine B with the intermediate isotope mixture, made from the calibration mixtures used in the measurements by MC-ICPMS as the isotope ratios of calibrants for the former measurements need to be in the range of natural isotope abundance variations for carbon.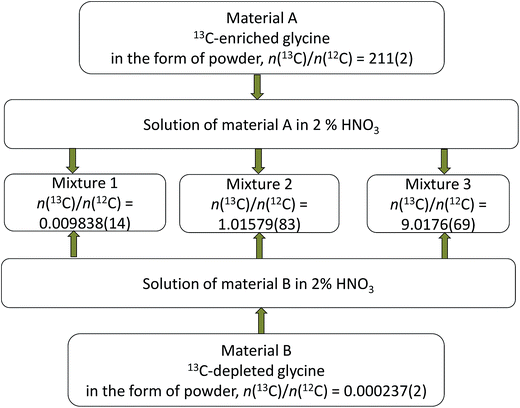 | ||
| Fig. 2 Diagram illustrating preparation of the synthetic isotope mixtures for characterisation measurements by MC-ICPMS. Combined standard uncertainties are given in parentheses. | ||
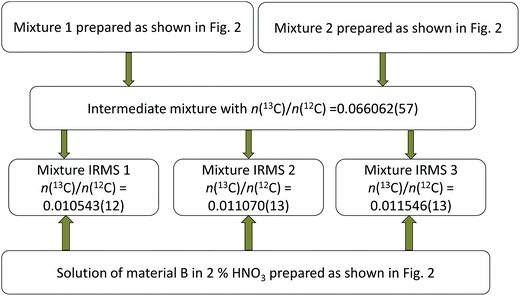 | ||
| Fig. 3 Diagram illustrating preparation of synthetic isotope mixtures for confirmatory measurements by IRMS. Combined standard uncertainties are given in parentheses. | ||
Pre-cleaned 40 mL borosilicate amber glass vials with caps were used in preparation of the solutions. A single source of 0.3 M ultrapure HNO3 was used a solvent. Weighing operations were performed in rooms with controlled temperature against operational mass standards traceable to the SI unit of kilogram. A Mettler-Toledo XP205 balance with a maximum load of 200 g and a sensitivity of 0.01 mg was used. A weighing uncertainty statement was provided for each weight by carrying out replicate measurements. Weighing operations are traceable to the SI through the use of calibrated weights traceable to the National Primary Standard of mass via the UK National Physical Laboratory (Teddington, UK).
Determination of impurities and water content of parent glycines A and B
Non-glycine forms of carbon in parent glycines A and B were quantified by 1H Nuclear Magnetic Resonance (NMR) using a Bruker Avance 600 MHz NMR spectrometer. The mass fraction of water in parent glycines A and B (wwater,A and wwater,B) were determined by coulometric Karl Fischer titration using a Metrohm 774 oven sample processor and a 831 Karl Fischer coulometer. The mass fractions of elemental impurities in parent glycines A and B (wimp,A and wimp,B) were quantified by analysis of 72 elements using a double-focusing sector field ICP-MS (Element-2, Thermo Fisher Scientific, Germany). Careful attention was given to resolving or correcting for spectral interferences in the measurements, which was achieved by selecting the isotopes least affected by potential interferences and measurements of many elements in medium resolution mode.Measurements of R(13C/12C) by MC-ICPMS
The isotope amount ratios n(13C)/n(12C) were determined using the Neptune MC-ICPMS (Thermo Scientific, Bremen, Germany) in high resolution mode. Important advantages of MC-ICPMS include (1) the capacity to measure ratios of the singly charged ions, 13C+ and 12C+, thus negating the need to correct measured data for the presence of isotopes of oxygen; (2) extremely stable conditions of instrumental mass bias over a prolonged period of time within a measurement session, thus allowing accurate correction for this effect; and (3) the carryover effect of carbon, even for the most highly 13C-enriched samples, is insignificant. The measurements followed the protocol described in detail elsewhere.7 Briefly, sample solutions were introduced into the plasma via a stable introduction system consisting of a peristaltic pump, a microconcentric PFA nebulizer and a tandem quartz spay chamber arrangement (cyclone and Scott double pass). The 12C+ and 13C+ ions were collected by Faraday cups at Low 3 and High 2 positions, respectively. Amplifier gain calibration was performed at the beginning of each measurement session. Typical operating conditions for the instrument are shown in Table 1. A single measurement consisted of 30 cycles of 8.4 s duration each. Procedural blanks were measured before and after each sample and synthetic isotope mixture. It was always verified using the on-line scan window that the signal from the previous sample had dropped to background level prior to starting measurement of the following sample. The on-line data processing included calculation of the ion beam intensity ratios and removal of outliers using a 2-σ test. Further treatment of measured data was performed off-line and included the correction for procedural blanks.| RF power, W | 1090 |
| Sample and H-type skimmer cones | Nickel, 1.1 and 0.8 mm orifice diameter, respectively |
| Argon gas flow rates, L min−1 | |
| Cool/plasma | |
| Auxiliary | |
| Nebulizer | |
| Sample uptake rate, mL min−1 | 0.06 |
| Mass resolution, R(5–95%) | 7800 |
| Ion lens settings | Optimised for maximum intensity of signal daily |
| Typical 12C+ sensitivity | 0.4 V mg−1 L−1 |
Measurements of R(13C/12C) by gas source IRMS
Flow injection analysis-chemical oxidation-isotope ratio mass spectrometry (FIA-CO-IRMS) was performed for confirmatory measurements of the glycine CRMs. A Dionex HPLC system coupled to a Delta V Advantage IRMS via a LC IsoLink chemical oxidation interface was used (Thermo Scientific, Bremen, Germany). ELGA water was used as the mobile phase with flow rate of 300 μL min−1. The chemical oxidation reagents were sodium persulfate (Sigma Aldrich 71890, 50 g in 500 mL of solution) and phosphoric acid (85% in water, Sigma Aldrich 79617, 660 μL in 500 mL of solution) which were prepared as a single solution and added to the mobile phase at a flow rate of 50 μL min−1 within the LC IsoLink. Backgrounds for m/z 18, 28, 32, 40 and 44 (predominately water, nitrogen, oxygen, argon and carbon dioxide, respectively) were checked prior to each analytical sequence and to ensure they were within the manufacturer's recommended limits. Linearity of the IRMS response was assessed via repeated injections (n = 9) of increasing injection volume of an in-house quality control glycine solution. The linearity of these injections was <0.06‰ V−1 for the m/z 44 signal. Similarly, the stability of the IRMS was assessed via repeated injections (n = 9) of the same volume of in-house glycine quality control material. Standard deviations of the raw δ(13C) values were <0.2‰ for the m/z 44 signal.All raw measurements were relative to pulses of CO2 working gas (CP grade, BOC, Guildford, UK) introduced to the IRMS in triplicate at the beginning and end of each run, via a separate open split to the sample gas. All six working gas pulses were included during data analysis. Each analytical run included five repeat injections of solution from a single vial. The raw data from the instrument consisted of ion current ratios and peak areas for the sample and working gas peaks for the three signals corresponding to m/z = 44, 45 and 46. The raw data were converted to R(13C/12C) values using the 17O correction algorithm by Santrock and co-authors as described in more detail previously.8,9 A blank correction was applied followed by normalisation using the gravimetrically prepared synthetic isotope mixtures (Fig. 3). BioUltra glycine sourced from Sigma Aldrich was used as an in-house quality control and was run at different amount levels at different time points throughout each sequence of analyses.
Measurements of δ(13C)VPDB by gas source IRMS
The same FIA-CO-IRMS system was used however the raw instrumental data (ion current ratios and peak areas for the sample and working gas peaks) were first converted into raw isotope delta values using the CIAAW-recommended 17O algorithm,10 then blank corrected, then normalised to the VPDB scale using USGS40 L-glutamic acid (δ(13C)VPDB = −26.39(4)‰); IAEA-CH-6 sucrose (δ(13C)VPDB = −10.45(3)‰); and USGS41 L-glutamic acid (δ(13C)VPDB = +37.63(5)‰).2 BioUltra glycine sourced from Sigma Aldrich was used as an in-house quality control and was run at different amount levels at different time points throughout each sequence of analyses. The δ(13C)VPDB notation was used as defined by the relationship: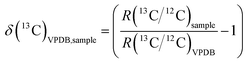 | (1) |
Uncertainty estimation
Combined standard uncertainties of R(13C/12C) and δ(13C)VPDB values measured by MC-ICPMS or FIA-CO-IRMS were obtained by propagating individual uncertainty components according to the JCGM guide.11 This was achieved by using a template in MS Excel for calculating the combined standard uncertainty of individual measurements based on the numerical method of differentiation by Kragten.12,13 In accordance with the JCGM guide, the parenthetic notation was used for reporting combined standard uncertainties, uc, whereas the plus-minus sign (±) was used to denote expanded uncertainties, U = kuc, where uc is the combined standard uncertainty and k is a coverage factor. Unless indicated otherwise, all expanded uncertainties shown in the paper are given with the coverage factor, k, equal to 2.Results and discussion
Primary preparation procedure for calibrators of R(13C/12C)
For a measurement result to be directly traceable to a base unit of the SI, it is necessary to use a primary method of analysis. The concept of primary methods in general and for the measurement of amount of substance in particular, has been discussed in detail previously.14–16 Definitions of a primary method of measurement and its equivalent term, a primary reference measurement procedure, have been developed by CCQM and the VIM, respectively.14,17 The essential feature of a primary method is that it allows a quantity to be measured in terms of a particular SI unit without reference to a standard or measurement already expressed in that unit.14,16However, due to difficulties of meeting strictly the aforementioned requirement of method independence, it was widely agreed that so far no procedure met the VIM definition of a primary reference measurement procedure in the area of isotope amount ratio measurements.18 Instead, a primary preparation procedure can be used to realise the SI measurement unit for number-ratio isotopic analysis.17,18 A recognised implementation of this procedure is a calibration approach based on the use of synthetic isotope mixtures, first described by Nier in 1950 and since then applied to determination of isotopic abundances of many elements.19–22
A detailed description of the theory behind the method and derivation of formulae in the case of carbon isotope ratio measurements can be found elsewhere.7,22 It can be shown that the following formula can be used to determine R(13C/12C) in glycine candidate RM:
 | (2) |
Correction for non-ideal properties of 13C-enriched and 13C-depleted glycines
In the ideal case, parent 13C-enriched and 13C-depleted glycines taken to prepare synthetic isotope mixtures would be entirely pure glycines. In reality however, the impurities present (whether water, trace elements, or carbon not in the form of glycine) have to be accounted for in the calculations. Mass fractions of water in the powdered 13C-enriched and 13C-depleted glycines immediately before dissolution were found to be wwc,A = 0.00020 ± 0.00006 and wwc,B = 0.00020 ± 0.00016 (expanded uncertainty, k = 2).Elemental impurities in the parent glycines A and B were estimated as the sum of the mass fractions of all elements detected by sector field ICP-MS. In an improved procedure to that reported previously,7 the glycines A and B were prepared in pre-cleaned plastic tubes in preference to glass for these analyses. This precluded the leaching of alkaline and alkaline earth metals into the glycine solutions between preparation and analysis which would bias the results. Na, Fe, Zn, Ca, Mg, Si, P and S were the main elemental impurities identified. Criteria for identifying matrix elements as main impurities in parent 13C-enriched and 13C-depleted materials were described elsewhere.23 Both parent glycines were characterised by a similar level of elemental impurities of less than 10 μg g−1. Conservative values of wimp,A = wimp,B = 10 ± 10 μg g−1 were used in subsequent calculations corresponding to a confidence level greater than 99% (coverage factor k = 4). The analysis by NMR showed that mass fractions of glycine were 0.9997 ± 0.0002 g g−1 and 0.9998 ± 0.0005 g g−1 in parent materials A and B, respectively (expanded uncertainty, k = 2).
Molecular weights of 13C-enriched and 13C-depleted parent glycines
In our previous work,7,8 the molecular weights (Mr) of 12C- and 13C-enriched glycines were calculated by using isotopic abundances of the elements provided by the supplier and the standard atomic weights reported in the IUPAC Technical Report “Atomic Weights of the Elements: Review 2000”.24 The uncertainties in Mr,glycine values also included a contribution from the presence of non-glycine forms of carbon as determined by qNMR. Therefore the uncertainty assigned to the Mr values corresponded to the expanded uncertainty (coverage factor k = 4) of measurements by NMR and was equivalent to 0.05%, giving values of 77.0452 ± 0.0385 g mol−1 and 75.0415 ± 0.0375 g mol−1 for the 13C-enriched and 12C-enriched glycines, respectively.A shortcoming of this approach is that the isotopic compositions of hydrogen, nitrogen and oxygen within the parent glycines were not investigated. The molecular weights of the 12C- and 13C-enriched glycines could therefore fall outside of the conservative uncertainty estimate above if there were any significant co-enrichment of hydrogen, nitrogen and/or oxygen isotopes (beyond that stated by the manufacturer). Therefore, subsamples of the 12C- and 13C-enriched glycines were sent to the US Geological Survey Stable Isotope Laboratory (Reston, Virginia, USA) where they were analysed by elemental analysis-isotope ratio mass spectrometry (EA-IRMS) for nitrogen isotopic composition and by high temperature conversion-isotope ratio mass spectrometry (HTC-IRMS) for hydrogen and oxygen isotopic compositions. For each measurement, the parent glycines were gravimetrically mixed with a glycine isotope delta reference material (USGS64 or USGS66) prior to measurement and the isotopic composition of the parent glycines determined via mass balance. As the parent glycines were not available in large quantities for this work, few measurements were performed, and therefore the measurement uncertainty associated to the results was expanded to provide sufficient confidence: measurement uncertainties assigned to the reported isotope delta values were assumed to be 50‰, 5‰ and 10‰ for δ(2H)VSMOW–SLAP, δ(15N)air–N2 and δ(18O)VSMOW–SLAP, respectively.
Isotope delta values for the parent glycines were used to determine the R(2H/1H)glycine, R(15N/14N)glycine and R(18O/16O)glycine values using the standard isotope delta equation and the CIAAW-recommended values for R(2H/1H)VSMOW, R(15N/14N)air–N2 and R(18O/16O)VSMOW. The δ(17O)VSMOW–SLAP value for the glycines was calculated using the reported δ(18O)VSMOW–SLAP value and the value for λ reported by Barkan and Luz (0.5279 ± 0.0001),25 and the following expression:
| δ(17O)VSMOW–SLAP,glycine = (1 + δ(18O)VSMOW–SLAP,glycine)λ − 1 | (3) |
The obtained δ(17O)VSMOW–SLAP value could then be used to determine the R(17O/16O)glycine value using the R(17O/16O)VSMOW value of 0.00038672 ± 0.00000087 (expanded uncertainty, k = 2)reported by Assonov and Brenninkmeijer.26 The R(13C/12C)glycine values for the parent glycines were determined at LGC following the approach described in detail elsewhere.7
The absolute isotope ratios thus obtained for the hydrogen, nitrogen, carbon and oxygen within the parent glycines were used to determine the corresponding amount fractions of the various isotopes x(1H)glycine, x(2H)glycine, x(12C)glycine, x(13C)glycine, x(14N)glycine, x(15N)glycine, x(16O)glycine, x(17O)glycine and x(18O)glycine. The amount fractions could then be used to determine the atomic weights of the four elements, Ar(H)glycine, Ar(C)glycine, Ar(N)glycine and Ar(O)glycine, within the glycines. The atomic weights could then be combined according to the molecular formula for glycine to result in the molecular weight Mr,glycine. The calculation sequence follows a similar calculation recently published in an IUPAC Technical Report.27 The calculation sequence was performed within a Kragten spreadsheet to allow estimation of the measurement uncertainty associated to the Mr,glycine values to be obtained.
The values obtained for Mr,13C-glycine and Mr,12C-glycine were 77.08481(14) and 75.06512(11), respectively (standard combined uncertainties). Note that these uncertainties do not include any contribution from the presence of non-glycine forms of carbon as determined by qNMR. These values lie within the conservative measurement uncertainty range of those applied during previous work and therefore there is no enrichment in hydrogen, nitrogen or oxygen isotopes in either of the parent glycines that significantly affects the Mr values.
Determination of calibration factors
Converting measured isotopic ion current ratios into unbiased isotope number ratios requires knowledge of calibration factors (K factors) which relate them. K factors are calculated from measurements of parent isotopically enriched materials and synthetic isotope mixtures prepared from them. The mathematical and physical background for the calculations is described in detail elsewhere.7,22,28 For a two-isotope system, the calculations can be made by using both the iterative procedure and analytical solution. The K factors for R(13C/12C) values obtained in four measurement sessions by MC-ICPMS are shown in Table 2. An important observation here is that the K factors determined for synthetic isotope mixtures with different isotope amount ratios n(13C)/n(12C) are statistically indistinguishable from each other within the limits of measurement uncertainty. As can also be seen from Table 2, there is an excellent agreement between K factors obtained through the iterative procedure and analytical solution.| K factor obtained using the iterative procedure | K factor obtained using the analytical solution which includes data obtained for the parent glycines | K factor obtained using the analytical solution which does not include data for the parent glycinesa | |||||
|---|---|---|---|---|---|---|---|
| Calibration mixture 1 with n(13C)/n(12C) ratio of 0.0099 | Calibration mixture 2 with n(13C)/n(12C) ratio of 1.0169 | Calibration mixture 3 with n(13C)/n(12C) ratio of 9.0624 | Calibration mixture 1 with n(13C)/n(12C) ratio of 0.0099 | Calibration mixture 2 with n(13C)/n(12C) ratio of 1.0169 | Calibration mixture 3 with n(13C)/n(12C) ratio of 9.0624 | Calibration mixture 2 with n(13C)/n(12C) ratio of 1.0169 | |
| a Measurement data for three calibration mixtures only were used in calculations. Details of the analytical solution is described by Meija (2012).22 | |||||||
| 1 day | 0.8930(12) | 0.8962(9) | 0.8977(9) | 0.8931(13) | 0.8963(9) | 0.8978(9) | 0.8960(7) |
| 2 day | 0.8925(12) | 0.8959(8) | 0.8981(7) | 0.8926(13) | 0.8960(8) | 0.8982(7) | 0.8956(7) |
| 3 day | 0.8857(12) | 0.8893(8) | 0.8904(8) | 0.8858(13) | 0.8894(8) | 0.8906(8) | 0.8892(7) |
| 4 day | 0.8871(12) | 0.8902(8) | 0.8912(7) | 0.8872(13) | 0.8903(8) | 0.8913(7) | 0.8902(7) |
| Average for all measurements | 0.8896(22) | 0.8929(20) | 0.8944(22) | 0.8897(22) | 0.8930(20) | 0.8945(22) | 0.8927(19) |
Homogeneity and stability assessment of the candidate RMs
The candidate reference materials were tested for homogeneity following sealing in ampoules. For each material, 10 units were selected using a random stratified approach, which were then analysed in triplicate using a random run order. All units and replicates from each material were analysed on a single day. Instrumental analysis was by FIA-CO-IRMS with calibration to the VPDB delta scale using the RMs listed above. Calibration by interpolation was applied except for LGC1711 as the calibration reference materials amenable to FIA-CO-IRMS did not cover its isotopic composition. The units of LGC1711 were therefore also analysed by Elemental Analyser IRMS (EA-IRMS) in a sequence that was identical other than the inclusion of LSVEC (lithium carbonate, δ(13C)VPDB = −46.6‰) as a check. An additional aim of the homogeneity study was to ensure that the isotopic equilibrium was reached for LGC1713 as this had been prepared by mixing natural and 13C-enriched glycines.The results were evaluated using linear mixed effects models with restricted maximum likelihood estimator (aka REML). From the fitted model coefficients, a standard uncertainty contribution due to possible inhomogeneity uhom was obtained for each material. Any significant within-run effects, such as trends in the results, were included in the model as fixed effects. The mixed model produces an unbiased estimate of the between-unit standard deviation. However, for an uncertainty assessment what is needed is a conservative estimate, that is, a figure which allows for the ‘masking’ of between-unit variation by within-unit variation. This can be addressed in different ways, and the approach adopted in this work was to take uhom as
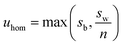 | (4) |
The results indicated that in all cases relatively little unit-to-unit variation in δ(13C)-values of the materials (Table 3). For the material LGC1711, both sets of data, obtained by FIA-CO-IRMS and EA-IRMS, gave very similar values and therefore the FIA-CO-IRMS value has been used for consistency between all three materials (therefore measurements of LSVEC do not contribute to the obtained uhom). The uhom delta values for the three candidate reference materials (Table 3) were converted to absolute ratios to give the values of 0.00000064 mol mol−1, 0.00000020 mol mol−1 and 0.00000017 mol mol−1 for the materials LGC1711, LGC1712 and LGC1713, respectively. The minimum recommended sample intake for the material is based on the amount taken for the homogeneity assessment, which was 5 μL for each solution.
| Material | Between unit SD, ‰ | Within unit SD, ‰ | u hom, ‰ | Degrees of freedom |
|---|---|---|---|---|
| LGC1711 (by FIA-CO-IRMS) | 0.0465 | 0.0990 | 0.0572 | 20 |
| LGC1711 (by EA-IRMS) | <0.00001 | 0.1002 | 0.0579 | 20 |
| LGC1712 | <0.00001 | 0.0271 | 0.0180 | 20 |
| LGC1713 | <0.00001 | 0.0271 | 0.0157 | 20 |
The nature of the glycine reference materials is such that deterioration is not anticipated over their lifetime when stored under the recommended conditions. The uncertainty associated with long-term instability was considered to be negligible compared with the uncertainty contributions from characterisation and possible heterogeneity and was therefore assigned a value of zero. However, regular stability checks will be carried out at three year intervals as part of LGC's on-going Reference Material Stability Monitoring Programme.
Characterisation measurements by MC-ICPMS
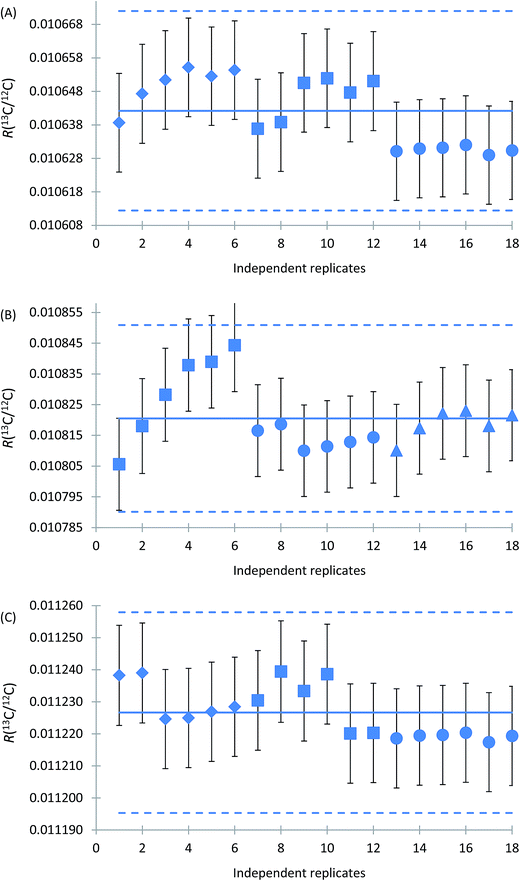
Characterisation of reference materials aims at obtaining a metrologically valid estimate of the true property values.29,30 It is worth noting that ISO 17034 recognises four main approaches for characterisation of RMs, including (1) a single (primary) method in a single laboratory, (2) two or more independent reference methods in one or several laboratories, (3) one or more methods of demonstrable accuracy, performed by a network of competent laboratories, and (4) an approach providing method-specific, operationally defined property values, using a network of competent laboratories.28 It is the first approach based on the use of a primary method which was used in characterisation of glycine solutions in CRM LGC171-KT.As noted above, calibration of measurements of isotope amount ratio n(13C)/n(12C) by using synthetic isotope mixtures provides results which are accepted without reference to a standard of the quantity being measured. The results obtained on different days of measurement for independent ampoules of the CRMs are shown in Fig. 4. As can be seen from this figure, R(13C/12C) values of the CRMs are very reproducible within the limits of standard uncertainties of individual results both within and between measurement sessions. The relative expanded uncertainty (k = 2) of the mean values corresponds to 0.28% for all three materials. The data for material LGC1711, which is a solution obtained by dissolving isotopic reference material ERM®-AE672a, are in excellent agreement with the certification data of ERM®-AE672a from the year 2013.
The uncertainty budget for the measurements is shown in Table 4. The major contribution to the uncertainties, equal to 72%, comes from the weighing operations during preparation of synthetic isotope mixtures. The second largest contribution, equal to 25%, is the uncertainty associated with molecular masses of the parent isotopically enriched glycines, largely due to the uncertainty in determination of the presence of non-glycine forms of carbon by qNMR. It is worth noting that standard deviations of measurements of isotope ratio n(13C)/n(12C) by MC-ICPMS in parent 13C-enriched and 13C-depleted enriched glycines, the calibration mixtures and sample solutions together account for 2.3% of total uncertainty.
| Uncertainty component | Contribution, % |
|---|---|
| Weighing operations | 72 |
| Molar masses of parent isotopically enriched glycines used to prepare calibration mixtures | 25 |
| Correction for water content in parent isotopically enriched glycines | 0.4 |
| 13C/12C isotope ratio measurements in the CRMs | 0.9 |
| 13C/12C isotope ratio measurements in calibration mixtures | 0.8 |
| 13C/12C isotope ratio measurements in parent isotopically enriched glycines | 0.6 |
Confirmatory measurements by IRMS
It has been a long discussion among metrologists about some ambiguity that remains in the interpretation of the definition of primary method.16 The definition of a primary method gives no criteria to determine whether the method has been implemented correctly or not, therefore some form of verification is required. IRMS with calibration using independently prepared synthetic isotope mixtures can be an alternative measurement method for R(13C/12C) values. The methodology for obtaining R(13C/12C) values in samples of glycines by IRMS was described previously elsewhere.8 The R(13C/12C) values for the glycine candidate reference materials obtained by FIA-CO-IRMS are shown in Table 5. As can be seen from this table, the isotope number ratio values obtained by IRMS and MC-ICPMS are in excellent agreement with each other.| Material | n(13C)/n(12C) ratio | Expanded uncertainty (k = 2) | Number of independent measurements |
|---|---|---|---|
| LGC1711 | 0.010633 | 0.000020 | 36 |
| LGC1712 | 0.010825 | 0.000016 | 36 |
| LGC1713 | 0.011232 | 0.000017 | 36 |
Certified R(13C/12C) values for LGC171-KT
Although a characterisation study determines the property values of reference materials it does not necessarily provide their correct uncertainties.31 It is the process of assigning realistic uncertainties to the property values that makes a distinction between characterisation and certification. The small uncertainty contribution arising from homogeneity testing was propagated to the final uncertainty statement of the materials together with the uncertainty arising from the characterisation measurements. Certified values of R(13C/12C) and associated expanded uncertainties of the certified reference materials are shown in Table 6. These values are traceable to the International System of Units (SI) and the traceability chain of the measurement results is illustrated in Fig. 5. Data obtained in this study afford calculation of isotope amount fractions and atomic weight of carbon in the LGC171-KT materials. The results of these calculations are shown in Table 7.| Solution name | n(13C)/n(12C) ratio | Expanded uncertainty (k = 2) |
|---|---|---|
| LGC1711 | 0.010642 | 0.000030 |
| LGC1712 | 0.010821 | 0.000030 |
| LGC1713 | 0.011227 | 0.000032 |
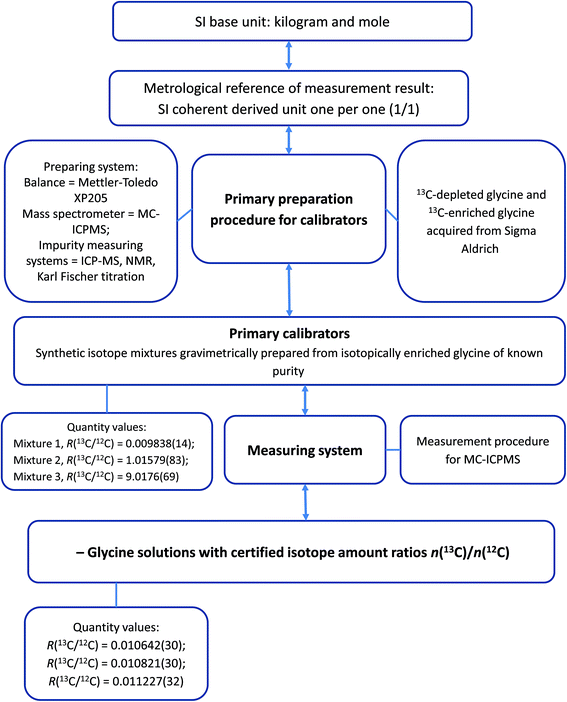 | ||
| Fig. 5 Flowchart illustrating the traceability chain of the property values of glycine CRM LGC171-KT. | ||
| Solution name | Isotope amount fraction, x | Atomic weight, Ar(C) | ||||
|---|---|---|---|---|---|---|
| x(12C) | U (k = 2) | x(13C) | U (k = 2) | A r(C) | U (k = 2) | |
| LGC1711 | 0.989470 | 0.000029 | 0.010530 | 0.000029 | 12.010565 | 0.000029 |
| LGC1712 | 0.989295 | 0.000029 | 0.010705 | 0.000029 | 12.010741 | 0.000029 |
| LGC1713 | 0.988898 | 0.000031 | 0.011102 | 0.000031 | 12.011140 | 0.000031 |
Indicative δ(13C)VPDB values for LGC171-KT
During the FIA-CO-IRMS measurement sequences used to provide the confirmatory R(13C/12C) values, RMs of known δ(13C)VPDB value were included to allow the determination of the candidate reference material δ(13C)VPDB values (Table 8). The values obtained were as follows: LGC1711 δ(13C)VPDB = −42.22 ± 0.34‰ (expanded uncertainty, k = 3.18); LGC1712 δ(13C)VPDB = −24.66 ± 0.24‰ (expanded uncertainty, k = 2.00) and LGC1713 δ(13C)VPDB = +12.55 ± 0.22‰ (expanded uncertainty, k = 4.30). Note that the uncertainty associated with δ(13C)VPDB for LGC1711 is larger because the calibration range afforded by the isotope delta RMs used for scale realisation do not cover the isotopic composition of LGC1711. Calibration via extrapolation was therefore necessary, which resulted in additional uncertainty.| RM | δ(13C)VPDB measured, ‰ | δ(13C)VPDB assumed, ‰ | ||
|---|---|---|---|---|
| Value | U (k = 1) | Value | Uncertainty (k = 1) | |
| a LSVEC was analysed only to check results. Results from sequences including LSVEC were neither used in the calculations of indicative δ(13C)VPDB values nor for the estimation of uhom. LSVEC was assumed to have a standard uncertainty of 0.2‰ to account for observed drift.38 | ||||
| IAEA-CH-6 | −10.42 | 0.09 | −10.45 | 0.03 |
| USGS40 | −26.41 | 0.09 | −26.39 | 0.04 |
| USGS41 | +37.62 | 0.09 | +37.63 | 0.05 |
| LSVECa | −46.80 | 0.21 | −46.6 | 0.2 |
An additional check of the δ(13C)VPDB values obtained was performed by running LGC171-KT together with the recently released USGS64, USGS65 and USGS66 glycine RMs within the same sequence. For the USGS RMs, the uncertainties reported by Schimmelmann et al. (2016) are likely underestimated as noted by Assonov and Gröning in the ESI from that paper.32 We have therefore assumed standard uncertainties for each of these RMs of ± 0.08‰. Normalisation using either set of RMs resulted in δ(13C)VPDB values that agreed with the expected values, within uncertainty (Table 9).
| RM | δ(13C)VPDB expected, ‰ | δ(13C)VPDB normalised to USGS64–66, ‰ | δ(13C)VPDB normalised to LGC171-KT, ‰ | |||
|---|---|---|---|---|---|---|
| Value | U (k = 2) | Value | U (k = 2) | Value | U (k = 2) | |
| USGS 64 | −40.81 | 0.16 | −40.81 | 0.19 | −40.89 | 0.25 |
| USGS 65 | −20.29 | 0.16 | −20.30 | 0.16 | −20.29 | 0.19 |
| USGS 66 | −0.67 | 0.16 | −0.67 | 0.20 | −0.58 | 0.21 |
| LGC1711 | −42.22 | 0.34 (k = 3.18) | −42.11 | 0.22 | −42.20 | 0.21 |
| LGC1712 | −24.66 | 0.24 | −24.67 | 0.16 | −24.69 | 0.17 |
| LGC1713 | +12.55 | 0.22 (k = 4.30) | +12.41 | 0.31 | +12.56 | 0.17 |
Re-determination of R(13C/12C)VPDB
The R(13C/12C)VPDB value of the zero-point of the VPDB isotope delta scale is the link between the relative isotope delta scale and the SI. The currently recommended value of R(13C/12C)VPDB = 0.011180 ± 0.000028 (expanded uncertainty, k = 2). This expanded uncertainty is equivalent to 2.5‰ when expressed as an isotope delta value, and is larger than the typical expanded uncertainty in δ(13C)VPDB values obtained by continuous-flow IRMS by a factor of 7 to 10.10,33 It was obtained from measurements of NBS19 reference material as follows: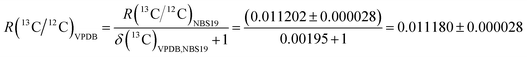 | (5) |
A reference value obtained from a number of different measurements can have an associated uncertainty which is smaller than any single measurement (depending on the reported data and on the method used to estimate the reference value). Kaiser (2008) suggested that the best estimate of R(13C/12C)VPDB was 0.011124(45) (standard uncertainty) this being the unweighted mean of previously reported measurements.6,34–37
Since the aforementioned work of Kaiser, there have been two newer determinations of R(13C/12C)VPDB: firstly the value which we previously reported during certification of ERM®-AE672a (0.011115 ± 0.000027, expanded uncertainty, k = 2),8 and secondly the value realised by the LGC171-KT reference set described herein (0.011091 ± 0.000023, expanded uncertainty, k = 2). These values are both based upon linear regression of the certified R(13C/12C) and indicative δ(13C)VPDB values of the reference materials. A re-assessment of the best estimate of R(13C/12C)VPDB is now possible. Simple inspection of the six R(13C/12C)VPDB values considered (those described as measurement results in Fig. 6) shows that uncertainty in the Valkiers et al. (2007)36 value is lower than the others, which is confirmed by a consistency plot constructed in Fig. 7. It is therefore not appropriate to include the uncertainties reported by the participants when estimating a consensus value and its associated uncertainty (e.g. by calculating the weighted mean). There is no evidence that any of the results is an outlier, or not part of normal distribution of R(13C/12C)VPDB values; however there is an additional dispersion between the values that cannot reasonably be explained by the reported uncertainties (the standard deviation of the reported values is larger than any of the reported expanded uncertainties). Due to the fact that the between-lab variation is a predominant contributor to the uncertainty of R(13C/12C)VPDB the classical mean and standard error of the six measurements provide a reasonable estimate of the true value of R(13C/12C)VPDB = 0.011117 ± 0.000039 (expanded uncertainty, k = 2.6) and we recommend that this value replaces that from Chang and Li (1990) as the current best estimate. The associated uncertainty of this mean value is lower than that of the previous consensus estimate of Kaiser, although somewhat larger than the currently accepted value from Chang and Li (1990).
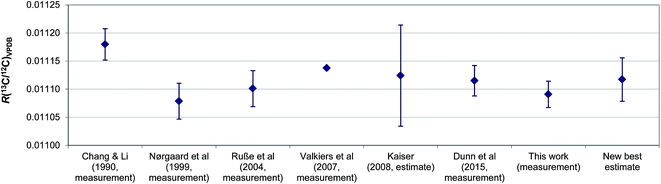 | ||
| Fig. 6 Comparison of R(13C/12C)VPDB values previously reported in the literature together with a new best estimate. Error bars show the expanded uncertainty. | ||
Conclusions
For the first time, a systematic description of the challenges associated with the characterisation of matrix reference materials for R(13C/12C) values traceable to the SI is reported. Three glycine solutions of the CRM LGC171-KT produced in this study are primarily intended for use in the calibration of instruments for the determination of absolute carbon isotope ratios. They can also be used as a quality control for validation of new measurement methods and for training and performance evaluation purposes. Many instrumental techniques, including MC-ICPMS, IRMS, cavity ring down spectroscopy and other isotope ratio infrared spectrometry methods, can perform carbon isotope ratio measurements and therefore benefit from the availability of the above materials.Certification of the LGC171-KT material has been made in accordance with latest methodological and statistical approaches. We have described in detail a development process for the CRM, including production, characterisation, homogeneity and stability assessment and assigning property values and their uncertainties. An improved approach for evaluating uncertainty contribution arising from homogeneity testing has been used in this work. Certified R(13C/12C) values for the glycine solutions are traceable to the International System of Units in the most direct way through calibration of the mass spectrometer by SI-traceable calibrators prepared from well characterised 13C-enriched and 13C-depleted glycines. Indicative δ(13C)VPDB values have also been determined for LGC171-KT. A new best-estimate for R(13C/12C)VPDB has also been determined and we recommend the value of R(13C/12C)VPDB = 0.011117 ± 0.000039 (expanded uncertainty, k = 2.6).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Tyler B. Coplen and Haiping Qi at the US Geological Survey Stable Isotope Laboratory, Reston, Virginia are gratefully acknowledged for performing isotopic analysis of hydrogen, nitrogen and oxygen in 13C-enriched and 13C-depleted glycines. Stephen Ellison and Philip Wilson at LGC are acknowledged for assistance and advice in statistical evaluation the measurement results and discussion. We also thank two anonymous reviewers for their helpful comments on an earlier version of this manuscript. The work described in this paper was funded in part by the UK Government Department for Business, Energy & Industrial Strategy (BEIS).References
- R. A. Werner and W. A. Brand, Rapid Commun. Mass Spectrom., 2001, 15(7), 501–519 CrossRef CAS PubMed.
- W. A. Brand, T. B. Coplen, J. Vogl, M. Rosner and T. Prohaska, Pure Appl. Chem., 2014, 86(3), 425–467 CAS.
- T. B. Coplen, W. A. Brand, M. Gehre, M. Gröning, H. A. Meijer, B. Toman and R. M. Verkouteren, Rapid Commun. Mass Spectrom., 2006, 20, 3165–3166 CrossRef CAS PubMed.
- T. B. Coplen, W. A. Brand, M. Gehre, M. Gröning, H. A. Meijer, B. Toman and R. M. Verkouteren, Anal. Chem., 2006, 78, 2439–2441 CrossRef CAS PubMed.
- J. Meija, personal communication.
- J. Kaiser, Geochim. Cosmochim. Acta, 2008, 72, 1312–1334 CrossRef CAS.
- D. Malinovsky, P. J. H. Dunn and H. Goenaga-Infante, J. Anal. At. Spectrom., 2013, 28, 1760–1771 RSC.
- P. J. H. Dunn, D. Malinovsky and H. Goenaga-Infante, Anal. Bioanal. Chem., 2015, 407, 3169–3180 CrossRef CAS PubMed.
- J. Santrock, S. A. Studley and J. M. Hayes, Anal. Chem., 1985, 57(7), 1444–1448 CrossRef CAS PubMed.
- W. A. Brand, S. S. Assonov and T. B. Coplen, Pure Appl. Chem., 2010, 82(8), 1719–1733 CAS.
- JCGM series - Evaluation of measurement data – Guide to the expression of uncertainty in measurement (ISO/IEC Guide 98-3), International Organisation for Standardization, Geneva, 2008, https://www.iso.org/sites/JCGM/GUM-introduction.htm Search PubMed.
- J. Kragten, Analyst, 1994, 119, 2161–2165 RSC.
- P. J. H. Dunn, L. Hai, D. Malinovsky and H. Goenaga-Infante, Rapid Commun. Mass Spectrom., 2015, 29, 2184–2186 CrossRef CAS PubMed.
- M. J. T. Milton and T. J. Quinn, Metrologia, 2001, 38, 289–296 CrossRef CAS.
- P. D. P. Taylor, H. Kipphardt and P. De Bièvre, Accredit. Qual. Assur., 2001, 6, 103–106 CrossRef.
- M. J. T. Milton, Metrologia, 2013, 58, 158–163 CrossRef.
- Joint Committee for Guides, in Metrology (JCGM), “International vocabulary of metrology – Basic and general concepts and associated terms (VIM)”, JCGM, 3rd edn, 2012 Search PubMed.
- P. De Bièvre, R. Dybkaer, A. Fajgelj and D. Brynn Hibbert, Pure Appl. Chem., 2011, 83(10), 1873–1935 Search PubMed.
- A. O. Nier, Phys. Rev., 1950, 77, 789–793 CrossRef CAS.
- J. R. De Laeter, P. De Bièvre and H. S. Peiser, Mass Spectrom. Rev., 1992, 11, 193–245 CrossRef CAS.
- M. Varlam, S. Valkiers, M. Berglund, P. Taylor, R. Gonfiantini and P. De Bièvre, Int. J. Mass Spectrom., 2008, 269, 78–84 CrossRef CAS.
- J. Meija, Anal. Bioanal. Chem., 2012, 403(8), 2071–2076 CrossRef CAS PubMed.
- D. Malinovsky, P. J. H. Dunn, P. Petrov and H. Goenaga-Infante, Anal. Bioanal. Chem., 2015, 407, 869–882 CrossRef CAS PubMed.
- J. R. De Laeter, J. K. Böhlke, P. De Bièvre, H. Hidaka, H. S. Peiser, K. J. R. Rosman and P. D. P. Taylor, Pure Appl. Chem., 2003, 75, 683–800 CAS.
- E. Barkan and B. Luz, Rapid Commun. Mass Spectrom., 2005, 19, 3737–3742 CrossRef CAS PubMed.
- S. S. Assonov and C. A. M. Brenninkmeijer, Rapid Commun. Mass Spectrom., 2003, 17, 1017–1029 CrossRef CAS PubMed.
- A. Possolo, A. M. H. van der Veen, J. Meija and D. Brynn Hibbert, Pure Appl. Chem., 2018, 90(2), 95–424 Search PubMed.
- G. Mana and O. Rienitz, Int. J. Mass Spectrom., 2010, 291, 55–60 CrossRef CAS.
- General requirements for the competence of reference material producers, ISO, Geneva, 2016, ISO 17034 Search PubMed.
- T. P. J. Linsinger and H. E. Emons, Accredit. Qual. Assur., 2013, 18, 149–152 CrossRef.
- A. M. H. van der Veen, T. P. J. Linsinger, H. Schimmel, A. Lamberty and J. Pauwels, Accredit. Qual. Assur., 2001, 6, 290–294 CrossRef.
- A. Schimmelmann, H. Qi, T. B. Coplen, W. A. Brand, J. Fong, W. Meier-Augenstein, H. F. Kemp, B. Toman, A. Ackermann, S. Assonov, A. T. Aerts-Bijma, R. Brejcha, Y. Chikaraishi, T. Darwish, M. Elsner, M. Gehre, H. Geilmann, M. Gröning, J. F. Helie, S. Herrero-Martin, H. A. S. Meijer, P. E. Sauer, A. L. Sessions and R. A. Werner, Anal. Chem., 2016, 88, 4294–4302 CrossRef CAS PubMed.
- J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. De Bièvre, M. Gröning, N. E. Holden, J. Irregeher, R. D. Loss, T. Walczyk and T. Prohaska, Pure Appl. Chem., 2016, 88(3), 293–306 CAS.
- T. L. Chang and W. Li, Chin. Sci. Bull., 1990, 35, 290–296 Search PubMed.
- J. V. Nørgaard, H. Kipphardt, S. Valkiers and P. D. P. Taylor, Certification report EUR 19061 EN, IRMM, 1999 Search PubMed.
- K. Russe, S. Valkiers and P. D. P. Taylor, Int. J. Mass Spectrom., 2004, 253, 255–262 CrossRef.
- S. Valkiers, M. Varlam, K. Russe, M. Berglund, P. D. P. Taylor, J. Wang, M. J. T. Milton and P. De Bièvre, Int. J. Mass Spectrom., 2007, 264, 10–21 CrossRef CAS.
- S. S. Assonov, Rapid Commun. Mass Spectrom., 2018, 32, 827–830 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2019 |