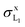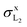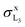L-shell X-ray production cross-sections for Mo by proton impact
Pablo D.
Pérez
 *ab,
Tabatha P.
Rodríguez
c,
Jorge C.
Trincavelli
*ab,
Tabatha P.
Rodríguez
c,
Jorge C.
Trincavelli
 ad,
José M.
Fernández-Varea
ad,
José M.
Fernández-Varea
 e and
Sergio G.
Suárez
ab
e and
Sergio G.
Suárez
ab
aConsejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina
bCentro Atómico Bariloche, Comisión Nacional de Energía Atómica (CNEA), San Carlos de Bariloche, Argentina. E-mail: pablo.perez@cab.cnea.gov.ar
cFacultad de Ciencias Naturales, Matemática y del Medio Ambiente, Universidad Tecnológica Metropolitana (UTEM), Santiago de Chile, Chile
dFacultad de Matemática, Astronomía, Física y Computación, Universidad Nacional de Córdoba (UNC), Córdoba, Argentina
eFacultat de Física (FQA and ICC), Universitat de Barcelona, Barcelona, Catalonia, Spain
First published on 26th November 2018
Abstract
Total L and Li subshell X-ray production cross-sections were determined experimentally for Mo by proton impact. The thick-target method was used, and the proton energies ranged from 200 keV to 3 MeV. The recorded X-ray spectra were fitted using novel open software for PIXE semi-quantitative analysis that takes into account X-ray emission, absorption and detection. K-shell X-ray production cross-sections of Ti and Cu samples were used to normalize our results for Mo. The measured Mo L X-ray production cross-sections are in excellent agreement with the predictions of the ECPSSR theory. The sensitivity of the theoretical L shell and Li subshell X-ray production cross-sections to the adopted fluorescence yields and Coster–Kronig coefficients was also studied.
Introduction
The accurate experimental determination of X-ray production cross-sections of atomic inner shells by the impact of protons and other ions is an active research topic in atomic collision physics, being important for testing theories and also for analytical techniques such as particle-induced X-ray emission (PIXE). Cross-section databases, once implemented in Monte Carlo simulation packages, find application in a large variety of disciplines ranging from materials science to medical physics. In a recent and very extensive compilation of measured cross-sections for L-shell ionization and X-ray production by protons,1,2 Miranda and Lapicki showed that for many atoms either there is a lack of experimental results or the existing ones are inconsistent.Experimental X-ray production cross-sections are often determined using thin samples. This thin-target method is effective and reliable although it has downsides related to the manufacture of samples and the characterization of their mass density or thickness. In turn, the thick-target method3 demands a more elaborate data analysis procedure, but it has been exploited fruitfully in the measurement of X-ray production cross-sections over a wide range of target elements and proton energies. Furthermore, it is amenable to be used for the measurement of low-probability events like multiple ionizations and radiative Auger emission.4
In this work, we address the ionization of the L subshells of Mo (Z = 42) by proton impact. On one hand, between around 600 keV and 4.5 MeV there is a lack of reliable experimental Mo L X-ray production cross-sections, and the existing values are much lower than the prediction of the ECPSSR formalism.5 On the other hand, experimental X-ray production cross-sections of individual Mo Li subshells are only available for energies below 300 keV. In order to help improve the status of the experimental database for this element, L shell and Li subshell X-ray production cross-sections were obtained using the thick-target method for protons with energies between 200 keV and 3 MeV. Novel software6 for semi-quantitative analysis of PIXE spectra was used to fit the acquired X-ray spectra. This software, called PAMPA (Parameter Assessment Method for PIXE Analysis), fits the spectrum by minimizing the quadratic differences between the predicted spectrum and the experimental one. The modelled spectrum considers the bremsstrahlung generated by the atoms in the sample, the emission of characteristic X-rays, absorption processes and several X-ray detection phenomena. A normalization factor is introduced in the thick-target equation [see eqn (1) below] to avoid the large uncertainties associated with the solid angle of the spectrometer and the calibration of the charge-integration device; hence, we rely on a relative measurement method. Then, K-shell X-ray production cross-sections for Ti and Cu are employed to determine this factor and place the X-ray production cross-sections for Mo on an absolute scale.
The cross-sections reported here are compared with the experimental values from the literature as well as with the predictions of the ECPSSR formalism and the binary-encounter approximation. The comparison with ECPSSR is made using fluorescence yields and Coster–Kronig coefficients published by Krause,7 Puri et al.8 (see also ref. 9) and Kolbe et al.10 with the intent to gauge the sensitivity of the theoretical Mo L and Mo Li X-ray production cross-sections to these atomic relaxation parameters.
Experimental
Samples
The analyzed sample was a bulk target of Mo. In order to normalize the measurements, Ti and Cu bulk samples were also required; these elements were selected because their K-shell X-ray production cross-sections are known with high accuracy. The three samples were metal plates polished and cleaned with a 50% (vol) nitric acid solution.X-ray spectrometer
The employed spectrometer was a Sirius Si drift detector (SDD) with an ultra-thin polymer window (Moxtek AP3.3) that allows us to measure X-rays emitted by elements down to Be. The active thickness of the Si crystal is 450 μm, and its area is 30 mm2 (nominal values quoted in the detector's data sheet). The SDD was located at a distance of 15 cm from the sample, and the observation angle β was set to 33° relative to the incidence direction of the proton beam. In a previous article, the intrinsic efficiency curve of this spectrometer was established by measuring the X-ray yields of several bulk samples bombarded with protons and comparing them with theoretical predictions.11Irradiation
The samples were irradiated in a NEC Pelletron 5SDH, 1.7 MV tandem ion accelerator located at the Centro Atómico Bariloche (San Carlos de Bariloche, Argentina).12 The ion source works by Cs sputtering of a solid cathode (SNICS II), and it was used for the extraction of H− ions from a ZrH2 cathode. The analysis chamber is a RC43 endstation equipped with several detectors for PIXE, RBS (Rutherford Backscattering Spectrometry), ERDA (Elastic Recoil Detection Analysis) and NRA (Nuclear Reaction Analysis).The samples were set up on a stage with micrometer precision perpendicular to the incident beam (α = 0°). All samples were bombarded with protons whose energies ranged from 200 to 3000 keV. The interval between incident energies was set smaller in regions where large variations in the X-ray production cross-sections were expected. The beam currents were registered by two current integrators, one connected to the sample stage and the other to the irradiation chamber. The currents were chosen between 1 nA and 2 nA so as to maintain low counting rates and avoid saturation of the SDD. The irradiations made at the highest proton energies were stopped when the accumulated charge reached 1 μC. As the energy decreased, the accumulated charge was increased up to 5 μC to partially compensate for the lower X-ray emission probabilities.
Data analysis
Methodology
Consider a vacancy in the Li subshell that is filled by a radiative transition from a higher subshell Xj (X = M or N in the case of Mo). The ensuing X-ray line will be denoted as LiXj. The thick-target method is based on two assumptions, namely (1) ions travel along straight trajectories losing energy gradually at a rate dictated by the stopping power and (2) LiXj characteristic X-rays are only emitted after ion-impact ionization, the contribution due to ionization by secondary electrons being negligible. The equation for the X-ray production cross-section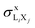 of an ion with kinetic energy E0 can be written in the form3,4,13
of an ion with kinetic energy E0 can be written in the form3,4,13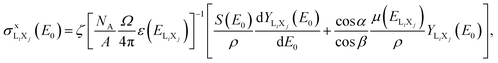 | (1) |
The procedure followed to obtain 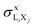 involves the following steps. (1) The X-ray yield of the LiXj line is measured for several energies of the incident proton beam. (2) The set of experimental X-ray yields is fitted with an appropriate analytical function
involves the following steps. (1) The X-ray yield of the LiXj line is measured for several energies of the incident proton beam. (2) The set of experimental X-ray yields is fitted with an appropriate analytical function 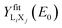 . (3)
. (3) 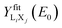 and its derivative are inserted in eqn (1) along with the mass stopping power, mass attenuation coefficient, intrinsic efficiency, etc.
and its derivative are inserted in eqn (1) along with the mass stopping power, mass attenuation coefficient, intrinsic efficiency, etc.
The X-ray production cross-section for subshell Li may be deduced directly from 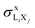 and ΓLiXj/ΓLi,total (the relative emission rate of the LiXj line) as
and ΓLiXj/ΓLi,total (the relative emission rate of the LiXj line) as
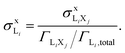 | (2) |
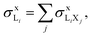 | (3) |
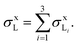 | (4) |
X-ray spectra
The collected X-ray spectra were fitted with the PAMPA program,6 specifically designed for PIXE. This software contemplates several physics phenomena related to the emission, absorption and detection of X-rays. PAMPA minimizes the quadratic differences between the experimental spectrum and an analytical function proposed to describe it, which depends on fundamental and instrumental parameters. Depending on the particular application of the program, different sets of parameters can be optimized; for example, elemental concentrations can be extracted for quantification purposes or the thicknesses of the spectrometer's dead layer and polymer window can be found to quantify the intrinsic efficiency at low energies. PAMPA implements realistic models for the peak profiles, instrumental parameters and bremsstrahlung background together with up-to-date fundamental parameters, thus enabling reliable fits to the acquired X-ray spectra. Here we will only outline briefly the main features of the program; for a full description, the reader may consult ref. 6.A characteristic X-ray of energy Ex and negligible natural width would produce a sharp peak (delta function) in the recorded spectrum. In a real energy-dispersive spectrometer, this line is broadened into a Gaussian distribution G(E) centered at Ex and with standard deviation
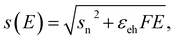 | (5) |
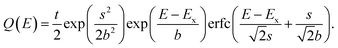 | (6) |
| H(E) = N[G(E) + Q(E)] | (7) |
The continuum background B(E) is modelled with a semi-empirical function6,16 derived from the following considerations: (1) the main contribution to the background is atomic bremsstrahlung, (2) the number of bremsstrahlung photons generated with a particular energy at each depth within the target is proportional to the number of ionized atoms at the same depth and to the differential atomic bremsstrahlung cross-section, and (3) the distribution of ionization with depth can be approximated by a step function.
The fundamental parameters used by PAMPA to predict the characteristic X-ray spectrum include the X-ray transition energies recommended by Deslattes et al.17 and relative emission rates tabulated by Campbell and Wang;18 all these quantities can be refined during the fitting process if so desired. Other quantities such as fluorescence yields,7,19 ionization cross-sections,5 mass stopping powers20 and mass attenuation coefficients21 are non-refinable.
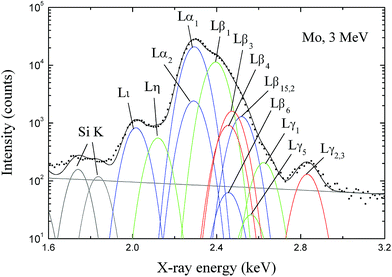
According to ref. 17, the characteristic lines emitted by transitions to the Mo L1 subshell are Lβ4 (L1M2), Lβ3 (L1M3) and Lγ2,3 (L1N2,3), the characteristic lines associated with transitions to the Mo L2 subshell are Lη (L2M1), Lβ1 (L2M4), Lγ5 (L2N1) and Lγ1 (L2N4), and the lines related to transitions to the Mo L3 subshell are L![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (L3M1), Lα2 (L3M4), Lα1 (L3M5), Lβ6 (L3N1) and Lβ15,2 (L3N4,5). In the fitting process, the energies of all these diagram lines were fixed to the values tabulated by Deslattes et al.17 and the relative emission rates within each subshell were set equal to the values tabulated by Campbell and Wang.18 Furthermore, the parameters sn and F of the detector response function as well as the asymmetry parameters t and b associated with each peak were assessed by Rodríguez et al.6 and kept unaltered during the optimization procedure. In turn, the three global scale factors that govern the intensities of the Li-subshell groups were treated as adjustable quantities. Including the offset and gain of the linear energy-channel relationship and the two empirical coefficients in the bremsstrahlung background model, the total number of adjustable parameters amounts to seven.
(L3M1), Lα2 (L3M4), Lα1 (L3M5), Lβ6 (L3N1) and Lβ15,2 (L3N4,5). In the fitting process, the energies of all these diagram lines were fixed to the values tabulated by Deslattes et al.17 and the relative emission rates within each subshell were set equal to the values tabulated by Campbell and Wang.18 Furthermore, the parameters sn and F of the detector response function as well as the asymmetry parameters t and b associated with each peak were assessed by Rodríguez et al.6 and kept unaltered during the optimization procedure. In turn, the three global scale factors that govern the intensities of the Li-subshell groups were treated as adjustable quantities. Including the offset and gain of the linear energy-channel relationship and the two empirical coefficients in the bremsstrahlung background model, the total number of adjustable parameters amounts to seven.
The energies of the lines belonging to the Mo L multiplet span from 2.0 to 2.8 keV. As a consequence of this small energy interval there is a strong overlap of the many contributing peaks, the most intense of which are Lα1 and Lβ1. Parasitic Si K X-rays also appear in the spectra, possibly generated by internal fluorescence in the Si dead layer of the SDD; fortunately they overlap with none of the Mo L lines. For illustration purposes, the region of interest of the spectrum pertaining to 3 MeV protons is depicted in Fig. 1. The contributions of the individual characteristic X-ray lines and the bremsstrahlung background to the fit are displayed too. As can be seen, the fitting procedure carried out by PAMPA with the set of characteristic energies and relative emission rates chosen from the literature led to a very good description of the spectrum.
X-ray yields
All the LiXj X-ray yields were fitted with the analytical function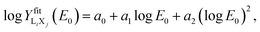 | (8) |
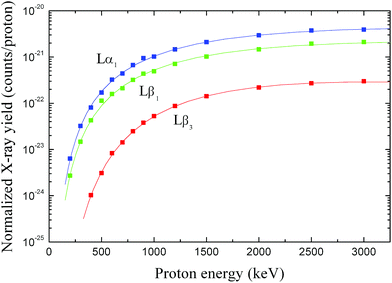 | ||
| Fig. 2 X-ray yields for the Lβ3, Lβ1 and Lα1 lines as a function of proton energy E0. The symbols are experimental data (the error bars are smaller than the symbol size) and the solid curves correspond to the analytical fits. The colour code is the same as that in Fig. 1. | ||
The 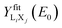 curves and their derivatives are replaced in eqn (1) to evaluate the
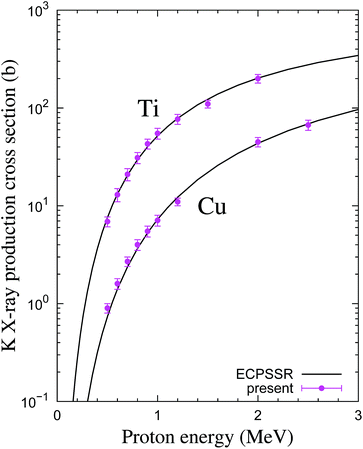
curves and their derivatives are replaced in eqn (1) to evaluate the 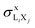 X-ray production cross-sections. The mass stopping powers and mass attenuation coefficients were taken from the SRIM2013 code20,22 and the XCOM database,23 respectively. As mentioned above, a normalization factor ζ was introduced in eqn (1) to circumvent some limitations of our experimental arrangement that are related to geometrical factors and charge integration. The uncertainty of the solid angle is large because we only know approximately the distance between the impact point of the beam on the sample and the active volume of the SDD and, moreover, we only have access to the nominal frontal area of the SDD. On the other hand, ζ also works as a parameter related to the calibration of the charge-collection device. This factor was found from additional measurements performed with the Ti and Cu samples. These elements were chosen because ECPSSR is in good agreement with the large body of measurements and also because of the availability of high-quality samples. The K-shell X-ray production cross-sections of these ‘reference’ elements, determined as explained in Subsection 3.1 (with ζ = 1), were divided by the theoretical values calculated from ECPSSR ionization cross-sections5,24 and the K-shell fluorescence yields recommended by Krause.7†. The ensuing ratios were averaged over all proton energies and the two elements, yielding ζ = 10.7 ± 0.8. The Ti K and Cu K X-ray production cross-sections normalized with this value of ζ are plotted and shown in Fig. 3. We have omitted the numerous experimental data published by other authors so as to avoid cluttering the figure.
X-ray production cross-sections. The mass stopping powers and mass attenuation coefficients were taken from the SRIM2013 code20,22 and the XCOM database,23 respectively. As mentioned above, a normalization factor ζ was introduced in eqn (1) to circumvent some limitations of our experimental arrangement that are related to geometrical factors and charge integration. The uncertainty of the solid angle is large because we only know approximately the distance between the impact point of the beam on the sample and the active volume of the SDD and, moreover, we only have access to the nominal frontal area of the SDD. On the other hand, ζ also works as a parameter related to the calibration of the charge-collection device. This factor was found from additional measurements performed with the Ti and Cu samples. These elements were chosen because ECPSSR is in good agreement with the large body of measurements and also because of the availability of high-quality samples. The K-shell X-ray production cross-sections of these ‘reference’ elements, determined as explained in Subsection 3.1 (with ζ = 1), were divided by the theoretical values calculated from ECPSSR ionization cross-sections5,24 and the K-shell fluorescence yields recommended by Krause.7†. The ensuing ratios were averaged over all proton energies and the two elements, yielding ζ = 10.7 ± 0.8. The Ti K and Cu K X-ray production cross-sections normalized with this value of ζ are plotted and shown in Fig. 3. We have omitted the numerous experimental data published by other authors so as to avoid cluttering the figure.
To determine the subshell X-ray production cross-sections 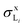 , the values of
, the values of 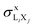 are summed for all the radiative transitions to the subshell Li [see eqn (3)].
are summed for all the radiative transitions to the subshell Li [see eqn (3)].
Uncertainty budget
The uncertainties of the X-ray production cross-section were found by propagating the errors in expression (1) as described by Pérez et al.4 For this matter, the uncertainty associated with the mass stopping power was 10% (see the graph for Mo given by Ziegler);20 the uncertainty of the mass attenuation coefficients was 10% because the X-ray energy range of interest is close to the Li absorption edges.26 The estimated uncertainty in the intrinsic efficiency of the SDD was 7%, as stated by Limandri et al.11Theory
The plane-wave Born approximation is an ab initio formalism that has been extensively used to calculate ionization cross-sections by proton impact. Binding-polarization and Coulomb corrections can be incorporated to improve the accuracy of the formalism at the energies employed in PIXE experiments. Chen and Crasemann27,28 calculated ionization cross-sections for the K, L and M (sub)shells of various atoms by adopting this corrected plane-wave Born approximation. The required inelastic form factors were computed from numerical bound and free relativistic wave functions of the active electron. Unfortunately, their tabulations do not include data for Mo.To facilitate the evaluation of ionization cross-sections within the corrected plane-wave Born approximation, Brandt and Lapicki developed the ECPSSR analytical model,5 which relies on non-relativistic hydrogenic inelastic form factors. A comprehensive overview of this model can be found in ref. 29. The ECPSSR has been very successful in predicting reliable cross-sections for many applications including PIXE. ECPSSR ionization cross-sections for the Mo Li subshells were extracted from the PIXE2010 database,24 choosing the ‘united atom’ approximation.‡
In addition, we have calculated ionization cross-sections for the Mo Li subshells having recourse to the binary-encounter approximation31 (BEA). This simple formalism only needs as an input the experimental binding energy of the considered subshell and its probability density of linear momentum, for which we adopted the analytical non-relativistic hydrogenic expressions with Slater's effective charges.32 The implementation of the BEA is more straightforward than that of the ECPSSR formalism although it is expected to be less accurate owing to the neglect of corrections for binding-polarization and Coulomb deflection.
From the Mo Li subshell ionization cross-sections one may compute the corresponding X-ray production cross-sections 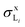 using the expressions
using the expressions
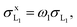 | (9) |
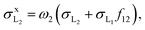 | (10) |
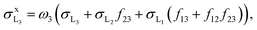 | (11) |
An internally consistent database of fluorescence yields and Coster–Kronig transition probabilities was compiled by Krause7 based on semi-empirical information. Later on, the atomic relaxation parameters ωi and fij that had been calculated in the Dirac–Hartree–Slater approximation were tabulated by Puri et al.8 as well as by Campbell.9 In recent work, Kolbe et al.10 used synchrotron radiation to measure ωi and fij for a few elements, among them Mo, with a traceable uncertainty budget. For the sake of completeness, the atomic relaxation data from these references are summarized in Table 1.
Results and discussion
We recall that in the fit of the X-ray spectra with PAMPA, the relative weights of the various radiative transitions LiXj to a given Mo Li subshell were kept fixed to ΓLiXj/ΓLi,total. Hence, we do not report the individual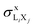 X-ray production cross-sections but, rather,
X-ray production cross-sections but, rather, 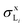 and σxL.
and σxL.
Total L-shell X-ray production cross-sections
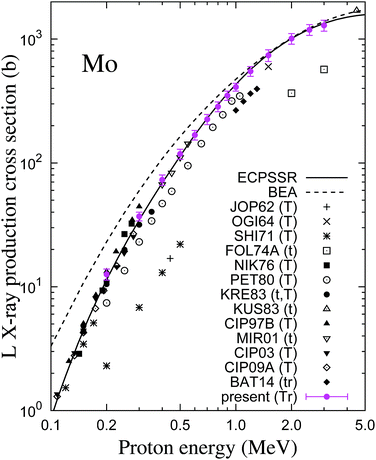
The present Mo L X-ray production cross-sections are listed in Table 2. They are also displayed in Fig. 4 along with the existing experimental data33–45 (the numerical values were taken from the review by Miranda and Lapicki1,2), and the theoretical ECPSSR and BEA σxL. Ratios of experimental to theoretical X-ray production cross-sections are shown in Fig. 5.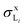 X-ray production cross-sections for Mo. The uncertainties correspond to one standard deviation
X-ray production cross-sections for Mo. The uncertainties correspond to one standard deviation
| E 0 (keV) | σ xL (b) | (b) | (b) | (b) |
|---|---|---|---|---|
| 200 | 12.6 ± 1.3 | 3.8 ± 0.5 | 8.8 ± 1.2 | |
| 300 | 37 ± 3 | 11.4 ± 1.5 | 26 ± 3 | |
| 400 | 73 ± 7 | 1.17 ± 0.15 | 22.1 ± 2.8 | 50 ± 6 |
| 500 | 118 ± 11 | 2.7 ± 0.3 | 35 ± 5 | 80 ± 10 |
| 600 | 168 ± 15 | 5.0 ± 0.6 | 50 ± 6 | 113 ± 14 |
| 700 | 225 ± 21 | 8.1 ± 1.0 | 67 ± 8 | 150 ± 19 |
| 800 | 285 ± 26 | 11.7 ± 1.5 | 84 ± 11 | 189 ± 24 |
| 900 | 350 ± 30 | 16.0 ± 2.0 | 103 ± 13 | 230 ± 30 |
| 1000 | 410 ± 30 | 20.6 ± 2.7 | 122 ± 16 | 270 ± 30 |
| 1200 | 550 ± 50 | 31 ± 4 | 160 ± 21 | 360 ± 50 |
| 1500 | 740 ± 80 | 46 ± 6 | 215 ± 29 | 480 ± 70 |
| 2000 | 1010 ± 100 | 67 ± 9 | 290 ± 40 | 650 ± 90 |
| 2500 | 1190 ± 120 | 78 ± 11 | 340 ± 50 | 770 ± 110 |
| 3000 | 1290 ± 130 | 81 ± 12 | 370 ± 50 | 840 ± 120 |
 | ||
| Fig. 4 Mo L X-ray production cross-section as a function of proton energy (logarithmic scale). The magenta circles with error bars are the present results. Other symbols are experimental data from the literature;33–45 the acronyms are those in the review,1,2 and the letters t and T indicate whether the thin-target or the thick-target method was used, respectively, whereas r means that the measurement was relative. The solid and dashed curves correspond to the ECPSSR theory5 and the BEA, respectively, with Krause's relaxation parameters.7 | ||
 | ||
| Fig. 5 Ratios of the present experimental Mo L X-ray production cross-sections to the predictions of the ECPSSR model, as a function of proton energy (logarithmic scale). The three plots correspond to the indicated choice of fluorescence yields and Coster–Kronig coefficients for the conversion of ionization to X-ray production cross-sections (see eqn (9)–(11)). The dotted lines delimit an energy-dependent uncertainty interval evaluated as a rough estimate of the accuracy of ECPSSR combined with the uncertainties of the ωi and fij coefficients. | ||
A few of the measurements reported in the literature were carried out using thin samples36,39,40,42,45 but in most cases the thick-target method was employed.33–35,37–39,41,43,44 Three of the older experimental X-ray production cross-section data sets from the sixties and seventies are about three to five times smaller than the rest of the data and should be discarded from the analysis. Our measured σxL are in satisfactory accord with those of the majority of experiments performed below around 300 keV. Between 400 and 550 keV, the present results are almost identical to those reported by Miranda's group,42 and these two data sets are somewhat larger than the cross-sections measured by Petukhov and co-workers.38 A similar trend is observed at 1.0–1.3 MeV, where the recent measurements by Batyrbekov and his colleagues45 are substantially smaller than our cross-sections. Therefore, between 600 keV and 3 MeV, the present σxL values are higher than those of all previous experiments.
Comparing the present Mo L X-ray production cross-sections with the ECPSSR theory we find excellent agreement in the investigated energy interval if the fluorescence yields and Coster–Kronig coefficients of Krause's classical compilation7 are adopted. As can be seen in Fig. 5, the agreement worsens slightly if the values of ωi and fij are taken from Puri et al.8 or Kolbe et al.10 Nevertheless, σxL is relatively insensitive to the selection of fluorescence yields and Coster–Kronig coefficients. Given the uncertainty of the experimental cross-sections and the accuracy attributed to the ECPSSR formalism, it is apparent that the theoretical σxL curves calculated with the three sets of atomic relaxation parameters are compatible with our measured Mo L X-ray production cross-sections. On the other hand, the simpler BEA yields too high cross-sections at energies below several hundred keV.
L subshell X-ray production cross-sections
The present Mo Li X-ray production cross-sections are listed in Table 2 and shown in Fig. 6. Included in the figure are the experimental data by Cipolla,41,44 who in these publications chose the L2,3, Lβ1 and Lα1,2 radiative transitions to evaluate the X-ray production cross-sections of the L1, L2 and L3 subshells, respectively, using eqn (2) with relative emission rates from Campbell and Wang.18 Theoretical subshell X-ray production cross-sections calculated from the ECPSSR Mo Li ionization cross-sections and the three aforementioned sets of fluorescence yields and Coster–Kronig coefficients7,8,10 are also displayed.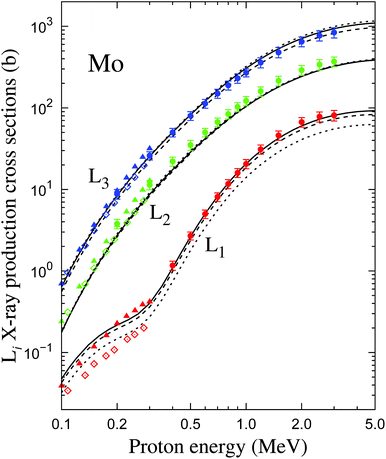 | ||
| Fig. 6 Mo Li subshell X-ray production cross-sections as a function of proton energy (logarithmic scale). The circles with error bars are the present results, whereas Cipolla's experimental data are depicted as triangles41 and diamonds;44 the red, green and blue symbols pertain to the L1, L2 and L3 subshells, respectively. The solid, dotted and dashed curves correspond to the theoretical values computed from ECPSSR subshell ionization cross-sections and relaxation parameters published by Krause,7 Puri et al.8 and Kolbe et al.,10 respectively. | ||
The experimental Mo L1 X-ray production cross-sections match perfectly with the theoretical 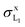 curve calculated with Krause's ω1. The curve computed with Puri et al.'s ω1 underestimates
curve calculated with Krause's ω1. The curve computed with Puri et al.'s ω1 underestimates 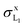 by around 30%, which can be attributed to the low value of the L1 fluorescence yield [see eqn (9) and Table 1]. Miranda and co-workers46 studied the effect of atomic relaxation parameters on L-shell X-ray production cross-sections by proton impact with energies below 1 MeV, concluding that Puri et al.'s relaxation data furnish the best overall agreement with a large number of experiments. However, they also highlight that
by around 30%, which can be attributed to the low value of the L1 fluorescence yield [see eqn (9) and Table 1]. Miranda and co-workers46 studied the effect of atomic relaxation parameters on L-shell X-ray production cross-sections by proton impact with energies below 1 MeV, concluding that Puri et al.'s relaxation data furnish the best overall agreement with a large number of experiments. However, they also highlight that 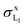 is not well predicted by Campbell and Wang's relative emission rates. The two sets of measurements by Cipolla are discrepant, which attests to the risk of relying on exclusively one radiative transition to infer the X-ray production cross-section of a subshell. Thus, although the Lγ2,3 peak is resolved in the X-ray spectra (see e.g.Fig. 1) it has a rather low intensity so that its area has a large uncertainty and might be affected by inaccuracies in the subtraction of the continuous bremsstrahlung component. Interestingly, if we sum the Lβ3,4 and Lγ2,3 X-ray production cross-sections of ref. 44, the results (not shown) are almost identical to the data of ref. 41 and more consistent with the trend of our
is not well predicted by Campbell and Wang's relative emission rates. The two sets of measurements by Cipolla are discrepant, which attests to the risk of relying on exclusively one radiative transition to infer the X-ray production cross-section of a subshell. Thus, although the Lγ2,3 peak is resolved in the X-ray spectra (see e.g.Fig. 1) it has a rather low intensity so that its area has a large uncertainty and might be affected by inaccuracies in the subtraction of the continuous bremsstrahlung component. Interestingly, if we sum the Lβ3,4 and Lγ2,3 X-ray production cross-sections of ref. 44, the results (not shown) are almost identical to the data of ref. 41 and more consistent with the trend of our 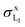 values.
values.
In the case of the Mo L2 X-ray production cross-sections, the present results and those of the older experiment by Cipolla41 are between 10% and 20% higher than the three curves, which are close to each other. Conversely, his more recent values44 fall nicely on the theoretical curves.
Finally, our measured 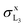 values as well as Cipolla's most recent data set44 support the fluorescence yields and Coster–Kronig coefficients of Kolbe et al. and Krause. The curve evaluated with Puri et al.'s atomic relaxation parameters exhibits a slightly worse agreement.
values as well as Cipolla's most recent data set44 support the fluorescence yields and Coster–Kronig coefficients of Kolbe et al. and Krause. The curve evaluated with Puri et al.'s atomic relaxation parameters exhibits a slightly worse agreement.
Conclusions
L-shell X-ray production cross-sections by proton impact were measured for Mo by means of the thick-target method. The results are compared to the previous experimental information and to the predictions of the ECPSSR model, paying attention to the choice of atomic relaxation parameters.The measured total Mo L X-ray production cross-sections are in good agreement with most previous experimental values below 300 keV. The data from the literature are inconsistent between 600 keV and 3 MeV, and in this energy interval our results are higher. In the whole energy range studied here, our measured L-shell X-ray production cross-sections match the theoretical predictions of the ECPSSR model, especially if the fluorescence yields and Coster–Kronig coefficients recommended by Krause are used.
Regarding the Mo Li X-ray production cross-sections, existing experimental data only extend up to 300 keV. The present results are consistent with them. The comparison of the measured 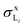 to the theoretical values is satisfactory if the atomic relaxation parameters of Krause or Kolbe et al. are employed. Puri et al.'s ω1 leads to L1 X-ray production cross-sections that deviate notably from those of the experiments. Further experimental and theoretical research is necessary to settle this issue.
to the theoretical values is satisfactory if the atomic relaxation parameters of Krause or Kolbe et al. are employed. Puri et al.'s ω1 leads to L1 X-ray production cross-sections that deviate notably from those of the experiments. Further experimental and theoretical research is necessary to settle this issue.
The fact that the X-ray spectra are fitted on the basis of sensible physics models and that PAMPA enables the possibility of setting up a fitting strategy enhances the confidence in the results, which would be difficult to achieve with commercial software. PAMPA has proven to be flexible and reliable for analyzing the measured X-ray spectra, allowing us to fit even the L lines that would only be resolved with high-resolution detectors such as wave-dispersive spectrometers.
The success of the presented combination of the thick-target method and data-analysis procedure opens up its application to investigate the ionization of the L subshells of other elements whose L lines overlap strongly. Moreover, this combination can be exploited in the measurement of the cross-sections of low-probability phenomena like multiple ionizations producing satellite lines.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Universidad Nacional de Cuyo (Argentina) for the financial support as well as Gimena Anibal and César Olivares for their technical assistance. We are also grateful to Prof. Javier Miranda (Universidad Nacional Autónoma de México) and Prof. Sam J. Cipolla (Creighton University) for valuable discussions. J. M. Fernández-Varea acknowledges the support from the Spanish Ministerio de Economía y Competitividad (project no. FIS2014-58849-P).References
- J. Miranda and G. Lapicki, At. Data Nucl. Data Tables, 2014, 100, 651–780 CrossRef CAS.
- J. Miranda and G. Lapicki, At. Data Nucl. Data Tables, 2018, 119, 444–453 CrossRef CAS.
- E. Merzbacher and H. W. Lewis, Handbuch der Physik, Springer-Verlag, 1958, vol. 34, pp. 166–192 Search PubMed.
- P. D. Pérez, A. Sepúlveda, G. Castellano and J. Trincavelli, Phys. Rev. A, 2015, 92, 062708 CrossRef.
- W. Brandt and G. Lapicki, Phys. Rev. A, 1981, 23, 1717–1729 CrossRef CAS.
- T. Rodríguez, S. Limandri, S. Suárez, I. Ortega-Feliu and J. Trincavelli, J. Anal. At. Spectrom., 2017, 32, 1020–1030 RSC.
- M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 307–327 CrossRef CAS.
- S. Puri, D. Mehta, B. Chand, N. Singh and P. N. Trehan, X-Ray Spectrom., 1993, 22, 358–361 CrossRef CAS.
- J. L. Campbell, At. Data Nucl. Data Tables, 2003, 85, 291–315 CrossRef CAS.
- M. Kolbe, P. Hönicke, M. Müller and B. Beckhoff, Phys. Rev. A, 2012, 86, 042512 CrossRef.
- S. Limandri, G. Bernardi and S. Suárez, X-Ray Spectrom., 2013, 42, 487–492 CrossRef CAS.
- S. Limandri, C. Olivares, L. Rodriguez, G. Bernardi and S. Suárez, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 318, 47–50 CrossRef CAS.
- Z. An and Q. Hou, Phys. Rev. A, 2008, 77, 042702 CrossRef.
- J. L. Campbell and J. A. Maxwell, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 129, 297–299 CrossRef CAS.
- C. Visñovezky, S. Limandri, M. E. Canafoglia, R. Bonetto and J. Trincavelli, Spectrochim. Acta, Part B, 2007, 62, 492–498 CrossRef.
- P. D. Pérez, A. P. L. Bertol, T. P. Rodríguez, M. A. Z. Vasconcellos and J. C. Trincavelli, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 318, 23–26 CrossRef.
- R. D. Deslattes, E. G. Kessler Jr, P. Indelicato, L. de Billy, E. Lindroth and J. Anton, Rev. Mod. Phys., 2003, 75, 35–99 CrossRef CAS.
- J. L. Campbell and J. X. Wang, At. Data Nucl. Data Tables, 1989, 43, 281–291 CrossRef CAS.
- S. T. Perkins, D. E. Cullen, M. H. Chen, J. H. Hubbell, J. Rathkopf and J. H. Scofield, UCRL-50400, Lawrence Livermore National Laboratory, 1991, vol. 30 Search PubMed.
- J. F. Ziegler, SRIM – The Stopping and Range of Ions in Matter, 2013, http://www.srim.org, accessed 2017 Search PubMed.
- K. Heinrich, 11th International Congress on X-Ray Optics and Microanalysis, 1987, pp. 67–119 Search PubMed.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- M. J. Berger, J. H. Hubbell, S. M. Seltzer, J. Chang, J. Coursey, R. Sukumar, D. Zucker and K. Olsen, XCOM: Photon Cross Section Database (version 1.5), http://physics.nist.gov/xcom, 2010 Search PubMed.
- M. G. Pia, G. Weidenspointner, M. Augelli, L. Quintieri, P. Saracco, M. Sudhakar and A. Zoglauer, IEEE Trans. Nucl. Sci., 2009, 56, 3614–3649 CAS.
- J. L. Campbell, Intl. Radiat. Phys. Soc. Bull., 2010, 24, 17–30 Search PubMed.
- C. T. Chantler, J. Phys. Chem. Ref. Data, 1995, 24, 71–643 CrossRef CAS.
- M. H. Chen and B. Crasemann, At. Data Nucl. Data Tables, 1985, 33, 217–233 CrossRef CAS.
- M. H. Chen and B. Crasemann, At. Data Nucl. Data Tables, 1989, 41, 257–285 CrossRef CAS.
- T. Mukoyama, Int. J. PIXE, 1991, 1, 209–239 CrossRef.
- G. Lapicki, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 115201 CrossRef.
- L. Vriens, Proc. Phys. Soc., 1967, 90, 935–944 CrossRef CAS.
- T. Mukoyama, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 354, 155–158 CrossRef CAS.
- R. C. Jopson, H. Mark and C. D. Swift, Phys. Rev., 1962, 127, 1612–1618 CrossRef CAS.
- W. T. Ogier, G. J. Lucas, J. S. Murray and T. E. Holzer, Phys. Rev., 1964, 134, A1070–A1072 CrossRef.
- K. Shima, I. Makino and M. Sakisaka, J. Phys. Soc. Jpn., 1971, 30, 611–619 CrossRef CAS.
- F. Folkmann, C. Gaarde, T. Huus and K. Kemp, Nucl. Instrum. Methods, 1974, 116, 487–499 CrossRef CAS.
- V. S. Nikolaev, V. P. Petukhov, E. A. Romanovsky, V. A. Sergeev, I. M. Kruglova and V. V. Beloshitshky, Invited lectures, review papers and progress reports from 9th ICPEAC, 1976, pp. 419–431 Search PubMed.
- V. P. Petukhov, E. A. Romanovskii, H. Kerkow and G. Kreysch, Phys. Status Solidi A, 1980, 60, 79–83 CrossRef CAS.
- G. Kreysch, H. Kerkow, R. I. Bogdanov, V. P. Petukhov and E. A. Romanovskii, Phys. Status Solidi A, 1983, 78, 507–525 CrossRef CAS.
- B. H. Kusko, K, L, and M-Shell X-Ray Production Cross Sections Induced by 4.5–67.5 MeV Protons, PhD thesis, University of California at Davis, Davis, 1983.
- S. J. Cipolla, AIP Conf. Proc., 1997, 392, 117–120 CrossRef CAS.
- J. Miranda, R. Ledesma and O. G. de Lucio, Appl. Radiat. Isot., 2001, 54, 455–459 CrossRef CAS.
- S. J. Cipolla, AIP Conf. Proc., 2003, 680, 15–19 CrossRef CAS.
- S. J. Cipolla, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 205201 CrossRef.
- E. Batyrbekov, I. Gorlachev, I. Ivanov and A. Platov, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 325, 84–88 CrossRef CAS.
- J. Miranda, C. Romo-Kröger and M. Lugo-Licona, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 189, 21–26 CrossRef CAS.
Footnotes |
| † The choice of ωK is, in this case, not critical: the discrepancy between the existing tabulated values is at most around 5% for Ti and somewhat smaller for Cu.25 |
| ‡ The version of ECPSSR that incorporates this specific refinement is sometimes called ECUSAR.30 |
| This journal is © The Royal Society of Chemistry 2019 |