Open Access Article
Open Access ArticleSpontaneous directional motion of water molecules in single-walled carbon nanotubes with a stiffness gradient†
Shuai
Chen
 ,
Yuan
Cheng
,
Yuan
Cheng
 ,
Gang
Zhang
,
Gang
Zhang
 * and
Yong-Wei
Zhang
* and
Yong-Wei
Zhang
Institute of High Performance Computing, A*STAR, 138632 Singapore. E-mail: zhangg@ihpc.a-star.edu.sg
First published on 21st December 2018
Abstract
Controlling water molecular motion at the nanoscale is critical for many important applications, such as water splitting to produce hydrogen and oxygen, biological and chemical cell reactions, nanofluidics, drug delivery, water treatment, etc. In this paper, we propose a new nanoscale device based on carbon nanotubes (CNTs) with a stiffness gradient to create a spontaneous directional motion of water molecules, and perform molecular dynamics simulations to analyze its transport characteristics. We find that the (6, 6) CNT possesses an optimal water transport rate. In the thinner CNTs, the water molecules are strongly confined by the CNT wall, resulting in a higher friction force; while in the thicker CNTs, the driving force is lower, and the water molecules tend to form ring-like configurations, resulting in a slower motion. For the (6, 6) CNT, water molecules tend to favor a chain-like configuration, through which the molecules are able to move synergistically along the stiffness gradient, and the transportation efficiency increases with the stiffness gradient but decreases with temperature. Both energetic and kinetic analyses are performed to elucidate this fascinating directional motion. Our work demonstrates a new strategy for controlling water molecular motion at the nanoscale without resorting to any active driving source, such as electric field, temperature or pressure difference.
Introduction
Investigation on the transportation of water molecules at the nanoscale has attracted much research interest1–10 due to their importance to biological activities,1 nanofluidic devices,2,3 water purification,4 drug delivery,5 seawater desalination,6 nanofiltration,7,8etc. In these applications, water molecules are often in a confined environment. As a result, the transport behaviors can be drastically different from their bulk counterpart. Hence, how to control the transport behavior of water molecules at the nanoscale is central to these applications.Since the demonstration of the excellent behavior of carbon nanotubes (CNTs) as a water transportation channel by Hummer et al.2 in 2001, many nanoscale water channels based on CNTs have been reported, and important progress has been made in understanding their transport behaviors.11–27 For example, for nanoscale channels based on CNTs, the structure of nanotubes16 and dopant atoms17 may greatly affect the water permeation rate. In multi-walled carbon nanotubes (MWCNTs), the nanotube type and layer number may also exert strong influence on the water transport behaviors.18,19 These studies on water molecules inside CNTs have not only unveiled new physics for confined water molecules, but also encouraged researchers to explore novel strategies to control the transport behaviors of water molecules at the nanoscale. Furthermore, the recent advances in precise and controllable fabrication of CNTs28,29 also pave the way towards efficient water transport at the nanoscale.
The directional motion of water molecules in CNTs has been typically realized by active means, including applications of pressure,16,25 electrical currents30 (or charge12,31), selective heating13,15 or complicated chemical reactions.32 For instance, Ma et al.25 found that the water flow velocity increases linearly with pressure between the two ends of a CNT. Zuo et al.14 introduced different types of external point charges outside a CNT, and realized directional motion of water molecules through the CNT channel under the influence of both thermal fluctuation and charge affinity. The directional migration of water molecules in CNTs can also be realized by using an electrical current.30 Very recently, Oyarzua et al.15 proposed a water pump based on CNTs with an imposed constant thermal gradient. The underlying mechanism for the fluid flow is the thermally induced asymmetric oscillations along the CNT, which propel the water in a constant, whip-like motion.
It is noted that all these aforementioned methods require active external means to drive water molecules.33 Then an interesting question is: is it possible to create a spontaneous directional motion of water molecules in CNTs without resorting to any external driving means? For this purpose, we propose a new device based on CNTs with a stiffness gradient to realize the spontaneous directional motion of water molecules. Our molecular dynamics simulations clearly show the spontaneous water motion through CNTs, without resorting to any active driving force, such as electric field, pressure or temperature difference. We further analyze the mechanism that underlies the spontaneous directional motion and factors that influence the transport rate.
Simulation method
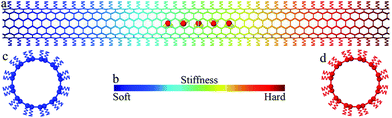
The large-scale atomic/molecular massively parallel simulator (LAMMPS) package34 was used to carry out the simulations. The simulated system is shown in Fig. 1a. In the system, water molecules were placed at the center of an uncapped (6, 6) nanotube (101.84 Å long and 8.02 Å in diameter). The adaptive intermolecular reactive empirical bond order (AIREBO) potential35 was used to describe the carbon–carbon interactions within the nanotube. The water model in this study is a transferable intermolecular potential with 3-points (TIP/3P),36 which has been widely used to simulate water in molecule dynamics simulations. This potential consists of a Coulomb interaction between partial point charges on the oxygen (−0.830e) and hydrogen (+0.415e) atoms and a Lennard-Jones interaction37 with σOO = 3.188 Å, and εOO = 0.102 kcal mol−1. The particle–particle particle–mesh (PPPM) method was applied to compute the long-range Coulomb interaction. An oxygen–hydrogen bond length of 0.9572 Å and a bond angle of 104.52° are maintained by harmonic potentials with spring constants of 450 kcal (mol−1 Å2)−1 and 55 kcal (mol−1 rad2)−1. The Lennard-Jones potential was also used to simulate the interaction between the nanotube and water with σCO = 3.298 Å, and εCO = 0.0828 kcal mol−1.Previous studies have shown that deposition of atoms or molecules on the external surface of a CNT, either physically or chemically, may change the local potential field of carbon atoms in the CNT, causing a modulation in both the structure and physical properties of the CNT.38–40 For example, asymmetric axial thermal conductance was observed in a CNT with inhomogeneously deposited mass, as a direct demonstration of a solid-state thermal rectifier.38 Similarly, by depositing atoms or molecules along the external surface of a CNT following certain distribution, a desired stiffness gradient can be created along the CNT. In our work, to introduce a stiffness gradient, each carbon atom was linked with an underlying spring pointing to the carbon ring center such that the nanotube is connected to a series of springs with linearly graded stiffness k along the nanotube axis direction (x direction) of the nanotube (cf.Fig. 1b–d). The range of spring stiffness (1 to 11 nN nm−1) and stiffness gradient (0 to 1 nN nm−2) considered in our simulations are comparable with those in previous experiments41 and simulations.39,40
In the present simulations, five water molecules in a chain configuration were initially placed in the CNT. All simulations were conducted under non-periodic boundary conditions for 50 ps. The system was relaxed for 10 ps at 300 K with a canonical (NVT) ensemble initially. During the relaxation, the center of mass of the nanotube was kept fixed in all directions, and the center of mass of the water chain was kept fixed along the nanotube axis direction. After that, a microcanonical (NVE) ensemble was adopted for another 40 ps and the confinement on the water chain was released. The integration time step is 1 fs, and the samples of the trajectories were stored every 1 ps.
Results and discussion
Directional motion of the water chain in the carbon nanotube
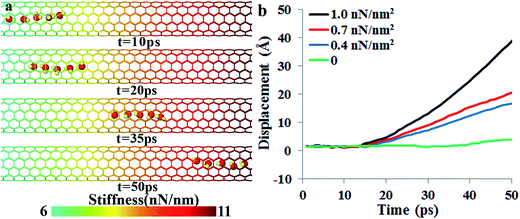
Fig. 2a shows a series of snapshots of the water chain positions at different simulation times, and Video S1 in the ESI† shows the water molecular motion and nanotube fluctuations. In this simulation, the midpoint stiffness km is 6 nN nm−1, and the stiffness gradient is 1 nN nm−2. Note that only the right half of the nanotube was plotted and for clarity, the fluctuations of carbon atoms are not shown in Fig. 2a. Our simulation clearly shows that a directional transportation of water molecules can be achieved by the stiffness gradient, and the water molecules move synergistically in a water-chain configuration from the soft region to the stiff region. In the “water-chain”, a water molecule is constantly interacting with its adjacent water molecules, in addition to the nanotube wall. To further show that the driving force of the spontaneous directional water transportation was the CNT stiffness gradient, three additional simulations with the same midpoint stiffness (km = 6 nN nm−1) but smaller gradients (∂k/∂x = 0, 0.4, 0.7 nN nm−2) were further carried out (Videos S2 and S3 in the ESI† show the water transportation processes when the stiffness gradient is 0.7 nN nm−2 and 0, respectively).Fig. 2b depicts the displacements of the water-molecule chain at different CNT stiffness gradients at every picosecond (details for calculating the displacements are given in the ESI†). It is found that the directional water transportation decreased with decreasing the stiffness gradient, and disappeared when there was no stiffness gradient. The motion of water molecules is not only influenced by the stiffness gradient, but also affected by the absolute value of stiffness of the initial location. We construct a model with water molecules initially located near the beginning of the soft region where the stiffness is 3 nN nm−1. The simulation results show that water molecules exhibit a slightly faster movement initially (cf. Fig. S1†), but the spontaneous directional transportation of water molecules and the subsequent speed are independent of the initial location.
Mechanism of directional water transportation induced by the stiffness gradient
In a mass-loaded CNT, each carbon atom is connected with its three nearest neighbor carbon atoms by covalent bonds, and also to a deposited atom or molecule by a bond (taken as a spring) as shown in Fig. 1. Within the first order approximation, the atomic vibration can be treated as a harmonic one with an effective spring constant. For the out-of-plane mode in the thermal vibration, each carbon atom moves perpendicular to the CNT surface influenced by its three nearest neighbors, and the vibrational amplitude ΔR is 〈ΔR2〉 ≈ 2kBT/Ke, where kB is the Boltzmann constant, T the temperature and Ke is the effective spring constant for the carbon atom including the contribution from the C–C covalent bonds and the interaction with the deposited mass. Therefore, the amplitude of thermal expansion at a “soft” section is much larger than that at a “stiff” section along the CNT. As a consequence, at the same temperature, with increasing the CNT stiffness, the average distance between the water-chain and CNT wall decreases, leading to a decrease in the potential energy. Therefore, the reduction in potential energy is the underlying physical origin for the directional motion of the water-chain from the “soft” section to the “stiff” section. In our simulations, the system was relaxed with a NVT ensemble initially. After that, a microcanonical NVE ensemble was adopted. In the NVE ensemble, no external thermostat was applied. Therefore, our directional motion is spontaneously achieved by the stiffness gradient without applying external driving forces, which is different from the motion realized by an external thermal gradient13,15 and stiffness gradient induced by a thermal gradient.42 It is worth noting that although the motion of water molecules inside the CNT is a spontaneous process without resorting to any active driving source, a certain amount of energy is still required to push water molecules entering the CNT, which is the general behaviour for any type of water channel.To gain further insight into the mechanism, we have calculated the variation of total potential energy for the water-chain and CNT wall as a function of stiffness. Fig. 3a indicates that the total potential energy for the water-chain and CNT wall decreases with increasing the stiffness. Evidently, there is a linear relationship between these quantities. From this linear relationship, we are able to calculate the driving force induced by potential energy reduction:
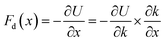 | (1) |
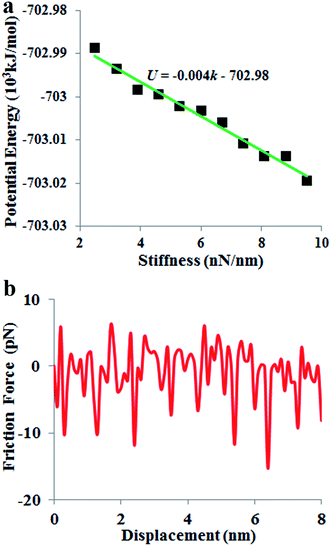 | ||
| Fig. 3 (a) Variation of potential energy with the nanotube stiffness. (b) Friction force of water molecules moving along the nanotube axis direction. | ||
Based on this linear relationship, the average value for the driving force Fd(x) is ∼6.6 pN.
During the directional motion of the water-chain within the CNT, in addition to the driving force induced by the stiffness gradient, the water-chain also experiences a friction force.43 The friction force is shown in Fig. 3b. It is seen that the values of the friction force are in the range from −15 to 5 pN. Compared with the aforementioned driving force (6.6 pN) contributed by the stiffness gradient, it is obvious that the driving force is not always larger than friction force during the motion process. The motion of water is similar to the energetically activated stick-and-slip motion, which, upon time averaged, resembles a steady-state motion. This phenomenon has also been observed on the motions of large nanoflakes (5 × 5 nm2) on a substrate,44 essentially resembling a particle moving in a periodic potential.
Temperature dependent directional water transportation in carbon nanotubes
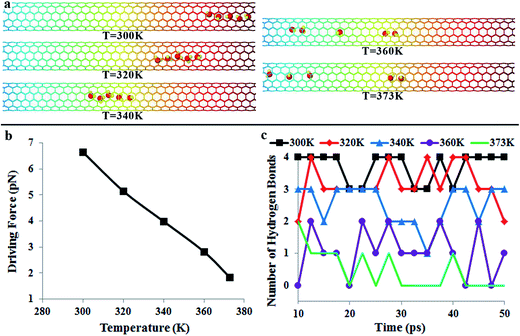
The directional motion of nanoflakes on a substrate with a stiffness gradient has been reported before.39 Although the spontaneous motion of water molecules observed in our work is also driven by the reduction in potential energy, there is a fundamental difference in the underlying mechanism. For a graphene nanoflake, there are strong covalent bonds between atoms. Therefore, the nanoflake moves as a whole. In the water chain, however, water molecules are linked by weak hydrogen bonds. Due to thermal vibrations, these hydrogen bonds may break and reform. It is expected that the temperature will have a significant effect on the directional motion of the water-chain.In the following, we would like to examine the effect of temperature on the directional transportation of water molecules. Fig. 4 shows the positions of water molecules after 50 ps simulation (cf.Fig. 4a), the driving force (cf.Fig. 4b), and the variation of the hydrogen bond45 number with time (cf.Fig. 4c) at different temperatures. It is interesting to see that although the water molecules also move in a water-chain manner at 320 K and 340 K, similar to the case at 300 K (1.0 Å ps−1), the average velocity is much slower (0.5 Å ps−1 and 0.2 Å ps−1). The underlying mechanism is the suppressed driving force at higher temperature (cf.Fig. 4b). When the temperature increases from 300 K to 340 K, the driving force decreases from 6.6 pN to 4.0 pN. Moreover, from Fig. 4c, it is clear that at 320 K, the number of hydrogen bonds is predominantly 2–3, much lower than that at 300 K, signifying the formation of the water-chain only occasionally. With increasing the temperature, the water chain configuration is no longer present in the CNT. For example, the number of hydrogen bonds is only in the range of 1–3 at 340 K, signifying the formation of fragmented smaller chains, but the absence of a complete water chain during the simulation time (cf. Video S4†).
When temperature further increases to 360 K (cf. Video S5†) and 373 K, the driving force is continuously reduced (2.8 pN and 1.8 pN in Fig. 4b). Correspondingly, Fig. 4a indicates that the directional water transportation is suppressed at 360 K and 373 K. Fig. 4c indicates that the number of hydrogen bonds is in the range of 0–2 at 360 K and 373 K, signifying further fragmentation of water chains and the absence of any complete water chain. The fragmentation of water chains, which is caused by the promoted thermal fluctuations, is also visible in Fig. 4a. A direct consequence of chain fragmentation is the reduction in the motion velocity of the water molecules, as shown in Video S4 (340 K) and S5 (360 K) in the ESI.† Our results clearly suggest that for a single water molecule, its “effective” length along the potential gradient field is limited, and thus the “effective” driving force is small. On the other hand, by forming the water-chain configuration, the “effective” length is remarkably increased, and therefore the water molecules can move spontaneously and collectively.
Diameter dependent directional water transportation in carbon nanotubes
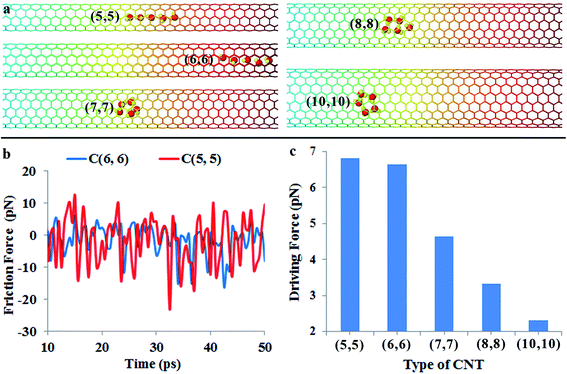
Nowadays, the chirality and diameter of single-walled carbon nanotubes can be controlled accurately during growth.28,29 This enables one to study water transportation in different sized CNTs. Here, we examine the effect of CNT diameter on the water transport behavior using MD simulations. Fig. 5a shows the positions of water molecules in (5, 5), (6, 6), (7, 7), (8, 8) and (10, 10) CNTs (their corresponding diameters are 6.68 Å, 8.02 Å, 9.36 Å, 10.70 Å and 13.37 Å, respectively) after 50 ps simulation. For the (5, 5) and (6, 6) CNTs, it is found that the water molecules are still able to keep the chain configuration. The motion of water molecules in the (5, 5) CNT (cf. Video S6 in the ESI†) is obviously slower than that in the (6, 6) CNT even if the driving force increases slightly from 6.6 pN for the (6, 6) CNT to 6.8 pN for the (5, 5) CNT (cf.Fig. 5c). When a water molecule moves within a CNT, it essentially resembles a particle moving in a periodic potential field, and the repeating energy barrier is the origin of the friction force. The radius of the (5, 5) CNT is about 3.34 Å, which is comparable to the equilibrium distance (3.2 Å) between the water molecule and graphene sheet governed by van der Waals interaction.46 Therefore, there is a strong confinement of the (5, 5) CNT on the water molecules. As a result, the potential energy field of the CNT wall can strongly distort the water-molecule chain, giving rise to a slower motion velocity. This is consistent with the larger friction force in the (5, 5) CNT (cf.Fig. 5b).On the other hand, the water transportation is also suppressed in larger carbon nanotubes even if the friction force is lower than that in the (6, 6) nanotube (cf. Fig. S2, Video S7 and S8 in the ESI†). The reason is that the driving force resulted from the gradient of potential energy decreases remarkably in larger nanotubes (cf.Fig. 5c). Moreover, when the diameter of the nanotube increases, the confinement of the CNT on water molecules becomes weaker, leading to increased movement space and flexibility for water molecules. In that case, water molecules are able to form a ring structure instead of a chain configuration. Moreover, the weak confinement permits more degrees of freedom, including the rotation degree of freedom and lateral space degree of water molecules to explore. The enhanced transversal and rotational degrees of freedom significantly reduce the spontaneous motion of water molecules.
Conclusions
In summary, the transport behavior of water molecules in a single-walled carbon nanotube with a stiffness gradient was studied by molecular dynamics simulations. A spontaneous directional transportation of water molecules from a “soft” region to a “stiff” region is achieved. The water transport rate is optimal in the (6, 6) CNT. The directional transportation decreased with decreasing the stiffness gradient, and disappeared when there was no stiffness gradient. The underlying mechanism was attributed to the total potential energy difference induced by the stiffness gradient. Furthermore, a theoretical calculation including the forces that water molecules experienced was carried out. Related analyses on driving force and friction force were made. Other factors such as temperature and diameter were also investigated. Our study has clearly shown that a CNT with a stiffness gradient is able to realize the spontaneous directional motion of water molecules, without resorting to any active driving force, such as electric field, pressure or temperature difference. This new way of controlling water molecules at the nanoscale may have potential applications in biology, nanofluidic devices, water purification, drug delivery, seawater desalination, nanofiltration, etc.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Agency for Science, Technology and Research (A*STAR), Singapore and the use of computing resources at the A*STAR Computational Resource Centre, and National Supercomputing Centre, Singapore. The authors are supported in part by a grant from the Science and Engineering Research Council (152-70-00017).References
- K. Murata, K. Mitsuoka, T. Hirai, T. Walz, P. Agrek, J. B. Heymann, A. Engel and Y. Fujiyoshi, Nature, 2000, 407, 599–605 CrossRef CAS PubMed.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190 CrossRef CAS PubMed.
- K. Besteman, J. O. Lee, F. G. M. Wiertz, H. A. Heering and C. Dekker, Nano Lett., 2003, 3, 727–730 CrossRef CAS.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- J. Shi, A. R. Votruba, O. C. Farokhzad and R. Langer, Nano Lett., 2010, 10, 3223–3230 CrossRef CAS PubMed.
- M. Elimelech and W. A. Phillip, Science, 2011, 33, 712–717 CrossRef PubMed.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Science, 2012, 335(6067), 442–444 CrossRef CAS PubMed.
- S. C. O'Hern, D. Jang, S. Bose, J. C. Idrobo, Y. Song, T. Laoui, J. Kong and R. Karnik, Nano Lett., 2015, 15, 3254–3260 CrossRef PubMed.
- Y. Zhu, F. Wang, J. Bai, X. C. Zeng and H. Wu, ACS Nano, 2015, 9(12), 12197–12204 CrossRef CAS PubMed.
- M. Ma, G. Tocci, A. Michaelides and G. Aeppli, Nat. Mater., 2016, 15, 66–71 CrossRef CAS PubMed.
- J. Li, X. Gong, H. Lu, D. Li, H. Fang and R. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3687–3692 CrossRef CAS PubMed.
- X. Gong, J. Li, H. Lu, R. Wan, J. Li, J. Hu and H. Fang, Nat. Nanotechnol., 2007, 2, 709–712 CrossRef CAS PubMed.
- A. Barreiro, R. Rurali, E. R. Hernández, J. Moser, T. Pichler, L. Forro and A. Bachtold, Science, 2008, 320, 775–778 CrossRef CAS PubMed.
- G. Zuo, R. Shen, S. Ma and W. Guo, ACS Nano, 2010, 4, 205–210 CrossRef CAS PubMed.
- E. Oyarzua, J. H. Walther, C. M. Megaridis, P. Koumoutsakos and H. A. Zambrano, ACS Nano, 2017, 11(10), 9997–10002 CrossRef CAS PubMed.
- X. Gong, J. Li, H. Zhang, R. Wan, H. Lu, S. Wang and H. Fang, Phys. Rev. Lett., 2008, 101, 257801 CrossRef PubMed.
- X. Li, Y. Shi, Y. Yang, H. Du, R. Zhou and Y. Zhao, J. Chem. Phys., 2012, 136, 05B602 Search PubMed.
- J. Zou, B. Ji, X.-Q. Feng and H. Gao, Nano Lett., 2006, 6(3), 430–434 CrossRef CAS PubMed.
- Z. Cui, D. Li and B. Ji, Int. J. Appl. Mech. Eng., 2015, 07(06), 1550084 CrossRef.
- X. Ma, S. Cambré, W. Wenseleers, S. K. Doorn and H. Htoon, Phys. Rev. Lett., 2017, 118(2), 027402 CrossRef PubMed.
- K. V. Agrawal, S. Shimizu, L. W. Drahushuk, D. Kilcoyne and M. S. Strano, Nat. Nanotechnol., 2017, 12(3), 267–273 CrossRef CAS PubMed.
- M. Nishi, T. Ohkubo, K. Urita, I. Moriguchi and Y. Kuroda, Langmuir, 2016, 32(4), 1058–1064 CrossRef CAS PubMed.
- K. Nomura, T. Kaneko, J. Bai, J. S. Francisco, K. Yasuoka and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(16), 4066–4071 CrossRef CAS PubMed.
- S. D. Bernardina, E. Paineau, J. B. Brubach, P. Judeinstein, S. Rouzière, P. Launois and P. Roy, J. Am. Chem. Soc., 2016, 138(33), 10437–10443 CrossRef PubMed.
- M. Ma, F. Grey, L. Shen, M. Urbakh, S. Wu, J. Z. Liu, Y. Liu and Q. Zheng, Nat. Nanotechnol., 2015, 10, 692–695 CrossRef CAS PubMed.
- K. Goh and Y. Chen, Nano Today, 2017, 14, 13–15 CrossRef CAS.
- R. H. Tunuguntla, R. Y. Henley, Y. C. Yao, T. A. Pham, M. Wanunu and A. Noy, Science, 2017, 357(6353), 792–796 CrossRef CAS PubMed.
- S. Zhang, L. Kang, X. Wang, L. Tong, L. Yang, Z. Wang, K. Qi, S. Deng, Q. Li, X. Bai, F. Ding and J. Zhang, Nature, 2017, 543(7644), 234–238 CrossRef CAS PubMed.
- F. Yang, X. Wang, D. Zhang, J. Yang, D. Luo, Z. Xu, J. Wei, J.-Q. Wang, Z. Xu, F. Peng, X. Li, R. Li, Y. Li, M. Li, X. Bai, F. Ding and Y. Li, Nature, 2014, 510(7506), 522–524 CrossRef CAS PubMed.
- D. Dundas, E. J. McEniry and T. N. Todorov, Nat. Nanotechnol., 2009, 4, 99–102 CrossRef CAS PubMed.
- O. E. Shklyaev, E. Mockensturm and V. H. Crespi, Phys. Rev. Lett., 2013, 110, 156803 CrossRef PubMed.
- M. G. L. van den Heuvel and C. Dekker, Science, 2007, 317, 333–336 CrossRef CAS PubMed.
- A. S. Barnard, Nature, 2015, 519(7541), 37–38 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. E. Lennard-Jones, Proc. R. Soc. London, 1924, 106(738), 463–477 CrossRef.
- C. W. Chang, D. Okawa, A. Majumdar and A. Zettl, Science, 2006, 314(5802), 1121–1124 CrossRef CAS PubMed.
- T. Chang, H. Zhang, Z. Guo, X. Guo and H. Gao, Phys. Rev. Lett., 2015, 114, 015504 CrossRef PubMed.
- M. Becton and X. Wang, RSC Adv., 2016, 6(56), 51205–51210 RSC.
- R. Li, H. Ye, W. Zhang, G. Ma and Y. Su, Sci. Rep., 2015, 5, 15828 CrossRef CAS PubMed.
- N. R. Raravikar, P. Keblinski, A. M. Rao, M. S. Dresselhaus, L. S. Schadler and P. M. Ajayan, Phys. Rev. B, 2002, 66(23), 235424 CrossRef.
- P. Liu and Y. W. Zhang, Carbon, 2011, 49, 3687–3697 CrossRef CAS.
- Y. Cheng, G. Zhang, Y. Zhang, T. Chang, Q. X. Pei, Y. Cai and Y. W. Zhang, Nanoscale, 2018, 10, 1660–1666 RSC.
- H. Xu and B. J. Berne, J. Phys. Chem. B, 2001, 105, 11929–11932 CrossRef CAS.
- T. Werder, J. H. Walther, R. L. Jaffe, T. Halicioglu and P. Koumoutsakos, J. Phys. Chem. B, 2003, 107, 1345–1352 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details and analyses. Videos of water transportation in the (6, 6) CNT with a stiffness gradient of 1 nN nm−2 (S1-Gradient1), 0.7 nN nm−2 (S2-Gradient2), and 0 nN nm−2 (S3-Gradient3). Videos of water transportation in the (6, 6) CNT with a stiffness gradient of 1 nN nm−2 at a temperature of 340 K (S4-340 K) and 360 K (S5-360 K). Videos of water transportation in the (5, 5) CNT (S6-(5, 5)CNT), (7, 7) CNT (S7-(7, 7) CNT) and (10,10) CNT (S8-(10,10) CNT) with a stiffness gradient of 1 nN nm−2. See DOI: 10.1039/c8na00322j |
| This journal is © The Royal Society of Chemistry 2019 |