Epitaxial highly ordered Sb:SnO₂ nanowires grown by the vapor liquid solid mechanism on m-, r- and a-Al₂O₃

Abstract

Epitaxial, highly ordered Sb:SnO₂ nanowires were grown by the vapor–liquid–solid mechanism on m-, r- and a-Al₂O₃ between 700 °C and 1000 °C using metallic Sn and Sb with a mass ratio of Sn/Sb = 0.15 ± 0.05 under a flow of Ar and O₂ at 1 ± 0.5 mbar. We find that effective doping and ordering can only be achieved inside this narrow window of growth conditions. The Sb:SnO₂ nanowires have the tetragonal rutile crystal structure and are inclined along two mutually perpendicular directions forming a rectangular mesh on m-Al₂O₃ while those on r-Al₂O₃ are oriented in one direction. The growth directions do not change by varying the growth temperature between 700 °C and 1000 °C but the carrier density decreased from 8 × 10¹⁹ cm⁻³ to 4 × 10¹⁷ cm⁻³ due to the re-evaporation and limited incorporation of Sb donor impurities in SnO₂. The Sb:SnO₂ nanowires on r-Al₂O₃ had an optical transmission of 80% above 800 nm and displayed very long photoluminescence lifetimes of 0.2 ms at 300 K. We show that selective area location growth of highly ordered Sb:SnO₂ nanowires is possible by patterning the catalyst which is important for the realization of novel nanoscale devices such as nanowire solar cells.

---

1 Introduction

Metal oxide semiconductor nanowires (NWs) such as Sb:SnO₂,¹ Sn:In₂O₃,² Al:ZnO³ and In:ZnO⁴ NWs have a high conductivity but they are also capable of light emission as shown for Sn:In₂O₃ NWs by O' Dwyer et al.⁵ and Gao et al.⁶ Despite ongoing efforts into the growth and properties of such metal oxide (MO) NWs only a few have obtained epitaxial, ordered networks which is essential for the realization of novel nanoscale devices with improved performance like nanowire solar cells (NWSCs). More specifically Wan et al.⁷ has obtained ordered Sn :In₂O₃ NWs by homo epitaxy on an Sn:In₂O₃ buffer layer while Nguyen et al.⁸ and Gao et al.⁶ have obtained ordered Sn:In₂O₃ NWs by hetero epitaxy on m-, a- and c-Al₂O₃. To the best of our knowledge all other MO NWs that have been obtained previously are not oriented in an epitaxial fashion along any particular direction. It is important then to obtain earth abundant MO NWs such as Sb:SnO₂ NWs as low cost alternatives to Sn:In₂O₃.

In the past we have grown SnO₂ NWs via the vapor liquid solid (VLS) mechanism at 800 °C and 10⁻¹ mbar which had a carrier density of the order of 10¹⁶ cm⁻³ and mobility of 70 cm² V⁻¹ s⁻¹, as determined from THz conductivity spectroscopy.⁹ High conductivity SnO₂ NWs have been obtained via the incorporation of Sb,¹⁰ Mo¹¹ and F¹² in SnO₂ NWs, while recently, Ma et al.¹³ showed theoretically that a semiconductor to semimetal transition is possible via the incorporation of Pb in SnO₂. However, in most cases Sb has been used as an n-type donor impurity in SnO₂ NWs.^14–24 All of the Sb:SnO₂ NWs have been obtained by using metallic Sn and Sb in the past, but they were not ordered.

Nevertheless, it is necessary to point out that Mathur et al.²⁵ has obtained un-doped SnO₂ NWs via the VLS mechanism that were ordered on TiO₂ (001) which is isostructural with the tetragonal rutile crystal structure of SnO₂. Similarly, Kim et al.²⁶ obtained un-doped, epitaxial, SnO₂ NWs on TiO₂ (101) while Leonardy et al.²⁷ investigated the structural properties of ordered, un-doped, SnO₂ NWs on m- and a-Al₂O₃ at 700 °C by using SnO under a flow of Ar at 10 mbar. Both Mathur et al.²⁵ and Leonardy et al.²⁷ obtained SnO₂ NWs which were oriented in two mutually perpendicular directions while the SnO₂ NWs of Kim et al.²⁶ were aligned in three directions. Others like Mazeina et al.²⁸ have grown vertical, un-doped SnO₂ NWs via the VLS mechanism on c-Al₂O₃ at 900 °C with limited ordering and uniformity. Lateral, but un-doped SnO₂ NWs have also been obtained by Kim et al.²⁹ and Choi et al.³⁰ while more recently Wang et al.³¹ investigated lateral SnO₂ NWs that were aligned on the surface of m-Al₂O₃. All of these studies on epitaxial, ordered un-doped SnO₂ NWs^25–30 focused primarily on their growth and structural properties. It is imperative then to investigate the electrical and optical properties of similar Sb:SnO₂ NWs which is critical in evaluating their potential for subsequent use in devices such as NWSCs.

Here we show that epitaxial, ordered Sb:SnO₂ NWs can be grown via the VLS mechanism on m-, r- and a- oriented Al₂O₃ only in a narrow window of growth conditions. We describe their morphology, structural, electrical and optical properties, in detail and show that selective area location growth of ordered Sb:SnO₂ NWs is possible which in turn is attractive for the realization of NWSCs as a low cost alternative to Sn:In₂O₃ NWs.

2 Methods

2.1. Epitaxial growth of Sb:SnO₂ NWs

The Sb:SnO₂ NWs were grown using a 1′′ hot wall, low pressure chemical vapour deposition (LPCVD) reactor, capable of reaching 1100 °C, which was fed via a micro flow leak valve positioned on the upstream side, just after the gas manifold which consists of four mass flow controllers. A chemically resistant, rotary pump that can reach 10⁻⁴ mbar was connected downstream. For the growth of the Sb:SnO₂ NWs, metallic Sn and Sb (Aldrich, 100 Mesh, 99.9%) were weighed with an accuracy of ±1 mg. We used an excess of Sb, i.e. a mass ratio of Sn/Sb ≈ 0.1, and the total mass of Sb and Sn was kept fixed and equal to 100 mg or 0.1 g. Square samples of 10 mm × 10 mm c-, m-, r- and a-Al₂O₃ were cleaned sequentially in trichloroethylene, methanol, acetone, isopropanol, rinsed with de-ionised water, dried with nitrogen and then coated with ≈1 nm Au. The elemental Sb and Sn as well as the c-, m-, r- or a-Al₂O₃ substrates were loaded in the same quartz boat which was positioned at the centre of the 1′′ LPCVD reactor. The latter was pumped down to 10⁻⁴ mbar and purged with 1000 sccm of Ar for 10 min at 1 mbar. Subsequently the temperature was ramped up to 800 °C at 30°C min⁻¹ using the same flow of Ar. Upon reaching 800 °C a flow of 10 sccm O₂ was added to the flow of Ar in order to grow the Sb:SnO₂ NWs over 10 min at 1 mbar, followed by cool down without O₂. We have grown Sb:SnO₂ NWs on c-, m-, r- and a-Al₂O₃ using these growth conditions and changed the growth temperature between 700 °C to 1000 °C.

2.2. Characterization of Sb:SnO₂ NWs

The morphology, crystal structure and composition of the Sb:SnO₂ NWs was determined by scanning electron microscopy (SEM), X-ray diffraction (XRD) and Energy Dispersive X-ray analysis (EDX). High resolution transmission electron microscopy (HRTEM) was carried out using a TECNAI F30 G² S-TWIN operated at 300 kV. The optical properties of the Sb:SnO₂ NWs were determined by steady state and transient absorption–transmission spectroscopy. The steady state and time resolved photoluminescence (PL) were also measured between 10 K and 300 K, while the electrical properties, i.e. carrier density and resistivity, were measured by the Hall effect in the Van der Pauw geometry similar to Costa et al.^23,24 In particular the Sb:SnO₂ NWs were transferred from the m-, r- or a-Al₂O₃ onto 10 mm × 10 mm c-Al₂O₃ by applying pressure. This results into a dry transfer of the ordered Sb:SnO₂ NWs onto the c-Al₂O₃ and the formation of a planar interconnected network. We then deposited In contacts over the Sb:SnO₂ NWs by thermal evaporation using a shadow mask. The Sb:SnO₂ NWs on c-Al₂O₃ was not heated up during the deposition, and the In contacts had diameters of ≈1 mm at the four corners of the 10 mm × 10 mm c-Al₂O₃, but we did not anneal them. The Hall effect was measured using a GMW3470 Electromagnet at 0.3 Tesla. The magnetic field was calibrated with a Hirst GM08 Gaussmeter. A Keithley 2635 A current source and Keithley 2182A nano-voltmeter, controlled by Lab View were used to provide a current and measure the voltages.

3 Results and discussion

In the past, we have shown that the reaction of Sn with O₂ at 800 °C and 10⁻¹ mbar results into a high yield and uniform distribution of SnO₂ NWs on Si (001) or fused SiO₂. The SnO₂ NWs have average diameters of ≈50 nm, lengths up to ≈100 μm and grow by the VLS mechanism whereby Sn enters the Au catalyst particles on the surface of Si (001) or fused SiO₂ and forms liquid Au:Sn particles. Upon saturation, solid SnO₂ forms beneath the liquid Au:Sn particles via the reaction with O₂ at the triple phase junction, as shown in Fig. 1(a), leading to one dimensional, bottom-up growth.³² However, the SnO₂ NWs obtained on Si (001) or fused SiO₂ were not oriented or ordered along any direction, and had a carrier density of the order of 10¹⁶ cm⁻³ with a mobility of 70 cm² V⁻¹ s⁻¹, as determined from THz conductivity spectroscopy.³³ Hence doping is required to increase their conductivity. Recently, we showed that higher carrier densities of the order of 10¹⁸ to 10¹⁹ cm⁻³ may be readily obtained in Sb doped SnO₂ NWs grown on both Si (001) and fused SiO₂.³⁴ We obtained a high carrier density of 4 × 10¹⁹ cm⁻³ in the Sb:SnO₂ NWs grown on c-Al₂O₃ at 800 °C and 1 mbar by adding metallic Sb to Sn but the Sb:SnO₂ NWs were not ordered or oriented in any particular direction, similar to those obtained previously on Si (001) and fused SiO₂.³⁴ This is in contrast to the findings of Mazeina et al.,²⁸ who obtained vertical but un-doped SnO₂ NWs via the VLS mechanism on c-Al₂O₃ at 900 °C with a limited degree of ordering and uniformity. Similarly, we did not obtain ordered Sb:SnO₂ NWs on c-Al₂O₃ by changing the growth temperature between 800 °C and 1000 °C. The epitaxial growth and ordering of Sb:SnO₂ NWs on c-Al₂O₃ is not favorable in view of the fact that SnO₂ has a tetragonal crystal structure which will not match the hexagonal crystal structure of the underlying c-Al₂O₃. However, we observed the formation of ordered Sb:SnO₂ NWs on the sides of the c-Al₂O₃, as described in more detail in the ESI,† which is related to its specific crystallographic orientation. Therefore we carried out the growth of the Sb:SnO₂ NWs on m- , r- and a-Al₂O₃ at 800 °C and 1 mbar using the same growth conditions described above.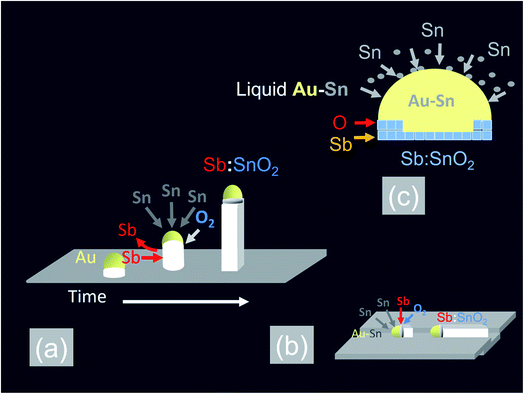

Fig. 1 Schematic representation of the VLS growth mechanism of Sb:SnO₂ NWs (a) bottom-up growth (b) lateral growth along a step or groove (c) Sb donor impurity incorporation mechanism.

3.1 Growth of Sb:SnO₂ NWs on m-, r- and a-Al₂O₃

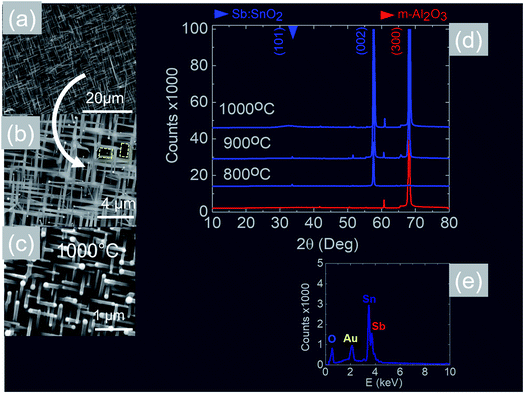
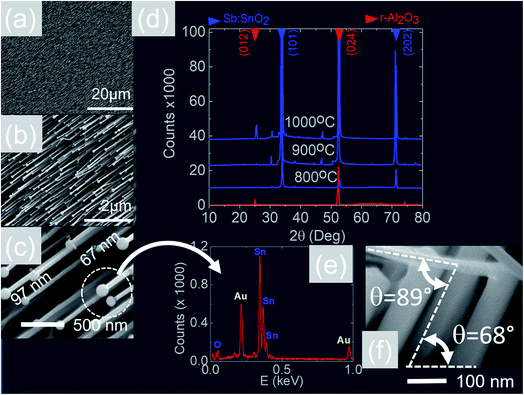
We readily obtained ordered Sb:SnO₂ NWs on all three surfaces i.e. m-, r- and a-Al₂O₃, as shown in Fig. 2, 3 and 4 respectively. The Sb:SnO₂ NWs on m-Al₂O₃ are aligned along two mutually perpendicular directions as shown by the SEM images in Fig. 2(a and b), but are inclined with respect to the surface, similar to the SnO₂ NWs obtained by Mathur et al.²⁵ and Leonardy et al.²⁷ In contrast, the Sb:SnO₂ NWs on r-Al₂O₃ are all oriented along one direction as shown in Fig. 3(a)–(c). However, upon closer inspection we find that the Sb:SnO₂ NWs on r-Al₂O₃ consist of two segments. The first segment is inclined at θ = 68° and the second segment is at an angle of θ = 89°, i.e. nearly perpendicular to the first, as shown in Fig. 3(f). This has also been observed by Jean et al.²⁰ who obtained Sb:SnO₂ NWs on 10 nm Au/Si (001) via the VLS mechanism at 1000 °C and 1 mbar using Sn/Sb = 50, 25 and 10 under Ar and trace amount of O₂, but their Sb:SnO₂ NWs were not aligned in any particular direction. The formation of the second segment can be prevented by reducing the growth time as will be described in more detail later. Similarly we find that the Sb:SnO₂ NWs on a-Al₂O₃ shown in Fig. 4(a–c) consist of two segments, similar to those obtained on r-Al₂O₃.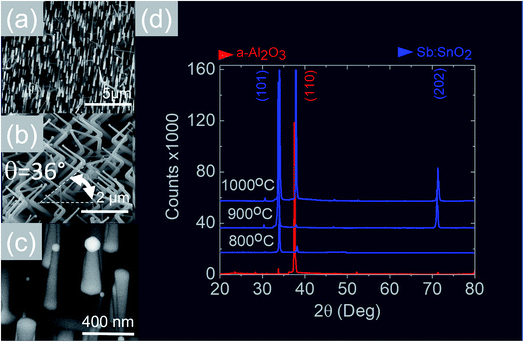

Fig. 2 SEM images of the Sb:SnO₂ NWs obtained at (a), (b) 800 °C and (c) 1000 °C on m-Al₂O₃ (d) XRD of m-Al₂O₃ (red) and Sb:SnO₂ NWs (blue) grown on m-Al₂O₃ at 800 °C, 900 °C and 1000 °C (e) EDX of the Sb:SnO₂ NWs.

Fig. 3 (a)–(c) SEM images of the Sb:SnO₂ NWs obtained at 800 °C on r-Al₂O₃ (d) XRD of r-Al₂O₃ and Sb:SnO₂ NWs grown at 800 °C , 900 °C and 1000 °C (e) EDX of an Au:Sn particle on the end of a Sb:SnO₂ NW (f) side view showing that the first segment of the Sb:SnO₂ NWs grows at θ = 68° and the second segment at θ = 89° with respect to the first.

Fig. 4 (a)–(c) SEM images of the Sb:SnO₂ NWs obtained at 800 °C on a-Al₂O₃ (d) XRD of a-Al₂O₃ (red) and Sb:SnO₂ NWs (blue) grown on a-Al₂O₃ at 800 °C, 900 °C and 1000 °C.

In all cases, we obtained a uniform distribution and ordering of Sb:SnO₂ NWs over the 10 mm × 10 m-, r- and a-Al₂O₃ in reproducible way, using Sn/Sb = 0.1 at 800 °C and 1 mbar as described above. Subsequently we varied the growth temperature between 700 °C to 1000 °C in order to find if any changes occur in the growth directions and ordering. The Sb:SnO₂ NWs obtained at 900 °C on m-Al₂O₃ were very similar to those obtained at 800 °C, but we find that the Sb:SnO₂ NWs obtained at 1000 °C are short, as shown in Fig. 2(c), due to the fact that the Sn and Sb are more or less completely transferred into the gas stream under the flow of Ar during the temperature ramp, before the onset of one dimensional growth. In fact, the depletion of Sb during the temperature ramp is more significant than Sn, due to the fact that Sn has a melting point of 232 °C and vapor pressure of 10⁻⁵ mbar, while Sb has a higher melting point of 630 °C, but a remarkably higher vapor pressure of 10⁻¹ mbar at 1000 °C. This in turn implies an important doping limitation when trying to obtain high carrier densities and conductivity in Sb:SnO₂ NWs using metallic Sn and Sb.³⁴ Likewise, the Sb:SnO₂ NWs obtained on m-Al₂O₃ at 700 °C were short, similar to those obtained at 1000 °C, due to the limited supply of Sn which has a lower vapor pressure at 700 °C, but they remained orthogonally oriented to each other. No changes occurred in the morphology and growth directions of the Sb:SnO₂ NWs on r- and a-Al₂O₃ by varying the temperature between 700 °C and 1000 °C. In contrast, the epitaxial growth and ordering of the Sb:SnO₂ NWs was critically dependent on the mass ratio of Sn/Sb. We obtained ordered Sb:SnO₂ NWs on m-, r- and a-Al₂O₃ only for Sn/Sb = 0.15 ± 0.05. One dimensional growth was completely suppressed when Sn/Sb < 0.1, and the Sb:SnO₂ NWs were not oriented in any particular direction for Sn/Sb > 0.2. Before elaborating further, it is important to mention that we did not obtain any Sb:SnO₂ NWs at all without adding O₂ to the flow of Ar during the growth step. In other words, the residual or background O₂ after purging and the temperature ramp was not significant, and the growth of the Sb:SnO₂ NWs occurred solely due to the oxygen supplied during the growth step.

Consequently the suppression of one dimensional growth for Sn/Sb < 0.1 is attributed to the total depletion and transfer of Sn into the gas stream during the temperature ramp, before the onset of growth, as it forms a liquid alloy with Sb. Note also that we did not obtain any SbO₂, Sb₂O₃ or Sb₂O₅ NWs by using only Sb.

On the other hand the Sb:SnO₂ NWs were not oriented in any particular direction for Sn/Sb > 0.2. From the above it is clear that an excess of Sb mixed with Sn provides flexible control over the Sn supplied to the Au particles which must be carefully tuned to a minimum for epitaxial growth and ordering to occur. This is further corroborated by the fact that we did not obtain ordered Sb:SnO₂ NWs without mixing the Sb and Sn even when Sn/Sb ≈ 0.15 ± 0.05.

In addition to the above it is important to point out that the epitaxial growth and ordering of the Sb:SnO₂ NWs also depends critically on the crystal quality of the m, r and a-Al₂O₃ surfaces. It has been shown that m-Al₂O₃ is thermodynamically unstable during high-temperature growth and nanostructured grooves composed of s- and r-facets develop along the [112̄0] direction.³⁵ In contrast Wang et al.³¹ claimed that both the a- and r-plane of Al₂O₃ retain their surface structure at elevated temperatures. We annealed the m-, r- and a-Al₂O₃ at 1000 °C for 30 min under Ar and O₂ without any Sn, Sb or Au and observed a drastic reduction in the strength of the XRD peaks of the m- and a-Al₂O₃ but the r-Al₂O₃ appeared to maintain its surface crystallinity. Subsequently we deposited 1 nm of Au over the pre-annealed m-, r- and a-Al₂O₃ and tried to grow epitaxial, ordered Sb:SnO₂ NWs at 800 °C and 1 mbar using Sn/Sb = 0.1. As expected, we obtained ordered Sb:SnO₂ only on r-Al₂O₃. It appears then, that the deposition of 1 nm Au over pristine m-, r-, and a-Al₂O₃ at room temperature, prevents in some way the deterioration of the surface crystal structure and allows the epitaxial growth of ordered Sb:SnO₂ NWs at elevated temperatures between 700 °C to 1000 °C. In fact, the deposition of a 1 nm Au layer on the m-, r-, and a-Al₂O₃, which contain grooves or steps along specific crystallographic directions, leads to instabilities and ruptures of the Au at elevated temperatures as described by Hughes et al.³⁶ These ruptures occur at high curvature sites, i.e., peaks and ridges, which act as retracting edges leading to a net flux of atoms away from the high positive curvature regions. For sufficiently thin layers, this process exposes the texture or steps of the underlying substrate, and a self-assembly of the Au particles will occur along specific crystallographic orientations.³⁷ This in turn will instigate one dimensional epitaxial growth along specific lateral crystallographic directions via the VLS mechanism, as shown in Fig. 1(b). When Sn is added to the Au particles, it is expected to reduce the surface tension and contact angle θ with the underlying m-, r- and a-Al₂O₃ surface, as a consequence of the fact that Sn and Sb have surface tensions of ≈500 mN m⁻¹ and 350 mN m⁻¹ respectively, but the surface tension of Au is ≈1000 mN m⁻¹. A large contact angle implies that the contact area is small, and vice versa, a smaller contact angle implies a larger contact area. Consequently, an excess of Sn is expected to lead to the formation of Au–Sn particles having a small contact angle and larger contact area with the underlying m, r and a-Al₂O₃ surface, in which case they might not be able to follow the variations in the surface topography which is necessary to obtain ordered Sb:SnO₂ NWs. The formation of ordered Sb:SnO₂ NWs is possible due to a reduction of the Sn by the excess of Sb during the temperature ramp, which in turn results into sufficiently small Au–Sn liquid particles that are able to follow steps or grooves on the surface during the growth step at elevated temperatures. Epitaxial growth, then, commences laterally, after which a transition to inclined growth occurs leading to the formation of the ordered networks of Sb:SnO₂ NWs shown in Fig. 2, 3 and 4.

All of the Sb:SnO₂ NWs on m-, r- and a-Al₂O₃ exhibited clear and well resolved peaks in the XRD, as shown in Fig. 2(d), 3(d) and 4(d) respectively, corresponding to the tetragonal rutile crystal structure of SnO₂. For comparison, we have included the XRD of the m-, r- and a-Al₂O₃ without the Sb:SnO₂ NWs. More specifically, the Sb:SnO₂ NWs on m-, r- and a-Al₂O₃ exhibit only one or two major peaks in their XRD, consistent with the fact that they grow along specific crystallographic directions. In contrast, we observed a multitude of major peaks from the Sb:SnO₂ NWs on c-Al₂O₃, due to the fact that they do not grow in an epitaxial fashion along specific directions, see ESI.† We did not observe any peaks related to oxides of Sb such as Sb₂O₃ or Sb₂O₅ which have melting points of 656 °C and 380 °C respectively. In addition, we do not observe any peaks suggesting the formation of Sb₂O₄, i.e. SbO₂ which is known to break down into Sb and O₂ at a higher temperature of 930 °C. Nevertheless the Sb:SnO₂ NWs contain Sb donor impurities as shown by the EDX spectrum in Fig. 2(e) and as confirmed previously by Raman spectroscopy.³⁴ Small differences in the amount of metallic Sb, i.e. for Sn/Sb = 0.15 ± 0.05, did not change the crystal structure or orientation of the Sb:SnO₂ NWs. We obtained exactly the same XRD spectra shown in Fig. 2, 3 and 4 for Sn/Sb = 0.1 and Sn/Sb = 0.15. However, it is important to point out that we did not detect any Sb in the Au particles on the ends of the Sb:SnO₂ NWs, as shown by the EDX spectrum in Fig. 3(e). This is consistent with the fact that we did not find Sb in the Au after trying to grow Sb₂O₃, Sb₂O₅ or SbO₂ NWs, using just Sb, and leads us to suggest that the Sb donor impurities are incorporated into the SnO₂ NWs by surface diffusion, from their sides, as depicted in Fig. 1(c).

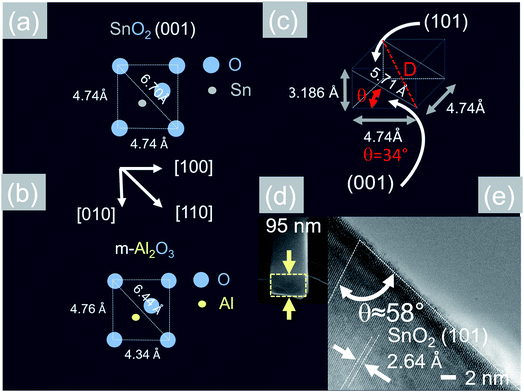
Now, the Sb:SnO₂ NWs on m-Al₂O₃ exhibited one dominant peak in the XRD, as shown in Fig. 2(d), corresponding to the (002), i.e. a multiple of (001), crystallographic planes of tetragonal rutile SnO₂. The two dimensional lattice of (001) SnO₂ and the oxygen terminated surface of m-Al₂O₃ are shown in Fig. 5(a) and (b) respectively. These have a small lattice mismatch of 0.5% so the Sb:SnO₂ NWs grow by a stacking of (001) planes on m-Al₂O₃ and the in-plane epitaxial relationship is SnO₂ (001)‖m-Al₂O₃. The growth of the Sb:SnO₂ NWs on m-Al₂O₃ is identical to that of SnO₂ NWs obtained by Leonardy et al.²⁷ on m-Al₂O₃ using SnO as opposed to Sn. For completeness, the tetragonal unit cell of SnO₂ is shown in Fig. 5(c), from which one may observe that the (101) crystallographic plane of SnO₂ is inclined at θ = 34° with respect to the (001). The Sb:SnO₂ NWs have rectangular sections, as shown in Fig. 5(d), and grow along the [101] crystallographic direction as confirmed by the HRTEM image of Fig. 5(e). Hence the Sb:SnO₂ NWs are inclined at θ = 34° with respect to the surface of m-Al₂O₃, and the fourth fold symmetry of the m-Al₂O₃ surface lattice gives rise to Sb:SnO₂ NWs oriented along two mutually orthogonal directions and the formation of the mesh structure observed in Fig. 2(a)–(c). This has also been confirmed by Wang et al.³¹ who showed that un-doped SnO₂ NWs also grow laterally along two perpendicular directions and cross each other on m-Al₂O₃.

Fig. 5 (a) Two dimensional lattice of the SnO₂ (001) that is grown in an epitaxial way on (b) oxygen terminated m-Al₂O₃ (c) crystal structure of tetragonal rutile SnO₂ (d) TEM and (e) HRTEM images of a Sb:SnO₂ NW after removing it from the m-Al₂O₃.

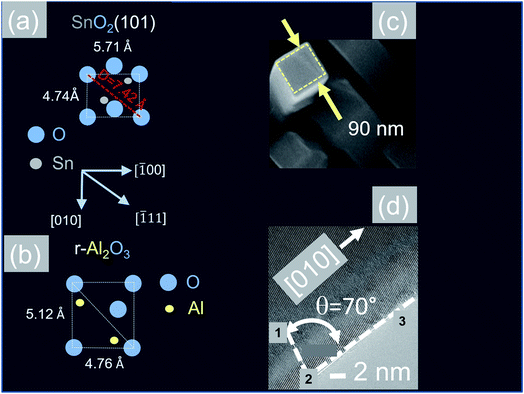
In contrast to the above we find that the Sb:SnO₂ NWs on r-Al₂O₃ exhibited two dominant peaks in the XRD, as shown in Fig. 3(d), corresponding to the (101) and (202) crystallographic planes of tetragonal rutile SnO₂. The two dimensional lattice of (101) SnO₂ and the oxygen terminated surface of r-Al₂O₃ are shown in Fig. 6(a) and (b) respectively. These have a larger lattice mismatch of 11%, and the in-plane epitaxial relationship is SnO₂ (101)‖r-Al₂O₃. The growth of the Sb:SnO₂ NWs on r-Al₂O₃ is very similar to the un-doped SnO₂ NWs of Kim et al.³⁸ which were also inclined at θ = 68° on r-Al₂O₃. Lateral SnO₂ NWs have also been obtained via the VLS mechanism by Kim et al.²⁹ on r-Al₂O₃ using C and SnO₂ as opposed to Sn but they did not observe the transition of growth from lateral to vertical SnO₂ NWs.

Fig. 6 (a) Two dimensional surface lattice of SnO₂ (101) which grows on (b) oxygen terminated surface of r-Al₂O₃ (c) TEM image of Sb:SnO₂ NWs after removing from r-Al₂O₃ (d) HRTEM image of the Sb:SnO₂ NWs showing the (010) lattice planes.

3.2 Selective area location growth of Sb:SnO₂ NWs on r-Al₂O₃

The VLS growth mechanism permits selective area location growth on m-, r- and a-Al₂O₃ as we did not obtain any Sb:SnO₂ NWs without using Au. We obtained hexagonally ordered Sb:SnO₂ NWs on r-Al₂O₃ by drop casting ∼10 μl of 9 μm diameter polystyrene spheres on r-Al₂O₃, followed by the deposition of a thin layer of ∼1 nm Au as shown in Fig. 7. Subsequently, the spheres were removed in isopropanol by ultrasonic vibration for 1 min, and the Sb:SnO₂ NWs were grown on the patterned Au on r-Al₂O₃ at 800 °C. The Sb:SnO₂ NWs on r-Al₂O₃ do not consist of two segments due to the reduced growth time. One may clearly observe that the Sb:SnO₂ NWs grow on the r-Al₂O₃ in a hexagonal pattern suggesting that one may also obtain different geometries in order to tailor the absorption–transmission spectrum in novel devices such as NWSCs.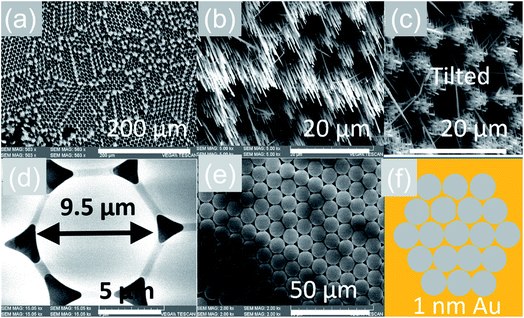

Fig. 7 Selective area location growth of Sb:SnO₂ NWs on r-Al₂O₃ (a) low magnification and (b) high magnification image (c) tilted view of the Sb:SnO₂ NWs on r-Al₂O₃ showing that they do not consist two segments as shown in Fig. 3(f); (d) an individual sphere in contact with its six closest neighbors (e) domain of ordered spheres (f) schematic representation of the spheres on r-Al₂O₃ after the deposition of 1 nm Au in between the spheres.

3.3 Electrical properties of Sb:SnO₂ NWs on m-, r- and a-Al₂O₃

The carrier density of the Sb:SnO₂ NWs grown on m-, r- and a-Al₂O₃ at 800 °C and 1 mbar with Sn/Sb = 0.1 was measured by the Hall effect. We obtained a carrier density of 8 × 10¹⁹ cm⁻³ which is significantly larger than that measured previously in un-doped SnO₂ NWs, that was of the order of 10¹⁶ cm⁻³.³³ The conductivity of the Sb:SnO₂ NWs was found to be ≈3 × 10² (Ω cm)⁻¹ giving a mobility of 20 cm² V⁻¹ s⁻¹ which is lower compared to 70 cm² V⁻¹ s⁻¹ in un-doped SnO₂ NWs that was previously measured by THz conductivity spectroscopy.³³ We did not observe a significant variation in the carrier density of the Sb:SnO₂ NWs on m-, r- and a-Al₂O₃, or due to slight variations of Sn/Sb = 0.15 ± 0.05. We measured the Hall effect of the Sb:SnO₂ NWs obtained with Sn/Sb = 0.15 and found a carrier density of 8.3 × 10¹⁹ cm⁻³ which is very close to that obtained with Sn/Sb = 0.1. However the carrier density in the Sb:SnO₂ NWs obtained at 900 °C was smaller i.e. 6 × 10¹⁸ cm⁻³ while those obtained at 1000 °C had an even smaller carrier density of 4 × 10¹⁷ cm⁻³ and conductivity of ≈3 (Ω cm)⁻¹. This is attributed to the transfer of the Sb into the gas stream during the temperature ramp, and before the onset of one dimensional growth, due to the high vapor pressure of Sb, which in turn limits the supply and incorporation of Sb impurities into the SnO₂ NWs during the growth step. This trend is consistent with the findings of Klamchuen et al.,²² who found that the doping level in SnO₂ NWs grown at 650 °C was twice that obtained at 750 °C, attributed to a suppression of impurity re-evaporation. They also observed that the doping level did not increase further upon reducing the growth temperature from 650 °C to 550 °C, which was explained by a suppression of the diffusion length of impurity ad-atoms on the surface of the SnO₂ NWs, and the presence of a temperature activated energy barrier which is necessary for the incorporation of the Sb impurities into the host lattice of SnO₂.

We suggest that the incorporation of Sb impurities into the SnO₂ NWs occurs through the sides of the SnO₂ NWs by thermal diffusion, or, via the triple phase junction, as shown in Fig. 1(c), similar to the mechanism proposed by Klamchuen et al.²² This is also corroborated by the fact that we did not detect any Sb in the Au particles after attempting to grow SbO₂, Sb₂O₃ or Sb₂O₅ NWs on r-Al₂O₃, by using only Sb, and also by the fact that we did not detect any Sb in the Au:Sn particles on the ends of the Sb:SnO₂ NWs, as shown in Fig. 3(e). It is also consistent with the findings of McGinley et al.,³⁹ who showed that the surface of SnO₂ nanoparticles is terminated by an oxygen rich layer, but when doped n-type with 9% or 17% Sb, the impurity atoms are concentrated near the surface of the SnO₂ nanoparticles with an oxidation state of five.

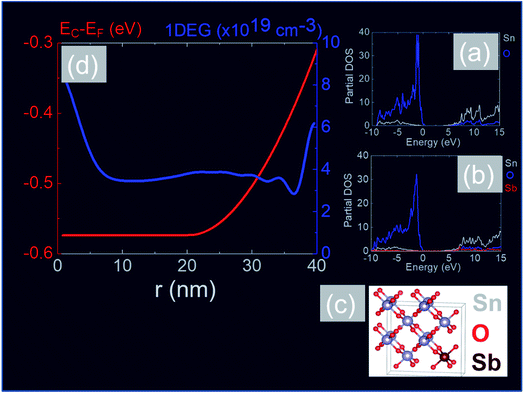
In order to obtain a more detailed understanding of the electronic properties of the Sb:SnO₂ NWs we carried out electronic structure calculations from first principles using the CASTEP plain wave DFT code^40,41 and the Heyd–Scuseria–Ernzerhof (HSE)⁴² exchange correlate-correlation energy functional. After relaxation of the cell, we obtained lattice constants of a = b = 4.82 Å and c = 3.23 Å which are in close agreement to reported values.⁴² DOS calculations were performed for the case of (a) the perfect SnO₂ cell and (b) the Sb-doped SnO₂ cell, shown in Fig. 8(a) and (b) respectively. The maximum of the valence band (VB) is set at zero energy level. It is evident from the partial density of states shown in Fig. 8(a) and (b) that the VB is dominated by O and the CB by Sn.⁶⁰ The band gap was found to be 3.6 eV for the perfect structure but a slight reduction of the band gap down to 3.5 eV was observed with doping. This semi-empirical method yields a much more accurate band gap than calculations performed based on the Perdew–Burke–Ernzerhof (PBE) GGA functional which are not shown here. In addition we find that the incorporation of Sb into the SnO₂ crystal does not produce any deep levels within the band gap which are in general detrimental to the operation of optoelectronic devices such as solar cells, light emitting diodes etc. In other words the Sb impurities are incorporated into the SnO₂ lattice as substitutional donors and our calculations show that the Fermi level resides 0.46 eV above the CB edge for 12.5 at% Sb (≡4 × 10²¹ cm⁻³).

Fig. 8 (a) DOS for un-doped SnO₂ and (b) DOS for Sb:SnO₂ with 12.5 at% (≡4 × 10²¹ cm⁻³) (c) structural model showing Sb substitutional donor impurity in SnO₂ (d) SCPS CB potential profile (red) and 1DEG charge distribution (blue) versus distance along the radial direction of a Sb:SnO₂ NWs with a diameter of 80 nm taking E_C − E_F = −0.3 eV at the surface and assuming a uniform distribution of ionized donor impurities N_D⁺ = 1 × 10¹⁹ cm⁻³ between r = 20 and 40 nm.

In addition, we calculated the conduction band (CB) potential profile, and one dimensional electron gas (1DEG) charge distribution, along the radial direction, via the self-consistent solution of the Poisson–Schrödinger (SCPS) equations, in the effective mass approximation, as described in detail elsewhere.⁴³ The SCPS calculations were carried out by taking into account the effective mass and dielectric constant of SnO₂ , i.e.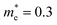 (ref. 44 and 45) and ε_r = 13.5 (ref. 46 and 47) respectively. In order to obtain a carrier density of 8 × 10¹⁹ cm⁻³ as determined from the Hall effect we have taken the Fermi level to be energetically located ≈0.3 eV above the CB edge, at the surface of the Sb:SnO₂ NWs. This is consistent with the electronic structure calculations of Mishra et al.,⁴⁸ who showed that the Sb impurities in SnO₂ form a band, which has an energetic overlap with the conduction band and a nearly free electron structure, i.e. behaves like a metallic band. It is also consistent with Li et al.,⁴⁹ who calculated the electronic structure of Sb:SnO₂ for 6.25% Sb, and found that the Fermi level moves into the CB upon the incorporation of Sb, and displays metallic character, but also with Farahani et al.,⁵⁰ who showed that the Fermi level resides ≈0.33 eV above the CB edge at the surface of Sb:SnO₂ epitaxial layers grown by molecular beam epitaxy on r-Al₂O₃.

The CB potential profile with respect to the Fermi level, i.e. E_C − E_F and 1DEG charge distribution, versus distance along the radial direction of the Sb:SnO₂ NWs, is shown in Fig. 8(d), where we have taken the donor impurities to be confined between r = 20 and 40 nm. The CB edge potential profile is near flat band in the vicinity of the core and the 1DEG charge distribution has a maximum at the core and a local maximum at the surface. It should be noted that we obtain similar band profiles and charge distributions by taking a uniform distribution of Sb impurities throughout the Sb:SnO₂ NWs. However the 1DEG in the vicinity of the core is expected to have a higher mobility when the density of donor impurities is larger at the surface than the core, as is the case in Fig. 9(d). In other words, the incorporation of Sb impurities into the SnO₂ NWs via surface diffusion is not a drawback in the end. We estimate that the mobility in the Sb:SnO₂ NWs with a maximum carrier density of the order of 10²⁰ cm⁻³ is a few tens of cm² V⁻¹ s⁻¹ (ref. 23 and 24) so the resistivity of the Sb:SnO₂ NWs is of the order of 10⁻³ Ω cm which in turn is attractive for the deposition of metal contacts with low resistance and the fabrication of high performance devices.

Fig. 9 Ultrafast, differential transient absorption dα versus optical delay τ (ps) and probe wavelength λ (nm) through the Sb:SnO₂ NWs grown on r-Al₂O₃ at (a) 800 °C, (b) 900 °C and (c) 1000 °C; (d) steady state transmission of light through the Sb:SnO₂ NWs grown on r-Al₂O₃ at different temperatures.

3.4 Optical properties of Sb:SnO₂ NWs on m-, r- and a-Al₂O₃

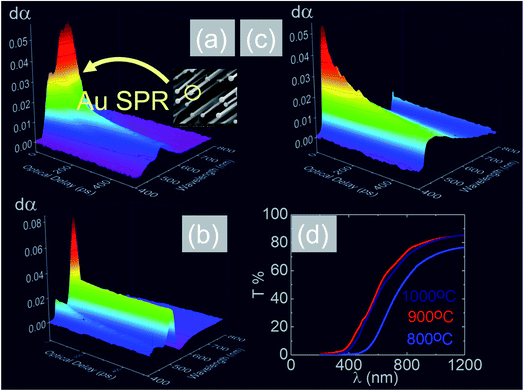
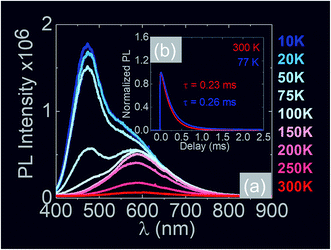
In the past the transmission of light through Sb:SnO₂ NWs^14–24 has not been investigated as they were not ordered or oriented along any particular direction which in turn leads to a considerable suppression of transmission and transparency. In contrast a higher transmission of light is expected to occur through ordered MO NWs. We measured the steady state transmission through the Sb:SnO₂ NWs that were grown at 800 °C on r-Al₂O₃ as shown in Fig. 9(d). The Sb:SnO₂ NWs have an optical transmission of 80% above 800 nm but they absorb light in the visible between 400 nm to 800 nm. We do not observe any interference effects since the spacing between the Sb:SnO₂ NWs is considerably smaller than the wavelength of light. In addition we find that the Sb:SnO₂ NWs on r-Al₂O₃ obtained at 900 °C and 1000 °C have a higher transparency compared to those obtained at 800 °C due to their shorter lengths. In order to understand the origin of the absorption we have measured the transient absorption through the Sb:SnO₂ NWs on an fs time scale as shown in Fig. 9(a)–(c). In all cases, we observe a strong peak in the time evolution of the differential absorption between 500 nm and 600 nm attributed to the surface plasmon resonance (SPR) of the Au–Sn particles, corresponding to sizes between 10 nm and 100 nm (ref. 51) and the existence of surface states lying energetically in the energy gap of SnO₂.⁵² One may observe a slight blue shift of the peak from 900 °C to 1000 °C in Fig. 9(b) and (c), consistent with that observed in the steady state transmission, that might be related to the smaller size of the Au–Sn particles due to the depletion of Sn that occurs during the temperature ramp and/or the elimination of mid gap states at elevated temperatures. It is important to point out, that the transparency of the Sb:SnO₂ NWs on r-Al₂O₃ may be increased further by selective area location growth as shown in Fig. 7 which leads to a higher transmission through the voids between the Sb:SnO₂ NW.

Finally it is worthwhile considering the PL obtained from the Sb:SnO₂ NWs, grown on r-Al₂O₃ at 800 °C, as shown in Fig. 10(a), in which case we observe emission at λ = 600 nm (≡2.1 eV) and 300 K. Bulk SnO₂ has a direct energy band gap of 3.7 eV but the even – parity symmetry of the conduction-band minimum and valence-band maximum states prohibits band – edge radiative transitions which has limited the use of SnO₂ for the fabrication of light emitting diodes. The PL at 2.1 eV is attributed to radiative recombination between deep donor and acceptor like states residing energetically in the energy band gap of SnO₂ that are related to oxygen vacancies. We observe a suppression of the maximum at λ = 600 nm and the emergence of emission at λ = 470 nm (≡2.6 eV) by decreasing the temperature from 300 K to 10 K due to radiative recombination via shallower levels as proposed by Luo et al.⁵³ However an interesting aspect of the PL emission at 2.1 eV and 2.6 eV is that it has a lifetime of τ ≈ 0.2 ms as shown by the time resolved PL in Fig. 10(b). This is considerably higher than the lifetimes extracted from SnO₂ rods and particles which are of the order of 100 ns (ref. 54) and comparable to Eu doped SnO₂ nanocrystals.⁵⁵ Hence, in principle, the Sb:SnO₂ NWs described here may be processed into devices capable of light emission but also NWSCs.^56,57

Fig. 10 (a) Temperature dependence of the PL obtained from the Sb:SnO₂ NWs grown on r-Al₂O₃ at 800 °C (b) time resolved PL taken at λ = 600 nm for 300 K and 77 K along with the corresponding lifetimes.

To the best of our knowledge no one has previously used ordered networks of Sn:In₂O₃ or Sb:SnO₂ NWs to make NWSCs despite the fact that Battaglia et al.⁵⁸ has showed that periodic photonic nanostructures outperform their random counterparts in trapping light in solar cells. It is desirable then to use these highly conductive, ordered networks, of Sb:SnO₂ NWs in order to improve the performance of all-solid state NWSCs. In addition the Sb:SnO₂ NWs can be used in perovskite solar cells as an electron transport layer (ETL). According to Jiang et al.⁵⁹ a traditional ETL such as TiO₂, is not very efficient for charge extraction at the interface, especially in planar structures. In addition, the devices using TiO₂ suffer from serious degradation under ultraviolet illumination. SnO₂ shows a better band alignment with the perovskite absorption layer and higher electron mobility, which is helpful for electron extraction. Consequently the specific ordered networks of Sb:SnO₂ NWs described here may serve as a scaffold on top of which one may deposit a perovskite absorber layer and a hole transport layer in order to create a p–n junction solar cell.

4 Conclusions

We have grown epitaxial, ordered Sb:SnO₂ NWs via the VLS mechanism on m-, r- and a-Al₂O₃ between 700 °C and 1000 °C using metallic Sn containing an excess of Sb i.e. for Sn/Sb = 0.15 ± 0.05 under a flow of Ar and O₂ at 1.5 ± 0.5 mbar. One dimensional growth was suppressed for Sn/Sb < 0.1 while the Sb:SnO₂ NWs were not oriented along any particular direction for Sn/Sb > 0.2. Consequently highly conductive and directional Sb:SnO₂ NWs may only be obtained in a narrow window of growth conditions. All of the Sb:SnO₂ NWs have the tetragonal rutile crystal structure and square sections. The Sb:SnO₂ NWs are oriented along two mutually perpendicular directions forming a rectangular mesh on m-Al₂O₃ with a maximum lattice mismatch of 0.1%. In contrast the Sb:SnO₂ NWs on r-Al₂O₃ are all oriented in one direction but have a larger lattice mismatch of 10%. The morphology and growth directions of the Sb:SnO₂ NWs on m-, r- and a-Al₂O₃ did not change by varying the growth temperature between 700 °C and 1000 °C but the carrier density changed from 8 × 10¹⁹ cm⁻³ to 4 × 10¹⁷ cm⁻³ due to the re-evaporation and limited incorporation of Sb donor impurities into the SnO₂ NWs with increasing temperature. All of the Sb:SnO₂ NWs had a high transmission of 80% above 800 nm and absorbed light between 400 nm to 800 nm primarily due to the SPR of the Au particles. The transmission may be improved significantly by selective area location growth which we have shown that is possible on r-Al₂O₃ by patterning the catalyst. In addition the Sb:SnO₂ NWs on m-, r- and a-Al₂O₃ are capable of light emission with remarkably long lifetimes of 0.2 ms and are attractive for the realization of NWSCs.

Conflicts of interest

There are no conflicts of interest to declare.

References

1. Q. Wan, E. N. Dattoli and W. Lu, Appl. Phys. Lett., 2007, 90, 222107.
2. M. Zervos, C. Mihailescu, J. Giapintzakis, C. Luculescu, N. Florini, P. Komninou, J. Kioseoglou and A. Othonos, APL Mater., 2014, 2, 056104.
3. S. N. Bai, H. H. Tsai and T. Y. Tseng, Thin Solid Films, 2007, 516, 155.
4. H. Duan, H. He, L. Sun, S. Song and Z. Ye, Nanoscale Res. Lett., 2013, 8(1), 493.
5. C. O. Dwyer, M. Szachowicz, G. Visimberga, V. Lavayen, S. B. Newcomb and C. M. S. Torres, Nat. Nanotechnol., 2009, 4, 239.
6. J. Gao, R. Chen, D. H. Li, L. Jiang, J. C. Ye, X. C. Ma, X. D. Chen, Q. H. Xiong, H. D. Sun and T. Wu, Nanotechnology, 2011, 22, 195706.
7. Q. Wan, E. N. Dattoli, W. Y. Fung, W. Guo, Y. Chen, X. Pan and W. Lu, Nano Lett., 2006, 6, 2909,  DOI:10.1021/nl062213d.
8. P. Nguyen, H. T. Ng, J. Kong, A. M. Cassell, R. Quinn, J. Li, J. Han, M. McNeil and M. Meyyappan, Nano Lett., 2003, 3, 925.
9. D. Tsokkou, A. Othonos and M. Zervos, Appl. Phys. Lett., 2012, 100, 133101.
10. Q. Wan, E. Dattoli and W. Lu, Small, 2008, 4, 451.
11. Z. H. Luo, D. S. Tang, H. Kuo, Y. Fang, Y. Q. Chen, X. W. He, Y. H. Peng, H. J. Yuan and Y. Yang, Chin. Phys. B, 2010, 19, 026102.
12. C. Amorim, C. Dalmaschio, E. Leite and A. Chiquito, J. Phys. D: Appl. Phys., 2014, 47, 045301.
13. F. Ma, Y. Jiao, G. Gao, Y. Gu, A. Bilic, S. Sanvito and A. Du, ACS Appl. Mater. Interfaces, 2016, 8, 25667.
14. Q. Wan and T. H. Wang, Chem. Commun., 2005, 30, 3841.
15. L. Li, J. Huang, T. Wang, H. Zhang, Y. Liu and J. Li, Biosens. Bioelectron., 2010, 25, 2436.
16. X. Rui-Jie and L. Hui-Xuan, Chin. Phys. B, 2012, 21, 088104.
17. Q. Wan, J. Huang, Z. Xie, T. Wang, E. N. Dattoli and W. Lu, Appl. Phys. Lett., 2008, 92, 102101.
18. J. Huang, A. Lu, B. Zhao and Q. Wan, Appl. Phys. Lett., 2007, 91, 073102.
19. B. R. Sathe, M. Patil, P. S. Walke, J. P. Vivek, A. Lele, V. K. Pillai and I. S. Mulla, Sci. Adv. Mater., 2009, 1, 38.
20. S. T. Jean and Y. C. Her, J. Appl. Phys., 2009, 105, 024310.
21. R. Kumar, K. Rao, K. Rajanna and A. Phani, Mater. Lett., 2013, 106, 164.
22. A. Klamchuen, T. Yanagida, K. Nagashima, S. Seki, K. Oka, M. Taniguchi and T. Kawai, Appl. Phys. Lett., 2009, 95, 053105.
23. I. Costa, Y. Colmenares, P. Pizani, E. Leite and A. Chiquito, Chem. Phys. Lett., 2018, 695, 125.
24. I. Costa, E. Bernardo, B. Marangoni, E. Leite and A. Chiquito, J. Appl. Phys., 2016, 120, 225109.
25. S. Mathur and S. Barth, Small, 2007, 3, 2070.
26. W. S. Kim, D. Kim, K. L. Choi, J. G. Park and S. H. Hong, Cryst. Growth Des., 2010, 10, 4747.
27. A. Leonardy, W. Z. Hung, D. S. Tsai, C. C. Chou and Y. S. Huang, Cryst. Growth Des., 2009, 9, 3958.
28. L. Mazeina, Y. N. Picard, J. D. Caldwell, E. R. Glaser and S. M. Prokes, J. Cryst. Growth, 2009, 311, 3158.
29. W. S. Kim, D. Kim and S. H. Hong, CrystEngComm, 2014, 16, 9340.
30. Y. H. Choi, J. Na, J. S. Kim, M. K. Joo, G. T. Kim and P. S. Kang, J. Korean Phys. Soc., 2014, 65, 502.
31. X. Wang, N. Aroonyadet, Y. Zhang, M. Mecklenburg, X. Fang, H. Chen, E. Goo and C. Zhou, Nano Lett., 2014, 14, 3014.
32. E. P. Stuckert, R. H. Geiss, C. J. Miller and E. R. Fisher, ACS Appl. Mater. Interfaces, 2016, 8, 22345.
33. D. Tsokkou, A. Othonos and M. Zervos, Appl. Phys. Lett., 2012, 100, 133101.
34. M. Zervos, A. Othonos, E. Tanasa and E. Vasile, J. Phys. Chem. C, 2018, 122, 22709.
35. D. Tsivion, M. Schvartzman, R. Popovitz-Biro and E. Joselevich, ACS Nano, 2012, 6, 6433.
36. R. A. Hughes, E. Menumerov and S. Neretina, Nanotechnology, 2017, 28, 282002.
37. A. L. Giermann and C. V. Thompson, Appl. Phys. Lett., 2005, 86, 121903.
38. W. S. Kim, D. H. Kim, Y. G. Jang and S. H. Hong, CrystEngComm, 2012, 14, 1545.
39. C. McGinley, S. A. Moussalami, M. Riedler, M. Pflughoe, H. Borchert, M. Haase, A. R. B. Castro, H. Weller and T. Möller, Eur. Phys. J. D, 2001, 16, 225.
40. M. D. Segall, P. J. D Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
41. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
42. W. Korner, D. F. Urban, D. M. Ramo, P. D. Bristowe and C. Elsasser, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195142.
43. M. Zervos and L. F. Feiner, J. Appl. Phys., 2004, 95, 1.
44. K. J. Button, C. G. Fonstad and W. Debrodt, Phys. Rev. B: Solid State, 1971, 4, 4539.
45. Y. Mi, H. Odaka and S. Iwata, Jpn. J. Appl. Phys., Part 1, 1999, 38, 3453.
46. H. J. Daal, J. Appl. Phys., 1968, 39, 4467.
47. M. Batzill and U. Diebold, Prog. Surf. Sci., 2005, 79, 47.
48. K. C. Mishra, K. H. Johnson and P. C. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 13972.
49. Z. Q. Li, Y. L. Yin, X. D. Liu, L. Y. Li, H. Liu and Q. G. Song, J. Appl. Phys., 2009, 106, 083701.
50. S. Farahani, T. Veal, J. Mudd, D. Scanlon, G. Watson, O. Bierwagen, M. White, J. Speck and C. McConville, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155413.
51. S. Link and M. El-Sayed, J. Phys. Chem. B, 1999, 103, 4212.
52. A. Othonos, M. Zervos and D. Tsokkou, Nanoscale Res. Lett., 2009, 4, 828.
53. S. Luo, P. K. Chu, W. Liu, M. Zhang and C. Lin, Appl. Phys. Lett., 2006, 88, 183112.
54. A. Kar, S. Kundu and A. Patra, J. Phys. Chem. C, 2011, 115, 118.
55. A. Kar and A. Patra, J. Phys. Chem. C, 2009, 113, 4375.
56. M. Zervos, E. Vasile, E. Vasile, E. Karageorgou and A. Othonos, J. Phys. Chem. C, 2016, 120, 11.
57. E. Karageorgou, M. Zervos and A. Othonos, APL Mater., 2014, 2, 116107.
58. C. Battaglia, C. M. Hsu, K. Soderstrom, J. Escarre, F. J. Haug, M. Charriere, M. Boccard, M. Despeisse, D. T. L. Alexander, M. Cantoni, Y. Cui and C. Ballif, ACS Nano, 2012, 6, 2790.
59. Q. Jiang, X. Zhang and J. You, Small, 2018, 14, 1801154.
60. J. Robertson, J. Phys. C: Solid State Phys., 1979, 12, 4767.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00074g

---