Formation of strong L1₀-FePd/α-Fe nanocomposite magnets by visualizing efficient exchange coupling

Abstract

Conceptual nanocomposite magnets (NCMs) composed of exchange-coupled hard/soft magnetic phases have been expected to show excellent magnetic performance based on simultaneous high coercivity (H_c) and high saturation magnetization (M_s). In our previous works, however, the H_c was considerably lower than its theoretical value (H_a), which prevented us from improving the performance of NCMs. Here, we show that the H_c of isolated particulate L1₀-FePd/α-Fe NCMs is dominated by their phase segregation into core/shell-like structures versus Janus-like structures. Using first-order reversal curve (FORC) analysis, we clearly distinguished a microscopically undetectable difference in the phase-segregation structure in the NCMs, finding both efficient and inefficient exchange coupling. The nanostructurally controlled NCMs dominated by core/shell-like structure with efficient exchange coupling showed the largest energy product ((BH)_max = 17.5 MGOe) in the Fe–Pd system and the highest H_c/H_a value (26.5%) among all NCM powders.

---

Introduction

Electric energy is mostly consumed by conversion into mechanical energy, where permanent magnets play an important role. Thus, highly efficient conversion of electric energy into mechanical energy depends on high-performance permanent magnets that have both high coercivity (H_c) and high saturation magnetization (M_s). Exchange-coupled nanocomposite permanent magnets (NCMs) composed of magnetically hard and soft phases have been theoretically expected to show higher performance than the neodymium magnets.^1–3 To bring out their full potential, NCMs should have soft magnetic phases within the nanoscale exchange-coupling length so they can derive a high M_s and H_c from their soft and hard phases, respectively.³ In many previous works, NCMs were synthesized at the necessary conditions for high performance, but their H_c was much lower than the anisotropy field (H_a), which is the H_c upper limit.^4–7 Thus, to improve the H_c of NCMs, we must clarify what determines their H_c.

In single-phase magnets, H_c is influenced by many factors such as magnetic-domain interaction,⁸ crystal structure,⁹ magnetic-domain size¹⁰ and magnetic-domain shape.^10,11 The H_c of NCMs, however, may be influenced by not only these factors but also the interface-inducing lattice strain between the soft/hard phases,⁴ the volume ratio^4,12 and the phase-segregation structure¹² of the soft/hard magnetic phases. However, the thermal annealing done at high temperatures to induce atomic diffusion, often necessary to form NCMs, makes it much more difficult to control the nanostructures of NCMs.^4,6,12 Because these several factors are intertwined complexly, improving H_c systematically in various NCMs has been very challenging.

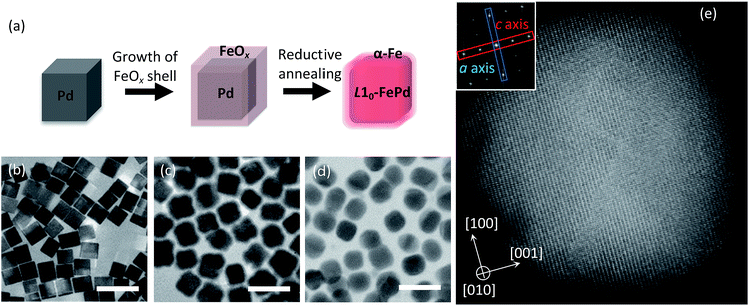
To find the dominant factor determining the H_c of NCMs, we must systematically control several factors that vary H_c. We selected L1₀-FePd as the hard magnetic phase and α-Fe as the soft magnetic phase, because α-Fe can coexist with L1₀-FePd, according to the Fe–Pd phase diagram.¹³ Moreover, we can easily control nanostructures such as the crystalline size of the L1₀-FePd phase corresponding to the magnetic-domain size under the single domain size (<330 nm), the hard/soft phase volume ratio and the magnetic-domain shape of the NCMs by the reduction–diffusion method (Fig. 1a and Table S1†).^4,5 Furthermore, we visualized the H_c change of NCMs with various nanostructures by using first-order reversal curves (FORCs) analysis, which is a powerful way to confirm the formation of NCMs.^2,4,14,15 This analysis can sensitively distinguish the magnetic circumstances affecting H_c, letting us quantitatively evaluate the hard/soft exchange coupling of well-defined L1₀-FePd/α-Fe NCMs (Fig. S9†).² By using FORCs, we visualized the H_c distributions in well-controlled NCMs, clarifying that the H_c of the NCMs is dominated by a slight change in the phase segregation between a core/shell-like structure and a Janus-like structure.

Fig. 1 (a) Synthesis of an L1₀-FePd/α-Fe NCM with a well-controlled nanostructure. (b–d) TEM images of (b) 19 nm Pd NCs, (c) Pd@FeO_x NCs with Fe/Pd = 66/34 at% and (d) L1₀-FePd/α-Fe NCMs synthesized under reductive annealing of (c) at 560 °C for 3 h. Scale bars are 50 nm. (e) High-angle annular dark-field scanning TEM (HAADF-STEM) image of (d) showing the L1₀ structure in the L1₀-FePd phase. The inset in (e) shows the fast Fourier transform (FFT) image, in which the spots surrounded by blue and red rectangles respectively imply the planes of the a axis and c axis of the L1₀ structure.

Results and discussion

Synthesis of L1₀-FePd/α-Fe NCMs

To fabricate well-defined L1₀-FePd/α-Fe NCMs with monodisperse L1₀-FePd crystalline size, magnetic-domain shape of the NCMs and volume ratio of the L1₀-FePd/α-Fe phases, we performed the following step-by-step synthesis (Fig. 1a): (1) synthesis of monodisperse Pd nanocubes (NCs) (Fig. 1b and S1a–f†);^16,17 (2) homogeneous growth of FeO_x shells on Pd NCs (Fig. 1c, S1g and Table S2†);¹⁸ (3) reduction–diffusion of Pd/FeO_x core/shell (Pd@FeO_x) NCs under the flow of 4% H₂ gas (Ar balance) (Fig. 1d, e and S5†).^4,5 This synthesis allowed us to finely tune the size of the Pd NCs, the thickness of the FeO_x shell and the reduction–diffusion conditions, so we could precisely control the L1₀-FePd crystalline size and the volume fraction of the L1₀-FePd/α-Fe phases. The nanostructure of Pd@FeO_x NCs also enabled the formation of a core/shell-like structure and a Janus-like structure under the reductive annealing (Fig. S4†). In addition, almost all particles were isolated after annealing because of the carbon shells formed from the organic ligands by Fe catalysis.¹⁹ The phenomenon could be observed in the particles annealed under several conditions from high-resolution transition electron microscopy (HRTEM) (Fig. S3†).¹⁹ We targeted a Pd grain size of 14–26 nm, which were estimated from TEM images, to facilitate the synthesis of the L1₀-FePd phase with a high ordering parameter.²⁰ We first focus on the samples synthesized by reductive annealing of Pd@FeO_x NCs (from 19 nm Pd NCs) with Fe/Pd = 66/34 atomic% (at%) at 540 °C for 5, 10, 15, 20 and 25 h. X-ray diffraction (XRD) patterns show the formation of L1₀-FePd and α-Fe phases (Fig. S2b†). Thus, we formed magnets composed of L1₀-FePd and α-Fe phases with well-controlled nanostructural characteristics such as the L1₀-FePd crystalline size, the shape of the magnets and the α-Fe/L1₀-FePd volume ratio.

Correlation of crystal and phase-segregation structures with H_c

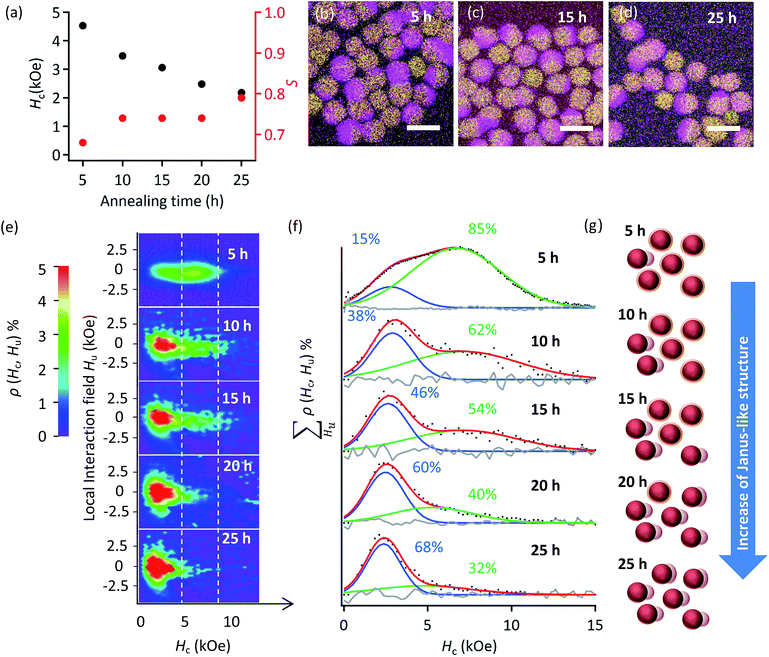
Using vibrating sample magnetometer (VSM) on a series of L1₀-FePd/α-Fe NCMs, we showed that H_c decreased monotonically with increasing annealing time (Fig. 2a). We attempted to explain this result by calculating the tetragonality—the ratio of lattice parameters (c/a)^9,21—and the ordering parameter (S)^22,23 of the L1₀-FePd phase grains. Strangely, S increased with annealing time (Fig. 2a) and c/a decreased monotonically (Fig. S2c†), usually indicating that the H_c of L1₀-FePd phase increased.²² The crystalline size of the α-Fe phase grains also did not show a significant difference in the calculated values obtained by the Scherrer equation for the 110 diffraction peaks (Scherrer constant K = 0.94) (Fig. S2†). Moreover, elemental maps measured with energy dispersive spectroscopy (EDS) did not show any differences in phase segregation among samples (Fig. 2b–d). These structural analyses could not explain the monotonic decrease in H_c with annealing time.

Fig. 2 (a) H_c and S values of the L1₀-FePd/α-Fe NCMs synthesized by reductive annealing of Pd@FeO_x NCs with Fe/Pd = 66/34 at% synthesized from 19 nm Pd NCs annealed at 540 °C for various times. (b–d) Elemental maps of the NCMs obtained by reductive annealing for (b) 5 h, (c) 15 h and (d) 25 h (purple: Fe–K, yellow: Pd–L). Scale bars are 25 nm. (e) FORCs diagrams of the L1₀-FePd/α-Fe NCMs with Fe/Pd = 66/34 at% synthesized from 19 nm Pd NCs. ρ(H_c, H_u) means the fraction of hysteron with a certain H_c and a certain H_u. When ρ(H_c, H_u) is over 5%, the colour becomes red. (f) H_c distributions obtained by calculating the ΣH_uρ(H_c, H_u) of (e). The black dots are raw data, the red curves are the sums of the fitting curves by a Gaussian function, the blue and green curves are fitting curves and the grey curves are the differences between the raw data and fitting curves. (g) Schematics of the fraction change of the core/shell-like and Janus-like structures estimated by FORCs analysis of (f).

Then, we used FORCs analysis on all the samples to clarify the nanostructure transformation that changed H_c (Fig. 2e and f). To better compare the H_c distributions, we integrated the height of the FORCs diagram (ρ(H_c, H_u)) with respect to the local interaction field (H_u). The obtained curve represents the fraction of hysteron for each H_c (Fig. S9†). These curves were fitted with a Gaussian function, whose number was determined by kernel density estimation (Fig. S9†), and the fractions of these distributions were calculated from the integral of the fitting curves (Fig. 2f). Each FORCs diagram showed two H_c distributions with quite high H_c compared with that of the α-Fe soft phase (H_c ≪ 1 kOe),^23,24 indicating that two types of NCMs formed.

The fraction of the low-H_c distribution increasing with annealing time corresponds to a structural transformation from a core/shell-like structure to a Janus-like structure (Fig. S4†) or to the coalescence of α-Fe phase; the L1₀-FePd/α-Fe exchange coupling weakened because larger α-Fe phase grains formed during annealing (Fig. 2g).^4,25–28 In other words, the different thicknesses of α-Fe phase within and beyond the threshold determining ‘efficient’ or ‘inefficient’ exchange coupling in the L1₀-FePd/α-Fe NCMs helped to form the two types of NCMs. Thus, a visualization of the exchange coupling by FORCs analysis could reveal that a slight change, which was microscopically undetectable, in the phase-segregation structure or the α-Fe thickness dominated the H_c of the NCMs.

Optimization of nanostructure in L1₀-FePd/α-Fe NCMs for high performance

By controlling the crystalline size of the L1₀-FePd phase and the volume ratio of the L1₀-FePd/α-Fe phases (Fig. 1a), we fabricated NCMs with the highest performance reported in the Fe–Pd system. We synthesized NCMs as follows: (1) synthesis of Pd NCs with sizes of 14, 19, 23 and 26 nm; (2) homogeneous growth of FeO_x shells on the Pd NCs with Fe/Pd molar ratios of approximately 62/38 and 66/34; (3) reductive annealing of Pd@FeO_x NCs under the conditions to produce NCMs with the highest H_c (Fig. S5 and Table S4†).

Among all these NCMs, the NCMs formed from 19 nm Pd NCs had the highest H_c regardless of Fe/Pd composition (Fig. S7a†). In the NCMs formed from 19 nm Pd NCs, we then controlled their L1₀-FePd/α-Fe volume fraction in the range of Fe/Pd = 53/47–75/25 at%, improving their M_s and maximizing their energy product ((BH)_max) and H_c/H_a ratio. These values became maximum ((BH)_max = 17.5 MGOe and H_c/H_a = 26.5%) at an Fe/Pd composition of 66/34 at% and decreased at >66/34 at% (Fig. 3a and b) due to the drastic decrease in H_c. These maximum values greatly exceeded the highest reported values ((BH)_max = 10.3 MGOe and H_c/H_a = 9%) in the Fe–Pd system.^4,5,25–28 Particularly, the H_c/H_a value (26.5%) was also highest among all NCM powders to our knowledge, which indicates that the performance of L1₀-FePd/α-Fe NCMs was efficiently brought out, compared with other systems.^{4–7,25–27}

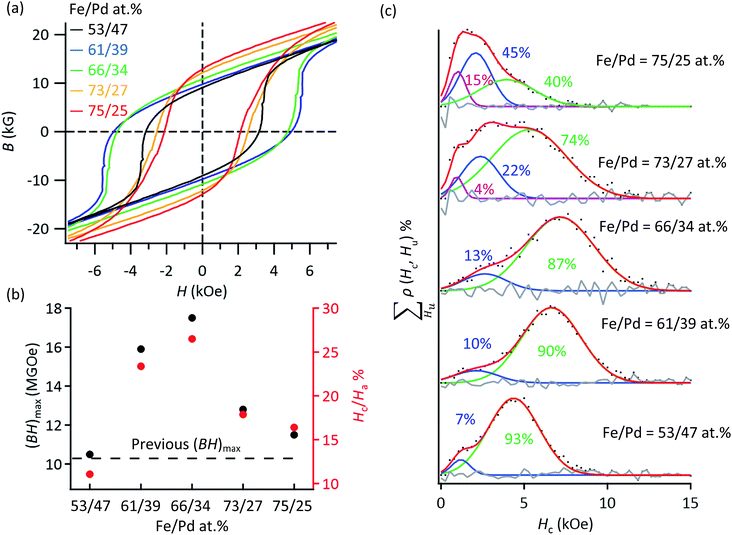Fig. 3 (a) B–H curves of the NCMs with Fe/Pd molar ratios of 53/47, 61/39, 66/34, 73/27 and 75/25 formed by reductive annealing at 590 °C for 3 h, at 570 °C for 10 h, at 560 °C for 3 h, at 540 °C for 3 h and at 540 °C for 3 h, respectively. The B values were obtained from the corrected M–H curve. (b) (BH)_max and the H_c/H_a values obtained from the B–H curves. (c) H_c distributions obtained by using the same method as in Fig. 2f. The cyan curves are also the H_c distributions derived from the L1₀-FePd/α-Fe NCMs.

To reveal which factor contributed to the high H_c/H_a and (BH)_max, we again conducted FORCs analysis on these NCMs (Fig. 3c). The H_c distributions revealed two types of exchange coupling derived from the Janus- and core/shell-like structures at Fe/Pd compositions of <66/34 at%. With more Fe, the lower H_c distribution appeared in addition to the two types of NCMs, which was also derived from the NCMs with the Janus-like structure because this H_c value is higher than that of α-Fe. On the other hand, the average H_c of almost pure L1₀-FePd magnets (Fe/Pd = 53/47 at%) was lower than those of the NCMs with Fe/Pd molar ratios of 61/39 and 66/34. Then, the surface anisotropic constant (K_s) of these NCMs were compared, which strongly suggested that the low K_s of pure L1₀-FePd magnets caused the lower H_cversus those of L1₀-FePd/α-Fe NCMs (Fig. S8†). This result means that the soft magnetic phase in NCMs contributes not only to the increase of the H_c with higher K_s value, but also to the decrease of the H_c due to the formation of Janus-like structure. Thus, the maximized (BH)_max and H_c/H_a at Fe/Pd = 66/34 at% came from the trade-off between the increase in K_s and the decrease in the fraction of the core/shell-like structure.

Clarification of the dominant factor determining the H_c of L1₀-FePd/α-Fe NCMs

We estimated the change in exchange coupling between the L1₀-FePd and α-Fe phases by the phenomenological eqn (1) of the micromagnetics model (Fig. S10†):²⁹

H_c = αH_aexp − N_effJ_s, (1)

where α is an effective microstructural parameter that varies from 0 to 1, which strongly depends on the exchange coupling factor;³⁰H_aexp is an anisotropy field of the NCMs, which is evaluated from the experimental results (Fig. S10†); N_eff is an effective demagnetization factor, which usually decreases with an increasing amount of the soft magnetic phase, because the soft magnetic phase in NCMs can weaken the local stray field;³⁰J_s is the saturation magnetic polarization. Thus, α and N_eff decreased as the fraction of the Janus-like structure increased. This behavior indicates that the structural change from core/shell- to Janus-like structures caused the decrease in exchange coupling between the L1₀-FePd and the α-Fe phases and the increase in α-Fe thickness, corresponding to the decrease in α and N_eff, respectively.

In fact, the micromagnetics model clearly explains the relationship between the fraction of the Janus-like structure and the α and N_eff by classifying the H_c distributions as follows (Fig. 4): (group I) low fraction of Janus-like structure, (group II) intermediate fraction of Janus-like structure and (group III) high fraction of Janus-like structure and transition from core/shell- to Janus-like structure. Thus, using FORCs analysis and the micromagnetics model, we showed that the H_c of NCMs was dominated by the phase-segregation structure, because the strength of exchange coupling between the L1₀-FePd and the α-Fe phases strongly depended on the thickness of the α-Fe phase.

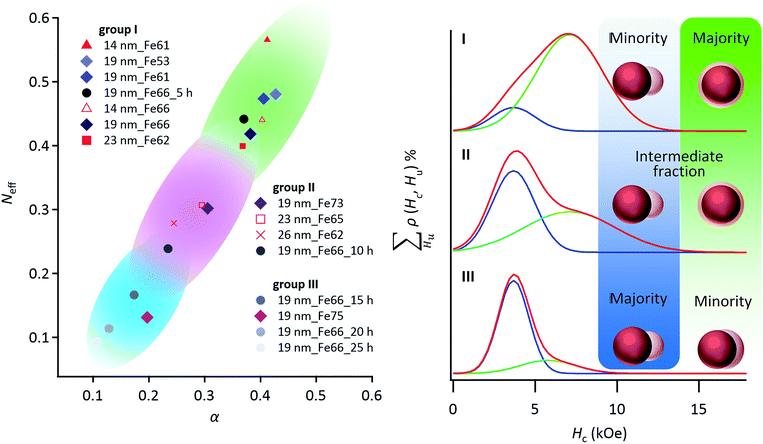Fig. 4 According to a phenomenological eqn (1) of the micromagnetics model, both the effective demagnetization factor (N_eff) and effective micromagnetics constant (α) were estimated for NCMs with different nanostructures. α and N_eff strongly depend on the exchange coupling factor and the crystalline size of the α-Fe soft magnetic phase,³² respectively. The α and N_eff values of the NCMs can be classified into groups I–III by using the H_c distributions as follows: group I is the minor fraction of the Janus-like structure; group II is the intermediate fraction of the Janus-like structure; group III is the major fraction of the Janus-like structure. The sample name comprises the starting Pd NC size, followed by the Fe fraction, followed by the annealing time, if any.

Conclusions

The FORCs analysis results consistent with the micromagnetics model revealed that the Janus-like structure in NCMs caused the drastic decrease in H_c. In other words, the NCMs largely dominated by the core/shell-like structure provided the largest (BH)_max (17.5 MGOe) in the Fe–Pd system and the highest H_c/H_a value (26.5%) among all NCM powders,^{4–7,25–28} because of the highly sensitive change of H_c induced by the extremely slight transformation of phase-segregation structures. In our previous works,^4,5 we could not correctly evaluate the decrease in H_c, because it was quite difficult to discuss the boundary between ‘efficient’ and ‘inefficient’ exchange coupling between the hard and soft magnetic phases by using conventional methods such as TEM, XRD and EDS elemental mapping. FORCs analysis enables us to visually distinguish the two types of NCMs, revealing the dominant factor determining the H_c of NCMs, that is, the phase-segregation fashion. These achievements can solve the mystery for the quite low H_c of NCMs, compared with the theoretical H_c. We believe that the optimization of nanostructures by FORCs analysis can realize the creation of high-performance NCMs in not only Fe–Pd system but also other systems.

Experimental procedure

Chemicals

All reagents and solvents were commercially available. Sodium tetrapalladate(II) (Na₂PdCl₄, 98%), polyvinylpyrrolidone (PVP, M_w ≈ 55k), ascorbic acid (AA, 99+%), potassium bromide (KBr, ≥99%), oleylamine (OAm, 80–90%), 1-octadecene (ODE, 90%) and eicosane (99%) were purchased from Sigma-Aldrich. Iron pentacarbonyl (Fe(CO)₅, 95%) was purchased from Kanto Chemical Corporation. Oleic acid (OA, >85%) was purchased from Tokyo Chemical Industry. Ethanol, acetone, n-hexane and chloroform were purchased from Wako Pure Chemical Industries. All chemical reagents were used as received without further purification.

Synthesis of Pd NCs

In typical synthesis of Pd NCs,¹⁶ 270 mL of an aqueous solution of PVP (2.8 g) and AA (0.66 g) was stirred at 80 °C for 1 h. Then, an aqueous solution (30 mL) of Na₂PdCl₄ (1.5 g) and KBr (16 g) was rapidly injected into the above solution. The aqueous solution was stirred at 80 °C for 3 h and then cooled to room temperature. This process synthesized Pd NCs with an edge length of 15.4(±1.4) × 13.4(±1.1) nm (Fig. S1a†). To synthesize larger Pd NCs (Fig. S1b–d†), after an aqueous solution (250 mL) of Na₂PdCl₄ (1.5 g) and KBr (3.0 g) was stirred at 40 °C for 1 h, an aqueous solution of Pd seeds (V mL), an aqueous solution (25 mL) of PVP (2.8 g) and an aqueous solution (25 mL) of AA (1.8 g) were injected every 30 min at 40 °C (Fig. S1†). Here, the volume of the seed solution (V mL) was determined by the equation of the seeded-growth method:¹⁷

d = d₀((n_i + n_m)/n_m)^1/3,

where d is the average length of the final Pd NCs, d₀ is the average length of the Pd seeds and n_i and n_m are the quantities of ionic and metallic Pd in the reaction solution. The solution was stirred at 40 °C for 48 h, heated from 40 °C to 60 °C and stirred at 60 °C for 48 h. After the reaction, the reaction solution was cooled to room temperature, and the Pd NCs were collected by centrifugation with acetone and then purified with ethanol/acetone (1/4 vol%).

Synthesis of Pd@FeO_x NCs

Before FeO_x growth on Pd NCs, we exchanged the organic ligand from PVP to OAm to disperse the Pd NCs in a low-polar solvent. The Pd NCs (0.50 mmol) protected by PVP were dispersed in the mixture of OAm (10 mL) and chloroform (20 mL) by sonication for 1 h, and then the solution was heated at 50 °C for 30 min. Then, the solution was cooled to room temperature, and the OAm-protected Pd NCs with sizes of 14 nm, 19 nm, 23 nm and 26 nm were collected with ethanol and purified n times (n = 4, 3, 2 and 1) with chloroform/ethanol (2/3 vol%), respectively. To cover the Pd NCs with FeO_x shells, the OAm-protected Pd NCs (0.50 mmol), OAm (0.50 mL) and OA (0.91 mL) were dispersed in ODE (63 mL).¹⁸ After the solution was stirred at 80 °C for 1 h under an N₂ atmosphere, Fe(CO)₅ (x mmol) was injected into the solution (Table S2†) and the reaction temperature was increased in steps of 3 °C min⁻¹ from 80 °C to 180 °C. Finally, after the solution was stirred at 180 °C for 2 h and cooled to room temperature, Pd@FeO_x NCs formed from the 14 nm, 19 nm, 23 nm and 26 nm Pd NCs were collected with ethanol and then purified three times with n-hexane/ethanol (3/1 vol%) including OAm (0.50 mL) and OA (0.50 mL).

Synthesis of L1₀-FePd/α-Fe NCMs

After the Pd@FeO_x NCs with sizes of 14 nm, 19 nm, 23 nm and 26 nm were washed m times (m = 7, 6, 5 and 4) with n-hexane, respectively, these NCs were dried in desiccator overnight. The L1₀-FePd/α-Fe NCMs were produced by reductive annealing—heating at 10 °C min⁻¹, holding at T °C for t h and cooling at 10 °C min⁻¹—of the Pd@FeO_x NCs under an Ar + 4% H₂ atmosphere (see Fig. S5 and S6, and Table S4† for detailed conditions).

Calculation of S of the L1₀-FePd phase in L1₀-FePd/α-Fe NCMs

An S of the L1₀-FePd phase was found with the following equation:²²

S² = (I₀₀₁/I₀₀₂)_meas./(I₀₀₁/I₀₀₂)_calc.,

where I₀₀₁ and I₀₀₂ are the peak intensities of the hkl diffraction peaks in the L1₀-FePd phase, and (I₀₀₁/I₀₀₂)_meas. and (I₀₀₁/I₀₀₂)_calc. are the measured and calculated intensity ratios. We used 0.9852 (PDF#03-65-9971) as a calculated intensity ratio.

Measurement of hysteresis loop at 300 K

The M–H curves were measured by a vibrating sample magnetometer (VSM, TOEI VSM-5) under a magnetic field (H) of −20 to 20 kOe, where the samples were prepared without aligning under the magnetic field. The samples were fixed with eicosane (melting point of 36.7 °C).

Evaluation of temperature-dependent magnetic properties

The magnetic properties of the samples fixed by eicosane were measured on a PPMS-VS (Quantum Design EverCool II). The anisotropy constant (K_u) and anisotropy field (H_aexp) were calculated from M–H curve fits based on the following equation:³¹

M(H) = J_s(1 − 4K_u²/15J_s²H²) + χH,

where M(H) is the magnetization at H and χ is the high-field susceptibility. α and N_eff were determined using eqn (1) from a micromagnetics model, drawing a linear function from the points of H_aexp, H_c and J_s depending on temperature (Fig. S10†).

FORCs analysis

The height of the FORCs diagram (ρ) was represented by the following equation:^14,15

ρ(H_A, H_B) = −∂²M(H_A, H_B)/2∂H_A∂H_B,

where H_A and H_B have the following relationship: a coercivity H_c = −(H_A − H_B)/2 and a local interaction field H_u = (H_A + H_B)/2. We applied a maximum H of 50 kOe to produce magnetic saturation and the measurement pitch for H_A and H_B was 0.5 kOe within −20 kOe to 20 kOe of H by using a superconducting quantum interference device (SQUID, Quantum Design MPMS XL) to measure the reversal magnetization in detail (Fig. S9†). The measurement temperature was 300 K. These samples were also fixed using eicosane.

Evaluation of H_a

H _a = 2(f_volumeK_uFePd + (1 − f_volume)K_uFe)/(f_volumeJ_sFePd + (1 − f_volume)J_sFe) = 2f_volumeK_uFePd/(f_volumeJ_sFePd + (1 − f_volume)J_sFe) (K_uFe ≪ K_uFePd),

where f_volume is the volume fraction of the L1₀-FePd in NCMs, K_uFePd (1.80 MJ m⁻³) and K_uFe (47.2 kJ m⁻³) are the anisotropic constants of the L1₀-FePd and the α-Fe phases, respectively and J_sFePd (13.8 kG) and J_sFe (21.5 kG) are the saturation magnetizations of the L1₀-FePd and the α-Fe phases, respectively.^3,5,24

Evaluation of (BH)_max

To calculate the (BH)_max, we measured the density of the NCMs and the demagnetization field of the magnets by using VSM.

(i) Volume ratio of L1₀-FePd/α-Fe phases

The volume fraction is calculated from the Fe/Pd at% as follows:

L1₀-FePd cm³: f_at(M_Fe + M_Pd)/d_FePd,

α-Fe cm³: (1 − 2f_at)M_Fe/d_Fe,

where f_at is the fraction of Pd atoms in the L1₀-FePd/α-Fe NCMs measured by XRF, M_Fe and M_Pd are the atomic weights of Fe and Pd atoms, respectively and d_FePd (9.75 g cm⁻³) and d_Fe (7.86 g cm⁻³) are the densities of the L1₀-FePd and α-Fe phases, respectively.⁴

(ii) Density of L1₀-FePd/α-Fe NCMs

From (i), we can estimate the density of the NCMs (d_NCMs) as follows:

d_NCMs = (f_at(M_Fe + M_Pd) + (1 − 2f_at)M_Fe)/(f_at(M_Fe + M_Pd)/d_FePd + (1 − 2f_at)M_Fe/d_Fe).

(iii) Conversion of magnetization unit from [emu g⁻¹] to [G]

We converted the magnetization unit from [emu g⁻¹] to [G] as follows:

J = Md_NCMs4π,

where J is the magnetic polarization and M is the magnetization.

(iv) Correction of magnetic field

To estimate the magnetic flux density (B), H should be corrected by removing the demagnetization field (N_zJ) as follows:

H_correct = H − N_zJ,

N_z = 1/(1 + c/a²(a(a + c))^1/2),

where H and H_correct are the magnetic fields before and after correction, N_z is a demagnetization factor of magnets along the z axis, and a and c are the radius and height of the cylinder, respectively, during the VSM measurement.³²

(v) Evaluation of (BH)_max

B = J + H_correct.

Finally, the (BH)_max values are obtained from B × H_correct in the second quadrants of the B–H curves.

TEM observation

The Pd NCs and Pd@FeO_x NCs were dispersed in ethanol and chloroform, respectively and then dropped on amorphous carbon-coated copper grids with a carbon thickness of about 30 nm. TEM samples for the L1₀-FePd/α-Fe NCMs were prepared by annealing the Pd@FeO_x NCs on TEM grids. TEM images were recorded on a JEM1011 (JEOL) at an acceleration voltage of 100 kV.

Powder XRD measurement

The XRD patterns were recorded on a PANalytical X'Pert Pro MPD diffractometer with Cu Kα radiation (λ = 1.542 Å) at 45 kV and 40 mA.

Evaluation of the composition of L1₀-FePd/α-Fe NCMs

The Fe/Pd molar ratios of the NCs and NCMs were measured by X-ray fluorescence (XRF) spectroscopy (JEOL JSX-3202C). The L1₀-FePd/α-Fe volume ratios were calculated on the hypothesis that the Pd phase grains were completely converted into the L1₀-FePd phase grains (Table S1†).

EDS elemental maps by HAADF-STEM and HRTEM

The TEM samples of the L1₀-FePd/α-Fe NCMs were prepared by annealing the Pd@FeO_x NCs on amorphous carbon-coated copper grids with a carbon thickness of about 5 nm. EDS maps by HAADF-STEM and HRTEM were performed on a JEM-ARM200F at an acceleration voltage of 200 kV.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by The Ministry of Education, Culture, Sports, Science and Technology (MEXT)/Japan Society for the Promotion of Science (JSPS) KAKENHI for Scientific Research B (Grant No. JP16H03826 (T. T.)) and for JSPS Research Fellowship (Grant No. JP18J15062 (K. M.)). This research was also supported by the ‘Development of magnetic material technology for high-efficiency motors’ program commissioned by the New Energy and Industrial Technology Development Organization (NEDO) and the Elements Strategy Initiative Center for Magnetic Materials (ESICMM) project from MEXT.

References

1. N. Jones, Nature, 2011, 472, 22–23.
2. J. P. Liu, E. Fullerton, O. Gutfleisch and D. J. Sellmyer, Nanoscale Magnetic Materials and Applications, ed. J. P. Liu, Springer, Berlin, 2009, pp. 309–335.
3. E. F. Kneller and R. Hawig, IEEE Trans. Magn., 1991, 27, 3588–3600.
4. N. Sakuma, T. Ohshima, T. Shoji, Y. Suzuki, R. Sato, A. Wachi, A. Kato, Y. Kawai, A. Manabe and T. Teranishi, ACS Nano, 2011, 5, 2806–2813.
5. T. Teranishi, A. Wachi, M. Kanehara, T. Shoji, N. Sakuma and M. Nakaya, J. Am. Chem. Soc., 2008, 130, 4210–4211.
6. H. Zeng, J. Li, J. P. Liu, Z. L. Wang and S. Sun, Nature, 2002, 28, 395–398.
7. F. Liu, J. Zhu, W. Yang, Y. Dong, Y. Hou, C. Zhang, H. Yin and S. Sun, Angew. Chem., Int. Ed., 2014, 53, 2176–2180.
8. Y. Tamada, S. Yamamoto, M. Takano, S. Nasu and T. Ono, Appl. Phys. Lett., 2007, 90, 162509.
9. T. Burkert, L. Nordström, O. Eriksson and O. Heinonen, Phys. Rev. Lett., 2004, 93, 027203.
10. Q. Song and Z. J. Zhang, J. Am. Chem. Soc., 2004, 126, 6164–6168.
11. A. Ramazani, M. A. Kashi and A. H. Montazer, J. Appl. Phys., 2014, 115, 113902.
12. V. Nandwana, G. S. Chaubey, K. Yano, C.-B. Rong and J. P. Liu, J. Appl. Phys., 2009, 105, 014303.
13. T. B. Massalski, H. Okamoto, P. R. Subramanian and L. Kacprzak, Binary Alloy Phase Diagrams, ed. T. B. Massalski, ASM intl., Almere, 2nd edn, 1990, vol. 2, pp. 1749–1751.
14. I. D. Mayergoyz, J. Appl. Phys., 1985, 57, 3803.
15. C.-I. Dobrotă and A. Stancu, J. Appl. Phys., 2013, 113, 043928.
16. T. T. Trinh, R. Sato, M. Sakamoto, Y. Fujiyoshi, M. Haruta, H. Kurata and T. Teranishi, Nanoscale, 2015, 7, 12435–12444.
17. R. Sato, M. Kanehara and T. Teranishi, Small, 2011, 7, 469–473.
18. H. Kura, M. Takahashi and T. Ogawa, J. Phys. Chem. C, 2010, 114, 5835–5838.
19. Z. He, J.-L. Maurice, A. Gohier, C. S. Lee, D. Pribat and C. S. Cojocaru, Chem. Mater., 2011, 23, 5379–5387.
20. K. Sato, Nat. Mater., 2009, 8, 924–925.
21. T. J. Klemmer, N. Shukla, C. Liu, X. W. Wu, E. B. Svedberg, O. Mryasov, R. W. Chantrell, D. Weller, M. Tanase and D. E. Laughlin, Appl. Phys. Lett., 2002, 81, 2220–2222.
22. S. Okamoto, N. Kikuchi, O. Kitakami, T. Miyazaki, Y. Shimada and K. Fukamichi, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 024413.
23. H. Gengnagel and U. Hofmann, Phys. Status Solidi, 1968, 29, 91–97.
24. M. W. Grinstaff, M. B. Salamon and K. S. Suslick, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 269–274.
25. Y. Yu, K. Sun, Y. Tian, X.-Z. Li, M. J. Kramer, D. J. Sellmyer, J. E. Shield and S. Sun, Nano Lett., 2013, 13, 4975–4979.
26. A. Kirkeminde and S. Ren, Nano Lett., 2014, 14, 4493–4498.
27. F. Liu, Y. Dong, W. Yang, J. Yu, Z. Xu and Y. Hou, Chem.–Eur. J., 2014, 20, 15197–15202.
28. S. H. Liu, C. C. Chen, S. N. Hsiao, S. K. Chen, Y. C. Chang, S. H. Su and K. F. Chiu, Appl. Phys. A, 2015, 119, 623–627.
29. X. C. Kou, H. Kronműller, D. Givord and M. F. Rossignol, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 3849–3860.
30. J. Bauer, M. Seeger, A. Zern and H. Kronműller, J. Appl. Phys., 1996, 80, 1667–1673.
31. G. Hadjipanayis, D. J. Sellmyer and B. Brandt, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 3349–3354.
32. R. J. Parker, Advances in Permanent Magnetism, Wiley, New York, 1990.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details on the synthesis and the material and magnetic characterization of NCMs with different size and compositions. See DOI: 10.1039/c9na00225a

---