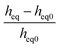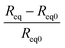Non-ohmic behavior and resistive switching of Au cluster-assembled films beyond the percolation threshold

Abstract

Networks based on nanoscale resistive switching junctions are considered promising for the fabrication of neuromorphic computing architectures. To date random networks of nanowires, nanoparticles, and metal clusters embedded in a polymeric matrix or passivated by shell of ligands or oxide layers have been used to produce resistive switching systems. The strategies applied to tailor resistive switching behavior are currently based on the careful control of the volume fraction of the nanoscale conducting phase that must be fixed close to the electrical percolation threshold. Here, by blending laboratory and computer experiments, we demonstrate that metallic nanostructured Au films fabricated by bare gold nanoparticles produced in the gas phase and with thickness well beyond the electrical percolation threshold, show a non-ohmic electrical behavior and complex and reproducible resistive switching. We observe that the nanogranular structure of the Au films does not evolve with thickness: this introduces a huge number of defects and junctions affecting the electrical transport and causing a dynamic evolution of the nanoscale electrical contacts under the current flow. To uncover the origin of the resistive switching behavior in Au cluster-assembled films, we developed a simple computational model for determining the evolution of a model granular film under bias conditions. The model exploits the information provided by experimental investigation about the nanoscale granular morphology of real films. Our results show that metallic nanogranular materials have functional properties radically different from their bulk counterparts, in particular nanostructured Au films can be fabricated by assembling bare gold clusters which retain their individuality to produce an all-metal resistive switching system.

---

Introduction

The looming end of Moore's scaling laws is stimulating the development of systems and architectures able to overcome the roadblock of CMOS-based digital computing.¹ The speed, spatial scale, circuit size, and energy dissipation required to maintain the ever increasing data flux between the memory and the processor is not any longer sustainable at extreme miniaturization:² a substantial paradigm shift in the design of computing hardware is mostly needed. An approach aiming at reproducing in hardware the human brain architectural and dynamical properties has been proposed as an alternative overcoming these limitations.³

Networks based on nanoscale resistive switching (RS) junctions are currently investigated for the fabrication of neuromorphic computing architectures, where the processing of cognitive and distributed data intensive tasks is performed similarly to synapses networks.^4–6 RS refers to physical phenomena where the resistance of a dielectric material changes reversibly in response to the application of a strong external electric field. RS has been reported in several systems including oxides, nitrides, chalcogenides, semiconductors, and organic materials.^6,7

For instance, random networks of nanowires, nanoparticles, and clusters, embedded in a polymeric matrix or passivated by shell of ligands or oxide layers (insulator-conductor nanocomposites), show RS phenomena resulting in features typical of neuromorphic systems.^6,8 This has been attributed to either polymer breakdown between junctions or conducting filament formation between individual metallic nanoobjects.^9–11 The evolution of the electrical properties of such nanocomposites, upon the application of an electric field, strongly depends on the volume fraction of the conductive phase and it can be described by the percolation theory.^12,13

Alternatively, networks of metallic nanoparticles produced in the gas phase and subsequently deposited on a substrate also exhibit RS,¹⁴ provided that the thickness of the resulting film is close to the percolation threshold. Switching events are argued to depend on the electric-field-induced formation/breaking of atomic wires in tunnel gaps between neighboring clusters.¹⁵ Recently, we reported that resistive switching networks can be fabricated by supersonic cluster beam deposition (SCBD) of Au clusters near the percolation threshold.¹⁶ In particular, we have studied the role of substrates in determining the characteristics of the observed switching behavior.¹⁷

Tailoring the conductivity of networks of nanoobjects showing RS is typically achieved by engineering the junctions between the different components and/or by the careful control of the volume fraction of the conducting phase that must be fixed close to the electrical percolation threshold.^11,15,18

Here, by blending laboratory and computer experiments, we report that nanostructured gold films fabricated by assembling bare gold nanoparticles and with thickness well beyond the percolation threshold, are in fact conductive, however show non-linear I–V curves together with reversible and reproducible resistive switching. Cluster-assembled gold films are of particular interest for the study of nanostructured metallic layers since they are not affected by oxidation of the nanoparticles during and after the deposition process. We characterize the evolution of the structure of the films with increasing thickness and provide robust evidence that the granularity, despite the evolving transport properties of the film, does not evolve since the nanoscale building blocks maintain their individuality.

To uncover the origin of the resistive switching behavior in Au cluster-assembled films, we developed a simple computational model for determining the evolution of the conduction properties of a model granular film under bias condition. The model exploits the information provided by experimental investigation about the nanoscale granular morphology of real films. As a result, the main electrical quantities (i.e. current and resistance) are calculated and monitored during the film evolution. Comparison with experimental data is eventually drawn.

Results and discussion

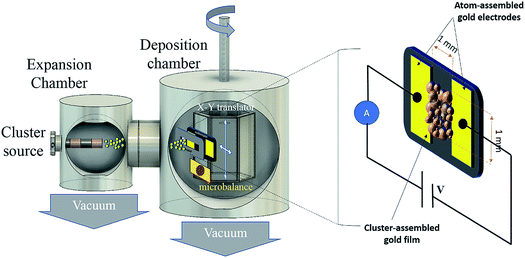
To test the electrical behavior of cluster-assembled Au films with different thicknesses, we fabricated two-terminal devices consisting in a pair of rectangular (2 × 7 mm) gold electrodes separated by a gap of 1 mm and deposited on an oxidized silicon substrate by standard thermal evaporation of gold in vacuum. (Scheme 1). Cluster-assembled films bridging the gap between the two gold electrodes have been deposited at room temperature by Supersonic Cluster Beam Deposition (SCBD) (see Methods).¹⁹ The experimental apparatus of the SCBD is schematically depicted in Scheme 1, the sample holder is equipped with electrical contacts for the in situ characterization of the evolution of the electrical properties of the film during the deposition process. Cluster-assembled films are also deposited on silicon substrates without electrodes or with a single electrode covering half of the substrate in order to perform structural and electrical characterization of the films by atomic force microscopy (AFM) (see Methods).

Scheme 1 Schematic representation (not to scale) of the apparatus for the deposition of cluster-assembled Au films. It consists of a pulsed microplasma cluster source mounted on the axis of differentially pumped vacuum chambers, the PMCS produces a supersonic expansion of an inert gas seeded with metallic clusters to form a cluster beam. The beam is intercepted by a substrate placed on a mobile holder (manipulator) in the deposition chamber. Substrates with gold electrodes previously deposited by thermal evaporation are mounted on the sample holder. A quartz microbalance attached to the manipulator is periodically exposed to the cluster beam to monitor the amount of deposited material. In situ electrical characterization during the cluster-assembled film growth is performed.

Au clusters, with a bimodal log-normal mass distribution peaked at 0.5 nm and 6 nm, were deposited using an apparatus equipped with a Pulsed Microplasma Cluster Source (PMCS) as described in detail in ref. 20 (see also Methods).

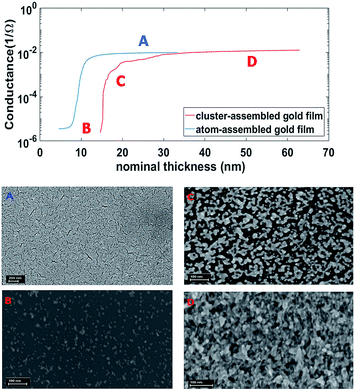
Fig. 1a shows the evolution of the electrical properties of a typical cluster-assembled film (red curve) compared to that of an atom-assembled one (blue curve) measured in situ during deposition. For different growth stages of the cluster-assembled film we associate a scanning electron microscopy (SEM) image (Fig. 1B, C and D) with its electrical behavior. For the atom-assembled film we report a SEM micrograph of a continuous layer (Fig. 1A).

Fig. 1 Top: percolation curves of an atomic-assembled gold film (blue) and of a cluster-assembled film (red), with the conductance (the inverse of the measured film resistance) on the y-axis in logarithmic scale and the film thickness on the x-axis; bottom: SEM images of the film morphology are associated to different film thicknesses and electrical behaviour. (A) continuous atom-assembled film (scale bar 200 nm). (B–D): Images of the principal steps of growth of a cluster-assembled metallic films are reported: (B) insulating stage; (C) close to percolation; (D) conducting regime: a fully connected thick-film (scale bar 100 nm).

We followed the evolution of the electrical properties of the different nanostructured film morphologies monitoring the evolution of the resistance as a function of thickness during the film growth. To describe the observed behavior we used the percolation theory based on the variation of the connectivity of elements, in our case clusters or nanoaggregates, in a random system.¹² In this framework, three principal growth stages of a random assembling of nanoparticles are easily identified from the conductance-thickness curve (percolation curve).^21,22 The evolution of the conductivity of cluster-assembled films with thickness (Fig. 1, red curve) shows that for a film characterized by isolated aggregates, an insulating behavior is observed.¹³ By increasing the thickness, the first percolation paths are formed (geometrical percolation stage) the conductivity abruptly increases, while the film is still in sub-monolayer regime. The critical thickness for the electrical percolation threshold, corresponding to the film morphology in Fig. 1C, can be determined by the occurrence of the maximum slope of the conductivity vs. thickness curve.²³ After the percolation transition, the cluster-assembled film is fully connected (Fig. 1D) and an ohmic behavior typical of a metallic regime is expected, as observed in atom-assembled metallic films.²⁴ We point out that in order to determine the thickness at which the transition to a ohmic behavior takes place, we consider the minimum of the product between the resistance and the squared thickness as function of the thickness.^25,26

For the sake of comparison, the evolution of the electrical properties of an atom-assembled film (blue curve) is also reported in Fig. 1, showing the percolation threshold always below 10 nm, whereas for cluster-assembled films such a threshold is found at thickness ∼10–15 nm.

The different surface mobilities of atoms and clusters are the origin of the different threshold thickness in the two systems.²⁷ For the atom-assembled film the transition to an ohmic behavior occurs at a thickness around 12 nm, while the cluster-assembled film shows the same transition in a range between 18 nm and 25 nm. We note also a faster increase of conductance in the case of the atom-assembled films; this also can be explained by the morphologic properties determined employing different building blocks for the two types of film fabrication.²⁸

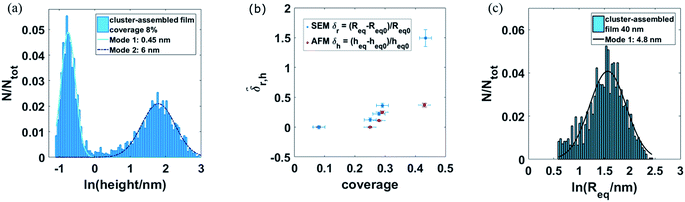
Multilayer cluster-assembled films are highly porous and characterized by a granular structure strongly reminiscent of the dimension distribution of the primeval building blocks. In order to observe the grain size distribution and the growth dynamics characterizing their structure, we performed a morphological analysis with atomic force microscopy (AFM) of the sub-monolayer cluster-assembled films. Fig. 2a reports the height distribution of deposited clusters (diameter in z direction, i.e. normal to the substrates) for a sub-monolayer film (coverage ∼8%). We observe very small aggregates with a broad distribution with height peaked at 0.4 ± 0.1 nm, while the median value of the population of the largest clusters is around 6 ± 2.5 nm. The equivalent radius distribution is bimodal, with the main two peaks around 0.7 and 4.4 nm.

Fig. 2 From left to right: (a) histogram in logarithmic scale of the height of the clusters measured by AFM on the smallest coverage sample. (b) relative island heights (measured by AFM) and the relative radius (measured from SEM micrographs, see Materials and methods) as a function of the coverage (the subscript ‘0’ refer to the smallest coverage sample). (c) histogram of the equivalent radius of the grains obtained segmenting a SEM micrograph of the thick film, in logarithmic scale.

By increasing the surface coverage from 0.08 to 0.45 (Fig. 1B and C), the mean value of the whole clusters heights increases of only 50%, on the other hand the equivalent radius increases of 160%. This suggests a preferential growth in x–y directions instead of z one in the first growth stages caused by the highest mobility of the small clusters.²⁷ By continuing the deposition we produce a fully connected film (Fig. 1D) with a thickness of 57 nm and characterized by a grain distribution substantially similar to that of the sub-monolayer films (quantitative granulometric characterization of SEM images is reported in Fig. 2c).^29,30

We underline the fact that the grain distribution nearly perfectly overlaps to that of the sub-monolayer film, thus suggesting that no significant grain growth is present even for very high thickness and that the nanoscale building blocks retain their individuality as reported in previous investigations.^31–33 This is at odd to what observed for the growth of gold films assembled by atoms: in this case the grain size increases linearly as films become thicker.^34–36

In Fig. 3 we report a comparison between two gold films assembled by atoms (Fig. 3a) and by clusters (Fig. 3b) respectively. The resistance values of an atom-assembled film (2 mm × 7 mm, 100 nm thickness) results in a resistivity ρ_atomic ∼ 10⁻⁸ Ωm, the same order of magnitude than the bulk gold ρ_bulk = 2.44 × 10⁻⁸ Ωm, while a cluster-assembled film 65 nm thick shows a resistivity ρ_cluster ∼ 10⁻⁷ − 10⁻⁶ Ωm, well above the bulk values.

Fig. 3 (a) electrical resistance and current of an atom-assembled Au film 100 nm thick as a function of time under the application of 0.5 V. (b) electrical resistance and current of a cluster-assembled Au film 65 nm thick as a function of time under the application of 12 V in the proximity of the forming step; the current is approximately equal to that circulating in the atom-assembled film (c) I–V curve of a cluster-assembled film after the activation of the switching activity in semilog-y scale.

Fig. 3b reports the temporal evolution of a cluster-assembled film with an initial resistance of about 33 Ω under a bias of 12 V: after few seconds we observe a switching towards substantially lower values of the circulating current and a corresponding steep increase of the resistance, followed by a sequence of switching events. The coexistence of two reversible switching regimes characterized by very different resistance ranges has already been reported in cluster-assembled gold films.¹⁷ The behavior reported in Fig. 3b is similar to what observed in silicon oxide-based devices used to emulate the generation of action potentials in neuronal assemblies³⁷

The cluster-assembled film is characterized by a higher initial resistance compared to the atom-assembled; for this reason we observe a larger voltage drop in the former for the same current circulating in both systems. Due to its extremely low resistance, the atom-assembled film has been tested at voltages lower than or equal to 0.5 V to keep the delivered power at a reasonable level. Nevertheless the atom-assembled film does not show any anomalous change in its electrical resistance under to flow of the same current travelling in the cluster-assembled film (see Scheme 1). Current has been limited in order to avoid macroscopic joule heating effects both in the atom-assembled electrodes and in the cluster-assembled film.

The difference in the resistivity values between atom-assembled and cluster-assembled films is due to the presence of an extremely large number of defects and grain boundaries typical of the low-energy cluster beam deposition regime^38–41 resulting in highly porous films.^42,43

The nanogranular and porous structure of the Au cluster-assembled films affects their electrical behavior, for thickness far beyond the percolation threshold, in a dramatic and unexpected way: we observe either a remarkable departure from an ohmic behavior and the onset of a resistive switching feature. The I–V curve of the cluster-assembled film is reported in Fig. 3c showing a non-linear behavior and the presence of hysteresis.

We characterized several cluster-assembled films with thicknesses beyond the percolation threshold and different initial resistances: all the films showed stable resistive switching behavior, with well-defined resistance levels that are recurrently explored under the application of a constant voltage bias, and whose order of magnitude depends by the applied voltage (see Fig. 3c and 4). This behavior is at the origin of the non-ohmic I–V curves. In all cases we observed a non-linear behavior after a given threshold voltage which reproducibly depends on several factors, namely: the initial resistance, the thickness, and the history of the sample (the applied voltage values before applying the electroforming one). Usually, the threshold voltage corresponds to a power of 3–4 W. Since the electrodes have a negligible resistance compared to the cluster-assembled film, the total areal power is about 4 × 103 W m⁻². After the first switching event, we observe a switching activity for a wide voltage range, above and below the critical value.

Fig. 4 (a) electrical resistance of a cluster-assembled film with thickness 30 nm under the bias of 20 V; several switch events in the interval time of 20 s are evident. (b) Histogram of the resistance values assumed by the sample under the application of 20 V in a time window of 200 s. (c) Electrical resistance of the same sample under the bias of 0.5 V. (d) Histogram of the resistance values assumed by the sample under the application of 0.5 V in a time window of 200 s.

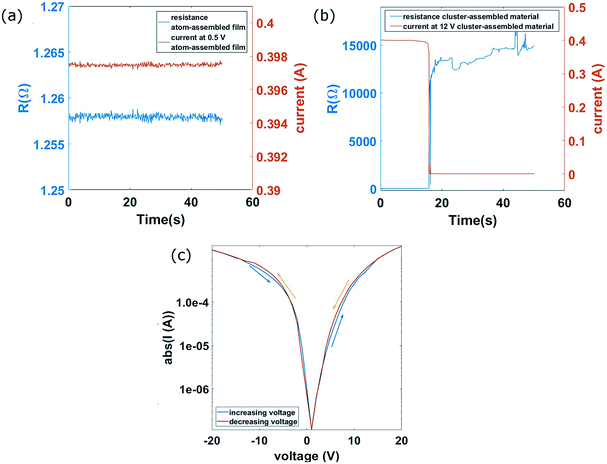
We report in Fig. 4a on the evolution of the resistance for a cluster-assembled film with a thickness of 30 nm under the application of 20 V bias after the activation: typical switching features are present, consisting in reversible switches in different resistance ranges. This is quantitatively represented in Fig. 4b reporting the histogram of the resistance values under a bias of 20 V in a time window of 200 s. The histogram shows different Gaussian type peaks around each resistance values reached after the switch events occur. It is to be noted that each level can be explored several times. In Fig. 4c and d we show the evolution of resistance with the histograms for the same sample under a lower voltage bias (0.5 V). The switching activity is always present although with a lower number of explored levels. A weakening of the switching activity can be observed, with a minor number of well distinct explored resistance values. This demonstrates the possibility to tune the switching activity of the device controlling the applied voltage in a reproducible manner.

The observed switching activity has a low amplitude with a dynamics and temporal behaviour that shows periods of activity separated by periods of inactivity.³⁷ This suggests that cluster-assembled gold films can electrically emulate the generation of action potentials typical of neural systems.³⁷

The observed behavior is radically different if compared to what observed in the atom-assembled films (Fig. 3a): here an ohmic regime is always found under similar current conditions consistently with all the literature reporting the electrical behavior of atom-assembled metallic films beyond the percolation threshold.³⁴

To date the characterization of the electrical behavior of cluster-assembled metallic films is limited to systems below or close to the percolation transition;^44–46 to the best of our knowledge no reports about the electrical properties of cluster-assembled gold films beyond the percolation threshold are available. This is mainly due to the fact that electrical characterization has been used to monitor the evolution of the cluster-assembled systems towards percolation (assuming that structural percolation and electrical percolation coincide)⁴⁵ and by the assumption that, after reaching percolation, the systems is characterized by a ohmic behavior, although with a very high number of defects, as described, for example, in the Sondheimer³⁸ or Mayadas–Shatzkes model.³⁹

To investigate in greater detail the link between the film nanogranular structure and the electrical transport properties, we performed measurements by AFM in PeakForce Tapping conductive mode, using the current-sensing scheme described in ref. 47. By applying a continuous voltage between an all-platinum conductive tip (Rocky Mountain Nanotechnology, tip radius <8 nm, k = 18 N m⁻¹ and resonance frequency 20 kHz) and another electrode connected to the sample it was possible to measure the continuous current which flows between them. This approach allows for recording both a topographic and an electrical current map, with the identical high spatial resolution.

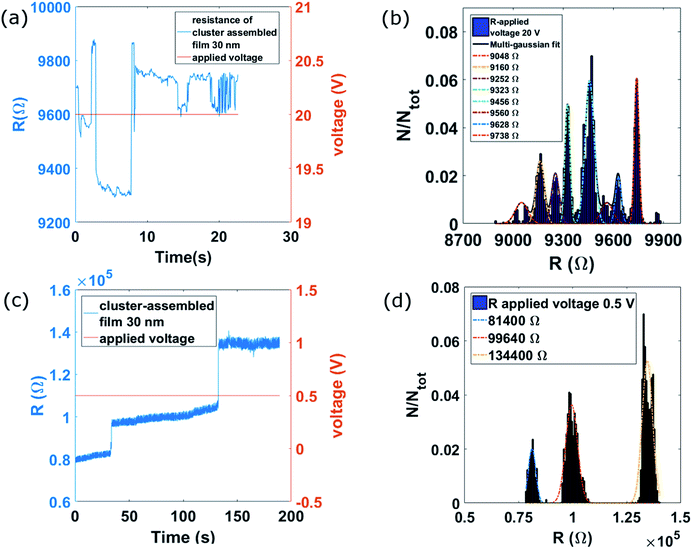
In the left column of Fig. 5 we report the morphology of an atom-assembled Au thin film (a), and of a cluster-assembled Au film with a thickness beyond the percolation transition (b). Each topographical image has a high imaging quality; the cleaning condition of the AFM tip is good and the acquired topographies reproduce accurately the morphologies of the different Au samples.

Fig. 5 Topographical AFM images of different Au films (left column) with the matching current map superimposed to the topographical one (right column), where the red regions are the conductive one. (a) Atom-assembled Au film. (b) Cluster-assembled Au film 37 nm thick.

In the right column of Fig. 5, we report the topographical maps with a modified color code: conductive regions (identified by applying to the current maps the threshold method described in the Materials and methods section) are uniformly colored in red, in order to directly associate the nanotopography to the electrical conductivity.

By inspecting the maps reporting in red the conductive regions of the atom-assembled films (Fig. 5a right), we observe that the red areas are disconnected: this is due to the fact that the dimension of the AFM tip radius (approximately 8 nm) does not allow to follow the entire profile of the rough film. The cluster-assembled film with a thickness of 37 nm beyond the percolation threshold (Fig. 5b right) shows also another non-uniform electrical behaviour, since the large uppermost nanoparticles appear no conductive, irrespective of those forming the film core. This evidence suggests that the clusters sitting on the film surface are in bad electrical contact with their neighbours, even if they are morphologically connected with them and well in contact with the AFM tip. We can conclude that the cluster-assembled film is not electrically homogeneous, also with a thickness beyond the percolation threshold.

Based on the above picture, we understand that the granular structure of cluster-assembled Au films largely determines the non-ohmic electrical properties of the system. Although the elemental building blocks can be considered metallic, their assembly does not result in an overall ohmic conductor.⁴⁸ Clusters are in fact physically connected (i.e. they form a porous but connected system, whose structure is beyond the percolation threshold), nevertheless the conduction features of the inter-cluster contacts is affected by the presence of defects and by the mismatch in the crystalline orientation of the touching faces.⁴⁹ These factors represent a barrier for the electric charge flow determining a distribution of different “resistances” among the film.⁵⁰ This distribution can dynamically change under the flow of the current due to the formation of local “hot spots” that induce atomic rearrangement, formation/destruction of contact depending of the power dissipated locally.⁸

We argue that a possible mechanism responsible for the resistive switching behaviour is represented by the modification/breaking of the physical contacts among nanoparticles and by the dynamical rearrangement of defects. More specifically, we guess that high electric fields could trigger the local rearrangement of matter so as to create new connection paths.⁵¹ On the contrary, a suitable power dissipation due to current flow along a percolative path could determine the breaking of a connection (a sort of local melting). The overall resistive switching naturally follows from the interplay of such counteracting mechanisms.

To test the validity of the above arguments, we developed a simple computer experiment aimed at modelling the microstructure evolution of a model granular film under bias condition. This model aims at a coarse-grained picture, with little insight on the actual details at the atomic scale. In this respect, the basic mechanisms driving the structural modifications of the system are introduced through a probabilistic description.

The approach we followed consists of a multi-step procedure. At first, the morphological features of real samples are extracted from experimental SEM images (see Methods section) and used to generate a corresponding computer model of granular films. Then, a resistive network is setup and all of the electrical quantities of the system are accordingly calculated. Finally, a probabilistic algorithm ruling over the evolution under suitable bias condition is elaborated and eventually applied to determine the related evolution of the system morphology and electrical characteristics. All steps are properly included in an iterative self-consistent scheme. Details are provided in the Methods section.

We assumed that a resistive model based on direct inter-grain conduction can describe the transport mechanisms.⁵² We did not consider quantum tunnelling between neighbouring grains, and activated conduction since we are addressing electrical transport beyond the percolation threshold, where electron transport is known to mainly occur by ordinary conduction between metallic islands in physical contact.⁵³

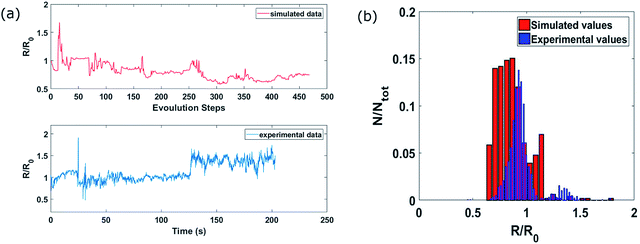
In order to effectively build an electrical model, a regular grid is superimposed to binary images obtained by SEM micrographs, thus establishing a one-to-one correspondence between the nodes of the grid and the pixels of the digital image. Next, a resistance is associated to each bond (connecting two neighbouring nodes) according to the following rules: (i) if the bond connects two pixels occupied by “Au matter”, then a finite resistance R is associated to the bond; (ii) if any of the neighbouring nodes connected by the bond lies in a “void” pixel, then an infinite value of resistance is used. The electrical network obtained by this approach is analysed by solving the Kirchoff circuit equations.⁵⁴ More specifically, calculations are performed using a matrix formulation reading in the form 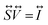, where 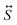is the conductance matrix as obtained from the actual resistive network implemented as above, while 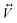and 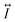are the nodal potential and the bond current matrix, respectively. The solution of such a linear system straightforwardly provides the current and potential maps over the simulated sample. In addition, the Joule dissipated power in each resistor and the electric field in the “void” pixels are as well calculated.

As a validation of our model, we preliminary performed a systematic analysis of the static electrical properties (i.e. no evolution occurring) of a large set of model systems with different coverage, here defined as the ratio between the number of pixels representing matter and void, respectively (see ESI†). The various model systems have been elaborated from a real sample by adopting different binarization processes of the original SEM micrographs. This procedure is beneficial in tuning the resulting connectivity of the model 2D granular system.

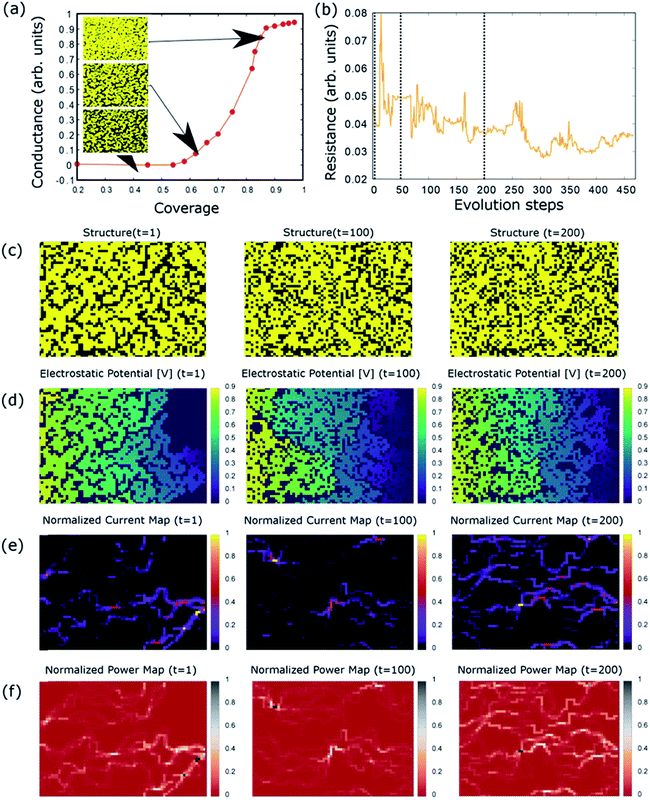
Fig. 6a shows the behaviour of the overall conductance as a function of the coverage. The results provide robust evidence of the percolative behaviour: very low conduction is found in low-coverage systems, while beyond the percolation threshold, occurring at a coverage 0.54, the conductance of the system rapidly increases. As expected, the maximum value is found only at maximum coverage: this situation indeed corresponds to the case of homogeneous (i.e. non-granular) metal conductor.

Fig. 6 (a) Percolation curve of conductance as a function of the coverage value. In the inset, images of some structural configurations are depicted. (b) Resistance as a function of simulation steps in a system of 50 × 70 pixels; the resistance values at the time steps corresponding to the shown configurations are highlighted. (c–f) The structure (c) and the maps of electrostatic potential (d), current (e) and dissipated power (f) in a system of 50 × 70 pixels, (coverage = 0.64). Values at three unlike microstructure arrangements are shown. Modifications in the structural parameters determine the continuous creation and destruction of percolative paths.

A deeper understanding of conduction processes can be achieved by investigating the electrostatic potential, current and dissipated power through the space maps (see ESI†). It is here evident how in very dilute systems conduction is suppressed due to absence of percolative paths within the sample. By increasing coverage, paths start to form and conductance rapidly increases. Finally, for very large values of coverage, the transport is mostly diffusive and current tends to flow uniformly along the sample.

Starting from the real sample of Fig. 1, we simulated the evolution of the system as described above. The resulting resistance is shown in Fig. 6b during the system evolution scanned by the synthetic events of modification/breaking of inter-cluster contacts described above. The system presents a value of coverage of 0.62, well beyond the percolation threshold for our systems. A resistive switching behaviour is indeed observed with the resistance assuming different values during the evolution of the contact network in the system, characterized by single variations opposite in sign. The dimension of the binary image used for the above analysis was 70 × 50 pixels: dense enough to capture the main morphological features, while resulting in an affordable computational cost.

We can now have a look at the maps of the electrostatic potential, current and dissipated power. In Fig. 6d–f these quantities are shown for three different sequential arrangements (corresponding to the three columns) collected during the system evolution under bias. An evolving network of current paths is observed, inducing rapid oscillations in the instantaneous values of the net through current and total resistance. It is important to remark that such evolving behaviour does not qualitatively change upon a modification of the coverage (beyond the percolation threshold) and construction and destruction probabilities (pC and pD). This makes us confident that the present computer model is trustworthy and the corresponding physical picture reliable and robust.

This model is too schematic to aim to quantitatively reproduce the electrical features of the cluster-assembled film, however it provides indications about the possible mechanisms of the observed behaviour. First, we highlight that the overall evolution of the resistance is reproduced as shown in Fig. 7a, where simulated and experimental normalized data are compared. Both the experiment and the model show discrete and reversible change in the resistance under a constant voltage bias and switching events. Both the sample and the model explore different resistance levels that are quite comparable in amplitude relatively to the initial resistance value and in frequency, as shown by the histogram in Fig. 7b, where two different peaks are clearly observed with a broadening determined by the switching events. This demonstrates that local random events of breaking/reconnection in the resistance network can determine a global behaviour of the systems like that observed for the cluster-assembled film.

Fig. 7 (a) Top: the resistance as function of simulation steps (the same data as in Fig. 6b) normalized to the initial resistance of a system 50 × 70 pixels; bottom: resistance evolution normalized to the initial resistance of the cluster-assembled film under a bias of 5 V as function of time. (b) The histogram of the resistance values both for the cluster-assembled film and the simulation.

We highlight also some differences: cluster-assembled films explore a larger number of resistance level (Fig. 4) compared to simulations and experimental resistance patterns are characterized by the presence of a larger number of switches. This reflects in the histogram that usually shows more distinct peaks with different broadening (see Fig. 3b and 7b). The higher complexity in the morphology of the cluster-assembled films causes different events of local breaking and reconstruction with different degree of influence on the global electrical resistance. The computational cost to simulate complex networks with a higher number of resistors and for a larger time interval, under different voltage bias is prohibitive. Anyway, this model gives a reasonable insight for the understanding of the resistive switching behaviour and how the nanostructure in a complex metallic film can give rise to the observed electrical properties.

Conclusions

We demonstrated that nanostructured Au films fabricated by bare gold nanoparticles produced in the gas phase and with thickness well beyond the electrical percolation threshold, show a non-ohmic behavior and reproducible complex resistive switching. This is ascribed to the nanogranular structure of the films that does not evolve with thickness causing the presence of a huge number of defects and junctions. The highly defective structure affects the electrical transport and dynamically rearranges under the current flow. A simple computational model based on a variable resistor network qualitatively reproduce the observed resistive switching behavior.

Our results show that metallic nanoscale materials have functional properties radically different from their bulk counterparts, in particular nanostructured Au films can be fabricated by assembling bare gold nanoparticles which retain their individuality to produce an all-metal resistive switching system. The presence of recurrent features in the switching behavior such as a threshold voltage for the appearance of the switching activity, recurrently and discrete explored resistance values and their dependence from the structural features of the cluster-assembled film (average thickness, resistance value reached on the percolation curve), offers the possibility to exploit such class of systems for the fabrication of complex networks suitable for reservoir computing,^5,18 using a straightforward bottom-up approach. Our results on nanostructured gold films opens new and important perspectives for the investigation of the fundamental mechanisms of electrical conduction in nanoscale metallic materials.

Methods

Substrate preparation and cluster-assembled film deposition

Silicon substrates are cleaned using an ultrasonic bath and subsequently heated at 1200 K in air for 4 hours in order to obtain the formation of an oxide insulating layer without significantly affect the original substrate rugosity (Rq = 0.34 nm).

A supersonic beam seeded with neutral gold clusters, with a bimodal log-normal mass distribution peaked at 0.5 nm and 6 nm, is intercepted by the silicon substrates mounted in the deposition chamber on a remotely controlled sample-holder (Scheme 1).²⁰ A quartz microbalance is periodically exposed to the cluster beam in order to carefully monitor the film thickness evolution. The sample holder is equipped with electrical contacts for the in situ characterization of the evolution of the electrical properties of the film during the deposition process. The cluster-assembled film density is determined ex situ by AFM characterization in order to provide a correction factor to the microbalance measurement of the film thickness: the densities of the evaporated and of the cluster-assembled films have been determined as 17.29 gr per cm³ and 8.56 gr per cm³ respectively.

The experimental apparatus of the SCBD consists of three differential pumped vacuum chambers: the source chamber, the expansion and the deposition one. The first chamber is equipped with Pulsed Microplasma Cluster Source (PMCS).¹⁹ The PMCS is characterized by a ceramic body where, after the injection of an inert gas, the production of clusters in gaseous phase is realized through the ablation of a metal target by a discharge plasma. The carrier gas (Ar) is pulsed injected in the source chamber. Then the cluster-gas mixture is extracted in a supersonic flow thanks to the pressure difference between the source chamber and the expansion one, where the beam is focused through a system of aerodynamic lenses.⁵⁵

Electrical characterization

The electrical measurements in situ are performed through a multimeter (Agilent model 34410A) controlled by a homemade LabView routine that coordinate data acquisition. In detail, the software performs a resistance measure every pre-determined time interval (usually 300 ms) when the cluster beam is directed against the substrate and it acquires the equivalent thickness measured by the quartz microbalance for each rastering step.

The investigation of the electrical properties of the fabricated samples are realized collecting the electrical resistance values at different voltage values. The measurements are performed through a standard two-probes method, employing High Power Source Measurement Unit (HPMSU, Agilent E52790A). The instrument can apply a dc voltage and measure a dc current, so the resistance is subsequently calculated using the Ohm's law. The sample properties are explored applying voltage with values that span an interval of 1–30 V, applying one voltage values for several seconds (2000 s) and performing one current measurement every 100 ms. To explore the current–voltage trend of the sample, voltage ramps are also applied starting from a minimum value up to a peak voltage, both for positive and negative values.

Topographical characterization by atomic force microscopy

The surface morphology of nanostructured gold thin films was characterized in air using a Multimode AFM equipped with a Nanoscope IV controller (BRUKER). The AFM was operated in Tapping Mode, using rigid silicon cantilevers mounting single crystal silicon tip with nominal radius 5–10 nm and resonance frequency in the range 250–350 kHz. Several 2 μm × 1 μm images were acquired on each sample with scan rate of 1 Hz and 2048 × 512 points. The images were flattened by line-by-line subtraction of first and second order polynomials in order to remove artifacts due to sample tilt and scanner bow.

Only globular objects from AFM images have been selected for the analysis of the cluster heights, by applying filtering selection criteria described in ref. 29 and 30. The height distribution of the objects identified is typically log-normal, as it is typical for systems resulting from aggregation processes,⁵⁶ and they appear Gaussian in a semi-log scale.⁵⁷ The distributions have been normalized with respect to the total number of counted particles and the median value of each Gaussian is associated to the diameter (in z direction) of the gold clusters.

The gold samples with the lowest coverage have been analyzed in order to characterize the size distribution of the incident clusters using a complementary approach and analysis based on SEM and AFM.²⁹

Analysis of SEM images

Analysis of the morphological properties of the fabricated samples was performed through a Scanning Electron Microscope (Zeiss Supra 40). We collected several grayscale images acquired with a 7 kV electron beam at different magnifications (300–750 kX) with a resolution comprises between 0.5 and 1 nm per pixels.

The grayscale image processing consists of two principal steps: (1) the binarization of the image and (2) the analysis of the geometrical properties of the recognized objects.²⁹ The first step is carried out choosing a threshold in a normalized gray-scale with values between 0 and 1 to segment the image distinguishing between substrate (below the threshold) and the aggregates (above the threshold). This is the most critical step²⁹ because of the resolution of nm per pixels and the error that can be introduced due to a wrong segmentation of an object on the image background with the presence of artefacts.²⁹ It is a good practice to examine the trend of the pixel value histogram to understand if there is a preferred method to set the threshold to binarize an image.⁵⁸

A comparison between several thresholding methods is realized: a local adaptive method (see adaptthresh in MATLAB), the Otsu's method,⁵⁹ a global one (using first order statistic, computing the global mean value of the image pixels) and a manual thresholding with the AFM software;²⁹ in this way it was possible to estimate the errors in measured values due to the pixel resolution or the different weights that carry some image characteristics, like the contrast or the homogeneity of the luminosity, affecting the segmentation of the image. For our SEM images and electrical AFM maps the adaptive method presents the advantage to provide a standard and reproducible approach. It works using a first-order statistics; a matrix of the same image size is calculated and each matrix element represents a threshold value chosen as the local mean intensity of the neighborhood of the pixel (usually the size neighborhood is calculated as the 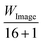, where W_Image is the image size).

On the binary image, the metallic aggregates (white regions) are discriminated from the substrate (black regions) and their geometrical properties are analyzed; a pre-analysis is performed taking the distribution of the number of pixels of the islands, in order to evaluate if applying a filter to smallest islands (since they carry a greater error in the measure of their dimensional features²⁹). A filter is usually chosen equal to 3 (all the aggregates with a number of pixels minor than or equal to three are ignored) if we observe a strong decrease (more than 50%) in the population of smallest islands (area between 1 and 100 pixels) in the presence of the filter. This choice is due to the fact that in an image with a resolution of about 1 or 0.5 nm per pixel the error on their measured dimension can be too high, and this is very important when there are few huge islands, because the weight of the smallest islands can affect the overall distribution population.

After the image processing is performed, we analyzed the geometrical properties of the metallic islands on the substrate plotting the equivalent radius distribution. The islands are identified by selecting the connected regions of the SEM images and the coverage is defined as the ratio between the number of the island pixels and the total one; the equivalent radius was computed as half of the diameter of the circle with the same area of the selected region, suitably rescaled in nm (see regionprops in MATLAB). For the images with coverages greater than 100%, the grains are recognized imposing some constraints on the surface radius.²⁹

Computer model

Given the initial structure of the granular film as obtained by SEM images and the corresponding calculated maps of electrical quantities, the new morphology is obtained by executing the following three-step procedure:

• Breaking inter-cluster connections: we identify all the sites where the local value of power dissipation is large enough to change the corresponding pixel from “matter” to “void” with a given probability p_d, thus mimicking the change that because of local melting the contact is lost. This affects the percolative paths followed by the charge flow, leading to a reduction of the net current passing through the film (in order to preserve the total amount of matter in the system, the closest “void” pixel is consequently “filled” with matter).

• Creating new inter-cluster connections: we identify the empty sites where the electric field is large enough to change the corresponding pixel from “void” to “matter” with a given probability p_c. In doing so, a general increase in the connections between clusters is yielded with a consequent increase of the overall current (in order to preserve the total amount of matter in the system, the closest “matter” pixel is consequently set to “void”).

• Introducing noise effects: in order to consider other possible source of modifications (e.g. mechanical stresses, or atom rearrangements at the interface of touching clusters) of the grain structure, a rearrangement is performed in the system on a local scale. Specifically, a small region in the system (with dimensions smaller than the grain size) is randomly selected and a local rearrangement of inter-grain contact features is performed.

Any step is followed by a local rearrangement, which is suitably applied to maintain the local compactness of the clusters. This reflects the fact that the morphological rearrangements taking place within our systems are not strong enough to cause the breaking of clusters into many smaller sub-units. Hence, among the possible rearrangements applied to the structure, only those which do not determine the production of too small matter aggregates are in fact allowed.

The overall microstructure evolution of a given sample is straightforwardly obtained by generating a sequence of synthetic inter-grain contact formation/breaking events, each followed by rearrangement. While the sequence is generated according to a probabilistic criterium, i.e. there is notion of “time evolution” in our model, the procedure is nevertheless truly effective in determining a new structure of the granular film at each sequence step so that monitoring of the resistive behaviour is addressed. Each advancement will be hereafter name “step”.

Finally, we remark that the threshold values for the dissipated power and electric field are established after analysing their values in different unevolved structures with the same coverage. Specifically, the maximum value of power and electric field obtained in this preliminary analysis are chosen as thresholds for the subsequent dynamical evolution. Such choice has proved satisfactory to generate structure evolutions where a statistically relevant number of rearrangements are performed.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Prof. A. Pullia for his assistance and insightful suggestions concerning the electrical characterization.

Notes and references

1. M. A. Zidan, J. P. Strachan and W. D. Lu, Nat. Electron., 2018, 1, 22–29.
2. R. A. Nawrocki, R. M. Voyles and S. E. Shaheen, IEEE Trans. Electron Devices, 2016, 63, 3819–3829.
3. A. V. Avizienis, H. O. Sillin, C. Martin-Olmos, H. Shieh, M. Aono and A. Z. Stieg, et al. , PLoS One, 2012, 7, 1–8.
4. T. Ohno, T. Hasegawa, T. Tsuruoka, K. Terabe, J. K. Gimzewski and M. Aono, Nat. Mater., 2011, 10, 591–595.
5. S. K. Bose, S. Shirai, J. B. Mallinson and S. A. Brown, Faraday Discuss, 2019, 213, 471.
6. J. S. Lee, S. Lee and T. W. Noh, Appl. Phys. Rev., 2015, 2, 031303.
7. Y. Yang and W. Lu, Nanoscale, 2013, 5, 10076–10092.
8. H. G. Manning, F. Niosi, C. G. Rocha, A. T. Bellew, C. O'Callaghan and S. Biswas, et al. , Nat. Commun., 2018, 9, 1–9.
9. Advances in Neuromorphic Memristor Science and Applications, ed. R. Kozma, R. Pino and G. E. Pazoneza, Springer Series in Cognitive and Neural Systems, Berlin, 2012.
10. P. Reissner, Y. Fedoryshyn, J. N. Tasserant and A. Stemmer, Phys. Chem. Chem. Phys., 2016, 18, 22783–22788.
11. P. N. Nirmalraj, A. T. Bellew, A. P. Bell, J. A. Fairfield, E. K. McCarthy and C. O'Kelly, et al. , Nano Lett., 2012, 12, 5966–5971.
12. D. Stauffer and A. Aharony, Introduction to percolation theory, Taylor & Francis, 1994.
13. G. Ambrosetti, I. Balberg and C. Grimaldi, Phys. Rev. B, 2010, 82, 134201.
14. A. Sattar, S. Fostner and S. A. Brown, Phys. Rev. Lett., 2013, 111, 136808.
15. S. Fostner and S. A. Brown, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052134.
16. C. Minnai, A. Bellacicca, S. A. Brown and P. Milani, Sci. Rep., 2017, 7, 7955.
17. C. Minnai, M. Mirigliano, S. A. Brown and P. Milani, Nano Futures, 2018, 2, 011002.
18. H. O. Sillin, R. Aguilera, H. H. Shieh, A. V. Avizienis, M. Aono and A. Z. Stieg, et al. , Nanotechnology, 2013, 24, 384004.
19. K. Wegner, P. Piseri, H. V. Tafreshi and P. Milani, J. Phys. D: Appl. Phys., 2006, 39, R439–R459.
20. C. Ghisleri, F. Borghi, L. Ravagnan, A. Podestà, C. Melis and L. Colombo, et al. , J. Phys. D: Appl. Phys., 2014, 47, 015301.
21. M. Sahimi, Heterogeneous Materials I: Linear Transport and Optical Properties, Springer, 2003.
22. S. Kirkpatrick, Rev. Mod. Phys., 1973, 45, 574–588.
23. T. Andersson, J. Phys. D: Appl. Phys., 1976, 9, 973–985.
24. R. F. Voss, R. B. Laibowitz and E. I. Allessandrini, Phys. Rev. Lett., 1982, 49, 1441–1444.
25. A. I. Maaroof and B. L. Evans, J. Appl. Phys., 1994, 76, 1047–1054.
26. F. A. Burgmann and S. H. Lim, et al. , Thin Solid Films, 2005, 474, 341–345.
27. P. Jensen, Rev. Mod. Phys., 1999, 71, 1695–1735.
28. P. Jensen and A. L. Barabasi, et al. , Phys. Rev. B, 1994, 50, 15316–15329.
29. F. Borghi, M. Mirigliano, P. Milani and A. Podestà, Quantitative Analysis of Gold Nano-aggregates by Combining Electron and Probe Microscopy Techniques, in Toward a Science Campus in Milan, Springer, 2018, pp. 67–80.
30. F. Borghi, A. Podestà, C. Piazzoni and P. Milani, Phys. Rev. Appl., 2018, 9, 044010.
31. L. Bardotti, B. Prével and P. Mélinon, et al. , Phys. Rev. B, 2000, 62, 2835–2842.
32. L. Bardotti, B. Prével and M. Treilleux, et al. , Appl. Surf. Sci., 2000, 164, 52–59.
33. F. Bisio, M. Palombo and M. Prato, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205428.
34. W. G. Ma, H. D. Wang, X. Zhang and W. Wang, J. Appl. Phys., 2010, 108, 064308.
35. D. I. Yakubovsky and A. V. Arsenin, et al. , Opt. Express, 2017, 25, 25574–25587.
36. P. B. Barna and M. Adamik, Thin Solid Films, 1998, 317, 27–33.
37. A. Mehonic and A. J. Kenyon, Front. Neurosci., 2010, 10, 1.
38. E. H. Sondheimer, Adv. Phys., 1952, 1, 1–42.
39. A. F. Mayadas and M. Shatzkes, Phys. Rev. B: Condens. Matter Mater. Phys., 1970, 1, 1382–1389.
40. G. Reiss, J. Vancea and H. Hoffmann, Phys. Rev. Lett., 1986, 56, 2100–2103.
41. J. Vancea, G. Reiss and H. Hoffmann, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 6435–6437.
42. G. B. Smith, A. I. Maaroof and M. B. Cortie, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 165418.
43. E. Barborini and G. Corbelli, et al. , New J. Phys., 2010, 12, 073001.
44. G. Fuchs and C. Montandon, et al. , J. Phys. D: Appl. Phys., 1993, 26, 1114–1119.
45. P. Jensen and P. Melinon, et al. , Phys. Rev. B, 1993, 47, 5008–5012.
46. S. Yamamuro and K. Sumiyama, et al. , J. Phys.: Condens. Matter, 1999, 11, 3247–3257.
47. V. Cassina and L. Gerosa, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115422.
48. S. B. Arnason, S. P. Herschfield and A. F. Hebard, Phys. Rev. Lett., 1998, 81, 3936–3939.
49. R. C. Munoz and C. Arenas, Appl. Phys. Rev., 2017, 4, 011102.
50. D. Valencia and E. Wilson, et al. , Phys. Rev. Appl., 2018, 9, 044005.
51. T. Sannicolo and D. Munoz-Rojas, et al. , Nano Lett., 2016, 16, 7046–7053.
52. Z. Wu and E. López, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 045101R.
53. B. Zeimetz, B. A. Glowacki and J. E. Evetts, Physica, 2002, 372, 767–770.
54. P. Clayton, Fundamentals of Electric Circuit Analysis, Wiley, New York, 2000.
55. P. Piseri, H. V. Tafreshi and P. Milani, Curr. Opin. Solid State Mater. Sci., 2004, 8, 195–202.
56. C. G. Granqvist and R. A. Buhrman, Appl. Phys. Lett., 1975, 27, 693–697.
57. E. Limpert, W. A. Stahel and M. Abbt, BioScience, 2001, 51, 341–352.
58. Digital Image Processing, ed. Gonzalez RC and Woods RE. Pearson, 2017.
59. A. N. Otsu, IEEE Trans. Syst. Man Cybern. B Cybern., 1979, SMC-9, 62–66.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00256a

---