Manipulating acoustic and plasmonic modes in gold nanostars

Abstract

In this contribution experimental evidence of plasmonic edge modes and acoustic breathing modes in gold nanostars (AuNSs) is reported. AuNSs are synthesized by a surfactant-free, one-step wet-chemistry method. Optical extinction measurements of AuNSs confirm the presence of localized surface plasmon resonances (LSPRs), while electron energy-loss spectroscopy (EELS) using a scanning transmission electron microscope (STEM) shows the spatial distribution of LSPRs and reveals the presence of acoustic breathing modes. Plasmonic hot-spots generated at the pinnacle of the sharp spikes, due to the optically active dipolar edge mode, allow significant intensity enhancement of local fields and hot-electron injection, and are thus useful for size detection of small protein molecules. The breathing modes observed away from the apices of the nanostars are identified as stimulated dark modes – they have an acoustic nature – and likely originate from the confinement of the surface plasmon by the geometrical boundaries of a nanostructure. The presence of both types of modes is verified by numerical simulations. Both these modes offer the possibility of designing nanoplasmonic antennas based on AuNSs, which can provide information on both mass and polarizability of biomolecules using a two-step molecular detection process.

---

1. Introduction

Label-free detection of protein molecules in their natural state at ultralow concentration is considered as the holy grail of biomedical research.¹ But, because of the acutely small size (<3 nm) of single protein molecules, their detection becomes exceptionally challenging.² One method to deal with this problem is to use the well-known localized surface plasmon effect of noble metal nanoparticles (NPs) which has been used for a wide variety of applications^3–7 including sensing,^8–10 imaging,¹¹ surface enhanced Raman spectroscopy (SERS),^12,13 quantum technologies and miniaturized photonic circuits.^14,15 Localized surface plasmon resonance (LSPR) of noble metal NPs can be tuned by changing their size, shape, material and the surrounding dielectric matrix.^16,17 NPs with sharp corners like nanotriangles,¹⁸ nanocubes,^19,20 nanorods,^21,22 nanostars,^23–26 or octahedral nanoparticles^27,28 are able to confine light in ultra-small regions tightly because of the lightning rod effect and the plasmonic resonance effect, resulting in higher electromagnetic energy concentration and thus higher electric field intensity at their hot-spots compared to the non-spiky NPs.^29–31 Thus spiky gold nanoparticles are ideal for plasmonic sensing because of their biocompatibility tunability and the large field enhancement at their hotspots. A small change in the surrounding dielectric media after the adsorption of protein molecules at the hot-spots results in a shift of the NP LSPR and thus helps to detect the presence of biomolecules. This opens new opportunities for design of next generation nano-devices for sensing applications.

Surface plasmons confined within the geometrical boundaries of flat nanoparticles give rise to radially symmetric plasmonic breathing modes.^32,33 A flat metal NP not only has edge modes³⁴ (dipolar, quadrupolar and higher order multipolar modes) because of LSPR, but also supports film modes. Breathing modes are dark modes that cannot be detected by photons as their net dipole moment is zero. However such modes can be detected by inelastic electron scattering in electron energy-loss spectroscopy as the electron wavelength is much smaller than the nanoparticle size.^35,36 The breathing modes are very important for near field coupling effects as they have a very high optical mode density. Several groups have investigated breathing modes of different metal nanostructures such as nanodisks,^32,35,37 nanoplates,³⁶ core–shell nanoparticles,^38,39 nanotriangles,⁴⁰ nanowires,^41,42 nanosphere–nanodisk trimers,⁴³ metal oligomers,⁴⁴ and graphene nanoellipses⁴⁵ but breathing modes of AuNSs have never been reported before.

AuNSs, because of having several polarization insensitive hot-spots generated after the interaction of light at the tip of the spikes randomly distributed over their core, are more advantageous than the other spiked nanoantennas like nanoellipsoids and nanorods^46–51 which have the ability to concentrate light like nanostars. AuNSs which are well known for their biomedical applications due to their low-toxicity, biocompatibility, high tunability and high electric field intensity enhancement at their hot-spots^46–49 have been synthesized using nano-chemistry strategies, including environmentally sensitive “green” synthesis routes^52–58 and surfactant-free routes. Here, for our study we have synthesized these highly tunable, stable, efficient AuNSs using a low-cost, simple, one-step (seedless), surfactant-free, high-yield wet chemistry method.⁵⁹

In this contribution we report experimental evidence of both the plasmonic edge modes and acoustic breathing modes in AuNSs. Results of optical and electron spectroscopy characterization of these highly stable nanoparticles (stability > 5 months in aqueous solution) are reported. Optical characterization provided integrated information regarding the collective behaviour of AuNSs in aqueous suspension while electron energy-loss spectroscopy (EELS), performed using a scanning transmission electron microscope (FEI Titan³ G2 STEM), provided local plasmonic responses of a single AuNS with high spatial resolution. Several groups have investigated plasmonic nanostructures including AuNSs via EELS,^60–74 but this high-resolution, low-loss EELS investigation into AuNSs has shown the presence of regular edge plasmon modes along with radial breathing modes, irrespective of the spike length.

This study is also supported by extensive theoretical investigations. The effect of tip displacement in response to excitation of the breathing modes has been calculated using the structural mechanics model of Comsol 5.4 which is based on the Finite Element Method. The maximum intensity enhancement of a single AuNS antenna has been calculated using the Radio Frequency (RF) module of Comsol 5.4. All these results indicate the possibility of creating a device based on the acousto-plasmonic AuNS antenna which will be useful for two-step clinical diagnostics.

2. Results and discussion

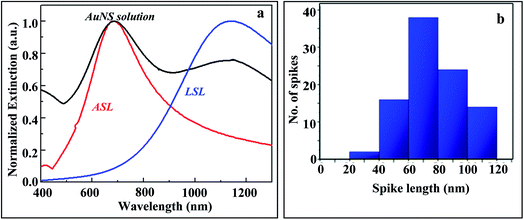
Gold nanostars are synthesized using a one-step (without seed) surfactant-free wet chemistry method as described elsewhere.⁵⁹ This method is briefly described in the Experimental section. Fig. 1(a) shows a typical high magnification TEM image of a gold nanoparticle while Fig. 1(b) shows a low magnification TEM image where almost all the nanoparticles have at least one spike on their surface, confirming the relatively high yield of the synthesis method. X-ray energy dispersive spectroscopy (XEDS) of the synthesized AuNSs confirms the presence of Au in the nanostars (Fig. S1†).

Fig. 1 (a) A high magnification TEM image of a randomly selected gold nanoparticle is shown. (b) A low magnification TEM image is shown here which is representative of almost all the nanoparticles observed.

Fig. 2(a) shows a comparative study between the normalized experimental extinction spectrum of the stable AuNS solution collected using a PerkinElmer Lambda 900 spectrophotometer and the corresponding theoretical investigations. Notably, in the experimental extinction spectra two major modes can be seen. The histogram for spike lengths of synthesized AuNSs is shown in Fig. 2(b). The average spike length (ASL) of the nanostars was measured and averaged from TEM images of nearly 100 AuNS nanoparticles and was found to measure 70 nm while the average diameter of the core measured almost 60 nm. The tip radius of the AuNS spike is varied here from 5 nm to 1 nm depending on the spike length. From the histogram in Fig. 2(b) one may observe that the AuNSs with an ASL of 70 nm are dominant in solution. AuNSs with a large spike length (LSL) of 90 nm are the second most dominant type of nanostar in the solution. The histogram in Fig. 2(b) supports the origin of the two peaks observed in the experimental extinction spectra. Complementarily, Finite Element Method (FEM) simulations were performed using Comsol 5.4 for the AuNSs with an ASL of 70 nm and LSL of 90 nm and the same core diameter (60 nm), permitting determination of extinction characteristics. The red and blue curves, shown in Fig. 2(a), represent the theoretically calculated normalized extinction spectra for AuNSs of spike lengths 70 nm and 90 nm, the convolution of which gives the resultant theoretical extinction spectra of the AuNS solution. From this figure we can conclude that the resultant theoretical extinction characteristics match well with the experimental ones, thus confirming our hypothesis.

Fig. 2 (a) Comparison of the normalized experimental extinction spectrum of the synthesized AuNS solution and the relevant theoretical investigation conducted on the extinction properties of AuNSs of two different spike lengths. Large spike length (LSL) and average spike length (ASL) are obtained based on the collected TEM information. (b) Histogram of the spike lengths of synthesized AuNSs is shown based on the collected TEM images of nearly 100 NPs.

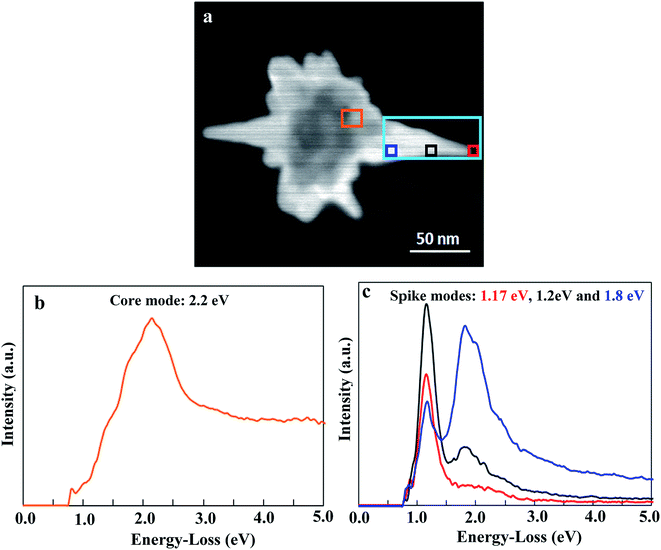
Although optical and computational studies of AuNSs dissolved in aqueous solution provided integrated information about the ensemble behaviour of AuNSs, STEM-EELS measurements revealed localized information about the plasmonic field distribution and resonances for different locations across a single nanostructure. Fig. 3 illustrates the EELS analysis for synthesized AuNSs with a LSL. EELS experiments allowed mapping of plasmonic edge modes in AuNSs and also the excitation and observation of optically dark radial breathing modes. The STEM-HAADF (High Angle Annular Dark Field) image of an AuNS with the LSL which was used for EELS analysis is shown in Fig. 3(a). The regions from which the EELS spectra were mapped and acquired are indicated by the colored boxes on the STEM image. Fig. 3(b) and (c) show the EELS spectra taken at the nanostar core and the nanostar spike. Fig. 3(b) shows a peak at 2.2 eV, which corresponds to the core mode of the AuNS as confirmed by the FEM simulation (Fig. S2†), which shows LSPR at 550 nm (2.2 eV) for a gold core of 60 nm. The strongest mode observed, at the pinnacle of the AuNS spike, was 1.17 eV, corresponding with one extinction peak from the UV-Vis-NIR spectra. FEM simulations carried out on similar types of AuNSs, having an 88 nm spike length and 60 nm core, indicate that the LSPR is expected to occur at 1060 nm (1.17 eV) and thereby confirm the dipolar (bright) edge mode nature at the pinnacle (see Fig. S3†).

Fig. 3 EELS characterization of AuNSs with a LSL: (a) AuNS with relative areas of investigation indicated by different colored boxes. (b) EELS spectrum of the AuNS core. (c) EELS spectra of different regions of the AuNS spike.

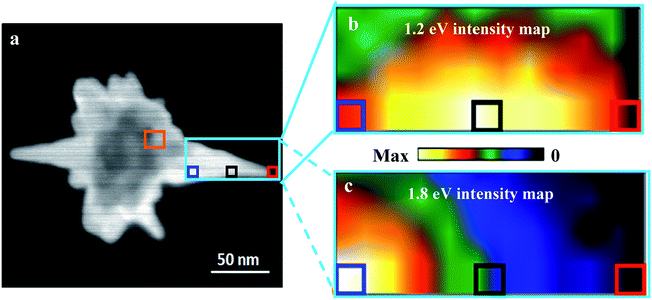
The EELS intensity maps for 1.2 eV and 1.8 eV, shown in Fig. 4(b) and (c), confirm the non-plasmonic edge nature observed at the spike of this AuNS.

Fig. 4 EELS intensity maps of different dominant modes in spikes of AuNSs with a LSL: (a) AuNS with relative areas of investigation indicated by different colored boxes. (b) EELS intensity map at 1.2 eV mode. (c) EELS intensity map at 1.8 eV mode. Here 1.2 eV and 1.8 eV modes are the major plasmonic modes located at the AuNS spike with LSL.

During STEM-EELS mapping, a 1.2 eV mode (Fig. 4(b)) was excited and observed in the central region of the spike. This mode shows a very different spatial and intensity distribution with respect to the edge mode. In addition, further away from the pinnacle, a similarly structured mode was observed at 1.8 eV. The comparison of the optical and EELS spectra of several nanostar spikes (small and large spike lengths) shows that the modes in the body of the spike are dark modes, since they cannot be excited by light and they are not observed in the optical spectra. To further confirm their non-plasmonic edge mode character a computational study was performed using FEM based Comsol 5.4 by analysing the mode shape at each mode frequency. Comsol simulations confirmed that the 1.2 eV mode possesses all the features of a radial breathing mode (Fig. 6) and it does not present the characteristic spatial distribution of plasmonic edge modes (dipolar, quadrupolar and higher order modes). However, the EELS maps were obtained by exciting the entire AuNS with a defocused electron beam, unlike the spectra in Fig. 3 obtained by spectrum imaging (SI) with a sub-nm electron probe. EELS intensity maps at 1.2 eV and 1.8 eV clearly show the mode localization away from the AuNS tip.

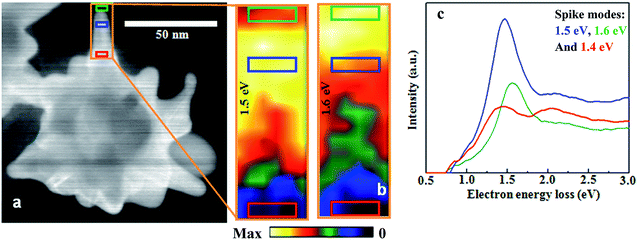
The presence of radial breathing modes and a dipolar edge mode is more evident for short spike than for long spike AuNSs, because of its larger interaction volume. The details of the EELS analysis of the AuNS with a small spike length (SSL) are shown in Fig. 5 and the relevant numerical results are given in Fig. 6.

Fig. 5 EELS of a AuNS with a short spike length: (a) AuNS image with relative areas of investigation (coloured boxes). (b) Intensity maps of major plasmonic modes at 1.5 eV and 1.6 eV located at the AuNS spike. (c) EELS spectra of different regions of the AuNS spike. The dominant mode at the pinnacle of the spike is 1.6 eV. The 1.6 eV EELS intensity map confirms its edge mode nature by showing a maximum intensity at the tip of the spike (green box area), whereas the 1.5 eV mode, which is dominant in the body of the spike (blue box region) confirms its non-plasmonic nature.

Fig. 6 (a) Single AuNS with a small spike length (SSL) is shown here. The enlarged portion of the black box shows different responses at different modes and thus is useful theoretically to predict the nature of the mode (either plasmonic edge mode or radial breathing mode). (b) Behaviour of a single AuNS with a SSL at 1.6 eV. (c) Behaviour of a single AuNS with a SSL at 1.5 eV. (d) Single AuNS with a LSL is shown. The enlarged portion of the black box shows different responses at different modes. (e) Behaviour of a single AuNS with a LSL at 1.17 eV. (f) Behaviour of a single AuNS with a LSL at 1.2 eV.

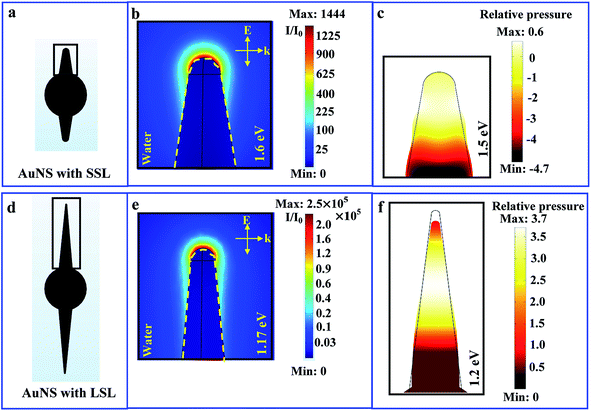
Fig. 6 illustrates the numerical study performed for the various observed modes, both edge and non-edge modes, in a single AuNS with a large spike length (LSL) and a small spike length (SSL), when excited by light and electron beams. Fig. 6(a) shows an illustration of a plasmonic SSL nanostar antenna determined by the quantitative parameters measured from the STEM images. Fig. 6(b) shows the resultant mode distribution at 1.6 eV when excited by light; the mode has its highest intensity at the pinnacle of the AuNS spike, as also observed in the EELS intensity map (Fig. 5(b)). Considering that the skin depth of gold in the wavelength range of 400–1200 nm is smaller than 5 nm, any plasmonic edge mode is not expected to penetrate into the body of the nanoparticle, rather it is confined at the metal–dielectric interface. Moreover, extinction studies also confirm the LSPR of this structure at 1.6 eV; thereby, this mode is a dipolar edge mode. Of note, the yellow dashed line in Fig. 6(b) represents the nanoparticle edge and does not appear to show evidence of structural modification. The intensity map in Fig. 5(b) exhibits an unexpected shape for the 1.5 eV mode; this mode was not observed in the optical extinction spectra, thereby indicating that it is formed by a non-plasmonic nature, as also supported by the simulations. The hypothesis that these modes are of an acoustic nature originated from multiple observations: the appearance of the highest intensity position away from the metal–dielectric interface, the radially symmetric nature of the mode and the corresponding absence of this mode in the extinction spectra, both for theoretical and experimental studies. To confirm this hypothesis, the mode at 1.5 eV of the SSL AuNS was investigated numerically using the structural mechanics module of Comsol 5.4 (the parameters for the simulation are given in the Numerical simulation section).^75–77Fig. 6(c) shows the 1.5 eV mode shape and distribution obtained via Comsol simulations for the SSL AuNS. The map of the relative pressure calculated via the structural mechanics module shows that the mode has the familiar, radial symmetry of a typical breathing mode.^32–34 The black contour line, shown in Fig. 6(c), represents the unperturbed morphology of the SSL AuNS, whereas the color map shows the relative pressure distribution at 1.5 eV and the modification of the structure because of the acoustic mode. Similarly, Fig. 6(f) shows the simulation obtained via Comsol of the LSL AuNS for the anomalous mode at 1.2 eV, as also shown in Fig. 4(b). Notably, the relative pressure is highest in the middle of the spike of the AuNS resulting in a significant contraction of the same structure. The map of the relative pressure, as calculated by structural mechanics, shows that the 1.2 eV mode exhibits the radial symmetry of a typical breathing mode,^32–34 again supporting the acoustic nature of the 1.2 eV mode of the LSL AuNS. Fig. 6(e) conversely shows the results for the analysis of the mode at 1.17 eV of the LSL AuNS, as reported in Fig. 3. The 1.17 eV mode has its highest intensity at the pinnacle of the AuNS spike, as observed in the EELS spectra (Fig. 3(c)). The 1.17 eV mode is a plasmonic edge mode, since its dipolar nature has been confirmed by calculating the LSPR from the extinction spectra and the electric field mapping using the RF module of Comsol 5.4.

Continued analysis of SI data for breathing modes revealed that the 1.5 eV mode is located along the spike where the diameter measured 7.4 nm (Fig. 5), whereas for the LSL AuNS the breathing mode at 1.2 eV is located along the spike where the diameter is 21.4 nm (Fig. 4). For any specific, non-symmetric structure, theoretical calculation of acoustic mode frequency is tedious.^78,79 Yet Lamb⁸⁰ introduced a very simple relationship between the acoustic breathing mode frequency and the size of the structure. According to Lamb's relationship, the acoustic breathing mode frequency varies inversely with the diameter of the spherically symmetric structures. If the spikes of the AuNS are considered to be a parallel combination of many disks,⁸¹ – the Lamb principle is also verified here for the two breathing modes – as the mode frequencies vary inversely with the structure diameter.

The plasmonic edge and breathing modes of AuNSs can be synergistically employed to determine the size and mass of target molecules, respectively, by combining the reactive sensing principle for plasmonic biosensing^82,83 and a nano-cantilever mechanism. According to the numerical investigation, the field intensity enhancement was found to be approximately 2.5 × 10⁵ in water media for the LSL AuNS at its LSPR (1060 nm). This indicates that the acousto-plasmonic AuNS based nanoantenna – supporting both plasmon edge and breathing modes – can be useful for two-step label free molecular detection at a point-of-care.

3. Conclusions

To summarize, we report the experimental evidence of both plasmonic edge and breathing modes in AuNSs. Here, AuNSs are synthesized via a known simple, one-step, surfactant-free wet-chemistry method with high yield and stability and characterized via optical spectroscopy and EELS. Low-loss EELS provided information about the local plasmonic modes of different regions of the nanostars and indicated the presence of optically dark breathing modes, allowing for the plasmonic edge and breathing modes of the synthesized AuNSs to be harnessed to determine the size and mass of adsorbed analytes based on both a plasmon resonance sensing mechanism and the cantilever principle, irrespective of the molecular shape. This study is also supported by the numerical investigations performed using FEM based Comsol 5.4 which confirms the presence of plasmonic edge and breathing modes in different AuNSs with different spike lengths. The numerical study predicts that for a AuNS nanoplasmonic antenna the field-intensity enhancement factor in the hot-spot region is around 10⁵. This indicates that these efficient acousto-plasmonic AuNS antennas might find applications in two-step label-free clinical diagnostics.

4. Experimental section

Materials

Gold(III) chloride trihydrate (HAuCl₄, 3H₂O), silver nitrate (AgNO₃), ascorbic acid (AA), hydrochloric acid (HCl) (35–37%), and polyvinylpyrrolidone (PVP) were purchased from Sigma Aldrich and used as received without further purification. The water used here was reagent-grade, produced using a Milli-Q SP ultrapure-water purification system.

Synthesis of the stabilized gold nanostars

At first, 10 ml of a 0.25 mM chloroauric acid (HAuCl₄) solution was mixed with 10 μl of a 1 M HCl solution in a glass vial. After that, at room temperature under moderate stirring (700 rpm), 100 μl of a 1 mM AgNO₃ solution and 50 μl of a 100 mM AA solution were added simultaneously. Within a few seconds the solution color turned to blue. After 2 minutes from the addition of the AA and AgNO₃, 5 ml of 2 mM polyvinylpyrrolidone (PVP) was added and was stirred for another 8 minutes maintaining the same stirring speed. Then the solution was kept for 3 hours at room temperature at rest. Afterwards, one centrifugal wash was performed at 4000 rcf for 20 minutes to wash out the extra PVP. After centrifugation, without disturbing the precipitate, the liquid containing extra PVP and the other chemicals was washed out and the solution was redispersed in DI water. Finally, the AuNS solution was kept at room temperature for future use. The characterization details of these synthesized AuNSs are given below.

Characterization

The synthesized nanoparticles are characterized using UV-Vis-NIR spectroscopy and scanning transmission electron microscopy:

UV-Vis-NIR spectroscopy

The UV-Vis-NIR spectra of the synthesized gold nanostar solution were obtained using a PerkinElmer Lambda 900 spectrophotometer. The extinction properties of the nanostar solution were measured in a wavelength range of 400 nm to 1300 nm.

STEM, XEDS, and EELS measurements

To probe the size and shape of the synthesized nanoparticles, a STEM (monochromated, image-corrected FEI Titan³ G2 STEM) was used. The electronic structure of the synthesized AuNSs was investigated with the help of low-loss EELS, and XEDS was used to determine the gold weight percentage in the solution. Sample preparation was done one day before the STEM measurements by drop casting and then drying the aqueous solution of gold nanoparticles on a standardized holey carbon film supported on a TEM grid. All experiments were performed at 60 kV with a high collection angle (∼25 mrad) to minimize the influence of Cherenkov radiation on the EELS signal.⁸⁴ The convergence angle and the probe size were measured to be approximately 13.2 mrad and 1.3 angstrom, respectively. The EELS energy resolution which is equivalent to the full width at half-maximum of the zero-loss peak was approximately 150 meV. To resolve the EELS signals spatially along and across each nano-object, spectrum imaging was used. All the EELS data were treated using the Gatan Digital Micrograph software package. No evidence of irradiation impairment was observed in the sample during EEL spectra acquisition. The zero-loss peak for each spectrum was removed using the standard reflected tail method which reflects the tail on the energy-gain side of the spectrum onto the energy-loss side, typically with a pre-defined scaling factor, and subtracts it.^85–88

Numerical simulation

FEM simulations are used here to find a correlation between the experimental data and the predicted properties of extinction (optical module) and acoustic modes (structural mechanics module) of AuNSs. During simulation, data regarding the different sizes and shapes of AuNS spikes and their cores are obtained from the STEM studies. The study is carried out to map the electric field for plasmonic modes and structural modification of the nanoantennas for phononic modes. The relative pressure due to the excitation of the breathing modes of AuNSs was calculated using the structural mechanics module of COMSOL 5.4 (ref. 75–77) where the mode frequency was obtained from the experimental EELS information. The Radio Frequency (RF) module of Comsol 5.4 is used to investigate the plasmonic modes. Numerical study is also carried out for hybrid AuNS antennas for different sizes of the nanospheres and gaps between each nanoantenna of that heterodimer. Scattering, absorption and extinction cross-sections of the AuNS plasmonic antennas are also calculated here. For the optical simulations the definitions in the Comsol material library are used for all the optical and physical properties of the surrounding media. Simulations considering both air (ε = 1.0) and water (ε = 1.77) as the homogeneous surrounding media are performed here. During this numerical investigation, the wavelength dependent permittivity of gold is obtained from the Johnson and Christy measurements⁸⁹ and plane waves are used as the excitation source. Electric field polarization of incident light is always chosen along the semi major axis of the AuNS spikes during extinction and electric field mapping. For the simulation of acoustic modes performed in air the material mechanical properties of Au are defined according to the bulk values. Physics controlled free tetrahedral meshes with an extremely fine size for the AuNSs and a normal size for surrounding media have been chosen for all analyses. For the simulation of acoustic modes, performed in air, the material mechanical properties of Au are defined according to the bulk values (Young's modulus = 79 GPa, Poisson's ratio = 0.4, and density = 19 300 kg m⁻³). The longitudinal speed of sound in gold is obtained as 3240 m s⁻¹.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We acknowledge support from the Ohio Third Frontier Project ‘Research Cluster on Surfaces in Advanced Materials (RC-SAM)’ at Case Western Reserve University.

References

1. N. Rezaei, Cancer Immunology, Springer, New York, 2014.
2. P. N. Prasad, Introduction to Biophotonics, John Wiley & Sons, New Jersey, 2003.
3. J. A. Schuller, E. S. Barnard, W. S. Cai, Y. C. Jun, J. S. White and M. L. Brongersma, Nat. Mater., 2010, 9, 193–204.
4. W. B. Hou and S. B. Cronin, Adv. Funct. Mater., 2013, 23, 1612–1619.
5. P. Reineck, G. P. Lee, D. Brick, M. Karg, P. Mulvaney and U. Bach, Adv. Mater., 2012, 24, 4750–4755.
6. H. C. Chen, S. W. Chou, W. H. Tseng, I. W. P. Chen, C. C. Liu, C. Liu, C. L. Liu, C. H. Chen, C. I. Wu and P. T. Chou, Adv. Funct. Mater., 2012, 22, 3975–3984.
7. S. S. Kelkar and T. M. Reineke, Bioconjugate Chem., 2011, 22, 1879–1903.
8. K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297.
9. K. V. Sreekanth, Y. Alapan, M. ElKabbash, E. Ilker, M. Hinczewski, U. A. Gurkan, A. De Luca and G. Strangi, Nat. Mater., 2016, 15, 621–627.
10. K. V. Sreekanth, Y. Alapan, M. ElKabbash, A. M. Wen, E. Ilker, M. Hinczewski, U. A. Gurkan, N. F. Steinmetz and G. Strangi, Adv. Opt. Mater., 2016, 4, 1767–1772.
11. J. S. Sekhon, H. K. Malik and S. S. Verma, RSC Adv., 2013, 3, 15427–15434.
12. B. Sharma, R. R. Frontiera, A. I. Henry, E. Ringe and R. P. Van Duyne, Mater. Today, 2012, 15, 16–25.
13. S. M. Nie and S. R. Emery, Science, 1997, 275, 1102–1106.
14. W. L. Barnes, A. Dereux and T. W. Ebbesen, Nature, 2003, 424, 824–830.
15. E. Ozbay, Science, 2006, 311, 189–193.
16. K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677.
17. J. A. Scholl, A. L. Koh and J. A. Dionne, Nature, 2012, 483, 421–428.
18. J. Nelayah, M. Kociak, O. Stephan, F. J. Garcia de Abajo, M. Tence, L. Henrard, D. Taverna, I. Pastoriza-Santos, L. M. Liz-Marzan and C. Colliex, Nat. Phys., 2007, 3, 348–353.
19. M. Rycenga, X. Xia, C. H. Moran, F. Zhou, D. Qin, Z. Y. Li and Y. Xia, Angew. Chem., Int. Ed., 2011, 50, 5473–5477.
20. Y. G. Sun and Y. N. Xia, Science, 2002, 298, 2176–2179.
21. H. J. Chen, L. Shao, Q. Li and J. F. Wang, Chem. Soc. Rev., 2013, 42, 2679–2724.
22. S. J. Lee and M. Moskovits, J. Am. Chem. Soc., 2012, 134, 11384–11387.
23. L. Rodríguez-Lorenzo, R. A. Alvarez-Puebla, I. Pastoriza-Santos, S. Mazzucco, O. Stéphan, M. Kociak, L. M. Liz-Marzán and F. J. García de Abajo, J. Am. Chem. Soc., 2009, 131, 4616–4618.
24. H. G. Liao, Y. X. Jiang, Z. Y. Zhou, S. P. Chen and S. G. Sun, Angew. Chem., Int. Ed., 2008, 47, 9100–9103.
25. H. L. Wu, C. H. Chen and M. H. Huang, Chem. Mater., 2008, 21, 110–114.
26. X. L. Liu, J. H. Wang, S. Liang, D. J. Yang, F. Nan, S. J. Ding, L. Zhou, Z. H. Hao and Q. Q. Wang, J. Phys. Chem. C, 2014, 118, 9659–9664.
27. J. Zhang, Y. Gao, R. A. Alvarez-Puebla, J. M. Buriak and H. Fenniri, Adv. Mater., 2006, 18, 3233–3237.
28. C. R. Li, N. P. Lu, J. Mei, W. J. Dong, Y. Y. Zheng, L. Gao, K. Tsukamoto and Z. X. Cao, J. Cryst. Growth, 2011, 314, 324–330.
29. V. Giannini, R. Rodríguez-Oliveros and J. A. Sánchez-Gil, Plasmonics, 2010, 5, 99–104.
30. R. Alvarez-Puebla, L. M. Liz-Marzan and F. J. García de Abajo, J. Phys. Chem. Lett., 2010, 1, 2428–2434.
31. P. G. Etchegoin and E. C. Le Ru, Surface Enhanced Raman Spectroscopy: Analytical, Biophysical and Life Science Applications, Chapter I – “Basic Electromagnetic Theory of SERS”, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2010.
32. F. P. Schmidt, H. Ditlbacher, U. Hohenester, A. Hohenau, F. Hofer and J. R. Krenn, Nano Lett., 2012, 12, 5780.
33. A. Chakrabarty, F. Wang, F. Minkowski, K. Sun and Q. H. Wei, Opt. Express, 2012, 20, 11615.
34. F. P. Schmidt, H. Ditlbacher, U. Hohenester, A. Hohenau, F. Hofer and J. R. Krenn, Nat. Commun., 2014, 5, 3604.
35. F. P. Schmidt, A. Losquin, F. Hofer, A. Hohenau, J. R. Krenn and M. Kociak, ACS Photonics, 2018, 5, 861.
36. M. Zhao, M. Bosman, M. Danesh, M. Zeng, P. Song, Y. Darma, A. Rusydi, H. Lin, C. W. Qiu and K. P. Loh, Nano Lett., 2015, 15, 8331.
37. M. K. Krug, M. Reisecker, A. Hohenau, H. Ditlbacher, A. Trugler, U. Hohenester and J. R. Krenn, Appl. Phys. Lett., 2014, 105, 1711031–1711033.
38. J. E. Sader, G. V. Hartland and P. Mulvaney, J. Phys. Chem. B, 2002, 106, 1399.
39. J. H. Hodak, A. Henglein and G. V. Hartland, J. Phys. Chem. B, 2000, 104, 5053.
40. A. Campos, A. Arbouet, J. Martin, D. Gérard, J. Proust, J. Plain and M. Kociak, ACS Photonics, 2017, 4, 1257.
41. N. Large, L. Saviot, J. Margueritat, J. Gonzalo, C. N. Afonso, A. Arbouet, P. Langot, A. Mlayah and J. Aizpurua, Nano Lett., 2009, 9, 3732.
42. K. Yu, T. A. Major, D. Chakraborty, M. S. Devadas, J. E. Sader and G. V. Hartland, Nano Lett., 2015, 15, 3964.
43. S. Tripathy, R. Marty, V. K. Lin, S. L. Teo, E. Ye, A. Arbouet, L. Saviot, C. Girard, M. Y. Han and A. Mlayah, Nano Lett., 2011, 11, 431.
44. C. Cherqui, N. W. Bigelow, A. Vaschillo, H. Goldwyn and D. J. Masiello, ACS Photonics, 2014, 1, 1013.
45. W. Wang and Z. Song, Phys. B, 2017, 530, 142.
46. S. A. Maier and H. A. Atwater, J. Appl. Phys., 2005, 98, 0111011.
47. H. Wang, D. W. Brandl, F. Le, P. Nordlander and N. J. Halas, Nano Lett., 2006, 6, 827–832.
48. J. W. Liaw, M. K. Kuo and C. N. Liao, Journal of Electromagnetic Waves and Applications, 2005, 19, 1787–1794.
49. M. B. Mohamed, V. Volkov, S. Link and M. A. El-Sayed, Chem. Phys. Lett., 2000, 317, 517–523.
50. C. F. Bohren and D. R. Huffman, Adsorption and Scattering of Light by Small Particles, Wiley-VCH, New York, 1983.
51. J. D. Jackson, Classical Electrodynamics, Wiley, New York, 1999.
52. L. N. Colleen, H. Liao and J. H. Hafner, Nano Lett., 2006, 6, 683–688.
53. P. S. Kumar, I. Pastoriza-Santos, B. Rodriguez-Gonzalez, F. J. García dé Abajo, F. Javier and L. M. Liz-Marzan, Nanotechnology, 2008, 19, 0156061–0156066.
54. Q. Chen, T. Kaneko and R. Hatakeyama, Condens. Matter, 2014, 1585, 1401–1417.
55. W. Moukarzel, J. Fitremann and J. D. Marty, Nanoscale, 2011, 3, 3285–3290.
56. H. Yuan, C. G. Khoury, H. Hwang, C. M. Wilson, G. A. Grant and T. Vo-Dinh, Nanotechnology, 2012, 23, 075102–075117.
57. A. Kedia and P. S. Kumar, J. Mater. Chem. C, 2013, 1, 4540–4549.
58. S. Chatterjee, A. B. Ringane, A. Arya, G. M. Das, V. R. Dantham, R. Laha and S. Hussain, J. Nanopart. Res., 2016, 18, 242–249.
59. S. Chatterjee, L. Ricciardi, J. I. Deitz, R. E. A. Williams, D. W. McComb and G. Strangi, Micromachines, 2018, 9, 664.
60. M. W. Chu, V. Myroshnychenko, C. H. Chen, J. P. Deng, C. Y. Mou and F. J. García dé Abajo, Nano Lett., 2009, 9, 399–404.
61. J. Nelayah, M. Kociak, O. Stephan, F. J. García dé Abajo, M. Tence, L. Henrard, D. Taverna, I. Pastoriza-Santos, L. M. Liz-Marzan and C. Colliex, Nat. Phys., 2007, 3, 348–353.
62. H. Wang, Y. Wu, B. Lassiter, C. L. Nehl, J. H. Hafner, P. Nordlander and N. J. Halas, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10856–10860.
63. A. L. Koh, K. Bao, I. Khan, W. E. Smith, G. Kothleitner, P. Nordlander, S. A. Maier and D. W. McComb, ACS Nano, 2009, 3, 3015–3022.
64. J. Morla-Folch, L. Guerrini, N. Pazos-Perez, R. Arenal and R. A. Alvarez-Puebla, ACS Photonics, 2014, 1, 1237–1244.
65. Y. Wu, G. Li, C. Cherqui, N. W. Bigelow, N. Thakkar, D. J. Masiello, J. P. Camden and P. D. Rack, ACS Photonics, 2016, 3, 130–138.
66. S. Mazzucco, O. Stéphan, C. Colliex, I. Pastoriza-Santos, L. M. Liz-Marzan, F. J. García dé Abajo and M. Kociak, Eur. Phys. J.: Appl. Phys., 2011, 54, 335121–335129.
67. F. J. García dé Abajo and M. Kociak, Phys. Rev. Lett., 2008, 100, 1068041–1068044.
68. V. Myroshnychenko, J. Nelayah, G. Adamo, N. Geuquet, J. Rodriguez-Fernandez, I. Pastoriza-Santos, K. F. MacDonald, L. Henrard, L. M. Liz-Marzan, N. I. Zheludev, M. Kociak and F. J. García dé Abajo, Nano Lett., 2012, 12, 4172–4180.
69. A. Losquin, L. F. Zagonel, V. Myroshnychenko, B. Rodriguez-Gonzalez, M. Tence, L. Scarabelli, J. Förstner, L. M. Liz-Marzan, F. J. García de Abajo, O. Stephan and M. Kociak, Nano Lett., 2015, 15, 1229–1237.
70. J. A. Scholl, A. L. Koh and J. A. Dionne, Nature, 2012, 483, 421–427.
71. V. Myroshnychenko, J. Rodríguez-Fernández, I. Pastoriza-Santos, A. M. Funston, C. Novo, P. Mulvaney, L. M. Liz-Marzán and F. J. García dé Abajo, Chem. Soc. Rev., 2008, 37, 1792–1805.
72. S. M. Novikov, A. Sánchez-Iglesias, M. K. Schmidt, A. Chuvilin, J. Aizpurua, M. Grzelczak and L. M. Liz-Marzán, Part. Part. Syst. Charact., 2014, 31, 77–80.
73. A. L. Koh, A. I. Fernández-Domínguez, D. W. McComb, S. A. Maier and J. K. W. Yang, Nano Lett., 2011, 11, 1323–1330.
74. F. V. Cube, J. Niegemann, S. Irsen, D. C. Bell and S. Linden, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1154341–1154345.
75. Comsol Multiphysics Structural Mechanics—User's Guide, Comsol, 2012, Version: 4.3.
76. T. Schumacher, M. Brandstetter, D. Wolf, K. Kratzer, M. Hentschel, H. Giessen and M. Lippitz, Appl. Phys. B: Lasers Opt., 2016, 122, 1–11.
77. L. Wang, T. Sagaguchi, T. Okuhata, M. Tsuboi and N. Tamai, ACS Nano, 2017, 11, 1180–1188.
78. W. M. Visscher, A. Migliori, T. M. Bell and R. A. Reinert, J. Acoust. Soc. Am., 1991, 90, 2154.
79. L. Saviot and D. B. Murray, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 214101–214111.
80. H. Lamb, Proc. London Math. Soc., 1882, 13, 189.
81. N. Large, L. Saviot, J. Margueritat, J. Gonzalo, C. N. Afonso, A. Arbouet, P. Langot, A. Mlayah and J. Aizpurua, Nano Lett., 2009, 9, 3732–3738.
82. V. R. Dantham, S. Holler, C. Barbre, D. Keng, V. Kolchenko and S. Arnold, Nano Lett., 2013, 13, 3347–3351.
83. I. Ament, J. Prasad, A. Henkel, S. Schmachtel and C. Sönnichsen, Nano Lett., 2012, 12, 1092–1095.
84. M. Stoger-Pollach, Micron, 2008, 39, 1092–1110.
85. J. I. Deitz, S. Karki, S. X. Marsillac, T. J. Grassman and D. W. McComb, J. Appl. Phys., 2018, 123, 1157031–1157036.
86. M. Contreras, J. Tuttle, D. Du, Y. Qi, A. Swartzlander, A. Tennant and R. Noufi, Appl. Phys. Lett., 1993, 63, 1824–1826.
87. D. B. Williams and C. B. Carter, Transmission Electron Microscopy: A Textbook for Materials Science, Springer, New York, 2009.
88. Digital Micrograph EELS Analysis User's Guide – EELS Analysis User Guide, Pleasanton, CA, 2003.
89. P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379.

---

Footnote

† Electronic supplementary information (ESI) available: Additional information including XEDS results of synthesized nanoparticles and the FEM simulation results is available. See DOI: 10.1039/c9na00301k

---