Mechanical anisotropy of two-dimensional metamaterials: a computational study

Abstract

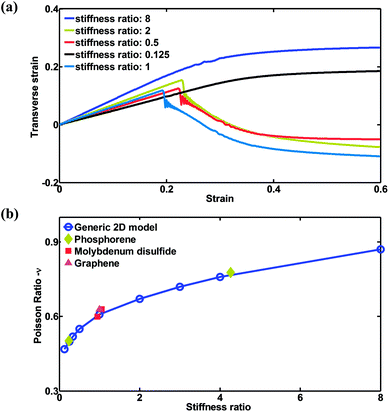
Metamaterials, rationally designed multiscale composite systems, have attracted extensive interest because of their potential for a broad range of applications due to their unique properties such as negative Poisson's ratio, exceptional mechanical performance, tunable photonic and phononic properties, structural reconfiguration, etc. Though they are dominated by an auxetic structure, the constituents of metamaterials also play an indispensable role in determining their unprecedented properties. In this vein, 2D materials such as graphene, silicene, and phosphorene with superior structural tunability are ideal candidates for constituents of metamaterials. However, the nanostructure–property relationship and composition–property relationship of these 2D material-based metamaterials remain largely unexplored. Mechanical anisotropy inherited from the 2D material constituents, for example, may substantially impact the physical stability and robustness of the corresponding metamaterial systems. Herein, classical molecular dynamics simulations are performed using a generic coarse-grained model to explore the deformation mechanism of these 2D material-based metamaterials with sinusoidally curved ligaments and the effect of mechanical anisotropy on mechanical properties, especially the negative Poisson's ratio. The results indicate that deformation under axial tensile load can be divided into two stages: bending-dominated and stretching-dominated, in which the rotation of junctions in the former stage results in auxetic behavior of the proposed metamaterials. In addition, the auxetic behavior depends heavily on both the amplitude/wavelength ratio of the sinusoidal ligament and the stiffness ratio between axial and transverse directions. The magnitude of negative Poisson's ratio increases from 0 to 0.625, with an associated increase of the amplitude/wavelength ratio from 0 to 0.225, and fluctuates at around 0.625, in good agreement with the literature, with amplitude/wavelength ratios greater than 0.225. More interestingly, the magnitude of negative Poisson's ratio increases from 0.47 to 0.87 with the increase of the stiffness ratio from 0.125 to 8, in good agreement with additional all-atom molecular dynamics simulations for phosphorene and molybdenum disulfide. Overall, these research findings shed light on the deformation mechanism of auxetic metamaterials, providing useful guidelines for designing auxetic 2D lattice structures made of 2D materials that can display a tunable negative Poisson's ratio.

---

1. Introduction

Recent years have witnessed the explosive growth of research into metamaterials, rationally designed multiscale composite systems which exhibit material properties not found in most conventional materials, due to their potential for a broad range of applications.^1–6 The unique properties of these materials, e.g. negative Poisson's ratio,^5,7,8 superior mechanical performance^9–11 and structural reconfiguration,^12–14 are usually dominated by their structure, although the influence of their composition cannot be neglected either. Among candidates for constituents of metamaterials, two-dimensional materials with one-atom thickness have attracted significant interest due to their unique physical and chemical properties.^{1,2,7,15–26} Lattice metamaterials made of two-dimensional materials such as graphene have attracted extensive research interest, indicating great potential in applications such as flexible electronic devices,^5,27–30 photonic and phononic devices,^31–34 and mechanically controllable thermal devices.^5,35–37 However, the microstructure–property relationship and composition–property relationship of metamaterials made of two-dimensional materials remain an open question. Previous research studies set up a solid foundation for future studies investigating the structure–property relationship for 2D lattice structures.^5,25,38,39 For 2D lattice structures with multiple cut patterns, several theoretical models have been proposed to predict the microstructure–property relationship, which could not be well explained through classical theory in composite materials.^5,25 Other studies focus on edge termination problems for 2D lattice structures made of 2D materials, which is a critical issue for mechanical performance and structural stability.^38,39 Despite these remarkable advances, the composition–property relationship has long been overlooked. For example, two-dimensional materials with a highly symmetric crystalline structure, such as graphene,⁴⁰ silicene,⁴¹ and molybdenum disulfide,⁴² exhibit isotropic mechanical properties while other materials with less symmetric structures, such as phosphorene,⁴³ are highly anisotropic along in-plane directions. The intrinsic mechanical anisotropy has potential to promote the tunability of mechanical properties of the associated metamaterials. Another important factor is the Föppl–von Kármán number,^44,45 an indication of the ratio between in-plane stiffness and out-of-plane bending stiffness, with high numbers corresponding to membranes that more easily bend and crumple than they stretch and shear. Graphene exhibits exceptional in-plane stretching stiffness, around 1 TPa in both armchair and zigzag directions,⁴⁶ due to the strong covalent bonding between adjacent carbon atoms, while the bending stiffness is significantly low due to its ultra-low thickness, ranging from 0.83 to 1.61 eV as measured experimentally⁷ and calculated theoretically.^47,48 In contrast, the in-plane stiffness of molybdenum disulfide is moderate, around 330 GPa, compared to graphene, while the bending stiffness (8.7–13.4 eV)⁴⁹ is much higher than that of graphene due to its three-atom thickness. Consequently, with a low Föppl–von Kármán number, metamaterials made of materials like graphene could exhibit low stability compared to those made of materials like molybdenum, in which the out-of-plane buckling appears early under external mechanical loading. Overall, the mechanical anisotropy of 2D materials would significantly influence the stability and property tunability of the associated metamaterials. In this paper, we strive to address the above issue through coarse-grained molecular dynamics simulations, a widely accepted computational technique for two-dimensional materials,^50,51 with a focus on the relationship between mechanical anisotropy and negative Poisson's ratio.

In recent years, extensive efforts have also been put into designing microstructures and understanding deformation mechanisms for metamaterials with auxeticity, also known as negative Poisson's ratio.^1,2,52,53 For most conventional engineering materials, transverse contraction (expansion) would happen in association with tension (compression) along the loading direction. Auxetic materials, however, will expand (shrink) transversely when they are axially stretched (compressed), which enhances the energy absorption capability and fracture toughness, and thus the stability and robustness of the associated nano-devices.^28–30 Various architectures, e.g. kirigami-based structures,^7,19,23 fractal hierarchical structures,^54,55 and dimpled elastic sheets,⁵² have been implemented in designing multifunctional materials. However, microstructures with a corrugated configuration, which may improve mechanical performance such as the stretchability of the associated metamaterials, have been overlooked.^56–58 Moreover, the J-shape mechanical responses⁵⁹ under external tension are intrinsically similar to those of many natural soft bio-materials,^60–62 potentially improving the physiological compatibility of the corresponding nano-devices.^30,63 Therefore, architectures with sinusoidally curved beams are implemented to design auxetic 2D lattice metamaterials. In this work, Section 2 will briefly summarize the structural design of the proposed metamaterial and the computational techniques implemented here. In Section 3, simulation results are presented and discussed, and the specific focus is the effect of amplitude/wavelength ratio and stiffness ratio on the magnitude of negative Poisson's ratio. Finally, we conclude in Section 4 the deformation mechanism and effects of both geometrical factors and mechanical anisotropy on the auxetic behavior of the proposed 2D material system.

2. Computational methods and models

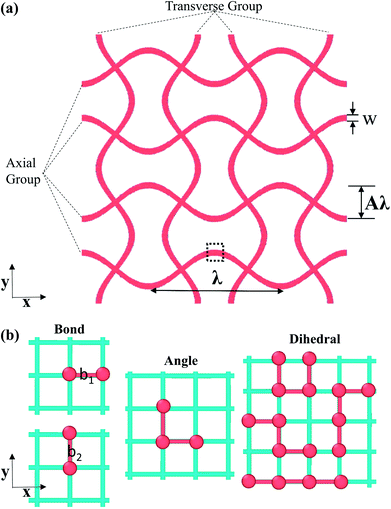
As discussed before, nanostructure designs with a curved configuration would dramatically improve the mechanical performance, such as stretchability, of 2D material systems.^56–58 In addition, the associated J-shape mechanical responses, similar to natural soft bio-matter, could enable good biocompatibility for nano-devices for biomedical applications.^30,63 Moreover, buckled structures are also promising in tuning phononic bandgaps, enabling many potential applications.³² Therefore, as shown in Fig. 1(a), two-dimensional networks with curved sinusoidal beams were created as the initial configuration. Three series of parameters, namely wavelength λ, amplitude/wavelength ratio A and band width w, can be tuned here to investigate their effects on the mechanical properties of two-dimensional kirigami, especially Poisson's ratio. Note that A is calculated by dividing the amplitude of sinusoidal curves by wavelength λ as shown in Fig. 1(a). For further quantitative analysis, the beams involved are classified into two groups: an axial group parallel to the loading direction and a transverse group perpendicular to the loading direction.

Fig. 1 (a) Schematic view of the two-dimensional kirigami. Note that three geometrical parameters, namely amplitude/wavelength ratio A, wavelength λ and band width w, are varied to systematically study their effect on mechanical properties, especially Poisson's ratio. (b) Interactions in the generic CG-MD model of 2D materials. Note that bonds along x and y directions (b₁ and b₂) may have different parameters in order to introduce mechanical anisotropy.

As mentioned in the introduction, there are huge differences in mechanical properties among 2D materials,^{40–43,53,64–67} which could bring interesting changes in the auxetic behaviors of 2D-material-based nanostructures. However, there are few general molecular models which could be tuned to accurately reproduce the mechanical properties of different 2D material systems. In order to model interactions among particles, a generic coarse-grained molecular dynamics (CG-MD) model of 2D materials is used as shown in Fig. 1(b), in which a squared lattice structure is connected by covalent bonds between adjacent particles. Each of those particles represents a cluster of atoms in a given 2D material system. The corresponding interactions can be divided into three categories, namely bond interactions which control the in-plane Young's modulus, angle interactions which define the in-plane shear modulus, and dihedral interactions which affect the out-of-plane bending stiffness. One of the advantages of this generic CG-MD model is that the mechanical properties can be tuned through varying the interaction parameters in a decoupled manner.⁵¹ For example, the Young's modulus along the x and y directions can be tuned through varying the stiffness of the b₁ and b₂ bonds respectively, as shown in Fig. 1(b), which provides a robust way to represent different kinds of 2D materials with widely varied and anisotropic mechanical properties. Accordingly, the total potential energy is calculated based on the following expressions

U = U_bond + U_angle + U_dihedral (1)

U_bond = k_bond(d − d₀)² (2)

U_angle = k_angle(θ − θ₀)² (3)

U_dihedral = k_dihedral(1 − cos(2φ)) (4)

for which detailed parameters can be found in Table 1. Those parameters are extracted from a CG-MD model initially developed for graphene.⁵⁰ Specifically, the bending stiffness in the current CG-MD model is two orders of magnitude higher to avoid buckling instability in the small strain regime. Note that most 2D materials behave linearly in the small strain regime while they exhibit strong non-linearity under large strains.^68–70 Notably the generic CG-MD may lose its capability in the large nonlinear deformation, but it suffices to study the Poisson's ratio of the proposed 2D lattice metamaterials in the small strain regime. Moreover, it would provide a theoretical limit for reference in the large strain regime.

Table 1 Parameters involved in the generic CG-MD potential for two-dimensional materials

Connection type	Analytical expression	Parameters
Bond 1	U bond(d1) = kbond1(d1 − d^01)^2	d ^01 = 2.8 Å
		k bond 1 = 20.46 eV Å^−2
Bond 2	U bond(d2) = kbond 2(d2 − d^02)^2	d ^02 = 2.8 Å
		k bond 2 = 2.56–20.46 eV Å^−2
Angle	U angle(θ) = kangle(θ − θ^0)^2	k angle = 17.75 eV
		θ ^0 = 90°
Dihedral	U dihedral(r) = kdihedral(1 − cos(2φ))	k dihedral = 100 × 0.180 eV

---

The simulation setup is briefly summarized as follows. The simulation box was fixed at 60 nm × 60 nm × 4 nm, in which periodic boundary conditions were applied along the x and y directions while shrink-boundary conditions were applied along the z direction. To perform a uniaxial tensile test, a strain-controlled loading method was adopted, in which a strain increment was added along the x direction every 10 000 time steps via elongation of the box while the lateral y direction was free to change through a pressure control set at 1 atm. The loading rate is around 1 × 10⁷ s⁻¹, falling into the conventional strain rate regime (10⁷ to 10⁹ s⁻¹) as commonly used in molecular dynamics studies.^71–73 To eliminate the effect of thermal fluctuations, temperature was controlled at around 1 K. Unless otherwise stated, time integration was performed on Nose–Hoover style non-Hamiltonian equations of motion from the isothermal–isobaric (NPT) ensemble,⁷⁴ in which the time step was set to 1 fs for both stability and accuracy. All the simulations were performed by implementing a parallel solver for molecular dynamics LAMMPS,⁷⁵ and the results were visualized through the OVITO⁷⁶ package.

3. Results and discussions

3.1 Deformation mechanism and geometry effect on Poisson's ratio

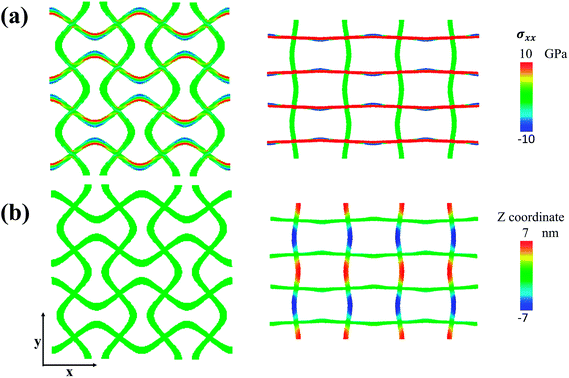
To obtain a comprehensive understanding of the auxeticity of our structure, the stress–strain and strain–strain behaviors of a typical sample were investigated first, in which the amplitude/wavelength ratio A is equal to 0.3, wavelength λ = 30 nm, and band width w = 2.4 nm. As shown in Fig. 2(a), the deformation history could be roughly divided into two stages, namely bending-dominated stage and stretching-dominated stage. The mechanical responses in the two stages are intrinsically different. In the bending-dominated stage, the axial group (marked in Fig. 1(a)) experiences both tension and bending due to its initial curved shape while the transverse group undergoes pure bending induced by bending of the axial group, resulting in unconventional transverse expansion under axial tension as shown in Fig. 2(a), which reveals a negative Poisson's ratio. In the bending-dominated stage, the local strain is much lower compared with the nominal strain of the whole sample, in which the deformation is mainly attributed to “rigid body rotation”. Consequently, the global nominal stress increases slowly. Simultaneously, the lateral expansion along the y direction is almost linearly related to the axial strain along the x direction as shown in Fig. 2(a), and the resultant Poisson's ratio is 0.625, which is in good agreement with the literature.³² Note that in this stage the out-of-plane buckling can be neglected as shown in Fig. 2(b). However, as the axial group is further “straightened” beyond a strain of 0.2, the transverse group tends to buckle to release its accumulated bending energy as we can see from Fig. 2(b). Profiles of the out-of-plane displacement can be found in Fig. S1 and S2 in the ESI material.† It can be seen that when the strain is below 0.2, the out-of-plane displacement for the entire structure is marginal, which is consistent with Fig. 2(b). Accordingly, the transverse group shrinks, and the whole sample experiences a sharp transition from negative Poisson's ratio to positive Poisson's ratio as shown in Fig. 2(a). In Fig. S1 and S2,† it can be seen that the out-of-plane displacement for the entire structure quickly increases when the strain is larger than 0.2, in which the shape of the entire structure is sinusoidal from the loading direction. Moreover, as the axial group is gradually straightened, instead of bending, stretching starts to dominate. Consequently, the nominal stress increases dramatically as shown in Fig. 2(a). The deformation patterns seen in the two different stages are further confirmed through the stress profile in the left-subfigure of Fig. 3(a). When the strain is equal to 0.1, it can be seen that the stress component σ_xx in the transverse group is around zero while σ_xx shows large variations in the axial group in which the stress is negative on one edge (compression) and positive (tension) on the other edge. Due to the unique structure, the transverse group cannot sustain loads along the x direction, while the axial group carries the most load along the x direction. Moreover, forces along the x direction not only induce tension inside the axial group but also produce bending, which cause rotation of the junctions, which also helps straighten out the transverse group. Consistent with Fig. 2(b), the out-of-plane coordinates of the whole sample are around zero as shown in the left sub-figure of Fig. 3(b) when strain is 0.1, indicating that there is no buckling in the bending-dominated stage. As the axial strain proceeds beyond 0.2, the load increment along the x direction can only generate minor bending moments due to the straightened shape of the axial group. Simultaneously, the axial group tends to be stretched rather than straightened under loads along the x direction. As shown in the right (0.4 strain) sub-figure of Fig. 3(a), the stress component σ_xx is positive in most areas of the axial group, despite several minor regions with negative stress when strain is equal to 0.4, indicating that the deformation is stretching-dominated. Meanwhile, the transverse group shows significant buckling as shown in the right (0.4 strain) sub-figure of Fig. 3(b), in which positive and negative z coordinates are expressed alternatively in adjacent regions within a single strand.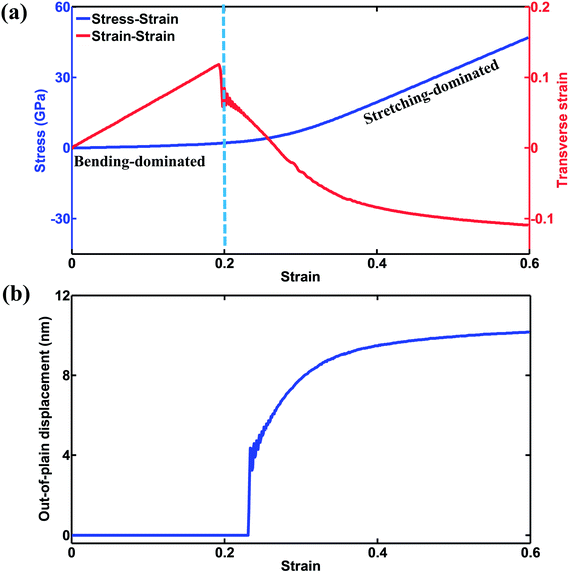

Fig. 2 (a) Stress–strain and strain–strain curves under uniaxial tension along the x direction. (b) Evolution of the out-of-plane displacement during uniaxial tensile tests along the x direction.

Fig. 3 Typical configurations under different deformation regimes colored by (a) axial stress along the x direction, and (b) out-of-plane displacement. Note that the images in the left column are extracted at a strain of 0.1 (bending-dominated) while images in the right column are extracted at a strain of 0.4 (stretching-dominated).

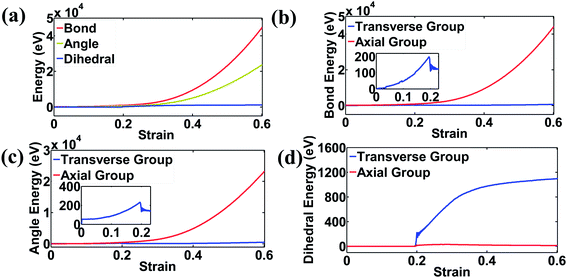
The energetic analysis results in Fig. 4 show the overall energy change classified as bond, angle and dihedral energy. As can be seen from Fig. 4(a), bond and angle energy changes are the main contributors to the global potential energy variation, while the dihedral energy change is at least one order of magnitude smaller than the former two terms, indicating the relative domination of in-plane deformation. Note that the angle energy change is significantly smaller than the bond energy change, indicating the larger role of bond energy towards in-plane deformation, which is consistent with the literature.⁵⁰ In accordance with Fig. 2(a), when the strain is below 0.2 (bending-dominated stage), the potential energy undergoes a slow increase, as the deformation at this stage is mainly attributed to “rigid body motion”. In contrast, in the stretching-dominated stage (>0.2 strain), the potential energy increases dramatically for all three terms, and most of the energy change comes from the axial group, as can be seen from Fig. 4(b) and (c). The transition between these two stages is reflected in the sharp potential energy drop in the graphs for bond and angle energies, as well as the sharp increase in the dihedral energy of the transverse group, as shown in the insets of Fig. 4(b–d).

Fig. 4 Potential energy evolution during the uniaxial tensile test along the x direction. (a) Global energy change. (b) Bond energy change for different groups. (c) Angle energy change for different groups. (d) Dihedral energy change for different groups.

As discussed in the literature,³² the amplitude/wavelength ratio is typically set as a relatively large value, such as 1/3, to ensure significant auxetic behaviors. However, a systematic understanding of the effect of amplitude/wavelength ratio is still lacking for topology optimization for proposed nanostructures. Next, a systematic parameter study is performed to understand the effect of amplitude/wavelength ratio (A) on the low-strain Poisson's ratio of the structure. As can be seen from Fig. 5(a), the curves can be divided into two stages, consistent with the results seen in Fig. 2(a). Interestingly, as A decreases, the critical strain for the transition from a negative Poisson's ratio to a positive Poisson's ratio will decrease, and is associated with an early out-of-plane buckling. Moreover, when A is 0.1, it can be seen that the strain–strain relation shows strong nonlinearity. Fig. 5(b) shows the relationship between the low-strain Poisson's ratio and A, in which the given Poisson's ratio has been calculated via a linear fitting of data points below a strain of 0.05. It can be observed that the magnitude of Poisson's ratio increases gradually and approaches 0.63, in good agreement with a value of 0.65 in the literature,³² as A increases. Due to this saturation effect, an amplitude of 0.3, falling into the saturation regime, is chosen for the amplitude in simulations hereafter. Note that wavelength λ and band width w also play an important role in the mechanical properties of the proposed 2D lattice structures, but these two geometrical parameters have a limited influence on the magnitude of Poisson's ratio,³² and are not investigated in this paper. Relevant results and discussions about the effect of wavelength λ and bandwidth w could be found in Fig. S3 in the ESI material.†

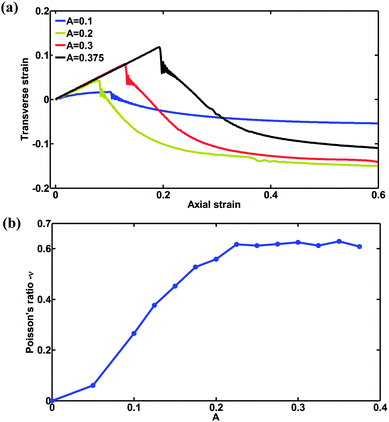Fig. 5 (a) Strain–strain responses for samples with different amplitude/wavelength ratios A as shown in Fig. 1(a). (b) Poisson's ratio versus amplitude/wavelength ratio A.

3.2 Effect of mechanical anisotropy

As is extensively investigated in the literature, 2D materials can exhibit exceptional mechanical performance, and among 2D materials some are isotropic while others are anisotropic.^{40–43,64–67} Moreover, due to the anisotropy of the underlying material, the Poisson's ratio of this proposed 2D lattice structure strongly depends on the stiffness ratio between the axial group and the transverse group, in which mechanical anisotropy plays a very important role. Therefore, it would be interesting to study the effect of stiffness ratio between the x and y directions on the magnitude of the Poisson's ratio, in order to expand our results to a plethora of potential 2D materials. In this section, the stiffness ratio, defined as the ratio between the Young's moduli in the x and y directions, can be tuned by varying the bond stiffness in the y direction, while the bond stiffness (and Young's modulus) in the x direction remains constant. Note that for stiffness ratios 8 and 0.125, tensile tests are performed for the same sample along the x and y directions, respectively, which is also true for stiffness ratios 2 and 0.5. Fig. 6(a) shows the strain–strain responses for samples with different stiffness ratios ranging from 0.125 to 8. The general trend of the curves is consistent with those in Fig. 2(a) and 5(a). However, significant differences are seen for the Poisson's ratio between samples with different stiffness ratios as shown in Fig. 6(b), in which the Poisson's ratio increases as the stiffness ratio increases. Additional all-atom molecular dynamics simulations are performed for isotropic molybdenum disulfide and anisotropic phosphorene as shown in Fig. S4 in the ESI material.† It can be seen that the resultant Poisson's ratios can be well fitted into the curve shown in Fig. 6(b), indicating that the stiffness ratio, or the ratio between Young's moduli of the x and y directions, is the dominating factor in determining the Poisson's ratio of the proposed 2D lattice structure among the given intrinsic mechanical properties of the material used.

Fig. 6 (a) Strain–strain responses for samples with different stiffness ratios, defined as the ratio between the Young's modulus along the x direction and that along the y direction. (b) Poisson's ratio versus stiffness ratio.

It is interesting to note that, for some cases, there would be a sharp transition of Poisson's ratio from negative to positive, indicating the out-of-plane buckling in Fig. 6 as well as Fig. 2, 5, and S3.† However, in other cases, there would be a smooth transition of Poisson's ratio from negative to zero as shown in Fig. 6 and S3.† Potential causes for these differences are detailed as follows: firstly, the out-of-plane buckling results from competition between out-of-plane bending and in-plane bending of transverse groups as shown in Fig. 1(a). Near the critical point, the huge bending energy stored in the transverse group would induce out-of-plane buckling. As shown in Fig. 4(b–d), the bond and angle energies, indicators of in-plane bending, experience a sharp drop while the dihedral energy, an indicator of out-of-plane buckling, experiences a sharp increase. Overall, the critical strain depends heavily on the ratio between out-of-plane bending stiffness and in-plane bending stiffness. Secondly, without out-of-plane buckling, Poisson's ratio of the lattice structures would experience a smooth transition from negative Poisson's ratio to zero Poisson's ratio as shown in Fig. 6(a) (stiffness ratio 8 and 0.125) and Fig. S3(c)† (width w = 1.2 nm). The negative Poisson's ratio at the initial stage results from the “straightening” and thus “elongation” of the transverse group induced by rotation of junctions due to the bending deformation of the axial group. In contrast, as the axial group is fully straightened out, the deformation of the axial group would not induce rotation of junctions, leading to zero Poisson's ratio. Given that the out-of-plane bending stiffness is sufficiently large, 2D lattice structures here would experience smooth transition from negative Poisson's ratio to zero Poisson's ratio.

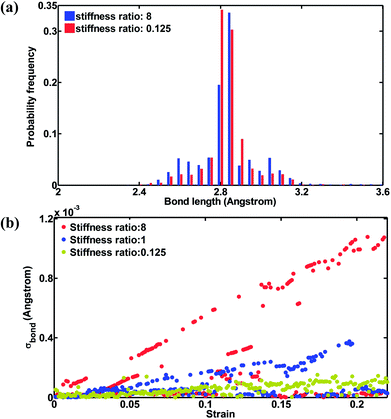
To understand the mechanical anisotropy effect from the perspective of the atomic structure, bond length changes are analyzed as shown in Fig. 7. Fig. 7(a) shows the bond length distribution of the transverse group when the axial strain is 0.2, in which the bond distribution for stiffness ratio 8 is skewed when compared with that for stiffness ratio 1. As discussed in Section 3.1, the transverse group experiences pure bending during uniaxial tension along the axial direction, and as such the bonds in the transverse group experience elongation or compression depending on the local bending moment generated. When the stiffness ratio is larger than 1, indicating that the initial bending stiffness of the transverse group is smaller than that of the axial group, the transverse group can be straightened more easily, comparatively. Consequently, the bonds in the transverse group experience larger changes in length than their counterparts when the stiffness ratio is no larger than 1, due to the difference in bond stiffness and geometry. This mechanism can be further confirmed in Fig. 7(b), which shows the standard deviation of bond lengths in the transverse group, σ_bond. As shown in Fig. 7(b), the values of σ_bond are larger at lower strain as the stiffness ratio increases from 0.125 to 1 to 8. The fluctuation of σ_bond could be attributed to the boundary conditions in the y direction, where pressure is controlled through controlling the box size in the transverse direction during axial elongation. Fig. 8 shows the stress profile at a strain of 0.2 for stiffness ratios of 8 and 0.125. It can be seen that the stress intensity of the transverse group for a stiffness ratio of 8 is lower and occurs over a smaller area. Based on the theory of elasticity, stress on a certain point of the cross section is proportional to both the curvature change and Young's modulus. For both cases with different stiffness ratios, the geometrical shapes of the transverse groups are identical. On the one hand, from Fig. 6(a), it can be seen that the transverse strain for a stiffness ratio of 8 is roughly 2 times that for a stiffness ratio of 0.125, indicating that the curvature change for a stiffness ratio of 8 is roughly 2 times that for a stiffness ratio of 0.125. On the other hand, the Young's modulus of the transverse group for a stiffness ratio of 8 is 0.125 times that of the transverse group for a stiffness ratio of 0.125. Therefore, at a given location, the stress of the transverse group for a stiffness ratio of 8 is roughly 0.25 times that for a stiffness ratio of 0.125. Consequently, the stress intensity for a stiffness ratio of 8 is much lower than that for a stiffness ratio of 0.125, as shown in Fig. 8. Overall, from these results, we can clearly see the major impact of stiffness anisotropy on the mechanical properties and behaviors of lattice-like metamaterials.

Fig. 7 (a) Bond length distribution of the transverse group for samples with different stiffness ratios when strain is 0.2. (b) Evolution of the standard deviation of bonds σ_bond for the transverse group from samples with different stiffness ratios.

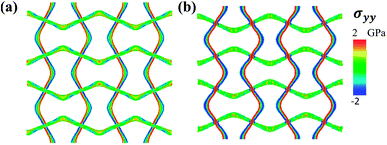Fig. 8 Global stress profile when strain is 0.2. (a) Stiffness ratio of 8. (b) Stiffness ratio of 0.125.

4. Conclusions

In this paper, we investigate the auxeticity of the proposed 2D lattice structure made of 2D materials through a systematic study of the effects of both geometrical factors and tuned mechanical anisotropy through implementing CG-MD simulations. First, the results indicate that the deformation of the proposed 2D lattice structure can be divided into two stages, namely bending-dominated, in which the Poisson's ratio is constant and negative, and stretching-dominated, where the Poisson's ratio becomes positive. The auxeticity could be attributed to the cooperative deformation of the axial group and the transverse group, where the bending moment generated by tension on the axial group causes rotation of the axial/transverse junctions, thus straightening out the transverse group. The transition between bending-dominated and stretching-dominated stages is associated with out-of-plane buckling, leading to the transition from a negative to a positive Poisson's ratio. Second, a systematic study of the effect of geometrical factors on Poisson's ratio reveals that it increases with the increase of amplitude/wavelength ratio A, representing the curvature of the beams, and that the Poisson's ratio reaches saturation at A = 0.225. Finally, the effect of mechanical anisotropy of the underlying 2D material forming the lattice on the structure's auxeticity is investigated. The results indicate that the magnitude of Poisson's ratio increases with the increase of the stiffness ratio between Young's moduli in the loading direction and the transverse direction. Additional all-atom MD simulations for phosphorene, graphene, and molybdenum disulfide were also performed to validate the relationship observed between the stiffness ratio and Poisson's ratio, indicating the general applicability of the obtained rule to 2D materials. The above relationship between the stiffness ratio and Poisson's ratio could be attributed to the cooperative deformation of the transverse and axial groups, in which the transverse group is more easily straightened at lower stiffness. Overall, these research findings can provide useful guidelines for the design of auxetic 2D lattice structures composed of anisotropic 2D materials, allowing for a tunable negative Poisson's ratio.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

N. L. and X. W. acknowledge the support from the National Science Foundation (Grant No. CMMI-1610812).

References

1. L. Wang and M. C. Boyce, Bioinspired Structural Material Exhibiting Post-Yield Lateral Expansion and Volumetric Energy Dissipation During Tension, Adv. Funct. Mater., 2010, 20, 3025–3030.
2. Q. Zhang, X. Xu, D. Lin, W. Chen, G. Xiong and Y. Yu, et al. Hyperbolically Patterned 3D Graphene Metamaterial with Negative Poisson's Ratio and Superelasticity, Adv. Mater., 2016, 28, 2229–2237.
3. J.-H. Lee, J. P. Singer and E. L. Thomas, Micro-/Nanostructured Mechanical Metamaterials, Adv. Mater., 2012, 24, 4782–4810.
4. T. Frenzel, C. Findeisen, M. Kadic, P. Gumbsch and M. Wegener, Tailored Buckling Microlattices as Reusable Light-Weight Shock Absorbers, Adv. Mater., 2016, 28, 5865–5870.
5. W. Yang, Q. Liu, Z. Gao, Z. Yue and B. Xu, Theoretical search for heterogeneously architected 2D structures, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, E7245–E7254.
6. J. Christensen, M. Kadic, O. Kraft and M. Wegener, Vibrant times for mechanical metamaterials, MRS Commun., 2015, 5, 453–462.
7. M. K. Blees, A. W. Barnard, P. A. Rose, S. P. Roberts, K. L. McGill and P. Y. Huang, et al. Graphene kirigami, Nature, 2015, 524, 204.
8. J. N. Grima, S. Winczewski, L. Mizzi, M. C. Grech, R. Cauchi and R. Gatt, et al. Tailoring Graphene to Achieve Negative Poisson's Ratio Properties, Adv. Mater., 2015, 27, 1455–1459.
9. X. Zheng, W. Smith, J. Jackson, B. Moran, H. Cui and D. Chen, et al. Multiscale metallic metamaterials, Nat. Mater., 2016, 15, 1100.
10. J. Bauer, A. Schroer, R. Schwaiger and O. Kraft, Approaching theoretical strength in glassy carbon nanolattices, Nat. Mater., 2016, 15, 438.
11. J. B. Berger, H. N. G. Wadley and R. M. McMeeking, Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness, Nature, 2017, 543, 533.
12. E. T. Filipov, T. Tachi and G. H. Paulino, Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials, Proc. Natl. Acad. Sci. U.S.A., 2015, 112, 12321–12326.
13. H. Yasuda, T. Tachi, M. Lee and J. Yang, Origami-based tunable truss structures for non-volatile mechanical memory operation, Nat. Commun., 2017, 8, 962.
14. B. Haghpanah, L. Salari-Sharif, P. Pourrajab, J. Hopkins and L. Valdevit, Multistable Shape-Reconfigurable Architected Materials, Adv. Mater., 2016, 28, 7915–7920.
15. S. Jianfeng, H. Yizhe, L. Chen, Q. Chen and Y. Mingxin, Synthesis of Amphiphilic Graphene Nanoplatelets, Small, 2009, 5, 82–85.
16. N. Levy, S. A. Burke, K. L. Meaker, M. Panlasigui, A. Zettl and F. Guinea, et al. Strain-Induced Pseudo–Magnetic Fields Greater Than 300 Tesla in Graphene Nanobubbles, Science, 2010, 329, 544–547.
17. S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Penta-graphene: A new carbon allotrope, Proc. Natl. Acad. Sci. U.S.A., 2015, 112, 2372–2377.
18. B. F. Grosso and E. J. Mele, Bending Rules in Graphene Kirigami, Phys. Rev. Lett., 2015, 115, 195501.
19. Z. Qi, D. K. Campbell and H. S. Park, Atomistic simulations of tension-induced large deformation and stretchability in graphene kirigami, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245437.
20. Y. Zhao, C. Wang, J. Wu, C. Sui, S. Zhao and Z. Zhang, et al. Carbon nanotubes kirigami mechanical metamaterials, Phys. Chem. Chem. Phys., 2017, 19, 11032–11042.
21. L. Tapasztó, G. Dobrik, P. Lambin and L. P. Biró, Tailoring the atomic structure of graphene nanoribbons by scanning tunnelling microscope lithography, Nat. Nanotechnol., 2008, 3, 397.
22. J. Annett and G. L. W. Cross, Self-assembly of graphene ribbons by spontaneous self-tearing and peeling from a substrate, Nature, 2016, 535, 271.
23. P. Z. Hanakata, Z. Qi, D. K. Campbell and H. S. Park, Highly stretchable MoS2 kirigami, Nanoscale, 2016, 8, 458–463.
24. Y. Wang, A. Vallabhaneni, J. Hu, B. Qiu, Y. P. Chen and X. Ruan, Phonon Lateral Confinement Enables Thermal Rectification in Asymmetric Single-Material Nanostructures, Nano Lett., 2014, 14, 592–596.
25. Y. Gao, W. Yang and B. Xu, Tailoring Auxetic and Contractile Graphene to Achieve Interface Structures with Fully Mechanically Controllable Thermal Transports, Adv. Mater. Interfaces, 2017, 4, 1700278.
26. O. Akhavan, Graphene Nanomesh by ZnO Nanorod Photocatalysts, ACS Nano, 2010, 4, 4174–4180.
27. A. Miyamoto, S. Lee, N. F. Cooray, S. Lee, M. Mori and N. Matsuhisa, et al. Inflammation-free, gas-permeable, lightweight, stretchable on-skin electronics with nanomeshes, Nat. Nanotechnol., 2017, 12, 907.
28. S. Xu, Y. Zhang, J. Cho, J. Lee, X. Huang and L. Jia, et al. Stretchable batteries with self-similar serpentine interconnects and integrated wireless recharging systems, Nat. Commun., 2013, 4, 1543.
29. J. A. Fan, W.-H. Yeo, Y. Su, Y. Hattori, W. Lee and S.-Y. Jung, et al. Fractal design concepts for stretchable electronics, Nat. Commun., 2014, 5, 3266.
30. J. Liu and Y. Zhang, A Mechanics Model of Soft Network Materials With Periodic Lattices of Arbitrarily Shaped Filamentary Microstructures for Tunable Poisson's Ratios, J. Appl. Mech., 2018, 85, 051003.
31. D. Mousanezhad, S. Babaee, R. Ghosh, E. Mahdi, K. Bertoldi and A. Vaziri, Honeycomb phononic crystals with self-similar hierarchy, Phys. Rev. B, 2015, 92, 104304.
32. Y. Chen, T. Li, F. Scarpa and L. Wang, Lattice Metamaterials with Mechanically Tunable Poisson's Ratio for Vibration Control, Phys. Rev. Appl., 2017, 7, 024012.
33. N. I. Zheludev and E. Plum, Reconfigurable nanomechanical photonic metamaterials, Nat. Nanotechnol., 2016, 11, 16.
34. Y. Tang, G. Lin, S. Yang, Y. K. Yi, R. D. Kamien and J. Yin, Programmable Kiri-Kirigami Metamaterials, Adv. Mater., 2017, 29, 1604262.
35. A. A. Balandin, Thermal properties of graphene and nanostructured carbon materials, Nat. Mater., 2011, 10, 569.
36. N. Wei, Y. Chen, K. Cai, J. Zhao, H.-Q. Wang and J.-C. Zheng, Thermal conductivity of graphene kirigami: Ultralow and strain robustness, Carbon, 2016, 104, 203–213.
37. Y. Gao and B. Xu, Controllable Interface Junction, In-Plane Heterostructures Capable of Mechanically Mediating On-Demand Asymmetry of Thermal Transports, ACS Appl. Mater. Interfaces, 2017, 9, 34506–34517.
38. Z. Gao, D. Liu and D. Tománek, Two-Dimensional Mechanical Metamaterials with Unusual Poisson Ratio Behavior, Phys. Rev. Appl., 2018, 10, 064039.
39. N. Karathanasopoulos, H. Reda and J.-f Ganghoffer, Designing two-dimensional metamaterials of controlled static and dynamic properties, Comput. Mater. Sci., 2017, 138, 323–332.
40. C. Lee, X. D. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385–388.
41. R. E. Roman and S. W. Cranford, Mechanical properties of silicene, Comput. Mater. Sci., 2014, 82, 50–55.
42. A. A. Tedstone, D. J. Lewis, R. Hao, S.-M. Mao, P. Bellon and R. S. Averback, et al. Mechanical Properties of Molybdenum Disulfide and the Effect of Doping: An in Situ TEM Study, ACS Appl. Mater. Interfaces, 2015, 7, 20829–20834.
43. Q. Wei and X. H. Peng, Superior mechanical flexibility of phosphorene and few-layer black phosphorus, Appl. Phys. Lett., 2014, 104, 5.
44. T. von Kármán Festigkeitsprobleme im maschinenbau, Teubner, 1910.
45. D. A. Foppl Vorlesungen uber technische mechannik, 1909.
46. C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene, Science, 2008, 321, 385–388.
47. P. Koskinen and O. O. Kit, Approximate modeling of spherical membranes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235420.
48. M. Arroyo and T. Belytschko, Finite crystal elasticity of carbon nanotubes based on the exponential Cauchy-Born rule, Phys. Rev. B, 2004, 69, 115415.
49. X. Si and C. Guoxin, Bending response of single layer MoS 2, Nanotechnology, 2016, 27, 105701.
50. L. Ruiz, W. Xia, Z. Meng and S. Keten, A coarse-grained model for the mechanical behavior of multi-layer graphene, Carbon, 2015, 82, 103–115.
51. S. Cranford, D. Sen and M. J. Buehler, Meso-origami: Folding multilayer graphene sheets, Appl. Phys. Lett., 2009, 95, 123121.
52. F. Javid, E. Smith-Roberge, M. C. Innes, A. Shanian, J. C. Weaver and K. Bertoldi, Dimpled elastic sheets: a new class of non-porous negative Poisson's ratio materials, Sci. Rep., 2015, 5, 18373.
53. G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Poisson's ratio and modern materials, Nat. Mater., 2011, 10, 823.
54. Y. Cho, J.-H. Shin, A. Costa, T. A. Kim, V. Kunin and J. Li, et al. Engineering the shape and structure of materials by fractal cut, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 17390–17395.
55. D. Lu, Y. F. Li, H. Seifi, S. Zhou, Z.-L. Zhao and Y. M. Xie, Designing novel structures with hierarchically synchronized deformations, Extreme Mech. Lett., 2018, 19, 1–6.
56. K.-I. Jang, S. Y. Han, S. Xu, K. E. Mathewson, Y. Zhang and J.-W. Jeong, et al. Rugged and breathable forms of stretchable electronics with adherent composite substrates for transcutaneous monitoring, Nat. Commun., 2014, 5, 4779.
57. K.-I. Jang, H. U. Chung, S. Xu, C. H. Lee, H. Luan and J. Jeong, et al. Soft network composite materials with deterministic and bio-inspired designs, Nat. Commun., 2015, 6, 6566.
58. Q. Ma, H. Cheng, K.-I. Jang, H. Luan, K.-C. Hwang and J. A. Rogers, et al. A nonlinear mechanics model of bio-inspired hierarchical lattice materials consisting of horseshoe microstructures, J. Mech. Phys. Solids, 2016, 90, 179–202.
59. C. Thurnherr, L. Ruppen, G. Kress and P. Ermanni, Non-linear stiffness response of corrugated laminates in tensile loading, Compos. Struct., 2016, 157, 244–255.
60. W. Yang, V. R. Sherman, B. Gludovatz, E. Schaible, P. Stewart and R. O. Ritchie, et al. On the tear resistance of skin, Nat. Commun., 2015, 6, 6649.
61. S. Ling, Q. Zhang, D. L. Kaplan, F. Omenetto, M. J. Buehler and Z. Qin, Printing of stretchable silk membranes for strain measurements, Lab Chip, 2016, 16, 2459–2466.
62. P. Chamiot-Clerc, X. Copie, J.-F. Renaud, M. Safar and X. Girerd, Comparative reactivity and mechanical properties of human isolated internal mammary and radial arteries, Cardiovasc. Res., 1998, 37, 811–819.
63. K. Bertoldi, V. Vitelli, J. Christensen and M. van Hecke, Flexible mechanical metamaterials, Nat. Rev. Mater., 2017, 2, 17066.
64. N. Liu, R. Pidaparti and X. Wang, Abnormal linear elasticity in polycrystalline phosphorene, Phys. Chem. Chem. Phys., 2018, 20, 8668–8675.
65. N. Liu, J. Hong, X. Zeng, R. Pidaparti and X. Wang, Fracture mechanisms in multilayer phosphorene assemblies: from brittle to ductile, Phys. Chem. Chem. Phys., 2017, 19, 13083–13092.
66. N. Liu, J. Hong, R. Pidaparti and X. Wang, Fracture patterns and the energy release rate of phosphorene, Nanoscale, 2016, 8, 5728–5736.
67. L. Ning, H. Jiawang, P. Ramana and W. Xianqiao, Abnormality in fracture strength of polycrystalline silicene, 2D Materials, 2016, 3, 035008.
68. S. J. Stuart, A. B. Tutein and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys., 2000, 112, 6472–6486.
69. J. Jin-Wu, Parametrization of Stillinger–Weber potential based on valence force field model: application to single-layer MoS 2 and black phosphorus, Nanotechnology, 2015, 26, 315706.
70. Q. Peng, X. Wen and S. De, Mechanical stabilities of silicene, RSC Adv., 2013, 3, 13772–13781.
71. G. Jung, Z. Qin and M. J. Buehler, Molecular mechanics of polycrystalline graphene with enhanced fracture toughness, Extreme Mech. Lett., 2015, 2, 52–59.
72. W. J. Xia and S. Keten, Size-dependent mechanical behavior of free-standing glassy polymer thin films, J. Mater. Res., 2015, 30, 36–45.
73. T. Zhang, X. Li, S. Kadkhodaei and H. Gao, Flaw Insensitive Fracture in Nanocrystalline Graphene, Nano Lett., 2012, 12, 4605–4610.
74. E. T. Mark, A. José, L.-R. Roberto, L. J. Andrea and J. M. Glenn, A Liouville-operator derived measure-preserving integrator for molecular dynamics simulations in the isothermal–isobaric ensemble, J. Phys. A: Math. Gen., 2006, 39, 5629.
75. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19.
76. S. Alexander, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00312f

---