Open Access Article
Open Access ArticleUnravelling the effects of size, volume fraction and shape of nanoparticle additives on crystallization of nanocomposite polymers†
Ahmad
Jabbarzadeh
 *ab and
Beny
Halfina
a
*ab and
Beny
Halfina
a
aFaculty of Engineering, School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, NSW 2006, Australia. E-mail: ahmad.jabbarzadeh@sydney.edu.au
bSydney Nano Institute, The University of Sydney, NSW 2006, Australia
First published on 17th October 2019
Abstract
We conducted large scale molecular dynamics simulations to understand the effects of size, shape and volume fraction of additive nanoparticles on the crystallization of nanocomposite polymers. We used spherical and cubic gold nanoparticles of various sizes ranging from 2 to 8 nm to create hexacontane (C60H122)–gold nanocomposites at various volume fractions of 0.84–19.27%. We show that, regardless of the shape, decreasing the size of particles at the same volume fraction results in decreased final crystallinity. Similarly, for the same particle size, increasing the volume fraction causes a decrease in the crystal growth rate and final crystallinity. We demonstrate that this is a confinement induced phenomenon, and the free interparticle space captures the combined effects of particle size and volume fraction. If this free space is smaller than the extended length of the molecule or the characteristic size of the crystal lamella thickness of the polymer, significant slow-down in crystallinity will emerge. In this confinement limit, the interparticle free space controls the crystal growth rate and final crystallinity. We have developed the equations that predict the critical volume fraction (φcr) for a given size or critical size (Dcr) for a given volume fraction. For φ > φcr or D < Dcr, one would expect confinement induced retardation of crystallization. We also show that cubic particles result in a higher growth rate and crystallinity in comparison to spherical particles, purely due to their shape. Furthermore, cubic particles due to flat surfaces lead to distinct two-tier crystallisation kinetics manifested by enhanced crystallization at the early stage of crystallization, followed by slow crystallization due to confinement effects. This two-tier crystallization is more distinct at higher volume fractions. For spherical particles, however, this two-tier crystallization is almost absent and molecular crystallization near the particle is frustrated by the curved shape of the nanoparticle.
1 Introduction
Understanding crystallization of polymers in the presence of secondary nanomaterials added to the melt such as nano-fillers, nucleating agents, conducting agents, colourants and reinforcing materials is of great importance in polymer processing and developing a new generation of hybrid nanomaterials. These secondary materials come in a variety of shapes, sizes, and quantities, and it is well known that their presence changes many properties of the end product. Additive nanoparticles are mixed with polymers for a variety of reasons, for example, nanofiller particles to make nanocomposites, conductive metallic nanoparticles such as gold, silver, and graphene to change the electrical properties of the polymer, and nucleating agents to provide heterogeneous nucleation surfaces for semicrystalline polymers. Experimental and modelling practitioners have studied the mechanical and structural properties of nanocomposite polymers for the past two decades, and excellent recent reviews1–3 offer a glimpse of the tremendous advancements in this field. A recent perspective review by Kumar et al.2 suggests the absence of explanation for the role of nanofillers in crystallization of polymers in simulation studies, as a critical missing piece of investigations in this area. The effect of nanoparticles on the crystallization of polymers is complex, and the experimental evidence in the literature suggests seemingly contradictory results. Some studies suggested reduced crystallization4,5 and some enhanced crystallization,6 and some reported no effect at all.7 Additive particles come in a variety of sizes and shapes and are mixed with the base polymer at various volume fractions. Therefore, unravelling the effects of shape, size, and volume fraction should help to explain some of the contradictions in the experiments and lead to optimized formulations for controlling the crystallinity of nanocomposite and hybrid materials.Experiments have shown the effect of additives on the morphology of low-density polyethylene8 and paraffin.9 Experimental studies have proved the strong effect of fibre inclusion on the crystallization kinetics and nucleation rate of poly(ethylene terephthalate) or PET.10,11 Experiments have shown the effect of talc additives on crystallization kinetics of semicrystalline poly(ether ether ketone) (PEEK)12 by using the Avrami model. In these experiments, two-tier crystallization is observed where nano-sized talc particles enhanced nucleation while impeding the growth rate. That is the time it took to crystallize the nanocomposite polymer increased by increasing the %wt of the talc nanoparticles. Similar two-tier crystallization was observed in experiments by Weng et al.13 who measured the effect of nano-graphite particles on the kinetics of crystallization of nylon-6. They found that while the half crystallization time decreased by adding the nano graphite particles, the total crystallization time increased. Furthermore, fitting the data to the Avrami model showed 3D growth for pure nylon-6 and 1D growth for the graphite–nylon6 nanocomposite. Experiments15 have also shown that shear-induced crystallization of isotactic polypropylene (iPP) is affected by the shape of the colourant used. It is shown that a spherical sodium aluminosulfosilicate or ultramarine blue (UB) colourant leads to a different morphology than that obtained with a Cu-phthalocyanine (CuPc) colourant which has a planar shape.14 The effect of surface topography of additives on the crystallization of polyolefins has been theoretically elaborated by Binsbergen16 who had ruled out the effect of epitaxial growth and particle size on the nucleation. Binsbergen has postulated that long stepwise ditches on a surface allow for alignment of the molecules and that subsequently enhances the crystallization. However, later studies by Wittmann and Lotz17 demonstrated the effect of epitaxy in the nucleating power of added particles. D'Haese et al.18,19 investigated the effect of the size,18 shape and concentration19 of nucleating particles in quiescent and flow-induced crystallization of iPP. Their initial work using 0.16% vol fraction zinc oxide spherical particles of different sizes of 35, 200, and 500, suggested that particle size did not have a measurable effect on the crystallization kinetics despite the expectation of seeing a link between the specific surface of the particle and nucleating efficiency.18 They did, however, report that under quiescent conditions a nanocomposite polymer with 200 nm particles crystallized much slower than that with 500 nm particles.18 They considered mostly spherical and oblate particles with different aspect ratios and showed that the crystallization time decreased when increasing the aspect ratio of the oblate particles. A series of experiments on polyethylene oxide (PEO) nanocomposites loaded with spherical silica particles have revealed the most interesting results. Using 25 nm grafted silica nanoparticles as a filler, Khan et al.5 showed that the final crystallinity of the nanocomposites decreases when increasing the % w loading of the silica particles. They showed that even at 10 w% loading there is a reduction in crystallinity. Zhao et al.20 using a similar poly(ethylene oxide)/grafted silica nanocomposite system compared the crystallization kinetics for 10 and 20 w% and neat PEO and reported a reduced rate of crystallization when increasing the volume fraction of the nanoparticles; however no significant effect on the final crystallinity was observed after long crystallization times. Papananou et al.21 studied the effect of the volume fraction and particle size of uncoated spherical silica particles on the final crystallinity of PEO nanocomposites. They used silica nanoparticles of 7–67 nm radius over a wide range of volume fractions. They reported that at the same volume fraction, decreasing the particle size results in a decrease in crystallinity. They also showed that for each particle size there is a critical volume fraction at which the crystallization slows down in comparison to that of the neat PEO.
While the experiments have shed some light on this complex problem, it has been difficult to control the shape of particles accurately, and larger particles often form aggregates with rough surfaces.19 This has made it difficult to discern the effects of volume fraction, effective surface area, and size and shape of the particles on crystallization. Computational modelling offers an alternative approach to study polymer crystallization under controlled conditions. We have previously used large scale molecular simulations to study polymer crystallization under quiescent22 and flow conditions23 and also to investigate surface-induced effects and crystallization.24,25 Dynamic Monte Carlo simulations have been used to study the effect of molecular anti plasticizer additive concentrations on crystallization.26 Daan Frenkel's group27 performed Monte Carlo simulations of hard colloid particle crystallization near surfaces of concave and convex additive particles. They studied the effect of additive particle size and curvature on nucleation. They showed that “flatter” additive particles with a larger radius (lower curvature) enhance the nucleation more than those with larger curvature. This phenomenon is attributed to the epitaxial effects of flatter surfaces. Atomistic molecular simulation of bulk polymers of complex shape in the presence of additives is scarce due to high computational requirements. However, attempts have been made to make coarse grained CG28 models and reduce computational needs. Yang et al.29 simulated crystallisation of polyethelene/fluorene composites as an isolated nanoparticle in a vacuum and showed that the crystalline content decreased when increasing the fluorene content. However, we are not aware of molecular simulations of bulk nanocomposites under constant pressure conditions, where the effects of size, shape and volume fraction are methodologically investigated.
To shed light on some of the contradictory results in the literature, and to understand the effect of nano-sized additive particles on polymer crystallization, we have conducted molecular dynamics simulations. In this work, we will consider the effect of particle size, volume fraction and shape only under quiescent crystallization. To keep the computational needs accessible, we have used n-hexacontane (C60H122, referred to as C60), a long linear alkane with 60 monomers. The molecule is a shorter version of polyethylene (PE) and is sufficiently long to show proper folding and crystallization features of polymeric materials. The crystallization time for this system is short enough to be studied by MD simulations which can typically cover tens of nanoseconds. We have used spherical particles of various diameters between 2.07 and 7.93 nm and cubic particles with sizes in the range of 1.27–6.44 nm. The simulations cover cases where effects of characteristic particle size, volume fraction, surface area, and shape are systematically studied. Here the objective is to isolate the effects of these parameters on the crystallization kinetics and final crystallinity. We have fitted the results in many cases to the Avrami model to obtain information on the growth rate and dimensionality. Also, we have analysed the crystal growth mechanism near the additive nanoparticle surfaces by calculating spatio-temporal properties during the crystallization process. The results provide a detailed picture of the crystal growth mechanism and the effect of volume fraction, size and shape of additive particles.
2 Methodology and results
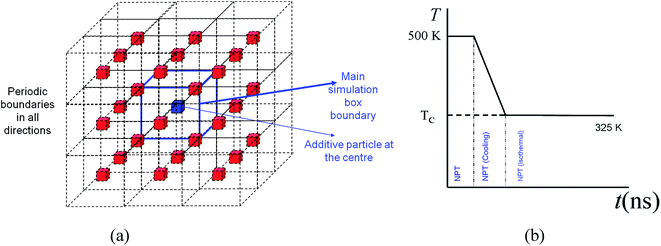
The simulations are conducted in four separate steps. The first step is to produce the polymer melt and additive particle. In this step, the molecular simulations are conducted at 500 K with the solid inclusion representing the additive nanoparticle placed at the centre of the simulation box. Therefore only one additive particle is simulated with the polymer melt surrounding the particle. Periodic boundary conditions (see Fig. 1a) are applied in all three dimensions so that the system represents uniformly distributed monodisperse additive nanoparticles in a matrix of the polymer melt. The system is then equilibrated under NVT conditions to allow for diffusion of the polymer melt molecules and creating a homogenous system. The system is further equilibrated under constant pressure (P = 1 atm) and isothermal conditions (T = 500 K). At this NPT stage, the simulation box is allowed to contract or expand. This process produces a melt with natural density at 500 K. In the fourth and final stage, the system is cooled under NPT conditions to a temperature of 325 K and is allowed to crystallize for an extended time of 37.6–56 ns. The contraction of the simulation box takes place during natural densification of the system under NPT conditions. Therefore the distance between the particles changes only slightly due to this densification. This assumption is validated by experimental evidence in the work of Khan et al.,5 who performed careful experiments to produce well-dispersed silica–PEO nanocomposite systems. Using small-angle X-ray scattering (SAXS), they measured the mean distance between silica nanoparticles in the melt and solidified state. Khan et al. concluded that the average particle spacing was essentially unchanged when the nanocomposite sample cooled below a crystallization temperature. In our model, we assume that the particles are well dispersed and there is no aggregation. Khan et al. also reported that there was no large scale particle aggregation.5 We note that MD simulations of a multi-particle system that includes a broad interparticle distance distribution are not feasible due to computational constraints. Nevertheless, the assumptions made here for modelling are reasonable and evidence-based and, as will be demonstrated later, can capture essential trends observed in experiments.2.1 Molecular model
A united atom molecular model is used in this work and the details can be found in our earlier work.22,30 In this model, the CH2 and CH3 groups of atoms on the linear hexacontane molecules are treated as single interaction sites. Intra-molecular interactions are governed through bond stretching and torsional and angle bending potentials. The non-bonded van der Waals interactions are governed by a 6-12 Lennard-Jones potential which is cut off at a radius of rc = 2.5σ = 0.9825 nm, where σ = 0.393 nm is the LJ length parameter of the methyl–methyl interaction. LJ interaction parameters for unlike groups i and j are calculated using Lorentz–Berthelot's combining rules so that εij = (εiεj)1/2 and σij = (σi + σj)/2.The additive nanoparticles are made of gold atoms and have an FCC structure, with lattice parameters a = b = c = 0.408 nm. For the simulations here the additive nanoparticle atoms have length and energy parameters of σw = 0.288 nm and εw = 2.25εCH2 = 239 K. Spherical and cubic particles are cut from a slab of gold to the nearest given diameter or size. In all cases, the additive particles are kept fixed at the centre of the simulation box. Experimental evidence has suggested that the distance between nanoparticles dispersed in a polymer remains mostly unchanged during crystallization.5 Therefore the particle is kept fixed at the centre of the simulation box. While for spherical particles there is no orientational preference, for cubic particles a mono-orientational system, as shown in Fig. 1a, is used. This approach allows us to use a single additive particle and saves significant computational time. To obtain an accurate picture of the effect of the particle size, D, (diameter for sphere and length for cube), the volume fraction, φ, was kept almost constant. Composite systems were created at φ = 6.75% by spherical particles of different sizes between D = 2.37–7.93 nm and by cubic particles of D = 1.94–6.41 nm. By using smaller particles of 1.55–3.1 nm for spherical additives and 1.26–2.51 nm for cubic particles, systems were also created at a lower volume fraction of 0.84%.
To isolate the effect of the volume fraction, φ, the nominal particle size was kept constant. We used spherical particles of 5.5 nm, and systems at volume fractions between 2.31 and 18.49% were created. For cubic additives, we created systems at a similar range of volume fractions 2.33–19.27% using a particle of 4.5 nm nominal size.
To save computational time, nanoparticles whose size was larger than 3.1 nm (much larger than twice the cut-off rc = 0.96 nm), a hollow core was used. To meet the periodic boundary conditions, in some instances the actual size and volume fraction of the particles were slightly different from the nominal size and volume fraction. The actual sizes and volume fractions are listed in Table 1. In most cases, the resulting size and volume fraction values for corresponding cubic and spherical particle systems were less than 1% different from the target values and were not larger than 4%. In all calculations, the actual size and volume fractions, as displayed in Table 1, are used. Fig. 2 shows the snapshots of cubic and spherical additive particles of 5 different sizes. The numerical values for various simulations can be found in Table 1.
| D, particle size [nm] | A, particle surface area [nm2] | V p, particle volume [nm3] | φ, volume fraction% | R ee/D, extended C60H122 molecule to particle size ratio | Number of united atoms of polymer (hexacontane C60H122) |
|---|---|---|---|---|---|
| Pure polymer with no additives | |||||
| — | — | — | — | — | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Spherical additives with different sizes and volume fractions (control) ( Fig. 8 ) | |||||
| 4.16 | 54.41 | 37.74 | 2.00 | 1.83 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 3.11 | 30.37 | 15.740 | 0.840 | 2.45 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cubic additives with the same nominal volume fractions as the control ( Fig. 8 ) | |||||
| 3.36 | 67.75 | 37.95 | 2.01 | 2.27 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 2.51 | 37.76 | 15.79 | 0.85 | 3.04 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Spherical additives with different sizes and the same nominal volume fraction (φ ∼ 0.84) ( Fig. 3a ) | |||||
| 3.11 | 30.37 | 15.74 | 0.84 | 2.45 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 2.72 | 23.25 | 10.54 | 0.84 | 2.80 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
| 2.33 | 17.08 | 6.64 | 0.84 | 3.27 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
| 1.94 | 11.86 | 3.84 | 0.84 | 3.92 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 1.55 | 7.59 | 1.97 | 0.84 | 4.90 | 7680 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cubic additives with different sizes and the same volume fraction (φ ∼ 0.84) ( Fig. 3b ) | |||||
| 2.51 | 37.76 | 15.79 | 0.85 | 3.04 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 2.20 | 28.92 | 10.58 | 0.85 | 3.47 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
| 1.88 | 21.26 | 6.67 | 0.85 | 4.05 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
| 1.57 | 14.77 | 3.86 | 0.86 | 4.86 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 1.27 | 9.47 | 1.98 | 0.85 | 6.07 | 7680 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Spherical additives with different sizes and the same nominal volume fraction (φ ∼ 6.75%) ( Fig. 4a ) | |||||
| 7.93 | 197.51 | 261.01 | 6.74 | 0.96 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 7.14 | 159.98 | 190.27 | 6.74 | 1.07 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
| 6.34 | 126.40 | 133.63 | 6.75 | 1.20 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 5.55 | 96.78 | 89.53 | 6.74 | 1.37 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
| 4.76 | 71.10 | 56.37 | 6.74 | 1.60 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
| 3.96 | 49.37 | 32.62 | 6.74 | 1.92 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 3.17 | 31.60 | 16.70 | 6.74 | 2.40 | 7680 |
| 2.38 | 17.77 | 7.05 | 6.75 | 3.20 | 3240 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cubic additives with different sizes and the same nominal volume fraction (φ ∼ 6.75%) ( Fig. 4b ) | |||||
| 6.41 | 246.68 | 263.61 | 6.80 | 1.19 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 5.77 | 199.96 | 192.39 | 6.81 | 1.32 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
| 5.13 | 158.15 | 135.32 | 6.87 | 1.48 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 4.50 | 121.24 | 90.84 | 6.81 | 1.70 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
| 3.86 | 89.23 | 57.35 | 6.89 | 1.98 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
| 3.22 | 62.12 | 33.31 | 6.87 | 2.37 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 2.58 | 39.91 | 17.16 | 6.92 | 2.95 | 7680 |
| 1.94 | 22.61 | 7.31 | 7.08 | 3.93 | 3240 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Spherical additives with different volume fractions and the same nominal size (∼5.5 nm) ( Fig. 6a ) | |||||
| 5.48 | 93.92 | 85.59 | 2.31 | 1.39 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 5.47 | 94.46 | 86.33 | 3.17 | 1.39 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
| 5.55 | 96.78 | 89.53 | 4.62 | 1.37 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 5.55 | 96.78 | 89.53 | 6.74 | 1.37 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
| 5.63 | 99.53 | 93.38 | 10.69 | 1.35 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
| 5.80 | 105.57 | 101.99 | 18.47 | 1.31 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cubic additives with different volume fractions and the same nominal size (∼4.5 nm) ( Fig. 6b ) | |||||
| 4.45 | 117.27 | 86.41 | 2.33 | 1.71 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 4.45 | 118.00 | 87.22 | 3.20 | 1.71 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
| 4.45 | 119.18 | 88.53 | 4.56 | 1.71 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
| 4.50 | 121.24 | 90.84 | 6.81 | 1.70 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
| 4.50 | 125.22 | 95.34 | 10.84 | 1.67 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
| 4.73 | 134.16 | 105.73 | 19.27 | 1.61 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
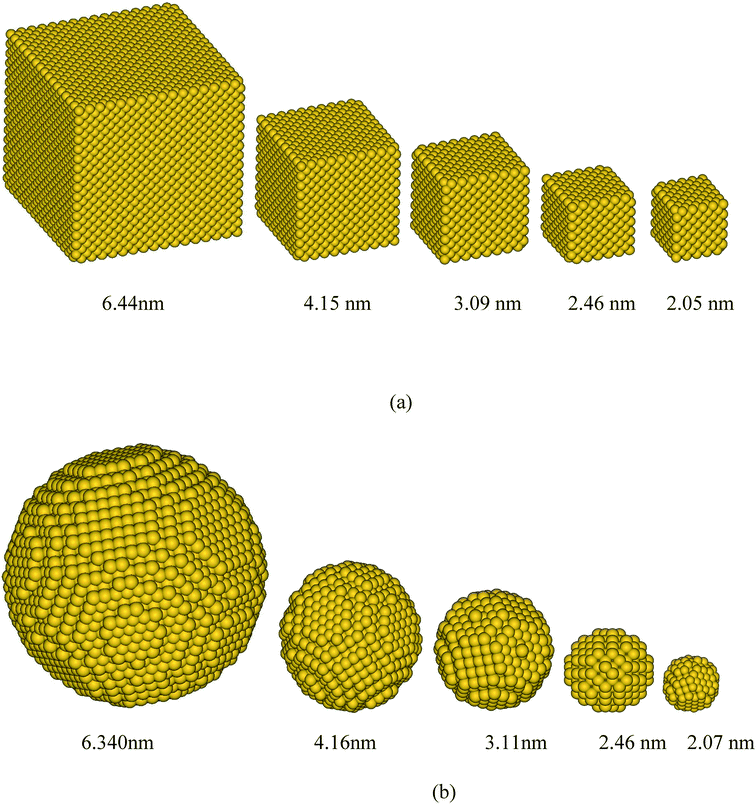 | ||
| Fig. 2 Some of the simulated gold additive nanoparticles of (a) cubic and (b) spherical shapes for various sizes. | ||
NVT simulations of hexacontane in pure or composite form were initially equilibrated under NVT conditions (constant number of molecules, volume and temperature) at a constant temperature of 500 K and a density of 750 kg m−3. The number of hexacontane molecules depending on the system ranged from 2000–250 molecules (120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–15
000–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 united atoms) for the simulations to study the effects of size and volume fraction. The length of the simulation box depended on the size of the additive so that all systems had approximately the same density. We also created a system for a pure polymer without additives. This system contained 61
000 united atoms) for the simulations to study the effects of size and volume fraction. The length of the simulation box depended on the size of the additive so that all systems had approximately the same density. We also created a system for a pure polymer without additives. This system contained 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 united atoms (1024 hexacontane molecules) and was used to compare the results with those of nanocomposite polymers and to discern the effect of additives. The temperature of 500 K was well above ∼368 K, which is the melting point of hexacontane.32 Periodic boundary conditions were applied in all three directions representing an infinite system of bulk composite polymeric melt with the additive nanoparticle volume fraction being the same as that of the main simulation box. The temperature was kept constant at 500 K using a Gaussian thermostat throughout the isothermal stages of the simulation. The resulting NVT configuration was equilibrated further under constant pressure and temperature conditions (NPT) at T = 500 K and P = 0.101 MPa. The SLLOD33,34 equations of motion (eqn (1)) governed the dynamics of hexacontane molecule motion.
440 united atoms (1024 hexacontane molecules) and was used to compare the results with those of nanocomposite polymers and to discern the effect of additives. The temperature of 500 K was well above ∼368 K, which is the melting point of hexacontane.32 Periodic boundary conditions were applied in all three directions representing an infinite system of bulk composite polymeric melt with the additive nanoparticle volume fraction being the same as that of the main simulation box. The temperature was kept constant at 500 K using a Gaussian thermostat throughout the isothermal stages of the simulation. The resulting NVT configuration was equilibrated further under constant pressure and temperature conditions (NPT) at T = 500 K and P = 0.101 MPa. The SLLOD33,34 equations of motion (eqn (1)) governed the dynamics of hexacontane molecule motion.
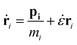 | (1) |
ṗi = Fi − ζpi − ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) pi pi |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 3 = 3![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) V V |
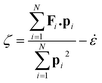 | (2) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 0,
= 0, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 0). For NPT simulations, the volume (V) can contract and expand according to eqn (1). Dynamics of the simulation box is governed by the dilation rate
= 0). For NPT simulations, the volume (V) can contract and expand according to eqn (1). Dynamics of the simulation box is governed by the dilation rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , which is calculated by integrating eqn (3).
, which is calculated by integrating eqn (3).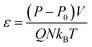 | (3) |
In this equation, P0 and P are the target pressure and the instantaneous pressure calculated at each time step. Q, N, kB and T, respectively, are the damping constant, the total number of atoms, the Boltzmann constant and the temperature. Note that Q = τ2, where τ is the response time of the feedback mechanism.33 We have adapted Q = 10/kB = 106/kBT500, which is close to the values used in other NPT simulation studies.33–36 After equilibration under NPT conditions at T = 500 K and P = 1 atm both the pure polymer melt and the nanocomposite polymer with additive systems achieve a density of approximately 771 kg m−3. This density is within 1.8% of the expected value (757 kg m−3) predicted by empirical equations given in ref. 37.
2.2 Crystallization simulations
2.3 Kinetics of crystallization and degree of crystallinity
The kinetics of crystallization is often described using Avrami's eqn (4):| 1 − χc = exp(−K(T)tn) | (4) |
In this equation χc is the relative crystallinity at time t, and K(T) and n are the Avrami time constant and Avrami exponent. K(T) is a function of the overall crystallization rate while n, the Avrami exponent, characterizes nucleation and the geometry of the growing crystallites.38
It is reported that all changes in n from 1 to 3 reflect the superposition of the homogeneous (in the bulk) and heterogeneous (near the interface) components of crystallization.39 If n = 0, it indicates that the crystallization has stopped. If the phase separation rate exceeds the crystallization rates, n is close to 3; otherwise, if the crystallization rate is much higher than phase separation n approaches 1.
Crystallinity is quantified by a method described in our earlier work.22,23 In this method, the relative orientation of the chord vectors within a molecule and neighbouring molecules is used to detect the crystallinity. The parallel orientation of these vectors is indicative of crystallization. This method is applied to quantify the degree of crystallinity. The chord vectors connect every other atom along the backbone of the chain. The chord vector that is between united atoms i and i + 2 is positioned at atom i, pointing to atom i + 2. This orientation order is monitored by the second and fourth rank correlation functions g2 and g4, which are used to detect nematic (parallel orientation) and tetratic31 (herringbone or mutually normal orientation) order in molecular systems. These functions are defined in eqn (5):
| g2(Γ) = 〈co2(θi − θj)〉; g4(Γ) = 〈co4(θi − θj)〉 | (5) |
3 Results and discussion
3.1 Effect of particle size on crystallization
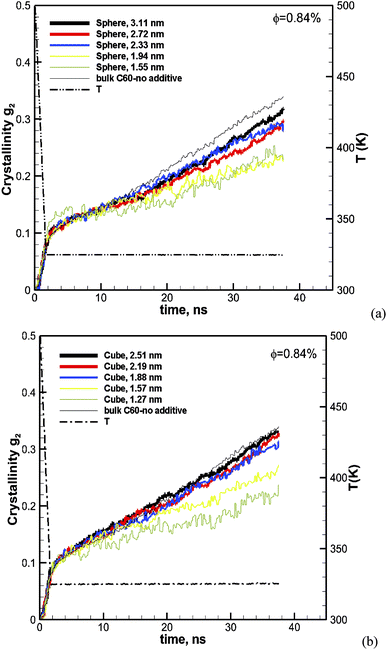
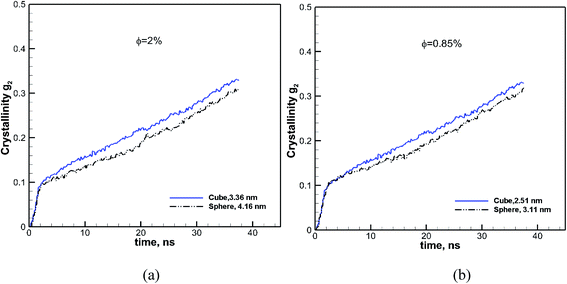
To evaluate the effect of the particle size, we have calculated the crystallization for spherical particles of various sizes between 1.55 and 3.1 nm and for cubic particles of 1.26–2.51 nm. The volume fraction of particles in the melt for all cases is kept the same at φ ∼ 0.84. The results for spherical particles are shown in Fig. 3a. The crystallization as a function of time for the pure bulk polymer melt of C60 without any additives is also shown on the same plot for comparison. We can see from this figure that the addition of spherical particles has resulted in a slower crystallization rate in comparison to that of the bulk pure polymer.Furthermore, the crystallization rate drops with the decreasing size of particles. It is notable that at the early cooling stage, the amount of crystallinity increases with the size of the particle; however as the crystallization proceeds the growth rate becomes slower with the decreasing size of the particle. The results for cubic particles are shown in Fig. 3b, which reveals a similar effect where the inclusion of additive particles resulted in slightly higher crystallinity at the beginning and a lower growth rate and final crystallinity at the end of the crystallization time, in comparison to the pure bulk polymer. For cubic particles, the enhanced crystallinity goes beyond the cooling stage and seems to be stronger than that for the spherical particles. For both the cubic and spherical particles, we can see that the final crystallinity decreases by decreasing the size of the particles at the same volume fraction of 0.84%.
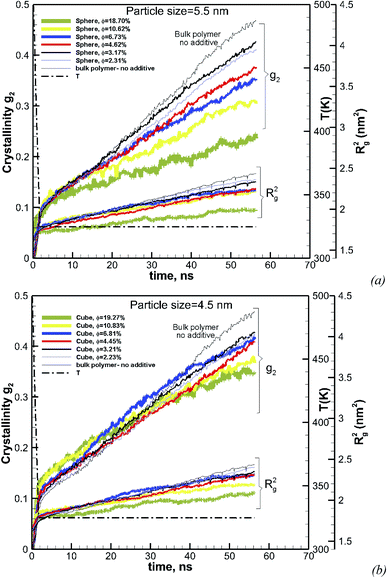
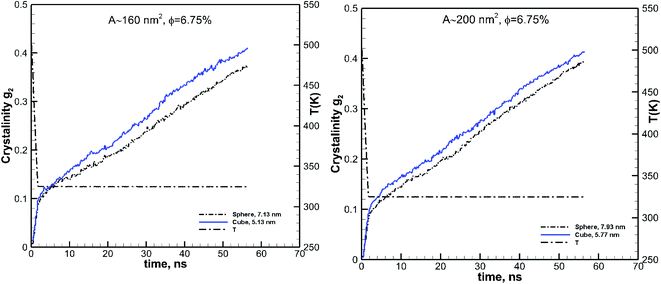
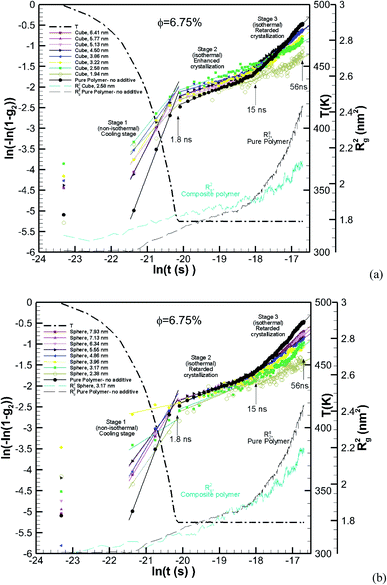
The effect of particle size at a higher nominal volume fraction of 6.75% was also examined. For these simulations, the particle size was varied over more extensive ranges of 2.38–7.93 nm for spherical and 1.94–6.41 nm for cubic additive nanoparticles. These simulations spanned larger particle sizes, and the simulation boxes were also larger. We also allowed the crystallization to occur for a longer time up to 56.3 ns. The degree of crystallinity (g2) versus time is plotted in Fig. 4a for spherical additive nanoparticles and in Fig. 4b for the cubic ones. Clearly, for the spherical particles in all cases, the crystallization rate and final crystallinity are lower than those for the pure polymer system without additives. This indicates that the spherical particles have impeded crystal growth. Furthermore, at the same volume fraction, as the particle size decreases the rate of crystal growth and final crystallinity decrease. Crystallization of the polymer with cubic particles at the same volume fraction exhibits a striking difference in the initial nucleation and growth. We can see in Fig. 4b that in all cases the initial crystallinity for the melt with additives is higher than that in the bulk pure polymer. However, as time proceeds, the crystal growth for the pure polymer system catches up. The rate of growth becomes slower for the nanocomposite polymers and the severity of this slow-down increases with the decreasing nanoparticle size. That is the growth rate decreases with the decreasing particle size. This is a clear sign of two-tier crystallization reported in some experiments [e.g.ref. 13]. For cubic particles, we see substantial two-tier crystallization, whereas this seems to be absent for spherical particles. This two-tier crystallization is also stronger at this higher volume fraction than that observed at φ = 0.84%. The slow-down in growth caused by increasing the volume fraction is somehow counterintuitive, as one expects a higher crystallinity as the available additive surface-induced crystallization increases. We will explain the mechanism of this two-tier crystallization process in the Discussion section.
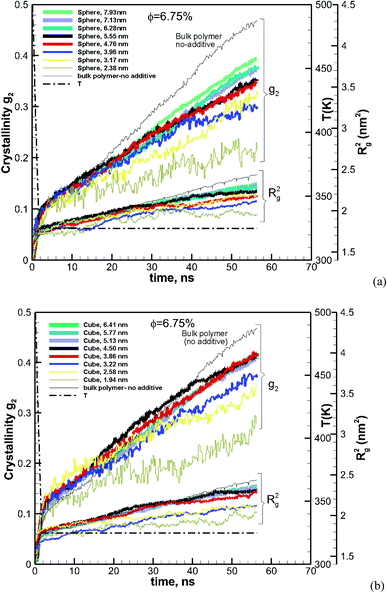 | ||
| Fig. 4 Same as Fig. 3 for a volume fraction of φ = 6.75% over ∼56 ns of crystallization time. The results also include the squared radius of gyration Rg2. The temperature ramp is shown by a black thick dash-dot line. | ||
The ensemble average square radius of gyration is defined in eqn (6):23
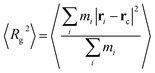 | (6) |
3.2 Effect of volume fraction on crystallization
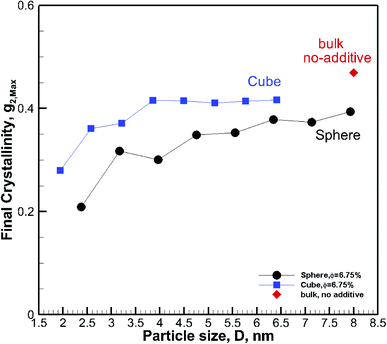
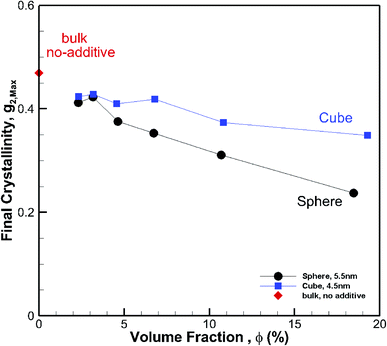
To understand the effect of volume fraction, we conducted simulations for nanocomposite polymers with spherical and cubic additives. In both cases, we kept the size of the nanoparticles almost the same and varied the simulation box size, so that volume fraction values of 2.31–19.27% were achieved for nanocomposite systems with spherical and cubic nanoparticles. The nominal particle size for spherical and cubic additives, respectively, was 5.5 nm and 4.5 nm. The crystallization plots for these systems are shown in Fig. 6a for spherical and in Fig. 6b for cubic additives. We can see that for both cases, the rate of growth and final crystallinity decreases when increasing the volume fraction. The effect is much more significant for the spherical particles. For cubic additives, a two-tier crystallization effect, where at early stages of crystallization the polymer with additives shows higher crystallinity, indicates that the presence of additives facilitates nucleation and growth. However, as time passes and crystallization grows the nanocomposite polymer systems with cubic additives show a slow-down in growth, whereas for the pure polymer crystallization continues at the same pace. The final crystallinity, as a function of volume fraction, is shown in Fig. 7. The results are shown for both the cubic and spherical additives and demonstrate that the final crystallinity decreases when increasing the volume fraction. Furthermore, again, nanocomposite systems with cubic particles show a higher final crystallinity than those with spherical particles. The difference between the cubic and spherical systems widens as the volume fraction increases; that is at lower volume fractions (∼2–3%) the difference is minor.3.3 Effect of particle shape
To obtain the local crystallinity, we have calculated the degree of crystallinity and other local properties by dividing the simulation domain into a number of volumetric cells. The number of cells is chosen so that several atoms on average fall in the cell for good statistics.
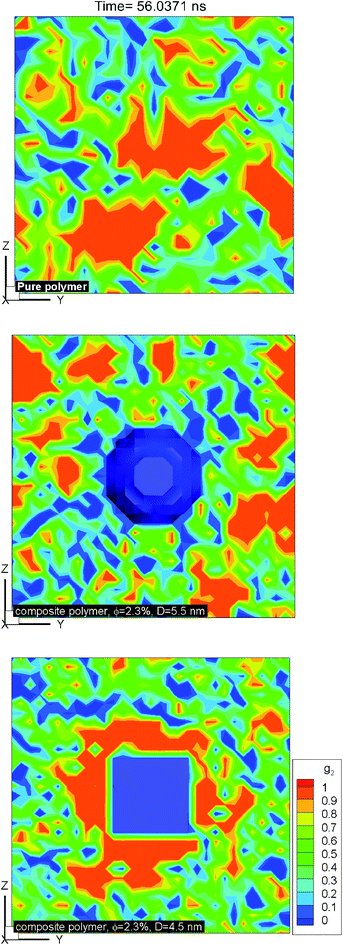
Fig. 10 shows the plot of iso-surfaces of 90% crystallinity (g2 ∼ 0.9) for pure and composite polymers with cubic and spherical additive nanoparticles of the same size (∼6.4 nm) and different volume fraction (6.75% for spherical and 12.5% for cubic additives) at different times during crystallization. These results show nucleation sites as they grow into fully crystalline regions and have not been reported in such detail before. We can see that as the time progresses, for the pure polymer these nucleation sites grow homogeneously and are randomly distributed across the simulation domain. For the composite systems, in the case of spherical additives, the crystalline regions form away from the additive particle and in the free space available for the polymer molecules. In contrast for the cubic additive, the crystal grows near the flat surfaces of the additive particle. Fig. 11 shows slices of the final crystallinity contour plots at the centre of the simulation box again for three systems of pure and composite polymers. In this case, the composite polymers have the same volume fraction of ∼6.75% and different particle sizes of ∼4.5 and ∼5.5 nm for cubic and spherical additive particles. Again we observe that crystalline regions (red colour) form near the surface of the cubic additive and away from the spherical particles. These pictures clearly show that the crystallization is frustrated by the curvature of the spherical particles and enhanced by the flat surfaces of the cubic particles. Furthermore, crystalline domains for the composite polymer with spherical particles are smaller than those for cubic additives, another indication that the shape of particles impacts the morphology. The slice of the crystallinity contour for the pure polymer in Fig. 11 shows much bigger regions of crystalline domains which are randomly distributed.
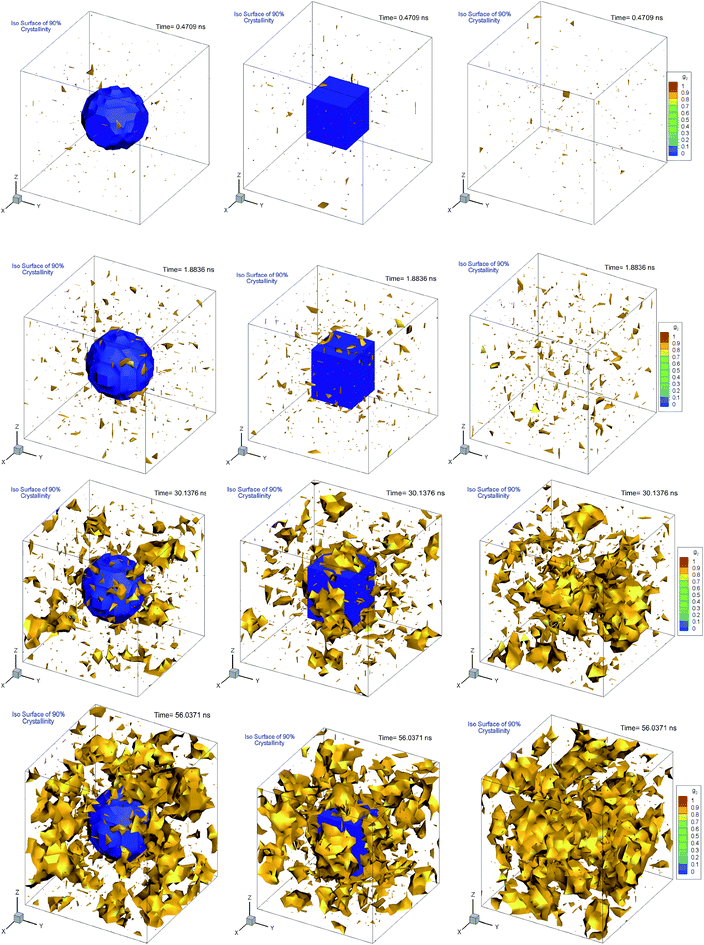 | ||
| Fig. 10 Iso-surfaces of 90% crystallinity for bulk pure hexacontane without additives (right column) and nanocomposite hexacontane with cubic (middle column) and spherical (left column) particles. The results are shown at different times during crystallization for 0.407, 1.88, 30.14, and 56.04 ns. The approximate position of the additive nanoparticle surface is determined from the iso-surface of zero melt density in blue colour. For nanocomposite polymers, spherical and cubic additives have approximately the same size (∼6.4 nm) whereas their volume fractions, respectively, are 6.75 and 12.5% (see also Movie 3–5 in the ESI†). | ||
ln[−ln(1 − g2)] = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) + n K(T) + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(t) ln(t) | (7) |
The Avrami constants ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) and n are the Avrami crystal growth function and exponent, respectively, and are determined by plotting ln(−ln(1 − g2)) as a function of ln(t) in Fig. 12a for the pure polymer with no additives and composite polymers with cubic additives of various sizes and at a volume fraction of (φ ∼ 6.75%). These are for the simulations whose kinetics of crystallization are shown in Fig. 4b. Linear fits are made into three stages of simulation that include stage 1 (non-isothermal, cooling stage, 1.8 ns), stage 2 (1.8–15 ns) which is the isothermal stage where all cubic additives enhanced the crystallization, and stage 3 (15–56 ns) which is the stage at which cubic additives retarded the crystallization. The extracted values for the Avrami exponent, n, and Avrami function ln
K(T) and n are the Avrami crystal growth function and exponent, respectively, and are determined by plotting ln(−ln(1 − g2)) as a function of ln(t) in Fig. 12a for the pure polymer with no additives and composite polymers with cubic additives of various sizes and at a volume fraction of (φ ∼ 6.75%). These are for the simulations whose kinetics of crystallization are shown in Fig. 4b. Linear fits are made into three stages of simulation that include stage 1 (non-isothermal, cooling stage, 1.8 ns), stage 2 (1.8–15 ns) which is the isothermal stage where all cubic additives enhanced the crystallization, and stage 3 (15–56 ns) which is the stage at which cubic additives retarded the crystallization. The extracted values for the Avrami exponent, n, and Avrami function ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) are tabulated in Table 2 for the cases shown in Fig. 12a. The results show that both ln
K(T) are tabulated in Table 2 for the cases shown in Fig. 12a. The results show that both ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) and n are higher for the pure polymer with no additives in comparison to the nanocomposite polymers. Furthermore, for stage 1 and stage 3, both ln
K(T) and n are higher for the pure polymer with no additives in comparison to the nanocomposite polymers. Furthermore, for stage 1 and stage 3, both ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) and n decrease with the decreasing additive particle size. For stage 2, there is no strong dependence on particle size. Furthermore, the two-tier crystallization can be observed from lower g2 values (lower ln(−ln(1 − g2)) for the pure polymer in stages 1 and 2 and higher g2 values at the end of stage 3. In Fig. 12a we also show Rg2 for the pure polymer and one of the nanocomposite systems. For the nanocomposite system, observation of higher values of Rg2 at the initial two stages of crystallization is consistent with their higher crystalline content. Note that the sharp change in the slope of the Avrami fit in stage 3 for the pure polymer coincides with a sharp increase in Rg2, whereas for the nanocomposite system the rate of increase in Rg2 is much slower.
K(T) and n decrease with the decreasing additive particle size. For stage 2, there is no strong dependence on particle size. Furthermore, the two-tier crystallization can be observed from lower g2 values (lower ln(−ln(1 − g2)) for the pure polymer in stages 1 and 2 and higher g2 values at the end of stage 3. In Fig. 12a we also show Rg2 for the pure polymer and one of the nanocomposite systems. For the nanocomposite system, observation of higher values of Rg2 at the initial two stages of crystallization is consistent with their higher crystalline content. Note that the sharp change in the slope of the Avrami fit in stage 3 for the pure polymer coincides with a sharp increase in Rg2, whereas for the nanocomposite system the rate of increase in Rg2 is much slower.
| Cubic additive nanoparticles (φ ∼ 6.75%) | ||||||
|---|---|---|---|---|---|---|
| Particle size (nm) | Stage 1 | Stage 2 | Stage 3 | |||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) (s−n) K(T) (s−n) |
N | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) (s−n) K(T) (s−n) |
n | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) (s−n) K(T) (s−n) |
n | |
| 6.41 | 30.94 | 1.64 | 3.69 | 0.29 | 12.53 | 0.79 |
| 5.77 | 28.04 | 1.50 | 4.28 | 0.33 | 11.83 | 0.75 |
| 5.13 | 24.01 | 1.31 | 4.25 | 0.33 | 12.21 | 0.77 |
| 4.50 | 31.96 | 1.69 | 3.88 | 0.30 | 10.18 | 0.65 |
| 3.86 | 23.57 | 1.28 | 2.96 | 0.25 | 11.05 | 0.70 |
| 3.22 | 24.11 | 1.31 | 3.93 | 0.31 | 10.69 | 0.69 |
| 2.58 | 19.64 | 1.08 | 3.68 | 0.29 | 6.85 | 0.47 |
| 1.94 | 17.39 | 0.98 | 2.23 | 0.23 | 5.46 | 0.40 |
| Pure polymer | 41.4 | 2.17 | 4.49 | 0.344 | 15.25 | 0.94 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Spherical additive nanoparticles (φ ∼ 6.75%) | ||||||
| 7.93 | 27.49 | 1.48 | 4.68 | 0.35 | 12.63 | 0.80 |
| 7.14 | 21.52 | 1.19 | 3.50 | 0.29 | 12.11 | 0.77 |
| 6.34 | 28.27 | 1.51 | 4.70 | 0.36 | 12.55 | 0.80 |
| 5.55 | 21.40 | 1.18 | 4.02 | 0.32 | 9.83 | 0.64 |
| 4.76 | 27.54 | 1.48 | 3.87 | 0.31 | 10.16 | 0.66 |
| 3.96 | 1.39 | 0.19 | 3.41 | 0.29 | 8.37 | 0.56 |
| 3.17 | 8.27 | 0.55 | 9.98 | 0.66 | 9.98 | 0.66 |
| 2.38 | 22.68 | 1.26 | 4.70 | 0.36 | 5.79 | 0.43 |
The fitting to the Avrami model for nanocomposite polymers with spherical particles of various sizes at a volume fraction of φ ∼ 6.75% is shown in Fig. 12b. Here there is a distinct difference with the cubic particles. The enhanced crystallization seen in stage 2 for nanocomposite polymers with cubic particles is absent here. Note that in stage 2 the ln(−ln(1 − g2) values for composite systems with spherical particles are almost the same as those for the pure polymer and even lower in some cases. The behaviour of Rg2 in Fig. 12b for the nanocomposite polymer with spherical particles is very similar to that of the pure polymer up to the beginning of stage 3, where the growth of crystals and molecular extension is severely retarded in the nanocomposite polymer. Here retarded crystallization for some cases begins at stage 2 and extends to stage 3. It is notable that retarded crystallization at stage 3 for spherical particles is more severe than that for the cubic particles. We note that the seeding effect of spherical particles evidenced by enhanced g2 values is only observed at the cooling stage 1. The lack of enhanced crystallization by spherical particles provides strong evidence that the two-tier crystallization depends on the particle shape and most likely will be observed when the additives have flat surfaces.
4 Discussion
4.1 The effect of additive particle size and volume fraction
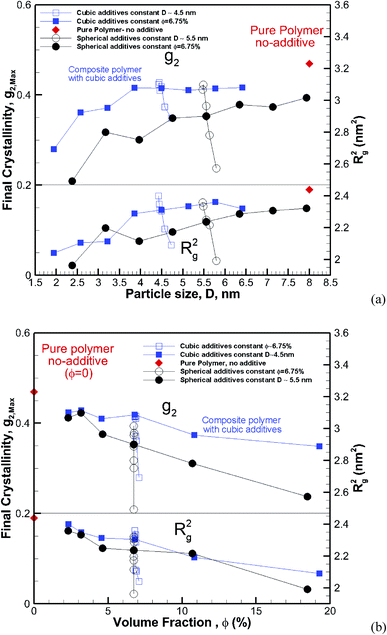
Clearly, the results here show both crystallization kinetics, and the final crystallinity has a strong dependence on additive size and volume fraction. However, it seems that neither of them on their own are good indicators of the final crystallinity and crystallization kinetics behaviour. We consider the two cases of constant particle size (D = ∼5.5 and ∼4.5 nm) and constant volume fraction (∼6.75%) and plot the final crystallinity versus particle size and volume fraction, respectively, in Fig. 13a and b. We can see in Fig. 13a that despite an almost constant size (open symbols) the final crystallinity changes significantly; this is due to a change in volume fraction. On a similar note in Fig. 13b, we can see cases (open symbols) where, despite an almost constant volume fraction, there is a significant change in crystallinity due to changes in particle size. Therefore, neither size nor volume fraction on its own can be used to control crystallinity. Therefore we need to find a measure to capture the combined effects of the size and volume fraction.Assuming a homogeneous distribution of additive particles, as is the case in our simulations, it is clear that at the same volume fraction, decreasing the particle size regardless of the shape results in smaller spacing between the particles. On the other hand, for the same particle size, increasing the volume fraction reduces the free space between particles. This squeezing action results in lower mobility and impedes molecular extension that is required as a precursor for crystallization.
4.2 Interparticle distance as a function of particle size and volume fraction
We can derive equations for minimum surface-to-surface interparticle free distance Dpp for a homogeneous monodisperse mono-orientational system of cubic particles (shown in Fig. 1a):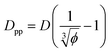 | (8) |
Analogous equation for spherical particles is given by:
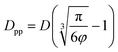 | (9) |
In the case of φ = 6.75%, for example, the spacing between the additive particles is Dpp = 0.98D for spheres and Dpp = 1.456D for cubes, where D is the size of the particle. For the same particle size, one can show:
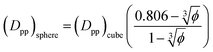 | (10) |
For φ = 6.75% and the same particle size (Dpp)sphere = 0.673(Dpp) cube. That is for the same particle size and volume fraction spherical particles have a significantly smaller minimum interparticle space than their cubic counterparts. Therefore, the big difference in final crystallinity shown in Fig. 5 for cubic and spherical particles may be related to this free interparticle distance.
Eqn (8) and (9) show that when decreasing the particles size, the available interparticle space filled by the melt molecules decreases. We define the normalized interparticle free distance as 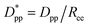 . Where Ree is the fully extended all-trans molecular length (7.62 nm for hexacontane). In the case of φ = 6.75%,
. Where Ree is the fully extended all-trans molecular length (7.62 nm for hexacontane). In the case of φ = 6.75%, 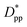 decreases from 1.04 to 0.33 for spherical particle systems and from 1.24 to 0.38 for cubic ones as the particle size decreases. This means confining the molecules into a smaller space, which results in slower growth. To demonstrate this, we plot the final crystallinity versus normalized interparticle free distance
decreases from 1.04 to 0.33 for spherical particle systems and from 1.24 to 0.38 for cubic ones as the particle size decreases. This means confining the molecules into a smaller space, which results in slower growth. To demonstrate this, we plot the final crystallinity versus normalized interparticle free distance 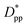 in Fig. 14. In this plot, we have included the results for constant volume fraction and also constant nanoparticle size cases (discussed in Fig. 13) for both cubic and spherical nanoparticles. This plot reveals a striking pattern where everything makes sense in the context of confinement induced slow-down in crystallization. Here, we can see an increase in the final crystallinity as the interparticle free space increases. This pattern of behaviour is regardless of the particle shape, size and volume fraction, and reveals a confinement induced phenomenon and critical spacing where this effect is most prominent. We can see that for cubic nanoparticles a plateau at
in Fig. 14. In this plot, we have included the results for constant volume fraction and also constant nanoparticle size cases (discussed in Fig. 13) for both cubic and spherical nanoparticles. This plot reveals a striking pattern where everything makes sense in the context of confinement induced slow-down in crystallization. Here, we can see an increase in the final crystallinity as the interparticle free space increases. This pattern of behaviour is regardless of the particle shape, size and volume fraction, and reveals a confinement induced phenomenon and critical spacing where this effect is most prominent. We can see that for cubic nanoparticles a plateau at 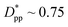 is achieved beyond which no significant effect is observed by increasing the
is achieved beyond which no significant effect is observed by increasing the 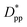 . For spherical particles, a less distinctive plateau appears to emerge at
. For spherical particles, a less distinctive plateau appears to emerge at 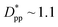 , and the increase in crystallinity with
, and the increase in crystallinity with 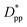 is more gradual. These correspond to a free spacing of 5.7 nm for cubic and 8.32 nm for spherical particles, comparable to the size of a partially folded or fully extended hexacontane molecule. This is the typical size of a lamella that forms in the crystallization of hexacontane. That is, the critical interparticle free space where the confinement-induced phenomenon is expected to emerge depends on the original size of the crystal lamella that forms in the pure polymer (see Movies 1 and 2 in the ESI† for crystallization of pure and nanocomposite polymer systems). Once this interparticle space is smaller than this size, confinement induced phenomena will significantly impact the growth rate of the crystal and final amount of crystallinity. We can see from the plots in Fig. 14 that at the same
is more gradual. These correspond to a free spacing of 5.7 nm for cubic and 8.32 nm for spherical particles, comparable to the size of a partially folded or fully extended hexacontane molecule. This is the typical size of a lamella that forms in the crystallization of hexacontane. That is, the critical interparticle free space where the confinement-induced phenomenon is expected to emerge depends on the original size of the crystal lamella that forms in the pure polymer (see Movies 1 and 2 in the ESI† for crystallization of pure and nanocomposite polymer systems). Once this interparticle space is smaller than this size, confinement induced phenomena will significantly impact the growth rate of the crystal and final amount of crystallinity. We can see from the plots in Fig. 14 that at the same 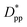 , cubic particles in the confinement limit
, cubic particles in the confinement limit 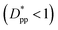 still lead to higher crystallinity than spherical ones, and particle shape plays an important role. However, for
still lead to higher crystallinity than spherical ones, and particle shape plays an important role. However, for 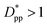 , particle shape only has a minor impact on the overall crystallinity.
, particle shape only has a minor impact on the overall crystallinity.
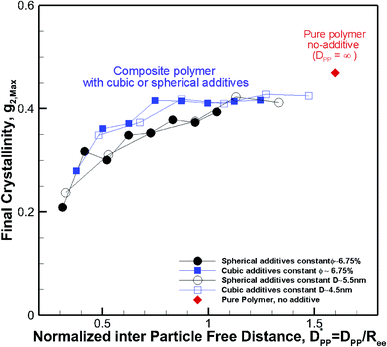 | ||
Fig. 14 Final crystallinity after 56 ns versus normalized interparticle free distance 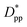 for several cases of nanocomposite polymers made from cubic or spherical particles of various sizes and volume fractions whose kinetics of crystallization are shown in Fig. 4 and 6. A red rhomboid symbol shows the final crystallinity for the pure polymer for comparison. for several cases of nanocomposite polymers made from cubic or spherical particles of various sizes and volume fractions whose kinetics of crystallization are shown in Fig. 4 and 6. A red rhomboid symbol shows the final crystallinity for the pure polymer for comparison. | ||
4.3 Critical volume fraction and particle size for confinement induced crystallization retardation
This significant insight leads us to develop relationships that will be useful as a guide to determine the critical volume fraction for a given nanoparticle size or critical nanoparticle size at a given volume fraction where the confinement-induced phenomenon is expected to retard the crystallization kinetics. Given a pure polymer with a crystal lamella thickness of Rc, one may use eqn (8) to calculate the critical volume fraction φcr-cube for a given cubic particle of size D by assuming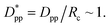 A similar approach leads to the development of an equation that gives the critical cubic particle size, Dcr-cube, for a given volume fraction φ. This leads to the equations:
A similar approach leads to the development of an equation that gives the critical cubic particle size, Dcr-cube, for a given volume fraction φ. This leads to the equations: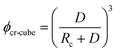 | (11) |
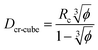 | (12) |
Eqn (11) provides a critical volume fraction for a given particle size D, and eqn (12) provides a critical particle size for a given volume fraction φ. For D < Dcr-cube and φ > φcr-cube one would expect confinement induced retardation of crystallization. Analogous equations for critical particle size or volume fraction of spherical particles can be derived, leading to eqn (13) and (14):
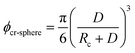 | (13) |
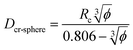 | (14) |
These equations provide guidelines for the choice of particle size and volume fraction where confinement effects are expected to retard crystallization. Such information is expected to be valuable in the formulation of nanocomposite polymers and hybrid molecular systems to achieve desirable control of crystallization.
Fitting the results to the Avrami model by using eqn (7), one can extract the Avrami exponent n and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) for the constant volume fraction and constant particle size discussed in Fig. 4 and 6. We have plotted n and ln
K(T) for the constant volume fraction and constant particle size discussed in Fig. 4 and 6. We have plotted n and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) as a function of normalized interparticle distance
K(T) as a function of normalized interparticle distance 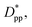 for all cases in Fig. 15. The results are shown for the three stages of crystallization identified in Fig. 12. The results for the pure polymer reveal that for the non-isothermal stage of crystallization the Avrami exponent n is close to ∼2.2, indicating almost 3D growth; however, for the nanocomposite systems, n is lower than the pure polymer value (see also Table 2). Therefore, we conclude that in stage 1, while the amount of crystallinity is enhanced in the composite polymers, the rate of crystallization and growth is much faster for the pure polymer. The results for ln
for all cases in Fig. 15. The results are shown for the three stages of crystallization identified in Fig. 12. The results for the pure polymer reveal that for the non-isothermal stage of crystallization the Avrami exponent n is close to ∼2.2, indicating almost 3D growth; however, for the nanocomposite systems, n is lower than the pure polymer value (see also Table 2). Therefore, we conclude that in stage 1, while the amount of crystallinity is enhanced in the composite polymers, the rate of crystallization and growth is much faster for the pure polymer. The results for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) show a similar pattern. Stage 2, however, shows a much slower growth rate with both n and ln
K(T) show a similar pattern. Stage 2, however, shows a much slower growth rate with both n and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) being much smaller than the stage 1 values. In stage 2, n and ln
K(T) being much smaller than the stage 1 values. In stage 2, n and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) show very similar values for the pure and composite systems, and there is no significant dependence on
K(T) show very similar values for the pure and composite systems, and there is no significant dependence on 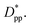 This suggests that there is a minimal confinement effect for nanocomposite systems in stage 2. Therefore, we conclude that in the enhanced crystallization stage while the amount of crystallinity is enhanced in composite polymers, the rate of crystallization and growth is almost the same as that in the pure polymer. In stage 3, both n and ln
This suggests that there is a minimal confinement effect for nanocomposite systems in stage 2. Therefore, we conclude that in the enhanced crystallization stage while the amount of crystallinity is enhanced in composite polymers, the rate of crystallization and growth is almost the same as that in the pure polymer. In stage 3, both n and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) increase significantly for all polymers; however, the growth rate is much higher for the pure polymer than for nanocomposite systems. Furthermore, both n and ln
K(T) increase significantly for all polymers; however, the growth rate is much higher for the pure polymer than for nanocomposite systems. Furthermore, both n and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) increase by increasing the interparticle space
K(T) increase by increasing the interparticle space 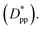 The initial crystalline content for the nanocomposite systems is seeded by the flat surfaces of the cubic additives. However, the faster growth rate in stage 1, and predominantly stage 3, catches up with the surface effects leading to a higher final crystallinity of the pure polymer. Note that it is in stage 3 that the confinement effects for nanocomposite systems kick in (see also Rg2 in Fig. 12a) causing a significant slow-down of the crystallization.
The initial crystalline content for the nanocomposite systems is seeded by the flat surfaces of the cubic additives. However, the faster growth rate in stage 1, and predominantly stage 3, catches up with the surface effects leading to a higher final crystallinity of the pure polymer. Note that it is in stage 3 that the confinement effects for nanocomposite systems kick in (see also Rg2 in Fig. 12a) causing a significant slow-down of the crystallization.
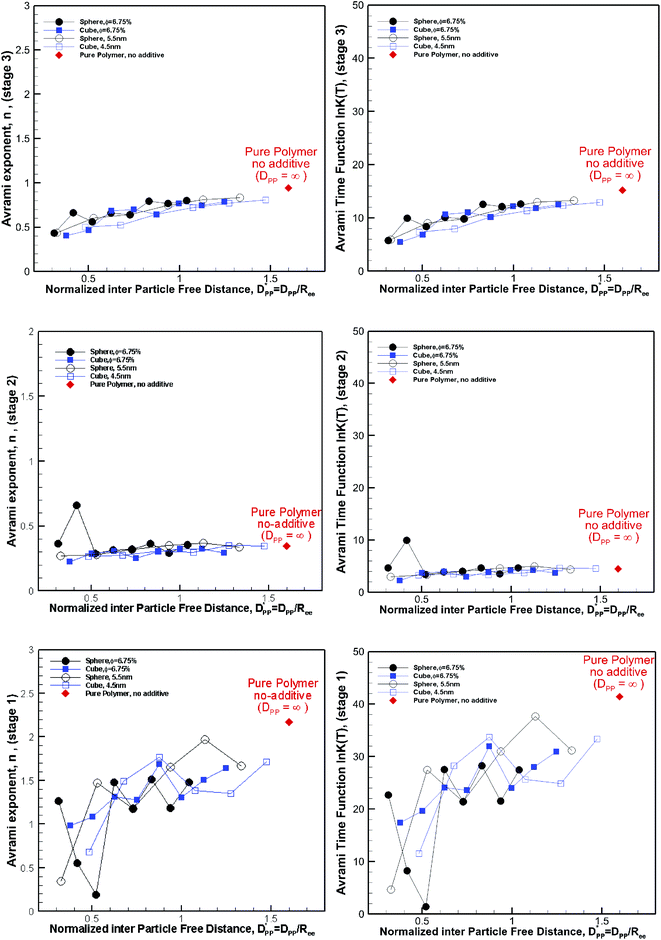 | ||
Fig. 15 Avrami exponent (n) (left column) and time function, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T), (right column) versus normalized free distance K(T), (right column) versus normalized free distance  for nanocomposite systems (as shown in Fig. 4 and 6) made of various particle sizes and volume fractions. The results are shown for both cubic and spherical particles and the three stages of crystallization identified in Fig. 12. The results are also shown for the pure polymer without additives for comparison using a single red rhomboid. for nanocomposite systems (as shown in Fig. 4 and 6) made of various particle sizes and volume fractions. The results are shown for both cubic and spherical particles and the three stages of crystallization identified in Fig. 12. The results are also shown for the pure polymer without additives for comparison using a single red rhomboid. | ||
We note that in all cases both n and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) are smaller for the nanocomposite systems; however in the limit, one sees that for
K(T) are smaller for the nanocomposite systems; however in the limit, one sees that for  these values approach those of the pure polymer. For the values shown in Fig. 15 comparing the spherical and cubic particles, it is clear that in most cases, ln
these values approach those of the pure polymer. For the values shown in Fig. 15 comparing the spherical and cubic particles, it is clear that in most cases, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(T) and n are smaller for the cubic particles. This is an indication that the growth dimensionality is restricted more by the cubic particles than the spherical ones. In the limit for
K(T) and n are smaller for the cubic particles. This is an indication that the growth dimensionality is restricted more by the cubic particles than the spherical ones. In the limit for  it is more likely for the spherical particle growth kinetics to be very similar to that of the pure polymer.
it is more likely for the spherical particle growth kinetics to be very similar to that of the pure polymer.
4.4 Experimental relevance and future prospects
With the insights obtained from the simulations here, we can explain some of the discrepancies and results reported in the literature. Perhaps the work by Papananou et al.21 is very relevant to the simulations presented here. They used uncoated spherical silica particles in their work and reported the loading of the particles in a PEO nanocomposite in terms of volume fraction. They used uncoated silica particles of 14, 37 and 134 nm diameters in their work. For the same particle size, they demonstrated that crystallinity decreases by increasing the volume fraction. They also showed that for the same volume fraction crystallinity decreases with the decreasing particle size. These are all in excellent agreement with our conclusions from the simulation work. Now we consider the applicability of eqn (13) in the context of their experiments. Papananou et al. showed that for silica nanoparticles of D = 134 nm (R = 67 nm) the crystallinity begins to decrease at a volume fraction of φ ∼ 30%. The lamella thickness for PEO was reported to be 25 nm.41 Using eqn (13) for predicting the critical volume fraction for spherical particles (Rc = 25 nm and D = 143 nm), φcr ∼ 31% can be obtained. This result is in excellent agreement with experimental observation, showing the effectiveness of eqn (13) for predicting critical volume fraction. Using 37 nm silica particles for analysis, the results of Papananou et al. (in Fig. 5a of ref. 21) showed that crystallinity starts decreasing at φ >∼10%; this is also in good agreement with the predicted value of φcr ∼ 11% using eqn (13). For the smallest particle of 14 nm the predicted value is φcr ∼ 2.42%; experimental values based on XRD measurement (Fig. S3. Ref. 21) showed reduced crystallinity at φ ∼ 7%, so this is also within the range.In the experiments by Khan et al.5 for the polyethylene oxide (PEO) nanocomposite with spherical silica particles, a significant decrease by up to ∼40% in crystallinity is observed. They reported a gradual decrease in crystallinity by increasing the w% loading from 10% to 60% for ∼25 nm size grafted nano-silica particles.5 The size of the core silica particles was ∼15 nm and the effective size of the nanoparticles including the grafted PMMA brushes was ∼25 nm. Considering that 15 nm silica particles of 2650 kg m−3 density are grafted with 5 nm PMMA of 1170 kg m−3 density, an average density of 1458 kg m−3 is calculated for the grafted 25 nm silica particles. The 100 kDa (Sigma Aldrich) PEO has a density of 1075 kg m−3 at 80 °C.42 Therefore, these w% values roughly translate to 7.37% to 44.2% volume fraction. Using eqn (13) for D = 25 nm and Rc = 25 nm, we obtain a φcr ∼ 6.54% showing that for φ > 6.54% one would observe confinement induced effects of reduced crystallinity. Therefore we can conclude that in Khan et al.'s experiment5 the loading of the nanoparticles was above the critical volume fraction limit and confinement effects manifested by crystallization retardation would be observed, a phenomenon that is reported in the experiments.
Zhao et al.20 studied a similar PEO nanocomposite using 14 nm core silica particles grafted with PMMA. They compared the crystallization for 10% and 20% loading. They reported that nanoparticles slow down the crystallization; however the final crystallinity after a long duration of crystallization was comparable. However, crystallinity (compared at the same time) decreased with increased % loading. We note that the cooling method in Khan et al.'s work was slow cooling and considered non-isothermal, whereas Zhao et al. quenched the PEO system in two stages and then crystallized under isothermal conditions. The different cooling method might explain the different results in the final crystallinity reported by Khan et al. and Zhao et al. Our simulations include a fast cooling (non-isothermal) stage followed by isothermal crystallization. Experiments by Papananou et al. used a fast cooling rate of 10 °C min−1 followed by isothermal crystallization, whereas Khan et al.5 used a very slow cooling rate of 5 °C h−1 (0.083 °C min−1) and Zhao et al. used two-stage quenching (first to 70 and then room temperature). Therefore we believe that in terms of the cooling method neither Khan et al.'s nor Zhao et al.'s work is entirely similar to that used in our simulations. However, the cooling method in Papananou et al.'s21 work is relatively close to that in our simulations. Such observations highlight the importance of the cooling rate in studying these systems.
The shape dependence of the two-tier crystallization that was discussed above may also explain why this was observed in the crystallization of graphite–nylon6 nanocomposite systems,13 where flat surfaces of graphite are expected to promote two-tier crystallization. However, two-tier crystallization was not reported in other experiments with spherical silica nanoparticles. The fact that cubic particles work better than spherical ones in enhancing nucleation and crystallization kinetics at the early stages of crystallization is due to epitaxial and surface curvature effects. This is consistent with the results in molecular simulation of crystallization of hard colloidal particles seeded by concave and convex segments of spherical particles where nucleation was enhanced more by flatter particles (particles with a larger radius).27
5 Conclusions
The results in our study showed that nanoparticle shape, size and volume fraction affect crystallization kinetics and final crystallinity. We found that the origin of two-tier crystallization is a combination of surface-induced enhancement and confinement induced retardation of crystallization. This phenomenon was shown to depend on particle shape and is most likely seen with nanofillers with flat surfaces. Furthermore, we demonstrated that the combined effects of nanoparticles size and volume fraction should be considered in formulating the nanocomposite and hybrid molecular systems. These combined effects on crystallization can be measured from the free interparticle space and are predominantly important in the confinement limit, where the free space is less than the original crystal size. We have developed equations for critical size and critical volume fraction of idealised monodisperse homogeneously distributed cubic and spherical nanoparticles, where these confinement effects are expected to be appreciable. While these equations are developed for idealized systems, we showed that they explain some of the results reported in experiments, and the predicted critical volume fraction values were in agreement with some of the results reported in the literature. Therefore these equations can be used as a guide in formulating nanocomposite and hybrid molecular systems for targeted crystalline content. The results also showed that spherical nanoparticles lead to lower crystallinity in comparison to the cubic nanofiller. This shape dependence observation was most significant in the confinement limit, where interparticle distance was smaller than the natural lamella thickness. The shape effect was independent of the particle size, volume fraction, and surface area, and was driven by different crystallization in regions near the surface of the particle. By examining local crystallinity and spatial distribution of crystalline regions, we showed that the spherical particles' curvature frustrated the crystallization near the surface and crystal domains were smaller and confined mostly to the interparticle free space.In contrast, for cubic particles with flat surfaces, crystallization was higher in regions near the surface of particles. Such differences suggested that the morphology of a crystallized polymer would be affected by the shape of particles. Shape induced changes in morphology are an area which should be explored with further simulations.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors gratefully acknowledge the support of this study by the Australian Centre of Advanced Computing and Communications, the National Computational Infrastructure (NCI) and the Sydney Informatics Hub at the University of Sydney for providing access to high-performance computational facilities (Artemis).References
- Modeling and prediction of polymer nanocomposite properties, ed. V. Mittal, John Wiley & Sons, 2012 Search PubMed.
- S. K. Kumar, V. Ganesan and R. A. Riggleman, J. Chem. Phys., 2017, 147, 020901 CrossRef PubMed.
- S. Fu, Z. Sun, P. Huang, Y. Li and N. Hu, Nano Materials Science, 2019, 1, 2–30 CrossRef.
- R. Jeziorska, A. Szadkowska, M. Zielecka, M. Wenda and B. Kepska, Polym. Degrad. Stab., 2017, 145, 70–78 CrossRef CAS.
- J. Khan, S. E. Harton, P. Akcora, B. C. Benicewicz and S. K. Kumar, Polymer, Macromolecules, 2009, 42, 5741–5744 CrossRef CAS.
- N. Bosq and D. Aht-Ong, Macromol. Res., 2018, 26, 13–21 CrossRef CAS.
- V. E. Reinsch and L. Rebenfeld, J. Appl. Polym. Sci., 1994, 52, 649–662 CrossRef CAS.
- Y. Tanaka, G. Chen, Y. Zhao, A. E. Davies, A. S. Vaughan and T. Takada, IEEE Trans. Dielectr. Electr. Insul., 2003, 10, 148–154 CrossRef CAS.
- A. Radulescu, L. J. Fetters and D. Richter,.Tailored Polymer Additives for Wax (Paraffin) Crystal Control, in Crude Oil Emulsions-Composition Stability and Characterization, ed. M. Abdel-Raouf, IntechOpen, 2012, pp. 205–230 Search PubMed.
- V. E. Reinsch and L. Rebenfeld, J. Appl. Polym. Sci., 1994, 52, 649–662 CrossRef CAS.
- X. L. Jiang, S. J. Luo, K. Sun and X. D. Chen, eXPRESS Polym. Lett., 2007, 1, 245–251 CrossRef CAS.
- S. Akhtar, D. Shukla and V. Kumar, Studies on effect of nano-talc filler on nucleation, crystal morphology and crystallization behaviour of semi-crystalline plastics, in Solid State Phenomena, Trans Tech Publications, 2008, vol. 136, pp. 161–174 Search PubMed.
- W. Weng, G. Chen and D. Wu, Polymer, 2003, 44, 8119–8132 CrossRef CAS.
- P. W. Zhu, A. Phillips, G. Edward and L. Nichols, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 051801 CrossRef PubMed.
- P. W. Zhu, G. Edward and L. Nichols, J. Phys. D: Appl. Phys., 2009, 42, 245406 CrossRef.
- F. L. Binsbergen, J. Polym. Sci., Polym. Phys. Ed., 1973, 11, 117–135 CAS.
- W. Stocker, M. Schumacher, S. Graff, A. Thierry, J. C. Wittmann and B. Lotz, Macromolecules, 1998, 31, 807–814 CrossRef CAS.
- M. D'Haese, P. Van Puyvelde and F. Langouche, Macromolecules, 2010, 43, 2933–2941 CrossRef.
- M. D'Haese, F. Langouche and P. Van Puyvelde, Macromolecules, 2013, 46, 3425–3434 CrossRef.
- D. Zhao, V. Gimenez-Pinto, A. M. Jimenez, L. Zhao, J. Jestin, S. K. Kumar and M. M. Khani, ACS Cent. Sci., 2017, 3, 751–758 CrossRef CAS PubMed.
- H. Papananou, E. Perivolari, K. Chrissopoulou and S. H. Anastasiadis, Polymer, 2018, 157, 111–121 CrossRef CAS.
- A. Jabbarzadeh and R. Tanner, J. Non-Newtonian Fluid Mech., 2009, 160, 11–21 Search PubMed.
- A. Jabbarzadeh and R. Tanner, Macromolecules, 2010, 43, 8136–8142 CrossRef CAS.
- A. Jabbarzadeh, Soft Matter, 2013, 9, 11598–11608 RSC.
- A. Jabbarzadeh and X. Chen, Faraday Discuss., 2017, 204, 307–330 RSC.
- A. K Dasmahapatra, H. Nanavati and G. Kumaraswamy, J. Chem. Phys., 2009, 131, 074905 CrossRef PubMed.
- A. Cacciuto, S. Auer and D. Frenkel, Nature, 2004, 428, 404–406 CrossRef CAS PubMed.
- T. Mandal, W. Huang, J. M. Mecca, A. Getchell, W. W. Porter and R. G. Larson, Soft Matter, 2017, 13, 1904–1913 RSC.
- H. Yang, X. J. Zhao, Z. S. Li and F. D. Yan, J. Chem. Phys., 2009, 130, 074902 CrossRef PubMed.
- L. Ramin and A. Jabbarzadeh, J. Chem. Phys., 2012, 137, 174706 CrossRef PubMed.
- A. Jabbarzadeh, P. Harrowell and R. I. Tanner, J. Phys. Chem. B, 2007, 111, 11354–11365 CrossRef CAS PubMed.
- P. Shashikanth and P. Prasad, Curr. Sci., 2001, 80, 1578–1581 CAS.
- D. Evans and G. Morriss, Statistical Mechanics of Nonequilibrium Liquids, Academic, Sydney, 1990 Search PubMed.
- P. J. Daivis and D. J. Evans, J. Chem. Phys., 1994, 100, 541–547 CrossRef CAS.
- J. Delhommelle and D. J. Evans, J. Chem. Phys., 2001, 115, 43–49 CrossRef CAS.
- H. C. Tseng, J. S. Wu and R. Y. Chang, J. Chem. Phys., 2008, 129, 014502 CrossRef PubMed.
- C. L. Yaws, Yaws' Thermophysical Properties of Chemicals and Hydrocarbons, Knovel, 2009 Search PubMed.
- M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- T. Irzhak, S. Mezhikovskii and V. Irzhak, Polym. Sci., Ser. B, 2008, 50, 201–203 CrossRef.
- A. Genovese, G. Amarasinghe, M. Glewis, D. Mainwaring and R. A. Shanks, Thermochim. Acta, 2006, 443, 235–244 CrossRef CAS.
- H. Wang, J. K. Keum, A. Hiltner and E. Baer, Macromolecules, 2010, 43, 3359–3364 CrossRef CAS.
- S. Mai, C. Booth and V. M. Nace, Eur. Polym. J., 1997, 33, 991–996 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00525k |
| This journal is © The Royal Society of Chemistry 2019 |