The interparticle distance limit for multiple exciton dissociation in PbS quantum dot solid films†
Naoki
Nakazawa
a,
Yaohong
Zhang
 *a,
Feng
Liu
a,
Chao
Ding
a,
Kanae
Hori
a,
Taro
Toyoda
a,
Yingfang
Yao
*a,
Feng
Liu
a,
Chao
Ding
a,
Kanae
Hori
a,
Taro
Toyoda
a,
Yingfang
Yao
 b,
Yong
Zhou
b,
Yong
Zhou
 b,
Shuzi
Hayase
c,
Ruixiang
Wang
d,
Zhigang
Zou
b and
Qing
Shen
b,
Shuzi
Hayase
c,
Ruixiang
Wang
d,
Zhigang
Zou
b and
Qing
Shen
 *a
*a
aFaculty of Informatics and Engineering, The University of Electro-Communications, Tokyo 182-8585, Japan. E-mail: yhzhang1021@live.com; shen@pc.uec.ac.jp
bEcomaterials and Renewable Energy Research Center, Jiangsu Key Laboratory for Nano Technology, National Laboratory of Solid State Microstructures, Nanjing University, Nanjing 210093, China
cFaculty of Life Science and Systems Engineering, Kyushu Institute of Technology, Fukuoka 808-0196, Japan
dBeijing Engineering Research Centre of Sustainable Energy and Buildings, Beijing University of Civil Engineering and Architecture, Beijing 102616, China
First published on 20th November 2018
Abstract
Understanding the behaviour of multiple exciton dissociation in quantum dot (QD) solid films is of fundamental interest and paramount importance for improving the performance of quantum dot solar cells (QDSCs). Unfortunately, the charge transfer behaviour of photogenerated multiple exciton in QD solid films is not clear to date. Herein, we systematically investigate the multiple exciton charge transfer behaviour in PbS QD solid films by using ultrafast transient absorption spectroscopy. We observe that the multiple exciton charge transfer rate within QD ensembles is exponentially enhanced as the interparticle distance between the QDs decreases. Biexciton and triexciton dissociation between adjacent QDs occurs via a charge transfer tunneling effect just like single exciton, and the charge tunneling constants of the single exciton (β1: 0.67 ± 0.02 nm−1), biexciton (β2: 0.68 ± 0.05 nm−1) and triexciton (β3: 0.71 ± 0.01 nm−1) are obtained. More importantly, for the first time, the interparticle distance limit (≤4.3 nm) for multiple exciton charge transfer between adjacent QDs is found for the extraction of multiple excitons rapidly before the occurrence of Auger recombination. This result points out a vital and necessary condition for the use of multiple excitons produced in PbS QD films, especially for their applications in QDSCs.
Conceptual insightsIn this study, we report the interparticle distance dependent multiple exciton dissociation behaviour in quantum dot (QD) solid films for the first time, and we systematically investigate the complex multiple exciton charge transfer behaviour in PbS QD solid films using ultrafast transient absorption spectroscopy. We found that the charge transfer rate constant ket of the single exciton, biexciton and triexciton within the QD solid film is exponentially enhanced as the interparticle distance between the QDs decreases, where charge transfer occurs via the tunneling effect between neighboring QDs. More importantly, when the QD center-to-center distance is smaller than 4.3 nm (or QD–QD spacing is smaller than 0.8 nm), multiple excitons can be rapidly extracted before the occurrence of Auger recombination. This result reveals the reason why above 100% incident photon to current conversion efficiency (IPCE) could only be observed in short surface-ligand treated QD based devices to date. Our finding points out a vital condition for using the multiple excitons in QD solid films and will be beneficial for the use of multiple exciton generation (MEG) in QDs to improve the performance of quantum dot solar cells and could have important implications in the development of this technology. |
Introduction
Quantum dot solar cells (QDSCs) are considered to be one of the most promising candidates for the new-generation photovoltaics due to multiple exciton generation (MEG) in QDs.1–10 In the MEG process, a single high energy photon can generate more than two excitons (electron–hole pairs) across the band gap, which is potentially vital for photocurrent improvements and thus the energy conversion efficiency of the solar devices. The MEG process is known as the inverse Auger recombination (AR) process,1 in which the electron (e)–hole (h) recombination energy is transferred to a third charge (e or h) that is re-excited to a higher-energy state.11 Quantum confinement of the exciton in a QD enhances the exciton–exciton interactions, which leads to MEG and AR processes.12 Thus, a detailed and deep understanding of the dynamics of multiple excitons, including their generation and dissociation, is very important for applying MEG to enhance the photovoltaic performance of QDSCs.The mechanism of MEG and AR processes in colloidal QDs have been studied using ultrafast transient absorption (TA) spectroscopy.2,11–13 The probability of MEG and AR can be greatly enhanced due to carrier confinement and increased e–h Coulomb interaction.4,14 It is known that MEG has been observed not only in solution but also in closely packed QD solid films such as PbS and PbSe QD films as the excitation photon energy exceeds 2.7 times Eg,2,4,15–23 and improvement of the incident-photon-to-current efficiency (IPCE) of over 100% has also been experimentally demonstrated.24,25 Surface passivation and modification of QDs is significantly important to enhance the photovoltaic performance of QDSCs.5,26–42 Designed surface treatment of QDs can improve the mobility of carriers and reduce the non-radiative carrier recombination.39,43–52 In particular, in QD solid films, the interparticle distance between the QDs can be controlled by the length of surface ligand of the QDs.53 It was reported that QD solid films treated with short ligands have strong electronic interaction between the QDs, which can improve carrier mobility.45,54 However, to date, the deeper reason behind this result has not been revealed and the charge transfer mechanism of multiple excitons between adjacent QDs is not fully understood. Thus, the study of the dynamics of multiple excitons in QD solid films is essential to realize the extraction of excitons and high performance of QDSCs based on MEG.
In this study, we report interparticle distance dependent multiple exciton dissociation in PbS QD solid films. Herein, PbS QD solid films were fabricated by a layer-by-layer method using different mercaptoalkanoic acids (MAA) such as 3-mercaptopropionic acid (3-MPA), 6-mercaptohexanic acid (6-MHA), 12-mercaptohexanic acid (12-MDA) and 16-mercaptohexadecanoic acid (16-MHDA) to replace the original surface ligands (i.e. oleic acid (OA)) of the colloidal PbS QDs. Based on this design, the interparticle distance between PbS QDs was well controlled by the length of the MAA.53 Using the same binding structure of these MAA ligands to the QDs, we observed the dependency of the exciton dissociation dynamics in PbS QD solid films to the QD center-to-center distance. We found that biexciton and triexciton dissociation between adjacent QDs can occur rapidly via charge transfer tunneling effects just like for single excitons, and the obtained charge tunneling constants of single exciton (β1), biexciton (β2) and triexcitons (β3) are 0.67 ± 0.02 nm−1, 0.68 ± 0.05 nm−1 and 0.71 ± 0.01 nm−1, respectively. More importantly, we discovered that when the QD center-to-center distance between the PbS QDs is smaller than 4.3 nm (or an interparticle spacing smaller than 0.8 nm), multiple excitons can be rapidly extracted before the occurrence of Auger recombination. This result reveals the reason why over 100% IPCE has only been observed in short surface ligand treated QD based devices to date.24,25 Our finding points out a necessary condition for using multiple excitons in QD solid films and will be beneficial for using the MEG in QDs to improve the performance of QDSCs.
Results and discussion
We initially investigated PbS QDs surface chemistry using Fourier transform infrared absorption (FTIR) spectroscopy. Fig. S1 (ESI†) shows the FTIR spectra of PbS QD solid films before and after MAA ligand exchanges. FTIR results confirm that new MAA ligand can be capped on the QDs surface after ligand exchange. In order to evaluate the interparticle distance between adjacent PbS QDs, which are capped by different MAA ligands, monolayer PbS QDs are deposited on an ultrathin carbon film and characterized by high resolution transmission electron microscopy (HRTEM). Fig. S2 (ESI†) shows the HRTEM images of PbS QD ensembles with various MAA ligands. It can be evidently seen that the size of PbS QD is about 3.5 nm and the borderlines of the MAA treated QDs are more distinct than that of OA-capped PbS QD film, which are in good agreement with the removal of OA ligands from the QDs surface. The averaged QD center-to-center distance was calculated as 4.0 ± 0.3 nm, 4.3 ± 0.4 nm, 4.8 ± 0.3 nm and 5.6 ± 0.4 nm for 3-MPA, 6-MHA, 12-MDA and 16-MHDA ligand treated QDs, respectively. And the averaged QD–QD spacing was calculated as 0.5 ± 0.2 nm, 0.8 ± 0.4 nm, 1.3 ± 0.4 nm and 2.1 ± 0.4 nm for 3-MPA, 6-MHA, 12-MDA and 16-MHDA ligand treated QDs, respectively. Interestingly, the averaged QD center-to-center distance and averaged QD–QD spacing in these MAA treated films was found to linearly increase from 4.0 nm to 5.8 nm and from 0.5 nm to 2.3 nm as the number of carbon atoms of the corresponding ligands increases from 3 to 18 as shown in Fig. 1 and Fig. S3 (ESI†), respectively.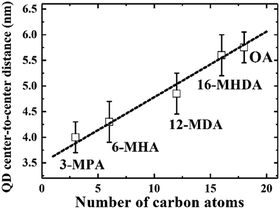 | ||
| Fig. 1 The linear relationship between the QD center-to-center distance and the number of carbon atoms in the capping ligands. | ||
Optical absorbance spectra of the four types of MAA ligand treated PbS QD solid films and isolated OA-capped PbS QDs solution are shown in Fig. S4a (ESI†). We investigated the exciton relaxation dynamics of the four types of PbS QD solid films using TA measurements. In Fig. 2a, as an example, the spectro-temporal TA map together with the ground-state absorption spectrum of 6-MHA treated PbS QD solid film are shown. It can be evidently observed that the optical absorption peak and TA bleaching peak around 1035 nm of the 6-MHA treated PbS QD solid film correspond to the lowest-energy excitons in the PbS QD solid film. In order to observe the single exciton (1 e–h pair) relaxation dynamics in the MAA treated PbS QD solid films, TA spectra were measured under low excitation fluences (∼10 μJ cm−2, which will be discussed in detail later), which is the condition for minimizing Auger recombination and maintaining signal-to-noise ratio during the TA measurement. Fig. S4b (ESI†) shows the TA responses of the lowest energy exciton in the 3-MPA, 6-MHA, 12-MDA and 16-MHDA treated PbS QD solid films and isolated OA-capped PbS QDs in an octane solution. In the TA measurements, all samples are pumped by 470 nm (2.64 eV) laser pulses, of which the photon energy is about 2.2 times of Eg, where Eg is the peak energy of the lowest-energy exciton in each PbS QD solid film. The photoinduced transmission changes ΔT/T of all samples are positive, representing the bleach of the lowest exciton state. As shown in Fig. S4b (ESI†), no significant decay of the TA signal intensities for 16-MHDA treated film and isolated PbS QDs in solution can be observed in the timescale up to 1 ns. This suggests that there is no exciton dissociation, i.e. no charge transfer from one QD to the neighbouring QD in both samples. This is because the QD center-to-center distance is too large for charge transfer between the two neighbouring QDs. In contrast, for the 3-MPA, 6-MHA and 12-MDA treated films, the TA signal intensities decay faster than that of the 16-MHDA treated film under the same excitation fluence. This indicates that an efficient charge transfer (1 e–h pair relaxation) channel appears in those three short-ligand (3-MPA, 6-HMA and 12-MDA) treated films. Then we can calculate the charge transfer rate constant k1et, i.e. the exciton lifetime τ1 (1/k1et) by fitting the TA decay curves with a single exponential function (Table S1, ESI†). As shown in Fig. S4b (ESI†) (solid lines), the fitting results reproduce the experimental results well. Interestingly, as shown in Fig. 2b, the relationship between the averaged QD center-to-center distance d and the charge transfer rate constant k1et of the 1 e–h pair can be well fitted by a single exponential decay function as reported in our earlier report.55 This behaviour can be explained very well by the Marcus theory in which the charge transfer rate constant ket (i.e. the k1et here) corresponds to the following model:56
| ket = k0e(−βd) | (1) |
 | ||
| Fig. 2 (a) Spectro-temporal TA map together with the ground-state absorption spectrum of 6-MHA treated PbS QD solid film. The negative signal in the changes of absorption (i.e., the positive value of ΔT) indicates the photobleaching of the exciton state. (b) Correlation between the averaged QD center-to-center distance (d) and the charge transfer rate constant (k1et) of 1 e–h pair from which the exciton lifetimes were calculated in Fig. S4b (ESI†). Single exponential decay fit (eqn (1)) (dotted line) indicates that the charge transfer occurs via tunneling of charge. | ||
Next, to explore the interparticle spacing dependent multiple exciton relaxation dynamics in the closely packed PbS QD solid films, the TA decay behaviours of the PbS QD solid films capped by different ligands were investigated under various excitation fluences of the pump light with the same wavelength of 470 nm (i.e., a photon energy of 2.64 eV). Fig. 3a and b show the TA responses of 16-MHDA and 3-MPA treated PbS QD solid films under various excitation fluences. As the excitation fluence increases, fast-decay components can be observed in both the 16-MHDA and 3-MPA treated PbS QD solid films. Fig. 3c and d show the excitation fluence dependence of TA signal intensities at a delay time of 1 ns (after the finish of AR) for 16-MHDA and 3-MPA treated films, respectively. For the 16-MHDA treated films, the TA signal intensity at 1 ns increases as the excitation fluence increases and saturates at about 150 μJ cm−2. Since AR occurs at a fast timescale from a few tens to hundreds of picosecond in the photoexcited QDs, almost all the photoexcited QDs include only one single exciton at longer times, such as 1 ns after the AR is finished. Thus, the TA signal intensities at the longer time correspond to the initial number of the photoexcited QDs. It is known that the probability of the initial generation of the multiple excitons (e–h pairs) in a QD can be expressed with a Poisson distribution, Pn(N0), where n is the number of the e–h pairs in a QD and N0 is the average number of the e–h pairs per QD immediately after photogeneration, respectively.47,58N0 is described by the product of the photon fluence Jp and the absorption cross section σ (N0 = Jpσ).59 Hence, TA signal intensities at 1 ns are given by:60
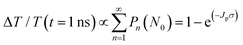 | (2) |
As shown in Fig. 3c, the fitted results by eqn (2) can reproduce the experimental results very well, which verifies that the multiple exciton relaxation in 16-MHDA treated film is dominated by AR. The value of σ is obtained to be 9.9(±0.5) × 10−15 cm2. The dependence of the TA signal intensity at 1 ns versus the photon fluence of the pump light for the 16-MHDA treated films, i.e., the decay behaviour of the multiple exciton is very similar to that of the isolated QD solution (Fig. S6e, ESI†), which confirms that the electronic interactions between the adjacent QDs in 16-MHDA treated film are negligible.
In contrast, for 3-MPA, 6-MHA and 12-MHDA treated films, the excitation-fluence dependent TA signal intensities at 1 ns of these three films are different from those of the 16-MHDA treated film and isolated QDs in solution (Fig. S6, ESI†). These results indicate that besides the AR relaxation process, other relaxation processes for the multiple exciton occurred in the closely packed films. One possible process is the dissociation of the multiple exciton through charge transfer between the neighbouring QDs in the closely packed films because the averaged QD center-to-center distance of the 3-MPA, 6-MHA and 12-MHDA treated films is shorter than that of 16-MHDA treated film: biexcitons and triexcitons in a single QD can transfer to the adjacent QDs like a single exciton as discussed above. According to the report of Kanemitsu et al.,60,61 the influence of this charge transfer process can be expressed by modifying eqn (2) for the TA signal intensities in the closely packed films at 1 ns as follows:
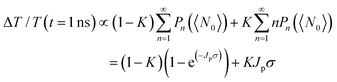 | (3) |
| Ligand | K | σ (cm2) |
|---|---|---|
| 3-MPA | 0.044(±0.002) | 1.4(±0.3) × 10−14 |
| 6-MHA | 0.023(±0.003) | 1.2(±0.1) × 10−14 |
| 12-MDA | 0.018(±0.003) | 1.0(±0.2) × 10−14 |
| 16-MHDA | 0 | 9.9(±0.5) × 10−15 |
| OA | 0 | 2.8(±0.9) × 10−15 |
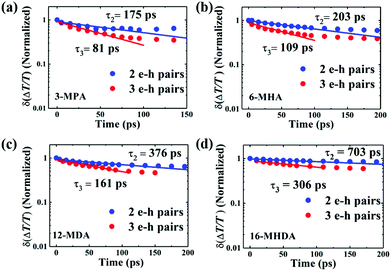
To gain a detailed understanding of the multiple exciton relaxation dynamics, we used a simple subtractive procedure to characterize the relaxation of different multiple-pair QD states from the TA decay curves.62 The average number of photoexcited e–h pairs per QD is calculated using N0 = Jpσ.59,62 When the range of the average number of e–h pairs per QD N0 is changed from 0.5 to 2.5 (Fig. S7, ESI†), the multiple exciton relaxation dynamics can be described by a triple exponential function:
| N(t) = A1e−t/τ1 + A2e−t/τ2 + A3e−t/τ3 | (4) |
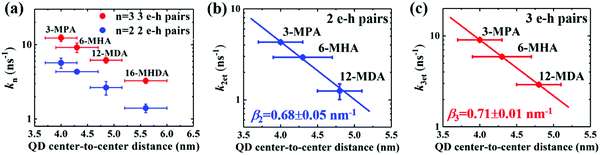
We sought to gain further insight into the multiple exciton dissociation dynamics through charge transfer. To do so, we calculated charge transfer rate constants k2et and k3et of the 2 and 3 e–h pairs, respectively. In 16-MHDA treated films, the multiple exciton relaxation dynamics is assumed to be only dominated by the AR process because of very weak electronic interactions between the QDs. Therefore, we can calculate the Auger recombination rate constants k2AR and k3AR, which are the inverse of the multiple exciton lifetimes τ2 and τ3 in the case of 16-MHDA treated film. Then, assuming that the Auger recombination rate constants k2AR and k3AR are the same in the PbS QD films treated by different MAA ligands in this study, we can calculate multiple charge transfer rate constants k2et and k3et from the measured exciton lifetimes of each MAA ligand-treated films via the following equation and the results are shown in Fig. 5b and c:
 | (5) |
From Fig. 5b, c and Fig. S8a and b (ESI†), we find that the charge transfer rates of the 2 and 3 e–h pairs are well described by a single exponential decay function of the QD center-to-center distance and the QD–QD spacing, similar to that of the 1 e–h pair. The values of the charge transfer rate constants k2et and k3et and Auger recombination rate constants k2AR and k3AR are summarized in Table 2. In particular, when the QD center-to-center distance (or interparticle spacing) is smaller than 4.3 nm (or 0.8 nm) in the case of 3-MPA and 6-MHA treated PbS QD solid films, the charge transfer rate constants k2et and k3et are larger than the Auger recombination rate constants k2AR and k3AR of those samples. This result indicates that in those samples, multiple excitons can be rapidly extracted before the onset of Auger recombination. Moreover, we determined the charge tunneling constants β2 and β3 by fitting Fig. 5b and c to eqn (1). The extracted values of the charge tunneling constantsβ2 and β3 are 0.68 ± 0.05 nm−1 and 0.71 ± 0.01 nm−1, respectively, which are close to that of the single charge tunneling constants β1. Therefore, we find that the dissociation of multiple exciton in closely packed films also occurs via the tunneling effect just like the behaviour of a single exciton in the QD films.
| QD center-to-center distance (nm) | k 2et (ns−1) | k 3et (ns−1) | k 2AR (ns−1) | k 3AR (ns−1) |
|---|---|---|---|---|
| 4.0 ± 0.3 (3-MPA) | 4.3 ± 0.2 | 9.0 ± 0.1 | 1.4 ± 0.1 | 3.2 ± 0.2 |
| 4.3 ± 0.4 (6-MHA) | 2.9 ± 0.1 | 5.9 ± 0.2 | 1.4 ± 0.1 | 3.2 ± 0.2 |
| 4.8 ± 0.3 (12-MDA) | 1.2 ± 0.2 | 2.9 ± 0.2 | 1.4 ± 0.1 | 3.2 ± 0.2 |
| 5.6 ± 0.4 (16-MHDA) | 0 | 0 | 1.4 ± 0.1 | 3.2 ± 0.2 |
Conclusions
In summary, the interparticle distance between the PbS QDs were well controlled by using different length MAA surface ligands, and the QD center-to-center distance in these MAA treated films was found to linearly increase as the number of carbon atoms in corresponding ligands increased. Evidence of interparticle distance dependent photogenerated multiple exciton dissociation in closely packed QD solid films has been shown for the first time. Our results show that the dissociation process of single exciton, biexciton and triexciton occur via tunneling of charges between neighboring QDs, and the obtained charge tunneling constants for the single exciton (β1), the biexciton (β2) and the triexciton (β3) are 0.67 ± 0.02 nm−1, 0.68 ± 0.05 nm−1 and 0.71 ± 0.01 nm−1, respectively. More importantly, for the first time, we found that the QD interparticle distance (or spacing) limit of multiple exciton extraction is 4.3 (or 0.8) nm, which clarifies one vital condition for using multiple excitons in packed QD solid films before the occurrence of Auger recombination. This result reveals the reason why above 100% IPCE could only be observed in short surface-ligand treated QD based devices to date. Our finding suggests that there is a large possibility to apply MEG in QDSCs. We consider that our results contribute to a further fundamental understanding of the improvement in the photovoltaic efficiency of QDSCs.Author contributions
Naoki Nakazawa, Yaohong Zhang and Qing Shen conceived and designed the experiments; Naoki Nakazawa, Feng Liu, Chao Ding, Kanae Hori and Taro Toyoda performed the experiments; Yaohong Zhang, Yingfang Yao, Yong Zhou, Zhigang Zou and Qing Shen analyzed the data; Shuzi Hayase, Ruixiang Wang and Qing Shen contributed reagents/materials/analysis tools; Naoki Nakazawa and Yaohong Zhang wrote the paper; Qing Shen corrected the paper.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research was supported by the Japan Science and Technology Agency (JST) PRESTO and CREST programs, Beijing Advanced Innovation Center for Future Urban Design, Beijing University of Civil Engineering and Architecture (Grant UDC2018031121), and the MEXT KAKENHI Grant (Grants 26286013, 17H02736).Notes and references
- A. J. Nozik, Inorg. Chem., 2005, 44, 6893–6899 CrossRef CAS PubMed.
- A. J. Nozik, M. C. Beard, J. M. Luther, M. Law, R. J. Ellingson and J. C. Johnson, Chem. Rev., 2010, 110, 6873–6890 CrossRef CAS PubMed.
- M. C. Beard, J. M. Luther, O. E. Semonin and A. J. Nozik, Acc. Chem. Res., 2013, 46, 1252–1260 CrossRef CAS PubMed.
- R. J. Ellingson, M. C. Beard, J. C. Johnson, P. Yu, O. I. Micic, A. J. Nozik, A. Shabaev and A. L. Efros, Nano Lett., 2005, 5, 865–871 CrossRef CAS PubMed.
- Y. Zhang, C. Ding, G. Wu, N. Nakazawa, J. Chang, Y. Ogomi, T. Toyoda, S. Hayase, K. Katayama and Q. Shen, J. Phys. Chem. C, 2016, 120, 28509–28518 CrossRef CAS.
- Y. Zhang, J. Zhu, X. Yu, J. Wei, L. Hu and S. Dai, Sol. Energy, 2012, 86, 964–971 CrossRef CAS.
- L. Hu, Z. L. Zhang, R. J. Patterson, Y. C. Hu, W. J. Chen, C. Chen, D. B. Li, C. Hu, C. Ge, Z. H. Chen, L. Yuan, C. Yan, N. Song, Z. L. Teh, G. J. Conibeer, J. Tang and S. J. Huang, Nano Energy, 2018, 46, 212–219 CrossRef CAS.
- A. A. Chistyakov, M. A. Zvaigzne, V. R. Nikitenko, A. R. Tameev, I. L. Martynov and O. V. Prezhdo, J. Phys. Chem. Lett., 2017, 8, 4129–4139 CrossRef CAS PubMed.
- S. Jiao, J. Du, Z. Du, D. Long, W. Jiang, Z. Pan, Y. Li and X. Zhong, J. Phys. Chem. Lett., 2017, 8, 559–564 CrossRef CAS PubMed.
- C. Ding, Y. Zhang, F. Liu, Y. Kitabatake, S. Hayase, T. Toyoda, R. Wang, K. Yoshino, T. Minemoto and Q. Shen, Nanoscale Horiz., 2018, 3, 417–429 RSC.
- H. Htoon, J. A. Hollingsworth, R. Dickerson and V. I. Klimov, Phys. Rev. Lett., 2003, 91, 227401 CrossRef CAS PubMed.
- Y. Kanemitsu, Acc. Chem. Res., 2013, 46, 1358–1366 CrossRef CAS PubMed.
- S. Garakyaraghi, C. Mongin, D. B. Granger, J. E. Anthony and F. N. Castellano, J. Phys. Chem. Lett., 2017, 8, 1458–1463 CrossRef CAS PubMed.
- A. Shabaev, A. L. Efros and A. J. Nozik, Nano Lett., 2006, 6, 2856–2863 CrossRef CAS PubMed.
- J. M. Luther, M. C. Beard, Q. Song, M. Law, R. J. Ellingson and A. J. Nozik, Nano Lett., 2007, 7, 1779–1784 CrossRef CAS PubMed.
- R. D. Schaller and V. I. Klimov, Phys. Rev. Lett., 2004, 92, 186601 CrossRef CAS PubMed.
- M. C. Beard, A. G. Midgett, M. Law, O. E. Semonin, R. J. Ellingson and A. J. Nozik, Nano Lett., 2009, 9, 836–845 CrossRef CAS PubMed.
- L. A. Padilha, J. T. Stewart, R. L. Sandberg, W. K. Bae, W.-K. Koh, J. M. Pietryga and V. I. Klimov, Acc. Chem. Res., 2013, 46, 1261–1269 CrossRef CAS PubMed.
- Q. Shen, K. Katayama, T. Sawada, S. Hachiya and T. Toyoda, Chem. Phys. Lett., 2012, 542, 89–93 CrossRef CAS.
- Q. Shen, K. Katayama and T. Toyoda, J. Energy Chem., 2015, 24, 712–716 CrossRef.
- S. Akhavan, A. F. Cihan, A. Yeltik, B. Bozok, V. Lesnyak, N. Gaponik, A. Eychmuller and H. V. Demir, Nano Energy, 2016, 26, 324–331 CrossRef CAS.
- V. Sukhovatkin, S. Hinds, L. Brzozowski and E. H. Sargent, Science, 2009, 324, 1542–1544 CrossRef CAS PubMed.
- J. B. Sambur, T. Novet and B. A. Parkinson, Science, 2010, 330, 63–66 CrossRef CAS PubMed.
- O. E. Semonin, J. M. Luther, S. Choi, H.-Y. Chen, J. Gao, A. J. Nozik and M. C. Beard, Science, 2011, 334, 1530–1533 CrossRef CAS PubMed.
- Y. Yan, R. W. Crisp, J. Gu, B. D. Chernomordik, G. F. Pach, A. R. Marshall, J. A. Turner and M. C. Beard, Nat. Energy, 2017, 2, 17052 CrossRef CAS.
- C.-H. M. Chuang, P. R. Brown, V. Bulović and M. G. Bawendi, Nat. Mater., 2014, 13, 796–801 CrossRef CAS PubMed.
- J. Tang, K. W. Kemp, S. Hoogland, K. S. Jeong, H. Liu, L. Levina, M. Furukawa, X. Wang, R. Debnath, D. Cha, K. W. Chou, A. Fischer, A. Amassian, J. B. Asbury and E. H. Sargent, Nat. Mater., 2011, 10, 765–771 CrossRef CAS PubMed.
- W. Shi, S. W. H. Eijt, C. S. Suchand Sandeep, L. D. A. Siebbeles, A. J. Houtepen, S. Kinge, E. Brück, B. Barbiellini and A. Bansil, Appl. Phys. Lett., 2016, 108, 081602 CrossRef.
- J. Y. Woo, S. Lee, S. Lee, W. D. Kim, K. Lee, K. Kim, H. J. An, D. C. Lee and S. Jeong, J. Am. Chem. Soc., 2016, 138, 876–883 CrossRef CAS PubMed.
- D. A. Hines and P. V. Kamat, J. Phys. Chem. C, 2013, 117, 14418–14426 CrossRef CAS.
- R. W. Crisp, D. M. Kroupa, A. R. Marshall, E. M. Miller, J. Zhang, M. C. Beard and J. M. Luther, Sci. Rep., 2015, 5, 9945 CrossRef CAS PubMed.
- P. R. Brown, D. Kim, R. R. Lunt, N. Zhao, M. G. Bawendi, J. C. Grossman and V. Bulović, ACS Nano, 2014, 8, 5863–5872 CrossRef CAS PubMed.
- J. Jean, T. S. Mahony, D. Bozyigit, M. Sponseller, J. Holovsky, M. G. Bawendi and V. Bulovic, ACS Energy Lett., 2017, 2, 2616–2624 CrossRef CAS.
- B. Sun, O. Voznyy, H. Tan, P. Stadler, M. Liu, G. Walters, A. H. Proppe, M. Liu, J. Fan, T. Zhuang, J. Li, M. Wei, J. Xu, Y. Kim, S. Hoogland and E. H. Sargent, Adv. Mater., 2017, 29, 1700749 CrossRef PubMed.
- M. Ono, T. Nishihara, T. Ihara, M. Kikuchi, A. Tanaka, M. Suzuki and Y. Kanemitsu, Chem. Sci., 2014, 5, 2696–2701 RSC.
- R. K. Capek, D. Yanover and E. Lifshitz, Nanoscale, 2015, 7, 5299–5310 RSC.
- C. R. Kagan, E. Lifshitz, E. H. Sargent and D. V. Talapin, Science, 2016, 353, 5523 CrossRef PubMed.
- D. Asil, B. J. Walker, B. Ehrler, Y. Vaynzof, A. Sepe, S. Bayliss, A. Sadhanala, P. C. Y. Chow, P. E. Hopkinson, U. Steiner, N. C. Greenham and R. H. Friend, Adv. Funct. Mater., 2014, 25, 928–935 CrossRef.
- Y. Gao, M. Aerts, C. S. S. Sandeep, E. Talgorn, T. J. Savenije, S. Kinge, L. D. A. Siebbeles and A. J. Houtepen, ACS Nano, 2012, 6, 9606–9614 CrossRef CAS PubMed.
- P. Galar, P. Piatkowski, T. T. Ngo, M. Gutierrez, I. Mora-Sero and A. Douhal, Nano Energy, 2018, 49, 471–480 CrossRef CAS.
- H. I. Wang, M. Bonn and E. Cánovas, J. Phys. Chem. Lett., 2017, 8, 2654–2658 CrossRef CAS PubMed.
- F. Liu, Y. Zhang, C. Ding, T. Toyoda, Y. Ogomi, T. S. Ripolles, S. Hayase, T. Minemoto, K. Yoshino, S. Dai and Q. Shen, J. Phys. Chem. Lett., 2018, 9, 294–297 CrossRef CAS PubMed.
- J. M. Luther, M. Law, Q. Song, C. L. Perkins, M. C. Beard and A. J. Nozik, ACS Nano, 2008, 2, 271–280 CrossRef CAS PubMed.
- S. J. Oh, Z. Wang, N. E. Berry, J.-H. Choi, T. Zhao, E. A. Gaulding, T. Paik, Y. Lai, C. B. Murray and C. R. Kagan, Nano Lett., 2014, 14, 6210–6216 CrossRef CAS PubMed.
- Y. Liu, M. Gibbs, J. Puthussery, S. Gaik, R. Ihly, H. W. Hillhouse and M. Law, Nano Lett., 2010, 10, 1960–1969 CrossRef CAS PubMed.
- Y. Zhang, G. Wu, C. Ding, F. Liu, Y. Yao, Y. Zhou, C. Wu, N. Nakazawa, Q. Huang, T. Toyoda, R. Wang, S. Hayase, Z. Zou and Q. Shen, J. Phys. Chem. Lett., 2018, 9, 3598–3603 CrossRef CAS PubMed.
- H. Zhang, B. Hu, L. Sun, R. Hovden, F. W. Wise, D. A. Muller and R. D. Robinson, Nano Lett., 2011, 11, 5356–5361 CrossRef CAS PubMed.
- S. J. Oh, D. B. Straus, T. Zhao, J. H. Choi, S. W. Lee, E. A. Gaulding, C. B. Murray and C. R. Kagan, Chem. Commun., 2017, 53, 728–731 RSC.
- Q. Lin, H. J. Yun, W. Liu, H.-J. Song, N. S. Makarov, O. Isaienko, T. Nakotte, G. Chen, H. Luo, V. I. Klimov and J. M. Pietryga, J. Am. Chem. Soc., 2017, 139, 6644–6653 CrossRef CAS PubMed.
- G. W. Guglietta, B. T. Diroll, E. A. Gaulding, J. L. Fordham, S. Li, C. B. Murray and J. B. Baxter, ACS Nano, 2015, 9, 1820–1828 CrossRef CAS PubMed.
- M. T. Frederick, V. A. Amin and E. A. Weiss, J. Phys. Chem. Lett., 2013, 4, 634–640 CrossRef CAS PubMed.
- E. A. Weiss, ACS Energy Lett., 2017, 2, 1005–1013 CrossRef.
- M. S. Kodaimati, C. Wang, C. Chapman, G. C. Schatz and E. A. Weiss, ACS Nano, 2017, 11, 5041–5050 CrossRef CAS PubMed.
- C. S. S. Sandeep, S. Ten Cate, J. M. Schins, T. J. Savenije, Y. Liu, M. Law, S. Kinge, A. J. Houtepen and L. D. A. Siebbeles, Nat. Commun., 2013, 4, 2360 CrossRef PubMed.
- J. Chang, Y. Ogomi, C. Ding, Y. H. Zhang, T. Toyoda, S. Hayase, K. Katayama and Q. Shen, Phys. Chem. Chem. Phys., 2017, 19, 6358–6367 RSC.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Biomembr., 1985, 811, 265–322 CrossRef CAS.
- J. J. Choi, J. Luria, B.-R. Hyun, A. C. Bartnik, L. Sun, Y.-F. Lim, J. A. Marohn, F. W. Wise and T. Hanrath, Nano Lett., 2010, 10, 1805–1811 CrossRef CAS PubMed.
- V. I. Klimov, J. Phys. Chem. B, 2000, 104, 6112–6123 CrossRef CAS.
- V. I. Klimov, D. W. McBranch, C. A. Leatherdale and M. G. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13740–13749 CrossRef CAS.
- T. Nishihara, H. Tahara, M. Okano, M. Ono and Y. Kanemitsu, J. Phys. Chem. Lett., 2015, 6, 1327–1332 CrossRef CAS PubMed.
- H. Tahara, M. Sakamoto, T. Teranishi and Y. Kanemitsu, Nat. Commun., 2018, 9, 3179 CrossRef PubMed.
- V. I. Klimov, A. A. Mikhailovsky, D. W. McBranch, C. A. Leatherdale and M. G. Bawendi, Science, 2000, 287, 1011–1013 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, FTIR spectra, HRTEM images of PbS QDs, light absorption spectra, TA time decay curves and fitting data of single exciton, excitation-fluences dependent TA time decay curves. See DOI: 10.1039/c8nh00341f |
| This journal is © The Royal Society of Chemistry 2019 |