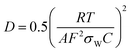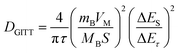Size control of zwitterionic polymer micro/nanospheres and its dependence on sodium storage

Abstract

In this study, the size control of organic materials and its dependence on sodium storage are investigated. Poly(pyrrole-squaraine) (PPS), a polymer containing zwitterionic repeating units, was selected as a proof for demonstration. The growth control of PPS micro/nanospheres could facilely be achieved via an in situ one-step polymerization. We found that the smallest-sized PPS showed the best rate performance and cycling performance, and the shortest activation process. Moreover, the Na-ion diffusion coefficient did not strictly correlate to the particle size. These results prove that the smaller size and the shorter ionic diffusion length rather than the ionic diffusion coefficient of the material dominated the charge transfer and ionic diffusion, thereby enhancing the rate performance.

---

New concepts

The size dependence of inorganic materials has been widely studied for fast-charging of batteries. Considering that organic materials are insensitive to the intercalation/extraction of large ions (e.g. Na⁺, K⁺), it is of particular importance to investigate if the rules for inorganic materials are applicable to organic materials likewise. However, the size control of organic materials and its dependence on electrochemical performance were not easily achievable because of the sensitivity to harsh post-treatments and poor solubility (required for batteries) of organic materials. We propose the concept that a zwitterionic polymer could be used to study the size control of organic materials and the subsequent size dependency of their electrochemical performance. As a proof-of-concept, poly(pyrrole-squaraine) (PPS), a polymer containing zwitterionic repeating units, was selected. The growth control of PPS micro/nanospheres was facilely achieved by tuning the reactants and solvents. The relationships among the particle size, the ionic diffusion length, the Na-ion diffusion coefficient and the electrochemical performance were studied. The results promote a deep understanding of the size effect on electrochemical performance and provide a universal route to enhance the electrochemical performance of organic electrodes.

Introduction

The increasingly growing demand for power supply promotes the development of alternatives, such as lithium-ion batteries (LIBs).¹ Among the various candidates, sodium-ion batteries (SIBs) have attracted extensive attention due to the abundant resources of sodium and their similar electrochemical properties as lithium.² However, the larger size of Na ions (1.02 Å vs. 0.76 Å of Li ions) always inhibits the Na-ion storage in traditional inorganic electrodes, leading to low capacity, poor rate performance and low cyclability. Organic materials (low cost, resource sustainability, structural diversity and flexibility) seem to be capable of solving these problems as they can accommodate the Na ions without obvious volume variations (e.g. <2% for sodium stilbene-dicarboxylate), leading to high rate performance and cyclability.^3,4

In order to enhance the electrochemical performance, especially to achieve high rate performance,^5–8 many strategies have been developed, mainly by the virtue of improving the charge transport and the ionic diffusion. The methods include particle size reduction (e.g. nanocrystallization),^9–12 morphological control (e.g. hollow structures, sheet morphologies or porous materials),^13–22 coating with conductive materials^23–26 and doping.^27,28 Among them, the size and morphology control significantly improve the rate and cycling performance, which have been extensively studied in inorganic materials. Based on these studies, it is widely accepted that size and morphology control can increase the electrode/electrolyte contact area and decrease the diffusion paths of ions and conduction paths of electrons. The short diffusion length is conducive to increase the utilization of active materials and improve the rate performance. However, there are few reports on the size effects of organic materials on batteries.^29–32 Considering that relatively weak intermolecular interactions can accommodate the Na ions and facilitate the intercalation/extraction of Na ions (e.g. <2% volume expansion after the intercalation of Na⁺ in organic materials⁴ compared with a volume expansion of ∼400% in inorganic materials³³), it is of particular importance to investigate if the aforementioned rules for inorganic materials are applicable to organic materials likewise. Moreover, the size and morphological control of inorganic materials seem to be easily achievable by various synthesis methods (e.g. hydrothermal method)^9,29 or post-treatments (e.g. mechanical milling, calcination, etc.).³⁴ The high stability of inorganic materials makes it possible to undergo various harsh conditions. On the contrary, the size and morphological control of organic materials are more difficult to achieve due to their low thermal stability (although it is acceptable for the cycling stability of batteries) and insolubility (that is required for batteries). A more convenient strategy is to control the particle size during synthesis, which has also not been widely studied in organic electrodes.

Herein, we have proposed a concept that uses the zwitterionic polymer to study the size control of organic materials and its subsequent effects on electrochemical performance. The zwitterionic nature makes it possible to control the size and morphology of the polymer by tuning the polar/nonpolar solvents and their ratio during synthesis. As a proof-of-concept, poly(pyrrole-squaraine) (PPS, Scheme 1), a polymer containing zwitterionic structure,³⁵ was selected as the cathode material to investigate the size control and its dependence on electrochemical behaviors in rechargeable SIBs. By controlling the experimental conditions, PPS micro/nanospheres with different sizes and regular shapes could be facilely synthesized by an in situ one-step polymerization technique of squaric acid with pyrrole. We found that the smallest-sized PPS nanospheres showed the best rate performance and cycling performance without a clear activation process. Moreover, through systematic analyses, we found that although the Na-ion diffusion coefficient did not strictly correlate to the particle size, the electrochemical performance (especially the fast-charge performance) enhanced with the downsizing of the particles. The results proved that the smaller size and the shorter ionic diffusion length of the nanometer-sized samples rather than their ionic diffusion coefficient dominated the charge transfer and ionic diffusion, which led to an enhanced electrochemical performance. These results promote a deep understanding of the size effect on electrochemical performance and provide a universal route to enhance the electrochemical performance of organic electrodes.

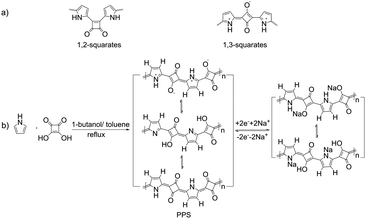Scheme 1 (a) Schematic of 1,2- and 1,3-squarates. (b) Schematic diagram of the synthesis of PPS and the storage mechanism of PPS in SIBs.

Results and discussion

Due to their unique optoelectronic properties, squaric acid-based dyes and polysquaraine have shown potential applications in photodetectors and solar cells.^36–39 Poly(pyrrole-squaraine) (PPS) was selected and synthesized here in view of the formation of a large π-conjugated system that facilitates fast charge and discharge in batteries,^3,4,40 the potential electrochemical activity of both the conjugated units (that benefits the high capacity), the abundant resources of raw materials, facile preparation, insolubility, stability and flexibility. Moreover, the zwitterionic nature made it possible to control the size and morphology by tuning the polar/nonpolar solvents and their ratio. Furthermore, a report⁴¹ has shown that azeotropic distillation using 1-butanol-benzene mixture as solvent facilitated the formation of PPS with a preference for 1,3-zwitterionic repeating units (Scheme 1), whereas the DMSO-acetic acid solvent condition at room temperature tended to form PPS with isomeric 1,2-diketonic repeating units. Considering the good electrochemical performance of the p-benzoquinone unit,^16,42 we selected the condition that can give 1,3-zwitterionic repeating units to be used for proof-of-concept.

The molar ratio of the two materials was kept at 1 : 1. We found that without the addition of butanol, no reaction was observed and no products were obtained (sample 1). With the addition of butanol, products were obtained with different morphologies (Fig. 1, Fig. S1, Table 1 and Table S1, ESI†). Interestingly, for all the conditions we tested, all the products are amorphous (Fig. S2 and S3, ESI†). However, all of them showed comparable Fourier transform infrared (FTIR) spectra (Fig. S4, ESI†) with a cyclobutenediylium-1,3-diolate moiety (as shown in Scheme 1a), which is consistent with the literature.^41,43–47 X-ray photoelectron spectroscopy (XPS) (Fig. S5, ESI†) and solid-state ¹³C nuclear magnetic resonance spectroscopy (¹³C NMR) (Fig. S6, ESI†) also confirmed the chemical composition of PPS. Moreover, we found that the morphology of PPS can be controlled (Fig. 1 and Table 1): (1) With the addition of butanol, micro/nanospheres could be achieved, although it should be noted that the morphology of the products was very sensitive to the concentration and ratio of the two solvents. For example, when butanol was used as the single solvent, we only obtained regular micro/nanospheres, provided the concentration was 0.0125 M. (2) With the increase in butanol in the mixture, the micro/nanospheres became smaller (from sample 4 to 6, Fig. 1c–e), leading to the smallest sized nanospheres when only butanol was used as the solvent (∼200 nm, Fig. 1f). Particularly, when the ratio of butanol and toluene increased from 3 : 1 to 5 : 1, smaller nanospheres of size at about 200 nm appeared, although the majority nanospheres were still sized at about 630 nm. This result undoubtedly indicated that the addition of butanol could lead to size reduction in PPS. (3) With the decrease in the concentration, the size of the micro/nanospheres also tended to decrease (from sample 2 to 4, Fig. 1a–c). All of these again proved that the morphology of the products was very sensitive to the concentration and ratio of the two solvents, which indicates that the size control of micro/nanospheres is highly dependent on the intermolecular interactions between the reactants and the solvents.⁴⁸ The indispensable presence of butanol suggested that the polar solvent (butanol) is essential for the formation of regular micro/nanospheres of PPS, due to the zwitterionic nature of PPS.

Fig. 1 (a–f) SEM images of the obtained PPS micro/nanospheres with different sizes: (a) 1200 nm, (b) 900 nm, (c) 800 nm, (d) 630 nm, (e) 630 nm with 200 nm small nanospheres and (f) 200 nm. The nanometer sized particles below the PPS micro/nanospheres in a and c are that of the substrate (conductive tape).

Table 1 The comparison of micro/nanospheres with different sizes and the corresponding experimental conditions

Sample index	Solvent ratio of 1-butanol and toluene	Concentration of reactants/mol L^−1	Size/nm	Figure
1	0 : 1	0.0125	No products
2 (PPS-XL)	2 : 1	0.2	∼1200	1a
3	2 : 1	0.1	∼900	1b
4 (PPS-L)	2 : 1	0.05	∼800	1c
5 (PPS-M)	3 : 1	0.05	∼630	1d
6 (PPS-S)	5 : 1	0.05	∼630 with small nanospheres (∼200 nm)	1e
7 (PPS-XS)	1 : 0	0.0125	∼200	1f

---

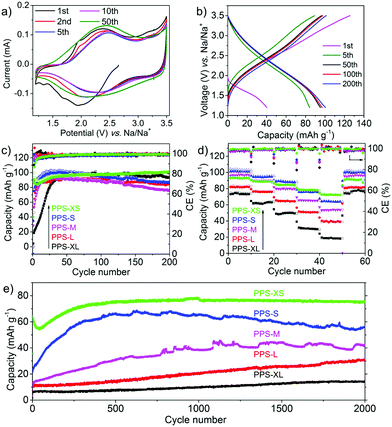
The controllable morphology and size of PPS made it possible to investigate the size dependency of PPS on the electrochemical performance. To compare the electrochemical characteristics of the PPS micro/nanospheres with different sizes, five samples (marked as XL, L, M, S and XS, respectively, see Table 1) were selected as representatives. Cathodes were obtained by mixing the PPS micro/nanospheres with Super P as the conductive additive and poly(vinylidene fluoride) (PVDF) as the binder. All the conditions were kept the same, giving a rough mass loading of ∼1 mg cm⁻² for all the five samples. Sodium metal was used as counter electrodes. Cyclic voltammetry (CV) measurements were recorded in the voltage range of 1.2–3.5 V at a scan rate of 0.5 mV s⁻¹. All the five samples showed only one pair of redox peaks located at 2.2–2.5 V (Fig. 2a and Fig. S7, ESI†). During the first cathodic scan, all the CV curves showed one reduction peak around 1.9–2.0 V. The reduction peaks from the second cathodic scan moved to a higher potential (∼2.25 V) and the currents roughly increased during cycling. These phenomena suggested the activation process during the first few cycles.^3,49,50 In addition, the smaller the size of the micro/nanospheres, the lesser were the cycles required to achieve symmetric redox peaks. Almost no obvious redox peaks were observed during several initial cycles for the large microspheres. After 50 cycles, all the five samples displayed obvious, symmetric and stable redox peaks. These results indicated that a longer activation process is required for larger micro/nanospheres. According to the total charge transferred, the stable currents generated subsequently correspond to one-electron transfer per conjugated unit, as shown in Scheme 1b. Such theoretical storage mechanism could be confirmed by the ex situ X-ray photoelectron spectroscopy (XPS) characterization of the PPS electrodes during the cycling process (Fig. S8, ESI†). The relative signal intensity between C=O double bonds and C–O single bonds relied on cycling, indicating the transformation of carbonyl groups (C=O double bonds) into C–O single bonds. Moreover, C–N–Na signal could also be observed, which showed the possible resonance structures between the neutral states and the zwitterionic states, as shown in Scheme 1b. No charge balancing anions (signal of PF₆⁻) were observed, indicating that the storage mechanism does not involve the intercalation of anions.

Fig. 2 (a) Typical CV curves of PPS electrodes (PPS-XS for example) in OSIBs at a scan rate of 0.5 mV s⁻¹; (b) typical voltage profiles of PPS electrodes (PPS-XS for example) in OSIBs; (c–e) cyclability of PPS electrodes in OSIBs: (c) at a current density of 50 mA g⁻¹; (d) rate cyclability (current density from left to right: 50, 100, 200, 500, 1000 and 50 mA g⁻¹). All the samples were firstly charged/discharged at a current density of 50 mA g⁻¹ till stable states for eliminating the activation process were achieved; (e) at a current density of 1000 mA g⁻¹.

The cycling performances of the five samples (PPS-XL, PPS-L, PPS-M, PPS-S and PPS-XS) were then tested at the rate of 50 mA g⁻¹ (50 mA g⁻¹ ∼0.56C). All the five samples showed similar sloping voltage profiles without distinct plateaus (Fig. 2b and Fig. S9, ESI†), although with the decrease in the particle size, plateaus tended to emerge in the voltage profiles. Moreover, all the five samples delivered similar and reversible capacities between 88–98 mA h g⁻¹ after 100 cycles (Fig. S10 and S11, ESI†), as shown in Fig. 2c. In addition, all of them showed a clear activation process with capacity enlargement in the first 20–30 cycles. With the increase in the particle size (from XS, S, M, L to XL), the activation process became severe and more cycles were necessary for achieving full utilization of active materials. PPS-XS, which had the smallest diameter, displayed the slightest activation process and best cyclability. These phenomena coincided well with the CV curves. Fig. 2d depicts the rate capability of the five samples. Most importantly, the capacities at high current densities (e.g. 500 and 1000 mA g⁻¹) became well-dependent on the particle size. The samples with smaller particle sizes delivered higher capacities. As expected, PPS-XS exhibited the best rate performance with a capacity of 91 mA h g⁻¹ at 50 mA g⁻¹ and 72 mA h g⁻¹ at 1000 mA g⁻¹, which corresponded to the capacity retention of 79% at the high rate. PPS-S and PPS-M showed slightly worse rate performances with capacity retentions of 61% and 55%, respectively, while the capacities of PPS-L and PPS-XL decreased dramatically with capacity retentions of 50% and 26%, respectively, at 1000 mA g⁻¹. We hence tested the long-term cycling of the five samples at a high rate of 1000 mA g⁻¹. As shown in Fig. 2e, the capacity, activation process and the long-term cyclability were highly dependent on the particle size. At a high current density, PPS-XS showed the shortest activation process and highest initial capacity. On the contrary, PPS-XL and PPS-L did not seem to saturate even after being charged/discharged for 1700 cycles. Furthermore, the capacity of PPS-XS became stable after the activation process, while the larger samples (e.g. PPS-S and PPS-M) were unstable afterwards. All of these results showed that the electrochemical performance (capacity, activation process, rate capability and long-term cyclability) is highly dependent on the particle size of PPS.

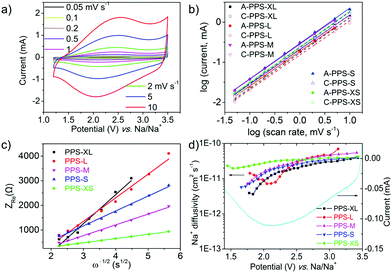
In order to further understand the size effect of PPS on the electrochemical performance, CV measurements at different scan rates, electrochemical impedance spectroscopy (EIS) and galvanostatic intermittent titration technique (GITT) were conducted. There is no doubt that smaller size increased the specific surface area (Table S2 and Fig. S12, ESI†) of the nanoparticles and hence the electrolyte/electrode interface, which shortened the ionic diffusion length. Dunn et al. have utilized the CV tests at different scan rates to study the contributions from capacitive and diffusion-controlled processes, according to the following equations:⁵¹

i = av^b

log i = b × log ν + log a

where the current i obeys a power law relationship with the scan rate v, and both a and b are adjustable parameters. From the second equation, b values can be determined from the slope of the plot of log i vs. log v. When the b value is close to 0.5, it is regarded as a diffusion-controlled phenomenon; when the b value is close to 1, it is defined as a surface capacitive process.^52,53 According to the CV curves of PPS at different scan rates (Fig. 3a and Fig. S13, ESI†) and the corresponding log relationship between the absolute values of peak currents and scan rates (Fig. 3b), all the b-values of five samples were close to 1 (Table S3, ESI†) for both cathodic and anodic scans, indicating that all the five samples were mainly controlled by surface capacitive effects.⁵⁴ In addition, the b values were relatively larger for particles with smaller size, which again proved that the smaller size and shorter ionic diffusion length weakened the role of diffusion-controlled process and led to the surface capacitive phenomenon.

Fig. 3 (a) CV curves of PPS-XS electrodes at various scan rates from 0.05 to 10 mV s⁻¹ (the sample was firstly cycled 50 times at a scan rate of 0.5 mV s⁻¹ for eliminating the activation process). (b) The log relationship of the absolute values of peak current and the scan rates for all the five PPS samples, A and C represent the anodic and cathodic scans, respectively. (c) The relationship between the resistance and ω^−0.5 at low frequencies. (d) Diffusivity of Na ions during the discharge process as calculated by the GITT method versus potential. The CV curve (PPS-XS as an example) during cathodic scan is also presented for comparison.

The EIS tests of the five samples after the first discharge were performed to investigate the charge transfer and ionic diffusion (as shown in Fig. S14, ESI†). The charge transfer resistance (Table S4, ESI†) was calculated from the semicircle in the EIS spectra.⁵⁵ The results showed that the diameter of the semicircle and the corresponding charge transfer resistances were generally decreasing with the decrease in the particle size. The PPS-XS sample showed the lowest charge transfer resistance. These results indicated that the smaller size of the nanoparticles benefited the charge transfer between the inner particles and the current collector (or conductive additives). The ionic diffusion could be monitored using the linear part of the Nyquist plot (at low frequencies). The Warburg coefficient σ_w was obtained from the plot of Z_revs. the reciprocal root square of the lower angular frequencies ω^−1/2 (Fig. 3c), according to the following equation:⁵⁶

Z_re = R_e + R_ct + σ_wω^−0.5

where R_e is the resistance of the electrolyte, R_ct is the charge transfer resistance and ω is the angular frequency. The Na-ion diffusion coefficients were then calculated accordingly:
where R is the gas constant, T is the absolute temperature, A is the surface area of the electrode, F is the Faraday's constant and C is the concentration of Na ions (Fig. S15 and Table S5, ESI†). In Fig. 3c, the lower slope represents the lower Warburg coefficient (σ_w) and higher Na ion diffusion coefficient. The results showed that the slopes and the corresponding Warburg coefficients were generally decreasing with the decrease in the particle size. It meant that the Na ion diffusion coefficient was increasing accordingly (details in ESI† and Table S4). These results reconfirmed that the smaller particle size is conducive to the ionic diffusion.

GITT measurement was exploited to investigate the diffusion coefficient of Na ions⁵⁷ (Fig. S15–S18 and Table S5, ESI†). The Na-ion diffusion coefficients were calculated via the following equation:^58,59

where τ is the constant current pulse time, m_B, V_M, M_B and S are the mass loading, molar volume, and molar mass of the repeating units of PPS, and the electrode–electrolyte interface area, respectively. ΔE_S is the voltage change between the steady and the initial state of every step, and ΔE_τ is the change of total voltage during a pulse step exclusive of the IR drop (Fig. S16, ESI†). The Na ion diffusion coefficient (D_GITT) calculated by the GITT method (details in ESI†) were about 10⁻¹¹–10⁻¹⁰ cm² s⁻¹ for both the discharge and charge processes of all the five samples (Fig. 3d and Fig. S18, ESI†). Moreover, the Na ion diffusion coefficients were roughly in agreement with the CV curves: during the discharge process, the Na-ion diffusion coefficients were relatively lower close to the peaks (or plateaus in the charge/discharge profiles), which corresponded to the intercalation of Na ions; during the charging process, the Na-ion diffusion coefficients were relatively larger near the CV peaks (or plateaus), corresponding to the extraction of Na ions. Moreover, the Na-ion diffusion coefficients showed kind of relevance with the particle size. The Na-ion diffusion coefficients of the samples with smaller particle sizes were generally higher than those of the larger ones. It is also worth noting that the Na-ion diffusion coefficients of samples with smaller particle sizes were more stable during the discharge/charge process, which meant that they were more independent of the intercalation/extraction process. These results showed that the charge transfer and ionic diffusion coefficient did not have a totally positive correlation with the particle size. However, the capacities at high current densities were totally in positive correlation with the particle size. Therefore, we further analyzed the CV curves to quantify the storage contributions of capacitive current and diffusion-controlled current (Fig. S19, ESI†).^51,60 The results showed that the process is diffusion dominated at low current densities. Therefore, the capacities of the five samples were similar and close to the theoretical capacity, provided that the current density was as low as possible. However, with the increase in the current density, the process became dominated by capacitive process. In this case, the higher surface area and the shorter Li-ion diffusion length due to the smaller particle size contribute to the higher capacity.^9,10,61,62 All of these results further proved that the smaller size and the shorter ionic diffusion length of the nanometer-sized samples rather than the Na-ion diffusion coefficient enhanced the charge transfer and ionic diffusion, which led to the higher electrochemical performance.

Conclusions

In summary, a polymer containing zwitterionic structure was developed as a proof-of-concept to investigate the size control and its dependence on the electrochemical behaviors in rechargeable OSIBs. By controlling the experimental conditions, PPS micro/nanospheres with different sizes and regular shapes were facilely synthesized by an in situ one-step polymerization technique. We found that the smallest sized PPS showed the best rate performance and cycling performance without clear activation process. Moreover, through systematic analyses, we found that although the Na-ion diffusion coefficient was not strictly correlated with the decrease in the particle size, the electrochemical performance (especially the fast-charge performance) enhanced with the downsizing of the particles. These results proved that the smaller size and the shorter ionic diffusion length of the nanometer-sized samples rather than the Na-ion diffusion coefficient enhanced the charge transfer and ionic diffusion, which led to the higher electrochemical performance. These results promote a deep understanding of the size effect on the electrochemical performance and provide a universal route to enhance the electrochemical performance of organic electrodes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National 1000-Talents Program, the National Natural Science Foundation of China (51773071), Wuhan Municipal Science and Technology Bureau (2017010201010141) and the Fundamental Research Funds for the Central Universities (HUST: 2017KFYXJJ023, 2017KFXKJC002, 2018KFYXKJC018).

Notes and references

1. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264.
2. J. Y. Hwang, S. T. Myung and Y. K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614.
3. M. Tang, S. Zhu, Z. Liu, C. Jiang, Y. Wu, H. Li, B. Wang, E. Wang, J. Ma and C. Wang, Chem, 2018, 4, 2600–2614.
4. C. Wang, Y. Xu, Y. Fang, M. Zhou, L. Liang, S. Singh, H. Zhao, A. Schober and Y. Lei, J. Am. Chem. Soc., 2015, 137, 3124–3130.
5. C. Jiang, M. Tang, S. Zhu, J. Zhang, Y. Wu, Y. Chen, C. Xia, C. Wang and W. Hu, Angew. Chem., Int. Ed., 2018, 57, 16072–16076.
6. Y. Ding and G. Yu, Chem, 2017, 3, 917–919.
7. Y. Lu, Q. Zhang, L. Li, Z. Niu and J. Chen, Chem, 2018, 4, 2786–2813.
8. N. Li, Y. Yin, S. Xin, J. Li and Y. Guo, Small Methods, 2017, 1, 1700094.
9. M. Okubo, E. Hosono, J. Kim, M. Enomoto, N. Kojima, T. Kudo, H. Zhou and I. Honma, J. Am. Chem. Soc., 2007, 129, 7444–7452.
10. K. T. Lee and J. Cho, Nano Today, 2011, 6, 28–41.
11. Y. Liu, Y. Qiao, W. Zhang, Z. Li, X. Ji, L. Miao, L. Yuan, X. Hu and Y. Huang, Nano Energy, 2015, 12, 386–393.
12. Z. Yi, N. Lin, W. Zhang, W. Wang, Y. Zhu and Y. Qian, Nanoscale, 2018, 10, 13236–13241.
13. Z. Tai, C. M. Subramaniyam, S. Chou, L. Chen, H. Liu and S. Dou, Adv. Mater., 2017, 29, 1700605.
14. M. Yu, Y. Huang, K. Wang, X. Han, M. Wang, Y. Zhu and L. Liu, Appl. Surf. Sci., 2018, 462, 955–962.
15. C. Yang, Y. Zhang, J. Zhou, C. Lin, F. Lv, K. Wang, J. Feng, Z. Xu, J. Li and S. Guo, J. Mater. Chem. A, 2018, 6, 8039–8046.
16. H. Li, M. Tang, Y. Wu, Y. Chen, S. Zhu, B. Wang, C. Jiang, E. Wang and C. Wang, J. Phys. Chem. Lett., 2018, 9, 3205–3211.
17. H. Li, C. Wu, Y. Bai, F. Wu and M. Wang, J. Power Sources, 2016, 326, 14–22.
18. Y. Zhao, L. Peng, B. Liu and G. Yu, Nano Lett., 2014, 14, 2849–2853.
19. C. Chen, Y. Wen, X. Hu, X. Ji, M. Yan, L. Mai, P. Hu, B. Shan and Y. Huang, Nat. Commun., 2015, 6, 6929.
20. Z. Yi, Q. Han, X. Li, Y. Wu, Y. Cheng and L. Wang, Chem. Eng. J., 2017, 315, 101–107.
21. J. Zhou, Z. Jiang, S. Niu, S. Zhu, J. Zhou, Y. Zhu, J. Liang, D. Han, K. Xu, L. Zhu, X. Liu, G. Wang and Y. Qian, Chem, 2018, 4, 372–385.
22. X. Zhang, Z. Hou, X. Li, J. Liang, Y. Zhu and Y. Qian, J. Mater. Chem. A, 2016, 4, 856–860.
23. W. Zhang, X. Wu, J. Hu, Y. Guo and L. Wan, Adv. Funct. Mater., 2008, 18, 3941–3946.
24. Y. Zhao, X. Cao, G. Fang, Y. Wang, H. Yang, S. Liang, A. Pan and G. Cao, Chem. Eng. J., 2018, 339, 162–169.
25. N. Wu, H.-R. Yao, Y.-X. Yin and Y.-G. Guo, J. Mater. Chem. A, 2015, 3, 24221–24225.
26. J. Meng, Z. Liu, C. Niu, L. Xu, X. Wang, Q. Li, X. Wei, W. Yang, L. Huang and L. Mai, Mater. Horiz., 2018, 5, 78–85.
27. R. Qing, J. Shi, D. Xiao, X. Zhang, Y. Yin, Y. Zhai, L. Gu and Y. Guo, Adv. Energy Mater., 2016, 6, 1501914.
28. Z. Jian, M. Zheng, Y. Liang, X. Zhang, S. Gheytani, Y. Lan, Y. Shi and Y. Yao, Chem. Commun., 2015, 51, 229–231.
29. X. Wu, J. Ma, Y.-S. Hu, H. Li and L. Chen, J. Energy Chem., 2014, 23, 269–273.
30. S. Bai, K. Zhu, S. Wu, Y. Wang, J. Yi, M. Ishida and H. Zhou, J. Mater. Chem. A, 2016, 4, 16812–16817.
31. C. Luo, R. Huang, R. Kevorkyants, M. Pavanello, H. He and C. Wang, Nano Lett., 2014, 14, 1596–1602.
32. S. Wang, L. Wang, K. Zhang, Z. Zhu, Z. Tao and J. Chen, Nano Lett., 2013, 13, 4404–4409.
33. J. W. Wang, X. H. Liu, S. X. Mao and J. Y. Huang, Nano Lett., 2012, 12, 5897–5902.
34. T. Sato, K. Sato, W. Zhao, Y. Kajiya and N. Yabuuchi, J. Mater. Chem. A, 2018, 6, 13943–13951.
35. A. Treibs and K. Jacob, Angew. Chem., Int. Ed. Engl., 1965, 4, 694.
36. M. Binda, T. Agostinelli, M. Caironi, D. Natali, M. Sampietro, L. Beverina, R. Ruffo and F. Silvestri, Org. Electron., 2009, 10, 1314–1319.
37. S. S. Pandey, T. Morimoto, N. Fujikawa and S. Hayase, Sol. Energy Mater. Sol. Cells, 2017, 159, 625–632.
38. D. Yang, Z. Guan, L. Yang, Y. Huang, Q. Wei, Z. Lu and J. Yu, Sol. Energy Mater. Sol. Cells, 2012, 105, 220–228.
39. M. Takeshi, T. Tatsuya, S. Ayaka, Y. Shigeyuki and N. Hiroyuki, Macromol. Chem. Phys., 2012, 213, 2590–2597.
40. Z. Guo, Y. Ma, X. Dong, J. Huang, Y. Wang and Y. Xia, Angew. Chem., Int. Ed., 2018, 130, 11911–11915.
41. C. R. Chenthamarakshan, J. Eldo and A. Ajayaghosh, Macromolecules, 1999, 32, 251–257.
42. C. Wang, C. Jiang, Y. Xu, L. Liang, M. Zhou, J. Jiang, S. Singh, H. Zhao, A. Schober and Y. Lei, Adv. Mater., 2016, 28, 9182–9187.
43. C. R. Chenthamarakshan, J. Eldo and A. Ajayaghosh, Macromolecules, 1999, 32, 5846–5851.
44. A. Ajayaghosh, C. R. Chenthamarakshan, S. Das and M. V. George, Chem. Mater., 1997, 9, 644–646.
45. D. E. Lynch, U. Geissler, I. R. Peterson, M. Floersheimer, R. Terbrack, L. Feng Chi, H. Fuchs, N. J. Calos, B. Wood, C. H. L. Kennard and G. John Langley, J. Chem. Soc., Perkin Trans. 2, 1997, 827–832.
46. D. E. Lynch, U. Geissler and K. A. Byriel, Synth. Met., 2001, 124, 385–391.
47. D. E. Lynch, U. Geissler, N. J. Calos, B. Wood and N. N. Kinaev, Polym. Bull., 1998, 40, 373–380.
48. C. Wang, H. Dong, L. Jiang and W. Hu, Chem. Soc. Rev., 2018, 47, 422–500.
49. C. Xia, S. Zhu, M. Tang, S. Xu, Y. Wu, C. Jiang, Y. Chen, S. Zhuo, B. Wang and C. Wang, J. Phys. Chem. C, 2018, 122, 21185–21191.
50. Y. Wang, Y. Ding, L. Pan, Y. Shi, Z. Yue, Y. Shi and G. Yu, Nano Lett., 2016, 16, 3329–3334.
51. J. Wang, J. Polleux, J. Lim and B. Dunn, J. Phys. Chem. C, 2007, 111, 14925–14931.
52. C. Wang, Y. Fang, Y. Xu, L. Liang, M. Zhou, H. Zhao and Y. Lei, Adv. Funct. Mater., 2016, 26, 1777–1786.
53. Z. Hu, L. Wang, K. Zhang, J. Wang, F. Cheng, Z. Tao and J. Chen, Angew. Chem., Int. Ed., 2014, 53, 12794–12798.
54. Y. C. Xiao, C. Y. Xu, P. P. Wang, H. T. Fang, X. Y. Sun, F. X. Ma, Y. Pei and L. Zhen, Nano Energy, 2018, 50, 675–684.
55. Y. Jing, Y. Liang, S. Gheytani and Y. Yao, Nano Energy, 2017, 37, 46–52.
56. Y. Cui, X. Zhao and R. Guo, Electrochim. Acta, 2010, 55, 922–926.
57. Q. Y. An, Y. F. Li, H. D. Yoo, S. Chen, Q. Ru, L. Q. Mai and Y. Yao, Nano Energy, 2015, 18, 265–272.
58. Y. Hu, B. Li, X. Jiao, C. Zhang, X. Dai and J. Song, Adv. Funct. Mater., 2018, 28, 1801010.
59. S. Yang, X. Wang, X. Yang, Y. Bai, Z. Liu, H. Shu and Q. Wei, Electrochim. Acta, 2012, 66, 88–93.
60. V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597.
61. X. Xia, D. Chao, Y. Zhang, J. Zhan, Y. Zhong, X. Wang, Y. Wang, Z. X. Shen, J. Tu and H. J. Fan, Small, 2016, 12, 3048–3058.
62. R. Sun, Q. Wei, J. Sheng, C. Shi, Q. An, S. Liu and L. Mai, Nano Energy, 2017, 35, 396–404.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S19 and Tables S1–S5. See DOI: 10.1039/c9nh00154a

---