Computational insight into the mechanism and origins of high selectivities in the acylation of polyamines with 5-benzoyl-5-phenyl-1,5-dihydro-4H-pyrazol-4-one†
Yan
Zhang
,
Yongsheng
Yang
,
Junxia
Yang
,
Lian
Yang
and
Ying
Xue
 *
*
College of Chemistry, Key Lab of Green Chemistry and Technology in Ministry of Education, Sichuan University, Chengdu 610064, People's Republic of China. E-mail: yxue@scu.edu.cn; Tel: +86 28 85418330
First published on 27th November 2018
Abstract
Amide bonds have gained much attention from numerous scientists and acyl transfer is a good way to form amide bonds. The acylation mechanism of polyamines and their high selectivity in dichloromethane were investigated by the use of the density functional theory (DFT), M06-2X/6-311+G (d, p)//M06-2X/6-31G (d, p) method combined with the solvation SMD model. The calculated results suggest that the reaction process involved two steps: an acylation step and a proton-transfer step, with the former being the rate-limiting step. Meanwhile, with the substituent group effects of amines and 5-acyl-5-phenyl-1,5-dihydro-4H-pyrazol-4-one (BCPP) on the acylation step, different substituent groups of amines have little influence on the kinetic properties of the acylation step, and the para-substituent groups of the phenyl group in BCPP lead to a linear relationship according to the electronegativity of the substituents. Furthermore, regarding the rate-selectivity of amines, the rate-selectivity of primary amines is higher than that of secondary amines, and polyamines very easily take part in acylation owing to the intramolecular hydrogen bond interaction. Moreover, it is harder for the amine group which has an α-position substituent group in polyamines to take part in an acylation reaction compared to the one without an α-position substituent group. The site-selectivity of the acylation process in polyamines is determined by steric hindrance. What's more, the auxiliary analysis of the distortion/interaction analysis and the frontier molecular orbital (FMO) analysis is used to investigate the origins of the rate- and site-selectivities.
1. Introduction
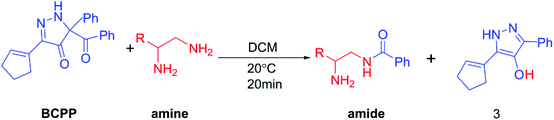
Amide bonds play an important role not only in biological systems, but also in medicinal chemistry. In biological systems, this key chemical bond can make peptides to produce proteins such as enzymes, which are essential in sustaining life.1 Meanwhile, the formation of amides also has great significance in organic synthesis. Typically, the most popular synthesis method of amides mainly depends on the combination of carboxylic acids and derivatives with amines or on the base catalyzed acylation of alcohols, phenols and so on.1a,2 In the meantime, with the development of chemistry, there have been some different synthesis methods coming into our sight, such as acyl transfer to form amide bonds.3 For example, the Danishefsky group reported that thio-formimidate carboxylate mixed anhydride (FCMA) intermediates can act as strong acyl donors to generate amide bond complexes.4 Also, Dawson and co-workers suggested a good way of protein synthesis by the removable acyl transfer auxiliary.3b Naturally, the formation of amide bonds has become a classic chemical reaction by acyl transfer, which has been widely researched and well applied.5 Up to now, the research of acyl transfer reagents has gradually increased.6 At the same time, a variety of metal catalysts have been used for acyl transfer, such as TaCl57 and CoCl2,8 with the rapid development of metal catalysts. However, nothing is perfect, including the performance of the metal catalysts, and the significance and limitations of the amide bond formation by the catalytic method have been already discussed.9Luckily, a new acylation reaction with no catalyst was reported by Doyle and his co-workers,6 as shown in Scheme 1. The high selectivity of the reaction between 5-acyl-5-phenyl-1,5-dihydro-4H-pyrazol-4-ones (BCPP) and amines has been amply demonstrated in this experimental literature.6 Besides the formation of amide bonds, it also produces N-heterocyclic compounds through the aromatization of the leaving group (the N-heterocycle part of BCPP). N-Heterocyclic compounds also have a significant role in chemistry, such as being a catalyst with the form of N-heterocyclic carbene.10 Perhaps, this reaction will develop into a good way to obtain N-heterocyclic compounds. From the viewpoint of kinetics, Doyle et al. found that the reaction rate of the secondary amine is slower than that of the primary amine, and the polyamine reaction rate is faster than that of monoamine.6 Here, we call this selectivity as rate-selectivity. That's to say, the rate-selectivity of the primary amine is higher than that of the secondary amine and also the rate-selectivity of polyamine is preferential than that of monoamine. More importantly, there was site-selectivity between the different amino groups in the polyamine. In brief, the selectivity of benzoyl transfer is mainly determined by the steric hindrance in the transfer process. At the same time, the mechanism was proposed by the author in the experimental paper, as shown in Scheme 2.6 For the monoamine, the key transition state is labeled as A, but for the polyamine, there are two different ways to generate the hydrogen bond interaction, which made by the other amino group, B and C as below.6 However, the mentioned mechanism doesn't include the aromatization of the leaving group, and there is little evidence to prove which mechanism is the best. Also, it cannot verify the specific interactions, such as electronic effect and interaction among the orbitals in the corresponding system.
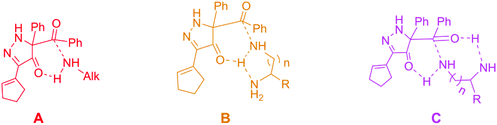 | ||
| Scheme 2 The proposed transition structures of the mechanisms of acylation in the experiment paper.6 | ||
With the recent advancement of theoretical methods, the combination of quantum chemical calculations with experiments has made significant advances in the development of chemistry. In particular, the density functional theory (DFT) method11 has been widely used in the study of mechanisms, intermolecular interactions, and the origins of selectivity in the reactions. In this report, we have adopted the DFT method to investigate this acylation reaction for the following key mechanistic questions: (1) what is the most feasible mechanism of the whole reaction, including the subsequent aromatization step? (2) Which factors will affect the reaction? (3) What are the fundamental reasons for the rate- and site-selectivities of polyamines in the acylation process? As a result, the conclusion of these problems was demonstrated by specific data and analysis, and the results were consistent with the experiments. What's more, this computational study firstly provides a full understanding of this acylation reaction6 from the molecular level, and it can provide some important suggestions for new kinds of reactions as well.
2. Computational details
All DFT calculations were performed with the Gaussian 0912 suite of electronic structure programs. The calculations employed the use of the M06-2X functional,13 which was widely applied in non-metallic systems, especially for main group elements,14 with the D3 Grimme dispersion correction. Geometry optimizations of all minima and transition states on the potential energy surface (PES) were performed in the gas phase with a standard basis set of 6-31G (d, p) for all atoms (abbreviated as BS1). To verify the structure of the minima without imaginary frequencies and transition states with only one imaginary frequency, harmonic vibrational frequency analysis was carried out at the M06-2X/BS1 level. Necessarily, through intrinsic reaction coordinate (IRC) calculations,15 the key transition state was confirmed to be the connection between the corresponding reactant and product.In order to simulate the real experimental solvent environment, the solvent effect was taken into consideration, and all structures obtained in the gas phase were re-optimized in dichloromethane (solvent used experimentally, ε = 8.93), with a self-consistent reaction field (SCRF) by using the SMD model,16 which includes radii and a nonelectrostatic term. By the way, there is little difference in structures between the gas phase and the solvent phase. Meanwhile, the single point (SP) energies were computed at the M06-2X/6-311+G (d, p) (donated as BS2) level based on the solvent-phase geometry structures. The auxiliary distortion/interaction analysis17 was under the M06-2X/BS2 level and the frontier molecular orbital (FMO)18 analysis was at the M06-2X/BS1 level. All free energy values in solution reported in this paper were the single-point energies in the solvent phase with Gibbs free energy correction of the gas phase, obtained at 298.15 K. The atoms in molecules (AIM) analysis was performed using the Multiwfn program developed by the Lu group.19 The total Cartesian coordinates for all minima points and transition states in the gas phase and the solvent phase were provided in the ESI.†
3. Results and discussion
3.1 Reaction mechanism
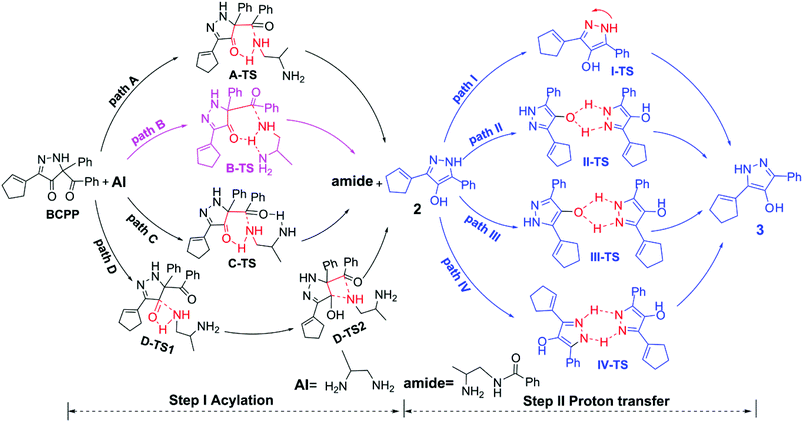
The reaction reported by Doyle6 involved two steps. The first one is the acylation step and the other one is the proton transfer step. Although the author of the experiment had proposed the possible mechanisms, it was not complete as it did not conclude the following aromatization step (proton transfer step). So, on this basis, we suppose four pathways in the step of acylation and four ways in the proton transfer process, which are summarized in Scheme 3.According to it, we chose 1,2-diaminopropane (AI) as the substrate. For the acylation step, the four pathways are path A, path B, path C, and path D, to obtain the amide product and the intermediate 2. The biggest difference between the former three pathways is the orientation of the other amino group that does not directly attack reaction center. In path A, the hydrogen of the terminal amino group in the amine molecule interacts with the carbonyl of the pyrazol ring, and the remaining nitrogen combines with the carbon atom of the benzoyl group in BCPP, via a six-membered ring transition state A-TS. Similarly, we changed the orientation of the other amino group close to the six-membered ring reaction center, generating the N–H hydrogen bond, shown as the form of B-TS in path B. Incidentally, the other amino group interacts with the hydrogen atom of the six-membered ring reaction center to make the transition state B-TS stable. However, the way that the hydrogen bond interacts is different in path C. In path C, the terminal amino group reacts with the benzoyl group of BCPP to generate a six-membered ring, and the other amino group interacts with the oxygen atom of the benzoyl group by the hydrogen bond like C-TS with a seven-membered ring. In brief, the former three pathways have a synergistic mechanism, and path B and path C both contain intramolecular hydrogen bond interactions. What's more, path D is the most special, with a stepwise mechanism. The first process is the transfer of the hydrogen atom of the terminal amino group in the amine molecule to the carbonyl group in the five-membered ring of BCPP and the nitrogen atom of the amino group interacts with the carbon atom of the carbonyl group via the four-membered ring transition state D-TS1 and this step is named hydroxylation as well. Then the corresponding intermediate goes through the benzoyl group transferring to the N-atom and then the C–N bond cleavage, via the four-membered ring transition state D-TS2, to produce an amide (the main product) and intermediate 2, which is called acylation.
Although the most focus is on acylation steps, the subsequent aromatization of intermediate 2 is well worth studying as well. For step II (proton transfer), starting with intermediate 2, it can go through four pathways to generate the N-heterocyclic compound product 3. In path I, as simply as seen, the proton transfers to the adjacent nitrogen atom by itself via I-TS, with just one molecule involved. However, in the other three pathways two molecules take part in the proton transfer. In path II, the hydroxyl group of intermediate 2 assists proton transfer, and forms the five-membered ring transition state II-TS. Similarly, the hydroxyl group of outcome 3 could also aid proton transfer through the five-membered ring transition state III-TS in path III. Meanwhile, the hydrogen of N–H in intermediate 2 can assist proton transfer too, and the six-membered ring transition state IV-TS comes into being in the last pathway.
For more intuitive representation, the free energy profiles of the mentioned pathways are depicted in Fig. 1. The black lines are the step of acylation (step I) and the blue ones represent proton transfer (step II). For step I, at first glance, the stepwise pathway (path D) is too difficult to take place with such a very high energy barrier. The free energy barrier of the hydroxylation step (D-TS1) is 41.6 kcal mol−1, and that of the following acylation process is 106.8 kcal mol−1, which is much higher compared with the other three pathways. As we can see, the difference among path A, path B, and path C is small in the value of the free energy barrier, being 21.0, 17.3 and 18.4 kcal mol−1 in paths A, B and C, respectively. Reviewing the whole step I, path B, the other amino group interacting with the hydrogen atom of the reaction center, is the most predominant way.
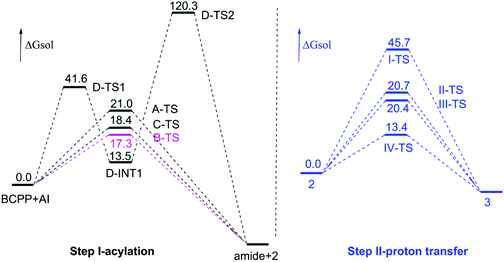 | ||
| Fig. 1 Calculated free energy profiles of acylation step pathways and proton transfer pathways. Gibbs free energies are given in kcal mol−1. | ||
As for the following step II, this proton transfer process, beginning with intermediate 2, includes four paths. As shown in Fig. 1 (to be brief, we selected 2 being the relative zero point of free energy), the free energy barrier of path I (one molecule) is 45.7 kcal mol−1. Obviously, this cannot occur easily. Maybe the higher energy barrier is caused by the larger ring tension of the three-membered ring transition state I-TS. By comparison, the other three dimolecular ways can take place more facilely. The proton transfer step assisted by the hydroxyl group of intermediate 2 has a free energy barrier of 20.7 kcal mol−1 through the five-membered ring transition state II-TS in path II. Similarly, with a free energy barrier of 20.4 kcal mol−1, the hydroxyl group of product 3 aids proton transfer by transition state III-TS in path III. Thus it can be seen that the little difference between two pathways is due to the minute disparity of intermediate 2 and product 3. Obviously, the most optimal way of path IV has the lowest free energy barrier, 13.4 kcal mol−1, by the six-membered ring transition state IV-TS generated by N–H of intermediate 2 helping the proton transfer. From here, we can conclude that the difference between the dimolecular path IV and path II/III is due to the predominant stability of the six-membered ring which makes IV-TS more stable. Therefore, path IV is the most favourable way in the proton transfer step. In a word, the whole mechanism is that the acylation step adopts the other amino group interacting with the H atom of the six-membered ring center to form an intramolecular hydrogen bond (path B in Scheme 3), and the proton transfer step goes through the N–H assisting proton transfer between two intermediate 2 molecules via the six-membered ring transition state (path IV in Scheme 3). By the way, the acylation step is the rate-limiting step of the title reaction. The concrete rectifies the conclusion of the experiment that the proton transfer step is the rate-determining one.6 Also the key intermediate and transition state structures are shown in Fig. 2.
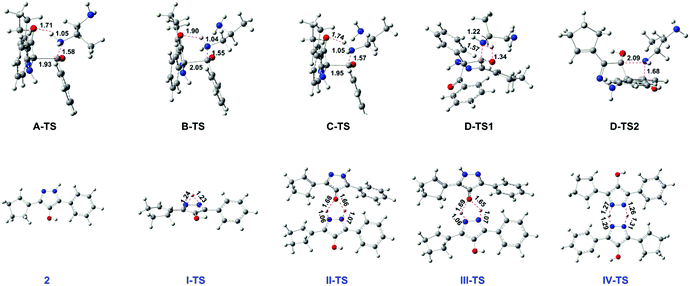 | ||
| Fig. 2 Optimized structures (in the gas phase) of key intermediate and transition states for the reaction mechanism. | ||
Next, with the confirmation of the predominant pathway, we pay more attention to the acylation process. Getting rid of the least possible way (path D), the difference among the other three pathways should be investigated in detail. Evidently, the transition state of A-TS has no interaction between the other amino groups and the six-membered ring reaction center, making it unstable. The small difference of free energy barrier is 1.1 kcal mol−1 between path B and path C, and the detailed comparison of B-TS and C-TS in the 3-D structure is shown as Fig. 3. During our study, we considered a different direction of the other amino group and obtained the aforementioned transition states, B-TS and C-TS. Comparing the two structures, there is little difference in the six-membered ring center except the distances of O3–H4 and C6–C1. The distance of O3–H4 is 1.90 Å in B-TS and 1.74 Å in C-TS, and they differ by 0.16 Å in O3–H4. There is a 0.1 Å difference in the distance of C6–C1 between two transition structures. However, for the hydrogen bond number, in C-TS, it includes only one hydrogen bond and the length of O7–H8 is 2.30 Å. But there are two hydrogen bonds in B-TS, O7–H8 and N9–H4, and the length is 2.20 Å and 2.27 Å, respectively. The length of each hydrogen bond in B-TS is shorter than the one in C-TS. It is the existence of the N9–H4 interaction that makes the distance of O3–H4 longer in the B-TS structure and the two hydrogen bonds in B-TS make it more stable (1.1 kcal mol−1 lower than C-TS). By the way, the energies of hydrogen bonds also agree with the results, with a total hydrogen bond energy of −68.31 kcal mol−1 for B-TS and −14.85 kcal mol−1 for C-TS, respectively. The difference in the hydrogen bond energy of 53.46 kcal mol−1 makes the two transition states different.
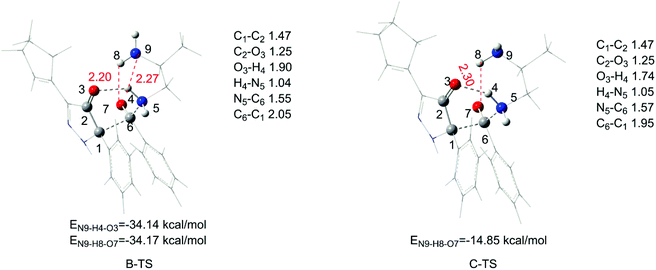 | ||
| Fig. 3 Transition states of path B and path C in the acylation process and the energy of each hydrogen bond (bond lengths are given in angstroms). | ||
3.2 Effect of the substituent group
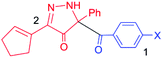
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), which was not taken into account in the experiment paper.6 The results of the free energy barrier are described in Table 1. One can see that there is little difference among the substituent groups and there is no regularity with the electron effects of the substituents here. The free energy barrier with the ethyl group is 16.5 kcal mol−1 and that with no substituent group (H) is 16.9 kcal mol−1. Also, the vinyl group has a 18.3 kcal mol−1 energy barrier and the phenyl group has a 17.1 kcal mol−1 energy barrier. From the concrete values of the free energy barrier difference, there is little difference. So, we can conclude that the change of the substituent group on amines has little influence and couldn't change the kinetic properties of the reaction.
CH2), which was not taken into account in the experiment paper.6 The results of the free energy barrier are described in Table 1. One can see that there is little difference among the substituent groups and there is no regularity with the electron effects of the substituents here. The free energy barrier with the ethyl group is 16.5 kcal mol−1 and that with no substituent group (H) is 16.9 kcal mol−1. Also, the vinyl group has a 18.3 kcal mol−1 energy barrier and the phenyl group has a 17.1 kcal mol−1 energy barrier. From the concrete values of the free energy barrier difference, there is little difference. So, we can conclude that the change of the substituent group on amines has little influence and couldn't change the kinetic properties of the reaction.
| Group | ΔG‡ | ΔΔG‡ |
|---|---|---|
| Et | 16.5 | −0.4 |
| H | 16.9 | 0 |
| Ph | 17.1 | 0.2 |
| Me | 17.3 | 0.4 |
–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
18.3 | 1.4 |
| Substituent | ΔG‡ | ΔΔG‡ | μ | χ | η | ω | N |
|---|---|---|---|---|---|---|---|
| OMe | 17.9 | 0.6 | −3.9 | 3.9 | 6.2 | 1.2 | 2.1 |
| H | 17.3 | 0 | −4.1 | 4.1 | 5.9 | 1.4 | 2.1 |
| Cl | 16.6 | −0.7 | −4.2 | 4.2 | 6.0 | 1.5 | 2.0 |
| CF3 | 14.7 | −2.6 | −4.3 | 4.3 | 5.8 | 1.6 | 1.9 |
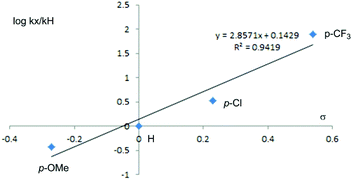
In order to explore the essential relationship, we adopted the conceptual density functional theory (conceptual DFT), a good way to obtain the qualitative character of chemical reactivity,21 to analyze the different para-substituted BCPP reactants. The corresponding characters and specific values are amply described in Table 2, in which μ means electronic chemical potential, χ presents electronegativity, η expresses chemical hardness, ω is the electrophilicity index, and N is the nucleophilicity. Associated with the preceding Hammett plot, we can easily find that the trend in the Hammett plot is consistent with the regularity of the electronegativity and the electrophilicity index in the table. That is to say the effect of these substituent groups of BCPP on this reaction is mainly manifested by the electronegativity of the substituent groups, with a good linear relationship. By the way, the electron donating group can make the energy barrier higher, and the electron withdrawing group leads to a lower energy barrier. In order to explore the electronic effect details, we divided BCPP into two parts, the benzoyl group (the blue part in Table 3) and the other part (the red part), and the NBO charge analysis of the two parts are shown in Table 3. As we can see, the two parts in the reactant complex (RC) have a negative charge for four different substituents. In the process of forming the transition states, part 1 acts as the electron-donating group and its negative charge becomes less negative. However, part 2 plays the part of the electron-accepting group with the negative charge being more negative. As the charge of part 1 changes more, the acylation process may be much more favorable. Therefore, the electron withdrawing group in BCPP can make the reaction feasible.
3.3 Origin of the rate-selectivity of amines
According to the experiment, we thought it was necessary to compare the reaction activity of monoamines with polyamines, and primary amines with secondary amines by a theoretical study. The calculated free energy profiles of monoamines and diamines are shown in Fig. 5(a). We chose 1-aminobutane as the monoamine (mono). From Fig. 5(a), the m-TS for the transition state of the monoamine and the B-TS for the transition state of the diamine mentioned before in Fig. 1, we can see that the free energy barrier of the monoamine is 19.5 kcal mol−1, which is 2.2 kcal mol−1 higher than that of the diamine (1,2-diaminopropane, di). Predictably, this difference is made by the intramolecular hydrogen bond in the diamine in the corresponding transition state, because there is no other amino group to generate hydrogen bonds in the monoamine, which is shown in Fig. 6. It is the existence of two hydrogen bond interactions (2.20 Å and 2.27 Å) that makes the free energy barrier difference of 2.2 kcal mol−1.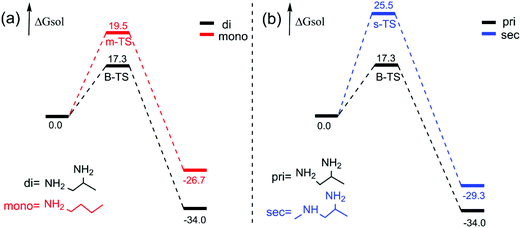 | ||
| Fig. 5 Calculated free energy profiles of the monoamine and the diamine (a) as well as the primary amine and the secondary amine (b) reacted with BCPP. The energies are in kcal mol−1. | ||
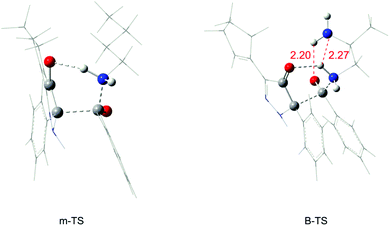 | ||
| Fig. 6 Optimized structures of the transition state (m-TS) in the monoamine and the transition state (B-TS) in the diamine (in the gas phase, the bond lengths are given in angstroms). | ||
As for the comparison of the primary amine (1,2-diamine-propane) with the secondary amine (sec), the result in the right part of Fig. 5 is more obvious. The free energy barrier of the secondary amine is 25.5 kcal mol−1, and that of the primary amine is 17.3 kcal mol−1, and the blue one is 8.2 kcal mol−1 higher than the black one, which reveals that the acylation reaction of the primary amine takes place easier than that of the secondary amine. That is to say, among the numerous amines, the rate-selectivity of acylation is that the primary amine is superior to the secondary amine and the polyamine is outstanding compared to the monoamine. Our computational conclusions are in agreement with the experimental results.6
To explore the origin of difference between the primary amine and the secondary amine, a distortion/interaction analysis17 of transition states (B-TS in the primary amine and s-TS in the secondary amine) was carried out. The results are shown as Fig. 7. Here, every transition state was separated into two distorted sections, BCPP and amine. The value of the distortion energy was defined as the difference between the distorted part in the transition state and the corresponding ground-state section (ΔEdis–BCPP for BCPP and ΔEdis-AI for amine (AI)). The activation energy ΔE‡ subtracting the total distortion energy was regarded as the interaction energy (ΔEint). With regard to the TS structures, the six-membered ring reaction center is identical, but in terms of distortion/interaction analysis, they are very different. By comparison, the distortion energy of BCPP in s-TS is much higher than that in B-TS (5.1 kcal mol−1), and for the other part AI, the distortion energy in B-TS is 3.4 kcal mol−1 lower than in s-TS. Meanwhile, the difference of ΔEint is 6.2 kcal mol−1 between the two structures. Thus it can be seen that the interaction energy decides the rate-selectivity between the primary amine and the secondary amine. This result explains the phenomenon that the secondary amine reacts more slowly, which was observed in the experiment.6
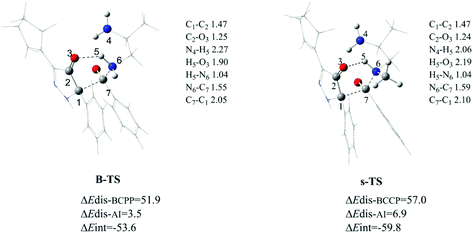 | ||
| Fig. 7 Optimized structures (in the gas phase) and distortion/interaction analysis of B-TS and s-TS (the energies are in kcal mol−1, and the bond lengths are in Å). | ||
3.4 Origin of site-selectivity of polyamines
From the observation of the experiment,6 we found that there was an obvious phenomenon, site-selectivity, when the reactants are polyamines. That's what got us interested, and we chose the different amines employed in the experiment (reactants 5 (1,2-diaminopropane), 19 (L-lysine methyl ester), and 21 (1,3-diaminopentane))6 to carry out computational study and the results are depicted in Fig. 8. We orderly named these three amines amine a, b, and c, respectively. The blue line represents the free energy surface for the amine group involved in the reaction, which is labeled in blue in the polyamine. The red line indicates the free energy surface for the reaction site marked in red, and the product of the red amine is the final outcome in the experiment. At first glance, the red lines are always below the blue lines in the free energy profile through the results of the computation study. For amine a, the energy barrier of the red amine group (17.3 kcal mol−1) is 1.9 kcal mol−1 lower than the blue one (19.2 kcal mol−1); similarly, the free energy of bTS′ (22.0 kcal mol−1) is 2.7 kcal mol−1 higher than bTS (19.3 kcal mol−1) for amine b. Also, the difference in the free energy barrier is 7.3 kcal mol−1 for amine c. It is worth noting that the greater the steric hindrance of the substituents, the more difficult the acylation at this site, just like the 19.2 kcal mol−1 for methyl (aTS′), the 20.2 kcal mol−1 for ethyl (cTS′) and the 22.0 kcal mol−1 for the ester group (bTS′). The site-selectivity that appeared in the computational study is consistent with the experimental phenomenon. Therefore, the calculated results agree with the experiment once more.6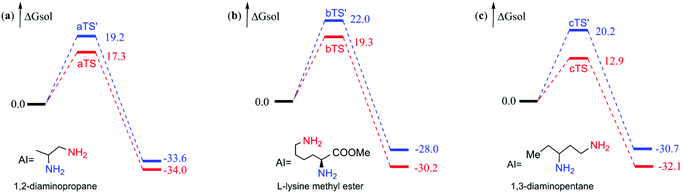 | ||
| Fig. 8 Calculated free energy profiles of different amine sites of polyamines (a, b, c) reacted with BCPP. The energies are kcal mol−1. | ||
Comparing the sites of two amino groups in the mentioned three polyamines, we pointed out that acylation of the amino group with a substituent group at its α-position C atom is harder to carry out compared to the one with no α-position substituent group. Therefore, we guess the site-selectivity of polyamines is decided by the steric hindrance during the process of acylation.
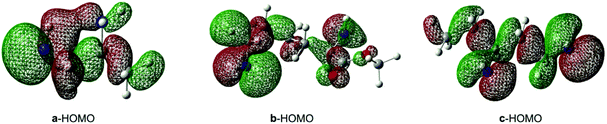
In order to explore the details deeply, the frontier molecular orbital (FMO) analysis was performed and the relevant results are shown in Table 4. We can see that the interaction orbitals of the acylation step are the HOMO of amines and the LUMO of BCPP. The energy gap Egap between BCPP and a, b, c amines is 6.64, 6.83 and 6.50 eV, respectively. Meanwhile, it also reveals that the electrons transfer from the amine HOMO to the BCPP LUMO.
| BCPP | a | b | c | |
|---|---|---|---|---|
| HOMO | −7.05 | −7.81 | −8.00 | −7.67 |
| LUMO | −1.17 | 3.13 | 1.74 | 3.07 |
As for the site-selectivity of the reaction, we analyzed it from the two amino sites of reactant amines. We found that the contributions of the amino group at different sites to their HOMO are different, as shown in Fig. 9. Obviously, among the HOMOs of the three amines, the nitrogen atom of the prior amino group (without the α-position substituent group) contributes more than the other one in their HOMOs and its HOMO energy is −7.81, −8.00 and −7.67 eV, respectively. In a word, the greater contribution of the prior amino group makes it more active and easy to interact with BCPP.
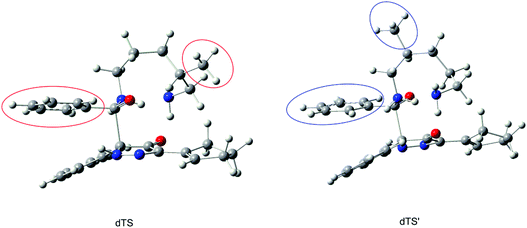
In addition, for the polyamine containing both the amino groups with and without the α-position substituent, the acylation reaction is only possible at the amino site without the α-position substituent. Interestingly, when there are no α-position substituent groups in polyamines, the multiple sites of amino groups can take part in the acylation reaction and generate diverse amides, such as the reactant d (reactant 2,5-diamino-2-methylpentane in the experiment6), and there is a certain degree of site-selectivity. Aiming at this reactant, we conducted a series of studies. Firstly, the free energy profile is displayed in Fig. 10 and there is a 0.8 kcal mol−1 difference between the two transition states, dTS and dTS′. With the ratio calculated by eqn (1) being 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, the result is in accord with the experiment (86
20, the result is in accord with the experiment (86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14).6 It also means that the acylation reaction is controlled by dynamics.
14).6 It also means that the acylation reaction is controlled by dynamics.
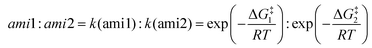 | (1) |
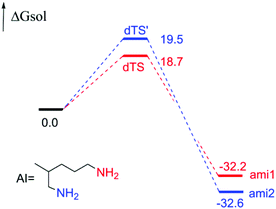 | ||
| Fig. 10 Calculated energy barrier profile of polyamines d reacted with BCPP (the energies are kcal mol−1). | ||
Among the multiple reaction sites, what factor decides which amine group is more prior? Here, we compared the transition structures of dTS and dTS′, as shown in Fig. 11. We can clearly observe the difference. In the dTS structure, the methyl substituent is farther away from the leaving group of the acylation step, but the corresponding distance is closer in the dTS′ structure. Combined with the previous conclusions, we can conclude that the site-selectivity is decided by the steric hindrance of the acylation step; the farther the substituent is from the reaction site, the more easily the amino group can take part in the acylation reaction. In other words, the amino group with a small steric hindrance is more predominant in this acylation reaction. The results are in accord with the experiment.6
4. Conclusion
The DFT M06-2X functional has been well applied to explore the reaction mechanism of the nonmetallic system. This method was adopted here to investigate the reaction mechanism, energetics, and rate- and site-selectivities of acylation of the polyamines with BCPP. The present studies have revealed that, as for the reaction mechanism, two steps, acylation and proton-transfer, were involved with the acylation (step I) being the rate-limiting step. For step I, comparing four possible ways, the way of the other amino group interacting with the reaction center is an almost feasible way which includes two hydrogen bonds in the transition state structure. With regard to the proton transfer step, the path of the N–H of intermediate 2 assisting proton transfer is an excellent pathway with a stable six-membered ring transition state. Regarding the effect of substituent groups, with the substituent group changed in amines, there is little influence on the dynamic characters of the acylation step. However, the effect is made obvious by the para-position substituent group of benzoyl in BCPP. The electron donor groups make the acylation step difficult to happen, but the electron absorption groups cause a lower energy barrier. There is a good linear relationship with a correlation coefficient of 0.9419. Besides, the rate-selectivity between the monoamines and the polyamines is decided by the intramolecular hydrogen bond interaction formed in the key transition state, so the reaction rate of polyamines is faster. Similarly, the rate-selectivity of primary amines and secondary amines is determined by the steric hindrance in the acylation step, where there is a large steric hindrance in secondary amines. More importantly, the site-selectivity of polyamines is confirmed by the position of the substituent groups, where an amino group without the α-position substituent group can take place in acylation. In a way, it is also decided by the steric hindrance. The longer the distance between the substituent group and the reaction site, the more active the amino site and the more predominant the site. These findings may provide some important information and provide a better understanding of the acylation reaction. In the meantime, the computational results may give some suggestion for similar reactions and help design new reactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has been supported by the National Natural Science Foundation of China (Grant No. 21573153).References
- (a) E. Valeur and M. Bradley, Chem. Soc. Rev., 2009, 38, 606–631 RSC; (b) C. L. Allen and J. M. J. Williams, Chem. Soc. Rev., 2011, 40, 3405–3415 RSC.
- (a) P. Saravanan and V. K. Singh, Tetrahedron Lett., 1999, 40, 2611–2614 CrossRef CAS; (b) R. G. Álvarez, P. Crochet and V. Cadierno, Green Chem., 2013, 15, 46–66 RSC.
- (a) E. R. Jarvo, G. T. Copeland, N. Papaioannou, P. J. Bonitatebus and S. J. Miller, J. Am. Chem. Soc., 1999, 121, 11638–11643 CrossRef CAS; (b) J. Offer, C. N. C. Boddy and P. E. Dawson, J. Am. Chem. Soc., 2002, 124, 4642–4646 CrossRef CAS; (c) H. U. Vora and T. Rovis, J. Am. Chem. Soc., 2007, 129, 13796–13797 CrossRef CAS.
- Y. Rao, X. C. Li and S. J. Danishefsky, J. Am. Chem. Soc., 2009, 131, 12924–12926 CrossRef CAS PubMed.
- (a) C. E. Muller and P. R. Schreiner, Angew. Chem., Int. Ed., 2011, 50, 6012–6042 CrossRef PubMed; (b) I. Kreituss and J. W. Bode, Acc. Chem. Res., 2016, 49, 2807–2821 CrossRef CAS PubMed.
- K. O. Marichev, E. C. Garcia, K. C. Bhowmick, D. J. Wherritt, H. Arman and M. P. Doyle, Chem. Sci., 2017, 8, 7152–7159 RSC.
- S. Chandrasekhar, T. Ramachander and M. Takhi, Tetrahedron Lett., 1998, 39, 3263–3266 CrossRef CAS.
- J. Iqbal and R. R. Srivastava, J. Org. Chem., 1992, 57, 2001–2007 CrossRef CAS.
- (a) T. Marcelli, Angew. Chem., Int. Ed., 2010, 49, 6840–6843 CrossRef CAS PubMed; (b) H. Charville, D. Jackson, G. Hodges and A. Whiting, Chem. Commun., 2010, 46, 1813–1823 RSC.
- (a) D. A. Culkin, W. Jeong, S. Csihony, E. D. Gomez, N. P. Balsara, J. L. Hedrick and R. M. Waymouth, Angew. Chem., Int. Ed., 2007, 119, 2597–2781 CrossRef; (b) C. Vincent, B. L. Stéphane and H. G. Lutz, Chem. Soc. Rev., 2004, 33, 619–636 RSC; (c) J. C. Garrison and W. J. Youngs, Chem. Rev., 2005, 105(11), 3978–4008 CrossRef CAS PubMed.
- (a) W. Kohn and L. J. Sham, J. Phys. Rev., 1965, 140, A1133 CrossRef; (b) R. M. Dreizler and E. K. U. Gross, Density Function Theory, Springer, 1990 CrossRef; (c) M. Steinmetz and S. Grimme, ChemistryOpen, 2013, 2, 115–124 CrossRef CAS; (d) W. Koch and M. C. Holthausen, A chemist's guide to density functional theory, Wiley-VCH, 2001 CrossRef; (e) R. M. Dreizler and E. K. U. Gross, Density Functional approach to time-dependent and to relativistic systems, Springer, 1985 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- (a) M. W. Andrew, J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600 CrossRef PubMed; (b) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed; (c) Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- (a) W. Koch and M. C. Holthausen, A chemist's guide to density functional theory, Wiley-VCH, 2001 CrossRef; (b) R. M. Dreizler and E. K. U. Gross, Density Functional approach to time-dependent and to relativistic systems, Springer, 1985, vol. 81, p. 140 Search PubMed.
- (a) R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed; (b) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- (a) J. L. Yu, S. Q. Zhang and X. Hong, J. Am. Chem. Soc., 2017, 139, 7224–7243 CrossRef CAS; (b) Y. Zhang, Y.-S. Yang, J.-M. Zhao and Y. Xue, Eur. J. Org. Chem., 2018, 3086–3094 CrossRef CAS; (c) X. Yang, Y.-S. Yang and Y. Xue, ACS Catal., 2016, 6, 162–175 CrossRef CAS.
- K. Fukul, Science, 1982, 218, 747–754 CrossRef PubMed.
- (a) T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed; (b) T. Lu, Multiwfn, version 3.5 Search PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- (a) P. Geerlings, F. D. Proft and W. Langenaker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS PubMed; (b) W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS; (c) S. B. Liu, Acta Phys.-Chim. Sin., 2009, 25, 590–600 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ob02722f |
| This journal is © The Royal Society of Chemistry 2019 |