Structural and thermodynamic aspects of water–carbonate exchange equilibrium for MIII/IV–EDTA–carbonate systems†
Rafał
Janicki
 * and
Anna
Mondry
* and
Anna
Mondry

University of Wrocław, Faculty of Chemistry, F. Joliot-Curie 14, 50-383 Wrocław, Poland. E-mail: rafal.janicki@chem.uni.wroc.pl
First published on 27th November 2018
Abstract
The results of a thermodynamic description of ternary M–EDTA–carbonate (where M = Er(III), Th(IV)) complex formation are presented. The crystal structures of the novel [C(NH2)3]3[Er(EDTA)(CO3)]·H2O (I) and [C(NH2)3]4[Th(EDTA)(CO3)2]·5H2O (II) compounds were determined. The structural and UV-vis-NIR spectroscopic results of crystal I served as the model data to analyze the stoichiometry and stability of the Er(III)–EDTA–carbonate system in aqueous solutions. The formation of the [Er(EDTA)(CO3)]3– complex in solution under different conditions was examined by complementary techniques including temperature dependent UV-vis-NIR and NMR spectroscopy as well as potentiometry. It was established that the affinity of the carbonate for the Er(III)–EDTA chelate is strongly pH dependent. Thus reaction (A) [Er(EDTA)(H2O)2]− + CO32– ⇄ [Er(EDTA)(CO3)]3– + 2H2O is more favoured at near neutral pH, while reaction (B) [Er(EDTA)(OH)(H2O)2]2– + CO32– ⇄ [Er(EDTA)(CO3)]3– + 2H2O + OH− occurs under more basic conditions. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values were found to be 3.66 ± 0.07 and 0.20 ± 0.12 for reactions (A) and (B), respectively. The temperature dependence of log
β values were found to be 3.66 ± 0.07 and 0.20 ± 0.12 for reactions (A) and (B), respectively. The temperature dependence of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β allowed the determination of the enthalpy and entropy changes of both reactions for the first time (ΔH(A) = −2.8 ± 0.8 kJ mol−1, ΔS(A) = 62 ± 3 J mol−1 K−1 and ΔH(B) = 28.1 ± 4.6 kJ mol−1, ΔS(B) = 92 ± 15 J mol−1 K−1). These data indicate that the carbonate anion more readily displaces H2O than the OH− ligand. The obtained results are important not only from the point of view of environmental lanthanide and actinide mobility, but also for designing MRI contrast agents.
β allowed the determination of the enthalpy and entropy changes of both reactions for the first time (ΔH(A) = −2.8 ± 0.8 kJ mol−1, ΔS(A) = 62 ± 3 J mol−1 K−1 and ΔH(B) = 28.1 ± 4.6 kJ mol−1, ΔS(B) = 92 ± 15 J mol−1 K−1). These data indicate that the carbonate anion more readily displaces H2O than the OH− ligand. The obtained results are important not only from the point of view of environmental lanthanide and actinide mobility, but also for designing MRI contrast agents.
Introduction
Besides citrates, succinates and oxalates, EDTA is one of the main organic ligands, which is present in liquid radioactive waste due to its use in the separation process and decontamination operations in the nuclear industry.1 For instance the Hanford mixed waste alone contains about 240 tons of radioactive waste containing the EDTA ligand, with initial concentrations of 0.1 M EDTA.1,2 This waste has unique characteristics of being extremely heterogeneous and highly basic, and having high ionic strength.1 The high solubility and thermodynamic stability of EDTA complexes with heavy metal ions may be a reason for the increased mobility of radionuclides to the environment, which may thus complicate the safe storage of radioactive waste. As an example, Tank241-T-106 at Hanford released 435 m3 of mixed radioactive waste containing Pu and EDTA into the subsurface during 1973.3,4 Recent study results of PuO2 solubility in EDTA solutions in the presence of Ca(II) cations and Fe(OH)3 suggest that the environmental mobility of plutonium due to Pu(IV)–EDTA complex formation is significantly overestimated.4 However, in that study, only binary M–EDTA, and not ternary M–EDTA–L, complexes were taken into consideration.3,4Ln(III) and An(III)/An(IV) ions which are entrapped by six donor atoms of EDTA ligands, possess two, three or four additional binding sites usually filled by an appropriate number of water molecules.5,6 These molecules, in turn, may be readily displaced by other bi- or tridendate ligands such as carbonates,7 phosphates, citrates etc.8 One of the most common inorganic O-donor ligands available in liquid nuclear waste9 and in the environment10 is a carbonate anion which strongly interacts with hard Pearson acids like trivalent lanthanides and actinides.10–12 In the presence of this anion ternary [M(EDTA)(CO3)m]n− complexes may be formed according to eqn (1):
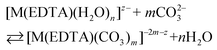 | (1) |
The available experimental data for this reaction are rather limited and provide equilibrium constant values that differ by several orders of magnitude. For instance the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βMLA values (where M = Ln(III), An(III/IV), L = EDTA, A = CO32–) for reaction (1) derived from the electronic spectroscopy results were found to be: log
βMLA values (where M = Ln(III), An(III/IV), L = EDTA, A = CO32–) for reaction (1) derived from the electronic spectroscopy results were found to be: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βNdLA = 0.83;13 log
βNdLA = 0.83;13 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuLA = 0.53,14 log
βEuLA = 0.53,14 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βHoLA = 0.6013 and log
βHoLA = 0.6013 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βErLA = 0.74,13 while those obtained from NMR data are by ca. two orders higher, log
βErLA = 0.74,13 while those obtained from NMR data are by ca. two orders higher, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βGdLA = 2.60 ± 0.02.15
βGdLA = 2.60 ± 0.02.15
The results of the potentiometric and spectroscopic study on An(III)–16 and An(IV)–EDTA–carbonate17 systems have shown that complexes of trivalent actinides are much weaker than those of tetravalent ones. For example the estimated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βAn(III)LA values (An = Am, Cm) were found to be between 3 and 4,16 whereas the log
βAn(III)LA values (An = Am, Cm) were found to be between 3 and 4,16 whereas the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βPu(IV)LA value is equal to 9.07 ± 0.2.17
βPu(IV)LA value is equal to 9.07 ± 0.2.17
The majority of the thermodynamic data on lanthanide and actinide coordination compounds are obtained at room temperature.18 Almost no data are available for the effects of temperature on the stability of ternary complexes in aqueous solutions, although, the temperature of nuclear waste in storage tanks is significantly above the ambient temperature and can be up to 90 °C.19
Therefore the aim of this paper is to describe thermodynamically reaction (1) at different temperatures between 283 and 333 K, at high ionic strength and various pH values. The crystal structures of novel ternary coordination compounds of [C(NH2)3]3[Er(EDTA)(CO3)]·H2O (I) and [C(NH2)3]4[Th(EDTA)(CO3)2]·5H2O (II) are presented. The UV-vis-NIR electronic spectroscopy results of crystal I and the Er(III)–EDTA–carbonate system in solution, extended by complementary potentiometric and 13C NMR results, enabled us to determine the thermodynamic functions ΔG, ΔH and ΔS for reaction (1) for the first time.
In this paper we attempt to find an answer to the question as to which of the structural and physicochemical factors determine the thermodynamic stability of ternary M(III/IV)–EDTA–carbonate complexes. This is particularly important for the study and prediction of the environmental An(III)/An(IV)–EDTA mobility process as well as for understanding the quenching of spin–lattice relaxation in some of the Gd(III)-based MRI contrast agents under physiological conditions.15 The presented study may elucidate what role the readily available carbonate coligand plays in both of these processes.
Results and discussion
X-ray crystal structure of [C(NH2)3]3[Er(EDTA)(CO3)]·H2O
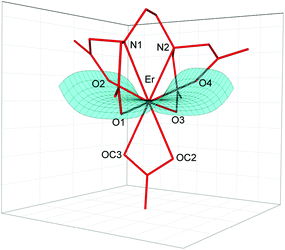
The crystal structure of [C(NH2)3]3[Er(EDTA)(CO3)]·H2O (I) was determined while the structural details of [C(NH2)3]2[Er(EDTA)(H2O)2]ClO4·6H2O (Ia) were taken from ref. 5 for comparison purposes. The details of the data collection and the structure refinement of I are given in Table S1 in the ESI.† In both compounds the Er(III) cation is eight coordinated and the EDTA ligand is bound to the Er(III) cation by four oxygen and two nitrogen atoms. The remaining coordination sites of Er(III) are filled by two oxygen atoms from the bidendate carbonate anion (in I) and two water molecules (in Ia). The views of both molecular anions are presented in Fig. 1.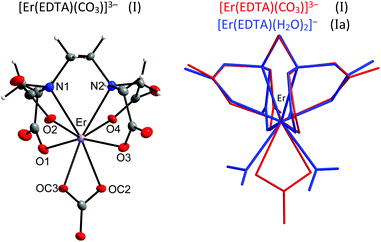 | ||
| Fig. 1 Molecular structure of [Er(EDTA)(CO3)]3– anion in I together with the atom labeling scheme and superimposed molecular structures of [Er(EDTA)(CO3)]3– (in red) and [Er(EDTA)(H2O)2]− (in blue) complexes. Coordinates of the [Er(EDTA)(H2O)2]− anion in Ia have been taken from ref. 5. | ||
To find the closest coordinates of the ideal polyhedron, the continuous symmetry measure parameter20 (hereinafter referred to as CSM) was calculated. Though the geometry of the first coordination sphere of Er(III) in I may be described as a biaugmented trigonal prism (BTPR-8, CSM = 11.9%) and that in Ia as a triangular dodecahedron (TDD-8, CSM = 1.604%) or a square antiprism (SAPR-8 CSM = 1.69%), the approximate symmetry of both complexes is C2. The substitution of two water molecules by a carbonate anion brings about only minute changes of bond lengths in the ErEDTA moiety; thus the EDTA ligand adopts very similar conformations in both crystals as shown in Fig. 1. The selected Er–L bond lengths in I and Ia5 are presented in Table 1.
| Bond | [Er(EDTA)(CO3)]3– (I) | [Er(EDTA)(H2O)2]− (Ia)5 | Δ Er–L |
|---|---|---|---|
| Er–O(CO2–) | 2.257(3)–2.321(3) | 2.2489(10)–2.2975(11) | |
| Er–O(CO 2 – ) av | 2.286(28) | 2.275(26) | 0.011 |
| Er–N | 2.570(4)–2.576(4) | 2.5995(12)–2.5816(11) | |
| Er–N av | 2.573(4) | 2.591(13) | −0.018 |
| Er–La | 2.328(3)–2.330(3) | 2.3445(10)–2.3444(10) | |
| Er–L av | 2.329(2) | 2.345(5) | −0.015 |
| Er⋯Er | 6.63 | 7.34 |
| [Th(EDTA)(CO3)2]4– (II) | [Th(EDTA)(H2O)4] (IIa)6 | Δ Th–L | |
|---|---|---|---|
| a L = CO32– in I and II or L = H2O in Ia and IIa. | |||
| Th–O(CO2–) | 2.481(4)–2.503(4) | 2.4014(15)–2.4576(15) | |
| Th–O(CO 2 – ) av | 2.491(10) | 2.428(26) | 0.063 |
| Th–N | 2.773(4)–2.801(5) | 2.790(2)–2.819(2) | |
| Th–N av | 2.787(20) | 2.805(21) | −0.018 |
| Th–La | 2.432(4)–2.484(4) | 2.5693(16)–2.4911(16) | |
| Th–L av | 2.454(24) | 2.532(33) | −0.078 |
As is seen, the Er–O(CO32–) and Er–OH2 bond lengths are similar; however the former ones are a little bit shorter due to larger formal negative charges on carbonate oxygen atoms. The Er(III) cation is located in a saddle point formed by four Er–O(CO2–) bonds (Fig. 2).
This point may be illustrated using the values of O1–Er–O3 (201.2°) and O2–Er–O4 (139.3°) angles, which are about 2° smaller in I than those in Ia. The binding of the CO32– anion or two H2O molecules with the [Er(EDTA)]− moiety occurs in such a way that the inserted coligands fit to the saddle point (Fig. 2) to minimize the repulsion between carboxylate donor atoms (O1, O2, O3, and O4) and OC2, OC3 in I or OW10 and OW11 in Ia coligands. This is a reason why the rotation of CO32–/H2O coligands around C2 axes is hindered. The encapsulation of the Er(III) ion seems to be slightly stronger in the [Er(EDTA)(CO3)]3– complex in comparison with that in the hydrated [Er(EDTA)(H2O)2]− species. This is due to a stronger electrostatic Er(III)–carbonate anion interaction and better fitting of the planar carbonate anion to the coordination vacancy of the [Er(EDTA)]− unit. To illustrate this problem it is worth comparing the distance between neighboring OC2⋯OC3 atoms from the CO32– anion in I with that between neighboring coordinated water molecules OW10⋯OW11 in Ia, which have been found to be 2.204(3) Å and 2.772(1) Å, respectively.
X-ray crystal structure of [C(NH2)3]4[Th(EDTA)(CO3)2]·5H2O
Thorium, which is characterised by a very stable +4 oxidation state, is thought to be a natural analog of tetravalent actinides. It seems to be important to elucidate how the increase of the oxidation state of the central metal cation disturbs the stoichiometry and in general the structure of the formed complexes. Crystals of the formula [C(NH2)3]4[Th(EDTA)(CO3)2]·5H2O (II) were obtained and the molecular structure of the [Th(EDTA)(CO3)2]4– anion is presented in Fig. 3. The details of the data collection and the structure refinement of II are provided in Table S1 in the ESI.†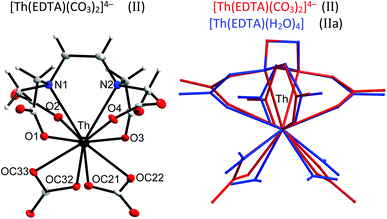 | ||
| Fig. 3 The molecular structure of the [Th(EDTA)(CO3)2]4– anion in II together with the atom labeling scheme and superimposed molecular structures of [Th(EDTA)(CO3)2]4– (in red) and [Th(EDTA)(H2O)4] (in blue) complexes. Coordinates of [Th(EDTA)(H2O)4] (IIa) have been taken from ref. 6. | ||
The EDTA ligand in the [Th(EDTA)(CO3)2]4– anion is coordinated to Th(IV) in the same fashion as in I and Ia; however the conformation of the EDTA ligand in II is different. Four remaining coordination sites of Th(IV) are occupied by two bidendate carbonate anions thus giving a coordination number of 10. This is the most common coordination number of Th(IV) which was also found in the hydrated [Th(EDTA)(H2O)4] complex.6 The superimposed molecular structures of [Th(EDTA)(CO3)2]4– and [Th(EDTA)(H2O)4] complexes are shown in Fig. 3. The increase of the coordination number from 8 in I and Ia up to 10 in II and IIa is caused by the increase of the charge density of Th(IV) (17.0 esu Å−1) in comparison with Er(III) (14.3 esu Å−1). The selected Th–L bond lengths in II and IIa are presented in Table 1. The Th–O(CO2–) bond lengths are slightly longer in II than in IIa, while the corresponding Th–N bond lengths for both crystals are similar within the error of experimental limits. The largest variation of bond lengths has been found for the case of Th–coligand interactions. The average Th–O(CO2–) bond lengths in II are about 0.078 Å shorter than the Th–O(H2O) ones in IIa. Interestingly the corresponding Er–coligand bond lengths in I and Ia differ only slightly. The binding of negatively charged coligands with Th(IV) (i.e. carbonate) brings about certain elongation of Th–O(CO2–) bonds while coordination of neutral coligands (i.e. H2O) causes their shortening. This is likely due to increased repulsion between negatively charged oxygen atoms from carboxylate and carbonate groups. The geometry of the first coordination sphere of Th(IV) in both complexes may be described as sphenocorona (JSPC-10) with CSM factors equal to 3.47% and 2.96% for II and IIa, respectively. The symmetry of the Th(IV) complexes under study may be approximated as C2.
UV-vis spectra of crystals I and Ia
Because the 4f electrons are essentially core orbitals, screened by the closed 5s and 5p subshells, they cannot participate significantly in covalent bonding. For instance the calculated values of ligand field stabilization for the Nd(Cp′′)3 complex (where Cp′′ is 1,3-bis-(trimethylsilyl)cyclopentadienyl) is about 58.6 kJ mol−1 (ref. 21) while for the substantially ionic compound [Nd(H2O)9](BrO3)3 this energy is only about 6.3 kJ mol−1.22 Therefore the geometry of ligands around Ln(III) ions is controlled mainly by steric factors. Thus only the nearest donor atoms of ligands bonded directly with Ln(III) may affect to some extent the 4f electrons. The influence of the outer coordination sphere is rather less important. Thus the spectral pattern of the f–f transitions, especially the hypersensitive ones, may be a “fingerprint” for a given system.The UV-vis-NIR spectra of I measured at room and liquid helium temperatures in the spectral range 250–900 nm are presented in Fig. S1 in the ESI.† The crystal field (CF) levels of the selected multiplets determined from the spectra of I and Ia, recorded at 4.2 K are presented in Table S2.† The number of CF components observed in the spectra of I indicates that there is one symmetry independent site of Er(III) which is consistent with the X-ray structural data; however some of the CF components of the 4S3/2 multiplets are additionally slightly split. The crystal field splitting (ΔCFS Table S2†) of the particular 2S+1LJ multiplets, except those of 4S3/2 and 4I11/2, are smaller in I than in Ia.5 The observed bathochromic shift of the highest energy CF component and the gravity center of all multiplets in the spectra of I in comparison with those in Ia may suggest some increase of the covalent contribution to Er–L bonding in I. It should be noted that the comparison of such spectroscopic properties is justified for systems with the same symmetry and is usually made for simple inorganic compounds which possess high point symmetry.23 Although the molecular systems under study have low symmetry (∼C2), the geometry of anionic complexes is substantially very similar. Therefore a comparison of crystal field splitting (ΔCFS) for the given multiplets in I and Ia can be done. The observed variation in the absorption spectra of f–f transitions may be attributed to different donor properties of binding coligands. The changes in the ΔCFS values and the energy of the gravicenter of the 2S+1LJ multiplets correspond to the positions of CO32– and H2O ligands in the spectrochemical and nephelauxetic series.24
A comparison of the spectral features of the hypersensitive transitions recorded for single crystals, containing a well-defined molecular lanthanide complex, with those of solutions, may provide crucial information about the stoichiometry, structure and concentration of the complex species in solution.12,25 The spectra of the 4I15/2 → 2H11/2 and 4I15/2 → 4S3/2 transitions of the Er(III) compounds are particularly informative in this regard. The absorption spectra of crystals I and Ia and solutions of the Er(III)–EDTA–carbonate complexes at pH ∼ 7.5 and ∼12 (μKCl = 3.5 M) were recorded and are shown in Fig. 4.
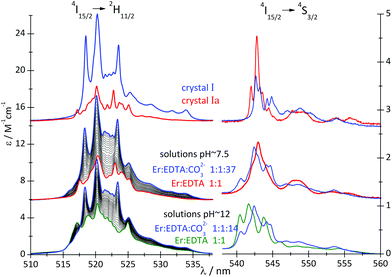 | ||
| Fig. 4 Absorption spectra of crystals I and Ia and solutions of the Er(III)–EDTA–carbonate systems (cErEDTA = 29.5 mM) at different concentrations of the carbonate, at pH ∼ 7.5 and 12. | ||
The different donor properties of both coligands are also reflected in the intensity of the f–f transitions, particularly of the hypersensitive ones. The oscillator strengths of the hypersensitive 4I15/2 → 2H11/2 transitions for the systems under study are presented in Table 2. The Judd–Ofelt26,27 analysis of the f–f transitions of I and Ia are discussed in the ESI (Table S3†).
| System | P × 108 |
|---|---|
| Solid | |
| I | 853 |
| Ia | 308 |
| Solution | |
Er![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EDTA 1 EDTA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; pH ∼ 7.5 1; pH ∼ 7.5 |
505 |
Er![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EDTA EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) carbonate 1 carbonate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15; pH ∼ 7.5 15; pH ∼ 7.5 |
1072 |
Er![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EDTA 1 EDTA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; pH ∼ 12 1; pH ∼ 12 |
705 |
Er![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EDTA EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) carbonate 1 carbonate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4; pH ∼ 12 4; pH ∼ 12 |
1128 |
The replacement of water molecules in Ia by more polarizable, bidendate CO32– anion in I brings about a significant increase in the intensities of the hypersensitive 4I15/2 → 4G11/2 and 4I15/2 → 2H11/2 transitions, as the polarizability of CO32– anions (αCO3 = 3.85 Å3) is about 2.7 times higher than that of water (αH2O = 1.442 Å3).28
Solution structure and stability of the ternary Er–EDTA–carbonate complex
The spectra of Er(III)–EDTA solutions at pH ∼ 7.5 in the absence of carbonate anions are similar to those in Ia. It has been shown previously that under these conditions [Er(EDTA)(H2O)2]− is the predominant species (∼95%).5 With the increase of the concentration of the carbonate anion the spectra of the Er(III)–EDTA–carbonate solution become more similar to that in I. Thus the following reaction (2) occurs in a solution of the Er(III)–EDTA–carbonate system at pH ∼ 7.5, for which the formation constant is described by eqn (3).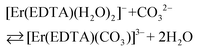 | (2) |
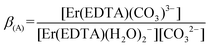 | (3) |
To examine reaction (2), the spectrophotometric titration of the Er(III)–EDTA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with the carbonate at pH ∼ 7.5 was performed (Fig. 4). Factor analysis29 of the set of these spectra was used to determine the molar fractions of Er(III) complexes existing in solutions and consequently to calculate the conditional stability constants β(A) (eqn (3)). The appropriate dependence needed for β(A) calculation is derived in Table S4 in the ESI† and the retrieved spectra of both [Er(EDTA)(H2O)2]− and [Er(EDTA)(CO3)]3– species are shown in Fig. S2 in the ESI.† The determined value of log
1 complex with the carbonate at pH ∼ 7.5 was performed (Fig. 4). Factor analysis29 of the set of these spectra was used to determine the molar fractions of Er(III) complexes existing in solutions and consequently to calculate the conditional stability constants β(A) (eqn (3)). The appropriate dependence needed for β(A) calculation is derived in Table S4 in the ESI† and the retrieved spectra of both [Er(EDTA)(H2O)2]− and [Er(EDTA)(CO3)]3– species are shown in Fig. S2 in the ESI.† The determined value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(A) is 3.66 ± 0.07.
β(A) is 3.66 ± 0.07.
To study the influence of the solution pH on the binding of the carbonate anion with the Er(III)–EDTA complex the titration of the Er(III)–EDTA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with the carbonate under basic conditions (pH ∼ 12) was also performed. It should be noted that the spectra of the Er(III)–EDTA system under neutral and basic conditions in carbonate free solutions differ remarkably. It may be caused by the hydrolysis of the [Er(EDTA)(H2O)2]− complex above pH > 9.30 Therefore an additional spectrophotometric titration of the [Er(EDTA)(H2O)2]− complex with KOH was performed (Fig. 5).
1 complex with the carbonate under basic conditions (pH ∼ 12) was also performed. It should be noted that the spectra of the Er(III)–EDTA system under neutral and basic conditions in carbonate free solutions differ remarkably. It may be caused by the hydrolysis of the [Er(EDTA)(H2O)2]− complex above pH > 9.30 Therefore an additional spectrophotometric titration of the [Er(EDTA)(H2O)2]− complex with KOH was performed (Fig. 5).
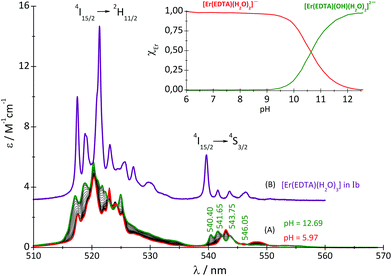 | ||
Fig. 5 Absorption spectra of the solutions of the Er(III)–EDTA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system at different pH (cErEDTA = 29.5 mM) (A); the [Er(EDTA)(H2O)3]− complex in a Na[Er(EDTA)(H2O)3]·5H2O crystal – Ib (B). 1 system at different pH (cErEDTA = 29.5 mM) (A); the [Er(EDTA)(H2O)3]− complex in a Na[Er(EDTA)(H2O)3]·5H2O crystal – Ib (B). | ||
The band shape and intensity of 4I15/2 → 2H11/2 and 4I15/2 → 4S3/2 transitions are almost the same in solutions at pH between 4 and 8. The predominant solution species under these conditions is [Er(EDTA)(H2O)2]−.5 Above pH > 8 considerable changes of the spectral patterns of 4I15/2 → 2H11/2 and 4I15/2 → 4S3/2 transitions are observed. Interestingly the final spectra of strongly basic solutions become more similar to those of the nine-coordinate [Er(EDTA)(H2O)3]− complex in a Na[Er(EDTA)(H2O)3]·5H2O crystal5 (hereinafter referred to as Ib) for which the UV-vis spectrum is also presented in Fig. 5, for comparison purposes. The resemblance of the spectra for both systems may suggest certain structural similarities of both complexes. It is particularly well observed in the spectra of the 4I15/2 → 4S3/2 transition which is very sensitive to the changes of the coordination number, as shown previously.5 As the pH value of the solution increases the additional peaks appear with the positions similar to those observed in the spectra of the nine-coordinate [Er(EDTA)(H2O)3]− complex in crystal Ib. The observed hypsochromic shift of the highest-energy CF components of the 4I15/2 → 4S3/2 transition in the spectra of Er(III)–EDTA solutions under basic conditions in comparison with those at neutral pH, may suggest the changes of the coordination sphere of the Er(III) ion due to the formation of the hydrolyzed complex according to the simplified equation
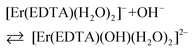 | (4) |
However, it should be noted that there is no convincing evidence for CN changes, except that obtained from the kinetic study results of the hydrolysis of a Yb–EDTA system.30c
To describe reaction (2) qualitatively, the factor analysis of the 4I15/2 → 2H11/2 and 4I15/2 → 4S3/2 spectra was performed assuming two principal equilibrium species: [Er(EDTA)(H2O)2]− and [Er(EDTA)(OH)(H2O)2]2–. The retrieved spectra of both species are shown in Fig. S3 in the ESI.† Because of the high thermodynamic stability of the Er–EDTA complex (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βErEDTA = 18.85 at μKNO3 = 0.1 M,31 log
βErEDTA = 18.85 at μKNO3 = 0.1 M,31 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βErEDTA = 17.45 ± 0.06 at μNaClO4 = 0.5 M)32 the concentrations of uncomplexed Er(III) and EDTA ions were neglected. The solutions under conditions under study were homogenous (no precipitate was formed). A speciation diagram, i.e. the molar fraction of the Er(III) species as a function of pH, is shown in an inset in Fig. 5. As is seen from this diagram, in solutions at the pH range between 6 and 9 the [Er(EDTA)(H2O)2]− complex is the predominant species. Above pH > 9 this complex starts to hydrolyse forming the [Er(EDTA)(OH)(H2O)2]2– species. At pH ∼ 10.6 the concentrations of both [Er(EDTA)(H2O)2]− and [Er(EDTA)(OH)(H2O)2]2– complexes are equal, and above this pH the hydrolysed complex begins to dominate. The obtained species concentrations were used to determine the hydrolysis constant βOH from eqn (5) of reaction (4):
βErEDTA = 17.45 ± 0.06 at μNaClO4 = 0.5 M)32 the concentrations of uncomplexed Er(III) and EDTA ions were neglected. The solutions under conditions under study were homogenous (no precipitate was formed). A speciation diagram, i.e. the molar fraction of the Er(III) species as a function of pH, is shown in an inset in Fig. 5. As is seen from this diagram, in solutions at the pH range between 6 and 9 the [Er(EDTA)(H2O)2]− complex is the predominant species. Above pH > 9 this complex starts to hydrolyse forming the [Er(EDTA)(OH)(H2O)2]2– species. At pH ∼ 10.6 the concentrations of both [Er(EDTA)(H2O)2]− and [Er(EDTA)(OH)(H2O)2]2– complexes are equal, and above this pH the hydrolysed complex begins to dominate. The obtained species concentrations were used to determine the hydrolysis constant βOH from eqn (5) of reaction (4):
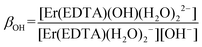 | (5) |
The final values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βOH determined on the basis of spectroscopic and potentiometric titrations are 3.40 ± 0.16 and 3.56 ± 0.21, respectively. These values are slightly higher in comparison with those obtained for the other Ln(III)–EDTA systems using other physical methods.30 The differences seem to be caused by the ionic medium effect as the presented results were obtained at a relatively high ionic strength (μKCl = 3.5 M).33 Because log
βOH determined on the basis of spectroscopic and potentiometric titrations are 3.40 ± 0.16 and 3.56 ± 0.21, respectively. These values are slightly higher in comparison with those obtained for the other Ln(III)–EDTA systems using other physical methods.30 The differences seem to be caused by the ionic medium effect as the presented results were obtained at a relatively high ionic strength (μKCl = 3.5 M).33 Because log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(A) = 3.66 ± 0.07 and log
β(A) = 3.66 ± 0.07 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βOH = 3.40 ± 0.16 are very similar, the competition between carbonate anion and OH− binding by the [Er(EDTA)(H2O)2]− complex is likely to arise. Thus under basic conditions (pH > 10.6) in the presence of carbonate anions the following reaction (6) should be expected. Reaction (6) is described using the formation constants β(B) (eqn. (7)).
βOH = 3.40 ± 0.16 are very similar, the competition between carbonate anion and OH− binding by the [Er(EDTA)(H2O)2]− complex is likely to arise. Thus under basic conditions (pH > 10.6) in the presence of carbonate anions the following reaction (6) should be expected. Reaction (6) is described using the formation constants β(B) (eqn. (7)).
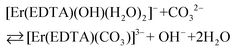 | (6) |
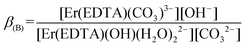 | (7) |
Because the molar fractions of the [Er(EDTA)(CO3)]3– and [Er(EDTA)(OH)(H2O)2]2– species are controlled by the concentrations of CO32– and OH− anions, the spectrophotometric and pH measurements were performed simultaneously. The determined value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(B) was 0.20 ± 0.12. It is worth noting that the calculated value of log
β(B) was 0.20 ± 0.12. It is worth noting that the calculated value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(B) = log
β(B) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(A) − log
β(A) − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βOH is equal to 0.26, and both log
βOH is equal to 0.26, and both log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(B) values, although obtained from the independent set of data, are in very good agreement. As is seen, the β(A) value is about three orders of magnitude larger than the β(B) one. It means that the carbonate anion substitutes water molecules more efficiently than the hydroxy anion. The latter is more strongly attracted by the Ln(III) cation than neutral H2O molecules. The determined log
β(B) values, although obtained from the independent set of data, are in very good agreement. As is seen, the β(A) value is about three orders of magnitude larger than the β(B) one. It means that the carbonate anion substitutes water molecules more efficiently than the hydroxy anion. The latter is more strongly attracted by the Ln(III) cation than neutral H2O molecules. The determined log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(A) value is comparable to that estimated for the Am(III)–EDTA–carbonate system for which the latter value was between 3 and 4.16 On the other hand it is significantly larger than 0.74 reported for the [Er(EDTA)(CO3)]3– complex in ref. 13. This underestimation of log
β(A) value is comparable to that estimated for the Am(III)–EDTA–carbonate system for which the latter value was between 3 and 4.16 On the other hand it is significantly larger than 0.74 reported for the [Er(EDTA)(CO3)]3– complex in ref. 13. This underestimation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(A) = 0.74 is likely due to the simplified model used for the description of reaction (1).
β(A) = 0.74 is likely due to the simplified model used for the description of reaction (1).
Because the geometries of the [Er(EDTA)]− moiety in crystals I and Ia are very similar, the substitution of H2O molecules by the CO32– anion (reaction (2)) is due to the changes of the Er–coligand interactions only. Thus the bond energies of Er–OH2 and Er–O(carbonate) (hereinafter referred to as EEr–L) may be estimated from eqn (8) and (9), respectively.
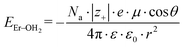 | (8) |
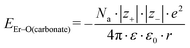 | (9) |
All the used quantities are presented in Table S5.† The bond energy change calculated in this way is defined as ΔEEr–L = EEr–O(carbonate) − EEr–OH2 and is equal to −22.1 kJ mol−1. The changes of the Th–L bond energy (ΔETh–L) values for the hypothetical reactions (10) and (11) calculated in the same way are equal to −29 kJ mol−1 and −58 kJ mol−1, respectively.
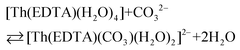 | (10) |
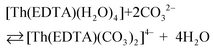 | (11) |
Although the presented model of the estimation of the M–L bond energy is simplified, as it does not take into account the covalent contribution to the M–L bonds,34 the obtained values may indicate that the Ln(III)–L bond energy is lower than the An(IV) one; moreover they may suggest that the dicarbonato [Th(EDTA)(CO3)2]4– complex should be more stable than the monocarbonate [Th(EDTA)(CO3)(H2O)2]2– species.
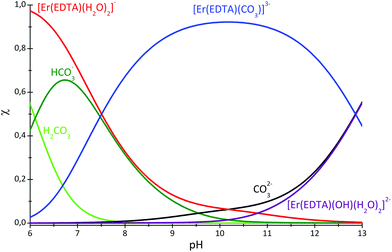
The speciation curves for the Er–EDTA–carbonate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system are presented in Fig. 6. The formation of [Er(EDTA)(CO3)]3– starts under slightly acidic conditions and it is the most stable species at pH 10. Above pH > 10 the binding of the carbonate anion competes with OH− anion coordination.
1 system are presented in Fig. 6. The formation of [Er(EDTA)(CO3)]3– starts under slightly acidic conditions and it is the most stable species at pH 10. Above pH > 10 the binding of the carbonate anion competes with OH− anion coordination.
To obtain a more comprehensive picture of the substitution of H2O/OH− ligands by carbonate anions, a study of the temperature effects on the stability of ternary complexes is required. Therefore reactions (2) and (6) were studied at elevated temperatures.
Thermodynamic description of [Er(EDTA)(CO3)]3– complex formation
Due to the low thermal stability of the carbonate/bicarbonate solutions, the reactions of (2) and (6) were studied in the temperature range between 283 and 333 K only.35 Because reactions (2) and (6) are pH dependent, the spectrophotometric and potentiometric measurements were performed simultaneously at a given temperature.The spectra of Er–EDTA–carbonate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 systems at pH ∼ 7.4 and ∼12.6 were measured at different temperatures between 283 and 333 K and are presented in Fig. S3 in the ESI.† It should be noted that the absorption spectra of the 4I15/2 → 2H11/2 and 4I15/2 → 4S3/2 transitions of solutions at pH around 12 are more temperature-sensitive than those at pH 7.4. It is likely connected with the change of the CN of the Er(III) ion in complexes under study under more basic solutions. The factor analysis of these spectra enabled us to determine the molar fractions of the Er(III) species in solutions under study at elevated temperatures. The combined glass electrode with a built-in temperature sensor was used to measure the pH of solutions at different temperatures.
1 systems at pH ∼ 7.4 and ∼12.6 were measured at different temperatures between 283 and 333 K and are presented in Fig. S3 in the ESI.† It should be noted that the absorption spectra of the 4I15/2 → 2H11/2 and 4I15/2 → 4S3/2 transitions of solutions at pH around 12 are more temperature-sensitive than those at pH 7.4. It is likely connected with the change of the CN of the Er(III) ion in complexes under study under more basic solutions. The factor analysis of these spectra enabled us to determine the molar fractions of the Er(III) species in solutions under study at elevated temperatures. The combined glass electrode with a built-in temperature sensor was used to measure the pH of solutions at different temperatures.
To calculate the ΔG values of reactions (2) and (6), the values of the ionic product of water (Kw) and the dissociation constants of carbonic acid K1 and K2 at various temperatures are also needed. The pKw values33 and the corresponding values of pK1, pK2 at μKCl = 3.5 M at a given temperature, which were calculated from the empirical model given in ref. 36 are presented in Table S6 in the ESI.† The obtained data sets of the molar fractions of the Er(III) and carbonate species with the calculated ΔG values at a given temperature and pH of the solution are compiled in Table S7.†
To enhance the obtained thermodynamic results, the temperature dependent 13C NMR spectra of Er(III)–EDTA–carbonate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solutions containing 13C enriched carbonate anions were measured at elevated temperature. It is known that the comparison of the intensities of carbon signals in the spectra of organic compounds is not recommended because of the low concentration of the 13C isotope in natural samples and different ordering of carbon atoms. Due to the same order of carbon atoms in bound and unbound carbonate species and the high concentration of the 13C isotope in the systems under study, the comparison of the intensities of the 13C NMR signals is justified.
1 solutions containing 13C enriched carbonate anions were measured at elevated temperature. It is known that the comparison of the intensities of carbon signals in the spectra of organic compounds is not recommended because of the low concentration of the 13C isotope in natural samples and different ordering of carbon atoms. Due to the same order of carbon atoms in bound and unbound carbonate species and the high concentration of the 13C isotope in the systems under study, the comparison of the intensities of the 13C NMR signals is justified.
Because of the low stability of the carbonate/bicarbonate solutions at pH ∼ 7 at elevated temperatures, only the 13C NMR spectra of the solutions at pH ∼ 12.4 could be recorded. Two 13C signals attributed to the bound (∼50 ppm) and unbound (∼160 ppm) CO32– anions were observed in the 13C NMR spectra, in which the intensity and position change with the temperature. The main conclusion that could be drawn from the 13C NMR spectroscopy data is that the formation of the ternary [Er(EDTA)(CO3)]3– complex is more favorable at higher temperatures. Unfortunately due to experimental difficulties it was not possible to measure the pD of solutions under study at different temperatures. Thus, only the molar fractions of bound and unbound carbonate species could be determined. The ratios of the molar fractions of the Er(III) species derived from the 13C NMR and UV-vis spectroscopy results calculated in this way are compiled in Fig. 7.
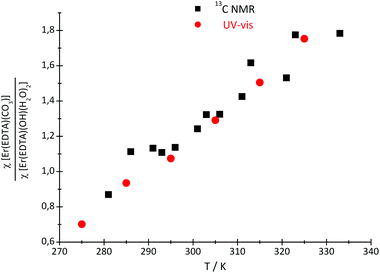 | ||
| Fig. 7 The ratio of the molar fractions of the Er(III) species, derived from the 13C NMR and UV-vis spectroscopy results. | ||
As seen in this figure the results obtained from both independent and compatible techniques are in very good accordance. The 13C NMR spectroscopy results are described and discussed in more detail in the Appendix.
By plotting ΔG versus temperature (Fig. 8) it was possible to determine the ΔH and ΔS of reactions (2) and (6). The determined values of the thermodynamic functions are provided in Table 3.
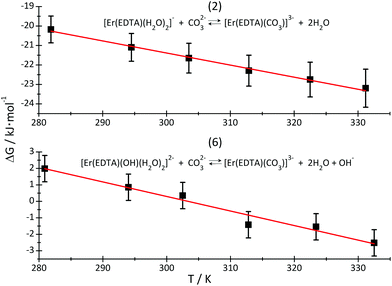 | ||
| Fig. 8 ΔG of reactions (2) – top and (6) – bottom, plotted as a function of temperature. The red lines are linear regression lines through the experimental data (black squares). | ||
As is seen, reaction (2) is slightly exothermic while reaction (6) is endothermic.
The replacement of H2O molecules by the carbonate anion is mainly entropy driven, although the formation of the [Er(EDTA)(CO3)]3– complex may be additionally enthalpy stabilized due to stronger electrostatic interactions of highly negatively charged oxygen carbonate atoms than neutral water molecules with Er(III) cations.
Because there is a lack of knowledge regarding thermodynamic data of carbonate binding by Ln(III) in general, we have referred the obtained data to those for the [Eu(CO3)]+ and [Eu(CO3)2]− systems, only. The enthalpy of formation of the [Eu(CO3)]+ and [Eu(CO3)2]− complexes are slightly positive and equal to 6.8 ± 2 kJ mol−1 and 7.5 ± 3 kJ mol−1, respectively.37 The enthalpy of reaction (6) is large and positive, as much more energy is needed to substitute the OH− anion than the H2O molecule, by the CO32– anion. Moreover this reaction is probably accompanied by a decrease of the coordination number from nine to eight. Such a decrease of the CN connected with the dissociation of water molecule(s) is usually endothermic for the other lanthanide systems.11,38 Both reactions are strongly entropy driven, resulting in the release of H2O/OH− ligands from the first coordination sphere of Er(III) and dehydration of carbonate anions. It is likely that the enthalpy changes reflect mainly the Er–L bond formation, while entropy changes are caused by disordering of the bulk solution “structure”. The other factor stabilising ternary eight coordinate [Er(EDTA)(CO3)]3– complexes is the spatial fitting of the planar bidentate CO32– anion to the coordination vacancies arising from the dissociation of H2O/OH− ligands.
Conclusions
The presented results are the first example of the thermodynamic description of carbonate ternary complex formation that was additionally structurally supported.The novel [C(NH2)3]3[Er(EDTA)(CO3)]·H2O I and [C(NH2)3]4[Th(EDTA)(CO3)2]·5H2O (II) compounds containing ternary [M(EDTA)(CO3)n]m− complexes were structurally characterized for the first time. In the eight coordinate [Er(EDTA)(CO3)]3– complex Er(III) is surrounded by six donor atoms (O4N2) from the EDTA ligand and two oxygen atoms from the bidendate carbonate anion. In the ten coordinate [Th(EDTA)(CO3)2]4– complex the EDTA ligand is bonded with Th(IV) in the same fashion as in [Er(EDTA)] systems, and the remaining four coordination sites are occupied by two bidendate carbonate anions. The increase of the oxidation state of the central metal cation from +3 to +4 is probably the main reason for the increase of the coordination number from 8 to 10, respectively.
The structural and UV-vis-NIR results of [C(NH2)3]3[Er(EDTA)(CO3)]·H2O (I), [C(NH2)3]2[Er(EDTA)(H2O)2]ClO4·6H2O (Ia) and Na[Er(EDTA)(H2O)3]·5H2O (Ib) were used as the model data to study carbonate binding with the Er(III)–EDTA complex and the hydrolysis reaction of the latter one in aqueous solutions.
Formation of the ternary [Er(EDTA)(CO3)]3– complex under different conditions (pH and temperature) was examined by UV-vis and NMR spectroscopy as well as by potentiometry. The equilibrium constant for reaction (A): [Er(EDTA)(H2O)2]− + CO32– ⇄ [Er(EDTA)(CO3)]3– + 2H2O was determined to be log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(A) = 3.66 ± 0.07. For the reaction that occurs in more basic solutions (B): [Er(EDTA)(OH)(H2O)2]2– + CO32– ⇄ [Er(EDTA)(CO3)]3– + 2H2O + OH−, the corresponding log
β(A) = 3.66 ± 0.07. For the reaction that occurs in more basic solutions (B): [Er(EDTA)(OH)(H2O)2]2– + CO32– ⇄ [Er(EDTA)(CO3)]3– + 2H2O + OH−, the corresponding log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(B) value was found to be 0.20 ± 0.12. It was also observed that the hydrolysis reaction [Er(EDTA)(H2O)2]− + OH− ⇄ [Er(EDTA)(OH)(H2O)2]2– is likely to accompany with the increase of the coordination number of Er(III) from eight to nine. The determined value of log
β(B) value was found to be 0.20 ± 0.12. It was also observed that the hydrolysis reaction [Er(EDTA)(H2O)2]− + OH− ⇄ [Er(EDTA)(OH)(H2O)2]2– is likely to accompany with the increase of the coordination number of Er(III) from eight to nine. The determined value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βOH is equal to 3.40 ± 0.16.
βOH is equal to 3.40 ± 0.16.
The temperature dependence of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(A) and log
β(A) and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(B) allowed us to determine the enthalpy and entropy of both (A) and (B) reactions, which were found to be ΔH(A) = −2.8 ± 0.8 kJ mol−1, ΔS(A) = 62 ± 3 J mol−1 K−1 and ΔH(B) = 28.1 ± 4.6 kJ mol−1, ΔS(B) = 92 ± 15 J mol−1 K−1. The obtained data indicate that the carbonate anion readily displaces H2O than the OH− ligand.
β(B) allowed us to determine the enthalpy and entropy of both (A) and (B) reactions, which were found to be ΔH(A) = −2.8 ± 0.8 kJ mol−1, ΔS(A) = 62 ± 3 J mol−1 K−1 and ΔH(B) = 28.1 ± 4.6 kJ mol−1, ΔS(B) = 92 ± 15 J mol−1 K−1. The obtained data indicate that the carbonate anion readily displaces H2O than the OH− ligand.
The formation of stable Ln(III)–EDTA–carbonate complexes at physiological pH is probably one of the reasons why Gd(III)–EDTA complexes could not be used as MRI contrast agents, as the high relaxivity of this complex is substantially reduced in the presence of carbonate anions.15 It may be expected that the other chelate complexes with two inner-sphere water molecules should also strongly interact with carbonate anions, due to spatial fitting of the carbonate ligand to the coordination vacancy that is formed as a result of water molecule dissociation.
The presented results are particularly important for the study and prediction of the environmental An(III)/An(IV)–EDTA mobility process. The binding of carbonate ligands with the An–EDTA moiety due to the formation of stable ternary [An(EDTA)(CO3)]3– and [An(EDTA)(CO3)2]4– complexes may certainly inhibit the hydrolysis of the An(III)/An(IV)–EDTA species to sparingly soluble hydroxo/oxo compounds. This, in turn, may enhance the mobility of trivalent and tetravalent actinides in the environment.
Experimental
Materials and sample preparation
Stock solutions of erbium chloride and erbium perchlorate were prepared by dissolving Er2O3 (99.9%, MERCK) in 2 M hydrochloric or chloric(VII) acids, respectively. The metal concentration was determined complexometrically by using xylenol orange as an indicator.Equimolar amounts of ErCl3 solution (6 mmol) and solid H4EDTA (98%, MERCK; 6 mmol) were mixed together and heated at 90 °C (±5 °C) until the precipitate was dissolved. Next, the solid [C(NH2)3]2CO3 (Aldrich) (30 mmol) was added to the solution to adjust the pH to ∼11. Large pink crystals of [C(NH2)3]3[Er(EDTA)(CO3)]·H2O (I) were formed after one weak.
In a similar way the crystals of the [C(NH2)3]4[Th(EDTA)(CO3)2]·5H2O (II) compound were obtained, but as a starting compound Th(NO3)4·5H2O (Serva Heidelberg) was used. The crystals of [C(NH2)3]2[Er(EDTA)(H2O)2]ClO4·6H2O (Ia) and Na[Er(EDTA)(H2O)3]·5H2O (Ib) were prepared according to the procedure described in ref. 5.
The solutions of Er(III)–EDTA systems used for spectroscopic measurements were prepared in deionised water with a specific conductivity of 0.05 μS cm−1. The concentration of Er(III) was 0.025–0.055 M. The ionic strength of the solution was adjusted with KCl to μ = 3.5 M.
For NMR spectroscopic measurements solutions of the Er(III)–EDTA–carbonate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 systems were prepared at concentrations of [ErEDTA] and [CO32–] equal to 0.049 M and 0.067 M, in D2O solution (μKCl = 3.5 M). For this experiment an isotopically enriched 13C (99%) NaH13CO3 sample (Cambridge Isotope Laboratories) was used. The final pD = 12.4 of the solution was adjusted with KOD. NMR spectra were recorded with an AMX Bruker 300 MHz NMR spectrometer.
1.4 systems were prepared at concentrations of [ErEDTA] and [CO32–] equal to 0.049 M and 0.067 M, in D2O solution (μKCl = 3.5 M). For this experiment an isotopically enriched 13C (99%) NaH13CO3 sample (Cambridge Isotope Laboratories) was used. The final pD = 12.4 of the solution was adjusted with KOD. NMR spectra were recorded with an AMX Bruker 300 MHz NMR spectrometer.
Temperature dependent measurements
For all samples the temperature was increased from 283 K to 333 K in steps of 10 K. At each temperature the sample was equilibrated for 15 min before an absorption UV-vis-NIR spectrum was recorded. No change of the spectra was observed after this time, proving that the thermodynamic equilibrium was reached.The pH of solutions at elevated temperatures was measured using a micro-combination pH electrode InLab Micro Pro-ISM (Mettler Toledo) with an integrated temperature sensor.
The standard solutions used for electrode calibration were prepared according to UPAC and NIST recommendations.39,40 The pure materials with indicated weights were dissolved in water with a specific conductivity 0.05 μS cm−1 at 25 °C.
| Recommended pH (at 298 K) | 7.41 | 10.12 | 12.45 |
|---|---|---|---|
| Composition | 0.025 M KH2PO4 0.025 M Na2HPO4 | 0.025 M NaHCO3 0.025 M Na2CO3 | Ca(OH)2 (saturated at 298 K) |
Electronic absorption spectra were recorded with a Cary 5000 UV/Vis/NIR spectrophotometer. The spectra of crystals were measured at different temperatures (298 K and 4.2 K) in a continuous flow helium cryostat (Optistat, Oxford). The spectra of solutions were measured in a home-made thermostated appliance. The experimental oscillator strengths (Pexp) were determined by using eqn (12):
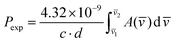 | (12) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) is the absorbance as a function of the wavenumber in cm−1. The experimental P values were used for the calculation of phenomenological Ωλ intensity parameters according to the Judd–Ofelt26,27 relationship:
) is the absorbance as a function of the wavenumber in cm−1. The experimental P values were used for the calculation of phenomenological Ωλ intensity parameters according to the Judd–Ofelt26,27 relationship: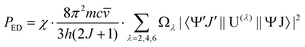 | (13) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is the wavenumber of the band maximum in cm−1, h is the Planck's constant, J is the ground state quantum number, and |〈ψ′J′||U(λ)||ψJ〉| are the reduced matrix elements of the respective unit tensor operator U(λ). The 〈ψ′J′||U(λ)||ψJ〉2 = U(λ) values were taken from the paper of Carnall et al.41
is the wavenumber of the band maximum in cm−1, h is the Planck's constant, J is the ground state quantum number, and |〈ψ′J′||U(λ)||ψJ〉| are the reduced matrix elements of the respective unit tensor operator U(λ). The 〈ψ′J′||U(λ)||ψJ〉2 = U(λ) values were taken from the paper of Carnall et al.41
The accuracy of the intensity parameter fitting was determined by the root mean square deviation (rms) using the following equation:
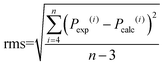 | (14) |
Factor analysis was performed according to the procedure described in ref. 29.
Crystal structure determination
Suitable crystals were cut from larger ones, mounted on a Kuma KM4 diffractometer equipped with a CCD counter and measured at 100 K. The structures were solved routinely by using Patterson synthesis. The C- and N-bonded hydrogen atoms were placed in positions calculated from the geometry, and those bonded to O atoms were found from the difference Fourier maps, but not all were found. The final refinement was anisotropic for all non-H atoms. The computations were performed with the SHELXS9742 and SHELXL43 programs, and the molecular graphic was prepared with DIAMOND.44C 14 H 32 ErN 11 O 12 (I), M = 713.76, monoclinic, space group P21/n, Z = 4, a = 14.749(3), b = 10.683(2), c = 15.594(3) Å, β = 92.30(2)°, V = 2455.2(1) Å3, μ = 3.50 mm−1, Dc = 1.931 g cm−3, F(000) = 1428, crystal size = 0.31 × 0.20 × 0.07 mm, θ = 3–28°, index ranges: −19 ≤ h ≤ 13, −13 ≤ k ≤ 14, −20 ≤ l ≤ 20. Final R indices Rint = 0.038, R[F2 > 2σ(F2)] = 0.039, wR(F2) = 0.105, S = 1.04. Largest diff. peak and hole: 2.15 and −1.21 e Å−3.
C 16 H 46 N 14 O 19 Th (II), M = 970.71, monoclinic, space group P21/c, Z = 4, a = 18.825(4), b = 8.827(1), c = 21.845(4) Å, β = 104.50(2)°, V = 3401.3(1) Å3, μ = 4.48 mm−1, Dc = 1.869 g cm−3, F(000) = 1928, crystal size = 0.41 × 0.35 × 0.03 mm, θ = 3–28°, index ranges: −18 ≤ h ≤ 23, −11 ≤ k ≤ 11, −26 ≤ l ≤ 28. Final R indices Rint = 0.043, R[F2 > 2σ(F2)] = 0.041, wR(F2) = 0.101, S = 0.99. Largest diff. peak and hole: 3.26 and −1.90 e Å−3.
CCDC 1870488 and 1870487 for I and II contain the supplementary crystallographic data for this paper.
Conflicts of interest
There are no conflicts to declare.Appendix
In order to examine the influence of the temperature on the formation of the [Er(EDTA)(CO3)]3– complex the 13C NMR spectra were measured at elevated temperatures. The solutions under study contained isotopically enriched 13C carbonate anions. The 13C labelling allowed shorter acquisition times which is remarkable in comparison with samples containing natural carbonates. Because the EDTA was not 13C enriched the 13C NMR signals attributed to this ligand were not observed in the experiment. Consequently only two signals of carbonate species attributed to the bound (∼50 ppm) and unbound (∼160 ppm) CO32– anions were observed in the spectrum of Er–EDTA–carbonate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 systems at different temperatures (Fig. 9).
1 systems at different temperatures (Fig. 9).
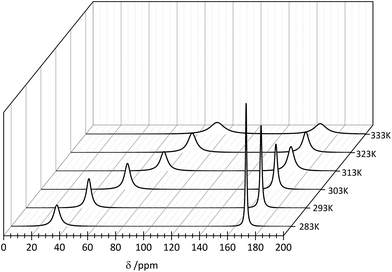 | ||
| Fig. 9 13C NMR spectra of the Er–EDTA–carbonate system at different temperatures. [ErEDTA] = 49.1 mM, [CO32–] = 67.6 mM, pD = 12.4. | ||
The observed temperature line broadening is caused by the increase of dynamic effects of carbonate exchange. A similar effect was observed for the other AnO22+–carbonate systems (where An = U, Pu, and Np).45 With the increase of the temperature, the signal at ∼50 ppm is gradually shifted to lower fields and its total intensity increases in comparison with the signal at 168 ppm. This indicates that the formation of the ternary [Er(EDTA)(CO3)]3– complex is more favorable at higher temperatures. Unfortunately due to experimental difficulties it was not possible to measure the pD of solutions under study at different temperatures. Thus, only the molar fractions of bound and unbound carbonate species could be determined from the intensity ratios of the 13C NMR peaks.
Acknowledgements
This work has been supported by the Program Operacyjny Kapitał Ludzki, Uniwersytet Wrocławski, POKL.04.01.01-00-054/10-00.References
- A. A. Okemgbo, H. H. Hill, S. G. Metcalf and M. Bachelor, Anal. Chim. Acta, 1999, 396, 105–116 CrossRef CAS.
- (a) S. G. Metcalf, Determination of EDTA and HEDTA in Hanford Defense Waste by High Performance Liquid Chromatography. Report no. RHO-SA-218, Rockwell Hanford Operations, 1981, pp. 1–32; (b) P. Thakur, J. L. Conca and G. R. Choppin, J. Solution Chem., 2012, 41, 599–615 CrossRef CAS.
- J. R. Freeman-Pollard, J. A. Caggiano and S. J. Trent, Engineering evaluation of the GAO-RCED-89-157, Tank 241-T-106 vadose zone investigations, 1994.
- D. Rai, D. A. Moore, K. M. Rosso, A. R. Felmy and H. Bolton Jr., J. Solution Chem., 2008, 37, 957–986 CrossRef CAS.
- R. Janicki and A. Mondry, Phys. Chem. Chem. Phys., 2014, 16, 26823–26831 RSC.
- M. Fairley, D. K. Unruh, A. Donovan, S. Abeysinghe and T. Z. Forbes, Dalton Trans., 2013, 42, 13706–13714 RSC.
- K.-N. Truong, P. Müller, R. Dronskowski and U. Englert, Cryst. Growth Des., 2017, 17, 80–88 CrossRef CAS.
- S. Gao, M.-L. Chen and Z.-H. Zhou, Dalton Trans., 2014, 43, 639–645 RSC.
- C. H. Delegard and S. A. Jones, Chemical Disposition of Plutonium in Hanford Site Tank Wastes, PNNL-23468 Rev. 1, WTP-RPT-234 Rev. 1, 2015, 3.10–3.12.
- D. L. Clark, D. E. Hobart and M. P. Neda, Chem. Rev., 1995, 95, 25–48 CrossRef CAS.
- D. A. Palmer and R. Van Eldik, Chem. Rev., 1983, 83, 651–731 CrossRef CAS.
- (a) R. Janicki, P. Starynowicz and A. Mondry, Eur. J. Inorg. Chem., 2011, 3601–3616 CrossRef CAS; (b) R. Janicki and P. Lindqvist-Reis, Dalton Trans., 2018, 47, 2393–2405 RSC.
- J. Dumonceau, S. Bigot, M. Treuil, J. Faucherre and F. Fromage, Rev. Chim. Miner., 1980, 17, 58–64 Search PubMed; S. Bigot, M. Treuil, J. Dumonceau and F. Fromage, J. Hydrol., 1984, 70, 133–148 CrossRef CAS.
- R. M. Supkowski and W. DeW Horrocks, Jr., Inorg. Chem., 1999, 38, 5616–5619 CrossRef CAS PubMed.
- L. Burai, V. Hietapelto, R. Király, E. Tóth and E. Brücher, Magn. Reson. Med., 1997, 38, 146–150 CrossRef CAS PubMed.
- T. L. Griffiths, L. R. Martin, P. R. Zalupski, J. Rawcliffe, M. J. Sarsfield, N. D. M. Evans and C. A. Sharrad, Inorg. Chem., 2013, 52, 3728–3737 CrossRef CAS PubMed.
- H. Boukhalfa, S. D. Reilly, W. H. Smith and M. P. Neu, Inorg. Chem., 2004, 43, 5816–5823 CrossRef CAS PubMed.
- R. M. Smith, A. E. Martell and R. J. Motekaitis, NIST Critically Selected Stability Constants of Metal Complexes Database, 2004 Search PubMed.
- A. P. Toste, J. Radioanal. Nucl. Chem., 1998, 235, 213–219 CrossRef CAS.
- (a) M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575 CrossRef CAS PubMed; (b) D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763 CrossRef CAS PubMed; (c) J. Cirera, E. Ruiz and S. Alvarez, Chem. – Eur. J., 2006, 12, 3162 CrossRef CAS PubMed.
- W. W. Lukens, M. Speldrich, P. Yang, T. J. Duignan, J. Autschbach and P. Kögerler, Dalton Trans., 2016, 45, 11508–11521 RSC.
- P. George and D. S. McClure, Prog. Inorg. Chem., 1959, 28, 381–463 Search PubMed.
- (a) C. K. Jorgensen, Modern Aspects of Ligand Field Theory, 1971 Search PubMed; (b) A. B. P. Lever, Inorganic Electronic spectroscopy, Elsevier, Amsterdam, 1984 Search PubMed; (c) M. Karbowiak, N. Edelstein, Z. Gajek and J. Drożdżyński, Spectrochim. Acta, Part A, 1998, 54, 2035–2044 CrossRef.
- (a) Y. Shimura and R. Tsuchida, Bull. Chem. soc. Jpn., 1953, 29, 311–316 CrossRef; (b) C. K. Jorgensen, Modern Aspects of Ligand Field Theory, 1971, pp. 343–353 Search PubMed.
- (a) A. Mondry and P. Starynowicz, Inorg. Chem., 1997, 36, 1176–1180 CrossRef CAS PubMed; (b) A. Mondry and P. Starynowicz, Dalton Trans., 1998, 859–863 RSC; (c) A. Mondry and P. Starynowicz, New J. Chem., 2000, 24, 603–607 RSC; (d) A. Mondry and P. Starynowicz, Eur. J. Inorg. Chem., 2006, 1859–1867 CrossRef CAS; (e) A. Mondry and R. Janicki, Dalton Trans., 2006, 4702–4710 RSC; (f) R. Janicki and A. Mondry, Eur. J. Inorg. Chem., 2013, 3429–3438 CrossRef CAS.
- B. R. Judd, Phys. Rev., 1962, 127, 750–761 CrossRef CAS.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511–519 CrossRef CAS.
- (a) J. W. Rohleder, Ann. Soc. Chim. Pol., 1972, 46, 2089–2097 CAS; (b) B. W. N. Lo, J. Phys. Chem. Solids, 1973, 34, 513–520 CrossRef CAS.
- A. Rossberg, T. Reich and G. Bernhard, Anal. Bioanal. Chem., 2003, 376, 631 CrossRef CAS PubMed.
- (a) D. Eckardt and L. Holleck, Z. Electrochem., 1955, 59, 202–206 CAS; (b) A. Merbach and F. Gnaegi, Chimia, 1969, 23, 271–273 CAS; (c) R. V. Southwood-Jones and A. Merbach, Inorg. Chim. Acta, 1978, 30, 77–82 CrossRef CAS; (d) K. Bukietyńska and A. Mondry, Inorg. Chim. Acta, 1987, 130, 145–150 CrossRef.
- G. Geier and U. Karlen, Helv. Chim. Acta, 1971, 54, 135–153 CrossRef CAS.
- T. F. Gritmon, M. P. Goedken and G. R. Choppin, J. Inorg. Nucl. Chem., 1977, 39, 2021–2023 CrossRef CAS.
- P. L. Brown and Ch. Ekberg, Hydrolysis of Metal Ions, Wiley-VCH, 2016, pp. 295–300 Search PubMed.
- M. L. Neidiga, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef.
- W. Stumm and J. J. Morgan, Aquatic chemistry: chemical equilibria and rates in natural waters, Wiley, 1996, pp. 148–204 Search PubMed.
- F. Millero, F. Huang, T. Graham and D. Pierrot, Geochim. Cosmochim. Acta, 2007, 71, 46–55 CrossRef CAS.
- K. J. Cantrell and R. H. Byrne, J. Solution Chem., 1987, 16, 555–566 CrossRef CAS.
- (a) G. Geier and U. Karlen, Helv. Chim. Acta, 1979, 54, 135–153 CrossRef; (b) N. Graeppi, D. H. Powell, G. Laurenczy, L. Zekany and A. E. Merbach, Inorg. Chim. Acta, 1995, 235, 311–326 CrossRef CAS; (c) R. Janicki and A. Mondry, Phys. Chem. Chem. Phys., 2015, 17, 29558–29565 RSC; (d) R. Janicki, A. Mondry and P. Starynowicz, Coord. Chem. Rev., 2017, 340, 98–133 CrossRef CAS.
- R. P. Buck, S. Rondinini, A. K. Covington, F. G. K. Baucke, C. M. A. Brett, M. F. Camões, M. J. T. Milton, T. Mussini, R. Naumann, K. W. Pratt, P. Spitzer and G. S. Wilson, Pure Appl. Chem., 2002, 74, 2169–2200 CAS.
- B. Modrzejewski, Pomiary pH, Wydawnictwo Naukowo Techniczne, Warszawa, 1971 Search PubMed.
- W. T. Carnall, P. R. Fields and B. G. Wybourne, J. Chem. Phys., 1965, 42, 3797–3806 CrossRef CAS.
- G. M. Sheldrick, SHELXS-97, Program for structure solution, University of Göttingen, 1997 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, A71, 3–8 CrossRef PubMed.
- DIAMOND-Visual Crystal Structure Information System, CRYSTALIMPACT, Postfach 1251, 53002 Bonn, Germany Search PubMed.
- (a) E. Brücher, J. Glaser and I. Toth, Inorg. Chem., 1991, 30, 2239–2241 CrossRef; (b) D. L. Clark, S. A. Ekberg, D. E. Morris, P. D. Palmer and C. D. Tait, Actinide(IV) and Actinide(VI) Carbonate Speciation Studies by PAS and NMR Spectroscopies, Los Alamos National Laboratory, report No LA-12820-MS, 1994; (c) C. D. Tait, P. D. Palmer, S. A. Ekberg and D. L. Clark, Report on Neptunium Speciation by NMR and Optical Spectroscopies, Los Alamos National Laboratory, report No LA-13012-MS, 1995.
Footnote |
| † Electronic supplementary information (ESI) available: Selected crystal data and structure refinement for I and II as well as spectroscopic and thermodynamic data. CCDC 1870487 and 1870488. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8qi01062e |
| This journal is © the Partner Organisations 2019 |