Soft nanohand grabs a growing nanoparticle

Abstract

Precise macromolecular recognition and self-sorting are essential in biological systems to maintain life. Herein, we report the self-assembly between one single dendritic macromolecule with discrete molecular weight and one single gold nanoparticle (Au NP) during the in situ growth of the Au NP. This process resembles an artificial, organic, and soft nanohand picking up a growing inorganic hard nanoparticle of a particular size (∼1.4 nm). Discrete 1 : 1 organic–inorganic hybrid nanostructures based on four finger-like dendritic macromolecules with different anchors have been investigated with their ability to wrap up a Au NP of different sizes. Both experimental and theoretical studies demonstrate that the dendrons with different anchoring groups can control the nucleation and growth, and stabilized the sizes of Au NPs. These results highlight the importance of the dendron's anchoring groups in the gold nucleation step before the small gold cluster grows into a Au NP and is then firmly wrapped within the whole dendron. These results provide the fundamental understanding of soft nanomachinery on sorting out nanosized products of particular size and shape.

---

Introduction

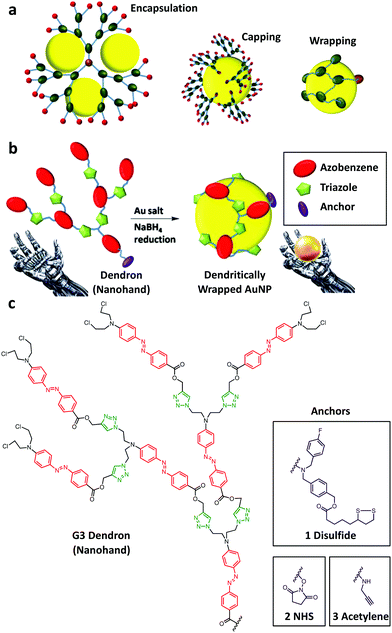
The manipulation, for example, picking-up, transporting, releasing and self-sorting, of bioactive molecular fragments by enzymes, has been utilized to maintain life. In a modern-day factory assembly line, programmable robotic arms are used to manipulate components. This idea has been recently extended to use an artificial small-molecule robotic arm to selectively transport a small molecular cargo on a molecular platform.¹ The idea of using an artificial macromolecular nanoarm to manipulate a nanoobject has not been explored before.

Dendrimers and dendrons are highly branched, monodisperse synthetic macromolecules. Owing to their tunable organic functionalities with “sticky” hetero-atoms (O, N, S) at the branching points, these macromolecules can encapsulate various inorganic nanoparticles (NPs) or drug molecules embedded in their internal void space.^2–4 Three types of dendrimer/dendron–inorganic NP hybrid structures can be distinguished, depending on the ratio of the number of dendrimers/dendrons to the number of NPs (Fig. 1a). Crooks et al. pioneered the synthesis of a series of dendrimer-encapsulated NPs through complexation between poly(amidoamine) (PAMAM) dendrimers and various metal NPs, such as Cu, Pd, Pt, Ni, Au, and Ru, etc.^5–9 In this approach, multiple NPs were grown in a single dendrimer macromolecule, possessing an “encapsulation” structure. By contrast, the second type possesses a single NP core “capped” by multiple dendrons at the surface of the NP.¹⁰ The third approach requires a sophisticated tuning of the ratio of dendrimers/dendrons to NPs to produce a 1 : 1 “wrapping” between one dendritic macromolecule and a single NP core. This dendritically wrapped structure allows a precise control of the NP size and yields a discrete architecture of the organic–inorganic hybrid material with better stability and solubility, suitable for catalysis, sensing, electronic and biological applications.¹¹ Systematic investigation of the formation of 1 : 1 dendritically wrapped NPs has not been reported before. Herein, we employ a series of nitrogen-rich (azobenzene, triazole, amine) dendrons (Fig. 1b) with three different anchoring groups, to systematically study the self-assembly between one single dendritic macromolecule with discrete molecular weight and one single gold nanoparticle (Au NP) during the in situ growth of the Au NP. This process resembles a nanohand picking up a growing nanoparticle of a particular size.

Fig. 1 (a) Graphical representations of dendrimer/dendron–nanoparticle (NP) hybrids, with NPs shown as yellow balls. Encapsulation: single dendrimer encapsulating multiple NPs; capping: single NP capped by multiple dendrons; wrapping: single NP wrapped by a single dendron; (b) in situ formation and growth of Au NP subsequently wrapped by a dendron, showing similarity with a nanohand picking up a gold ball with a suitable size; and (c) chemical formula of the nitrogen-rich (azobenzene, triazole, amine) third-generation (G3) dendron with three different anchor groups shown in insets: disulfide (called G3-1 dendron in this work), N-hydroxysuccinimide (NHS, G3-2) and acetylene (G3-3).

We shall first present our experimental observations, followed by theoretical simulation to quantify the interactions between dendrons and Au NPs. In particular, we shall address the 1 : 1 and 2 : 1 wrapping ratios and the effect of the anchor groups on Au NP nucleation and growth. Then our major experimental and theoretical methods will be described, while we present other methods and results in the ESI.†

Experimental results

To rationally study the structure–property relationship of dendrons for stabilizing NPs through wrapping to obtain the 1 : 1 and 2 : 1 dendritically wrapped NPs, we have used N-rich dendrons carrying amine branches with azobenzene and 1,2,3-triazole linkers^12,13 for in situ Au NP formation (Fig. 1c and ESI,† Fig. S1–S3). The 1,2,3-triazole ring is known as a good ligand for stabilizing inorganic NPs such as Pd and Au NPs.^14,15 Furthermore, the azobenzene group can bind with metal ions to exhibit energy storage properties.¹⁶ Thus, our proposed N-rich dendrons (one with N-hydroxysuccinimide, NHS) are expected to provide effective Au NP stability. We investigated dendron characteristics such as the dendron's generation number (which counts the degree of branching, being 3 in Fig. 1) and the anchor functional groups.

Dendritically wrapped Au NPs were prepared in situ by reducing a Au(III) salt in the presence of various dendrons and NaBH₄ in different ratios. To prepare a stable group of dendritically wrapped Au NPs, an optimal ratio of 1 : 3 (dendron : Au(III) was achieved in a toluene/dimethylformamide mixture. The as-prepared dendritically wrapped Au NPs were characterized by transmission electron microscopy (TEM) to determine their sizes and morphologies.

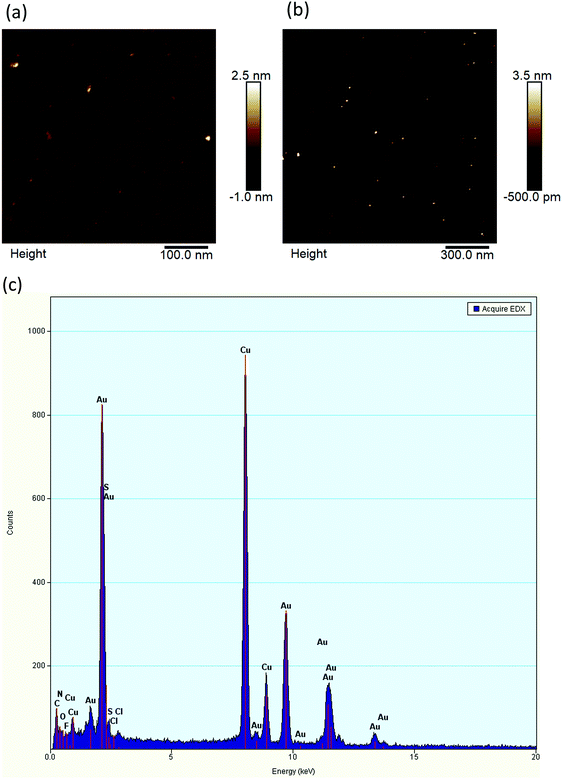
Based on the initial atomic force microscopy (AFM) analyses, the G3-1(disulfide)@AuNP (Fig. 2a), shows an average height of 1.96 ± 1.10 nm while the G2-3(acetylene)@AuNP (Fig. 2b) shows an average height of 2.61 ± 1.13 nm. These are among the smallest particle size and largest size of our dendritically wrapped AuNPs. The particle sizes of the specific G3 and G2-dendritically wrapped AuNPs were analyzed by transmission electron microscopy (TEM). Energy dispersive X-ray (EDX) analysis (Fig. 2c) of the G2-3(acetylene)@AuNP shows the presence of the elements Au, C, N, O, F, S and Cl, revealing the successful complexation between the dendron and the AuNP. The Cu signals originate from the Cu grid.

Fig. 2 (a) Atomic force microscopy (AFM) images of G3-1(disulfide)@AuNP with average height of 1.96 ± 1.10 nm; atomic force microscopy (AFM) images of G2-3(acetylene)@AuNP (b) 2.61 ± 1.13 nm; and (c) energy dispersive X-ray (EDX) spectroscopy spectrum of G2-3(acetylene)@AuNP revealing elements Au, C, N, O, F, S, Cl and Cu (grid).

Based on the TEM observations (ESI,† Fig. S4 and S5), the as-prepared G3-dendritically wrapped Au NPs are basically spherical. Furthermore, the resulting Au NP sizes wrapped with G3-1(disulfide), G3-2(NHS), and G3-3(acetylene) are 1.4 ± 0.2, 2.2 ± 0.2, and 2.3 ± 0.3, respectively (Table 1). These results reveal clearly that the anchor groups of dendrons can influence the resulting Au NP size of the dendritically wrapped Au NP and also that the G3 dendrons stop the growth of the Au NPs at the observed sizes. As seen in control experiments on the dendritic size effect, second-generation (G2) dendritically^12,13 wrapped Au NPs have an overall Au NP size >2.6 nm (ESI,† Fig. S6). In other control experiments, colloidal Au NPs (4–10 nm) were obtained without the use of any dendron (ESI,† Fig. S7). In particular, all G3-dendritically wrapped Au NPs were characterized by UV/visible absorption spectroscopy, revealing local maxima at 420–430 nm of dendron^12,13 and 545–555 nm of Au NP^17–19 (ESI,† Fig. S8). From the UV spectra, the local maximum at 420–430 nm (dendron) of the G3-1(disulfide)@AuNP has a larger red-shift than both the G3-2(NHS)@AuNP and G3-3(acetylene)@AuNP. The red-shift trend at 420–430 nm (dendron) is: G3-1(disulfide)@AuNP > G3-2(NHS)@AuNP > G3-3(acetylene)@AuNP. On the other hand, the local maximum at 545–555 nm (Au NP) of the G3(disulfide)@AuNP with a Au NP size of 1.4 nm showed a larger blue-shift than the local maxima of both G3-2(NHS)@AuNP and G3-3(acetylene)@AuNP. The blue-shift trend at 545–555 nm (AuNP) is: G3-1(disulfide)@AuNP > G3-2(NHS)@AuNP > G3-3(acetylene)@AuNP. These results are coherent with their corresponding Au sizes and with the fact that the G3-1(disulfide) dendron is presumably bound more tightly to the Au NP compared to the two other dendrons.

Table 1 Average sizes of the Au NP cores of the dendritically wrapped Au NPs determined by transmission electron microscopy (TEM) analysis

Hybrid structure	Au NP diameter (nm)
G3-1(disulfide)@AuNP	1.4 ± 0.2
G3-2(NHS)@AuNP	2.2 ± 0.2
G3-3(acetylene)@AuNP	2.3 ± 0.3

---

It is crucial to confirm the ratio between the dendron and Au NP in the as-prepared G3-dendritically wrapped Au NPs. Experimentally, thermogravimetric analysis (TGA) provides the information of weight percentages of both the organic (dendron) and the inorganic (Au) components (Table 2). Based on the thermo-decomposition studies at 550 °C (ESI,† Fig. S9), the weight percentage of the sample residue is the weight of the Au whereas the organic dendrons are decomposed and calcinated. The weight percentages of residue Au for G3-1(disulfide)@AuNP, G3-2(NHS)@AuNP, and G3-3(acetylene)@AuNP are 85.1 ± 0.1, 86.2 ± 0.1, and 86.9 ± 0.1, respectively. Given the experimentally determined Au NP size, the numbers of Au atoms for 1.4, 2.2, 2.3 nm Au NPs are approximately 85, 329, and 376, respectively (ESI,† Table S1). With the known molecular weights of all three G3 dendrons and the corresponding Au NP atom numbers (ESI,† Table S2), the weight percentages needed to form 1 : 1 dendron : Au NP hybrid structures can be calculated (ESI,† Table S3). The weight percentages of Au of the G3-1(disulfide)@AuNP hybrid structure show coherence between the experimental value (85.1%) and the calculated value (83.8%). That is, the weight percentages of organic (dendron, 14.9%) : inorganic (Au, 85.1%) in the G3-1(disulfide)@AuNP hybrid structure reveal a 1 : 1 dendron : Au NP ratio, a genuine “wrapping” structure. However, the experimental weight percentages of Au for G3-2(NHS)@AuNP and G3-3(acetylene)@AuNP hybrid structures deviate from the calculated values (ESI,† Table S3). Therefore, these two hybrid structures are not in a 1 : 1 ratio between their dendrons and Au NP, but preferably form “capping” hybrid structures with two dendrons capping a single Au NP: we thus observe 2 : 1 wrapping ratio for G3-2 and G3-3 dendrons, vs. 1 : 1 for G3-1.

Table 2 Thermo gravimetric analysis (TGA) of the dendritically wrapped Au NPs

Hybrid structure	Weight% organic (dendron)	Weight% inorganic (Au)
G3-1(disulfide)@AuNP	14.9	85.1
G3-2(NHS)@AuNP	13.8	86.2
G3-3(acetylene)@AuNP	13.5	86.9

---

The G3-1(disulfide)@AuNP, which has the smallest Au NP size (1.4 nm), was analyzed by zeta potential (−81.33 ± 2.18 mV) and mobility (6.35 × 10⁻⁴ ± 1.83 × 10⁻⁵ cm² V⁻¹ s⁻¹). The group of G3-3(acetylene) dendron and G3-3(acetylene)@AuNP was characterized by infrared (IR) spectroscopy. The IR spectroscopic analysis of the G3-3(acetylene)@AuNP showed (ESI,† Fig. S10) observable absorption signals at 2900 and 1640 cm⁻¹, which are originated from the bare AuNP and G3-3(acetylene) dendron, respectively. These results provide further experimental evidence that the dendron was complexed with AuNP, forming the dendritically wrapped Au NP. However, the IR absorption signal of acetylene stretching at 2140 cm⁻¹ of the G3-3(acetylene)@AuNP is too low to be observed.

From the TGA result, the G3-3(acetylene)@AuNP may have two dendrons capping a single Au NP (2.3 nm) core. Presumably the anchor acetylene group would not bind to the Au NP, such that the anchor group would be away from the Au NP. The particular structure of two dendrons capping a single Au NP core would have two unbound acetylene anchor groups sticking out from the Au NP core, yielding a discretely divalent NP.^20–26 It is of interest to perform an acetylenic HOMO-coupling reaction (ESI,† Fig. S11) to join two of these bis-G3-3(acetylene)@AuNPs together by forming a diacetylene bond. Such a HOMO-coupling reaction was performed using a Pd(PPh₃)₂Cl₂ catalyst and triethylamine. TEM analysis of the resulting structures reveals oligomeric (three or four) linear Au NP arrays (ESI,† Fig. S11). The inter-particle spacing is approximately 1.5 nm between any two Au NPs. Therefore, it is reasonable to believe that there are two G3-3(acetylene) dendrons capping a single Au NP. If there were multiple (acetylene-anchor) dendrons capping a single Au NP, such homo-coupling reaction would produce a Au NP cross-linking network instead of a linear array.

Our experimental results reveal that the nature of the anchor group on the G3 dendrons can affect the diameter of the Au NP core in dendritically wrapped Au NPs. The anchor groups—disulfide, NHS, and acetylene—could bind to Au atoms by forming Au–S, Au–N/O, and Au–C≡C dynamic bonds, respectively. Our prediction from experiment is therefore that a stronger binding (Au–S) between the anchor of the G3-1(disulfide) dendron and Au atom is the key parameter to obtain a smaller sized dendritically wrapped Au NPs (1.4 nm).

Theoretical simulations and discussion

To further investigate the foregoing observations and interpretations based on our experiments, we employ density-functional theory.^27–31 We calculate and compare the total energies for a variety of relevant structures to study the synthesis, wrapping, and binding of dendron molecules around Au NPs. These total energies will also allow us to derive optimized binding energies and compare the resulting structures.

The binding between two extended atomic assemblies (e.g., NP and molecule) primarily involves close-range “bonding” between atoms, reducing the total energy. However, larger-scale reshaping of the two assemblies is often required to geometrically match them together and thus allow this bonding to occur: this “deformation” increases the total energy.³² To gauge the relative cost of this deformation, we calculate, in addition to the binding energy E_b, also the individual deformation energies of the Au NP, E_deform(Au_n), and of the dendron, E_deform(G3). Then we can define a “frozen binding energy” that excludes deformation, = E_b − E_deform(Au_n) − E_deform(G3): it represents the close-range “bonding” between atoms. All these energies are derived from certain total energies for suitably chosen optimized vs. constrained geometric configurations, as defined in more detail in the ESI.†

For a system of hundreds of atoms, we must remain aware of the very large number of possible geometric structures. Even though the experimental TEM images show approximately spherical NP shapes and suggest internal crystallinity, the Au NPs synthesized in solution and binding to dendron molecules need not have complete atomic shells around a central Au core (or a corresponding high symmetry void).^33–35 Further, Au NPs need not be exactly crystalline in their outer atomic layers. For comparison, real Au NPs with up to about 20 atoms in vacuum³⁶ exhibit an internal structure quite different from that of an ideal Au crystal. This is equivalent to Au crystal surfaces in vacuum being “reconstructed”, i.e. their structure deviates strongly from the bulk Au crystal structure in their outer atomic layer^37–39). In addition, the exact number of Au atoms in the NPs is not known. However, the experiment observed two distinct NP diameters at 1.4 nm and 2.2–2.3 nm for different anchor groups, which reflects a diameter ratio of close to 1.6, cf.Table 1. This can be simulated by NPs that have full outer atomic shells and a highly symmetric shape:³⁵ we assume clusters of fcc lattice structure confined by six square (100) and eight hexagonal (111) crystal facets denoted as Au(k,m) NPs, following the nomenclature Here we select a Au(3,2) NP which, applying a bulk Au lattice constant of 0.407 nm, has a diameter of 1.47 nm and contains 116 atoms with a complete outer shell of 78 atoms (for comparison with the experimental NP diameter, we quote only the diameter of the smallest sphere enclosing all Au nuclei). We also compare experiment to a larger Au(4,3) NP of a diameter 2.37 nm, i.e. 60% larger than for Au(3,2) NP, containing 405 atoms with a complete outer shell of 204 atoms. The dendrons appear to remain intact in the experiment, so that we only need to optimize their wrapping geometries, as described in the Theoretical and computational methods section. Our notation to label the different clusters examined in this work is given in Table 3.

Table 3 Cluster notation. The notation Au(k,m) and properties of polyhedral nanoparticles are further described in ESI, Section S3

Cluster name	Description
G3	Third generation dendron
G3-1(disulfide) = G3-1	Third generation dendron, with anchor of type 1, 2 or 3
G3-2(NHS) = G3-2
G3-3(acetylene) = G3-3
G3-A	Truncated H-terminated dendron anchor 1, 2, or 3
G3-1A, G3-2A, G3-3A
Au, Au NP	Au nanoparticle, with n atoms in outer shell if hollow
Aun, Aun NP
Au(k,m)	Polyhedral Au NP with 6 k × k square facets and 8 k × m hexagonal facets
Au78	Outer shell of a Au(3,2) NP
G3@Au, G3-1@Au, etc.	Dendron attached to a Au nanoparticle
G3@Aun, G3-1@Aun, etc.
G3-A@Au, G3-1A@Au, etc.	Dendron anchor attached to a Au nanoparticle
G3-A@Aun, G3-1A@Aun, etc.

---

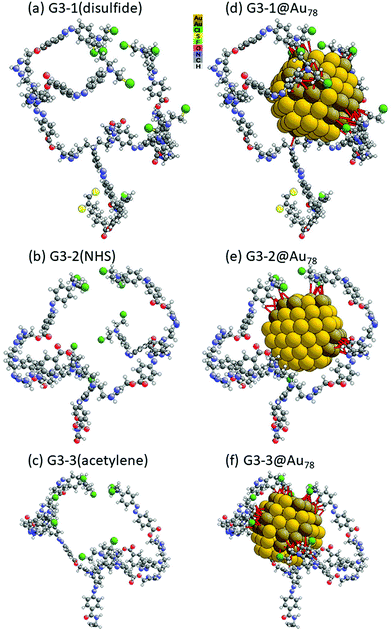
We first consider the wrapping structures and energies of complete dendrons around a Au NP of diameter 1.4 nm, modeled by a Au₇₈ NP (which represents the outer shell of a Au(3,2) NP with an unrelaxed diameter of 1.467 nm). Fig. 3 shows the resulting structure for the G3-1 dendron with disulfide anchor wrapped around a Au₇₈ NP (to better visualize the wrapping geometry, movies rotating the three whole clusters are provided and described in ESI,† Movies, cf. ESI,† Fig. S21–S23). The Au₇₈ NP in Fig. 3 shows slight rounding of its corners and edges, so that the 3 × 3 square facets and 3 × 2 hexagonal facets are no longer planar and the overall shape of the NP is more spherical; the rounding of “protruding” atoms is realistic, as is known in particular from corrugated stepped surfaces, including the ridges of Au(110).⁴⁰ As a result of this rounding (and partly also because of the empty core), the diameter of this bare Au₇₈ NP has shrunk to about 1.29 nm, i.e. by about 0.1 nm or 12% from its unrelaxed bulk-like dimensions (when wrapped with dendrons, it re-expands to about 1.43 nm, a 3% contraction from the unrelaxed value 1.47 nm). Such values are consistent with experimentally known contractions of 4 to 5% in Au(111) and Au(100) surfaces and Au NPs,^37,39 as well as the well-known re-expansion due to binding to atoms and molecules added to the surface (adsorbates).⁴¹

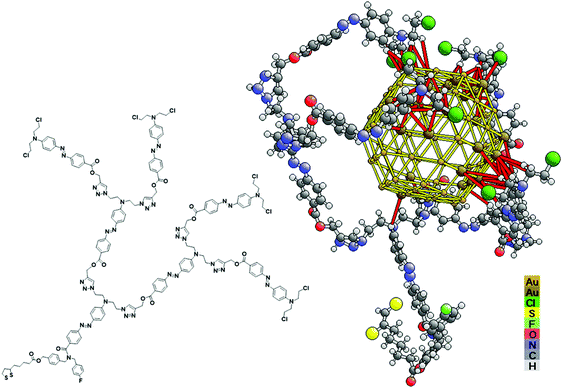Fig. 3 Left: Molecular structure of dendron G3-1 (drawn planar, with disulfide anchor pointing to bottom left). Right: Perspective view of optimized cluster G3-1@Au₇₈ (with disulfide anchor pointing down, and an empty gold shell), also shown in Fig. 4d. The ends of the four dendrites are visible as four pairs of (green) Cl atoms. The red interatomic links show Au–dendron internuclear distances up to 0.4 nm; those Au atoms that are linked in this way to the dendron are shown larger and darker (brown).

We found that the three anchors point away from the Au NP, toward the bottom in Fig. 3 and 4, while in each case the dendrites bind to the Au NP (the far ends of the four dendrite arms are clearly seen as four pairs of Cl atoms). The three wrapping configurations seen in Fig. 4 for the three different anchors are shown with different viewpoints to illustrate different sides and different aspects; in fact, the three configurations are very similar, as shown in ESI,† Fig. S21–S23 (and the corresponding movies) which use the same viewpoints for all anchors.

Fig. 4 Perspective views of ball-and-stick models of three dendron molecules G3-1(disulfide), G3-2(NHS) and G3-3(acetylene) (a–c) shown with their structures taken from the corresponding optimized Au–dendron clusters G3-1@Au₇₈, G3-2@Au₇₈, and G3-3@Au₇₈ (d–f), see text. Au atoms are shown with bulk-like touching-sphere radii. The red interatomic Au–dendron links refer to atom distances up to 0.4 nm, with dendron-linked gold atoms emphasized by darker color (brown).

It is clear from Fig. 3 and 4 that the Au₇₈ NP does not completely fill the space provided within the dendron “nanohand”, since parts of the dendrites arch significantly away from the Au NP. It is in fact likely that the larger set of observed Au NPs (wrapped by G3-2 and G3-3 dendrons) could easily be accommodated in that space, probably with significant reconfigurations of the dendrons, allowing larger parts of the dendrons to lie against and “bond” to the Au NP. This is especially facilitated by the fact that the ends of the dendrites need not touch each other on the far side of the NP. Indeed, the “nanohand” need not be completely closed. This allows Au NPs of larger size to be accommodated within the dendron nanohand. While the G3-1(disulfide) dendron is found to wrap around a Au NP with diameter of 1.4 ± 0.2 nm, the G3-2(NHS) and G3-3(acetylene) dendrons are wrapped around Au NPs with diameters of 2.2 ± 0.2 nm (57% larger), resp. 2.3 ± 0.3 nm (64% larger). The latter diameters can be easily realized by Au(4,3) NPs with 405 atoms, which yield an approximately 65% larger unrelaxed diameter than does our Au(3,2) shown in Fig. 2. This strongly suggests that in the latter two cases, namely G3-2(NHS) and G3-3(acetylene), the larger (4,3) NPs are more realistic models for the NP wrapping.

Of interest in terms of the experimentally observed 1 : 1 and 2 : 1 dendron : NP wrapping ratios is the area of the Au NP covered by the dendrons in the calculated results. This area can be defined in at least two ways: the area that is sterically blocked from access to a second dendron; or the number of Au atoms to which the dendrons bond. We think that the first definition is more relevant to the situation at hand, especially as the second definition relies on specifying what constitute Au–dendron “bonds”, which do not have clear-cut criteria and, in the case of Au, are relatively weak, as we discuss further below. The steric blocking can be roughly evaluated by visual inspection. Fig. 4 suggests that a large part, about 60–70%, of the Au₇₈ NP surface is inaccessible to further attachment by other dendrons, making the wrapping of a complete second dendron to the same NP impossible, in agreement with the experimental observations for the G3-1 dendron. Larger NPs, like those observed with the G3-2 and G3-3 dendrons, have surface areas that are about 2.6 times larger (obtained by comparing the unrelaxed areas of Au NPs (4,3) and (3,2) given in ESI,† Table S4), and thus can well accommodate two dendrons each, again as observed experimentally.

In keeping with the relative weakness of bonding to Au, we find rather long interatomic distances between the dendron atoms and the Au nanocluster. Fig. 4 shows all Au–dendron internuclear “links” up to 0.4 nm for the three dendrons (most of these connections are far too long to be called “bonds”). Here the limit of 0.4 nm is arbitrary and only serves as a guide to illustrate proximity rather than bonding. Reference values are given in Table 4. We found no Au–S or Au–F pairs within 0.4 nm. It is notable that the terminal Cl atoms of the dendrites do not bond to or even approach the Au NP. The nearest atoms to the Au are multiple H and C. This will be seen to also be the case for dendron anchor groups binding to smaller Au₆ and Au₈ clusters, cf. below.

Table 4 Experimental and calculated interatomic distances (in nm). The “minimum calculated” values are the minimum interatomic distances found in G3@Au₇₈ clusters in this work

Atom pair	vdW	H-Bonding	Non-bonding	Covalent bonding	Minimum calculated
Au–H	0.395	0.260–0.287^42		0.154–0.165^43	0.22
Au–C			0.364–0.397^42	0.197–0.206^44	0.29
Au–Cl					0.34
Au–O					0.37
Au–N					0.39
Au–S				0.23–0.24^45	>0.4
Au–F					>0.4

---

The calculated binding energies for the three Au NP plus dendron clusters are given in Table 5. These results indicate rather large overall binding energies E_b for the three dendrons attached to Au₇₈, decreasing from −81 eV to −78 eV and −63 eV from dendrons G3-1 to G3-2 and G3-3, respectively. This represents about −2 eV on average for each interatomic “link” shown in Fig. 3 and 4, giving a very rough measure of local “bonding” strength. As these links do not involve covalent bonding (in view of the large interatomic distances), we ascribe the attraction mainly to electrostatic and van der Waals forces. Since the dendron anchor groups point away from the Au NPs and therefore likely contribute little to the binding to the Au NPs, the variation of binding energy between the dendrons may thus primarily be due to different local wrapping geometries (seen clearly in Fig. 4) that can greatly affect both the electrostatic and the van der Waals interactions. This interatomic “bonding” is weakened by deformation of the Au NP and dendron, as seen in the more negative values of E^frozen_b. This indicates that the cost of deformation is about +21 eV, +7 eV and +19 eV for dendrons G3-1, G3-2 and G3-3, respectively. This deformation energy is needed to bend and twist the dendrons and Au NPs so as to get close enough to “bond”. Table 5 also shows that this deformation energy is fairly constant for structural relaxations in the Au NP (cf. the values of 6.2 to 7.6 eV for E_deform(Au₇₈)), but that it varies considerably among the dendrons (cf. values of 15 eV, 1 eV and 11 eV for E_deform(G3)). Since all the dendrite branches are inherently the same in the three dendrons, we ascribe these variations to the different wrapping geometries adopted in our optimization scheme, i.e. they may correspond to different local energy minima rather than inherently different properties between the dendrons.

Table 5 Summary of binding and deformation energies for three different G3@Au₇₈ clusters and their gold and dendron components G3-1(disulfide), G3-2(NHS), and G3-3(acetylene), see text. For definitions of the energy contributions see ESI Section S2

Energy (eV)	G3-1@Au78	G3-2@Au78	G3-3@Au78
E b	−80.86	−77.76	−63.03
E ^frozenb	−102.35	−84.89	−82.06
E deform(Au78)	6.15	6.41	7.60
E deform(G3)	15.34	0.72	11.43

---

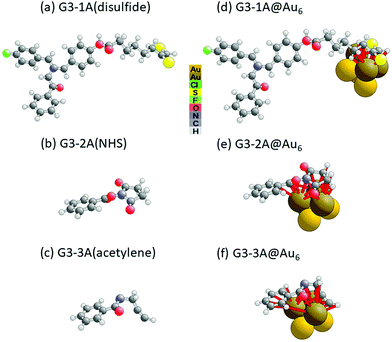
We next address the question of nucleation of the Au NPs. There is experimental evidence that small Au NP nuclei first form at anchor sites, before migrating to the dendrite sites which we simulated for G3@Au₇₈ clusters. To examine this possibility, we calculated binding energies between anchor sites and smaller Au₆ and Au₈ clusters. The Au clusters are structure optimized using an initial octahedral Au(1,2) NP which represents Au₆, while for Au₈ two Au atoms are added to Au₆ above midpoints of two of its opposite triangular facets. As described above, we truncated the dendrons by removing their dendrite branches and saturating open anchor bonds with H atoms. The resulting optimized structures are illustrated in Fig. 5 for the Au₆ clusters (the corresponding very similar structures with Au₈ clusters are shown in ESI,† Fig. S24).

Fig. 5 Perspective views of ball-and-stick models of three dendron anchor molecules G3-1A, G3-2A, and G3-3A (a–c), shown with their structures taken from the corresponding geometry-optimized Au–dendron clusters G3-1A@Au₆, G3-2A@Au₆, and G3-3A@Au₆ (d–f), see text. The red interatomic links refer to Au–anchor internuclear distances up to 0.4 nm, with anchor-linked gold atoms emphasized by darker color (brown).

Comparing Fig. 5 with ESI,† Fig. S24, we see that the Au–anchor binding is structurally similar for Au₆ and Au₈ clusters, but there are differences due to the different number of Au atoms directly exposed to the dendrons: 3 for Au₆vs. 4 for Au₈. This is borne out by the energetics, listed in ESI,† Table S7. This is also apparent from inspecting ESI,† Tables S5 and S6 which list minimum internuclear distances (d_min) below 0.4 nm of Au–G3A pairs and their frequency of occurrence in the clusters. The relevant pairs for Au₆ can be described as mainly Au–H (d_min = 0.22 nm), Au–C (d_min = 0.22 nm), Au–O (d_min = 0.24 nm), and Au–S (d_min = 0.23 nm) with only little participation of Au–N links at larger distance (d_min = 0.34 nm). These distance results differ only little for Au₈, namely by 0.01 to 0.05 nm.

Table S7 (ESI†) indicates that the S-containing anchor (G3-1A) shows the strongest binding to the small Au NPs, while the NHS- and acetylene-containing anchors (G3-2A and G3-3A) show weaker binding, with E_b for G3-3A(acetylene) being overall smallest for both Au₆ and Au₈.

Comparing Table 5 with Table S7 (ESI†), it emerges that, for each anchor, the large Au₇₈ NP binds more strongly to the full dendrons than do the small Au NPs to the anchor groups. This finding supports the hypothesis that the large Au NPs bind preferably within the dendrite nanohand. This can be expected from the larger number of Au–dendrite links in the larger clusters, see Fig. 4, 5 and Fig. S24 (ESI†). The binding between large Au NP and full dendrons is spread out among many more connected Au–dendron atoms, so that the average binding energy per individual Au–dendron connection is actually rather small. By contrast, because of their size, the small Au NPs cannot connect to many dendrite atoms, so that it is more favorable for the small Au NPs to bind to the anchor groups, where individual links are relatively strong.

Conclusion

We have synthesized and studied a series of hybrid dendrimer structures consisting of dendrons (with three different anchor groups) wrapped around gold nanoparticles of particular sizes, resembling a nanohand selecting/grabbing/picking up a gold ball. Gold NPs nucleate, grow and stabilize at two different sizes, depending on the nature of the dendron's anchor. For the smaller Au NP size with diameter 1.4 nm (TEM) and height 1.9 nm (AFM), experiment indicates a 1 : 1 ratio of dendron : NP, while a 2 : 1 ratio appears for the larger Au NP size with diameter 2.2 nm (TEM) and height 2.6 nm (AFM). The nucleation appears to take place at the anchor groups of the dendrons and the Au NP sizes would be affected by the binding strengths between the anchor groups and Au atom as well as the structural complimentary and surface coverage between the dendron and AuNP.⁴⁶

By atomic-scale simulation using density functional theory, we have examined how the dendrons can wrap themselves around a Au NP, both configurationally and energetically. The results confirm the dendron : NP wrapping ratio of 1 : 1 for the smaller NP size and the 2 : 1 ratio for the larger Au NPs. Modeling of smaller Au NPs attached to the dendron anchors clearly supports the experimental suggestion that nucleation of the Au NPs is initiated at the anchor sites, while the larger stabilized Au NPs bind to the dendron arms as a ball caught in the hand. Therefore, we can confirm the value of pursuing experimental and theoretical research on dendrons and Au NPs. In particular, our results provide guidance for choosing appropriate sizes of Au NPs and for designing useful dendron@NP clusters. Overall, this indicates that further insight into the dendron@NP induced by various anchor groups, a focus of ongoing work, must be continued to be fully understood. A critical challenge for the use of dendron@NP under real world is going on.

These results provide the fundamental understanding of nanomachinery for grabbing a growing nanoparticle of a particular size with a four-finger nanohand. The study of nanomachine transportation and a nanoassembly line using the nanohand with both catching and releasing of nanoparticle is currently on-going in our laboratory. With a porous Au NP, drugs or selected substrates can be trapped inside the Au NP, targeting for drug/substrate transportation and release by the nanohand. Similarly, this process can selectively remove unwanted counterparts from a mixture of nanoparticles with a broad size distribution.

Major experimental methods

General preparation of dendritically wrapped gold nanoparticles

1% Au(III) solution (29.4 mM) was prepared using the following procedure: chloroauric acid (HAuCl₄) (117.8 mg) and tetraoctylammonium bromide (663 mg) were dissolved in 10 mL deionized water and 11.8 mL toluene. The mixture was stirred vigorously for 10 min under N₂. The organic layer was collected for further use. A sodium borohydride solution (NaBH₄) (100 mM) was prepared by dissolving 18.9 mg NaBH₄ in 5 mL of deionized water. The Au(III) solution (1%, 0.33 mL) and the dendron solution (toluene/dimethylformamide 1 : 1 v/v) were separately stored in the dark for 24 h. The two solutions were mixed in the dark and toluene (5 mL) was then added to the mixture. After stirring for 30 min, NaBH₄ (4 equiv.) was added to reduce the Au ions and allow the mixture to stir in the dark over 2 h. The product dendritically wrapped Au NPs were precipitated from the reaction mixture by adding excess deionized water. The precipitate was collected and washed with ethyl acetate and acetone three times separately. The dendritically wrapped Au NPs were dried in vacuum. For a typical example, the G3-1(disulfide) dendron (161 mg) was dissolved in 5 mL toluene/dimethylformamide (1 : 1 v/v) to a final concentration of G3-1(disulfide) of 10 mM. A 1% Au(III) solution (0.30 mL), G3-1(disulfide) dendron solution (0.0588 mL) and toluene (4.64 mL) were stirred vigorously for 30 min. A NaBH₄ solution (0.353 mL) was added dropwise to the reaction mixture and the reaction was stirred for 2 h in the dark. The as-prepared G3-1(disulfide)@AuNPs were precipitated by adding deionized water and then washed with acetone and ethyl acetate. The G3-1(disulfide)@AuNPs were dried in vacuum overnight.

Major theoretical and computational methods

The initial molecular models of the different dendrons and the gold clusters are designed by a molecular builder together with optimizations based on force fields using the ATK software.⁴⁷ Further geometric analysis and visualization is performed with the Balsac software.⁴⁸ With the initial model structures as input, we apply the VASP (Vienna Ab initio Simulation Package) software,^30,31 together with the LDA (Local Density Approximation) functional²⁷ to optimize the different models, which yields corresponding equilibrium structures. VASP calculations, based on the GGA (Generalized Gradient Approximation) functional of Perdew–Burke–Ernzerhof (PBE)^28,29 are then employed to evaluate the final electronic structure and total energies of the different models: the separated gold NPs and dendrons, and the combined gold + dendron clusters. In additional calculations, simulating small nucleating Au₆ and Au₈ clusters, we performed both geometry optimizations and final electronic structure calculations using the GGA functional.

In all calculations, the projector augmented wave (PAW) method, as implemented in the VASP code, was applied with plane-wave basis sets constrained to a 400 eV cut-off energy. Further, the Brillouin zone is sampled by a 1 × 1 × 1 k-point grid.

The complete dendrons were built piecewise with the ATK tool, starting from the anchor groups and terminating with the four dendrite branches. Each added piece was given a spherical curvature that approximates the shape of the Au NP of approximately 1.4 nm diameter, so as to avoid the need for large-scale reconfigurations inherent in wrapping a large molecule around a large NP. The resulting isolated dendron was then structurally optimized to a nearby local energy minimum E_tot(G3), thus retaining its curved shape. As described earlier and in the ESI,† for the Au NP a bulk fcc crystal was cut to give a highly symmetrical compact Au₁₁₆ cluster of 1.47 nm diameter with a complete outer polyhedral shell. All internal Au atoms are then removed, leaving a hollow shell of 78 atoms, which we call Au₇₈ NP. This Au₇₈ NP is structurally optimized towards a local energy minimum E_tot(Au₇₈) (causing a minor inward rounding of the corners of the particle; global optimization would have been unrealistic as it would have collapsed the empty Au₇₈ shell into a much smaller compact NP). Next the dendron and hollow Au₇₈ NP are combined “manually” to produce reasonable Au–dendron interatomic distances, and then optimized together using VASP to yield the locally minimized energy E_tot(G3@Au₇₈).

To investigate nucleation of Au NPs at the anchor groups, we calculate binding energies between the anchor groups and smaller compact Au₆ and Au₈ NPs. The latter are both constructed from an initial octahedral Au(1,2) NP representing Au₆ while for Au₈ two Au atoms are added to Au₆ above midpoints of two of its opposite triangular facets. The dendrites are removed from the anchors and the cut bonds are then saturated by hydrogen, resulting in dendron anchor groups labeled G3-A. The neglect of the dendrites is justified because they are distant from the anchor sites and play no role in the anchor–Au interactions.

It must be stressed that we cannot guarantee finding the globally optimum structures. Also, we must bear in mind that in the experiment thermal energy will introduce a dynamic distribution of structures. Furthermore, we ignore the solvent in which the NPs and dendrons are immersed. However, we do expect to find realistic and representative structures that can help understand the system at hand, and especially the wrapping behavior of the dendrons around the Au NPs.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. K. C.-F. L. conceived and designed the experiments. K. C.-F. L., M. A. V. H. and K. E. H. directed the study. X. L., S. F. L., P. M. M. and K. C.-F. L. completed the synthesis and characterization. J. C. Y. and P. M. M. analyzed the experimental data. X.-B. L. performed the DFT calculations. K. E. H. analyzed the structures and produced the graphics. K. C.-F. L., X.-B. L., M. A. V. H. and K. E. H. wrote the paper.

Funding sources

We received financial support from the University Grants Committee of Hong Kong (AoE/P-03/08) and from the Collaborative Research Fund of the Research Grants Council of Hong Kong (Grant No. C2014-15G). ICTS is supported by the HKBU Institute of Creativity, which is sponsored by Hung Hin Shiu Charitable Foundation (). We are also grateful for computing resources of the High Performance Computing Service at Hunan Key Laboratory of Super-Microstructure and Ultrafast Process, Central South University, Changsha, China, and the Tianhe-2 cluster at the National Supercomputer Center in Guangzhou, China. We thank Prof. Meng-Qiu Long at Central South University for the software support of VASP and ATK.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Prof. Klaus E. Hermann is grateful for support by the ICTS at HKBU. We also thank Prof. Rui-Qin Zhang at City University of Hong Kong for valuable discussions. We thank Winnie Wu (HKBU) for the AFM analysis and Anna Chan (HKBU) for the EDX measurements.

References

1. S. Kassem, A. T. L. Lee, D. A. Leigh, A. Markevicius and J. Solà, Nat. Chem., 2016, 8, 138.
2. C.-S. Kwan, R. Zhang, M. A. Van Hove, Z. Cai and K. C.-F. Leung, Nat. Commun., 2018, 9, 497.
3. D. A. Tomalia, J. B. Christensen and U. Boas, Dendrimers, Dendrons, and Dendritic Polymers: Discovery, Applications, and the Future, Cambridge University Press, 2012.
4. D. Astruc, E. Boisselier and C. Ornelas, Chem. Rev., 2010, 110, 1857.
5. D. F. Yancey, E. V. Carino and R. M. Crooks, J. Am. Chem. Soc., 2010, 132, 10988.
6. L. K. Yeung and R. M. Crooks, Nano Lett., 2001, 1, 14.
7. R. M. Crooks, M. Zhao, L. Sun, V. Checkik and L. K. Yeung, Acc. Chem. Res., 2001, 34, 181.
8. V. S. Myers, M. G. Weir, E. V. Carino, D. F. Yancey, S. Pande and R. M. Crooks, Chem. Sci., 2011, 2, 1632.
9. N. Li, P. Zhao, L. Salmon, J. Ruiz, M. Zabawa, N. S. Hosmane and D. Astruc, Inorg. Chem., 2013, 52, 11146.
10. F. Sander, U. Fluch, J. P. Hermes and M. Mayor, Small, 2014, 10, 349.
11. D. Thompson, J. P. Hermes, A. J. Quinn and M. Mayor, ACS Nano, 2012, 6, 3007.
12. S.-F. Lee, Q. Wang, D. K.-L. Chan, P.-L. Cheung, B. S. Ong, K.-W. Wong, J. C. Yu and K. C.-F. Leung, New J. Chem., 2014, 38, 3362.
13. Q. Wang, S.-F. Lee, C. Y. Tang, K. C.-F. Leung and K.-W. Wong, RSC Adv., 2014, 4, 18193.
14. P. Zhao, N. Salmon, L. Li, N. Liu, J. Ruiz and D. Astruc, Chem. Commun., 2013, 49, 3218.
15. C. Ornelas, J. R. Aranzaes, L. Salmon and D. Astruc, Chem. – Eur. J., 2008, 14, 50.
16. T. J. Kucharski, N. Ferralis, A. M. Kolpak, J. O. Zheng, D. G. Nocera and J. C. Grossman, Nat. Chem., 2014, 6, 441.
17. C.-P. Chak, S. H. Xuan, P. M. Mendes, J. C. Yu, C. H. K. Cheng and K. C.-F. Leung, ACS Nano, 2009, 3, 2129.
18. C.-P. Chak, L.-H. Chau, S.-Y. Wu, H.-P. Ho, W. J. Li, P. M. Mendes and K. C.-F. Leung, J. Mater. Chem., 2011, 21, 8317.
19. C.-P. Chak, J. M. Y. Lai, K. W. Y. Sham, C. H. K. Cheng and K. C.-F. Leung, RSC Adv., 2011, 1, 1342.
20. J. P. Hermes, F. Sander, U. Fluch, T. Peterle, D. Thompson, R. Urbani, T. Pfohl and M. Mayor, J. Am. Chem. Soc., 2012, 134, 14674.
21. A. W. Shaffer, J. G. Worden and Q. Huo, Langmuir, 2004, 20, 8343.
22. S. E. Lohse, J. A. Dahl and J. E. Hutchison, Langmuir, 2010, 26, 7504.
23. J. G. Worden, Q. Dai, A. W. Shaffer and Q. Huo, Chem. Mater., 2004, 16, 3746.
24. G. A. DeVries, M. Brunnbauer, Y. Hu, A. M. Jackson, B. Long, B. T. Neltner, O. Uzun, B. H. Wunsch and F. Stellacci, Science, 2007, 315, 358.
25. F. Huo, A. K. R. Lytton-Jean and C. A. Mirkin, Adv. Mater., 2006, 18, 2304.
26. C. Krüger, S. Agarwal and A. Greiner, J. Am. Chem. Soc., 2008, 130, 2710.
27. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
30. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
31. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
32. L. Li, L. Wang and E. Alexov, Front. Mol. Biosci., 2015, 2, 5.
33. B. K. Teo and N. J. A. Sloane, Inorg. Chem., 1985, 24, 4545.
34. Y. Ding, F. R. Fan, Z. Q. Tian and Z. L. Wang, J. Am. Chem. Soc., 2010, 132, 12480.
35. K. Hermann, Crystallography and Surface Structure: An Introduction for Surface Scientists and Nanoscientists, Wiley, Weinheim, 2nd edn, 2017.
36. J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, J. Am. Chem. Soc., 2008, 130, 3756.
37. C. Wöll, S. Chiang, R. J. Wilson and P. H. Lippel, Phys. Rev. Lett., 1989, 39, 7988.
38. T. Gritsch, D. Coulman, R. J. Behm and G. Ertl, Surf. Sci., 1991, 257, 297.
39. S. Bengió, V. Navarro, M. A. González-Barrio, R. Cortés, I. Vobornik, E. G. Michel and A. Mascaraque, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045426.
40. W. Moritz and D. Wolf, Surf. Sci., 1985, 163, L655.
41. U. Starke, M. A. Van Hove and G. A. Somorjai, Prog. Surf. Sci., 1994, 46, 305.
42. M. Abu Bakar, M. Sugiuchi, M. Iwasaki, Y. Shichibu and K. Konishi, Nat. Commun., 2017, 8, 576.
43. H. Schmidbaur, H. G. Raubenheimer and L. Dobrzańska, Chem. Soc. Rev., 2014, 43, 345.
44. D. Benitez, N. D. Shapiro, E. Tkatchouk, Y. M. Wang, W. A. Goddard and F. D. Toste, Nat. Chem., 2009, 1, 482.
45. A. H. Pakiari and Z. Jamshidi, J. Phys. Chem. A, 2010, 114, 9212.
46. J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103.
47. ATK ((Atomistix ToolKit) version 16.0, software package for calculating electronic and transport properties) by QuantumWise A/S see https://quantumwise.com/.
48. Balsac (Build and Analyze Lattices And Clusters), visualization and analysis software, Version 4.21, by K. Hermann (FHI Berlin, 2018) see also hhttp://ttp://www.fhi-berlin.mpg.de/KHsoftware/Balsac/index.html.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental procedures, spectra, and modeling results. G3-1@Au₇₈ movie (MovS1_Au78DeG31movie_(new), MPG), G3-2@Au₇₈ movie (MovS2_Au78DeG32movie_(new), MPG), G3-3@Au₇₈ movie (MovS3_Au78DeG33movie_(new), MPG). See DOI: 10.1039/c9qm00132h

---