Understanding the Z selectivity of the metal-free intermolecular aminoarylation of alkynes: a DFT study†
Huining
Bai
a,
Huimin
Zhang
a,
Yuen
Guo
a,
Hui
Chen
b,
Donghui
Wei
 a,
Shijun
Li
a,
Shijun
Li
 a,
Yanyan
Zhu
a and
Wenjing
Zhang
a,
Yanyan
Zhu
a and
Wenjing
Zhang
 *a
*a
aCollege of Chemistry and Molecular Engineering, Zhengzhou University, Zhengzhou, Henan Province 450001, P. R. China. E-mail: zhangwj@zzu.edu.cn
bInstitute of Chemistry, Henan Academy of Sciences, Zhengzhou 450002, P.R. China
First published on 26th November 2018
Abstract
The transition metal-catalyzed hydro- or carboamination of alkynes usually yields cis enamines, indicating that the hydrogen or the unsaturated carbon group is located at the same side of the olefin bond with the amine group. Recently, Greaney and coworkers reported a metal-free intermolecular aminoarylation of alkynes, affording tetrafunctionalized enamines with the amine and aryl groups in trans geometry. The Smiles rearrangement was proposed to account for the aminoarylation mechanism, but the Z selectivity (i.e. trans enamine as the main product) is quite difficult to understand. In the present paper, the aminoarylation mechanism has been thoroughly studied and accordingly, the origin of the Z selectivity has been discussed in detail. The calculated results reveal that the Smiles rearrangement mechanism is able to occur under experimental conditions, but the novel mechanism, in which an alternative pathway is proposed for transformation of the anionic adduct, is more reasonable on account of the lower energy barrier and the more rational explanation for the roles of the additive K2CO3. The Z selectivity is determined by the inherent requirements of the dynamic preference of pathways (the CTI-first pathway in the Smiles rearrangement mechanism and the QZ pathway in the novel mechanism) that promise the Z-geometry product, rather than the conventional isomerization of the E-geometry product in situ with the assistance of K2CO3.
Introduction
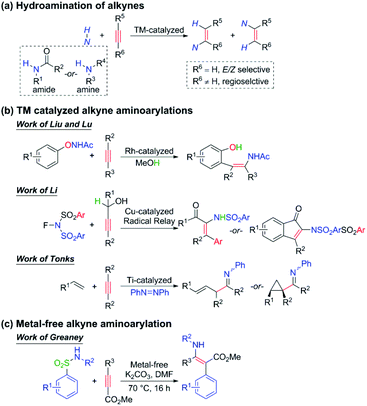
The densely functionalized enamine and its derivatives have extensive applications in heterocycle chemistry, natural product synthesis, chiral β-amino acid preparation, and so on.1–4 For tetrasubstituted species, difunctionalization of alkynes is often the only efficient way to synthesize since the classical disconnections across the double bond lead to very sterically hindered reactions that are low yielding and lack regioselectivity.5 During the past few decades, the hydroamination of alkynes (Scheme 1a) to give trisubstituted enamines has been extensively developed and widely applied in the synthesis of various products such as polymers, pharmaceuticals, and natural products.6 Nevertheless, the analogous carboamination reaction of alkynes to afford tetrasubstituted enamines is still challenging and rare to be reported. Some progress has recently been achieved by the Liu and Lu,7 Li,8 and Tonks9 groups using transition metal catalysis (Scheme 1b), but a general protocol is still strongly desired to be built.Aminoarylation of alkynes can simultaneously induce nitrogen and aryl sources onto the carbon–carbon triple bonds. When the alkyne is substituted by a conjugated carbonyl group, the resulting product can be endowed with both nucleophilicity (the nitrogen and the β-carbon) and electrophilicity (the α-carbon and the carbonyl group), which makes the densely functionalized enamine a most important intermediate in organic synthesis. Encouragingly, Greaney and coworkers have recently made exciting progress in the one-step intermolecular aminoarylation of alkynes under user-friendly and metal-free conditions (Scheme 1c). The widely commercially available aryl sulfonamides and methyl formate-substituted alkynes were used as the substrates, 3 equivalents of K2CO3 as the additive, and N,N-dimethylformamide (DMF) as the solvent. This affords a universal strategy because alkyl-, aryl-, and heteroaryl substituted alkynes are all able to furnish the corresponding products in good to excellent yields, and both electron-donating and electron-withdrawing groups are well tolerated. As for the scope of aryl sulfonamides, it is found that the electron-withdrawing group, which is desired to stabilize the Meisenheimer intermediate10 of the Smiles rearrangement, is not an essential factor here. By contrast, moderately electron-donating groups could also give excellent yields (89% or 91%). Besides, the reaction can be extended to heteroaryl sulfonamides and secondary N-alkyl sulfonamides as well, which opens a way to novel enaminotates.
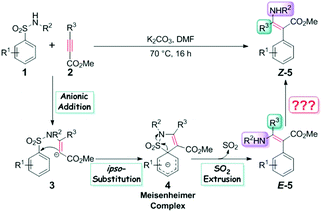
We are deeply intrigued by this reaction not only because of the novel points of the reaction itself, such as metal-free conditions and the densely functionalized product which features a concentration of both electrophilic and nucleophilic reactive substituents, but more importantly due to the Z-enamines as the main products. As displayed in Scheme 1, the transition metal-catalyzed hydro- or carboamination of alkynes usually yields cis enamines, indicating that the hydrogen or the unsaturated carbon group is located at the same side of the olefin bond with the amine group, but Scheme 1c shows that the title metal-free aminoarylation of alkynes affords the trans product, which features the Z selectivity. The anionic addition/ipso-substitution/SO2 extrusion sequence is proposed to account for the reaction mechanism (Scheme 2), but it cannot explain the Z selectivity since the extrusion of SO2 from the Meisenheimer intermediate 4 should result in the E-geometry product, and the isomerization of a typical and highly conjugated double bond is commonly considered difficult. Then how does this isomerization occur? Are there any alternative pathways to avoid this isomerization and reach the Z-geometry product? Except for furnishing ammonia anions to facilitate the anionic addition, what roles do the additive K2CO3 play? Why is it necessary to be excessive? To pursue answers to these queries, we conducted thorough studies on the reaction mechanism and the origin of the Z selectivity in the present work by using the density functional theory (DFT)11 method. During the past decade, the DFT method has been widely used in mechanism and reaction selectivity studies toward organic and catalytic reactions.12–20 More detailed information about the reaction process can be provided by scientists to gain better insights into the reaction mechanism and the origin of the enantio-, stereo-, chemo-, and regioselectivities, which provides important guidance for new reactions and more efficient catalyst designs in the future.
The reaction of 4-nitrobenzenesulfonamide (R1 = 4-NO2, R2 = H in Scheme 2) and methyl 3-(4-fluorophenyl)propiolate (R3 = 4-fluorophenyl in Scheme 2) was selected as the model reaction because it performs best in yield (95%) among all the 24 reported examples. For the sake of brevity, we will denote these two reactants in the remaining sections of this paper as R1 and R2, respectively.
Computational details
All theoretical calculations were performed by using the Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 suit of program. All structures were optimized in the solution phase (DMF is used in the experiment) by using the integral equation formalism polarizable continuum model (IEFPCM)22,23 at the M06-2X24/6-31G(d, p)11,25,26 level of theory (denoted as Level A). The vibrational frequencies were calculated at the same level with the temperature set as 343.15 K and the pressure as 1 atm. All reactant, intermediates, and products were ensured to have no imaginary frequency, while each transition state has one but only one imaginary frequency. The intrinsic reaction coordinate (IRC)27,28 calculations were also conducted at the same level to help confirm that each transition state leads to the expected reactants and products. The Parr functions29 were calculated to estimate the electrophilicity and nucleophilicity of the key atoms in related structures.
21 suit of program. All structures were optimized in the solution phase (DMF is used in the experiment) by using the integral equation formalism polarizable continuum model (IEFPCM)22,23 at the M06-2X24/6-31G(d, p)11,25,26 level of theory (denoted as Level A). The vibrational frequencies were calculated at the same level with the temperature set as 343.15 K and the pressure as 1 atm. All reactant, intermediates, and products were ensured to have no imaginary frequency, while each transition state has one but only one imaginary frequency. The intrinsic reaction coordinate (IRC)27,28 calculations were also conducted at the same level to help confirm that each transition state leads to the expected reactants and products. The Parr functions29 were calculated to estimate the electrophilicity and nucleophilicity of the key atoms in related structures.
On basis of the optimized geometries, all energies were further refined through single-point calculations at the M06-2X/6-311++G(2df, 2pd)30–32//IEFPCMDMF level (denoted as Level B). The Gibbs free energies were applied for all discussions, and were calculated by adding the thermal corrections to Gibbs free energies calculated at Level A to the single-point energies refined at Level B. We chose to conduct discussions based on Gibbs free energies rather than the Born–Oppenheimer energies, which are the electronic (including nuclear-repulsion) energies plus the zero-point energies (ZPEs), because the entropy effect is not included in Born–Oppenheimer energies, and they are independent of temperature.
Results and discussion
Reaction mechanism
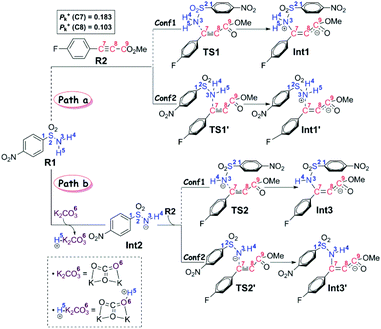
On the basis of the anionic addition/ipso-substitution/SO2 extrusion reaction sequence and our computational results, we have proposed the reaction to go through three stages, in particular the anion formation and anionic addition (Stage I), the 4-nitrophenyl rearrangement (Stage II), and finally the isomerism and product release (Stage III). For each stage, more than one possible reaction pathway have been carefully considered. Thus in this section, we will present all the calculated results and discussion in a stage-by-stage fashion.Stage I: anion formation and anionic addition It is a common view that the Smiles rearrangement is triggered by the anionic addition.33,34 Nevertheless, besides the addition of anion Int2 to R2, the nucleophilic attack by the neutral aryl sulfonamide R1 to the alkyne R2 has also been calculated to serve as a comparison and verification to the selected computational method and level. As shown in Scheme 3, these two reaction pathways are denoted as Path a and Path b, respectively.
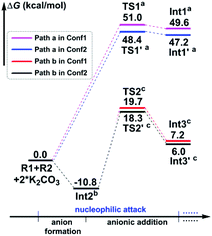
In particular, it is presumed that Path a involves the direct attack of the N3 atom of R1 on the C7 atom of R2. While in Path b, the substrate R1 should firstly be transformed into its anion Int2 with the assistance of the additive K2CO3, which accordingly results in the delivery of a molecule of K2CO3–H+, and then the electron-rich N3 atom of Int2 would attack on the C7 atom of R2via the transition state TS2/TS2′, affording the corresponding anion complex Int3/Int3′. The anion formation is a barrierless process which can be demonstrated by the results of the flexible scanning of the H5–O6 bond from the optimized complex CP1 (see Fig. S1 in the ESI† for more details). Beyond the subject of nucleophilic attack, the combination conformations of substrates with the 4-nitrophenyl group oriented to the methyl formate group (Conf1) or the 4-flurophenyl group (Conf2) have also been studied in detail. Please see the optimized geometries of all related structures in Fig. S4 in the ESI.†Fig. 1 gives the Gibbs free energy profiles of all the calculated possible pathways in Stage I. As we can see, the anionic attack rather than the sulfonamide attack can be definitely confirmed by the extremely higher energy barrier of Path a (51.0/48.4 kcal mol−1viaTS1/TS1′, respectively) than that of Path b (30.5/29.1 kcal mol−1viaTS2/TS2′, respectively). The significantly stronger nucleophilicity of the anion than the neutral molecule should obviously account for these results. Regarding the combination conformations, it is easy to figure out that Conf2 is relatively more energetically favourable over Conf1 for no matter Path a or Path b. This may be partly due to the slightly stronger π⋯π interaction between the two aryl groups than that between the 4-nitrophenyl and the carbonyl group.
In short, the whole reaction should be initiated by the anion formation with the assistance of K2CO3, followed by anionic addition of Int2 to the aryl alkyne R2 with the conformation of Conf2 to give anion complex Int3′. Accordingly, all calculations afterward were based on Int3′. As for why the nucleophilic addition occurs at the C7 atom rather than the C8 atom, we have checked their reactivity through electrophilic Parr function Pk+ calculations. The results show that the Pk+ of C7 and C8 atoms in R2 is 0.183 and 0.103, respectively, indicating that the C7 atom is more reactive as an electrophilic center.
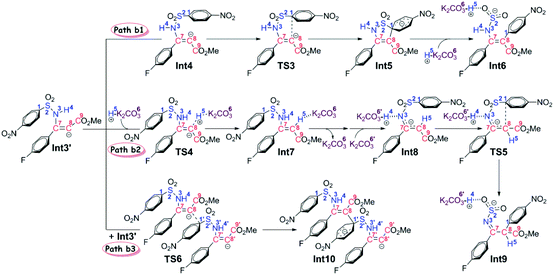
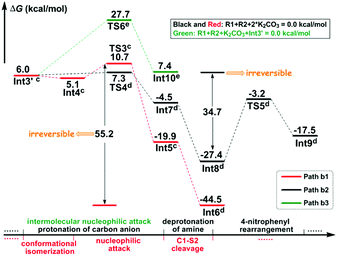
Stage II: 4-nitrophenyl rearrangement Given the anion complex Int3′, three possible mechanisms have been proposed for rearrangement of the 4-nitrophenyl group (Scheme 4), in particular the conformational isomerization from Int3′ to Int4, followed by nucleophilic attack viaTS3, and finally the ipso-substitution due to cleavage of the C1–S2 bond (denoted as Path b1), the protonation of the carbon anion viaTS4, followed by deprotonation from the amine to give Int8, and finally the 4-nitrophenyl rearrangement viaTS5 (denoted as Path b2), and the bimolecular mechanism with another Int3′ involved (denoted as Path b3). Noteworthily, only the first step of Path b3 is illustrated in Scheme 4 since the energy barrier of this step is obviously higher than the other two pathways (Fig. 2). More details about the mechanism and energy profiles of the whole process of Path b3 can be found in Part 3 of the ESI.†
 | ||
| Fig. 2 Gibbs free energy profiles of the possible pathways in Stage II. The superscripts represent adding energies of (c) K2CO3–H+ + K2CO3, (d) K2CO3, and (e) K2CO3–H+. | ||
As shown in Scheme 4, in Path b1, complex Int3′ is firstly converted to the slightly more stable complex Int4 to facilitate the following nucleophilic attack of the C8 anion center to the C1 atom of the 4-nitrophenyl moiety. The gradual decrease of the distance between C1 and C8 atoms results in the formation of the so-called spirocyclic anion intermediate (Meisenheimer complex) Int5. The energy barrier of this nucleophilic attack is 5.6 kcal mol−1, and the anionic intermediate Int5 is located 19.9 kcal mol−1 lower than the substrates of the reaction, which corresponds well to the fact that the Meisenheimer complex is a stable intermediate of the Smiles rearrangement. The direct cleavage of the C1–S2 bond has been demonstrated to be very difficult (see Part 4 in the ESI† for more details), but when the K2CO3–H+, which is delivered during the anion formation, is added to stabilize the negative charge that is concentrated on the SO2 moiety, the C1–S2 bond would be broken barrierlessly. Similarly, we confirm this barrierless feature on account of the results of flexible scanning. Please see Fig. S2 in the ESI† for more details. It is worth noting that the ipso-substituted product Int6 is located more than 55 kcal mol−1 under the transition state TS3, indicating that the nucleophilic attack followed by C1–S2 bond cleavage is irreversible.
Path b2 was proposed mainly on account of the experimental fact that excessive K2CO3 has been added to the reaction system. Since K2CO3–H+ has been delivered during the anion formation, we consider that the instant protonation of the carbon anion by K2CO3–H+ should be very likely to occur. As is shown in Fig. 2, the energy barrier is calculated to be only 1.3 kcal mol−1, which is 4.3 kcal mol−1 lower than that of the nucleophilic attack in Path b1. Beyond, the transition state TS4 of the protonation process is located 3.4 kcal mol−1 lower than the transition state TS3 of the nucleophilic attack process in Path b1. Although the barrier of the reverse reaction from Int7 back to Int3′ is only 11.8 kcal mol−1, the instant formation of intermediate Int8 makes the reaction irreversible. In particular, the transformation from Int7 to Int8 involves the successive changes including the release of a molecule of K2CO3 and barrierless proton transfer of H4 (see Fig. S3 of the ESI† for the scanning results) from the N3 atom to the O6′ atom of the second molecule of K2CO3. Int8 features a delocalized negative charge around the N3, C7 and C8 atoms, and the instantaneous charge rearrangement facilitates the nucleophilic attack of the C8 atom on the C1 atom via the transition state TS5. Since the nucleophilicity of the C8 atom has been decreased due to the charge delocalization, which can be demonstrated by the nucleophilic Parr functions Pk− (1.008 in Int3′, and 0.716 in Int8), the energy barrier for this step (24.2 kcal mol−1) is higher than the corresponding process in Path b1 (5.6 kcal mol−1viaTS3), but easy to overcome under the experimental conditions.
Inspired by our previous study35 about the reaction mechanism of stereoselective C(2)-vinylation of 1-substituted imidazoles with 3-phenyl-2-propynenitrile, the bimolecular reaction mechanism through Path b3 has also been studied. As shown in Scheme 4, the first step is the nucleophilic attack of the C8 atom of Int3′ on the C1 atom of the second molecule of Int3′, which affords intermediate Int10. However, it is different from what has been concluded in that previous study, the energy barrier of this step (21.7 kcal mol−1) is demonstrated to be significantly higher than the intramolecular reactions viaTS3 or TS4, so Path b3 has been definitely excluded. As mentioned above, more details about Path b3 can be found in Part 3 of the ESI.†
Stage III: isomerism and product release
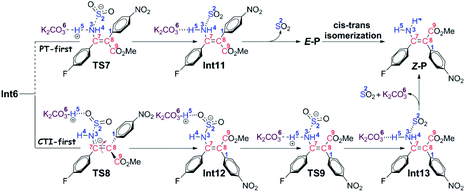
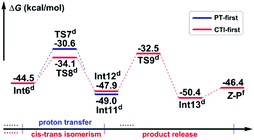
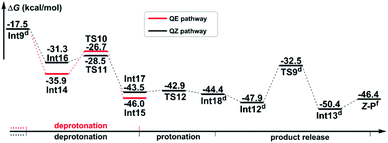
Path b1 Given the zwitterion intermediate Int6, the reaction is possible to go through two pathways (as shown in Scheme 5), i.e. the concerted proton transfer of the H5 atom from K2CO3–H+ to the N3 atom and the SO2 extrusion, followed by a cis–trans isomerization with the assistance of the K2CO3 to give the Z-geometry product Z-P (denoted as the PT-first pathway), or the cis–trans isomerization from Int6 to Int12 goes preferentially over the proton transfer of the H5 atom from K2CO3–H+ to the amine group to give the final product (denoted as the CTI-first pathway). The calculated results reveal that the energy barrier (Fig. 3) of the concerted step of the PT-first pathway via transition state TS7 is 3.5 kcal mol−1 higher than that of the isomerism transformation of the CTI-first pathway via transition state TS8, indicating that the latter pathway is more favourable. Accordingly, calculations about the PT-first mechanism after Int11 have not been carried out.
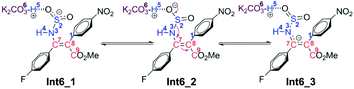
As for the CTI-first mechanism, the barrier of the cis–trans isomerization viaTS8 is 10.4 kcal mol−1, indicating that it is easy to occur under mild conditions. This seems in contrast to the common view that rotation along the carbon–carbon double bond is very difficult. Actually, in this elementary step, the length of the N3–S2 bond is 1.83 Å in Int6 (see Fig. S5 and S6 in the ESI†), obviously longer than the normal N–S single bond. We consider that this relatively weak bonding interaction should be partly attributed to the resonance structures of Int6 (as shown in Scheme 6), and due to these resonance structures (especially Int6_3), the double bond of C7–C8 has been weakened, making the isomerization much easier to occur.36 As a result, the E-geometry carbon–carbon double bond in Int6 can be isomerized to the Z-geometry in Int12.
The last step is to transfer the proton H5 to the N3 atom accompanied by the release of the SO2 molecule. The IRC computational result of transition state TS9 demonstrates that these two processes can be accomplished in a concerted step. The barrier of this step is 15.4 kcal mol−1, which is easy to overcome under the experimental conditions. As a result, given the complex Int13, the final aminoarylation product of alkyne can be released by removing the SO2 and K2CO3 molecule.
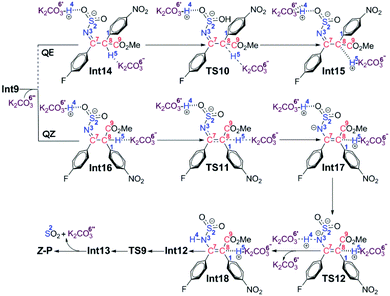
Path b2 As shown in Scheme 7, there are three steps included in Stage III of Path b2, i.e. the deprotonation from the C8 atom, the protonation of the N3 atom, and finally the product release. Since the C7–C8 bond has been transformed into a typical single bond in Int9 (1.58 Å), the K2CO3 molecule (the third one for the whole reaction) is possible to combine with Int9 to give Int14 in quasi E geometry (denoted as the QE pathway) or with the rotation isomer of Int9 to give Int16 in quasi Z geometry (denoted as the QZ pathway). The computational results (Fig. 4) disclose that the energy barriers of the following deprotonation of the C8 atom via the QE and QZ pathways are 9.2 and 2.8 kcal mol−1, respectively, which clearly indicates the preference of the latter reaction pathway.
The remaining steps are to extrude the molecule of SO2 and to transfer the H4 and H5 atoms to the N3 atom to give the enamine product. The computational results reveal that the energy barrier to transfer the H4 atom via transition state TS12 is 0.6 kcal mol−1 only, indicating that it is able to go very fast. Transfer of the H5 atom and extrusion of SO2 can be accomplished in one concerted step via transition state TS9, which is the same as that in the CTI-first mechanism. But before that, the intermediate Int18 should be transformed into Int12 as in the CTI-first mechanism, then the rest of the reactions are the same.
Discussion
Taking all above discussions into consideration, we can conclude that the Smiles rearrangement mechanism (denoted as Mechanism I) for the title reaction should go specifically through Path b with conformation Conf2 in Stage I, Path b1 in Stage II, and the CTI-first pathway in Stage III. In other words, the whole reaction going through Mechanism I should include seven steps, in particular the anion formation, anionic attack, conformational isomerization, nucleophilic attack, C1–S2 bond cleavage, cis–trans isomerization and finally product release. The anionic attack of the anion Int2 on the alkyne substrate R2 is the rate-determining step, with the energy barrier of 29.1 kcal mol−1, which is a rational value for the experimental conditions (see Fig. S9† for energy profiles of the whole reaction going through Mechanism I). All these results are also well consistent with the common proposal that the SNAr process (anionic attack) for the formation of the Meisenheimer complex goes slow, and thus is the rate-determining step of the Smiles rearrangement.32,33Mechanism II provides an alternative pathway for further transformation of the anionic adduct Int3′. It states to go through Path b with conformation Conf2 in Stage I, Path b2 in Stage II, and the QZ pathway in Stage III. There are eight steps included, in particular anion formation, anionic attack, protonation of the anionic carbon, deprotonation of the amine, 4-nitrophenyl rearrangement, deprotonation from the C8 atom, protonation of the N3 atom, and finally product release. As what has been illustrated, K2CO3 plays important roles as a proton transfer medium in processes of anion formation, activation of the olefin intermediate Int7 to facilitate the 4-nitrophenyl group transfer, and product release including the double bond restoration and the SO2 extrusion. Namely, excessive K2CO3 is conducive to the reaction to occur through Mechanism II, which corresponds well to the experimental fact. The rate-determining step of Mechanism II is also the anionic attack reaction, a common step of Mechanisms I and II, with the energy barrier of 29.1 kcal mol−1. Thus we consider that Mechanism II should also be a possible mechanism of the title reaction. Please see Fig. S10† for energy profiles of the whole reaction going through Mechanism II.
The bimolecular reaction mechanism (denoted as Mechanism III) has been disclosed to be unlikely to occur because of the much higher energy barrier viaTS6, so it is excluded from our further discussion.
As shown in Scheme 4, the most essential difference in Mechanisms I and II is whether the nucleophilic attack viaTS3 goes first (Path b1) or the proton transfer viaTS4 is more likely to occur (Path b2). The barriers for conversion of Int3′via transition states TS3 and TS4 are 5.6 and 1.3 kcal mol−1, respectively, indicating that the proton transfer from K2CO3–H+ to the C8 atom to form the neutral functionalized olefin Int7 is more favourable than the conformational isomerization followed by a nucleophilic attack to give the Meisenheimer complex Int5. More importantly, the instant conversion of Int5 and Int7 to respectively Int6 and Int8 makes these two reactions irreversible, so we consider that Mechanism II is more energetically favourable, although the barrier afterwards is higher than that in Mechanism I. In addition, there is only one molecule of additive that participates in the reaction through the whole process of Mechanism I, but in Mechanism II, the K2CO3 molecule has been demonstrated to play important roles in three steps, which is in excellent agreement with the experimental reports about 3 equivalents of K2CO3 which is an indispensable reaction condition. In summary, on account of the energetic preference and the more consistent results with experimental observations, it is reasonable to infer that Mechanism II is more likely to occur under the title reaction conditions than the conventional Smiles rearrangement mechanism. Additional studies towards the substituent effects provide further support to the preference of Mechanism II (see Part 6 in the ESI†). A brief discussion about the mechanism of reaction of allene is an interesting extension of this study. It is of great importance to help gain deeper insight into the mechanism of aminoarylation of unsaturated bonds (see Part 7 in the ESI† for more details).
Understanding the Z-selectivity
Given the possible reaction mechanisms in hand, we can now turn to discussion on the origin of the unexpected Z selectivity when the reaction goes through Mechanisms I and II, respectively.According to Mechanism I, the most important Meisenheimer intermediate Int5 is a pre-E-geometry olefin, leading the following intermediate Int6 to be in absolute E geometry. The PT-first pathway (Scheme 5) indicates that Int6 should be firstly converted to the E-geometry aminoarylated product (E-P) according to the synergetic proton transfer and SO2 extrusion, and then E-P is isomerized to the product in Z geometry (Z-P) with the assistance of K2CO3, which is thermodynamically driven since Z-P is more stable than E-P (G(E-P) − G(Z-P) = 3.1 kcal mol−1), while the CTI-first pathway suggests that the cis–trans isomerization from Int6 in E geometry to Int12 in Z geometry should occur before the synergetic proton transfer and SO2 extrusion. The resulted aminoarylation product can be in Z geometry only. On the basis of all abovementioned discussion about Mechanism I, the latter pathway is more energetically favourable, so Z-P should be the only product. That is to say, after generation of the Meisenheimer intermediate, the inherent requirement of the preference of cis–trans isomerism of Int6 (CTI-first pathway) over the synergetic proton transfer and SO2 extrusion (PT-first pathway) should be the essential reason to produce Z-P rather than E-P through Mechanism I.
The general strategy of Mechanism II is firstly to transform the double bond of the anionic adduct Int3′ into a single bond through the protonation of the carbon anion (C8 atom) and the rearrangement of the 4-nitrophenzyl group, followed by rotating around the single bond to the conformational isomer which promises Z geometry, and finally to restore the double bond through deprotonation from the carbon atom. As shown in Fig. 4, after combination with the third molecule of K2CO3, the deprotonation along the QZ pathway is obviously more favourable than the QE pathway, indicating that Z-P should be the dominant product. In other words, the stereoselectivity of the title reaction going through Mechanism II is determined by the preference of proton transfer in quasi Z geometry over that in quasi E geometry.
Conclusions
To gain deep insights into the unusual Z selectivity of the recently reported metal-free intermolecular aminoarylation of alkynes, thorough DFT investigations have been carried out towards the reaction mechanism. The main contributions to gaining a deeper understanding about the mechanism of similar reactions and valuable guidance for the design of more efficient reactions to synthesize novel tetrafunctionalized enamine and its derivatives can be concluded as follows:(i) The conventional Smiles rearrangement mechanism (Mechanism I) has been presented in very detail. It is indicated that the reaction should include generally seven steps, and the anionic attack reaction of Int2 to alkyne R2 is the rate-determining step. The nucleophilic attack of the sulfonamide R1 on R2 has been definitely excluded on account of the much higher energy barrier. As for further reaction of the intermediate after the Meisenheimer complex, the CTI-first pathway is proved to be more energetically favourable than the PT-first pathway, enabling the reaction to afford the Z-geometry product as the main product, which accounts well for the essential mechanism of transformation from the Meisenheimer complex which promises E-geometry to the Z-geometry product.
(ii) An alternative reaction mechanism (Mechanism II) has been proposed and demonstrated to be more reasonable. The rate-determining step is the same as Mechanism I, which predicts a rational barrier for the experimental conditions. The essential difference in Mechanisms I and II is whether the 4-nitrophene rearrangement or the protonation of the anionic intermediate occurs preferentially. Our computational results reveal that the energy barrier of the latter transformation is 4.3 kcal mol−1 lower the former reaction. So Mechanism II is more likely to occur for the studied reaction. Moreover, Mechanism II is able to interpret the experimental fact of 3 equivalents of K2CO3 as an indispensable condition in a more reasonable way than Mechanism I.
(iii) The bimolecular reaction mechanism (Mechanism III) for the 4-nitrophenyl rearrangement has also been studied but excluded due to the significantly higher energy barrier than the other two mechanisms.
(iv) The origin of the unusual Z selectivity of the title reaction going through Mechanisms I and II has been clearly stated. It is commonly thought that the Z-geometry product should be formed according to the isomerization of the E-geometry enamine in situ because Z-P can be stabilized by an internal hydrogen bond. But our calculations disclose that the stereoselectivity of the title reaction through Mechanisms I and II should be determined by the inherent requirements of the dynamic preference of the pathway which promises a product in the Z geometry. In particular, the preference of the CTI-first pathway in Mechanism I and the QZ pathway in Mechanism II determines the reaction to give the Z-geometry product as the dominant product.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work described in this study was supported by the National Natural Science Foundation of China (No. 21503191, 21502045) and the China Postdoctoral Science Foundation (No. 2015M572115).Notes and references
- B. Stanovnik and J. Svete, Chem. Rev., 2004, 104, 2433–2480 CrossRef CAS
.
- P.-Q. Huang, W. Ou and J.-L. Ye, Org. Chem. Front., 2015, 2, 1094–1106 RSC
.
- R. G. Vaswani, B. K. Albrecht, J. E. Audia, A. Côté, L. A. Dakin, M. Duplessis, V. S. Gehling, J.-C. Harmange, M. C. Hewitt, Y. Leblanc, C. G. Nasveschuk and A. M. Taylor, Org. Lett., 2014, 16, 4114–4117 CrossRef CAS
.
- Y. K. R. And and A. Chartrand, Org. Lett., 2007, 9, 1029–1032 CrossRef
.
- P. T. G. Rabet, S. Boyd and M. F. Greaney, Angew. Chem., Int. Ed., 2017, 56, 4183–4186 CrossRef CAS
.
- L. B. Huang, M. Arndt, K. Gooßen, H. Heydt and L. J. Gooßen, Chem. Rev., 2015, 115, 2596–2697 CrossRef CAS
.
- G. Liu, Y. Shen, Z. Zhou and X. Lu, Angew. Chem., Int. Ed., 2013, 52, 6033–6037 CrossRef CAS
.
- J. Q. Sun, G. F. Zheng, T. Xiong, Q. Zhang, J. B. Zhao, Y. Li and Q. Zhang, ACS Catal., 2016, 6, 3674–3678 CrossRef CAS
.
- Z. W. Davis-Gilbert, L. J. Yao and I. A. Tonks, J. Am. Chem. Soc., 2016, 138, 14570–14573 CrossRef CAS
.
- A. J. J. Lennox, Angew. Chem., Int. Ed., 2018, 57, 14686–14688 CrossRef CAS
.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS
.
- Y. Y. Wang, D. H. Wei, Y. Wang, W. J. Zhang and M. S. Tang, ACS Catal., 2016, 6, 279–289 CrossRef CAS
.
- X. L. Zhang, M. S. Tang, Y. Wang, Y. Y. Ran, D. H. Wei, Y. Y. Zhu and W. J. Zhang, J. Org. Chem., 2016, 81, 868–877 CrossRef CAS
.
- W.-J. Zhang, D.-H. Wei and M.-S. Tang, J. Org. Chem., 2013, 78, 11849–11859 CrossRef CAS
.
- Y. Wang, L. J. Zheng, D. H. Wei and M. S. Tang, Org. Chem. Front., 2015, 2, 874–884 RSC
.
- Y. Y. Ran, M. S. Tang, Y. Wang, Y. Y. Wang, X. L. Zhang, Y. Y. Zhu, D. H. Wei and W. J. Zhang, Tetrahedron, 2016, 72, 5295–5300 CrossRef CAS
.
- H. M. Zhang, H. Xu, H. N. Bai, D. H. Wei, Y. Y. Zhu and W. J. Zhang, Org. Chem. Front., 2018, 5, 1493–1501 RSC
.
- H. N. Bai, H. Xu, H. M. Zhang, Y. E. Guo, J. K. Shan, D. H. Wei, Y. Y. Zhu, S. R. Zhang and W. J. Zhang, Catal. Sci. Technol., 2018, 8, 5165–5177 RSC
.
- P.-C. Tu, L. Zhou, A. M. Kirillov, R. Fang and L. Yang, Org. Chem. Front., 2018, 5, 1356–1365 RSC
.
- Y. Wang, D. H. Wei and W. J. Zhang, ChemCatChem, 2018, 10, 338–360 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C. 01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed
.
- W. Sang-Aroon and V. Ruangpornvisuti, Int. J. Quantum Chem., 2008, 108, 1181–1188 CrossRef CAS
.
- J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
- M. M. Francl, W. J. Petro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS
.
- V. Rassolov, J. A. Pople, M. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS
.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS
.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS
.
- L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494 RSC
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS
.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS
.
- J.-P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016–5021 CrossRef CAS
.
-
J. J. Li, Name Reactions. A Collection of Detailed Reaction Mechanisms, Springer, Heidelberg, 2nd edn, 2003 Search PubMed
.
-
L. Kürti and B. Czakó, Strategic Applications of Named Reactions in Organic Synthesis, Elsevier, Dorecht, 2005 Search PubMed
.
- D. H. Wei and M. S. Tang, J. Phys. Chem. A, 2009, 113, 11035–11041 CrossRef CAS PubMed
.
- D. Z. Sun, Y. Y. Zhu, D. H. Wei, C. Zhang, W. J. Zhang and M. S. Tang, Chem. Phys. Lett., 2010, 495, 33–39 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Flexible scanning results from CP2, Int5 and Int8 (Part 1); optimized geometries of all structures involved in Mechanisms I and II (Part 2); mechanism of Path b3 (Part 3); the overall Gibbs free energy profiles of the possible direct cleavage of the C1–S2 bond (Part 4); the overall free energy profiles of the reaction going through Mechanisms I and II. (Part 5); substituent effect studies (Part 6); possible reaction mechanisms of allene (Part 7); a list of Cartesian coordinates of all structures involved in this work (Part 8). See DOI: 10.1039/c8qo01093e |
| This journal is © the Partner Organisations 2019 |