Exploring the necessity of an acidic additive for Pd(II)-catalyzed exclusive C4-fluoroalkylation of 3-acetylindole: a detailed DFT study on the mechanism and regioselectivity

Abstract

The reaction mechanisms of Pd(II)-catalyzed exclusive C4-fluoroalkylation of indole, with an acetyl group as the directing group at the C3 site, were explored via density functional theory calculations (DFT). Our results reveal that the regioselectivity of the C4 site over the C2 site is mainly achieved in the step of C–H activation. Compared to original Pd(OAc)₂, Pd(TFA)₂ formed via the addition of acidic TFA (Trifluoroacetic Acid) has important advantages. At first, it reduces the energy barrier of the C–H activation step for both the C4 site and C2 site. Furthermore, it leads to a larger degree of lowering of the energy barrier of C4–H activation when compared to that of C2–H activation. These advantages could give rise to the experimental observation of an exclusive C4 product with good yield under mild reaction conditions. Thus the necessity of an acidic additive of TFA should arise from its capability of leading to the formation of Pd(TFA)₂. Detailed analysis indicates that, in the C–H activation step, electron density is donated from the indole substrate to the Pd-catalyst as the acceptor. Compared to Pd(OAc)₂, the ability of Pd(TFA)₂ as the electron acceptor is enhanced due to more electron-withdrawing ligands of CF₃COO⁻. This enhanced accepting ability could lead to a larger amount of donated electron density which will give rise to a lower energy barrier and thus to a higher degree of feasibility of the reaction. Furthermore, this enhanced accepting ability will also lead to a higher degree of preference to the C4 site since its donating ability is verified to be stronger than that of the C2 site. Based on this analysis, other acidic additives, capable of introducing a strong electron-withdrawing ligand into the Pd-catalyst, could also realize the exclusive C4 functionalization under mild reaction conditions. This prediction was theoretically verified in the case of HOTf, whose acidity is stronger than that of TFA. Thus we hope that our theoretical results would promote related experimental exploration in the near future.

---

Introduction

As commonly occurring heterocycle motifs in numerous natural products, indole and its derivatives have possessed great application in the fields of pharmaceuticals, agrochemicals, and biologically active compounds as well as molecular materials with novel properties (electronic, optical or transmission devices).¹ Clearly, the synthesis of various substituted indoles is crucial not only to our fundamental understanding of indole-based compounds but also to their practical application.²

As representatives of indole derivatives, C4-substituted compounds are known as privileged frameworks due to their roles of backbone of ergot alkaloids.³ Because of their great value,⁴ lots of interest have been dedicated to the synthetic research of 4-substituted indoles.⁵ However, the regioselective functionalization of the C4 site of indole has become a challenging task which is still far away from successful accomplishment. This point has been clearly indicated in the literature as the number of reports of synthesis of the C4-site product of indole is notably fewer when compared with the functionalization of other carbon sites.⁵

The reason for this difficulty is mainly attributed to the quite weak reactivity of the C4 site of indole.⁶ Actually this site has been described as the least reactive one in indole.⁷ Due to this intrinsic inertia, traditional synthetic routes of the C4 product of indole were usually forced to adopt harsh stoichiometric metallation⁸ or radical processes.⁹ In many of these reactions, a stoichiometric amount of toxic metallation, e.g., thallation^8a or mercuriation,¹⁰ or forcing reaction conditions^9,11 are necessary. Thus, although with successful synthesis of target products, these approaches are usually precluded from gaining broad application.

However, it is a comfort to see that new strategies, based on transition metal (TM)-catalyzed activation of C–H bonds,¹² enzymatic catalysis¹³ as well as the photoredox process,¹⁴ have given rise to positive progress towards C4 functionalization of indole under mild reaction conditions. Among these new advances, TM-catalyzed C–H bond activation has contributions significantly with the advantage as a type of atom- and step-economical transformation with satisfactory yield.¹⁵

The majority of these TM-catalyzed reactions need a directing group (DG) installed on the C3 position.^6,16 Most of the DGs arise from the carbonyl-based group, e.g., aldehyde, ketone, carboxyl and acylamide.¹⁷ According to Prabhu's report,^6a C4-functionalization of indole could be achieved by weak coordinating DGs, e.g., –CHO, –COCF₃, while strong coordinating DGs, e.g., –CONHMe, –COMe, prefer C2-site reactions. This categorization has been supported by the reports from different research groups.^6b,16a,d,18

However, in a recent report of exclusive C4-fluoroalkylation of indoles under mild conditions (Scheme 1),¹⁹ the reaction was achieved in the presence of strong coordinating –COMe at the C3 position which is crucial to the good yield of this reaction. Furthermore, acidic additive TFA is crucial to this reaction as the yield of C4-fluoroalkylation reduces completely to zero without this additive. These novel results could raise several questions: What is the underlying reason for the exclusive regioselectivity of the C4 site over the C2 site in this work? Why is the acidic additive necessary and what kind of role does the additive play?

Scheme 1 Palladium-catalyzed regioselective C–H fluoroalkylation of indoles at the C4 site.

Clearly, mechanistic insights, from the theoretical viewpoint, into these experimental results are highly valuable and crucial to subsequent rational design of the reactions dedicated to certain C4 functionalization of indoles. However, according to the best of our knowledge, such a type of study, focusing on the underlying reason for the regioselectivity, is still sparse.⁵

Therefore, we conduct herein systematic DFT²⁰ calculations to understand the regioselectivity of C2 and C4 sites in the target reactions as shown in Scheme 1. Besides the roles of indole substrates 1a and Pd(II)-catalyst, the importance of acidic additives, e.g., TFA, were explored too. As believed by us, a thorough and reliable theoretical interpretation of the regioselectivity of this reaction would provide a valuable guide for related experimental reports which are expected to come soon.

Computational details

The B3LYP functional,²¹ together with the 6-31G(d) basis set for main group elements and LANL2DZ²² for Pd and I (denoted as BS1 hereafter), was used to locate all the stationary points involved. Frequency analysis at the same level of optimization was performed to confirm the nature of the stationary points as the local minimum or transition state (TS) and to evaluate the zero-point vibration energy (ZPVE) as well as thermal corrections. Intrinsic reaction coordinate (IRC) calculations²³ were further performed to verify the located TS.

To provide more accurate results, electronic energies were also calculated with the M06-2X functional²⁴ and a larger basis set which is a combination of 6-311+G(d,p)²⁵ for main group elements and SDD²⁶ for Pd and I (denoted as BS2). The results have suggested that the influence of a basis set and functional on relative energies is small (Table S1 in the ESI†). For the sake of accuracy, the solvent effect should also be included for dichloromethane (DCM), which was the solvent used in the experiment. Thus the free energy of solvation was evaluated, on the gas-phase structures, at the M06-2X/BS1 level via the self-consistent reaction field (SCRF) method using the SMD model.²⁷ In the following content, the analysis of the reaction mechanism was mainly based on the free energies, i.e., ΔG_sol, including electronic energies from the B3LYP/BS2 level, free energy of solvation in DCM, and the zero-point vibration energy (ZPVE) as well as thermal corrections based on gas-phase optimization.

In order to verify the reliability of gas-phase optimization, some important stationary points were also optimized in the DCM solvent. The obtained results are close to those from gas-phase structures and thus our analysis is mainly based on results from gas-phase structures. In addition, in order to explore the influence of dispersion correction on the results,²⁸ some important stationary points were also reoptimized at both B3LYP-D3(BJ)/BS1 and M06-2X/BS1 levels. The results suggest that the differences of geometry among these methods are small and the corresponding results are close to each other (in ESI†). Therefore, in this system, we have employed the geometry from the B3LYP/BS1 level to discuss the following reaction mechanism. The natural population analysis (NPA)²⁹ has been carried out to obtain detailed information on the transferred electron density (Δe) between the catalyst and substrate in the reaction. The transferred electron density (Δe) is defined as the amount of electron density flowing from the substrate to the catalyst, equal to the difference between the isolated catalyst and the catalyst moiety in the transition state structure.

All calculations were performed with the Gaussian 09 program³⁰ and Multiwfn software³¹ was used for wavefunction analysis.

Results and discussion

In the aspect of palladium acetate, previous experiments have suggested that different forms, e.g., monomeric form Pd(OAc)₂, and polymeric form [Pd(OAc)₂]_n (n = 2, 3), could coexist in solution.³² Our calculated results indicate that monomeric form Pd(OAc)₂ could be generated from the dimer form in the DCM solvent since the free energy change is only 1.2 kcal mol⁻¹ (Scheme S1(c)†). The generation of [Pd(OAc)]⁺ from monomer Pd(OAc)₂ should be quite difficult due to the need for a large amount of free energy (58.6 kcal mol⁻¹ in Scheme S1(e)†). Therefore, in the case of palladium acetate, its monomeric form Pd(OAc)₂ will be mainly used for subsequent discussions.

Based on the proposed mechanism in previous reports,¹⁹ the whole catalytic cycles, for both C4–H and C2–H fluoroalkylation of the indole substrate 1a, should consist of 3 steps (Fig. 1): (1) C–H activation promoted by the Pd(II)-catalyst, (2) oxidative addition by 2,2,2-trifluoroethyl(mesityl)iodonium triflate salt (2a) and (3) reductive elimination leading to the final products 3aa or 3ba.

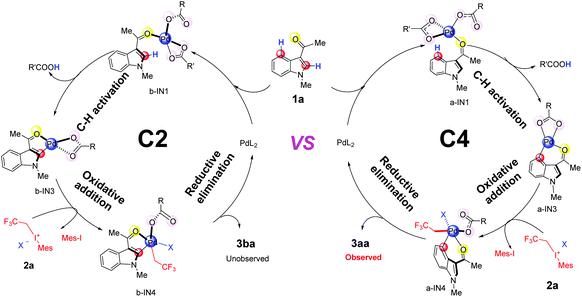Fig. 1 The catalytic cycles of C4 & C2-trifluoroalkylation of indole promoted by Pd(II)L₂, including C–H activation, oxidative addition and reductive elimination.

It has been widely accepted that various DGs would coordinate to the Pd center of the catalyst via their heteroatoms and this coordination could lead to the formation of the initial intermediates which were thermodynamically favorable.³³ Therefore, in this work, we propose that the DG of the substrate 1a coordinates to the catalyst and leads to the formation of the complexes IN1 as shown in Fig. 2. Formally, the coordination mode of one of the two L ligands changes from η² to η¹ in IN1 while the other one remains to be of η² mode (Fig. 2).

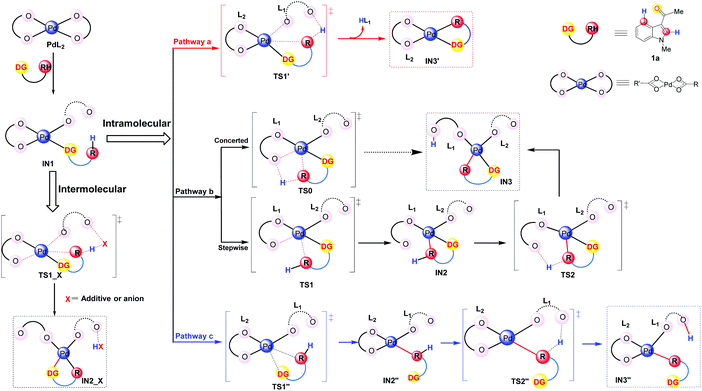Fig. 2 Possible pathways in the C–H activation step: concerted pathway (a), directed stepwise/concerted pathway (b), and undirected pathway (c).

It should be clarified that IN1 represents the whole group of isomers sharing the same coordination mode around the Pd center. Starting from IN1, according to the best of our knowledge, the C–H activation would proceed in two patterns: intermolecular and intramolecular (in Fig. 2). For the intermolecular one, the proton is abstracted by an external group, e.g., additive or its derivatives. In the case of the intramolecular pattern, where the abstraction of a proton is accomplished by ligand L of the Pd-catalyst, three different pathways (a–c of Fig. 2) were explored.

Pathway a is a concerted metalation deprotonation process (CMD)^15a,34 as both the formation of Pd⋯π interaction and the proton transfer at the C4/C2 position proceed via a single transition state TS1′. The ligand which abstracts the proton H will be denoted as L₁ and the other as L₂ hereafter. It should be noted that the proton transfer in this pathway is accomplished by the ligand L₁ which formally coordinates to the Pd center in the η¹ mode, i.e., η¹–L₁. Besides the release of one equivalent acid HL, the intermediate IN3′, participating in the subsequent step of oxidative addition, is also produced. During the whole pathway, DG always coordinates to the Pd center and thus pathway a could be indicated as a directed concerted process.

As shown in Fig. 2, pathway b is also a directed one.^33c,d,35 Besides leading directly to the final product IN3 in a concerted pattern viaTS0, there is another possibility for pathway b to proceed in a directed stepwise process. The latter consists of two steps: first the formation of Pd⋯π interaction, leading to IN2, occurs viaTS1 and then the proton at the C4/C2 position of IN2 transfers viaTS2, leading to IN3 eventually. Being different from pathway a, the proton transfer here is completed by the ligand L₁ which is formally in the η² coordination mode to the Pd center, i.e., η²-L₁.

Although the above pathways are all directed, previous reports of Pd-catalyzed C–H activations of some aromatic substrates, e.g., anisole and chlorobenzene, do indicate the possibility of undirected processes in which the Pd–O_DG bond in IN1 could be broken in the subsequent steps.^33d Thus, in order to provide a thorough exploration of the reaction mechanism, an undirected stepwise process, i.e., pathway c in Fig. 2, is also taken into account in this work. This pathway includes two steps: firstly, viaTS1′′, the formation of Pd⋯π interaction replaces the Pd–O_DG bond in IN1 and leads to IN2′′; secondly, viaTS2′′, the abstraction of a proton at the C4/C2 position of IN2′′ is achieved by a η¹–L₁, resulting in IN3′′ eventually.

C–H activation catalyzed by Pd(OAc)₂

We firstly study here the mechanism of C4–H activation catalyzed by the original Pd(OAc)₂ catalyst. In the intramolecular pattern, for pathway a (the red line in Fig. 3), the formation of the common starting intermediate a₀′-IN1 is an endergonic process requiring an amount of energy of 9.3 kcal mol⁻¹. From a₀′-IN1, the reaction proceeds via a concerted TS a₀′-TS1 of the 6-membered palladium-cycle structure, in which η¹-OAc abstracts the proton H to result in the species a₀′-IN2. After the release of one equivalent of HOAc, this pathway ends at the formation of a₀′-IN3. As shown in Fig. 3, the energy barrier of the C4–H activation step of pathway a here is 35.8 kcal mol⁻¹. This value is too high for the reaction to proceed at room temperature which is the experimental condition. Thus this concerted pathway should not be available.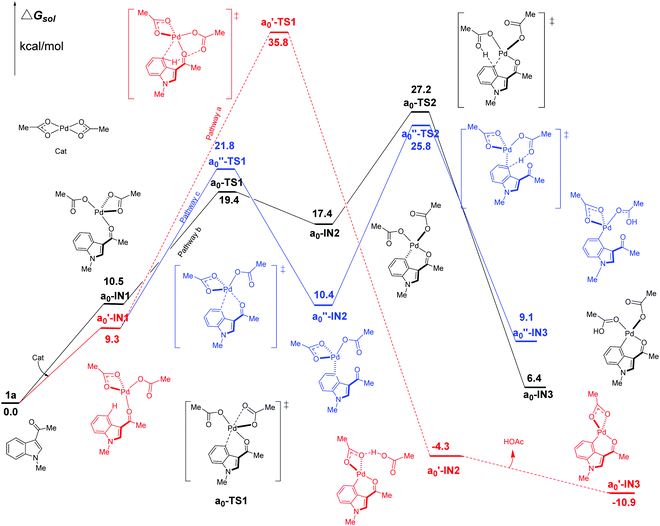

Fig. 3 Three possible pathways (intramolecular pattern) of C4–H activation in indole with Pd(OAc)₂ as the catalyst.

In the case of pathway b, we first investigate its stepwise version (the black line in Fig. 3). From the starting point of an endergonic intermediate of a₀-IN1 (10.5 kcal mol⁻¹), which is an isomer of a₀′-IN1, the step of the formation Pd⋯π interaction proceeds via the ligand-exchange TS a₀-TS1 as a Pd–O_L coordination bond (O_L refers to the O atom of ligand (L₁ L₂) in the palladium-catalyst) is weakened by the Pd⋯π interaction. As the product of this step, the intermediate a₀-IN2 is higher in energy than a₀-IN1 by 6.9 kcal mol⁻¹. The reason for this increase in energy might be attributed to the unfavorable replacement of a Pd–O_L coordination bond by the weak Pd⋯π interaction. The subsequent step of the proton transfer, starting from a₀-IN2, proceeds via the TS a₀-TS2 of a structure of 6-membered palladium cycle, leading to a₀-IN3 which is an isomer of a₀′-IN2. The calculated free energy data suggest that the step of proton transfer is rate-determining as a₀-TS2 is the highest TS of the whole pathway b. The energy barrier of this step is calculated to be 27.2 kcal mol⁻¹. Although lower than that of pathway a, this high energy barrier still denies the possibility of pathway b, in this stepwise fashion, at room temperature. Another point, worthy of being noted, is that the obtained intermediate a₀-IN3 is energetically unfavorable (6.4 kcal mol⁻¹) when compared with the reactants (Fig. 3).

Besides the stepwise version, the corresponding concerted one of pathway b is also found. In this version, starting from a similar intermediate a₀-IN1′, a barrier of 26.4 kcal mol⁻¹ ought to be overcome. Thus this one should be impossible at room temperature too (see ESI, Fig. S2†).

In the case of undirected pathway c, via the TS a₀′′-TS1 which is higher in free energy than a₀′-IN1 by 12.5 kcal mol⁻¹, the Pd⋯π interaction replaces the Pd–O_DG bond intramolecularly and leads to the intermediate a₀′′-IN2. Then the proton transfers, via the TS a₀′′-TS2, to form the species a₀′′-IN3. In this pathway, a₀′′-TS2 is the highest TS and thus the rate-determining free energy barrier is calculated to be 25.8 kcal mol⁻¹. Clearly, at room temperature, it is still hard for pathway c of C4–H activation to proceed even though its energy barrier is lower than those of pathways a and b.

As shown above, under the catalyst of original Pd(OAc)₂ alone, all the intramolecular pathways should be impossible at room temperature. For C2–H activation, similar results exist as shown in Fig. S4 (see the ESI†). These calculated results are consistent with the experimental observation in which the yield of the reaction is near zero without acidic TFA as the additive.

It has been reported that the additive itself could be involved directly, as an assistant, in the step of C–H activation (intermolecular pattern in Fig. 1). Thus we firstly investigate the role of acidic TFA within this pattern.

According to previous reports, there are several possible modes to involve TFA to abstract a proton: neutral TFA molecule, CF₃COO⁻ anion, or new complex formed by TFA with substrate 2a.^33g,36 In this work, when neutral TFA is involved, the energy barriers of C4/C2–H activation are 22.6/25.2 kcal mol⁻¹ (Fig. S5†) and thus they are still difficult to proceed at room temperature. For the involvement of either a CF₃COO⁻ anion or new complex compositing of TFA, the barriers of C4/C2–H activation reach up to 30–43 kcal mol⁻¹, which are even higher (Fig. S6 and S7†). Thus, instead of acting as an assistant, the necessity of addition of TFA should arise from other possibilities which promote C–H activation.

Actually TFA could change the electronic structure and geometrical structure of the original Pd-catalyst via the introduction of a strong electron-withdrawing trifluoroacetate ligand.³⁷ According to our calculations, two possible Pd salts, i.e., Pd(TFA)₂ and Pd(OAc)(TFA), could be feasibly generated from Pd(OAc)₂ by adding TFA (Scheme S1†). Thus, we have explored both the C4–H and C2–H activation catalyzed by these new possible Pd salts.

C–H activation catalyzed by Pd(TFA)₂

Firstly, the C4–H activation catalyzed by Pd(TFA)₂ was explored for all the possible pathways in Fig. 4. Being different from Pd(OAc)₂, Pd(TFA)₂ is capable of forming exergonic intermediates a₁-IN1 and a₁′-IN1via the coordination to the substrate 1a (Fig. 4).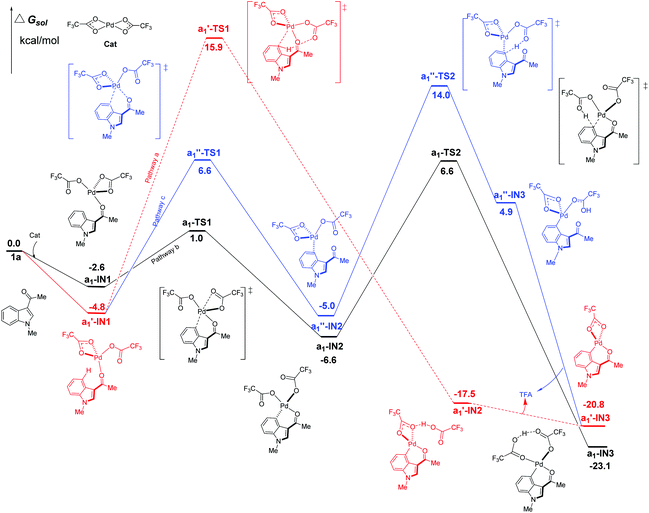

Fig. 4 Three possible pathways of C4–H activation (intramolecular pattern) in indole with Pd(TFA)₂ as the efficient catalyst.

As shown in Fig. 4, the most kinetically favorable pathway is b in stepwise pattern (the black line), where the a₁-TS2 is characterized as the highest TS giving a free-energy barrier of only 13.2 kcal mol⁻¹, i.e., the energy difference between a₁-IN2 and a₁-TS2. Obviously, this energy barrier is consistent with the experimental observation of a room-temperature reaction. In the aspect of thermodynamics, pathway b is also favorable due to the release of an amount of energy of 23.1 kcal mol⁻¹ after the formation of the 6-membered intermediate a₁-IN3.

Compared to pathway b, the energies of the corresponding TS of the pathways a and c are all higher than that of a₁-TS2 (6.6 kcal mol⁻¹) by 9.3 (a₁′-TS1) and 7.4 kcal mol⁻¹ (a₁′′-TS2) respectively. Thus, these two paths should be less favorable.

In the case of C2–H activation catalyzed by Pd(TFA)₂ as shown in Fig. 5, the free energy barrier of b, calculated to be 17.8 kcal mol⁻¹ (between b₁-IN1 and b₁-TS2), is remarkably lower than those of pathways a and c, which are 25.1 and 21.1 kcal mol⁻¹, respectively. The energies of the corresponding TS of pathways a and c are higher than that of b₁-TS2 (13.0 kcal mol⁻¹) by 6.3 (b₁′-TS1) and 2.4 kcal mol⁻¹ (b₁′′-TS2) respectively. In the aspect of thermodynamics, pathway b here is also an exothermic one, releasing an amount of energy of 18.3 kcal mol⁻¹ after the formation of the 5-membered intermediate b₁-IN3. Additionally, the energies of the final products (b₁′-IN3) of pathways a and c are also higher than that of b (b₁-IN3) as shown in Fig. 5. Therefore, in the aspects of both kinetics and thermodynamics, pathway b is the most favorable one for C2–H activation here.

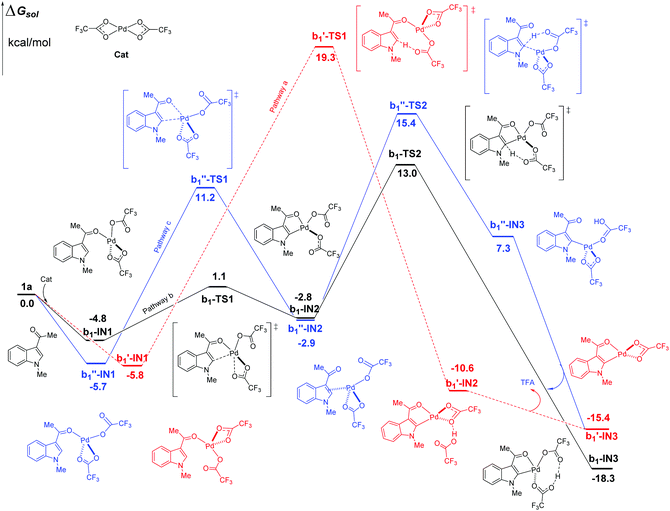Fig. 5 Three possible pathways of C2–H activation (intramolecular pattern) in indole with Pd(TFA)₂ as the efficient catalyst.

As shown above, when Pd(TFA)₂ plays the role of a catalyst, the energy barriers of the most favorable pathways, for either C4–H or C2–H activation, are significantly reduced to certain values (13.2, 17.8 kcal mol⁻¹ for both C4 and C2–H, respectively), with which a room-temperature reaction should be feasible. Furthermore, the most favorable rate-determining energy barrier of C2–H activation (b₁-TS2) is higher than that of C4–H activation (a₁-TS2) by 4.6 kcal mol⁻¹. The free energy of b₁-TS2 is also higher than that of a₁-TS2 by 6.4 kcal mol⁻¹. Such large energy differences should successfully lead to the exclusive regioselectivity of C4–H activation which is the experimental observation.

It should be mentioned that the other possible TSs of pathway b, in both C4–H and C2–H activation catalyzed Pd(TFA)₂, are also found in our calculations (Fig. S8–S10†). However, their energies are quite close to that of either a₁-TS2 or b₁-TS2, with the differences lying within 0.3–0.8 kcal mol⁻¹.

Similar to Pd(OAc)₂ in Section.1, we have also explored the intermolecular pattern of C–H activation catalyzed by Pd(TFA)₂ where one external TFA is involved (Fig. S11†). The corresponding energy barriers of C4–H and C2–H activation are 13.0 and 17.8 kcal mol⁻¹, respectively. These values are quite close to the results of the cases without TFA, 13.2 and 17.8 kcal mol⁻¹ (Fig. 4–5). Thus the necessity of the addition of TFA mainly comes from its capability of providing Pd(TFA)₂ as the efficient catalyst.

Pd(OAc)(TFA) as the catalyst

When Pd(OAc)(TFA) is employed as the catalyst, there is more than one possibility on the ligand abstracting the H atom (Fig. S12–S15 in the ESI†) because of the existence of two different ligands OAc⁻, and CF₃COO⁻. Here we use Pd(OAc)(TFA) to denote the case where the OAc⁻ ligand works to abstract the proton H and Pd(TFA)(OAc) means that the CF₃COO⁻ ligand plays the role of abstracting the proton H.

In the case of Pd(OAc)(TFA), the most favorable pathway is b of concerted fashion, irrespective of C4–H or C2–H activation (Fig. S12 and S13†). The calculated energy barriers are 13.2 (a₂-TS0) and 17.0 (b₂-TS0) kcal mol⁻¹ for C4–H and C2–H activation, respectively. Significantly, the energy barrier of C4–H activation is lower than that of C2–H activation by 3.8 kcal mol⁻¹, which could achieve the regioselectivity of the C4 site over C2. For pathways a and c, the rate-determining barriers of other pathways lie within the range of 20–37 kcal mol⁻¹ which are remarkably higher than those of pathway b.

Similar to Pd(TFA)₂, Pd(OAc)(TFA) is also capable of facilitating the reaction at room temperature and leading to the regioselectivity of the C4 site. However, the free energy of the TS for the most favorable pathway for C4–H activation here is remarkably higher than that of Pd(TFA)₂ by 6.6 kcal mol⁻¹ (Table 1). Therefore, as catalysts, the efficiency of Pd(OAc)(TFA) should be significantly lower than that of Pd(TFA)₂.

Table 1 Comparison of the overall free energies/energy barriers of the rate-determining TS of various pathways in the intermolecular pattern between C2–H and C4–H activations (kcal mol⁻¹)

	Pathway a		Pathway b		Pathway c
The free energies	C2/C4–H	Δ	C2/C4–H	Δ	C2/C4–H	Δ
Pd(OAc)2	37.0/35.8	1.2	28.2/27.2	1.0	25.5/25.8	−0.3
Pd(TFA)(OAc)	24.5/22.3	2.2	25.4/21.7	3.7	21.7/21.4	0.3
Pd(OAc)(TFA)	36.6/29.7	6.9	16.9/13.2	3.7	21.4/20.7	0.7
Pd(TFA)2	19.3/15.9	3.4	13.0/6.6	6.4	15.4/14.0	1.4
			7.4/0.6^a	6.8^a
			12.5/6.1^b	6.4^b

---

The energy barriers	C2/C4–H	Δ	C2/C4–H	Δ	C2/C4–H	Δ
a With electronic energies at the M06-2X/BS2 level. b From the results based on solvent-phase geometries.
Pd(OAc)2	37.0/35.8	1.2	28.2/27.2	1.0	25.5/25.8	−0.3
Pd(TFA)(OAc)	26.8/23.9	2.9	25.4/21.7	3.7	24.0/23.0	1.0
Pd(OAc)(TFA)	36.6/29.7	6.9	17.0/13.2	3.8	21.4/20.7	0.7
Pd(TFA)2	25.1/20.7	4.4	17.8/13.2	4.6	21.1/19.0	2.1
			18.1/15.3^a	2.8^a
			19.5/4.2^b	5.3^b

---

In the case of Pd(TFA)(OAc), for both C4–H and C2–H activations, the most favorable pathway is c with the energy barriers of 23.0 and 24.0 kcal mol⁻¹, respectively (Fig. S14 and S15†). These values are remarkably higher than those of both Pd(TFA)₂ and Pd(OAc)(TFA). Therefore, it is hardly possible for Pd(TFA)(OAc) to work as the efficient catalyst under the coexistence of Pd(TFA)₂ and Pd(OAc)(TFA).

It is indicated that the performance of Pd(OAc)(TFA) as the catalyst is highly dependent on the ligand which abstracts the proton H. When OAc⁻ abstracts the proton H, Pd(OAc)(TFA) works similarly to Pd(TFA)₂ with lower efficiency. When CF₃COO⁻ abstracts the proton H, Pd(OAc)(TFA) works similarly to Pd(OAc)₂ with high energy barriers for all the pathways.

Through the discussion above, Pd(TFA)₂ is calculated to be the most efficient catalyst for the C–H activation step, which not only decreases the barriers of the reaction, but also leads to the regioselectivity of the C4 site over C2. In order to verify the reliability of the results, firstly, we have performed the optimization of some important stationary points in the DCM solvent. As shown in Fig. S16 and S17 and Tables S2–S6 (in the ESI†), not only the difference between gas-phase geometry and that in solvent are actually small (seen in Tables S2–S6†), but also the calculated energy barriers are close to each other.

In addition, we have employed both B3LYP-D3(BJ) or M06-2X methods to include dispersion corrections in the optimization of some important stationary points. As shown in Fig. S18 and S19 and Table S7 in the ESI,† the energy barriers, from different methods, are close to each other. For example, in C4–H activation, the energy barriers from B3LYP, B3LYP-D3(BJ), and M06-2X are 13.2, 11.5, and 13.6 kcal mol⁻¹, respectively; the corresponding differences are 0.4–1.8 kcal mol⁻¹. Similar results exist in C2–H activation too (Table S7 in the ESI†). In the aspect of optimized geometry, the difference from various methods is small too (Tables S8–S21†). As shown in Table S8,† the average differences of inter-atomic distances and the corresponding average deviations lie within the range of 0.000–0.009 Å and 0.000–0.020 Å, respectively. For some important inter-atomic distances, the corresponding differences lie within the range of 0.000–0.021 Å (Table S9†). Thus the geometries at the B3LYP level should be reliable in this system and the obtained results should be reasonable.

Finally, in order to explore the influence of functionals and basis set on the results, we have calculated the electronic energies at other levels, e.g., B3LYP/BS1, M06-2X/BS1, and M06-2X/BS2. The results indicate that our conclusion is preserved although there are indeed mild differences in numerical details (Table S1 in the ESI†). For example, at the M06-2X/BS2 level, the difference of the activation free energies between C2 and C4–H activations is 6.8 kcal mol⁻¹, quite close to that of the B3LYP/BS2 level (6.4 kcal mol⁻¹ in Table 1). In addition, these results further support the conclusions that the influence of the basis set and functional on relative energies is small.

Knowing that Pd(TFA)₂ is calculated to be the most efficient catalyst for the C–H activation step, the subsequent oxidative addition and reductive elimination steps were also explored. As shown in Fig. S20 and S21,† the free energies of the TS of these two steps are quite lower than those of C–H activation. These results support that the C–H activation is the key step for regioselectivity in the whole catalytic cycle.

The underlying basis of the improvement of the performance of Pd(TFA)₂ as the catalyst

Based on the discussion above, the necessity of additive TFA should be attributed to its capability of generating a Pd-catalyst, especially Pd(TFA)₂. As shown in Table 1, for the most favorable pathways of both C4–H and C2–H activations, the energy barriers, as well as the overall free energies of the TS, are significantly reduced from those of original Pd(OAc)₂ to Pd(TFA)₂. Moreover, under the catalysis of Pd(TFA)₂, the energy barrier of the most favorable pathway for C4–H activation is remarkably lower than that for C2–H activation by 4.6 kcal mol⁻¹. In the aspect of the free energy of the rate-determining TS, the value of C2–H activation is higher than that of C4–H activation by 6.4 kcal mol⁻¹. Thus, besides facilitating the reaction at room temperature, the most important role of the addition of TFA is to result in large differences between C4–H and C2–H activations which should give rise to the exclusive C4 selectivity eventually.

In order to explore the underlying reason for the improved efficiency of Pd(TFA)₂, detailed analysis was performed on the calculated data. According to the theory of frontier molecular orbital (FMO), the feasibility of a reaction could be measured by the energy difference between the highest occupied molecular orbital (HOMO) of one reactant and the lowest unoccupied molecular orbital (LUMO) of the other. The lower this difference is, the easier it is for the reaction to proceed.

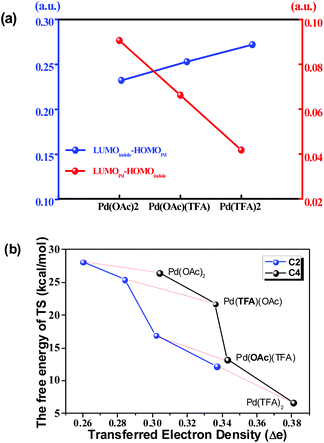
As shown in Fig. 6(a), the energy gap between the LUMO of the Pd-catalyst (LUMO_Pd) and the HOMO of indole substrate 1a (HOMO_indole) gradually reduces along the order of Pd(OAc)₂, Pd(OAc)(TFA) and Pd(TFA)₂. This trend is consistent with the order of efficiency of these 3 Pd-catalysts shown above. In comparison, the gap between LUMO_indole and HOMO_Pd, with values significantly larger than those of LUMO_indole–HOMO_Pd, is opposite to the order of catalyst efficiency. Thus the FMO analysis implies that electron density is donated from 1a to the Pd-catalyst.

Fig. 6 (a) The LUMO–HOMO gap involving different Pd-catalysts. (b) The correlation between the free energy of the TS and the amount of transferred electron density in pathway b under various Pd-catalysts.

Taking the implication from the LUMO_Pd–HOMO_indole gap, the amount of transferred electron density (Δe), from 1a to the Pd-catalyst, might provide further information on the step of C–H bond activation. As shown in Fig. 6(b), there is a clear correlation between the free energy of the TS and the amount of Δe in pathway b. This correlation is consistent with the implication from FMO analysis. That is to say, a smaller LUMO_Pd–HOMO_indole gap leads to a larger amount of transferred electron density and thus a higher degree of feasibility of C–H activation eventually. Moreover, the regioselectivity of the C4 site over the C2 site is also represented in this correlation since the amount of Δe of C4–H activation is larger than that of C2–H activation under the same Pd-catalyst (Fig. 6(b)). Similar results exist in other pathways too (Fig. S23†).

This correlation could be explained that a larger amount of Δe is capable of giving rise to stronger attractive interaction between substrate 1a and the Pd-catalyst which stabilizes the TS. This explanation is confirmed by the activation strain mode³⁸ as shown in Fig. S29 and S30.†

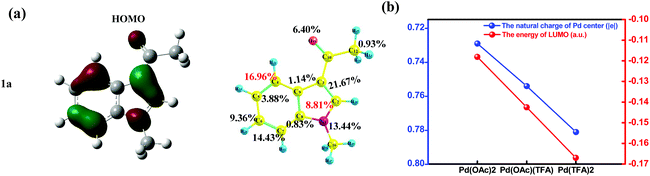
As shown in Fig. 7(a), for substrate 1a, HOMO_indole is mainly of delocalized π type and its contribution from the C4 site (16.96%) is almost as large as twice of that from C2 site (8.81%). Thus, the donation of electron density from this MO is more feasible to take place at the C4 site when compared to that at the C2 site. The results of Fukui function f⁺ of 1a provide the same prediction as the absolute value of the C4 site (0.130) is remarkably larger than that of the C2 site (0.047) as shown in Fig. S25.† These ought to be the reason for the results that, in most pathways of C–H activation explored here, the C4 site reaction is calculated to be more feasible than the C2 site reaction (Table 1). In addition, these results are also consistent with the larger amount of Δe of C4–H activation than that of C2–H activation under the same Pd-catalyst (in Fig. 6(b)).

Fig. 7 (a) The HOMO distribution of substrate 1a and the corresponding atomic contributions. (b) The comparisons of the energies of the LUMO for various Pd-catalysts and the corresponding natural charges of the Pd center in the Pd-catalyst.

It is easy to understand that the most important contribution to LUMO_Pd comes from the Pd(II) center (∼60%) which should be the most important site to accept electron density donated from 1a. Besides lowering the energy of LUMO_Pd (Fig. 7(b), blue line), the addition of acidic TFA also increases the amount of positive charges of the Pd center of the catalyst (Fig. 7(b), red line). All these results support the increase of the accepting ability of the catalyst due to the addition of TFA. In other words, the demand for electron density, donated from 1a, grows up because of TFA. This increased demand would strengthen the discrimination between carbon sites of different donating ability, e.g., C4 vs. C2, and thus sharpens the regioselectivity of the C4 site over the C2 site.

Based on the discussion above, other acidic additives, which are capable of introducing strong electron-withdrawing ligands into the Pd-catalyst, would also realize the exclusive C4-fluoroalkylation under mild reaction conditions according to the discussion above. This prediction was theoretically explored in the case of HOTf, whose acidity is stronger than that of TFA. Our results suggest that new Pd-catalysts including the OTf⁻ ligand, e.g., Pd(OTf)₂ and Pd(TFA)(OTf), could be generated via adding HOTf. The performances of these Pd-catalysts were calculated to be even better than that of Pd(TFA)₂ (Table S26†). These results might provide a useful guide for subsequent condition optimization of reactions of this type.

The correspondence between the theoretical prediction and experimental observation is an important issue that should not be ignored. While the experimental examination of these predictions is beyond the scope of this theoretical work, we do find some experimental and theoretical reports which describe the priority of the usage of Pd(TFA)₂ or the collection of Pd(OAc)₂ and HOTf than Pd(OAc)₂ alone as the catalyst.^37c,39 Although in an indirect way, these reports could be considered as support of the predictions based on our calculations. Thus, we have thought that the proposed mechanism in this work should be reasonable.

Conclusions

A detailed mechanistic study of Pd(II)-catalyzed C4-fluoroalkylation of 3-ethylindole (1a), with 2,2,2-trifluoroethyl(mesityl)iodonium triflate salt (2a) as the fluoroalkylation reagent, was performed via DFT calculations. The whole catalytic cycle consists of three steps: C–H activation, oxidative addition and reductive elimination. The experimentally observed regioselectivity of the C4 site over the C2 site is mainly achieved in the step of C–H activation according to theoretical results.

In the step of C–H activation, both intermolecular and intramolecular patterns were explored. With original Pd(OAc)₂ as the catalyst alone, neither C4–H nor C2–H activation could proceed under the experimental condition of room temperature because of the calculated high energy barriers of all the possible pathways (Table 1). These theoretical results are consistent with the experimental observation that the yield of the reaction is near zero if no additive is included.

If additive TFA itself acts as an assistant, directly involved in the C–H activation, the reaction, which is of an intermolecular pattern, is still difficult to proceed under the experimental conditions even though the energy barriers are reduced a little. However, the addition of TFA could give rise to other possible Pd-catalysts, i.e., Pd(TFA)₂ and Pd(OAc)(TFA), from the view of thermodynamics.

Compared to Pd(OAc)₂, Pd(TFA)₂ would lead not only to the higher degree of feasibility for the step of C–H activation but also to the enhanced regioselectivity of the C4 site over the C2 site. The performance of Pd(OAc)(TFA) lies between Pd(OAc)₂ and Pd(TFA)₂. Therefore, together with the results on Pd(OAc)₂, the experimentally observed necessity of the acidic TFA is reproduced in our theoretical results.

Further detailed analysis indicates that transfer of electron density, from indole substrate 1a to the Pd-catalyst, should take place in the C–H activation step. Furthermore, there exists a correlation between the larger amount of transferred electron density and lower free energy of the TS, i.e., higher degree of feasibility of the reaction. Thus this transfer of electron density, which could induce attractive interaction between 1a and the Pd-catalyst in TS, should be important.

When a strong electron-withdrawing ligand of CF₃COO⁻ is introduced into Pd(TFA)₂via adding TFA, its abilities of accepting electron density from 1a should be enhanced according to both the lower LUMO energies and the larger amount of positive charge of the Pd center. This enhanced accepting ability should lead to stronger attractive interaction in the TS and thus to a lower energy barrier, i.e., higher degree of feasibility of the reaction. Furthermore, this enhanced accepting ability will also give rise to a higher degree of preference to the C4 site, of which the donating ability is verified to be stronger than that of the C2 site. Thus the experimentally observed necessity of acidic TFA should arise from the fact that it could lead to other Pd-catalysts, e.g., Pd(TFA)₂, with stronger ability as an electron acceptor due to the strong electron-withdrawing ligand CF₃COO⁻.

Based on this explanation, other acidic additives, which are capable of introducing strong electron-withdrawing ligands into the Pd-catalyst, would also realize the exclusive C4 functionalization under mild reaction conditions. This prediction was theoretically explored in the case of HOTf, whose acidity is stronger than that of TFA. Our results suggest that the performance of the potential catalysts of Pd(OTf)L (L = OAc⁻, TFA⁻ and OTf⁻) would be superior to that of Pd(OAc)₂ or even to Pd(TFA)₂. We hope our theoretical prediction would promote related experimental research in near future.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We want to express our sincere thanks to Prof. De-Cai Fang of Beijing Normal University and Dr Shi-Jun Li of Zhengzhou University for their kind comments and discussions which are quite important for the improvement of this work. This work was supported by the National Natural Science Foundation of China (No. 21103137, 21572177 and 21673173), China Postdoctoral Science Foundation (No. 2017M623225), the Natural Science Foundation of Shaanxi Province (No. 2016JZ004, 2016JQ2038 and 2018JQ3038), and the Northwest University Science Foundation for Postgraduate Students (No. YZZ17123 and YZZ17124). B. Yin is grateful to the “Excellent Young Scholar Plan” of Northwest University for a fellowship grant (No. 338050094).

References

1. (a) L. Jing, J. Susan, E. Lothar and G. H. Patrick, Angew. Chem., Int. Ed., 2001, 40, 4765–4769; (b) J. Li, A. W. Burgett, L. Esser, C. Amezcua and P. G. Harran, Angew. Chem., Int. Ed., 2001, 40, 4770–4773; (c) K. C. Nicolaou, D. Y. K. Chen, X. Huang, T. Ling, M. Bella and S. A. Snyder, J. Am. Chem. Soc., 2004, 126, 12888–12896; (d) A. J. Kochanowska Karamyan and M. T. Hamann, Chem. Rev., 2010, 110, 4489–4497; (e) N. K. Kaushik, N. Kaushik, P. Attri, N. Kumar, C. H. Kim, A. K. Verma and E. H. Choi, Molecules, 2013, 18, 6620–6662; (f) K. Liang, T. Wu and C. Xia, Org. Biomol. Chem., 2016, 14, 4690–4696; (g) M. A. Corsello, J. Kim and N. K. Garg, Chem. Sci., 2017, 8, 5836–5844.
2. (a) S. Cacchi and G. Fabrizi, Chem. Rev., 2005, 105, 2873–2920; (b) G. R. Humphrey and J. T. Kuethe, Chem. Rev., 2006, 106, 2875–2911; (c) Q. L. Xu, L. X. Dai and S. L. You, Chem. Sci., 2013, 4, 97–102; (d) H. Ikemoto, T. Yoshino, K. Sakata, S. Matsunaga and M. Kanai, J. Am. Chem. Soc., 2014, 136, 5424–5431; (e) Y. Feng, D. Holte, J. Zoller, S. Umemiya, L. R. Simke and P. S. Baran, J. Am. Chem. Soc., 2015, 137, 10160–10163; (f) Y. Yang, X. Qiu, Y. Zhao, Y. Mu and Z. Shi, J. Am. Chem. Soc., 2016, 138, 495–498.
3. (a) W. Oppolzer, J. I. Grayson, H. Wegmann and M. Urrea, Tetrahedron, 1983, 39, 3695–3705; (b) H. Liu and Y. Jia, Nat. Prod. Rep., 2017, 34, 411–432.
4. C. Wallwey and S. M. Li, Nat. Prod. Rep., 2011, 28, 496–510.
5. J. Kalepu, P. Gandeepan, L. Ackermann and L. T. Pilarski, Chem. Sci., 2018, 9, 4203–4216.
6. (a) V. Lanke, K. R. Bettadapur and K. R. Prabhu, Org. Lett., 2016, 18, 5496–5499; (b) J. Lv, B. Wang, K. Yuan, Y. Wang and Y. Jia, Org. Lett., 2017, 19, 3664–3667.
7. A. H. Sandtorv, Adv. Synth. Catal., 2015, 357, 2403–2435.
8. (a) R. A. Hollins, L. A. Colnago, V. M. Salim and M. C. Seidl, J. Heterocycl. Chem., 1979, 16, 993–996; (b) M. Iwao and F. Ishibashi, Tetrahedron, 1997, 53, 51–58; (c) T. Mesganaw, N. F. Fine Nathel and N. K. Garg, Org. Lett., 2012, 14, 2918–2921.
9. J. Xiu and W. Yi, Catal. Sci. Technol., 2016, 6, 998–1002.
10. M. A. Brown and M. A. Kerr, Tetrahedron Lett., 2001, 42, 983–985.
11. O. Yonemitsu, P. Cerutti and B. Witkop, J. Am. Chem. Soc., 1966, 88, 3941–3945.
12. (a) H. M. L. Davies and D. Morton, Chem. Soc. Rev., 2011, 40, 1857–1869; (b) T. Furuya, A. S. Kamlet and T. Ritter, Nature, 2011, 473, 470–477; (c) M. Simonetti, D. M. Cannas, A. Panigrahi, S. Kujawa, M. Kryjewski, P. Xie and I. Larrosa, Chem. – Eur. J., 2017, 23, 549–553; (d) J. A. Leitch, Y. Bhonoah and C. G. Frost, ACS Catal., 2017, 7, 5618–5627; (e) J. A. Leitch, C. J. Heron, J. McKnight, G. Kociok-Kohn, Y. Bhonoah and C. G. Frost, Chem. Commun., 2017, 53, 13039–13042.
13. L. Y. P. Luk, Q. Qian and M. E. Tanner, J. Am. Chem. Soc., 2011, 133, 12342–12345.
14. G. L. Gao, C. Yang and W. Xia, Chem. Commun., 2017, 53, 1041–1044.
15. (a) D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823; (b) J. Wencel-Delord, T. Dröge, F. Liu and F. Glorius, Chem. Soc. Rev., 2011, 40, 4740–4761; (c) J. Wencel-Delord and F. Glorius, Nat. Chem., 2013, 5, 369; (d) Y. Yang and Z. Shi, Chem. Commun., 2018, 54, 1676–1685.
16. (a) V. Lanke and K. Ramaiah Prabhu, Org. Lett., 2013, 15, 6262–6265; (b) Q. Liu, Q. Li, Y. Ma and Y. Jia, Org. Lett., 2013, 15, 4528–4531; (c) X. Chen, G. Zheng, Y. Li, G. Song and X. Li, Org. Lett., 2017, 19, 6184–6187; (d) S. Chen, B. Feng, X. Zheng, J. Yin, S. Yang and J. You, Org. Lett., 2017, 19, 2502–2505; (e) Y. Q. Yang, P. Gao, Y. Zhao and Z. Z. Shi, Angew. Chem., Int. Ed., 2017, 56, 3966–3971; (f) K. R. Bettadapur, R. Kapanaiah, V. Lanke and K. R. Prabhu, J. Org. Chem., 2018, 83, 1810–1818.
17. (a) X. Liu, G. Li, F. Song and J. You, Nat. Commun., 2014, 5, 5030; (b) T. J. Potter, D. N. Kamber, B. Q. Mercado and J. A. Ellman, ACS Catal., 2017, 7, 150; (c) V. Lanke and K. R. Prabhu, Chem. Commun., 2017, 53, 5117–5120.
18. M. S. Sherikar, R. Kapanaiah, V. Lanke and K. R. Prabhu, Chem. Commun., 2018, 54, 11200–11203.
19. A. J. Borah and Z. Shi, Chem. Commun., 2017, 53, 3945–3948.
20. R. G. Parr, Density-functional theory of atoms and molecules, Oxford University Press, Oxford, U.K., 1989.
21. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
22. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
23. (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368; (b) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
24. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
25. (a) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648; (b) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
26. (a) P. Fuentealba, H. Preuss, H. Stoll and L. Von Szentpály, Chem. Phys. Lett., 1982, 89, 418–422; (b) D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141.
27. U. Domańska, M. Laskowska and A. Pobudkowska, J. Phys. Chem. B, 2009, 113, 6397–6404.
28. (a) P. R. Schreiner, L. V. Chernish, P. A. Gunchenko, E. Y. Tikhonchuk, H. Hausmann, M. Serafin, S. Schlecht, J. E. P. Dahl, R. M. K. Carlson and A. A. Fokin, Nature, 2011, 477, 308; (b) T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586.
29. (a) J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218; (b) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746; (c) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, E.01, Gaussian, Inc., Wallingford CT, 2009.
31. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
32. W. A. Carole and T. J. Colacot, Chem. – Eur. J., 2016, 22, 7686–7695.
33. (a) Y. Lan, C. Wang, J. R. Sowa and Y. D. Wu, J. Org. Chem., 2010, 75, 951–954; (b) Y. Lan and K. N. Houk, J. Org. Chem., 2011, 76, 4905–4909; (c) L. Zhang and D. C. Fang, J. Org. Chem., 2013, 78, 2405–2412; (d) L. Zhang and D. C. Fang, J. Org. Chem., 2016, 81, 7400–7410; (e) L. Zhang and D. C. Fang, Organometallics, 2017, 36, 4943–4951; (f) L. Zhang and D. C. Fang, Org. Chem. Front., 2017, 4, 1250–1260; (g) D. Wen, B. Yuan, R. He, W. Shen and M. Li, Tetrahedron Lett., 2018, 59, 462–468.
34. (a) S. Rousseaux, M. Davi, J. Sofack-Kreutzer, C. Pierre, C. E. Kefalidis, E. Clot, K. Fagnou and O. Baudoin, J. Am. Chem. Soc., 2010, 132, 10706–10716; (b) L. David and F. Keith, Chem. Lett., 2010, 39, 1118–1126; (c) D. L. Davies, S. A. Macgregor and C. L. McMullin, Chem. Rev., 2017, 117, 8649–8709.
35. B. Lian, L. Zhang, S. J. Li, L. L. Zhang and D. C. Fang, J. Org. Chem., 2018, 83, 3142–3148.
36. L. Guo, F. Zhang and X. Zhang, J. Mol. Model., 2016, 22, 280.
37. (a) P. Y. Lee, P. Liang and W. Y. Yu, Org. Lett., 2017, 19, 2082–2085; (b) K. Pandey, K. Rangan and A. Kumar, J. Org. Chem., 2018, 83, 8026–8035; (c) S. Kumar, R. K. Saunthwal, M. Mujahid, T. Aggarwal and A. K. Verma, J. Org. Chem., 2016, 81, 9912–9923.
38. (a) W. J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127; (b) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967.
39. (a) Y. Wu, B. Li, F. Mao, X. Li and F. Y. Kwong, Org. Lett., 2011, 13, 3258–3261; (b) A. N. Campbell, E. B. Meyer and S. S. Stahl, Chem. Commun., 2011, 47, 10257–10259; (c) C. Zhang and Y. Rao, Org. Lett., 2015, 17, 4456–4459; (d) L. Y. Shao, L. H. Xing, Y. Guo, K. K. Yu, W. Wang, H. W. Liu, D. H. Liao and Y. F. Ji, Adv. Synth. Catal., 2018, 360, 2925–2937; (e) B. Wang, C. Jiang, J. Qian, S. Zhang, X. Jia and Y. Yuan, Org. Biomol. Chem., 2018, 16, 101–107; (f) D. Wang and S. S. Stahl, J. Am. Chem. Soc., 2017, 139, 5704–5707.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8qo01338a

---