Open Access Article
Open Access ArticleA DFT study on nanocones, nanotubes (4,0), nanosheets and fullerene C60 as anodes in Mg-ion batteries†
Esmail Vessally *ab,
Ibon Alkorta
*ab,
Ibon Alkorta *b,
Sheida Ahmadia,
Robab Mohammadia and
Akram Hosseinian
*b,
Sheida Ahmadia,
Robab Mohammadia and
Akram Hosseinian c
c
aDepartment of Chemistry, Payame Noor University, Tehran, Iran. E-mail: vessally@yahoo.com
bInstituto de Química Medica (CSIC), Juan de la Cierva, 3, Madrid 28006, Spain. E-mail: ibon@iqm.csic.es
cSchool of Engineering Science, College of Engineering, University of Tehran, P. O. Box 11365-4563, Tehran, Iran
First published on 8th January 2019
Abstract
In this article, we studied the interactions between Mg atom and Mg2+ ion and four nanostructures, including a nanocone, nanotube (4,0), nanosheet, and C60 nanocage, to obtain the cell voltages (V) for Mg-ion batteries (MIBs). Total energy, geometry optimization, frontier molecular orbital (FMO) and density of states (DOS) analyses have been performed using the ωB97XD level of theory and the 6-31G(d) basis set. The DFT calculations clarified that the changes in energy adsorption between Mg2+ ion and the nanostructures, Ead, are in the order tube > cone > sheet > cage. However, Vcell for the nanocone is the highest. The changes in Vcell of the MIBs are in the order cone > tube > sheet > cage. This study theoretically considers the possibilities of Mg as an anode in batteries due to its high Vcell values.
1 Introduction
Secondary batteries or rechargeable batteries are very important for producing electricity in various devices. In addition to wet batteries, such as lead-acid batteries, which contain liquid electrolyte in an unsealed container, dry batteries, such as zinc–carbon, nickel–cadmium, nickel–zinc and lithium-ion batteries, are well-known and have attracted much attention due to the facility of their transportation. Some dry batteries have disadvantages, including heavy metals, which are significant environmental pollutants due to their toxicity and transport issues.Lithium (Li) is a suitable anode metal for rechargeable batteries because of its low density, high specific capacity, and lowest electrochemical potential in the periodic table.1 Regarding the battery systems in Li batteries, the movement of Li+ ions through the electrolyte and electrons through the external electrical circuit to the cathode lead to a suitable battery system. Therefore, we have designed a simple model system in the present work which can reveal preliminary knowledge about the possibilities of electron transfer. This model can reveal some details about the electron transfer process which have not been thoroughly studied in experimental research on Li–CO2 batteries. We hope that the computational data reported in the present work will motivate experimental researchers to investigate this simple model system and compare their experimental results.
Li-ion batteries have some disadvantages, such as low-voltage energy storage, high cost and environmental issues.1 Sodium-ion batteries (SIBs)2 and magnesium-ion batteries (MIBs)3–5 have been suggested as useful alternatives because of their low cost and high availability. However, SIBs have high gravimetry; thus, they are not suitable for vehicles and electronic instruments.3 Rechargeable Mg-ion batteries are a promising candidate technology for future electrical energy storage because of the abundance of magnesium and its divalent character, which leads to strong interactions of Mg2+.6
There are a few reports in the literature of theoretical or experimental studies on MIBs. Matsui and coworkers experimentally studied α-MnO2 as a cathode material for rechargeable Mg batteries. Their studies showed that α-MnO2 is a promising candidate as a cathode material for rechargeable Mg batteries if its capacity retention can be significantly improved.7 J. Chen and co-workers reported that TiS2 nanotubes can be used as cathode materials in rechargeable Mg-ion batteries, indicating important advantages in terms of environmental considerations, safety and relatively high capacity.8
A few theoretical studies have been carried out on potential Mg-ion batteries (MIBs). In 2018, J. Sun and co-workers9 reported density functional theory calculations for the evaluation of phosphorene as a potential anode material for magnesium batteries. They estimated that the average voltage of Mg adsorption in phosphorene is 0.833 V, which is suitable for its application as an anode in MIBs. A. O. Pereira and co-workers reported a first-principles investigation of transition metal dichalcogenide nanotubes for Li and Mg ion battery applications.10 They investigated the adsorption and diffusion properties of Li and Mg in MoS2 and WS2 nanotubes. They found that the Mg intercalation in WS2 and MoS2 nanotubes showed remarkable diffusion properties in comparison to Li insertion.10
Recently, various nanoparticles have been studied for application in the electronics, optics and sensor fields.11–13 It has been indicated that some nanoparticles are suitable for use in ion batteries.14–17 Nanotubes, nanosheets and fullerenes have been studied as anode electrodes for lithium-ion batteries (LIBs) and SIBs.14,18 Some inorganic nanosheets, such as ZnO, SiC and MgO, have been reported as anodes in ion batteries.14,19,20
Our goal in this work is to study the use of carbon nanostructures with different shapes as anodes in Mg-ion batteries. Different shapes of nanostructures lead to different interactions between Mg2+/Mg and the nanostructures, which causes variations in the cell voltage. We investigated the interactions between Mg atom and Mg2+ ion and four nanostructures, including a nanocone, nanotube (4,0), nanosheet, and C60 nanocage (Fig. 1). The aim of this work was to obtain the cell voltages (V) of Mg-ion batteries based on the four nanostructures (Table 1).
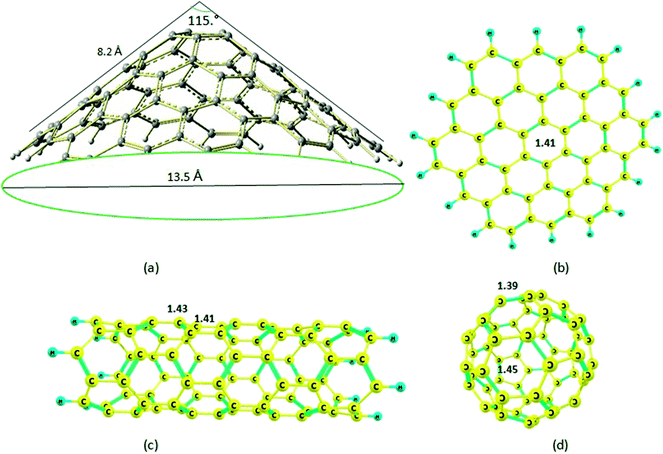 | ||
| Fig. 1 Optimized molecular structures of the (a) nanocone; (b) nanosheet; (c) nanotube; (d) nanocage. | ||
| Nanostructure | Ead non-BSSE | Ead BSSE | EHOMO | ELUMO | Eg | % ΔEg | ΔEcell | Vcell |
|---|---|---|---|---|---|---|---|---|
| a Energies of the HOMO, LUMO, and HOMO–LUMO gap (Eg) are in eV. ΔEg indicates the change in Eg of the nanostructure after Mg/Mg2+ adsorption. The total energy changes (ΔEcell, kcal mol−1) and cell voltages (V) of the nanostructure-based Mg-ion batteries are shown.b Amounts in parenthesis are for interactions over the six-membered ring. | ||||||||
| Cone | — | — | −6.5 | −1.3 | 5.2 | — | −191.2 | −4.1 |
| Cone/Mg2+ | −194.9 (−192.1)b | −192.8 (−190.2)b | −10.6 (−10.6) | −7.4 (−7.4) | 3.2 (3.3) | −38.5 (−37.1) | (−188.0) | (−4.1) |
| Cone/Mg | −2.6 (−3.1) | −1.7 (−2.2) | −6.4 (−6.5) | −1.4 (−1.4) | 5.0 (5.1) | −3.4 (−2.0) | ||
| Tube | — | — | −6.4 | −2.2 | 4.2 | — | −177.2 | −3.8 |
| Tube/Mg2+ | −239.6 | −236.8 | −11.8 | −8.0 | 3.8 | −8.5 | ||
| Tube/Mg | −62.7 | −59.5 | −6.0 | −2.1 | 3.8 | −8.7 | ||
| Sheet | — | — | −6.4 | −0.8 | 5.7 | — | −173.4 | −3.8 |
| Sheet/Mg2+ | −177.6 | −176.1 | −11.7 | −8.0 | 3.7 | −34.7 | ||
| Sheet/Mg | −3.5 | −2.7 | −6.4 | −0.8 | 5.6 | −1.7 | ||
| C60 | — | — | −7.8 | −1.8 | 6.0 | — | −142.6 | −3.1 |
| C60/Mg2+ | −145.7 | −143.6 | −13.3 | −8.7 | 4.6 | −23.2 | (−141.4) | (−3.1) |
| (−144.7) | (−142.7) | (−13.4) | (−8.7) | (4.8) | (−21.3) | |||
| C60/Mg | −1.8 | −1.1 | −6.9 | −1.8 | 5.1 | −16.1 | ||
| (−2.2) | (−1.2) | (−6.7) | (−1.9) | (5.0) | (−17.1) | |||
2 Computational methods
Total energy, geometry optimization, Frontier molecular orbital (FMO) and density of states (DOS) analyses were carried out at the ωB97XD level of theory using the 6-31G(d) basis set.21 The ωB97XD method has a higher % HF exchange, which predicts Eg more accurately than other general DFT methods, such as B3LYP.22 All calculations were performed using the G09 program.23 In the optimization process, all atoms were optimized, and none of the atoms were fixed. The vibrational frequencies were calculated for our systems. All the structures were true minima on the potential energy surface. The first vibration wavelength numbers of the nanostructures and their complexes are presented in Table 2; the results indicate that no imaginary frequencies were found.| Nanostructure | ΔG kcal mol−1 | ΔΔG kcal mol−1 | TΔS kcal mol−1 | ν1−1 cm−1 |
|---|---|---|---|---|
| Cone | — | — | 36.7 | |
| Cone/Mg2+ | −195.6 | −198.5 | −16.4 | 36.4 |
| Cone/Mg | 2.9 | −16.4 | 17.8 | |
| Tube | — | — | 100.4 | |
| Tube/Mg2+ | −239.2 | −186.6 | −17.0 | 53.0 |
| Tube/Mg | −52.5 | −17.1 | 38.0 | |
| Sheet | — | — | 40.7 | |
| Sheet/Mg2+ | −178.3 | −180.5 | −21.4 | 41.4 |
| Sheet/Mg | 2.2 | −21.4 | 19.7 | |
| C60 | — | 269.9 | ||
| C60/Mg2+ | −145.8 | −148.6 | −15.4 | 150.4 |
| C60/Mg | 2.9 | −15.5 | 10.7 |
The wB97XD includes a dispersion term proposed by Grimme to properly describe weak interactions.24 The molecular formulas of the studied nanostructures are nanocone, C80H20; nanotube, C56H8; nanosheet, C54H18; and nanocage, C60. Hydrogen atoms were used to cap the boundary carbon atoms of the nanostructures.
The natural bond orbitals (NBO) of the Mg2+/Mg-nanocone complex were calculated for charge and hybridization analysis.
The Mg and Mg+ adsorption energies were computed by the following equation:
| Ead = Ecomplex − Enanostructure − EMg/Mg2+ + EBSSE | (1) |
The HOMO–LUMO energy gap (Eg) is computed as:
| Eg = ELUMO − EHOMO | (2) |
| ΔEg = [(Eg2 − Eg1)/Eg1] × 100 | (3) |
3 Results and discussion
For each nanostructure [the nanocone, nanotube (4,0), nanosheet or C60 nanocage], the physical parameters of the isolated nanostructures and their interaction energies with Mg atom or Mg2+ ion were considered first. Finally, the cell voltages (V) of the four nanostructure-based Mg-ion batteries (MIBs) were calculated and discussed.We examined all the regions at the top of the pentagon or hexagon rings, especially the top carbon atoms, for possible interactions with ionic or neutral Mg. The global minima for interactions between the metal and cone were obtained when Mg was located in the top middle of the pentagon or hexagon ring.
3.1 Adsorption of Mg/Mg2+ over the nanocone
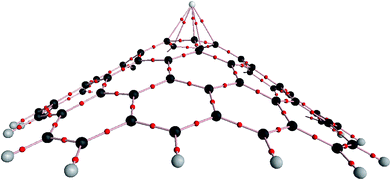
The structure of the nanocone, with a five-membered ring at its tip and six-membered rings connected to the five-membered ring, is shown in Fig. 1. A detailed description of the geometrical parameters of the carbon nanocone is presented in Fig. 1. The opening angle of the cone is about 115°. The length and diameter of the cone are 8.2 and 13.5 Å, respectively.27 The bond length of the C–C bonds of the nanocone in the five-membered ring is 1.42 Å, which is consistent with a previous article.16 The HOMO and LUMO energies are −6.51 and −1.33 eV, respectively; thus, the HOMO–LUMO gap energy is 5.18 eV (Table 1). In order to study the adsorption behavior of Mg2+/Mg on the nanocone, it was necessary to examine all possibilities of interaction between Mg2+/Mg and the five and six-membered rings of the nanocone.The formation of a complex with Mg2+ decreases the energies (more negative) of both the HOMO and LUMO levels (Fig. 3). However, the shift of the LUMO level is more significant, from −1.33 eV in the isolated molecule to −7.43 eV in the Mg2+ nanocone complex (Table 1). Therefore, Eg of the nanocone decreased from 5.18 in the pristine nanocone to 3.18 in the Mg2+-nanocone complex.
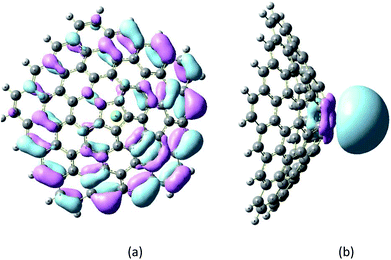
These large changes in Eg are attributed to large changes in the size and shape of the LUMO. The LUMO in the Mg2+-nanocone complex lies on the Mg2+ cation. The changes in the HOMO, LUMO and Eg are illustrated in Fig. 4 by density of states (DOS) diagrams. The plot of the partial density of states (PDOS, Fig. 5) clearly indicates that a new level produced at the Eg gap of the pristine nanocone mostly arises from the Mg2+ cation, which leads to a decrease in Eg of the Mg2+-nanocone complex.
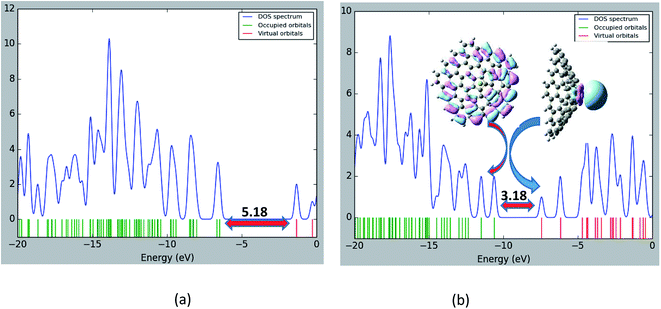 | ||
| Fig. 4 Density of states (DOS) plots of (a) the pristine nanocone; (b) the Mg+2-nanocone complex. The Eg units are in eV. | ||
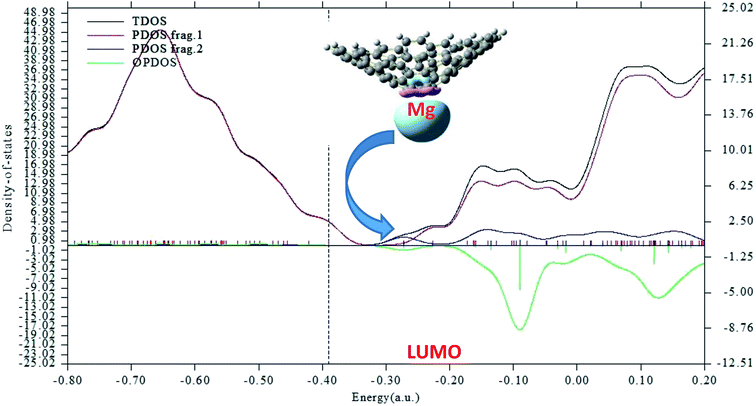 | ||
| Fig. 5 Partial density of states (PDOS) plot of the Mg2+-nanocone complex. The red and blue lines indicate the nanocone and Mg2+, respectively. The LUMO profile of this complex is also depicted. | ||
In contrast, the Mg atom does not significantly change the HOMO or LUMO levels or, consequently, the Eg value. The Mg atom slightly decreases the LUMO level and increases the HOMO level.
The NBO analysis shows a charge transfer of 0.19e from the nanocone to the Mg2+ cation. This value is higher than that of an analogous system with Na+.14 In the neutral complex, only 0.004e are transferred from the Mg atom to the nanocone, which is less than the corresponding complex with Na atom.
The hybridization of the carbon atoms in the five-membered ring in the center of the nanocone is sp2.11. After the adsorption of Mg2+, the hybridization of the carbon atoms changes to sp2.21. The DFT calculations indicate that the p character of the carbon atoms in the five-membered ring increases with adsorption of Mg2+ because these carbon atoms tend to interact with the Mg2+ cation. Strong interactions between carbon atoms in the five-membered ring and Mg2+ lead to an increment of the p character of the carbon atoms and, consequently, to an increment of the bond length from 1.419 in the pristine nanocone to 1.433 Å in the Mg2+-nanocone complex.
The electron density (ρ) and the Laplacian of the electron density (∇2ρ) are two significant criteria to evaluate the strength and character of a chemical bond.32,33 In this regard, we investigated ρ and ∇2ρ for the C–C and Mg–C chemical bonds in the five-membered ring based on AIM theory,28 as shown in Fig. 6. According to our results, the magnitude of ρ (0.300 a.u.) and the negative sign of ∇2ρ (−0.792 a.u.) for the C–C chemical bonds in the pristine nanocone and the magnitude of ρ (0.291 a.u.) and the negative sign of ∇2ρ (−0.736 a.u.) for the Mg2+-nanocone complex reflect the covalent character of the C–C chemical bonds, while the magnitude decreases for the Mg2+-nanocone complex due to interactions between the five-membered carbon atoms and Mg2+. In contrast to the C–C chemical bonds, the character of the Mg2+–C chemical bonds should be non-covalent due to the small value of ρ (0.032 a.u.) and the positive sign of ∇2ρ (0.168 a.u.).
As in the case of the adsorption of Mg2+ on the five-membered ring, both the HOMO and LUMO levels change to lower energies, and the effect on the LUMO is greater than on the HOMO. The LUMO level changes from −1.33 eV in the pristine nanocone to −7.37 eV in the Mg2+-nanocone complex (Table 1). Therefore, Eg of the nanocone decreased from 5.18 in the pristine nanocone to 3.26 in the Mg2+-nanocone complex. Based on the adsorption energy, Ead, and the HOMO–LUMO gap, Eg, we may conclude that the adsorption of Mg2+ over the five-membered ring in the nanocone is more suitable for Mg-ion batteries than adsorption over the six-membered rings.
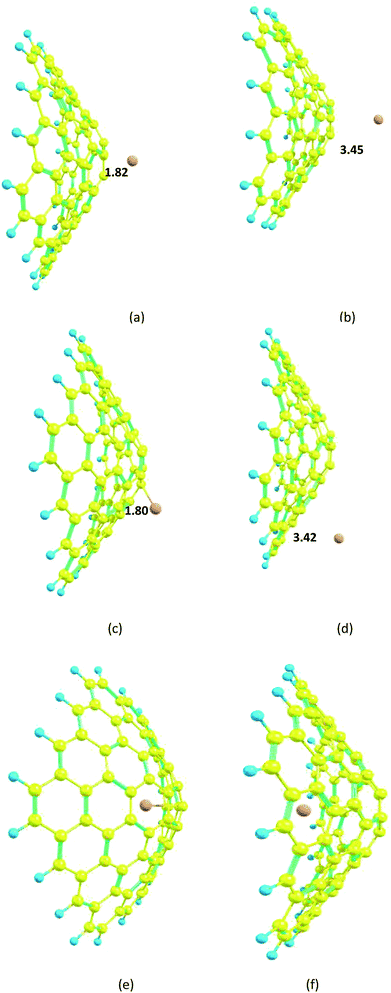
In the case of the nanocone, adsorption can occur on concave or convex surfaces (Fig. 2e and f). It is important and interesting to compare the calculated data for both cases. The interaction between Mg2+ and the nanocone on a concave surface is greater (−1.1 kcal mol−1) than on a convex surface. However, the stronger interaction between Mg and the nanocone on a concave surface (−4.0 kcal mol−1) with respect to a convex surface leads to low ΔEcell and Vcell values.
3.2 Adsorption of Mg/Mg2+ over the nanotube (4,0)
The carbon nanotube (4,0) with a zigzag configuration is shown in Fig. 7; its terminal carbons are capped with hydrogen atoms. There are two types of C–C bonds in the nanotube, whose bond lengths are 1.41 and 1.43 Å; this shows that the two bonds are different and form a boat structure. The HOMO and LUMO energies of the nanotube are −6.42 and −2.23 eV, respectively; thus, the HOMO–LUMO gap energy is 4.19 eV. The Mg2+ ion and Mg atom interact with the six-membered ring; after optimization, the distances between the Mg2+ ion and Mg atom and the plane of the nanotube become 1.61 and 1.68 Å, respectively, indicating strong interactions between the nanotube and both Mg2+ and Mg. The surprisingly strong interactions for both Mg2+ ion and Mg atom can be attributed to the boat conformation of the rings in the nanotube, which act as molecular clips. These results resemble the ionic structure described for a C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li complex.30
Li complex.30
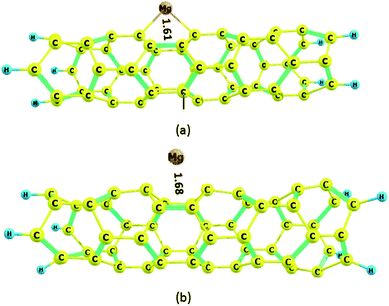 | ||
| Fig. 7 Optimized structures of the Mg2+ and Mg-nanotube complexes: (a) Mg2+-nanotube complex, (b) Mg-nanotube complex. Distances are in Å. | ||
The adsorption energy, Ead, of Mg2+ ion on the nanotube is −236.8 kcal mol−1, and that of Mg atom is −59.5 kcal mol−1 (Table 1). Our results indicate that the adsorption energies, Ead, of both Mg2+ ion and Mg atom on the nanotube are stronger than on the nanocone.
Both the HOMO and LUMO levels of the Mg2+ and Mg-complexes change to lower energies (more negative), where the shift of the Mg2+-complex is greater. However, the Eg of the nanotube slightly decreased from 4.19 in the pristine nanotube to 3.84 in the Mg2+-nanotube complex, which indicates a low sensing effect with absorption of Mg2+ on the nanotube. The ΔEg of the Mg2+-nanotube complex is −8.5, which is smaller in absolute value than that of the Mg2+-nanocone complex (−38.5).
3.3 Adsorption of Mg/Mg2+ over the nanosheet
The carbon nanosheet model used in the calculation and formed only with six-membered rings is shown in Fig. 1. The bond length of the C–C bond in the nanosheet is 1.41 Å, which is consistent with previous work.14 The HOMO and LUMO energies are −6.44 and −0.76 eV, respectively; thus, the HOMO–LUMO gap energy is 5.69 eV. The Mg2+ ion and Mg atom interact over the six-membered ring with distances 1.86 and 3.35 Å from the plane of the nanosheet, respectively (Fig. 8); this indicates strong interactions between Mg2+ and the nanosheet. The Ead of the Mg2+ ion on the nanosheet is −176.1 kcal mol−1 and Ead for the Mg atom is −2.7 kcal mol−1 (Table 1).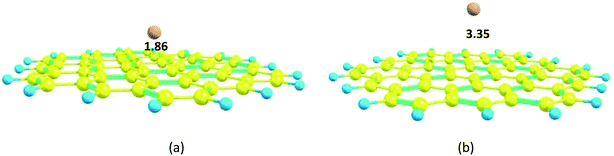 | ||
| Fig. 8 Optimized structures of the Mg2+ and Mg-nanosheet complexes: (a) Mg2+-nanosheet complex, (b) Mg-nanosheet complex. Distances are in Å. | ||
Both the HOMO and LUMO levels change to lower energies, where the shift of the LUMO level to a lower energy is greater. The LUMO level changed from −0.76 eV in the nanosheet to −7.99 eV in the Mg2+-nanosheet complex (Table 1). Therefore, Eg of the nanosheet decreased from 5.69 in the pristine nanosheet to 3.71 in the Mg2+-nanosheet complex, which indicates that the nanosheet interacts sensitively with Mg2+ ion. The ΔEg of the Mg2+-nanosheet complex (−34.7) has a larger absolute value than that of the Mg2+-nanotube complex (−8.5).
3.4 Adsorption of Mg/Mg2+ over the nanocage
The carbon nanocage, C60, shows five-membered and six-membered rings, as illustrated in Fig. 1. The bond length of the C–C bonds in the five-membered ring of the nanocage is 1.45 Å, which is longer than that in the six-membered ring (1.39 Å). The HOMO and LUMO energies for the isolated nanocage are −7.83 and −1.79 eV, respectively; thus, the HOMO–LUMO gap energy is 6.04 eV. The Eg values for the four nanostructures considered here are in the order cage > sheet > cone > tube, which indicates that the nanocage can have high stability and low interaction energy with Mg2+. Because there are two interaction sites in the cage, it was necessary to consider two types of adsorption sites between Mg2+/Mg and the nanocage over both the five and six-membered rings.The optimized distances of the Mg2+ ion and Mg atom located over the five-membered ring are 1.87 and 3.59 Å, respectively; meanwhile, the distances of Mg2+ ion and Mg atom over the six-membered ring are 1.88 and 3.60 Å, respectively (Fig. 9).
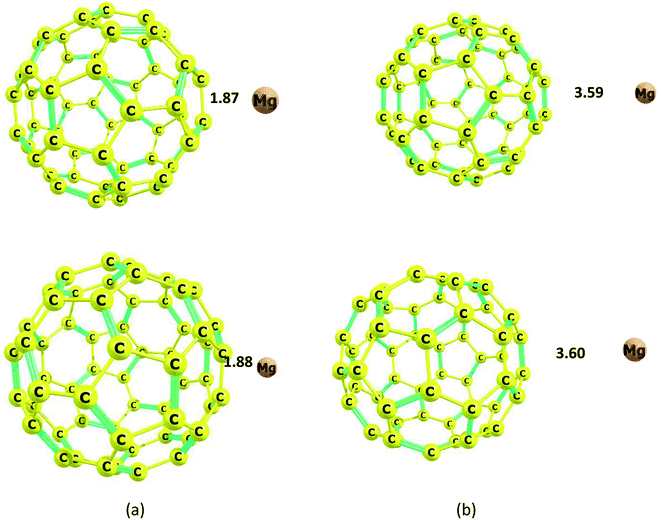 | ||
| Fig. 9 Optimized structures of the Mg2+ and Mg-nanocage complexes. (a) Mg2+-nanocage complex, (b) Mg-nanocage complex. Distances are in Å. | ||
The adsorption energy, Ead, of Mg2+ ion on the five-membered ring of the nanocage is −143.6 kcal mol−1, which is larger than that of Mg atom (−1.1 kcal mol−1); meanwhile, the adsorption energies, Ead, of Mg2+ ion and Mg atom on the six-membered ring are −142.7 and −1.2 kcal mol−1, respectively (Table 1). Thus, the Ead of the Mg2+-cage has the lowest adsorption energy, and Ead changes in the order tube > cone > sheet > cage.
Both the HOMO and LUMO levels of the Mg2+-cage complex transfer to lower energies; the shift of the LUMO level to a lower energy is greater. The LUMO level changed from −1.79 eV to −8.69 eV (Table 1). Therefore, Eg of the nanocage decreased from 6.04 to 4.63 in the Mg2+-nanocage complex, and the ΔEg of the Mg2+-nanostructure became −23.2.
The Gibbs free energies (G), relative free energies (ΔG), energy differences between the nanostructure-Mg2+ and nanostructure-Mg complexes (ΔΔG), and entropy terms (TΔS) are shown in Table 2. The more negative values of ΔΔGad indicate that adsorption of Mg2+/Mg on the nanostructures can proceed spontaneously. The adsorptions of Mg2+ on all the nanostructures and Mg on the nanotube proceed spontaneously, while the adsorptions of neutral Mg on the cone, sheet and cage do not proceed spontaneously.
The value of TΔSad decreases during the adsorption process, which is due to a decrease of the degrees of freedom for the nanostructure-Mg2+/Mg complexes. The entropy terms (TΔS) are identical for both the nanostructure/Mg2+ and nanostructure/Mg complexes. The TΔS values for both the cone/Mg2+ and cone/Mg species are 16.4 kcal mol−1, which may be negligible compared to the ΔG value of −195.6 kcal mol−1.
The calculated adsorption energies, Ead, are consistent with the relative free energies, ΔG (Tables 1 and 2). The highest ΔG values for the nanostructure-Mg2+ and -Mg complexes correspond to the nanocone and nanotube, respectively. The energy differences between the nanostructure-Mg2+ and nanostructure-Mg complexes, ΔΔG, are consistent with ΔEcell (Tables 1 and 2).
3.5 Comparison of the nanostructures in Mg2+-ion batteries (MIBs)
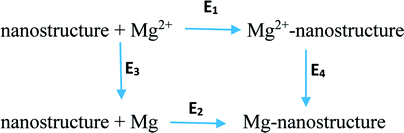
Four types of nanostructures were suggested as anodes for MIBs. The formal reactions in the anode and cathode are as follows:29| Anode: Mg-nanostructure ↔ Mg2+-nanostructure + 2e− | (4) |
This reaction can be divided into several formal reactions that are presented below:
| Cathode: Mg2+ + 2e− ↔ Mg | (5) |
The total reaction of the cell can be defined as:
| Mg2+ + Mg-nanostructure ↔ Mg2+-nanostructure + Mg + ΔGcell | (6) |
This equation is related to the binding energy on one hand and to the ionization potential of Mg on the other hand.
The Nernst equation is used to obtain the cell voltage (Vcell) as follows:
| Vcell = −ΔGcell/zF | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 C mol−1) and the charge of Mg2+ (z = 2, the cation in the electrolyte), respectively. The ΔGcell is the Gibbs free energy difference of the total reaction of the cell. For DFT calculations at 0 K, it can be presented as:
500 C mol−1) and the charge of Mg2+ (z = 2, the cation in the electrolyte), respectively. The ΔGcell is the Gibbs free energy difference of the total reaction of the cell. For DFT calculations at 0 K, it can be presented as:| ΔGcell = ΔEcell + PΔV − TΔS | (8) |
In previous reports, we confirmed that the volume and entropy contributions to Vcell are very small (<0.01 V).29 Therefore, Vcell for the Mg2+- or Mg-nanostructure complexes can be determined by calculating the internal energy change (ΔE) from eqn (6) and (8) as follows:
| ΔEcell ∼ ΔGcell = EMg + EMg(2+)-nanostructure − EMg(2+) − EMg-nanostructure | (9) |
Eqn (9) indicates that the simultaneous strong interaction between Mg2+ and the nanostructure and the weak interaction between Mg atom and the nanostructure affords a more negative and higher ΔEcell. In conclusion, the strong adsorption of Mg2+ and the weak adsorption of Mg on the nanostructure lead to a high Vcell (Table 1). ΔEcell and Vcell were calculated for the four nanostructures and are presented in Table 1 and illustrated in Fig. 10. The ΔEcell and Vcell values for the four nanostructures in MIBs changed in the same order: cone > tube > sheet > cage. The largest ΔEcell and Vcell values are −191.2 kcal mol−1 and 4.1 V, respectively, which are related to the nanocone. ΔEcell and Vcell for the nanotube in a MIB are −177.2 kcal mol−1 and 3.8 V, respectively, which are lower than the values for the nanocone. However, Vcell of the nanotube (3.8 V) is larger than that reported for Li-ion batteries (1.45 V) by Gao et al.,31 which was calculated at the B3LYP/6-31G(d) level of theory. The strongest interaction between Mg2+ and the nanotube implies that the MIB-nanotube will have the largest Vcell value; meanwhile, the strong interaction between the Mg atom and the nanotube led to a decrease in the Vcell value. The lowest Vcell value belongs to the MIB-nanocage due to the weakest interaction between Mg2+ and the nanocage, which was confirmed by the high Eg of the nanocage; this is probably due to the spherical structure of fullerene 60. In general, the Vcell values for the MIBs-nanostructures range from −3.1 to −4.1 V; thus, these nanostructures are promising candidates for application as anodes in the manufacture of MIBs. We can conclude that the advantages of Mg, including its low cost, availability and high Vcell value, will encourage the battery scientists to study these MIBs-nanostructures after overcoming their technical issues.
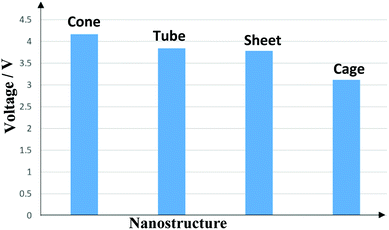 | ||
| Fig. 10 Diagram of the cell voltages of the different nanostructures as anodes in Mg ion batteries (MIBs). | ||
All calculations were performed in the gas phase. Certainly, the study of solvent effects on these systems would be useful to further support the experimental data.
4 Conclusions
In this work, the adsorption of Mg2+ and Mg on nanostructures, including a nanocone, nanotube (4,0), nanosheet, and C60 nanocage, was studied to scrutinize their possible application as anodes of MIBs. The interactions between Mg2+ and the surfaces of the nanostructures are clearly stronger than those with Mg, which clarifies that these nanostructures are appropriate as anodes of MIBs.The Ead, in kcal mol−1, between Mg2+ and the nanotube showed the highest adsorption energy; the Ead values changed in the order tube (−236.8) > cone (−192.8) > sheet (−176.1) > cage (−143.6). However, the cell voltage, Vcell, was the highest for the nanocone. The changes in Vcell of the MIBs are in the order cone (−4.14 V) > tube (−3.84 V) > sheet (−3.76 V) > cage (−3.09 V). The interactions between Mg2+ and Mg and the nanostructures play remarkable roles in the determination of the cell voltage. The strong interaction between Mg2+ and the nanostructures and the weak interaction between Mg and the nanostructures led to high Vcell values. In a comparison between the nanotube and nanocone, strong interactions between Mg and the nanotube led to a decreased Vcell of the nanotube with respect to that of the nanocone.
This study confirms that the advantages of Mg, including its low cost and availability, combined with its high Vcell value are of benefit to the battery scientists to study MIBs-nanostructures after overcoming technical issues.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to acknowledge to “Instituto de Quimica and Medica (CSIC)” for their support of this research.References
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. Zhang, Energy Environ. Sci., 2014, 7, 513–537 RSC.
- S. W. Kim, D. H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710–721 CrossRef CAS.
- P. Novak, R. Imhof and O. Haas, Electrochim. Acta, 1999, 45, 351–367 CrossRef CAS.
- D. Aurbach, Y. Gofer, Z. Lu, A. Schechter, O. Chusid, H. Gizbar, Y. Cohen, V. Ashkenazi, M. Moshkovich and R. Turgeman, J. Power Sources, 2001, 97, 28–32 CrossRef.
- D. Aurbach, Z. Lu, A. Schechter and Y. Gofer, Nature, 2000, 407, 724 CrossRef CAS PubMed.
- M. M. Huie, D. C. Bock, E. S. Takeuchi, A. C. Marschilok and K. J. Takeuchi, Coord. Chem. Rev., 2015, 287, 15–27 CrossRef CAS.
- R. Zhang, X. Yu, K.-W. Nam, C. Ling, T. S. Arthur, W. Song, A. M. Knapp, S. N. Ehrlich, X.-Q. Yang and M. Matsui, Electrochem. Commun., 2012, 23, 110–113 CrossRef CAS.
- Z. Tao, L. Xu, X. Gou, J. Chen and H. Yuan, Chem. Commun., 2004, 40, 2080–2081 RSC.
- X. Han, C. Liu, J. Sun, A. D. Sendek and W. Yang, RSC Adv., 2018, 8, 7196 RSC.
- A. O. Pereira and C. R. Miranda, J. Phys. Chem. C, 2015, 119, 4302–4311 CrossRef CAS.
- (a) S. A. Siadati, E. Vessally, A. Hosseinian and L. Edjlali, Synth. Met., 2016, 220, 606–611 CrossRef CAS; (b) R. Rostamoghli, M. Vakili, A. Banaei, E. Pourbashir and K. Jalalierad, Chem. Rev. Lett., 2018, 1, 31–36 Search PubMed; (c) M. Heidari Nezhad Janjanpour, M. Vakili, S. Daneshmehr, K. Jalalierad and F. Alipour, Chem. Rev. Lett., 2018, 1, 45–49 Search PubMed.
- S. A. Siadati, E. Vessally, A. Hosseinian and L. Edjlali, Talanta, 2017, 162, 505–510 CrossRef PubMed.
- E. Vessally, S. Soleimani–Amiri, A. Hosseinian, L. Edjlal and A. Bekhradnia, Phys. E, 2017, 87, 308–311 CrossRef CAS.
- A. Hosseinian, E. Saedi Khosroshahi, K. Nejati, E. Edjlali and E. Vessally, J. Mol. Model., 2017, 23, 354 CrossRef CAS PubMed.
- K. Nejati, A. Hosseinian, L. Edjlali and E. Vessally, J. Mol. Liq., 2017, 229, 167–171 CrossRef CAS.
- P. Subalakshmi and A. Sivashanmugam, J. Alloys Compd., 2017, 690, 523–531 CrossRef CAS.
- K. Nejati, A. Hosseinian, A. Bekhradnia, E. Vessally and L. Edjlal, J. Mol. Graphics Modell., 2017, 74, 1–7 CrossRef CAS PubMed.
- M. Li, Y.-J. Liu, J.-x. Zhao and X.-g. Wang, Appl. Surf. Sci., 2015, 345, 337–343 CrossRef CAS.
- Y. Xing, Z. Xi, Z. Xue, X. Zhang, J. Song, R. Wang, J. Xu, Y. Song, S. Zhang and D. Yu, Appl. Phys. Lett., 2003, 83, 1689–1691 CrossRef CAS.
- M. Nayebzadeh, A. A. Peyghan and H. Soleymanabadi, Phys. E, 2014, 62, 48–54 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- U. Salzner and A. Aydin, J. Chem. Theory Comput., 2011, 7, 2568–2583 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li,H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg,M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 program, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–561 CrossRef CAS.
- N. O'Boyle, A. Tenderholt and K. Langner, J. Comput. Chem., 2018, 29, 839–845 CrossRef PubMed.
- H. F. Dos Santos, L. A. De Souza, W. B. D. Almeida and T. Heine, J. Phys. Chem. C, 2014, 118, 24761–24768 CrossRef CAS.
- R. F. W. Bader, in Atoms in Molecules: A Quantum Theory, ed. J. Halpen and M. L. H. Green, The international series of monographs of chemistry, Clarendon Press, Oxford, 1990 Search PubMed.
- P. A. Denis and F. Iribarne, Chem. Phys. Lett., 2013, 573, 15–18 CrossRef CAS.
- D. Datta, J. Li and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 1788–1795 CrossRef CAS PubMed.
- Z. Gao, C. S. Chin, J. H. K. Chiew and J. J. C. Zhang, Energies, 2017, 10, 1503 CrossRef.
- F. Gharibzadeh, S. Gohari, K. Nejati, B. Hashemzadeh and S. Mohammadiyan, Chem. Rev. Lett., 2018, 1, 16–22 Search PubMed.
- I. Torkpoor, M. Heidari Nezhad Janjanpour, N. Salehi, F. Gharibzadeh and L. Edjlali, Chem. Rev. lett., 2018, 1, 2–8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra06031b |
| This journal is © The Royal Society of Chemistry 2019 |