A new metallic π-conjugated carbon sheet used for the cathode of Li–S batteries

Abstract

Lithium–sulfur (Li–S) batteries are considered as the most promising next generation high density energy storage devices. However, the commercialization of Li–S batteries is hindered by the shuttle effect of polysulfides, the low electronic conductivity of the sulfur cathode and a large volume expansion during lithiation. Herein, we predict a new two dimensional sp² hybridized carbon allotrope (PHE-graphene) and prove its thermodynamic and kinetic stability. If it is utilized to encapsulate the cathode of Li–S batteries, not only will the shuttle effect be avoided but also the electronic conductivity of the sulfur cathode will be improved significantly owing to its metallic electronic band structure. The thermal conductivity of PHE-graphene was found to be very high and even comparable with graphene, which is helpful for the heat dissipation of cathodes. In addition, PHE-graphene also exhibited superior mechanical properties including ideal tensile strength and in-plane stiffness.

---

1 Introduction

With the continuous consumption of finite fossil fuels and serious environmental pollution issues, the demand for renewable and clean energy sources such as solar and wind has increased substantially. Correspondingly, it is necessary to develop efficient rechargeable energy storage systems for these intermittent energy sources.^1,2 Rechargeable lithium-ion (Li-ion) batteries are regarded as a suitable choice for energy storage devices.^3,4 However, Li-ion batteries can still not meet the rising demands of large scale applications owing to their limited energy density and high cost.^3–5 Accordingly, new economical energy storage systems with a high specific capacity are needed. Li–air and Li–S batteries have attracted increasing attention due to their high theoretical capacities of 3000 W h kg⁻¹ and 2600 W h kg⁻¹, respectively.^1,6 Unfortunately, there are many insurmountable obstacles existing in Li–air batteries such as a low practical energy density,⁶ lots of detrimental side reactions,⁷ instability towards moisture,⁸ etc. In contrast, it is more practical to deal with the challenges of Li–S batteries, and sulfur is environmentally friendly and abundant in nature.⁹ Therefore, Li–S batteries are widely viewed as promising energy storage systems to replace the present Li-ion batteries. Nevertheless, there are still a few challenges faced with Li–S batteries. Firstly, sulfur and its reaction products (Li₂S and Li₂S₂) exhibit poor electronic conductivity, which results in a low rate capability and poor cycle performance of Li–S batteries.^10–12 Secondly, the dissolved intermediate lithium polysulfides (Li₂S_n, 3 ≤ n ≤ 8) can diffuse freely between the cathode and anode during charge/discharge processes. This “shuttle effect” results in lithium anode corrosion, a poor cycle stability of the sulfur cathode, and low coulombic efficiency in Li–S batteries.^13–15 Thirdly, the large volumetric expansion of the sulfur cathode during lithiation leads to electrode pulverization and fast capacity fading.^16–18

To solve these problems faced with Li–S batteries, finding new cathode materials which not only have high electrical conductivity but also are able to confine polysulfides in the cathodes are crucial. Various sulfur-based composites have been proposed, such as carbon–sulfur composites,^19–22 polymer–sulfur composites,^23–25 and carbon–polymer–sulfur composites.^26–28 Among the numerous available cathode materials, graphene has high interest due to its advantageous intrinsic properties for Li–S batteries, such as superior electrical conductivity and high theoretical surface area for sulfur loading.^29–31 However, graphene–sulfur composites have failed to eliminate the shuttle effect in Li–S batteries.^32,33 To confine polysulfides effectively, methods using graphene oxide to replace graphene³⁴ and encapsulating graphene–sulfur composites with polymers³⁰ have been tried. However, both approaches will deteriorate the electrical conductivity of cathodes.³² Metal oxide–sulfur composites can also alleviate the shuttle effect by transforming soluble polysulfides into insoluble lower-order sulfides,^35–37 but the poor electronic conductivity of these metal oxides limits their behavior for improving cell lifetimes.³⁸ A recent study showed that two dimensional (2D) multiporous carbon sheets can be used to encapsulate the cathodes of Li–S batteries.³⁹ Relative to sulfur-based composites, this multiporous carbon has a higher electrical conductivity. For new cathode materials, excellent mechanical properties are essential to bear possible volumetric expansion. In addition, high thermal conductivities are also expected for new cathode materials in order to facilitate the heat dissipation of electrodes.

In this study, we firstly predicted a new 2D sp² hybridized carbon allotrope (PHE-graphene), and suggested its synthesis by a dehydrogenation reaction of small molecules. Secondly, its thermodynamic and kinetic stability were examined and electronic band structures were investigated. Thirdly, the phonon lifetimes and group velocity in PHE-graphene were calculated. The phonon and electron thermal conductivities were evaluated, then the ideal tensile strength of PHE-graphene was determined. The upper limits of in-plane stiffness were systematically investigated for twenty 2D carbon sheets. Finally, the energy barriers of Li and S atoms diffusing through PHE-graphene were studied and its potential applications in Li–S batteries are discussed.

2 Methods

Our ab initio calculations were performed using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation⁴⁰ and implemented in the VASP code.^41,42 Blöchl’s projector augmented wave (PAW) method^43,44 was utilized to describe the interactions between the nucleus and the valence electrons of carbon. A plane-wave basis with a cutoff energy of 400 eV was used to expand the wave functions. The geometries of all of the carbon allotropes investigated in this work were fully relaxed including the atomic positions and lattice parameters until the residual forces on each atom were less than 0.0001 eV Å⁻¹. The Brillouin zone sample meshes were dense enough and the k spacing was less than 0.3 Å⁻¹ for all of the structures. The phonon band structure was determined by the direct supercell method as implemented in the Phonopy program.⁴⁵ Lattice thermal conductivity was calculated by solving the linearized phonon Boltzmann equation within the single-mode relaxation time approximation (RTA) and implemented by the Phono3py code.⁴⁶ Electron thermal conductivity was calculated according to the rigid-band approximation (RBA) using BoltzTraP2 code.⁴⁷ The energy barriers of S and Li atoms diffusing were investigated using both PBE and dispersion corrected (DFT-D3)⁴⁸ density functionals.

3 Results and discussion

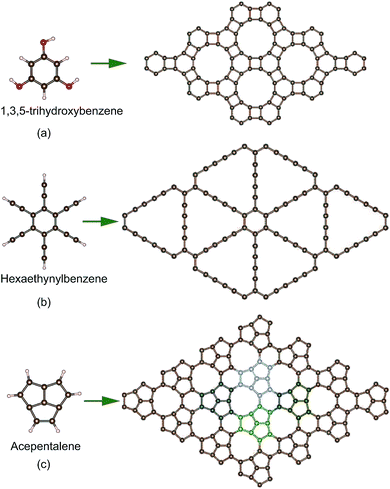
Many methods can be utilized to prepare graphene, such as top-down exfoliation, bottom-up chemical vapor deposition (CVD) or chemical synthesis methods.⁴⁹ However, new 2D carbon materials usually cannot be obtained by the exfoliation method due to the lack of bulk layer precursors. CVD is also not suitable for the synthesis of 2D carbon except for graphene. Chemical synthesis from small molecules is a promising route to prepare new 2D carbon sheets, although it is still very challenging. Experimentally, two 2D carbon sheets have been synthesized by the dehydration or dehydrogenation chemical reactions of small molecules as shown in Fig. 1a and b. A 4–6 carbophene (i.e. DHP-graphene)^39,50 was synthesized by the dehydration reaction of 1,3,5-trihydroxybenzene molecules and graphdiyne⁵¹ was obtained by the dehydrogenation reaction of hexaethynylbenzene molecules. Likewise, a new conjugated π-bonding planar carbon structure might be achieved by the dehydrogenation reaction of acepentalene⁵² molecules as shown in Fig. 1c. This carbon allotrope has also been found in structure research based on particle swarm optimization for a system with ten carbon atoms. Its structure consists of pentagonal, hexagonal and enneagonal rings, and thus it is named PHE-graphene. PHE-graphene belongs to the space group P6̄m2 (D_3h). Its lattice constant a is 5.738 Å. In the unit cell of PHE-graphene, there are four nonequivalent chemical bonds, whose lengths are 1.385, 1.448, 1.392 and 1.514 Å, respectively. The ratio of chemical bond numbers is 1 : 2 : 1 : 1. Thus the average bond length is 1.438 Å which is a little higher than that of graphene (1.42 Å).

Fig. 1 (a) The 4–6 carbophene (i.e. DHP-graphene) prepared by the dehydration reaction of 1,3,5-trihydroxybenzene molecules. (b) Graphdiyne synthesized by the dehydrogenation reaction of hexaethynylbenzene molecules. (c) A possible preparation method for PHE-graphene by the dehydrogenation reaction of acepentalene molecules.

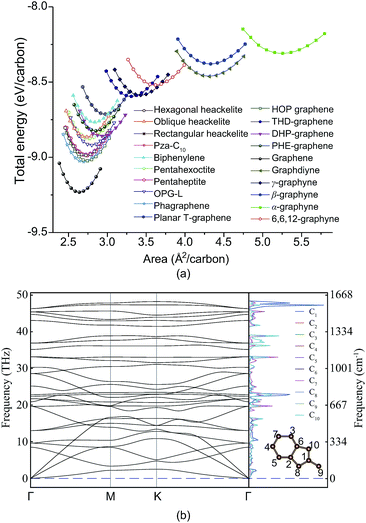
To add PHE-graphene into the carbon material family, we should firstly check its thermodynamic and kinetic stability. Fig. 2a shows the total energies of PHE-graphene and nineteen other 2D carbon allotropes, including DHP-graphene,³⁹ graphdiyne,⁵¹ THD-graphene,⁵³ planar T-graphene,⁵⁴ rectangular heackelite,⁵⁵ pza-C₁₀,⁵⁶ phagraphene,⁵⁷ pentahexoctite,⁵⁸ pentaheptite,⁵⁹ OPG-L,⁶⁰ oblique heackelite,⁵⁵ HOP graphene,⁶¹ hexagonal heackelite,⁵⁵ graphene,⁶² γ-graphyne,⁶³ biphenylene,⁶⁴ β-graphyne,⁶⁵ α-graphyne⁶⁵ and 6,6,12-graphyne.⁶⁵ As expected, graphene is the most stable 2D carbon layer. Five sp + sp² hybridized structures (including α-graphyne, β-graphyne, γ-graphyne, 6,6,12-graphyne and graphdiyne) were less stable relative to the other sp² hybridized carbon sheets. Among them, the α-graphyne is the least stable sp + sp² hybridized structure and graphdiyne is the least stable structure experimentally synthesized. PHE-graphene also exhibited a high thermodynamic stability. At equilibrium geometry, its total energy was lower than not only the sp + sp² hybridized 2D carbon structures but also sp² hybridized biphenylene, planar T-graphene and THD-graphene. Fig. 2b shows the phonon dispersion and projected phonon density of states (PhDOS) of PHE-graphene. Since no imaginary phonon frequencies were found, PHE-graphene is kinetically stable. The highest phonon frequency of PHE-graphene was calculated to be 48.24 THz (or 1609 cm⁻¹), which is extremely close to that (around 1600 cm⁻¹ (ref. 66 and 67)) of graphite and graphene. In addition, we could find two phonon bandgaps in the frequency regions of 33–35 and 39–42 THz. From the PhDOS, it can be seen that the high frequency phonons were mainly from the contribution of the C₁ atom. Furthermore, a NVT ab initio molecular dynamics simulation was performed, which also confirmed the stability of PHE-graphene (see Fig. S1 in the ESI†).

Fig. 2 (a) Total energy as a function of volume for the 2D carbon allotropes. (b) Phonon dispersion of PHE-graphene and projected phonon density of states (PhDOS). The insert shows the ten non-equivalent carbon atoms in the unit cell.

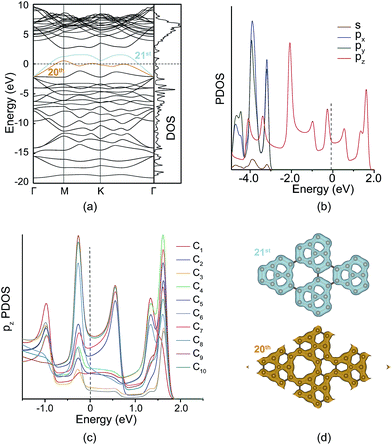
PHE-graphene has ten carbon atoms and forty 2s²2p² electrons in its unit cell. If PHE-graphene is semiconductive, the 20^th band should be below the Fermi level (E_F) and the 21^st band should be above the E_F. From Fig. 3a, we can find that both the 20^th and 21^st bands were partially occupied and crossed the E_F. Therefore, PHE-graphene is a metallic carbon material. Fig. 3b shows the projected density of states (PDOS: s, p_x, p_y and p_z). The PDOS near E_F completely results from the p_z electrons, which discloses the π-conjugated nature of PHE-graphene. If the p_z DOS is projected on each carbon atom, it can be seen that the PDOS near the E_F is mainly ascribed to the contributions of the C₈, C₉ and C₁₀ atoms as shown in Fig. 3c. Based on the DOS analysis, we can conclude that PHE-graphene is a metallic π-bonding carbon structure with excellent electrical conductivity. Fig. 3d shows the charge densities of the 20^th and 21^st bands. It can be seen that the electrons in PHE-graphene are delocalized especially for the 20^th band, in which the electrons behave just like the free electrons in metals.

Fig. 3 (a) Band structures and the density of states (DOS) of PHE-graphene. (b) Partial density of states (PDOS) of s, p_x, p_y and p_z. (c) The p_z PDOS of the C₁–C₁₀ atoms. (d) Charge densities of the 20^th and 21^st bands.

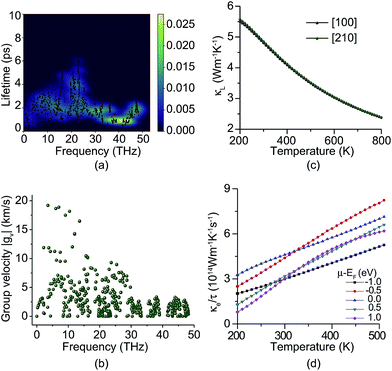
The thermal conductivity of a material results from the transportation of electrons and phonons. Fig. 4a shows the phonon lifetimes calculated from the imaginary part of phonon self energy.⁴⁶ We find that most phonons have short lifetimes, especially the high frequency phonons. The longest phonon lifetime around 20 THz is still less than 7 ps. Fig. 4b shows the phonon group velocity. Only a few low frequency phonons have group velocities of more than 10 km s⁻¹ and most phonons’ group velocities are less than 5 km s⁻¹. Two phonon bandgaps around 33–35 and 39–42 THz can also be found from Fig. 4a and b. Due to low phonon lifetimes and group velocity, the lattice thermal conductivity (κ_L) of PHE-graphene is quite low. At room temperature (300 K), the κ_L is only 4.8 W m⁻¹ K⁻¹. Along the [100] and [210] directions, thermal transport is almost isotropic as shown in Fig. 4c. With increasing temperature, κ_L decreases drastically due to the enhancement of phonon dispersion. The electron thermal conductivity (κ_e) is the function of both temperature and chemical potential (μ). Owing to the metallic electronic band structure, κ_e should dominate the thermal transport of PHE-graphene just like other metals. Fig. 4d shows κ_e/τ as functions of temperature for five μ − E_F, where μ is chemical potential. It can be seen that κ_e/τ increases with rising temperature. While μ − E_F is −1 eV, κ_e/τ is 2.986 × 10¹⁴ W m⁻¹ K⁻¹ s⁻¹. Accurate electron relaxation time of PHE-graphene is not available at present. However, a few studies of 2D carbon materials have confirmed that τ is usually tens of picoseconds (ps). For instance, τ is 14.6 ps for THD-graphene,⁵³ 13–14 ps for graphene⁶⁸ and 16–19 ps for graphdiyne.⁶⁹ Supposing the τ of PHE-graphene is 14 ps, close to sp² hybridized THD-graphene and graphene, κ_e is estimated to be up to 4180 W m⁻¹ K⁻¹ while μ − E_F is −1.0 eV. Such a high thermal conductivity of PHE-graphene is even comparable with single-layer graphene (5300 W m⁻¹ K⁻¹),⁷⁰ and superior to few-layer graphene (1300–2800 W m⁻¹ K⁻¹),⁷¹ bulk graphite (2000 W m⁻¹ K⁻¹),⁷² carbon nanotubes (3000 W m⁻¹ K⁻¹)⁷³ and diamond (1000–2200 W m⁻¹ K⁻¹).⁷⁴

Fig. 4 (a) Phonon lifetimes. (b) Phonon group velocity. (c) Lattice thermal conductivity (κ_L) of PHE-graphene as a function of temperature. (d) Electron thermal conductivity (κ_e) divided by relaxation time (τ) as a function of temperature.

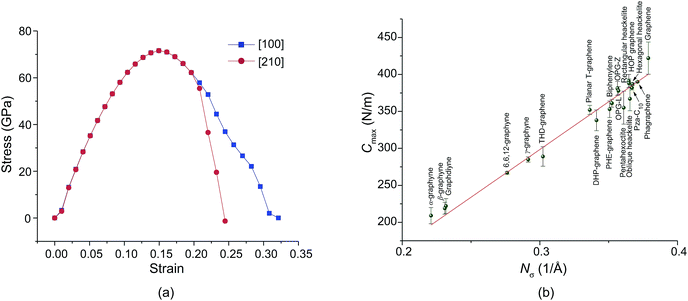
Fig. 5a shows the stress–strain relations. We found that the ideal tensile strength of PHE-graphene is up to 71.6 GPa which is far less than that (130 ± 10 GPa) of graphene.⁷⁵ However, PHE-graphene still has a higher tensile strength relative to most 2D materials, such as MoS₂ (25 GPa),⁷⁶ silicene (12.5 GPa)⁷⁷ and phosphorene (4.45 GPa).⁷⁸ Before yielding, PHE-graphene can endure 15% tensile strain. As for 2D PHE-graphene, its elastic behavior under strain should be evaluated by in-plane stiffness C rather than Young’s modulus. If S₀ is defined as the area of PHE-graphene at equilibrium geometry, the in-plane stiffness can be given by C = (1/S₀) × (∂²E/∂ε²), where E is the strain energy calculated by subtracting the total energy of the strained system from the equilibrium total energy and ε is the strain. In this study, we applied strain ε on both the [100] and [010] directions at the same time, which meant that the 2D lattice constants or the unit cell were enlarged (1 + ε) times. Thus, we calculated the upper limit of the stiffness, i.e. C_max. Fig. 5b shows the C_max of the twenty carbon allotropes. It can be found that the C_max significantly depends on the number of carbon atoms per unit area, N_σ. For sp + sp² hybridized carbon sheets (α-graphyne, β-graphyne, graphdiyne, 6,6,12-graphyne, and γ-graphyne), they usually have a lower C_max due to their small N_σ. In contrast, C_max is usually higher than 300 N m⁻¹ for sp² hybridized carbon allotropes except for THD-graphene. Graphene has the highest N_σ (0.379 Å⁻¹) and its C_max is up to 422 N m⁻¹, which is very close to the experimental upper limit (about 419 N m⁻¹) of graphene.⁷⁵ The C_max of PHE-graphene was also up to 353 N m⁻¹ and thus it possesses excellent mechanical properties.

Fig. 5 (a) The stress–strain relations of PHE-graphene in the [100] and [210] directions. (b) The upper limit of in-plane stiffness (C_max) as a function of the number (N_σ) of carbon atoms per unit area.

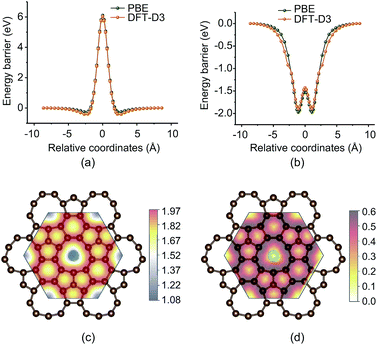
Fig. 6a shows the energy barrier of sulfur atoms passing through the enneagonal rings of PHE-graphene. It can be seen that a very high barrier prevents the sulfur atoms from penetrating through PHE-graphene. When one sulfur atom gradually approaches PHE-graphene, the total energy drops by 0.5 eV. This indicates that PHE-graphene has weak adsorption for sulfur atoms. The effects of the PBE functional and the DFT-D3 dispersion corrected functional on energy barriers are negligible. Surprisingly, we find that PHE-graphene strongly adsorbs Li atoms as shown in Fig. 6b. For the most stable adsorption geometry, the distance between Li and PHE-graphene was about 1.08 Å and the adsorption energy was 1.97 (1.90) eV at the PBE (DFT-D3) level. If one Li atom passes through the PHE-graphene, only an energy barrier around 0.47–0.48 eV needs to be overcome. In view of PHE-graphene preventing sulfur passing through it, PHE-graphene could be used to encapsulate the cathodes of Li–S batteries, by which the “shuttle effect” could be effectively avoided. The adsorption geometries and energies of Li₂S_n (n ≤ 8) and S₈ on PHE-graphene were also evaluated as shown in Table. S1 and Fig. S2 (see the ESI†). The adsorption energy was the highest for Li₂S but was relatively weak for Li₂S_n (3 ≤ n ≤ 8) and S₈ species. In addition, the low conductivity faced in Li–S batteries at present can also be significantly improved because PHE-graphene is a metallic carbon material. Fig. 6c shows the vertical distance (Δd) between Li and PHE-graphene during Li atom diffusion on the PHE-graphene surface. The minimum Δd occurred at the enneagonal hollow sites and was around 1.08 Å. In contrast, the Δd was at a maximum on the top of C, which was about 1.97 Å. The Li atom diffusion barriers on the PHE-graphene surface are presented in Fig. 6d. The diffusion barriers between adjacent carbon rings were 0.589, 0.548, 0.301, and 0.302 eV for enneagon⇀hexagon, enneagon⇀pentagon, hexagon⇀pentagon, and pentagon⇀pentagon, and 0.395, 0.339, 0.286, and 0.302 eV for the reverse processes, respectively. Therefore, Li atoms shift readily along the path of ⋯hexagon⇀pentagon⇀pentagon⇀hexagon⋯ and the corresponding barriers were close to that (0.327 eV) of Li atom diffusion on the graphene surface.⁷⁹

Fig. 6 (a) and (b) show the energy barriers of S and Li atoms diffusing through the enneagon rings, respectively. (c) The vertical distance (Δd) between Li and the PHE-graphene during Li atom diffusion on the surface of PHE-graphene. (d) A 2D contour plot of the energy barrier for Li atom diffusion on the surface of PHE-graphene.

4 Conclusions

In summary, we proposed a new carbon sheet (PHE-graphene) and suggested its preparation by a dehydrogenation reaction of small molecules. The thermodynamic and kinetic stability of PHE-graphene were examined by means of ab initio calculations. Electronic band structure calculations showed that PHE-graphene is a metallic carbon material. The density of states near the Fermi energy level completely result from the contributions of delocalized p_z electrons. Similar to graphene, PHE-graphene is a typical π-conjugated system. Anharmonic lattice dynamics calculations revealed the low phonon lifetimes and group velocity in PHE-graphene, which directly results in its low lattice thermal conductivity. However, the electron thermal conductivity was found to be very high and even comparable with graphene. The enneagonal rings in PHE-graphene provide a passage for Li atoms but prevent S atoms from passing through. If PHE-graphene is utilized in cathodes, the major challenges faced by Li–S batteries, including low conductivity and the shuttle effect can be solved. Its high thermal conductivity is also helpful for the heat dissipation of cathodes. In addition, PHE-graphene also exhibits superior mechanical properties. Its ideal tensile strength was up to 71.6 GPa and the upper limit of its in-plane stiffness was 353 N m⁻¹.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported financially by the National Natural Science Foundation of China (Grant No. 11464028), the Natural Science Foundation of Jiangxi Province, China (Grant No. 20171ACB21007) and the Department of Education of Jiangxi Province, China (Grant No. GJJ150025).

Notes and references

1. M. Arumugam, C. Sheng-Heng and Z. Chenxi, Adv. Mater., 2015, 27, 1980–2006.
2. J.-Q. Huang, T.-Z. Zhuang, Q. Zhang, H.-J. Peng, C.-M. Chen and F. Wei, ACS Nano, 2015, 9, 3002–3011.
3. X. Yu, Z. Bi, F. Zhao and A. Manthiram, ACS Appl. Mater. Interfaces, 2015, 7, 16625–16631.
4. A. Manthiram, Y. Fu and Y.-S. Su, Acc. Chem. Res., 2013, 46, 1125–1134.
5. J. Xiao, J. Z. Hu, H. Chen, M. Vijayakumar, J. Zheng, H. Pan, E. D. Walter, M. Hu, X. Deng, J. Feng, B. Y. Liaw, M. Gu, Z. D. Deng, D. Lu, S. Xu, C. Wang and J. Liu, Nano Lett., 2015, 15, 3309–3316.
6. A. Kraytsberg and Y. Ein-Eli, J. Power Sources, 2011, 196, 886–893.
7. L. Li, S.-H. Chai, S. Dai and A. Manthiram, Energy Environ. Sci., 2014, 7, 2630–2636.
8. L. Jang-Soo, T. K. Sun, C. Ruiguo, C. Nam-Soon, L. Meilin, L. K. Tae and C. Jaephil, Adv. Energy Mater., 2010, 1, 34–50.
9. Q. Wang, N. Yan, M. Wang, C. Qu, X. Yang, H. Zhang, X. Li and H. Zhang, ACS Appl. Mater. Interfaces, 2015, 7, 25002–25006.
10. D. Bing, Y. Changzhou, S. Laifa, X. Guiyin, N. Ping and Z. Xiaogang, Chem.–Eur. J., 2013, 19, 1013–1019.
11. P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2011, 11, 19.
12. X. Ji and L. F. Nazar, J. Mater. Chem., 2010, 20, 9821–9826.
13. B. Zhang, X. Qin, G. R. Li and X. P. Gao, Energy Environ. Sci., 2010, 3, 1531–1537.
14. K. Kumaresan, Y. Mikhaylik and R. E. White, J. Electrochem. Soc., 2008, 155, A576–A582.
15. Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2004, 151, A1969–A1976.
16. Y. Wei, Y. Tao, C. Zhang, J. Wang, W. Qiao, L. Ling and D. Long, Electrochim. Acta, 2016, 188, 385–392.
17. G. Zheng, Y. Yang, J. J. Cha, S. S. Hong and Y. Cui, Nano Lett., 2011, 11, 4462–4467.
18. J. Zang, T. An, Y. Dong, X. Fang, M. Zheng, Q. Dong and N. Zheng, Nano Res., 2015, 8, 2663–2675.
19. H. Wang, Y. Yang, Y. Liang, J. T. Robinson, Y. Li, A. Jackson, Y. Cui and H. Dai, Nano Lett., 2011, 11, 2644–2647.
20. X. Ji, K. T. Lee and L. F. Nazar, Nat. Mater., 2009, 8, 500.
21. X. Li, Y. Cao, W. Qi, L. V. Saraf, J. Xiao, Z. Nie, J. Mietek, J.-G. Zhang, B. Schwenzer and J. Liu, J. Mater. Chem., 2011, 21, 16603–16610.
22. S. Wei, H. Zhang, Y. Huang, W. Wang, Y. Xia and Z. Yu, Energy Environ. Sci., 2011, 4, 736–740.
23. Y. Fu and A. Manthiram, J. Phys. Chem. C, 2012, 116, 8910–8915.
24. Y. Zhang, Z. Bakenov, Y. Zhao, A. Konarov, T. N. L. Doan, M. Malik, T. Paron and P. Chen, J. Power Sources, 2012, 208, 1–8.
25. L. Xiao, Y. Cao, J. Xiao, B. Schwenzer, M. H. Engelhard, L. V. Saraf, Z. Nie, G. J. Exarhos and J. Liu, Adv. Mater., 2012, 24, 1176–1181.
26. Y. Bu, J. Wu, X. Zhao, K. Ding, Q. Liu, Y. Huang, J. Lv and Y. Wang, RSC Adv., 2016, 6, 104591–104596.
27. G. Zheng, Q. Zhang, J. J. Cha, Y. Yang, W. Li, Z. W. Seh and Y. Cui, Nano Lett., 2013, 13, 1265–1270.
28. X. Li, M. Rao and W. Li, J. Solid State Electrochem., 2016, 20, 153–161.
29. G. Zhou, L.-C. Yin, D.-W. Wang, L. Li, S. Pei, I. R. Gentle, F. Li and H.-M. Cheng, ACS Nano, 2013, 7, 5367–5375.
30. Z. Chenxi and M. Arumugam, Adv. Energy Mater., 2013, 3, 1008–1012.
31. T. Lin, Y. Tang, Y. Wang, H. Bi, Z. Liu, F. Huang, X. Xie and M. Jiang, Energy Environ. Sci., 2013, 6, 1283–1290.
32. X. Yang, L. Zhang, F. Zhang, Y. Huang and Y. Chen, ACS Nano, 2014, 8, 5208–5215.
33. Z. Li, Y. Huang, L. Yuan, Z. Hao and Y. Huang, Carbon, 2015, 92, 41–63.
34. L. Ji, M. Rao, H. Zheng, L. Zhang, Y. Li, W. Duan, J. Guo, E. J. Cairns and Y. Zhang, J. Am. Chem. Soc., 2011, 133, 18522–18525.
35. Z. Wei Seh, W. Li, J. J. Cha, G. Zheng, Y. Yang, M. T. Mcdowell, P.-C. Hsu and Y. Cui, Nat. Commun., 2013, 4, 1331.
36. X. Tao, J. Wang, Z. Ying, Q. Cai, G. Zheng, Y. Gan, H. Huang, Y. Xia, C. Liang, W. Zhang and Y. Cui, Nano Lett., 2014, 14, 5288–5294.
37. Q. Pang, D. Kundu, M. Cuisinier and L. F. Nazar, Nat. Commun., 2014, 5, 4759.
38. T. Zeng, X. Hu, P. Ji and G. Zhou, Solid State Ionics, 2016, 291, 47–68.
39. Y. Cai, Y. Guo, B. Jiang and Y. Lv, Sci. Rep., 2017, 7, 14948.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
42. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
43. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
44. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
45. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
46. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306.
47. G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
49. X. Cai, Y. Luo, B. Liu and H.-M. Cheng, Chem. Soc. Rev., 2018, 47, 6224–6266.
50. Q.-S. Du, P.-D. Tang, H.-L. Huang, F.-L. Du, K. Huang, N.-Z. Xie, S.-Y. Long, Y.-M. Li, J.-S. Qiu and R.-B. Huang, Sci. Rep., 2017, 7, 40796.
51. M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593–2600.
52. A. de Meijere, P. R. Schreiner, F.-M. Schüngel, F. Gerson and P. Merstetter, Chem. Commun., 1999, 2189–2190.
53. X. Xu, B. Jiang, Y. Guo and Y. Cai, Mater. Chem. Phys., 2017, 200, 50–56.
54. H. Huang, Y. Li, Z. Liu, J. Wu and W. Duan, Phys. Rev. Lett., 2013, 110, 029603.
55. H. Terrones, M. Terrones, E. Hernández, N. Grobert, J.-C. Charlier and P. M. Ajayan, Phys. Rev. Lett., 2000, 84, 1716–1719.
56. X. Luo, L.-M. Liu, Z. Hu, W.-H. Wang, W.-X. Song, F. Li, S.-J. Zhao, H. Liu, H.-T. Wang and Y. Tian, J. Phys. Chem. Lett., 2012, 3, 3373–3378.
57. Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186.
58. B. R. Sharma, A. Manjanath and A. K. Singh, Sci. Rep., 2014, 4, 7164.
59. V. H. Crespi, L. X. Benedict, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, R13303–R13305.
60. C. Su, H. Jiang and J. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075453.
61. B. Mandal, S. Sarkar, A. Pramanik and P. Sarkar, Phys. Chem. Chem. Phys., 2013, 15, 21001–21006.
62. J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60.
63. N. Narita, S. Nagai, S. Suzuki and K. Nakao, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 11009–11014.
64. M. A. Hudspeth, B. W. Whitman, V. Barone and J. E. Peralta, ACS Nano, 2010, 4, 4565–4570.
65. D. Malko, C. Neiss, F. Viñes and A. Görling, Phys. Rev. Lett., 2012, 108, 086804.
66. J. Maultzsch, S. Reich, C. Thomsen, H. Requardt and P. Ordejón, Phys. Rev. Lett., 2004, 92, 075501.
67. O. Dubay and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035401.
68. J. Xi, M. Long, L. Tang, D. Wang and Z. Shuai, Nanoscale, 2012, 4, 4348–4369.
69. M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593–2600.
70. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907.
71. S. Ghosh, W. Bao, D. L. Nika, S. Subrina, E. P. Pokatilov, C. N. Lau and A. A. Balandin, Nat. Mater., 2010, 9, 555.
72. A. A. Balandin, Nat. Mater., 2011, 10, 569.
73. H.-Y. Chiu, V. V. Deshpande, H. W. C. Postma, C. N. Lau, C. Mikó, L. Forró and M. Bockrath, Phys. Rev. Lett., 2005, 95, 226101.
74. A. Sukhadolau, E. Ivakin, V. Ralchenko, A. Khomich, A. Vlasov and A. Popovich, Diamond Relat. Mater., 2005, 14, 589–593.
75. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
76. T. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235407.
77. Q.-X. Pei, Z.-D. Sha, Y.-Y. Zhang and Y.-W. Zhang, J. Appl. Phys., 2014, 115, 023519.
78. Z.-D. Sha, Q.-lX. Pei, Z. Ding, J.-W. Jiang and Y.-W. Zhang, J. Appl. Phys., 2015, 48, 395303.
79. C. Uthaisar and V. Barone, Nano Lett., 2010, 10, 2838–2842.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra07074a

---