Open Access Article
Open Access ArticleThe mechanistic investigations of photochemical decarbonylations and oxidative addition reactions for M(CO)5 (M = Fe, Ru, Os) complexes†
Zheng-Feng Zhanga and
Ming-Der Su *ab
*ab
aDepartment of Applied Chemistry, National Chiayi University, Chiayi 60004, Taiwan. E-mail: midesu@mail.ncyu.edu.tw
bDepartment of Medicinal and Applied Chemistry, Kaohsiung Medical University, Kaohsiung 80708, Taiwan
First published on 21st January 2019
Abstract
The mechanisms for the photochemical CO-dissociation and the oxidative addition reactions are studied theoretically using three model systems: M(CO)5 (M = Fe, Ru, and Os) and the CASSCF/Def2-SVP (fourteen-electron/ten-orbital active space) and MP2-CAS/Def2-SVP//CASSCF/Def2-SVP methods. The structures of the intersystem crossings and the conical intersections, which play a decisive role in these CO photo-extrusion reactions, are determined. The intermediates and the transition structures in either the singlet or triplet states are also computed, in order to explain the reaction routes. These model studies suggest that after the irradiation of Fe(CO)5 with UV light, it quickly loses one CO molecule to generate a 16-electron iron tetracarbonyl, in either the singlet or the triplet states. It is found that the triplet Fe(CO)4 plays a vital role in the formation of the final oxidative addition product, Fe(CO)4(H)(SiMe3), but the singlet Fe(CO)4 plays a relatively minor role in the formation of the final product. However, its vacant coordination site interacts weakly with solvent molecules ((Me3)SiH) to yield the alkyl-solvated iron complexes, which are detectable experimentally. The theoretical observations show that Ru(CO)5 and Os(CO)5 have similar photochemical and thermal potential energy profiles. In particular, this study demonstrates that the oxidative addition yield for Fe is much greater than those for its Ru and Os counterparts, under the same chemical conditions.
I. Introduction
Over the past forty years, the photochemistry of coordinatively saturated pentacarbonyl transition-metal complexes that feature the group 8 elements, M(CO)5 (M = Fe, Ru, and Os), has been extensively studied.1,2 The prevailing photochemical operation for these metal pentacarbonyl compounds is CO ligand dissociation, which produces highly reactive coordination positions at the transition metal center. Therefore, understanding the formation mechanisms and reactivity patterns for these important intermediates is necessary for both the synthetic and catalytic fields of inorganic and organometallic chemistry.In particular, the photochemistry of Fe(CO)5 has been the subject of study for many years because of its applications in various areas, including photocatalysis and synthesis.3–10 The photolytic dissociation of a CO ligand from Fe(CO)5 to generate Fe(CO)4 (ref. 11–14) is the most important aspect of its reaction to UV irradiation.15–25 Starting from this unsaturated 16-electron iron carbonyl intermediate Fe(CO)4, it can easily react with different types of molecules to undergo oxidative addition reactions,26–28 which are of both academic and commercial importance in inorganic and organometallic chemistry.29–32 As a consequence, the study of the photochemistry of Fe(CO)5 has been the subject of a great many experimental and theoretical studies that seek to determine the fundamental aspects of its reaction chemistry.33–37 Along the entire group 8 metal triad (Fe, Ru, and Os), the photochemistry of Ru(CO)5 and Os(CO)5 has not been the subject of extensive study.38–47 The reason for this could be that iron is cheap and environmentally benign but ruthenium and osmium are expensive and toxic. The instability of the Ru(CO)5 and Os(CO)5 complexes with respect to the respective formation of the well-known Ru3(CO)12 and Os3(CO)12 species could be another reason.45 Nevertheless, Fe(CO)5 is quite toxic as well.
The available experimental observations show that upon CO-photolysis of the pentacarbonyl metal complex M(CO)5,2 it yields the coordinatively unsaturated intermediate, Fe(CO)4, which has the triplet ground state. This result has been verified both experimentally11–25,48–53 and theoretically.54–61 However, both Ru(CO)4 and Os(CO)4 are predicted to have a singlet ground state.38–47 In particular, iron tetracarbonyl fragments are an exceedingly active catalyst, as mentioned previously,11–14,26–28 but ruthenium and osmium tetracarbonyl fragments are not easily formed photochemically from the corresponding M(CO)5 reactants, because unlike Fe(CO)4, these can be produced but immediately combine with one CO molecule.11–14,38–47
The activation of the Si–H bond in alkylsilane by this a d8 organometallic photoproduct Fe(CO)4 has been studied using picosecond time-resolved infrared (TRIR) spectroscopy.62–66 Therefore, if the reactants and products have different spin states, the way in which the species in a particular spin state transform into the final products of the same spin state by way of several intermediates of different spin state and the spin crossovers is of interest.
After several decades of intensive research into the oxidative addition of alkanes on Fe(CO)4,67–76 much is still not known about its initial CO-photoextrusion mechanism, nor about that for the analogous Ru(CO)5 and Os(CO)5 molecules.54–63,77–79 It is astonishing how little is understood about the role that is played by the either the photo-generated singlet or triplet unsaturated d8 M(CO)4 intermediates in the oxidative addition reaction with organic molecules, considering the importance of these tetracarbonyl metal complexes in the fields of catalytic and synthetic chemistry.
In principle, understanding the characteristics of the potential energy surfaces is of great importance in determining the functions of different possible courses. In spite of the large number of photochemical results for the Fe(CO)4 species, which may help in interpreting the potential energy surfaces for pentacarbonyl transition-metal complexes, the entire mechanistic detail remains unexplained. Indeed, it is not possible to locate intermediates or the transition states because of the limitations of current experimental techniques. Theoretical computations, which are a major source of dependable essential information, are an extremely useful tool with which to study the photochemistry so a theoretical study of the mechanisms for the photodissociation of d8 M(CO)5 (M = Fe, Ru, and Os) and the Si–H bond–activation reaction for correspondingly photo-generated M(CO)4 with trimethylsilane, eqn (1), is undertaken.
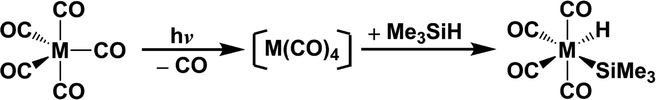 | (1) |
This theoretical study demonstrates that either the spin crossover (usually from the triplet excited state to the singlet ground state) or the conical intersection (generally from the singlet excited state to the singlet ground state)80–85 mechanisms play a vital role in interpreting the mechanisms for the photochemical oxidative addition reactions for the pentacarbonyl transition-metal complexes, M(CO)5 (M = Fe, Ru, and Os). The theoretical results for all three transition metals are also compared to determine the implications for the photochemistry of iron, ruthenium and osmium pentacarbonyl molecules. This study gives a better understanding of the photochemical reactions of the group 8 triad, M(CO)5, and supports experimental observations.2,11–14,38–47
II. Methodology
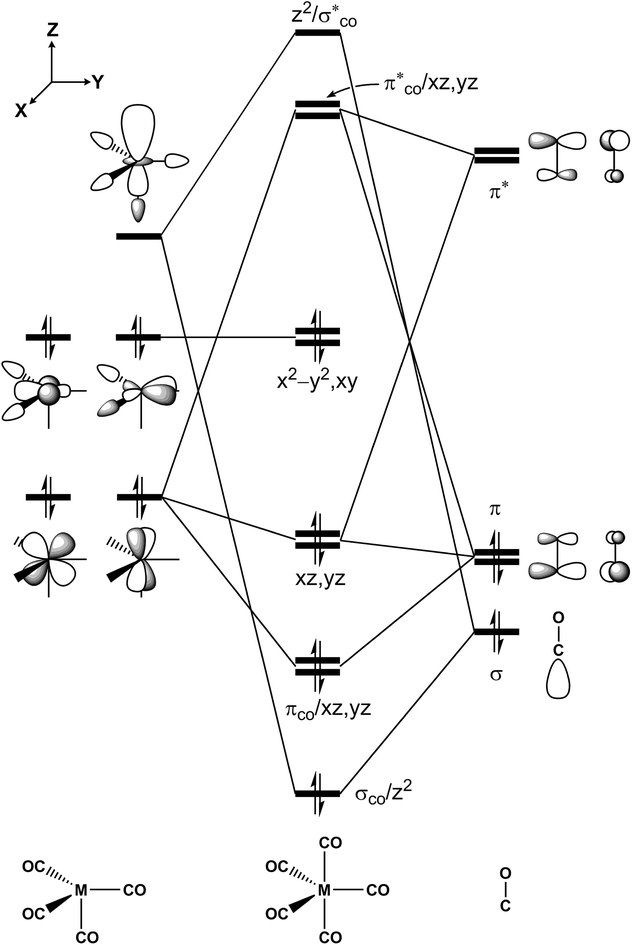
The intersection points for the ground state (S0), the first singlet excited state (S1) and the lowest triplet excited state (T1) surfaces and the transition states and the local minima for the photochemical reactions of d8 M(CO)5 complexes (eqn (1)) on S0, S1 and T1 surfaces are determined at the CASSCF (the complete-active-space SCF) level of calculations, using the Def2-SVP basis set.86 Starting from the bipyramidal geometry of d8 M(CO)5, CASSCF optimizations have been executed for the electronic ground state and a few low lying excited states in order to pursue the geometry change. The singlet ground-state configuration complies with a closed shell (σCO/z2)2(πCO/yz)2(πCO/xz)2(3dxz)2(3dyz)2(3dxy)2(3dx2−y2)2 configuration (Fig. 1). Low-lying virtual orbitals conform to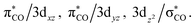 The minima, crossing minima and transition states are determined using Cartesian coordinates so the computational geometries are independent of any specific choice of internal variables. Each stationary point is executed by its harmonic frequencies, which are computed analytically at the CASSCF(14,10) level of theory.
The minima, crossing minima and transition states are determined using Cartesian coordinates so the computational geometries are independent of any specific choice of internal variables. Each stationary point is executed by its harmonic frequencies, which are computed analytically at the CASSCF(14,10) level of theory.
For better energetic values, the multi-reference Møller–Plesset (MP2-CAS) algorithm87 is used for electron correlations. Therefore, the relative energies that are obtained in this study are those established at the MP2-CAS(14,10)/Def2-SVP level, using the CASSCF(14,10)/Def2-SVP geometry, which are hereafter designated as MP2-CAS and CASSCF, respectively. The GAUSSIAN 09 package of programs88 is used for all of the computations. The absolute energies and the Cartesian coordinates for the stationary points are available as ESI.†
III. Results and discussion
(1) The photoactivation reaction for Fe(CO)5
In this section, the photochemical CO-dissociation reaction pathways for iron pentacarbonyl complex Fe(CO)5 (Fe-S0-Rea) is presented since its photochemistry has been extensively studied by many research groups.2–66,89 A schematic overview of the CO-extrusion mechanism with the relative energies is shown in Fig. 2. The corresponding optimized molecular structures are all listed in Fig. 3.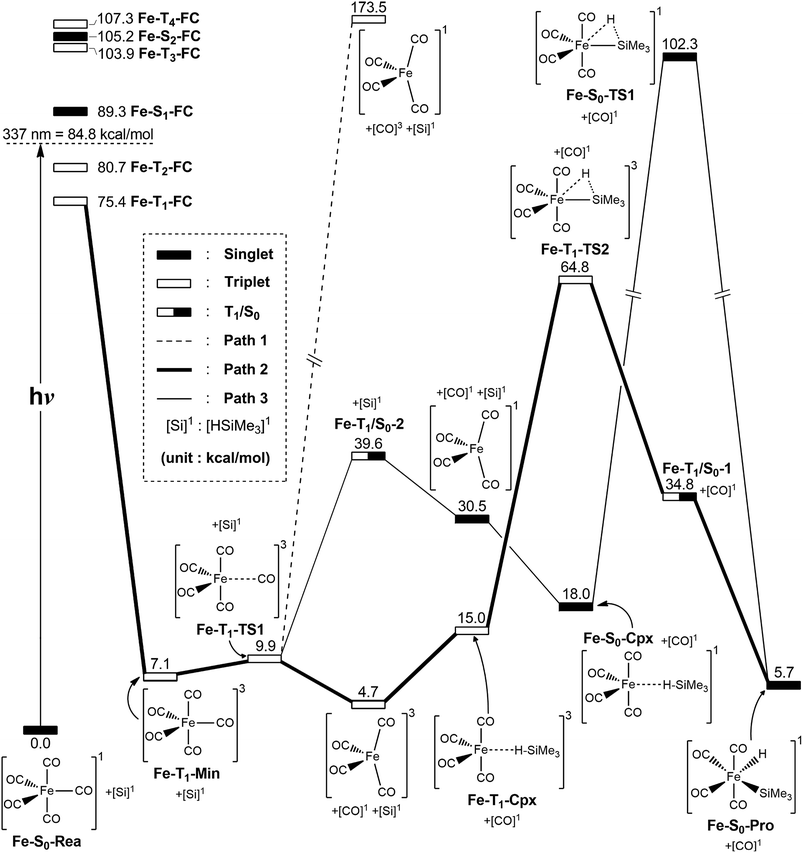 | ||
| Fig. 2 The potential energy surface based on the MP2-CAS(14,10)/Def2-SVP//CAS(14,10)/Def2-SVP level of theory for the CO-photoextrusion reaction and the oxidative addition reaction mechanisms of Fe(CO)5 (Fe-S0-Rea). FC and CI stand for Franck–Condon and conical intersection, respectively. All energies (in kcal mol−1) are given with respect to the reactant (Fe-S0-Rea). For the key points of the CASSCF optimized structures, see Fig. 3. | ||
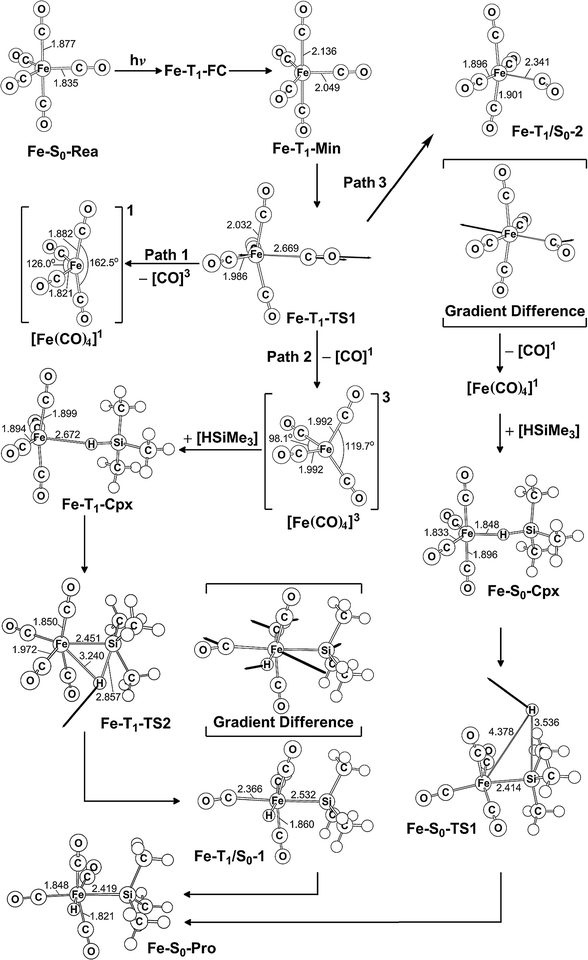 | ||
| Fig. 3 CAS(14,10)/Def2-SVP optimized geometries (in Å and deg) for the key points of the reactant Fe(CO)5 (Fe-S0-Rea) on the potential energy surfaces of paths 1, 2, and 3. The bold arrows indicate the principal atomic motions in the transition state eigenvector. The relative energies for each point are given in Fig. 2. Some hydrogen atoms are omitted for clarity. | ||
The MP2-CAS//CAS/Def2-SVP computations given in the left-hand side of Fig. 2 demonstrate that the relative energies (kcal mol−1) of the excited Franck–Condon region for Fe(CO)5 increase in the order: Fe-S0-Rea (0.0) < Fe-T1-FC (75.4) < Fe-T2-FC (80.7) < Fe-S1-FC (89.3) < Fe-T3-FC (103.9) < Fe-S2-FC (105.2) < Fe-T4-FC (107.3). It is noted that these MP2-CAS results reveal that the energy of the singlet first excited state (Fe-S1-FC) is higher than those of two triplet excited states (Fe-T1-FC and Fe-T2-FC). Additionally, the reported experimental absorption band is 337 nm (=84.8 kcal mol−1),2,15 which is lower in energy than Fe-S1-FC by 4.5 kcal mol−1. These evidences strongly suggest that once Fe-S0-Rea is photo-irradiated with 337 nm light into an excited electronic state, this species may subsequently relax to the triplet lowest excited state (Fe-T1-FC). However, one reviewer pointed out that since the vertical Franck–Condon S1 energy of (Fe-S1-FC), which differs with respect to the experimentally observed UV absorption energy, it is could be possible that UV excitation does not purely populate the S1 state, but instead populates a state that involves several configurations, hence the discrepancy in energy value. Nevertheless, our theoretical findings concluded that the photochemical carbonylation reaction of Fe-S0-Rea should occur from a triplet first excited state within the FC zone (Fe-T1-FC), which agrees satisfactorily with the experimental observations.2–66
As seen in Fig. 2, after irradiation with UV light,2–66 the reactant (Fe-S0-Rea) can relax to a local minimum at the triplet state Fe-T1-Min, whose conformation is near to the S0 geometry, as shown in Fig. 3. The MP2-CAS computations show that its energy is calculated to be about 7.1 kcal mol−1 greater than Fe-S0-Rea, as illustrated in Fig. 2. From Fe-T1-Min, a transition state search for the Fe–CO bond breaking, using the geometry of Fe-T1-Min, is undertaken. The optimized structure of Fe-T1-TS1 and the calculated transition vector at the CASSCF level are given in Fig. 3. These computations show that this transition state (Fe-T1-TS1) lies only 2.8 kcal mol−1 above the Fe-T1-Min point. From the Fe-T1-TS1 point, the Fe(CO)4 species then undergoes an oxidative addition reaction with trimethylsilane to yield the final product, Fe-S0-Pro. This gives rise to three types of reaction routes (paths 1, 2, and 3), as shown in Fig. 2.
On path 1, after the Fe-T1-TS1 point, the species separates into two molecules with different spin states. One is the Fe(CO)4 molecule in the singlet state, which is denoted [Fe(CO)4]1, and the other is the CO molecule at the triplet excited state, which is denoted [CO]3. The MP2-CAS computations show that the energies of [Fe(CO)4]1 and [CO]3 are 174 kcal mol−1 higher than that of the corresponding reactant (Fe-S0-Rea). Since this relative energy much higher than the available experimental observations for UV irradiation,2,54–66 it is not possible to generate both products ([Fe(CO)4]1 and [CO]3). Therefore, path 1 is unlikely because of the high activation energy that is required. The computations indicate that the reaction mechanism for path 1 is as follows: ([Si]1 acts for trimethylsilane in the singlet state.)
| Path 1: Fe-S0-Rea + [Si]1 + hν → Fe-T1-Min + [Si]1 → Fe-T1-TS1 + [Si]1 → [Fe(CO)4]1 + [CO]3 + [Si]1 |
On path 2, after the Fe-T1-TS1 point, the species divides into two fragments: one triplet intermediate [Fe(CO)4]3 and one singlet CO molecule. The [Fe(CO)4]3 then interacts with trimethylsilane to yield the triplet precursor complex (Fe-T1-Cpx), which is estimated to be 15.0 kcal mol−1 above the corresponding reactants. Fortunately, the activation barrier from Fe-T1-Cpx to Fe-T1-TS2 is calculated to be 49.8 kcal mol−1, which is much greater than the complex energy (15.0 kcal mol−1), so Fe-T1-Cpx should be readily observed in experiments. The Si–H bond-breaks via the triplet Fe-T1-TS2, and then this species loosens to produce the final insertion product (Fe-S0-Pro) across the intersystem crossing point (Fe-T1/S0-1). Because the activation energy (49.8 kcal mol−1) for path 2 is computed to be much less than the reported energy of the UV irradiation,2,15–28 path 2 should be energetically accessible. Consequently, the mechanism for path 2 is as follows:
| Path 2: Fe-S0-Rea + [Si]1 + hν → Fe-T1-Min + [Si]1 → Fe-T1-TS1 + [Si]1 → [Fe(CO)4]3 + [CO]1 + [Si]1→ Fe-T1-Cpx + [CO]1 → Fe-T1-TS2 + [CO]1 → Fe-T1/S0-1 + [CO]1 → Fe-S0-Pro + [CO]1 |
On path 3, many experimental observations2,15–28 show that the photochemical loss of a CO ligand from the Fe(CO)5 molecule results in the formation of the triplet [Fe(CO)4]3 intermediate and then proceeds ultimately along the singlet ground state path. This strongly implies that the crossing point for the triplet and singlet surfaces plays a central role in describing the mechanistic CO-photoelimination reaction for Fe-S0-Rea. Therefore, intersystem crossing from triplet to singlet states occurs in the region of the T1/S0 intersection Fe-T1/S0-2, as given in Fig. 2. These MP2-CAS calculations predict that Fe-T1/S0-2 lies 39.6 kcal mol−1 above Fe-S0-Rea. This molecule then relaxes to a singlet [Fe(CO)4]1 intermediate and one singlet CO molecule, whose relative energy is computed to be 30.5 kcal mol−1, with respect to Fe-S0-Rea. [Fe(CO)4]1 then reacts with trimethylsilane to generate a singlet precursor complex (Fe-S0-Cpx), which is computed to be 18.0 kcal mol−1 higher in energy than the initial reactants. This precursor complex then undergoes an insertion process to reach the transition state Fe-S0-TS1, initially via a Si–H bond stretching with a hydrogen migrating to the iron center, as shown in Fig. 3. Fig. 2 demonstrates that the activation barrier from Fe-S0-Cpx to Fe-S0-TS1 is calculated to be 84.3 kcal mol−1. This theoretical evidence strongly suggests that it is difficult for the precursor complex (Fe-S0-Cpx) to override barrier since this barrier is too high to be reached to the final insertion product (Fe-S0-Pro). It is, therefore, predicted that Fe-S0-Cpx could be easily detected experimentally. Indeed, this theoretical prediction has been confirmed by several experimental observations.29–32
Based on these theoretical calculations, the mechanism for path 3 is as follows:
| Path 3: Fe-S0-Rea + [Si]1 + hν → Fe-T1-Min + [Si]1 → Fe-T1-TS1 + [Si]1 → Fe-T1/S0-2+ [Si]1 → [Fe(CO)4]1 + [CO]1 + [Si]1→ Fe-T1/S0-3 + [CO]1 + [Si]1→ [Fe(CO)4]3 + [CO]1 + [Si]1 → Fe-T1-Cpx + [CO]1 → Fe-T1-TS2 + [CO]1 → Fe-T1/S0-1+ [CO]1 → Fe-S0-Pro + [CO]1 |
In brief, these theoretical computations show that under irradiation by UV light, Fe(CO)5 (Fe-S0-Rea) generates a coordinately unsaturated 16-electron tetracarbonyl iron (0) intermediate that exists in either the singlet or the triplet states by way of the photochemical loss of one CO ligand. After this CO-photodissociation, the dynamic Fe(CO)4 species readily experiences oxidative addition of an Si–H bond to an iron center to produce an insertion product. These model studies show there are three possible reaction pathways (path 1, path 2, and path 3) for the photo-assisted Si–H bond activation reaction. Only path 2 is shown to be energetically favorable reaction route for the alkylsilane oxidative addition reactions because this reaction pathway allows the production of the Fe(CO)4 fragment at the triplet ground state, but the other routes (path 1 and path 3) generate the singlet excited Fe(CO)4 intermediate. In other words, these model observations demonstrate that the singlet excited tetracarbonyl iron (0) plays no role in the photochemical oxidative addition reactions of alkylsilanes. However, the singlet excited Fe(CO)4 moiety interacts with alkylsilane to yield a singlet van der Waal's complex (Fe-S0-Cpx), which is readily experimentally detectable. Because of the moderate barrier height for the triplet Fe-T1-Cpx species, as shown in Fig. 2, this triplet van der Waal's complex should also be experimentally observable.11–37,48–79
(2) The photoactivation reaction for Ru(CO)5
The co-photoextrusion and the oxidative addition reaction mechanisms of the pentacarbonyl complex that contains the next transition metal element in the group 8 family, Ru(CO)5 (Ru-S0-Rea), is examined. Since previous several theoretical studies38,39,43–45 have demonstrated that the ground state of the Ru(CO)4 fragment favors a low-spin electronic ground state and its calculated triplet–singlet energy splitting (=Etriplet − Esinglet) is about 13.1–25.0 kcal mol−1 at different levels of theory, the conical intersection pathway is used to study the CO-photodissociation mechanism of Ru-S0-Rea. A sketch of the potential energy surfaces for the reaction routes that lead to the CO dissociation and the Si–H bond oxidative addition reactions is shown in Fig. 4. The calculated geometrical structures for specific parameters at the CASSCF level of theory are all shown in Fig. 5.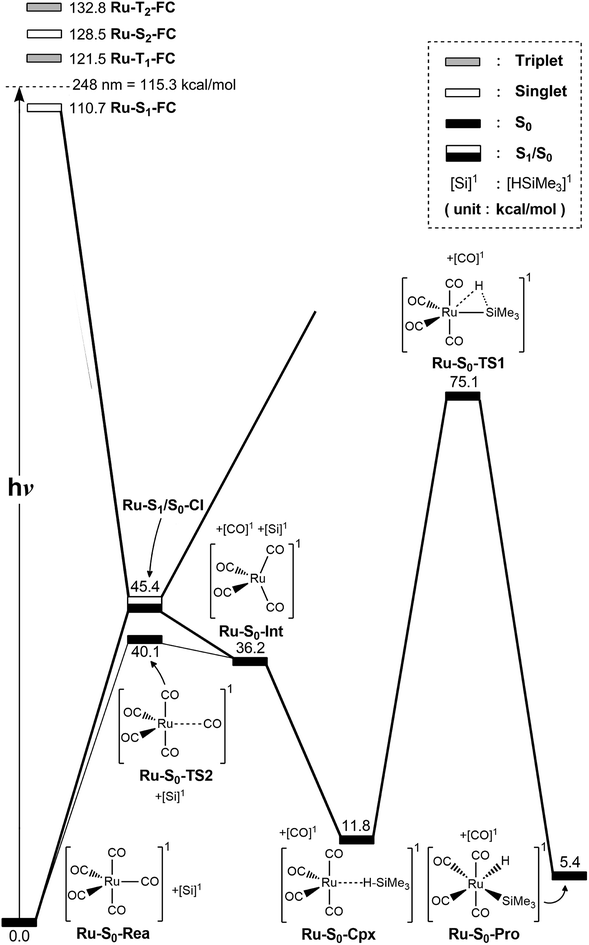 | ||
| Fig. 4 The potential energy surface based on the MP2-CAS(14,10)/Def2-SVP//CAS(14,10)/Def2-SVP level of theory for the CO-photoextrusion reaction and the oxidative addition reaction mechanisms of Ru(CO)5 (Ru-S0-Rea). FC and CI stand for Franck–Condon and conical intersection, respectively. All energies (in kcal mol−1) are given with respect to the reactant (Ru-S0-Rea). For the key points of the CASSCF optimized structures, see Fig. 5. | ||
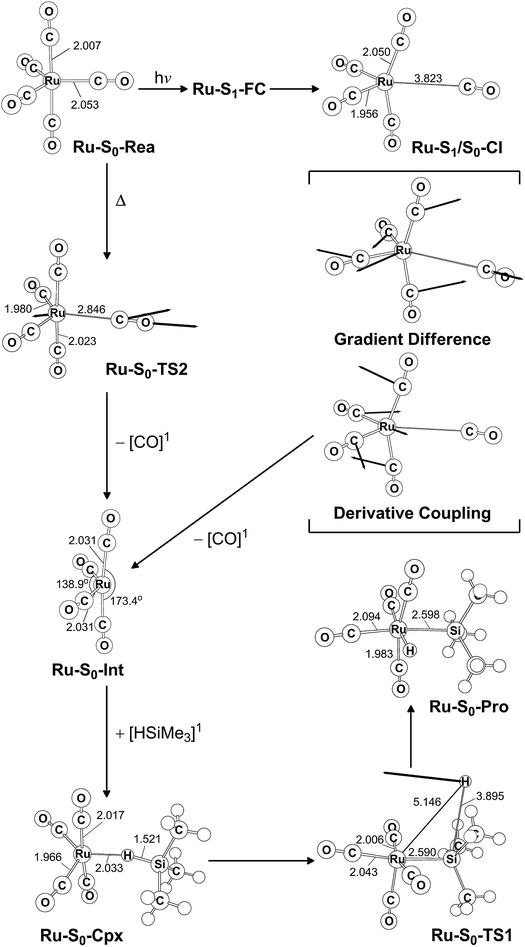 | ||
| Fig. 5 CAS(14,10)/Def2-SVP optimized geometries (in Å and deg) for the key points for the reactant, Ru(CO)5 (Ru-S0-Rea), on the potential energy surfaces. The bold arrows indicate the principal atomic motions in the transition state eigenvector. The relative energies for each species are shown in Fig. 4. Some hydrogen atoms are omitted for clarity. | ||
Initially, the reactant (Ru-S0-Rea) is promoted to the singlet excited state by way of a vertical excitation (Ru-S1-FC), as shown on the left-hand side of Fig. 4. It is noted that the calculated vertical singlet excitation energy at the MP2-CAS level of theory (110.7 kcal mol−1) agrees with the available experimental results. Bogdan and Weitz reported that the unsaturated 16 electron Ru(CO)4 is a photoproduct of the irradiation of Ru(CO)5 by 248 nm (=115.3 kcal mol−1) radiation.45 As mentioned previously, the theoretical calculations show that the Ru(CO)4 fragment should have a singlet electronic ground state.38,39,43,46,47 These results show that the only excited state that is involved in the photochemical carbonyl elimination reaction for Ru(CO)5 (Ru-S0-Rea) is the singlet.
From the Franck–Condon point (Ru-S1-FC), the species relaxes to a conical intersection (Ru-S1/S0-CI) between the singlet excited- and ground-electronic states. As seen in Fig. 5, funneling through the Ru-S1/S0-CI point results in two different reaction routes on the ground state surface, via either the derivative coupling vector or the gradient difference vector.80–85 The derivative coupling vector for Ru-S1/S0-CI is almost an antisymmetric bending motion, which produces a vibrationally hot species in the singlet ground-state configuration. Its gradient difference vector produces one equatorial Ru–CO bond breaking. Therefore, following the gradient difference vector from Ru-S1/S0-CI and dissociating one equatorial Ru–CO bond leads to a ruthenium complex with tetracarbonyls (Ru-S0-Int) and one CO molecule. The MP2-CAS calculations show that the energy of Ru-S1/S0-CI, relative to the initial reactant (Ru-S0-Rea), is 45.4 kcal mol−1, but it is 71.7 kcal mol−1 lower than Ru-S1-FC. In other words, beginning from the Ru-S1-FC point, Ru(CO)5 enters an efficacious decay tunnel (Ru-S1/S0-CI). From this conical intersection, the 16-electron photoproduct (Ru-S0-Int) and the initial reactant (Ru-S0-Rea) are readily obtained via a barrierless ground-state relaxation path.
The unsaturated Ru(CO)4 species then reacts with trimethylsilane to form a precursor complex (Ru-S0-Cpx) at the singlet ground state. Subsequently, one hydrogen migrates from the silicon atom to the ruthenium center via a transition state (Ru-S0-TS1). The insertion product (Ru-S0-Pro) is then produced. The barrier energy from Ru-S0-Cpx to Ru-S0-TS1 is computed to be 63.3 kcal mol−1 but the MP2-CAS computations show that the energy of Ru-S1/S0-CI lies 71.7 kcal mol−1 below that of Ru-S1-FC. This evidence shows that the large excess energy of 72 kcal mol−1 that is a result of the relaxation from Ru-S1-FC to Ru-S1/S0-CI is the driving force for further oxidative addition reactions with alkylsilane on the ground state surface. These theoretical findings demonstrate that the photochemical reaction for Ru(CO)5 is as follows:
| Ru(CO)5 (photo): Ru-S0-Rea + [Si]1 + hν → Ru-S1-FC + [Si]1 → Ru-S1/S0-CI + [Si]1 → Ru-S0-Int + [CO]1 + [Si]1 → Ru-S0-Cpx + [CO]1 → Ru-S0-TS1 + [CO]1 → Ru-S0-Pro + [CO]1 |
The thermal (dark) reaction of Ru(CO)5 (Ru-S0-Rea) is also examined. As shown in Fig. 4, the energy of Ru(CO)4 (Ru-S0-Int) and one CO molecule is calculated to be 36.2 kcal mol−1 above that of the corresponding reactant (Ru-S0-Rea). Close to the conical intersection region (Ru-S1/S0-CI), a CO-thermal-dissociation transition state (Ru-S0-TS2) lies on the singlet ground state surface, whose energy is only 5.3 kcal mol−1 below that of Ru-S1/S0-CI, as shown in Fig. 4. That is to say, the computations predict that the activation energy from Ru-S0-Rea to Ru-S0-TS2 is 40.1 kcal mol−1, but the barrier height from Ru-S0-Int to Ru-S0-TS2 is only 3.9 kcal mol−1. This theoretical evidence strongly suggests that Ru(CO)4 and CO recombine to regenerate the singlet reactant, Ru(CO)5, and that this process is very fast. This theoretical result is in agreement with the available experimental observations.12,45 According to some experimental reports,12,45 the singlet Ru(CO)4 fragment i generated during the irradiation of Ru(CO)5, but this ruthenium tetracarbonyl also instantly recombines with CO to form the parent molecule. This is in sharp contrast to the case of Fe(CO)5, as shown in Fig. 2,11–14 where the photochemical combination of a CO ligand occurs on a potential energy surface with a different spin multiplicity, as discussed in the previous section.
(3) The photoactivation reaction for Os(CO)5
The photochemical reaction mechanisms of the third member of the group 8 triad, Os(CO)5, are reported. Since the Os(CO)4 fragment is known to have the ground-state singlet electronic state, as demonstrated by several experimental47 and theoretical39,44 studies, the CO-photodissociation mechanism for Os(CO)5 (Os-S0-Rea) from the conical intersection mechanism viewpoints is studied. Fig. 6 shows the potential energy surface for the reaction pathways that give rise to the CO dissociation and the Si–H bond oxidative addition reaction with trimethylsilane. Fig. 7 also shows the CASSCF/Def2-SVP computed structures with some key geometrical parameters.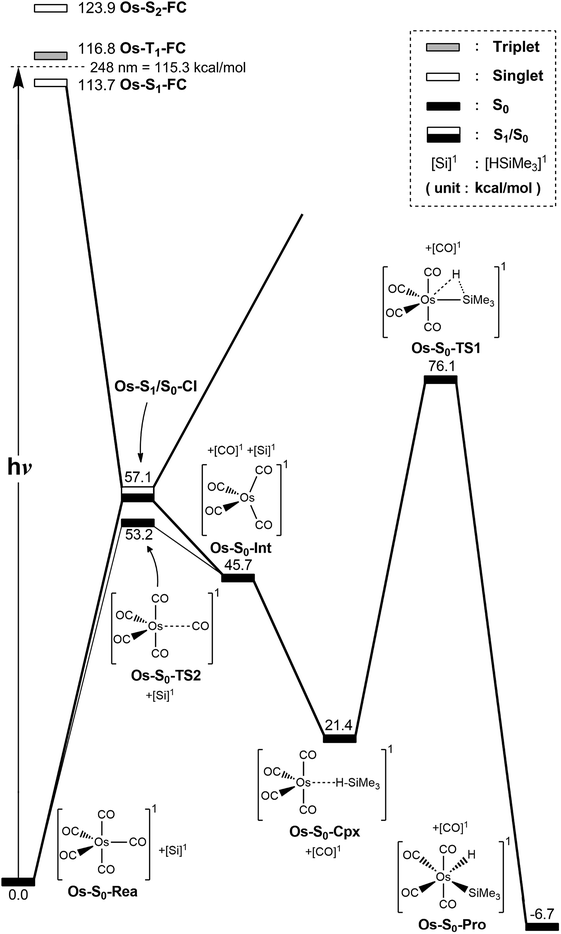 | ||
| Fig. 6 The potential energy surface based on the MP2-CAS(14,10)/Def2-SVP//CAS(14,10)/Def2-SVP level of theory for the CO-photoextrusion reaction and the oxidative addition reaction mechanisms of Os(CO)5 (Os-S0-Rea). FC and CI stand for Franck–Condon and conical intersection, respectively. All energies (in kcal mol−1) are given with respect to the reactant (Os-S0-Rea). For the key points of the CASSCF optimized structures, see Fig. 7. | ||
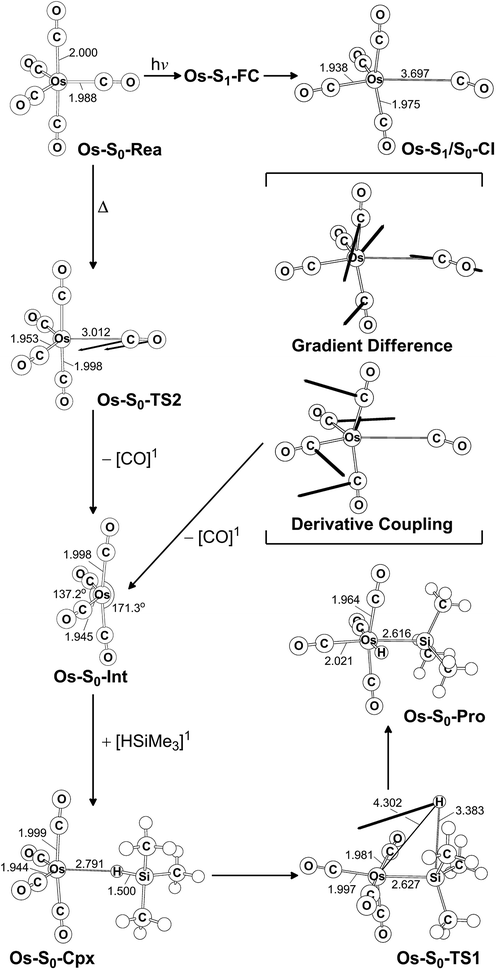 | ||
| Fig. 7 CAS(14,10)/Def2-SVP optimized geometries (in Å and deg) for the critical points for the reactant, Os(CO)5 (Os-S0-Rea), on the potential energy surfaces. The bold arrows indicate the principal atomic motions in the transition state eigenvector. The relative energies for each species are shown in Fig. 6. Some hydrogen atoms are omitted for clarity. | ||
Similarly to Ru(CO)5 as shown in Fig. 4, Fig. 6 shows that the irradiation of Os(CO)5 with light promotes it to the singlet first excited state in the Franck–Condon region, (Os-S1-FC). Calculations at the MP2-CAS level of theory show reveal the promotion energy for Os-S0-Rea is estimated to be 113.7 kcal mol−1. This theoretical value is in good agreement with the reported experimental data (248 nm = 115.3 kcal mol−1).47 This agreement means that the subsequent computational results for the photochemical reaction for Os(CO)5 are reliable.
The photoexcited Os(CO)5 undergoes radiation-less relaxation to the singlet ground state surface through the conical intersection point, (Os-S1/S0-CI), whose geometrical structure is shown in Fig. 7. Previous experience of the CO photoelimination mechanism for Ru(CO)5 shows that the breaking of an equatorial Os–CO bond plays a central role in the photoextrusion reaction for Os-S0-Rea. Indeed, along the Os–CO stretching reaction path, Os-S1/S0-CI is acquired at the Os–CO bond length of 3.697 Å. The MP2-CAS results show that the energy of Os-S1/S0-CI lies 57.1 kcal mol−1 above the initial reactant, but 63.2 kcal mol−1 below Os-S1-FC. This species then decays to an Os(CO)4 fragment (Os-S0-Int) and one CO molecule. The computational data that is shown in Fig. 6 shows that the large excess energy of 74.6 kcal mol−1 that results from the relaxation from Os-S1-FC to Os-S0-Int is the driving force for a further oxidative addition reaction with alkylsilane on the singlet ground state surface (see below).
This unsaturated 16-electron Os-S0-Int fragment also reacts with trimethylsilane to form the initial precursor complex, Os-S0-Cpx, whose energy is computed to be 21.4 kcal mol−1, relative to parent molecules. The species then undergoes a 1,2-hydrogen shift via a transition state (Os-S0-TS1) to yield the final insertion product (Os-S0-Pro). Because of the large excess energy (74.6 kcal mol−1) mentioned previously, the species readily overcomes the barrier (54.7 kcal mol−1) from Os-S0-Cpx to Os-S0-TS1. The theoretical findings show that similarly to the photochemical mechanism for Ru(CO)5 studied earlier, Os(CO)5 proceeds along the following photochemical reaction pathway:
| Os(CO)5 (photo): Os-S0-Rea + [Si]1 + hν → Os-S1-FC + [Si]1 → Os-S1/S0-CI + [Si]1 → Os-S0-Int + [CO]1 + [Si]1 → Os-S0-Cpx + [CO]1 → Os-S0-TS1 + [CO]1 → Os-S0-Pro + [CO]1 |
The thermal (dark) reaction mechanism for Os(CO)5 is also examined using the same level of theory. As is seen in Fig. 6, the MP2-CAS results show that the energies for Os-S0-TS2, and Os-S0-Int + [CO]1 are respectively calculated to be 53.2 and 45.7 kcal mol−1, with respect to the corresponding reactant. In other words, the reverse barrier height from Os-S0-Int + [CO]1 to Os-S0-TS2 is estimated to be 7.5 kcal mol−1. This theoretical finding shows that the unsaturated Os(CO)4 fragment easily recombines with one CO molecule to return to the parent molecule, Os(CO)5. In other words, this theoretical study shows that the reactivity of the unsaturated Os(CO)4 complex is quite similar to that of the analogous Ru(CO)4 compound.12,46,47
IV. Conclusion
The photochemical reaction mechanisms for the CO dissociation and the related oxidative addition with alkylsilane for group 8 metal pentacarbonyl complexes are studied. Taking the group 8 triad systems together, the following conclusions can be drawn:These computational results are in good agreement with the formation of an intermediate of a metal tetracarbonyl fragment (d8 M(CO)4) by the photochemical loss of one CO ligand from the parent molecule (d8 M(CO)5), which is in good agreement with many experimental findings.2–79
For the Fe(CO)5 model molecule, the theoretical findings show that the singlet–triplet energy difference of Fe(CO)4 is calculated to be 25.8 kcal mol−1 (MP2-CAS/Def2-SVP//CASSCF/Def2-SVP) and it has a triplet electronic ground state.90 Knowledge of the intersystem crossing mechanism for the Fe(CO)5 complex is of great importance in understanding its reaction mechanisms because it is the driving force for photochemistry. The theoretical evidence shows that the triplet iron tetracarbonyl activates the Si–H bond of alkylsilane much more readily than its singlet counterpart.
However, these theoretical results show that it is difficult for the CO molecule to recombine with the Fe(CO)4 complex, which has a vacant coordination site because the iron tetracarbonyl is proven to have a triplet electronic ground state but CO has a singlet ground state. Therefore, according to spin selection rules, it should be difficult for the triplet Fe(CO)4 and the singlet CO to recombine to generate the parent Fe(CO)5 molecule. This theoretical observation is in good agreement with many experimental results.2,11–25,33–37
For the Ru(CO)5 and Os(CO)5 model compounds, both ruthenium and osmium pentacarbonyls have similar photochemical and thermal potential energy profiles. The computations also show that both Ru(CO)4 and Os(CO)4 fragments feature a singlet electronic ground state. Therefore, the computations demonstrate that the conical intersection mechanism plays a vital role in the photochemical reactions for the Ru(CO)5 and Os(CO)5 transition metal complexes. The theoretical observations also show that the activation barrier for the thermal fragmentation reactions for Ru and Os pentacarbonyls are much higher than those for the thermal recombination reactions for the corresponding M(CO)4 fragments and CO. Therefore, after the loss of CO from Ru(CO)5 or Os(CO)5, the CO molecule readily recombines with Ru(CO)4 or Os(CO)4 to form the parent compounds. This finding is in agreement with several experimental observations.11–25,38–47
This theoretical evidence demonstrates that Fe(CO)5 readily undergoes one CO ligand dissociation upon irradiation with light to form the very reactive unsaturated intermediate Fe(CO)4 species, but it is difficult for either Ru(CO)5 or Os(CO)5 to dissociate one CO group. Therefore, the yield of oxidative addition product for the Fe(CO)5 molecule should be much larger than those for the Ru(CO)5 and Os(CO)5 systems, for the same reactive conditions.
The photochemistry of d8 M(CO)5 is salient to many types of photochemical reaction. The subtle variation poses a mechanistic challenge and it is hoped that this study will stimulate further study of this subject.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the National Center for High-Performance Computing of Taiwan for generous amounts of computing time, and the Ministry of Science and Technology of Taiwan for the financial support. In particular, one of the authors (M.-D. Su) also wishes to thank Professor Michael A. Robb, Dr S. Wilsey, Dr Michael J. Bearpark, (University of London, UK) and Professor Massimo Olivucci (Universita degli Studi di Siena, Italy), for their encouragement and support during his stay in London. Special thanks are also due to reviewers 1, 2, and 3 for very helpful suggestions and comments.References
- For reviews, see: M. Warighton, Photochemistry of metal carbonyl, Chem. Rev., 1974, 74, 401 CrossRef.
- For reviews, see: N. Leadbeater, Enlightening organometallic chemistry: the photochemistry of Fe(CO)5 and the reaction chemistry of unsaturated iron carbonyl fragments, Coord. Chem. Rev., 1999, 188, 35 CrossRef CAS.
- F. W. Grevels, in Photoprocesses in Transition Metal Complexes, Biosystems and Other Molecules, ed. E. Kochanski, Kluwer, Amsterdam, 1992 Search PubMed.
- G. L. Geoffroy and M. S. Wrighton, in Organometallic Photochemistry, Academic Press, New York, 1979 Search PubMed.
- V. Balzani and V. Carassiti, in Photochemistry of Coordination Compounds, Academic Press, London, 1970 Search PubMed.
- A. Marquez, C. Daniel and J. F. Sanz, The vacuum-ultraviolet spectrum of iron pentacarbonyl: an experimental analysis supported by a CASSCF CCI study of the Rydberg states, J. Phys. Chem., 1992, 96, 121 CrossRef CAS.
- F. Asinger and O. Berg, Über die Isomerisierung der olefinischen Doppelbindung durch Metallcarbonyle, Chem. Ber., 1955, 88, 445 CrossRef CAS.
- E. N. Frankel, E. A. Emken, H. M. Peters, V. L. Davison and R. O. Butterfield, Homogeneous Hydrogenation of Methyl Linoleate Catalyzed by Iron Pentacarbonyl. Characterization of Methyl Octadecadienoate—Iron Tricarbonyl Complexes, J. Org. Chem., 1964, 29, 3292 CrossRef CAS.
- F. K. Velichko and L. V. Vinogradova, Izv. Akad. Nauk SSSR, Ser. Khim., 1970, 1628 CAS.
- M. S. Sigman and B. E. Eaton, Catalytic Iron-Mediated [4 + 1] Cycloaddition of Diallenes with Carbon Monoxide, J. Am. Chem. Soc., 1996, 118, 11783 CrossRef CAS.
- M. Poliakoff, II Fe(CO)4, Chem. Soc. Rev., 1978, 527 RSC.
- M. Poliakoff and E. Weitz, Shedding light on organometallic reactions: the characterization of tetracarbonyliron (Fe(CO)4), a prototypical reaction intermediate, Acc. Chem. Res., 1987, 20, 408 CrossRef CAS.
- M. Poliakoff, S. M. Howdle and S. G. Kazarian, Vibrational Spectroscopy in Supercritical Fluids: From Analysis and Hydrogen Bonding to Polymers and Synthesis, Angew. Chem., Int. Ed., 1995, 34, 12751 CrossRef.
- J. P. Lomont, S. C. Nguyen and C. B. Harris, Ultrafast Infrared Studies of the Role of Spin States in Organometallic Reaction Dynamics, Acc. Chem. Res., 2014, 47, 1634 CrossRef CAS PubMed.
- A. B. Callear and R. J. Oldman, Absorption Spectra of Excited Atoms and Excited Ions produced by Isothermal Flash Photolysis of Metal Carbonyls in the Gas Phase, Nature, 1966, 210, 730 CrossRef CAS.
- M. Poliakoff and J. J. Turner, Reactions of organodigermanes, J. Chem. Soc., Dalton Trans., 1973, 1357 Search PubMed.
- M. Poliakoff, Infrared spectrum of matrix isolated tricarbonyliron, J. Chem. Soc., Dalton Trans., 1974, 210 RSC.
- M. Poliakoff and J. J. Turner, Structure and reactions of matrix-isolated tetracarbonyliron(0), J. Chem. Soc., Dalton Trans., 1974, 2276 RSC.
- M. Poliakoff and J. J. Turner, A new route to matrix isolated iron atoms, J. Chem. Soc., Faraday Trans. 2, 1974, 70, 93 RSC.
- T. J. Barton, R. Grinter, A. J. Thomson, B. Davies and M. Poliakoff, Magnetic circular dichroism evidence for the paramagnetism of tetracarbonyliron(0): low-temperature matrix studies, J. Chem. Soc., Chem. Commun., 1977, 841 RSC.
- Z. Karny, R. Naaman and R. N. Zare, Production of excited metal atoms by UV multiphoton dissociation of metal alkyl and metal carbonyl compounds, Chem. Phys. Lett., 1978, 59, 33 CrossRef CAS.
- G. Nathanson, B. Gitlin, A. M. Rosan and J. T. Yardley, Ultraviolet laser photolysis: primary photochemistry of Fe(CO)5 in PF3, J. Chem. Phys., 1981, 74, 361 CrossRef CAS.
- M. Poliakoff and J. J. Turner, The Structure of [Fe(CO)4]—An Important New Chapter in a Long-Running Story, Angew. Chem., Int. Ed., 2001, 40, 2809 CrossRef CAS PubMed.
- M. Poliakoff, The infra-red laser-induced photochemistry of Fe(CO)4, Spectrochim. Acta, 1987, 43A, 217 CrossRef CAS.
- H. Ihee, J. Cao and A. H. Zewail, Ultrafast Electron Diffraction of Transient [Fe(CO)4]: Determination of Molecular Structure and Reaction Pathway, Angew. Chem., Int. Ed., 2001, 40, 1532 CrossRef CAS PubMed.
- J. C. Mitchener and M. S. Wrighton, Photogeneration of very active homogeneous catalysts using laser light excitation of iron carbonyl precursors, J. Am. Chem. Soc., 1981, 103, 975 CrossRef CAS.
- J. C. Mitchener and M. S. Wrighton, Low-temperature photochemistry of tetracarbonylethyleneiron and tetracarbonylpropyleneiron. Spectroscopic observation of catalytically significant intermediates, J. Am. Chem. Soc., 1983, 105, 1065 CrossRef CAS.
- M. Bergt, T. Brixner, B. Kiefer, M. Strehle and G. Gerber, Controlling the Femtochemistry of Fe(CO)5, J. Phys. Chem. A, 1999, 103, 10381 CrossRef CAS.
- A. J. Ouderkirk, P. Wermer, N. L. Schultz and E. Weitz, Observation of coordinatively unsaturated intermediates following the pulsed UV photolysis of iron pentacarbonyl (Fe(CO)5), J. Am. Chem. Soc., 1983, 105, 3354 CrossRef CAS.
- T. A. Seder, A. J. Ouderkirk and E. Weitz, The wavelength dependence of excimer laser photolysis of Fe(CO)5 in the gas phase. Transient infrared spectroscopy and kinetics of the Fe(CO)x (x = 4, 3, 2) photofragments, J. Chem. Phys., 1986, 85, 1977 CrossRef CAS.
- R. J. Ryther and E. Weitz, Diode laser probes of the product distribution of coordinatively unsaturated iron carbonyls produced following excimer laser photolysis of iron pentacarbonyl in the gas phase, J. Phys. Chem., 1992, 96, 2561 CrossRef CAS.
- P. Portius, J. X. Yang, X.-Z. Sun, D. C. Grills, P. Matousek, A. W. Parker, M. Towrie and M. W. George, Unraveling the Photochemistry of Fe(CO)5 in Solution:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Observation of Fe(CO)3 and the Conversion between 3Fe(CO)4 and 1Fe(CO)4(Solvent), J. Am. Chem. Soc., 2004, 126, 10713 CrossRef CAS PubMed.
Observation of Fe(CO)3 and the Conversion between 3Fe(CO)4 and 1Fe(CO)4(Solvent), J. Am. Chem. Soc., 2004, 126, 10713 CrossRef CAS PubMed. - R. J. Ryther and E. Weitz, Reaction kinetics of coordinatively unsaturated iron carbonyls formed on gas-phase excimer laser photolysis of iron pentacarbonyl, J. Phys. Chem., 1991, 95, 9841 CrossRef CAS.
- V. Bachler, F.-W. Grevels, K. Kerpen, G. Olbrich and K. Schaffner, A Novel Facet of Carbonyl iron-Diene Photochemistry:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The η4-s-trans Isomer of the Classical Fe(CO)3(η4-s-cis-1,3-butadiene) Discovered by Time-Resolved IR Spectroscopy and Theoretically Examined by Density Functional Methods, Organometallics, 2003, 22, 1696 CrossRef CAS.
The η4-s-trans Isomer of the Classical Fe(CO)3(η4-s-cis-1,3-butadiene) Discovered by Time-Resolved IR Spectroscopy and Theoretically Examined by Density Functional Methods, Organometallics, 2003, 22, 1696 CrossRef CAS. - E. Weitz, Studies of Coordinatively Unsaturated Metal Carbonyls in the Gas Phase by Transient Infrared Spectroscopy, J. Phys. Chem., 1987, 91, 3945 CrossRef CAS.
- M.-C. Heitz and C. Daniel, Photodissociation Dynamics of Organometallics: Quantum Simulation for the Dihydride Complex H2Fe(CO)4, J. Am. Chem. Soc., 1997, 119, 8269 CrossRef CAS.
- P. T. Snee, C. K. Payne, S. D. Mebane, K. T. Kotz and C. B. Harris, Dynamics of Photosubstitution Reactions of Fe(CO)5: An Ultrafast Infrared Study of High Spin Reactivity, J. Am. Chem. Soc., 2001, 123, 6909 CrossRef CAS.
- J. J. Levison and S. D. Robinson, Transition-metal complexes containing phosphorus ligands. Part II. Triaryl phosphite derivatives of ruthenium and osmium, J. Chem. Soc. A, 1970, 639 RSC.
- T. Ziegler, Coordination geometries and relative donor-acceptor abilities of CX and X2 (X = O, S, Se, Te) and CX2 and H2CX (X = O, S) complexed to Ru(CO)4. Theoretical study by the Hartree-Fock-Slater transition-state method, Inorg. Chem., 1986, 25, 2721 CrossRef CAS.
- M. F. Gregory, M. Poliakoff and J. J. Turner, Infrared spectra of 13CO-enriched Ru(CO)5 in liquid xenon: the energy-factored force field, J. Mol. Struct., 1985, 127, 247 CrossRef CAS.
- A. W. Ehlers and G. Frenking, Structures and Bond Energies of the Transition-Metal Carbonyls M(CO)5 (M = Fe, Ru, Os) and M(CO)4 (M = Ni, Pd, Pt), Organometallics, 1995, 14, 423 CrossRef CAS.
- S. A. Decker and M. Klobukowski, The First Carbonyl Bond Dissociation Energies of M(CO)5 and M(CO)4(C2H2) (M = Fe, Ru, and Os): The Role of the Acetylene Ligand from a Density Functional Perspective, J. Am. Chem. Soc., 1998, 120, 9342 CrossRef CAS.
- L. A. Barnes, M. Rosi and C. W. Baushlicher Jr, An ab initio study of Fe(CO)n, n = 1, 5, and Cr(CO)6, J. Chem. Phys., 1991, 94, 2031 CrossRef CAS.
- J. Li, G. Schreckenbach and T. Ziegler, A Reassessment of the First Metal-Carbonyl Dissociation Energy in M(CO)4 (M = Ni, Pd, Pt), M(CO)5 (M = Fe, Ru, Os), and M(CO)6 (M = Cr, Mo, W) by a Quasirelativistic Density Functional Method, J. Am. Chem. Soc., 1995, 117, 486 CrossRef CAS.
- P. L. Bogdan and E. Weitz, A transient infrared spectroscopy study of coordinatively unsaturated ruthenium carbonyls, J. Am. Chem. Soc., 1989, 111, 3163 CrossRef CAS.
- M. Poliakoff and J. J. Turner, Structure and reactions of matrix-isolated tetracarbonyliron(0), J. Chem. Soc., Dalton Trans., 1974, 2276 RSC.
- P. L. Bogdan and E. Weitz, A transient infrared spectroscopy study of coordinatively unsaturated osmium carbonyl compounds, J. Am. Chem. Soc., 1990, 112, 639 CrossRef CAS.
- W. Wang, A. A. Narducci, P. G. House and E. Weitz, Gas-Phase Study of the Formation and Dissociation of Fe(CO)4H2:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kinetics and Bond Dissociation Energies, J. Am. Chem. Soc., 1996, 118, 8654 CrossRef CAS.
Kinetics and Bond Dissociation Energies, J. Am. Chem. Soc., 1996, 118, 8654 CrossRef CAS. - L. Banares, T. Baumert, M. Bergt, B. Kiefer and G. Gerber, The ultrafast photodissociation of Fe(CO)5 in the gas phase, J. Chem. Phys., 1998, 108, 5799 CrossRef CAS.
- O. Rubner, T. Baumert, M. Bergt, B. Kiefer, G. Gerber and V. Engel, Theoretical analysis of femtosecond excitation and fragmentation dynamics of Fe(CO)5, Chem. Phys. Lett., 2000, 316, 585 CrossRef CAS.
- O. Rubner and V. Engel, Fragmentation dynamics of Fe(CO)5 upon femtosecond excitation: a time-dependent statistical description, Chem. Phys. Lett., 1998, 293, 485 CrossRef CAS.
- M. Erdmann, O. Rubner, Z. Shen and V. Engel, Time-resolved photoelectron spectroscopy of Fe(CO)5 multiple fragmentation: theoretical considerations, Chem. Phys. Lett., 2001, 341, 338 CrossRef CAS.
- P. T. Snee, C. K. Payne, S. D. Mebane, K. T. Kotz and C. B. Harris, Dynamics of Photosubstitution Reactions of Fe(CO)5: An Ultrafast Infrared Study of High Spin Reactivity, J. Am. Chem. Soc., 2001, 123, 6909 CrossRef CAS.
- L. A. Barnes, M. Rosi and C. W. Bauschlicher, An ab initio study of Fe(CO)n, n = 1, 5, and Cr(CO)6, J. Chem. Phys., 1991, 94, 2031 CrossRef CAS.
- B. J. Persson, B. O. Roos and K. Pierloot, A theoretical study of the chemical bonding in M(CO)x (M = Cr, Fe, and Ni), J. Chem. Phys., 1994, 101, 6810 CrossRef.
- B. Delley, M. Wrinn and H. P. Luthi, Binding energies, molecular structures, and vibrational frequencies of transition metal carbonyls using density functional theory with gradient corrections, J. Chem. Phys., 1994, 100, 5785 CrossRef CAS.
- W. Wang and E. A. Weitz, Theoretical Study of the Reaction H2 + Fe(CO)4 ⇌ H2Fe(CO)4, J. Phys. Chem. A, 1997, 101, 2358 CrossRef CAS.
- O. Rubner, V. Engel, M. R. Hachey and C. Daniel, A CASSCF/MR-CCI study of the excited states of Fe(CO)5, Chem. Phys. Lett., 1999, 302, 489 CrossRef CAS.
- O. GonzalezBlanco and V. Branchadell, J. Chem. Phys., 1999, 110, 778 CrossRef CAS.
- A. Ricca, Heats of formation for Fe(CO)n (n = 1-4), Chem. Phys. Lett., 2001, 350, 313 CrossRef CAS.
- J. N. Harvey and M. Aschi, Modelling spin-forbidden reactions: recombination of carbon monoxide with iron tetracarbonyl, Faraday Discuss., 2003, 124, 129 RSC.
- S. A. Trushin, W. Fuss, K. L. Kompa and W. E. Schmid, Femtosecond Dynamics of Fe(CO)5 Photodissociation at 267 nm Studied by Transient Ionization, J. Phys. Chem. A, 2000, 104, 1997 CrossRef CAS.
- P. T. Snee, C. K. Payne, K. T. Kotz, H. Yang and C. B. Harris, Triplet Organometallic Reactivity under Ambient Conditions: An Ultrafast UV Pump/IR Probe Study, J. Am. Chem. Soc., 2001, 123, 2255 CrossRef CAS PubMed.
- V. Bachler, F.-W. Grevels, K. Kerpen, G. Olbrich and K. Schaffner, A Novel Facet of Carbonyliron-Diene Photochemistry: The η4-s-trans Isomer of the Classical Fe(CO)3(η4-s-cis-1,3-butadiene) Discovered by Time-Resolved IR Spectroscopy and Theoretically Examined by Density Functional Methods, Organometallics, 2003, 22, 1696 CrossRef CAS.
- M. Besora, J. L. Carreón-Macedo, A. J. Cowan, M. W. George, J. N. Harvey, P. Portius, K. L. Ronayne, X. Z. Sun and M. Towrie, A Combined Theoretical and Experimental Study on the Role of Spin States in the Chemistry of Fe(CO)5 Photoproducts, J. Am. Chem. Soc., 2009, 131, 3583 CrossRef CAS PubMed.
- J. P. Lomont, S. C. Nguyen and C. B. Harris, Ultrafast Studies of Stannane Activation by Triplet Organometallic Photoproducts, Organometallics, 2012, 31, 3947 CrossRef CAS.
- M. A. Schroeder and M. S. Wrighton, Pentacarbonyliron(0) photocatalyzed hydrogenation and isomerization of olefins, J. Am. Chem. Soc., 1976, 98, 551 CrossRef CAS.
- E. A. McNeill and F. R. Scholer, Molecular structure of the gaseous metal carbonyl hydrides of manganese, iron, and cobalt, J. Am. Chem. Soc., 1977, 99, 6243 CrossRef CAS.
- R. L. Sweany, J. Am. Chem. Soc., 1981, 103, 2410 CrossRef CAS.
- P. J. Krusic, D. J. Jones and D. C. Roe, Photochemical activation of molecular hydrogen by Fe(CO)5, Organometallics, 1986, 5, 456 CrossRef CAS.
- D. M. Hayes and E. Weitz, A Study of the Kinetics of Reaction of Fe(CO), and Fe(CO),(L) with H2 and C2H4 for L = H2 and C2H4 by Transient Infrared Spectroscopy: Reactions Relevant to Olefin Hydrogenation Kinetics, J. Phys. Chem., 1991, 95, 2723 CrossRef CAS.
- S. K. Nayak, G. J. Farrell and T. J. Burkey, Photosubstitution of Two Iron Pentacarbonyl CO's in Solution via a Single-Photon Process: Dependence on Dispersed Ligands and Role of Triplet Intermediates, Inorg. Chem., 1994, 33, 2236 CrossRef CAS.
- S. K. Nayak and T. J. Burkey, Photosubstitution of iron pentacarbonyl, with triethylphosphine in cyclohexane: Fe(CO)4PEt3 and Fe(CO)3(PEt3)2 are single-photon products, Inorg. Chem., 1992, 31, 1125 CrossRef CAS.
- A. J. Ouderkirk and E. Weitz, The kinetics of reaction of photolytically generated Fe(CO)x (x = 2, 3, 4) with CO, J. Chem. Phys., 1983, 79, 1089 CrossRef CAS.
- E. A. Glascoe, K. R. Sawyer, J. E. Shanoski and C. B. Harris, The Influence of the Metal Spin State in the Iron-Catalyzed Alkene Isomerization Reaction Studied with Ultrafast Infrared Spectroscopy, J. Phys. Chem. C, 2007, 111, 8789 CrossRef CAS.
- J. N. Harvey and R. Poli, Computational study of the spin-forbidden H2 oxidative addition to 16-electron Fe(0) complexes, Dalton Trans., 2003, 4100 RSC.
- C. Daniel, M. Benard, A. Dedieu, R. Wiest and A. Veillard, Theoretical Aspects of the Photochemistry of Organometallics. 3. Potential Energy Curves for the Photodissociation of Fe(CO), J. Phys. Chem., 1984, 88, 4805 CrossRef CAS.
- J. N. Harvey and R. Poli, Computational study of the spin-forbidden H2oxidative addition to 16-electron Fe(0) complexes, J. Chem. Soc., Dalton Trans., 2003, 4100 RSC.
- J. N. Harvey, Computational study of the energetics of 3Fe(CO)4, 1Fe(CO)4 and 1Fe(CO)4(L), L = Xe, CH4, H2, and CO, Phys. Chem. Chem. Phys., 2006, 8, 93 RSC.
- F. Bernardi, M. Olivucci and M. A. Robb, Modelling Photochemical Reactivity of Organic Systems — A New Challenge to Quantum Computational Chemistry, Isr. J. Chem., 1993, 265 CrossRef CAS.
- M. Klessinger, Conical Intersections and the Mechanism of Singlet Photoreactions, Angew. Chem., Int. Ed. Engl., 1995, 34, 549 CrossRef CAS.
- F. Bernardi, M. Olivucci and M. A. Robb, Potential energy surface crossings in organic photochemistry, Chem. Soc. Rev., 1996, 321 RSC.
- F. Bernardi, M. Olivucci and M. A. Robb, The role of conical intersections and excited state reaction paths in photochemical pericyclic reaction, J. Photochem. Photobiol., A, 1997, 105, 365 CrossRef CAS.
- M. Klessinger, Theoretical models for the selectivity of organic singlet and triplet photoreactions, Pure Appl. Chem., 1997, 69, 773 CAS.
- M. Klessinger and J. Michl, in Excited States and Photochemistry of Organic Molecules, VCH Publishers, New York, 1995 Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- M. J. Bearpark, M. A. Robb and H. B. Schlegel, A direct method for the location of the lowest energy point on a potential surface crossing, Chem. Phys. Lett., 1994, 223, 269 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian, Inc., Wallingford CT, 2013.
- C. Daniel, M. Benard, A. Dedieu, R. Wiest and A. Veillard, Theoretical Aspects of the Photochemistry of Organometallics. 3. Potential Energy Curves for the Photodissociation of Fe(CO), J. Phys. Chem., 1984, 88, 4805 CrossRef CAS.
- However, it has been shown by Harvey and Aschi that the energy difference between triplet ground state (Fe-T1-Int) and the singlet excited state (Fe-S1-Int) was estimated to be 8.0 kcal/mol. See: ref. 61.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra07669c |
| This journal is © The Royal Society of Chemistry 2019 |