Theoretical investigation on the electronic structure of one dimensional infinite monatomic gold wire: insights into conducting properties

Abstract

Mixed-valence metal–organic nanostructures show unusual electronic properties. In our pervious investigation, we have designed and predicted a unique one-dimensional infinite monatomic gold wire (1D-IMGW) with excellent conductivity and the interesting characteristic of mixed valency (Au_c³⁺ and Au⁰_i). For further exploring its conduction properties and stability in conducting state, here we select one electron as a probe to explore the electron transport channel and investigate its electronic structure in conducting state. Density functional theory (DFT) calculations show the 1D-IMGW maintains its original structure in conducting state illustrating its excellent stability. Moreover, while adding an electron, 1D-IMGW is transformed from a semiconductor to a conductor with the energy band mixed with Au_c (5d) and Au_i (6s) through the Fermi level. Thus 1D-IMGW will conduct along its gold atom chain demonstrating good application prospect in nanodevices.

---

1. Introduction

One-dimensional metallic nanowires have received significant attention due to their particular physicochemical properties^1–21 as well as their potential applications in nanodevices. Previous experimental and theoretical studies have been conducted to illuminate the formation of atomic wires and their unique properties,^22–32 in particular, various novel gold nanostructures with unusual stoichiometries and structures have been synthesized because of the unique interactions between Au–Au, such as metallophilic interaction originating from electronic correlation being reinforced by relativistic effects,^{23–29,33–42} and short d¹⁰–d¹⁰ contacts³⁶ arising from the bonding stabilization. However, the finite length limit the applications of Au monatomic chain. With the aim to obtain one-dimensional infinite monatomic gold wire with highly conductive and stability, we adopt the strategy to construct one-dimensional infinite monatomic metal wire by alternately connecting the organic metal macrocyclic compound and the single metal atom.

As is well-known, corroles,^43–50 are constructed by four conjugated pyrrole rings with three pyrrole-type nitrogen atoms and one pyridine-type nitrogen atom. Comparing with porphyrins,⁵¹ corroles' cavities are smaller due to the lack of one meso-carbon atom, which makes corroles superior tri-anionic ligands^52,53 in stabilizing high oxidation-state transition metals and trivalent metals [M(III), M(IV) or M(V), M = Au, Mn, Fe, Co, Ni, Cu, Cr, Rh, Ga].^54–63 The trivalent gold is generally stabled by a trianionic ligand to form stable complex. Furthermore, a stable square-planar Au(III)–corrole⁶³ has been synthesized with excellent long-wavelength phosphorescence at ambient temperature.

Based on this stable isolated subunit, we have designed and investigated a novel one-dimensional (1D) infinite monatomic gold wire (1D-IMGW)²² with each of central Au at corrole rings connected by the single Au atoms, which has stabilized by tri-anionic corrole ligands. The 1D-IMGW exhibits excellent stability by the strong interaction between the d_z² orbitals of the Au_c atoms in the centers of the corrole rings and the 6s orbitals of the Au_i atoms in the middle of adjacent corrole rings. Moreover, the 1D-IMGW demonstrated the unique characteristic of mixed valency (Au³⁺ and Au⁰) and strong absorption across the entire visible range. We also further predicted the exceptional conductivity along the monatomic Au chains perpendicular to the corrole rings. However, the mechanism of charge transport on the materials of 1D-IMGW remains unclear. To explore it, here we have charged one electron on the 1D-IMGW and studied the electronic properties of this monatomic Au wire. In this work, the stable structure of charged 1D-IMGW ([1D-IMGW]⁻) has been optimized using density functional theory (DFT), and the band structure, the density of states (DOS), projection density of states (PDOS), Bader charges analysis and the partial charge densities have been calculated. These results presented here, help us to understand the micro mechanism of charge transport of 1D-IMGW that the electron transport along the energy band mixed with Au_c (5d) and Au_i (6s) through the Fermi level of [1D-IMGW]⁻.

2. Computational details

As used in our previous work,²² we performed ab initio calculations on the structural and electronic properties of the 1D-IMGW with one electron (the same amount of homogeneous positive background charge is added to ensure the charge neutrality by VASP program)^64,65 under periodic boundary conditions using the plane-wave technique implemented in the Vienna ab initio simulation package (VASP).^66,67 The generalized gradient approximation (GGA) with the PBE functional,⁶⁸ including spin–orbit coupling (SOC), was employed to describe the exchange–correlation functional in all calculations. Here we've summed up over the data of quantisation axis (s_x, s_y, s_z) for s, p, d orbitals of every atoms and given the total spin–orbit coupling effects for s, p and d orbitals for Au atoms in 1D gold wire. The projector-augmented wave (PAW) method⁶⁹ was used to describe the electron–ion interactions, and the cutoff energy was set to 400 eV. All atomic positions were optimized by the conjugated gradient method with a converging tolerance of 0.02 eV Å⁻¹ for the force on all atoms. The 1D periodic boundary conditions were considered along the growth direction of the nanowire. Two vacuum distances in the b and c directions over 15 Å were set to eliminate interactions between nanowires in adjacent cells. A Monkhorst–Pack grid 11 × 1 × 1 was used to sample the 1D periodic Brillouin zone, and 31 × 1 × 1 k-point meshes were used in the structure densities of states (DOS) integral for the periodic systems. The Brillouin zone was sampled by 31 k-points with line-mode used to calculate their electronic band structures.

3. Results and discussion

3.1 The electronic structure of the [1D-IMGW]⁻

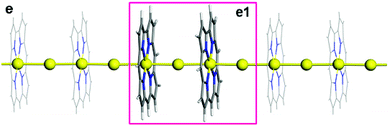
Our designed and predicted a unique one-dimensional (1D) infinite monatomic gold wire (1D-IMGW),²² in which monatomic Au wire is stabilized by the organic macrocyclic corrole compounds, and there are strong σ chemical bonding between the 5d_z² orbitals of the Au_c (Au atom at the centre of the corrole rings) and the 6s orbitals of the Au_i (Au atom between corrole rings) atoms. The 1D-IMGW displays excellent conductivity and strong absorption across the entire visible range. We here further investigate the mechanism of electron transport of 1D-IMGW. The optimized stable structure of charged 1D-IMGW ([1D-IMGW]⁻) is presented in Fig. 1. The partial bond lengths and the Bader charges analysis of Au_c and Au_i atoms are collected in Table 1. As seen from Fig. 1 and Table 1, the bond lengths of Au–N range from 1.967 Å to 1.987 Å, and from 1.971 Å to 1.993 Å, and the Au–Au bond lengths are 2.757 Å and 2.785 Å, and 2.766 Å and 2.777 Å in 1D-IMGW and [1D-IMGW]⁻, respectively. These bond lengths have slightly altered before and after charging on 1D-IMGW, indicating that the skeleton structure of 1D-IMGW has not distorted after charging and is relatively stable.

Fig. 1 (e) The structure of the [1D-IMGW]⁻ and (e1) the primitive cell structure of the [1D-IMGW]⁻.

Table 1 The bond lengths of Au–N (D_Au–N) and Au–Au (D_Au–Au) (Å), and the Bader charges of Au atoms in the [1D-IMGW]⁻ and [1D-IMGW]

System	Bond lengths		Au charges
	DAu–N	DAu–Au	Auc	Aui
1D-IMGW	1.967–1.987	2.757–2.785	0.96, 0.98	−0.15, −0.16
[1D-IMGW]^−	1.971–1.993	2.766–2.777	0.94, 0.97	−0.35, −0.35

---

As is our known, the mixed-valence character is usually determined by the spin density obtained under the broken symmetry approach^70,71 in molecular systems. However, for the stable periodic system of [1D-IMGW]⁻, we adopt the Bader charges analysis on Au atoms to investigate the possible oxidation states of Au atoms. As seen from Table 1, the Bader charges of the two Au_c atoms in [1D-IMGW]⁻ are 0.94 |e| and 0.97 |e|, which are also very close to the Bader charges of 0.96 |e| and 0.98 |e| in 1D-IMGW, showing that the oxidation states of Au_c atoms in [1D-IMGW]⁻ are still triplet valence.²² The Bader charges of Au_i atoms are −0.35 |e| in [1D-IMGW]⁻, higher than that (−0.15 |e| and −0.16 |e|) in 1D-IMGW, indicating that the added electron located mainly on the 6s of Au_i atoms in [1D-IMGW]⁻. Obviously, these Bader charges demonstrate that the structure of [1D-IMGW]⁻ remain the characteristic of mix valences with Au_c³⁺ and Au_i⁻, respectively.

3.2 The electron properties of [1D-IMGW]⁻

Here we used electron probe to further understand the electron transport mechanism of 1D-IMGW. Based on the optimized structure of charged 1D-IMGW ([1D-IMGW]⁻), the calculated electronic band structure, density of states (DOS) and the projection densities of states (PDOS) of [1D-IMGW]⁻ are shown in Fig. 2 and 3. As seen from Fig. 2, the calculated electronic band structure of [1D-IMGW]⁻ shows a metallic property, which is different from the direct semiconductor of neutral 1D-IMGW, because the partial electronic bands of [1D-IMGW]⁻ have already crossed the Fermi level. We can also see that the distribution of the energy densities of states nearby the Fermi level is relatively higher in [1D-IMGW]⁻ than that in 1D-IMGW,²² showing that the electron conduction is very excellent on 1D-IMGW materials.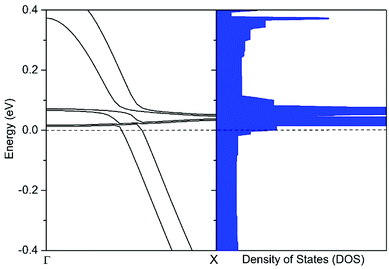

Fig. 2 The band structure (left) and density of states (right) of the [1D-IMGW]⁻ calculated by PBE. The Fermi level is set at zero.

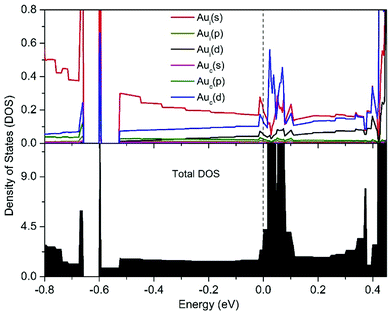Fig. 3 Calculated projection densities of states (PDOS) (up) and total densities of states (down) of the [1D-IMGW]⁻.

To investigate the component of total DOS nearby the Fermi level of [1D-IMGW]⁻, the projection densities of states (PDOS) by calculating the total spin–orbit coupling effects for s, p and d orbitals for Au atoms in 1D gold wire, is presented in Fig. 3. Comparing the total DOS and the PDOS in Fig. 3, we can see the orbital-projected densities of states of Au_c and Au_i nearby the Fermi level are mainly 5d and 6s orbitals, respectively, indicating that there is a strong orbital interaction between the 5d orbitals of the Au_c atoms and the 6s orbitals of the Au_i atoms about the Fermi level. Therefore, as predicted by our previous research,²² 1D-IMGW has remarkable conductivity and its electron conducting channel is along the monoatomic Au chains through the 5d_z² orbitals of the Au_c atoms and the 6s orbitals of the Au_i atoms.

3.3 The partial charge densities of [1D-IMGW]⁻

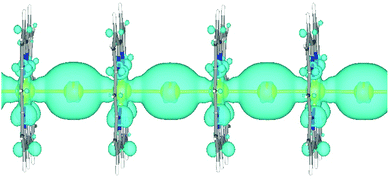
To further show the visualized strong interaction between the 5d orbitals of the Au_c atoms and the 6s orbitals of the Au_i atoms at Fermi level in [1D-IMGW]⁻, The partial charge densities of the Fermi level of [1D-IMGW]⁻ are provided in Fig. 4. As seen from Fig. 4, the major contributions of the partial charge densities of the Fermi level arise from the strong σ bond formed by the 5d_z² orbitals of the Au_c atoms and the 6s orbitals of the Au_i atoms in the [1D-IMGW]⁻. Moreover, the extending σ bond in [1D-IMGW]⁻ is very similar to that in 1D-1MGW and the charge densities on Au_i of [1D-IMGW]⁻ is much greater than that of 1D-IMGW, leading to the high stability for 1D-IMGW with electron transporting. Obviously, the conduction mechanism of 1D-IMGW is the electron transporting along the monoatomic Au chains perpendicular to the corrole rings through the electronic energy bands consisting of 5d_z² orbitals of the Au_c atoms and the 6s orbitals of the Au_i atoms.

Fig. 4 The partial charge densities (isovalue = 0.0003 au) of the Fermi level of [1D-IMGW]⁻.

4. Conclusions

Based on our previous study of the newly-constructed 1D-infinite monatomic Au wire (1D-IMGW) with excellent conductivity, extensive density functional calculations have been performed to further investigate the electronic properties of 1D-IMGW after adding one electron ([1D-IMGW]⁻), which will bring us insight into the electron transport mechanism on 1D-IMGW. The optimized structure of the [1D-IMGW]⁻ still remain linear, however, its electronic energy band structure displays a conductor property. Moreover, this theoretical work provide a method to study the electron transport mechanism of one-dimensional monoatomic Au chains and the calculated PDOS and partial charge densities indicate that the 1D-IMGW has extremely strong conductivity where electrons conduct along the monoatomic Au chains perpendicular to the corrole rings by their 5d_z² and 6s orbitals of Au_c and Au_i, respectively. Despite charging on the 1D-IMGW, the Au_c and Au_i still show mixing oxidation valence states of Au³⁺ and Au⁻.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge simulating discussions with Professors Zexing Cao, Jun Li and Yi Zhao. This work was supported by the National Natural Science Foundation of China (No. 21663008, 21763006, and 21503046), Natural Science Foundation of Guizhou Province of China (No. [2017]1029), Science and Technology Project of Guizhou Province (No. 2017[5788]), Natural Science Foundation of Guizhou Province of China (No. QKJ[2015]2122), Natural Science foundation of Department of Education of Guizhou Province (No. QJTD[2015]55), the construction project for Guizhou Provincial Key Disciplines (No. ZDXK[2015]10) and the undergraduate research program of GZEU (No. 2018DXS112). This project is partially supported by the Open Fund of Shaanxi Key Laboratory of Catalysis to J. X. L. (No. SXKLC-2017-01). We also thank the computational resources assistance by the State Key Laboratory of Physical Chemistry of Solid Surfaces (Xiamen University), the Shenzhen Supercomputing Center.

Notes and references

1. H. J. Seo, W. Jeong, S. Lee and G. D. Moon, Nanoscale, 2018, 10, 5424.
2. L. Gao, L. Chen, H. Wei and H. Xu, Nanoscale, 2018, 10, 11923.
3. R. MacKenzie, C. Fraschina, B. Dielacher, T. Sannomiya, A. B. Dahlin and J. Vörös, Nanoscale, 2013, 5, 4966.
4. L. Shi, R. Wang, H. Zhai, Y. Liu, L. Gao and J. Sun, Phys. Chem. Chem. Phys., 2015, 17, 4231.
5. C. J. Murphy and N. R. Jana, Adv. Mater., 2002, 14, 80.
6. T. M. Whitney, P. C. Searson, J. S. Jiang and C. L. Chien, Science, 1993, 261, 1316.
7. Z. L. Wang, Adv. Mater., 2000, 12, 1295.
8. M. Wu, J. D. Burton, E. Y. Tsymbal, X. C. Zeng and P. Jena, J. Am. Chem. Soc., 2012, 134, 14423.
9. T. Nishinaka, A. Takano, Y. Doi, M. Hashimoto, A. Nakamura, Y. Matsushita, J. Kumaki and E. Yashima, J. Am. Chem. Soc., 2005, 127, 8120.
10. H.-F. Wang, X.-Q. Gong, Y.-L. Guo, Y. Guo, G. Lu and P. Hu, J. Phys. Chem. C, 2009, 113, 6124.
11. F. Wang, Y. Dai, J. Zhao and Q. Li, Phys. Chem. Chem. Phys., 2014, 16, 24716.
12. E. B. Guidez and C. M. Aikens, Nanoscale, 2012, 4, 4190.
13. K. A. Dick and P. Caroff, Nanoscale, 2014, 6, 3006.
14. L. Liu, J. Yuan, L. Cheng and J. Yang, Nanoscale, 2017, 9, 856.
15. S. Ding, Y. Tian, J. Jiu and K. Suganuma, RSC Adv., 2018, 8, 2109.
16. M. Hu, J. Gao, Y. Dong, S. Yang and R. K. Y. Li, RSC Adv., 2012, 2, 2055.
17. G.-C. He, H. Lu, X.-Z. Dong, Y.-L. Zhang, J. Liu, C.-Q. Xie and Z.-S. Zhao, RSC Adv., 2018, 8, 24893.
18. Y. C. Kim and S. Y. Kim, RSC Adv., 2018, 8, 19532.
19. S. J. Percival, N. E. Vartanian and B. Zhang, RSC Adv., 2014, 4, 10491.
20. X. Wang, X. Yin, H.-L. Yu and Y.-T. Liu, ChemistrySelect, 2018, 3, 6156.
21. H. Joshi, D. P. Rai, P. K. Patra, K. C. Bhamu and R. K. Thapa, Nanosci. Nanoeng., 2016, 4, 59.
22. C. Zhu, J.-X. Liang and G. Wei, Phys. Chem. Chem. Phys., 2016, 18, 12338.
23. H. Ohnishi, Y. Kondo and K. Takayanagi, Nature, 1998, 395, 780.
24. G. Rubio-Bollinger, S. R. Bahn, N. Agraït, K. W. Jacobsen and S. Vieira, Phys. Rev. Lett., 2001, 87, 026101.
25. V. Rodrigues and D. Ugarte, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 073405.
26. S. B. Legoas, D. S. Galvão, V. Rodrigues and D. Ugarte, Phys. Rev. Lett., 2002, 88, 076105.
27. S. R. Bahn, N. Lopez, J. K. Nørskov and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 081405.
28. F. D. Novaes, A. J. R. da Silva, E. Z. da Silva and A. Fazzio, Phys. Rev. Lett., 2003, 90, 036101.
29. N. V. Skorodumova and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 121404.
30. X. Li, H. Lv, J. Dai, L. Ma, X. C. Zeng, X. Wu and J. Yang, J. Am. Chem. Soc., 2017, 139, 6290.
31. C. Hermosa, J. Vicente Álvarez, M.-R. Azani, C. J. Gómez-García, M. Fritz, J. M. Soler, J. Gómez-Herrero, C. Gómez-Navarro and F. Zamora, Nat. Commun., 2013, 4, 1709.
32. J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864.
33. H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370.
34. H. Schmidbaur, Gold Bull., 2000, 33, 3.
35. H. Schmidbaur, Gold Bull., 1990, 23, 11.
36. A. Muñoz-Castro and R. G. Maturana, J. Phys. Chem. C, 2014, 118, 21185.
37. R. G. Maturana, M. P. Vargas and A. Muñoz-Castro, J. Phys. Chem. A, 2012, 116, 8737.
38. A. I. Yanson, G. R. Bollinger, H. E. van den Brom, N. Agrait and J. M. van Ruitenbeek, Nature, 1998, 395, 783.
39. R. H. M. Smit, C. Untiedt, A. I. Yanson and J. M. van Ruitenbeek, Phys. Rev. Lett., 2001, 87, 266102.
40. E. Z. da Silva, F. D. Novaes, A. J. R. da Silva and A. Fazzio, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 115411.
41. A. Thakur, A. Kumar and P. K. Ahluwalia, AIP Conf. Proc., 2013, 1512, 190.
42. V. G. Pol, E. Koren and A. Zaban, Chem. Mater., 2008, 20, 3055.
43. C. Zhu, J. Liang, B. Wang, J. Zhu and Z. Cao, Phys. Chem. Chem. Phys., 2012, 14, 12800.
44. I. Aviv and Z. Gross, Chem. Commun., 2007, 20, 1987.
45. V. S. Shetti, U. R. Prabhu and M. Ravikanth, J. Org. Chem., 2010, 75, 4172.
46. D. T. Gryko, Eur. J. Org. Chem., 2002, 2002, 1735.
47. I. Aviv-Harel and Z. Gross, Chem.–Eur. J., 2009, 15, 8382.
48. C. Zhu, J.-X. Liang and Z. Cao, J. Phys. Chem. C, 2018, 122, 20781.
49. C. Zhu and J.-X. Liang, New J. Chem., 2015, 39, 3624.
50. C. Zhu, J. Liang and Z. Cao, J. Phys. Chem. C, 2013, 117, 13388.
51. C. Zhu and Z. Cao, Acta Chim. Sin., 2013, 71, 1527.
52. W. Liu, X. Huang, M.-J. Cheng, R. J. Nielsen, W. A. Goddard and J. T. Groves, Science, 2012, 337, 1322.
53. S. Leininger, B. Olenyuk and P. J. Stang, Chem. Rev., 2000, 100, 853.
54. W. Nam, Acc. Chem. Res., 2007, 40, 522.
55. G. Golubkov, J. Bendix, H. B. Gray, A. Mahammed, I. Goldberg, A. J. DiBilio and Z. Gross, Angew. Chem., Int. Ed., 2001, 40, 2132.
56. E. Vogel, S. Will, A. S. Tilling, L. Neumann, J. Lex, E. Bill, A. X. Trautwein and K. Wieghardt, Angew. Chem., 1994, 106, 771.
57. H. Schlaich, G. G. Lindner, J. Feldmann, E. O. Göbel and D. Reinen, Inorg. Chem., 2000, 39, 2740.
58. A. E. Meier-Callahan, H. B. Gray and Z. Gross, Inorg. Chem., 2000, 39, 3605.
59. S. Will, J. Lex, E. Vogel, V. A. Adamian, E. Van Caemelbecke and K. M. Kadish, Inorg. Chem., 1996, 35, 5577.
60. G. Golubkov and Z. Gross, Angew. Chem., 2003, 115, 4645.
61. J. Liang, C. Zhu and Z. Cao, Phys. Chem. Chem. Phys., 2013, 15, 13844.
62. C. Zhu and J.-X. Liang, J. Power Sources, 2015, 283, 343.
63. E. Rabinovich, I. Goldberg and Z. Gross, Chem.–Eur. J., 2011, 17, 12294.
64. H. He, P. Zapol and L. A. Curtiss, J. Phys. Chem. C, 2010, 114, 21474.
65. C. Ouyang, Y. Du, S. Shi and M. Lei, Phys. Lett. A, 2009, 373, 2796.
66. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
67. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
68. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
69. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
70. D. Mac-Leod Carey, C. Morales-Verdejo, A. Muñoz-Castro, F. Burgos, D. Abril, C. Adams, E. Molins, O. Cador, I. Chávez, J. M. Manríquez, R. Arratia-Pérez and J. Y. Saillard, Polyhedron, 2010, 29, 1137.
71. A. Muñoz-Castro, D. Mac-Leod Carey, C. Morales-Verdejo, I. Chávez, J. M. Manríquez and R. Arratia-Pérez, Inorg. Chem., 2010, 49, 4175.

---