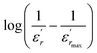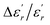Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Study of diffuse phase transition and relaxor ferroelectric behavior of Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic
Z. Raddaouia,
S. El Kossia,
J. Dhahri *a,
N. Abdelmoulab and
K. Taibic
*a,
N. Abdelmoulab and
K. Taibic
aLaboratoire de la Matière Condensée et des Nanosciences, Université de Monastir, Faculté des Sciences de Monastir, Avenue de l'environnement, 5019 Monastir, Tunisia. E-mail: j.dhahri3000@gmail.com
bLaboratoire des Matériaux Ferroélectriques, LR-Physique-Mathématiques et Applications, Université de Sfax, Faculté des Sciences, Route de Soukra km 3.5 B.P 1171, 3000 Sfax, Tunisia
cLaboratoire de Sciences et Génie des Matériaux, Faculté de Génie Mécanique et Génie des Procédés, Université des Sciences et de la Technologie Houari Boumediene BP32, Bab Ezzouar 16111, Alger, Algeria
First published on 18th January 2019
Abstract
In the present work, structural and dielectrics properties of polycrystalline sample Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 (BBTZN) prepared by a molten-salt method were investigated. X-ray diffraction analyses revealed the formation of a single-phase pseudocubic structure with a Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Unlike the trend observed in classic ferroelectrics, the temperature dependence of the dielectric constants showed the presence of three sequences of structural phase transitions. In fact, the local disorder provides a frequency dependent relaxor like behaviours attributed to the dynamic of polar nanoregions (PNRs). The diffuse phase transition (DPT) analyzed using the modified Curie–Weiss law and Lorenz formula confirms the presence of short-range association between the nanopolar domains. The obtained values of the degree of diffuseness are found to be in the range of 1.58–1.78 due to the existence of different states of polarization and, hence, different relaxation times in different regions. The frequency dependence of temperature at dielectric maxima, which is governed by the production of PNRs at a high temperature, satisfies the Vogel–Fulcher (V–F) law. The temperature dependence of the electric modulus for various frequencies indicating a thermally activated relaxation ascribed to the Maxwell–Wagner (M–W) space charge relaxation phenomenon.
m space group. Unlike the trend observed in classic ferroelectrics, the temperature dependence of the dielectric constants showed the presence of three sequences of structural phase transitions. In fact, the local disorder provides a frequency dependent relaxor like behaviours attributed to the dynamic of polar nanoregions (PNRs). The diffuse phase transition (DPT) analyzed using the modified Curie–Weiss law and Lorenz formula confirms the presence of short-range association between the nanopolar domains. The obtained values of the degree of diffuseness are found to be in the range of 1.58–1.78 due to the existence of different states of polarization and, hence, different relaxation times in different regions. The frequency dependence of temperature at dielectric maxima, which is governed by the production of PNRs at a high temperature, satisfies the Vogel–Fulcher (V–F) law. The temperature dependence of the electric modulus for various frequencies indicating a thermally activated relaxation ascribed to the Maxwell–Wagner (M–W) space charge relaxation phenomenon.
1. Introduction
New industrial applications require advanced materials with interesting properties. Perovskite materials fall into this category of materials fall into this category of materials owing to their promising physical properties and potential manipulation in many industrial and engineering fields such as multilayer ceramic capacitors MLCCs, positive-temperature-coefficient resistors PTCRs, and piezoelectric transducers.1–3 However, these days much research is directed towards lead free relaxor materials with a perovskite structure characterized by a translational symmetry breaking to form polar nanoregions (PNRs), which explains the origin of relaxor behavior.4 In this respect, compositional inhomogeneity plays a central role, and discrete ferroelectric nano-regions have been proposed to explain the diffused dielectric response.5 The first evidence of these inhomogeneities was provided by Burns and Dacol6 who observed a deviation from the linear temperature dependence of the optical index of refraction below a certain temperature during the cooling of the La-doped PbZr(1−x)TixO3 samples.Despite, the discovery of many attractive properties in some perovskite structures including relaxor behavior in Pb(Mg1/3Nb2/3)O3–PbTiO3,7,8 Pb(Mg1/3Nb2/3)O3 Pb(Zr0.52Ti0.48)O3,9 and Pb(Zn1/3Nb2/3)O3–PbTiO3,10 they have net been put to application due to their volatility and toxicity. So many researchers have attempted to overcome this problem by doping BaTiO3 in the A or/and B sites to become a relaxor.11 In fact, the discovery of the high-permittivity of the ferroelectric ceramic BT in 1943 (ref. 12) mode it subject of investigation in order to understand and manipulate its properties. These compounds present several polymorphic phase transitions used to correlate important dielectric/ferroelectric properties, such as variations in polymorphic phase transition temperatures, permittivity, and dielectric loss with chemical doping and ceramic microstructure.13–15
Incorporating Bi3+ in to this structure at Ba site was reported in many works and assumed that the relaxor behavior is induced by heterovalent substitution can be explained by the random-field-induced domain state.16–19
Moreover, other researchers studied the effect of doping at Ti4+ site using more stable chemical ions and larger ionic size as Zr4+. They report a decrease of the electronic hopping conduction, and the existence of introduce a relaxor behavior in the BT attributed to the distribution of micro-polar regions along the structure.20 Introducing disorder on BT using Nb5+ lead to small inhomogeneities distribution and the creation of titanium vacancies.21 It is evident that more efforts are needed in this area in order to produce an ideal, low loss, highdielectric constant material that could be used for advanced capacitive applications.22
Therefore, in this work we have synthesized the Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 (BBTZN) ceramic by the molten-salt method. We have studied the effect of structure and microstructure on the dielectric properties of the polycrystalline BBTZN.
2. Experimental details
2.1. Preparation of Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 perovskite sample
A polycrystalline BBTZN sample was produced by the molten salt method using stoichiometric amounts of BaCO3, Bi2O3, TiO2, ZrO2 and Nb2O5 (having a purity of more than 99.9% for each of them). The precursors were weighed, then, thoroughly mixed in an agate mortar for 2 h. The salt-precursor mixture was placed in an alumina crucible and heated at 800 °C for 24 h. After cooling to room temperature, the mixture was washed with distilled water and filtered to remove the salts. After being dried at 100 °C in air and ground thoroughly, the compounds were pressed into disks (with a diameter of 8 mm and a thickness about 2 mm), and sintered in air at 900 °C for 24 h.2.2. Characterization of the sample
The composition and microstructure of the BBTZN ceramic were analysed using scanning electron microscopy (SEM) equipped with an energy dispersive X-ray system (EDX). The pictures were taken at room temperature on a Phillips XL30 microscopy.The crystal structure, as well as its purity were checked by X-ray diffraction (XRD) using “PANalytical X'Pert Pro” diffractometer with CuKα radiation. Data a were collected at room temperature in the range of 2θ from 10 to 70° with a step size of 0.017° and a counting time of 18 s per step. The structural analysis was carried out by the standard Rietveld method.23
The dielectric properties were measured on discs under helium atmosphere as a function of both temperature (290–800 K) and frequency (1 kHz to 1 MHz) using a Wayne-Kerr 6425 component analyzer. All the dielectric data were collected while heating at a rate of 2 K min−1.
3. Results and discussion
The EDX chemical analysis of Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 sample is shown in Fig. 1(a). The EDX spectrum reveals the presence of Ba, Bi, Ti, Zr, Nb and O elements, which confirms that there is no loss of any integrated element during sintering, within the experimental errors. EDX analysis also showed that the chemical composition of the sample is close to the nominal one within the experimental uncertainties.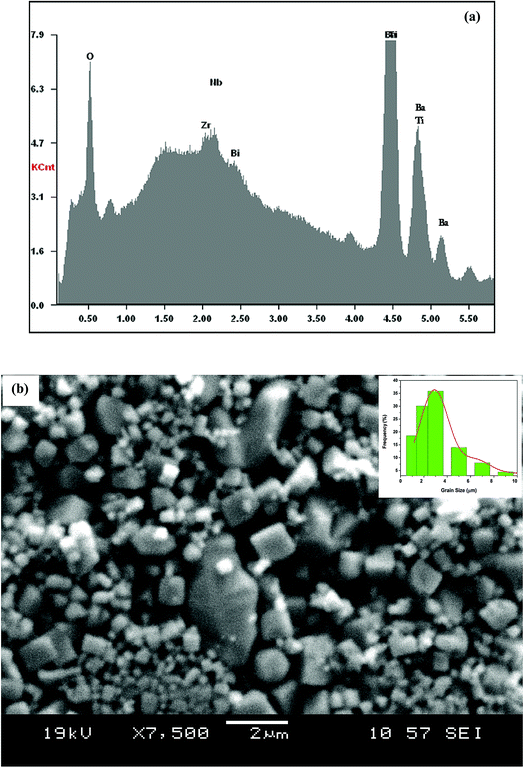 | ||
| Fig. 1 (a) EDX analysis spectrum of Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic; (b) SEM image of the sample. The inset shows the size distribution histogram. | ||
The surface of the BBTZN sample is shown in Fig. 1(b). It can be seen from the micrograph that the inhomogeneous microstructures of the grains and may be advantageous to explain the dielectric properties.24
The size distribution of particles presented in the inset of Fig. 1(b) was analysed quantitatively by fitting the histogram using a Lorentzian function. The mean diameter of BBTZN is of 2.5 μm order.
The X-ray diffraction patterns for the polycrystalline BBTZN sample taken at room temperature are presented in Fig. 2. This figure, shows that the sample is in a single-phase condition with minor secondary phases identified as Bi2O3 phase arising from a small contamination during the sample preparation, which is in agreement with the results found by A. Aoujgal et al.25 The concentration of this impurity is obviously very small (a few percent). The structural parameters, unit cell volume and fitting parameters of the sample were refined by the standard refinement analysis. This refinement was performed with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group in the pseudocubic unit cell. The related results are listed in Table 1.
m space group in the pseudocubic unit cell. The related results are listed in Table 1.
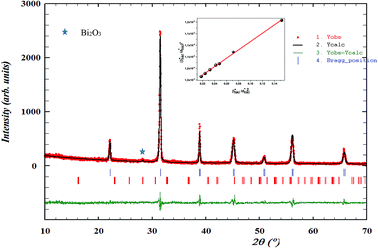 | ||
| Fig. 2 Room temperature XRD pattern and Rietveld refinement result for Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic. The inset shows their crystal structure and fitted curves of the H–W analysis. | ||
| Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 | ||
|---|---|---|
| Structure pseudo-cubic | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase m phase |
|
| Cell parameters | a = b (Å) | 4.0135(4) |
| V (Å3) | 64.652(1) | |
| Thermal agitation | (Ba/Bi) Biso (Å2) | 1.488 |
| (Ti/Zr/Nb) Biso (Å2) | 1.731 | |
| (O1) Biso (Å2) | 2.002 | |
| Bond lengths and Bond angles | dTi–O (Å) | 2.006(7) |
| θ(Ti–O–Ti) (°) | 180.00 | |
| Discrepancy factors | Rp (%) | 9.57 |
| Rwp (%) | 12.5 | |
| χ2 | 1.78 | |
| Experimental density | dtheo (g cm−3) | 6.142 |
| Theoretical density | dexp (g cm−3) | 5.97 |
| Compactness | C | 0.97 |
| Average crystallite size | 〈D〉XRD (nm) | 64.2 |
| 〈D〉H–W (nm) | 91 | |
| ε | 0.002 | |
XRD profile analysis is a simple and powerful method to determine the average crystallite size DXRD. Debye–Scherrer's formula showed the broadening of the XRD pattern attributed to the crystallite size-induced broadening:26
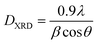 | (1) |
The crystallite size calculated by XRD data (DXRD) was smaller than that obtained by SEM image, which indicates that each particle observed by SEM is formed by several crystallized grains.27
According to the Halder–Wagner (H–W) method, the crystallite size (DH–W) and the strain (ε) of the powder can be determined using the βhkl and planar spacing dhkl (the distance between adjacent planes in the set (hkl)):28
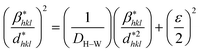 | (2) |
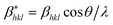 and
and 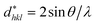 . The results of crystallite size and micro-strain are summarized in Table 1. The plot of eqn (2) is a straight line with a positive slope and a nonzero y-intercept (the inset of Fig. 2). The crystallite size DH–W was determined from the slope inverse of the linearly fitted data and the root of the y-intercept gave the microstrain. The value of the crystallite size (DH–W) obtained from the H–W analysis was compared to that obtained by Scherrer's method (DXRD).
. The results of crystallite size and micro-strain are summarized in Table 1. The plot of eqn (2) is a straight line with a positive slope and a nonzero y-intercept (the inset of Fig. 2). The crystallite size DH–W was determined from the slope inverse of the linearly fitted data and the root of the y-intercept gave the microstrain. The value of the crystallite size (DH–W) obtained from the H–W analysis was compared to that obtained by Scherrer's method (DXRD).
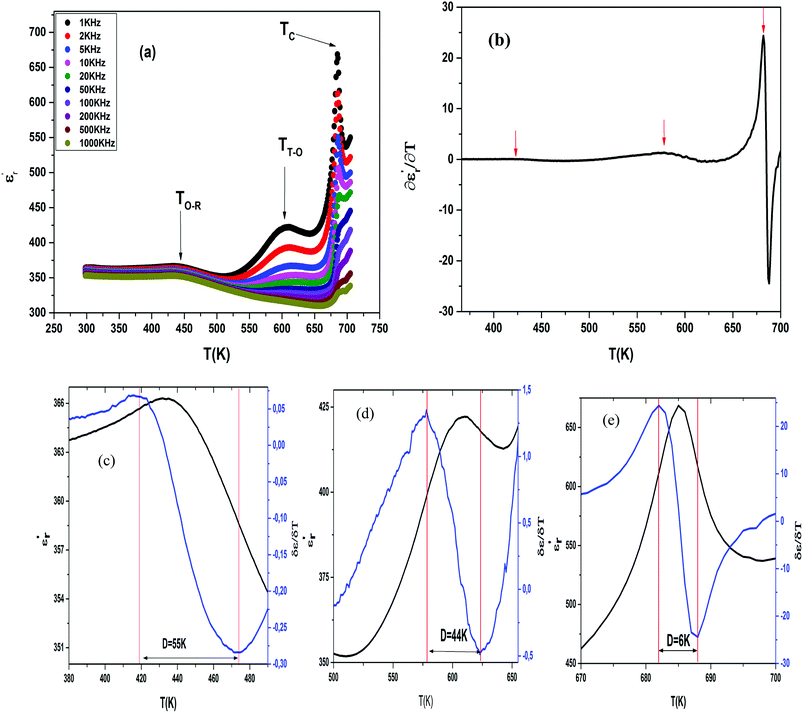
The temperature and frequency variations of the dielectric constant of BBTZN ceramics are shown in Fig. 3(a). To highlight the phase transitions, we plotted the curve of the differential dielectric constant 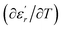 vs. temperature in the insets of Fig. 3(b). Three peaks were observed on the dielectric curves. They originated from phase transitions from a cubic paraelectric to a tetragonal ferroelectric at the Curie temperature (TC), then to an orthorhombic ferroelectric (at TT-O), and finally to a rhombohedral ferroelectric (at TO-R). These transitions are identical than those obtained on pure BT ceramics.29 Some researchers have reported low values of dielectric constant at Tc such that Li et al.30 report the maximum dielectric constant
vs. temperature in the insets of Fig. 3(b). Three peaks were observed on the dielectric curves. They originated from phase transitions from a cubic paraelectric to a tetragonal ferroelectric at the Curie temperature (TC), then to an orthorhombic ferroelectric (at TT-O), and finally to a rhombohedral ferroelectric (at TO-R). These transitions are identical than those obtained on pure BT ceramics.29 Some researchers have reported low values of dielectric constant at Tc such that Li et al.30 report the maximum dielectric constant 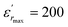 , Hayashi et al.31 is of the order
, Hayashi et al.31 is of the order 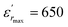 .
.
Three regions of dielectric relaxations were observed in the present perovskite at the temperature ranges of 350–500 K, 500–620 K and 620–720 K with a maximum in the dielectric permittivity that shifted to a higher temperature with increasing frequency (Fig. 3(a)). This shift of each maximum in the dielectric permittivity for the three regions indicating diffused type phase transition. All the observed dielectric behaviours confirm the diffuse relaxor character for our composition. This indicates an important property of a disordered perovskite structure. In addition, we notice coexistence of low dielectric constant and high dielectric constant regions in dielectric materials. It was explained by the charge accumulation at the interface between the grain and grain boundaries (as shown in SEM images (Fig. 1(b))) and lead to a Maxwell–Wagner (MW) interfacial polarization.32
Compared to literature 33–35 (Table 2), we note that a low dielectric constant of the BBTZN sample, attribute able to the presence of Bi, Zr, Nb in the BaTiO3 lattice, which can minimize the local constraints and facilitate the motions of the domain. This great mobility of the domain walls in this ceramic, led to a low dielectric constant.
The broad peak or diffusiveness in ε′(T) occurred due to fluctuations in the composition and structural disorder in the cationic arrangement on one or more site of the crystal structure. The local disorder in the system led to the formation of polar nanoregions (PNRs) of different sizes and local curie points. The dynamics of these PNRs is responsible for the diffuse phase transition (DPT).36
The width of the transition represents the DPT, which is very important in ferroelectric materials.
We can define ‘D’ is the characterizing parameter of diffuseness degree. It is the temperature interval where the volume of polar microscopic regions changes due to the appearance of new microscopic polar regions. This is defined as:37
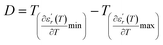 | (3) |
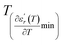 and
and 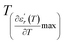 are the temperature when
are the temperature when 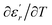 reaches the minimum and maximum, respectively. The curves for the
reaches the minimum and maximum, respectively. The curves for the 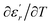 against (T) for the three regions I, II and III are shown in Fig. 3(c–e). The temperature interval between
against (T) for the three regions I, II and III are shown in Fig. 3(c–e). The temperature interval between 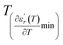 and
and 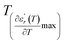 reflects the diffuseness degree microscopically. The vertical dashed lines in Fig. 3(c–e) correspond to
reflects the diffuseness degree microscopically. The vertical dashed lines in Fig. 3(c–e) correspond to 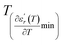 and
and 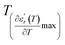 values. D is the interval between
values. D is the interval between 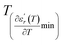 and
and 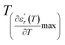 .
.
The values of diffuseness decreases with the increase in temperature. This indicates that the phase transition from paraelectric-ferroelectric is the transition that occurs with less diffuse (D = 6 K) disorder, while the phase transition tetragonal to orthorhombic phase transition is the transition that occurs with more diffuse (D = 44 K) disorder. The orthorhombic to rhombohedral phase transition is the transition more diffuse (D = 55 K) disorder.
To explain the ferroelectric behavior with DPT phenomenon of the dielectric materials, Curie and Weiss propose the Curie–Weiss law.38 When the temperature is above Tc, the dielectric normal behavior follows the C–W law as follows:
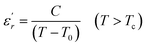 | (4) |
The inverse of dielectric constant 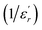 as a function of temperature at 1 kHz for BBTZN ceramic sample is plotted in Fig. 4. The two parameters C and T0 obtained by fitting the inverse dielectric to eqn (4) are summarized in Table 2.
as a function of temperature at 1 kHz for BBTZN ceramic sample is plotted in Fig. 4. The two parameters C and T0 obtained by fitting the inverse dielectric to eqn (4) are summarized in Table 2.
The value of Curie constant obtained is in the order of 105 that is normally observed for displacive ferroelectrics type. (TC ≠ T0) shows that the phase transition is of a first order type.39 All these dielectric results are in agreement with relaxor ferroelectric behavior for three regions.
In addition, we notice that the curves can be divided into three regions. The first region represents the ferroelectric behavior up to the transition at Tm. The second region, near the transition, indicates a diffused transition up to a temperature TC–W. The third region represents the linear behavior of 1/ε′ as a function of temperature following the Curie–Weiss relation. It is clear from the above figures that for both samples at T > TC–W, a normal Curie–Weiss behavior is found.
The parameter ΔTm, which is often used to show the degree of deviation from the Curie–Weiss law, is defined as follows:
| ΔTm = TC–W − Tm | (5) |
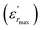 and TC–W represents the temperature from which the dielectric constant starts to deviate from the Curie–Weiss law. The various constants are listed in Table 2. The deviation from the Curie–Weiss behavior was qualified to a short-range association between the nanopolar domains. In addition, the deviation from Curie–Weiss law within a certain temperature interval above Tm is one of the salient features of relaxor ferroelectrics.
and TC–W represents the temperature from which the dielectric constant starts to deviate from the Curie–Weiss law. The various constants are listed in Table 2. The deviation from the Curie–Weiss behavior was qualified to a short-range association between the nanopolar domains. In addition, the deviation from Curie–Weiss law within a certain temperature interval above Tm is one of the salient features of relaxor ferroelectrics.
The relaxor behavior in ferroelectric compound is usually affected by the compositional fluctuation, the merging of micropolar regions into macropolar regions, or a coupling of order parameter and local disorder mode through the local strain.40
Because the radius of Bi3+ (0.117 nm) is smaller than that of Ba2+ (0.161 nm) and Zr4+ (0.072 nm), and the radius of Ti4+ (0.061 nm) is close to that of Nb5+ (0.064 nm),41 the complex substitution at A-site and B-site tends to cause inhomogeneous composition distribution and disordered crystal structure.
Therefore, according to our results, the observed relaxation phenomena is attributed to the multi-ion coexistence at the A and B-sites. Different effects of A-site substitution on cation ordering and the stability of the polar region are considered to be based on the polarizability of cations and the tolerance factor of the perovskite structure. For perovskites with the ABO3 general formula, the following equation can be used to calculate the tolerance factor (t):
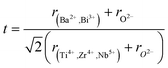 | (6) |
The tolerance factor value was estimated t = 0.93. It was found within the range of a stable perovskite structure.
So, Ba2+ cations can stabilize normal ferroelectrics due to the larger ionic diameter and higher polarizability. While Bi3+ cations in A-sites behave as a typical destabilizer against normal ferroelectrics and induce paraelectric behavior due to smaller ionic diameter and lower polarization. In this case more macrodomains (long-range ordered regions) in Bi substituted ceramic will breakup into micropolar regions than those in BaTi0.9Zr0.05Nb0.04O3 ceramic. Mechanical stress in the grain is one of the causes of relaxor behavior in the Ti4+, Zr4+ and Nb5+ mixed composition.
Similar behaviors are reported for Ba(1−x)Bi2x/3Zr0.15Ti0.85O3 and was attributed to the diffuse ferroelectric phase transition.42 N. Haddadou et al.43 report for the Ba0.925Bi0.05(Ti0.95−xZrx)Sn0.05O3 (0.05 ≤ x≤ 0.30) ceramics than the low Zr-composition was found to exhibit a flat 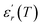 curve with stable dielectric permittivity in a large range of temperature, promising for the X7R specifications.
curve with stable dielectric permittivity in a large range of temperature, promising for the X7R specifications.
An empirical relaxation strength characterizes the frequency dispersion and could be defined by the parameter ΔTrelax = Tm (1 MHz) − Tm (1 kHz).44 The values of ΔTrelax, as shown in Table 2, the values of ΔTrelax are higher in the regions (I and III). The substitution of Bi3+ for Ba2+ in site A promote the relaxor behavior with a low amplitude of dielectric constant.45 Also substituting Nb5+, Zr4+ for Ti4+ to heightens the transition temperatures. According to the bibliography for rate of ion Zr4+ = 5% we found the diffuse phase transition46,47 and the effect of the Nb5+ ions to improve the dielectric property.48
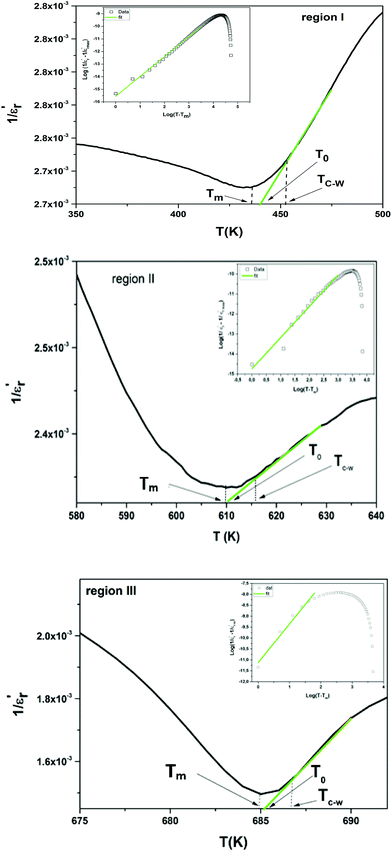
To further study the phase transition behavior of the BBTZN sample, we calculated the diffuseness parameter using the modified Curie–Weiss law:49
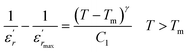 | (7) |
The diffuseness coefficient γ allows understanding the character of the phase transition; C1 is a constant quantity and 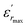 is the peak dielectric permittivity at temperature Tm. In general, the value of γ between these limits (1 <γ < 2) provide an incomplete diffuse phase transition. For normal ferroelectrics γ approximate to 1 but relaxor ones approximate to 2.
is the peak dielectric permittivity at temperature Tm. In general, the value of γ between these limits (1 <γ < 2) provide an incomplete diffuse phase transition. For normal ferroelectrics γ approximate to 1 but relaxor ones approximate to 2.
The inset of Fig. 4 shows the plots of 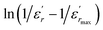 versus ln(T − Tm) at 1 kHz for BBTZN ceramic sample. The obtained values of ‘γ’ are found to be in the range of 1.58–1.78 (Table 2), which corresponds to the diffuse phase transition due to the existence of different states of polarization and, hence, different relaxation times in different regions.50
versus ln(T − Tm) at 1 kHz for BBTZN ceramic sample. The obtained values of ‘γ’ are found to be in the range of 1.58–1.78 (Table 2), which corresponds to the diffuse phase transition due to the existence of different states of polarization and, hence, different relaxation times in different regions.50
The values of ‘γ’ indicate that the paraelectric-ferroelectric phase transition (γ = 1.78) is the transition that occurs with more disorder, while the phase transition from orthorhombic to rhombohedral (γ = 1.58) is the transition that occurs with less disorder.
The incorporation of Bi2O3 induced the ferroelectric relaxor behavior in the Ba0.8Sr0.2TiO3 perovskite. The relaxor character based on empirical parameters such as γ and the originated is form the micro-polar clusters, which stemmed from the heterovalent substitutions of Bi3+ at A site.42
In addition, the relaxor behavior with DPT occurs at the B site of the ABO3 perovskite structure, where Nb5+ and Ti4+ also possess different valences and ionic radii, as reported by Z. Sun et al.51 for the perovskite Ba(Zr0.2Ti0.8)(1−x)NbxO3 ceramics. This difference for ionic radii produce the formation of the local electric fields owing to the local charge imbalance and the local elastic fields due to local structure distortions, prevents the long-range dipole alignment, i.e., giving rise to the PNRs.
Therefore, the origin of the observed relaxor character in BBTZN is the substitution of Bi3+ for Ba2+ in A site and (Zr4+, Nb5+) for Ti4+ in B site. This inhomogeneous distribution leads to the compositional fluctuation which may result in microscopic heterogeneity with different Curie points and cause the observed diffuseness.52 Furthermore, it creates the different states of polarization and hence different relaxation time in different regions and also to the formation of a local charge imbalance and defects, which cause, in turn, the thermal activation conduction of mobile ions/or the other defects contributing to the observed dielectric dispersion.53 However, many studies have shown that γ is not a good parameter to give the exact degree of dielectric relaxation in perovskites.54 Recently, both empirical relations, Gaussian-distribution above Tm and the better Lorentz type above and below Tm, have been attempted to express fairly the relaxor feature. Smolenskii and co-works55 introduced the concept of Gaussian distribution of the Tm to the small micro-regions considered noncorrelated. According to such an assumption, the permittivity εr as a function of temperature is expressed as:56
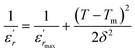 | (8) |
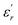 is the dielectric constant,
is the dielectric constant, 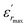 is its maximum value, Tm is the temperature corresponding to this maximum, and δ is the Gaussian coefficient of diffuseness.
is its maximum value, Tm is the temperature corresponding to this maximum, and δ is the Gaussian coefficient of diffuseness.
Fig. 5 shows the fitted results from eqn (8). The best Gaussian fitting parameter (δ) is shown in Table 3.
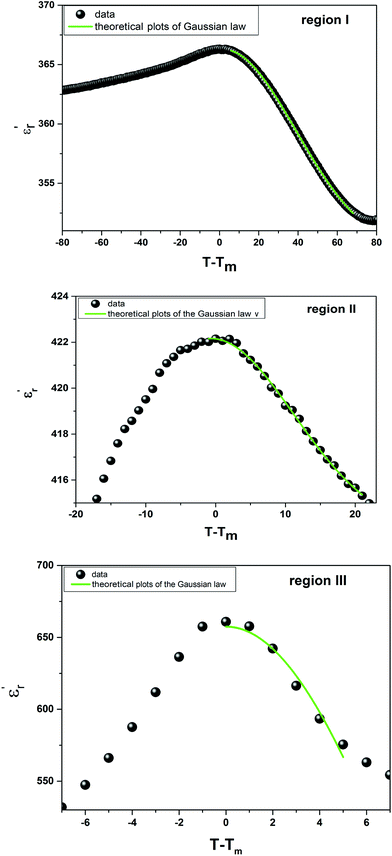 | ||
| Fig. 5 The experimental and fitted dielectric data as a function of temperature for Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic using the Gaussian distribution. | ||
| Dielectric fitting parameters | Ba0.97Bi0.02Ti0.9Zr0.05Nb0.3 | ||||
|---|---|---|---|---|---|
| Regions I | Regions II | Regions III | |||
| Gaussian distribution | T < Tm | δ (K) | 35.9 | 113.48 | 9.17 |
| χ2 | 0.99 | 0.95 | 0.97 | ||
| Lorenz type | T < Tm | εA | 366.5 | 430 | 695 |
| TA (K) | 448.39 | 628.35 | 689.69 | ||
| δA (K) | 443.4 | 126 | 25 | ||
| χ2 | 0.98 | 0.997 | 0.986 | ||
| T > Tm | εA | 366.22 | 438.21 | 747 | |
| TA (K) | 433.19 | 516.08 | 677.1 | ||
| δA (K) | 182.96 | 346 | 16.86 | ||
| χ2 | 0.99 | 0.995 | 0.984 | ||
It has been emphasized in the literature that a description of the high temperature slope of the dielectric peak in ferroelectrics with or without DPT, and classical relaxor materials can be well described above and below Tm with the Lorenz formula empirical relation:57
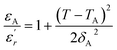 | (9) |
 measured on BBTZN ceramic could be fitted by the Lorentz-type quadratic relation in the two different temperature ranges T < Tm and T > Tm, respectively. The values of δA, TA and εA obtained from the experimental data, fitted by eqn (9) are listed in Table 3, and the fitting curves are shown in Fig. 6.
measured on BBTZN ceramic could be fitted by the Lorentz-type quadratic relation in the two different temperature ranges T < Tm and T > Tm, respectively. The values of δA, TA and εA obtained from the experimental data, fitted by eqn (9) are listed in Table 3, and the fitting curves are shown in Fig. 6.
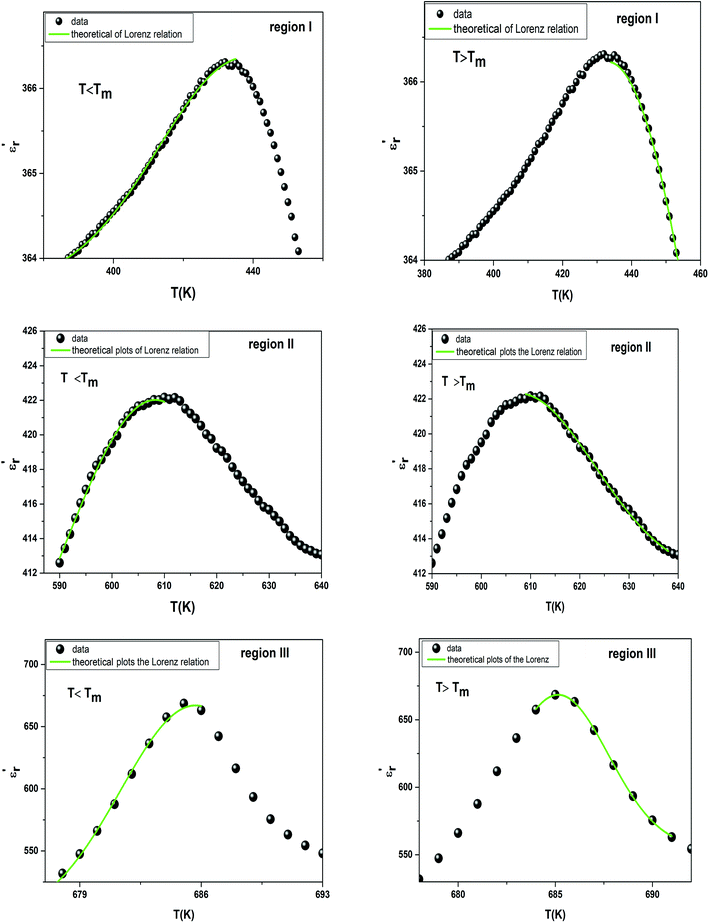 | ||
| Fig. 6 The experimental and fitted dielectric data as a function of temperature for Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic using the Lorenz type. | ||
We notice the very different fitting parameters δA in two different temperature ranges (T < Tm and T > Tm), which indicates that there should be two polarization processes in these compound for the three transitions. Furthermore, δA increased in the two ranges of temperature, which suggests increasing the diffuseness. This behavior explains by the Bi3+ substitution in A site and (Zr4+, Nb5+) for Ti4+ in B site is found to induce chemical and structural inhomogeneity that leads to structural disorder reflected as increasing diffuseness in the transition.
Comparing the Lorenz type and Gaussian distribution for T > Tm, we note that the diffuseness of the dielectric relaxation are close. From the temperature dependence of 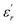 for the compound BBTZN and the fitting process, it is noted that the Lorenz formula is more accurate than the Gaussian formula for description the ferroelectric phase transition. It is deduced that the Curie–Weiss law which describes the temperature dependence of the dielectrics in the three phase transitions. The difference of eqn (8) and (9) is that the former supposes Gaussian distribution of PNRs at TC, and the latter supposes Lorentz-type distribution. From the above analysis, eqn (9) could describe the experience phenomenon precisely.
for the compound BBTZN and the fitting process, it is noted that the Lorenz formula is more accurate than the Gaussian formula for description the ferroelectric phase transition. It is deduced that the Curie–Weiss law which describes the temperature dependence of the dielectrics in the three phase transitions. The difference of eqn (8) and (9) is that the former supposes Gaussian distribution of PNRs at TC, and the latter supposes Lorentz-type distribution. From the above analysis, eqn (9) could describe the experience phenomenon precisely.
In addition, the diffuseness of the phase transition of relaxation can also be described by another empirical parameter such as ΔTdiffuse defined as:58
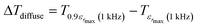 | (10) |
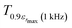 corresponding to 90% of the temperature of the maximum of the real dielectric permittivity εrmax and
corresponding to 90% of the temperature of the maximum of the real dielectric permittivity εrmax and 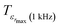 is their associated maximum at 1 kHz.
is their associated maximum at 1 kHz.
In order to quantify the frequency dispersion in the dielectric behavior, we define a parameter 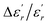 as:
as:
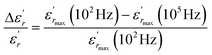 | (11) |
The values of ΔTdiffuse and 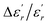 calculated and summarized in Table 2.
calculated and summarized in Table 2.
To further understand the relaxor nature of our compound, three models were used to describe the evolution of the maximum peak temperature of permittivity depending on frequency. The first model is that of Debye model based upon classical dielectric media. In Debye relaxation, dipoles are free to rotate and are thermally activated. The dipoles moments have the same values and there is no interaction between the dipoles; which can be written as follows:59
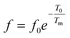 | (12) |
To better understand relaxor ferroelectric character, the maximum dielectric constant (Tm) is found to obey Vogel–Fulcher (V–F) model.60 This model takes into account the interactions between the dipoles. These interactions make the dipoles freeze at a particular temperature called freezing temperature. This model, described by the relation similar to that recognized for glasses,61 can be expressed as follows:
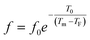 | (13) |
The experimental values are fitted to eqn (12) and (13), and are shown in Fig. 7. The fitting results were computed for the sample and are given in Table 3, for TF = 586 K and Ea = 0.052 eV for region II and TF = 669 K and Ea = 0.033 eV for region III. Similarly, the low values of the activation energy are also found by Zhang et al.62 for 0.9Pb(Mg1/3Nb2/3)O3-0.1PbTiO3 relaxors (Ea ≈ 0.012 eV), F. Bourgiba et al.63 for BaTi0.5(Fe0.33W0.17)O3 ceramics (Ea ≈ 0.0494–0.0586 eV) and Tinberg64 (1 − x)BaTiO3–xBiScO3 films (Ea ≈ 0.05–0.12 eV). The activation energy Ea, much lower in our ceramic, reflected a lower barrier between two potential wells. This range of features relating to the potential well reflected different polarization mechanisms. The parameters (Ea, TF) indicate that the relaxation behavior is triggered by monopolars and similar to the thermally activated process of the spin glass in which the freezing process is controlled by cluster flipping and the intercluster interaction mechanism.
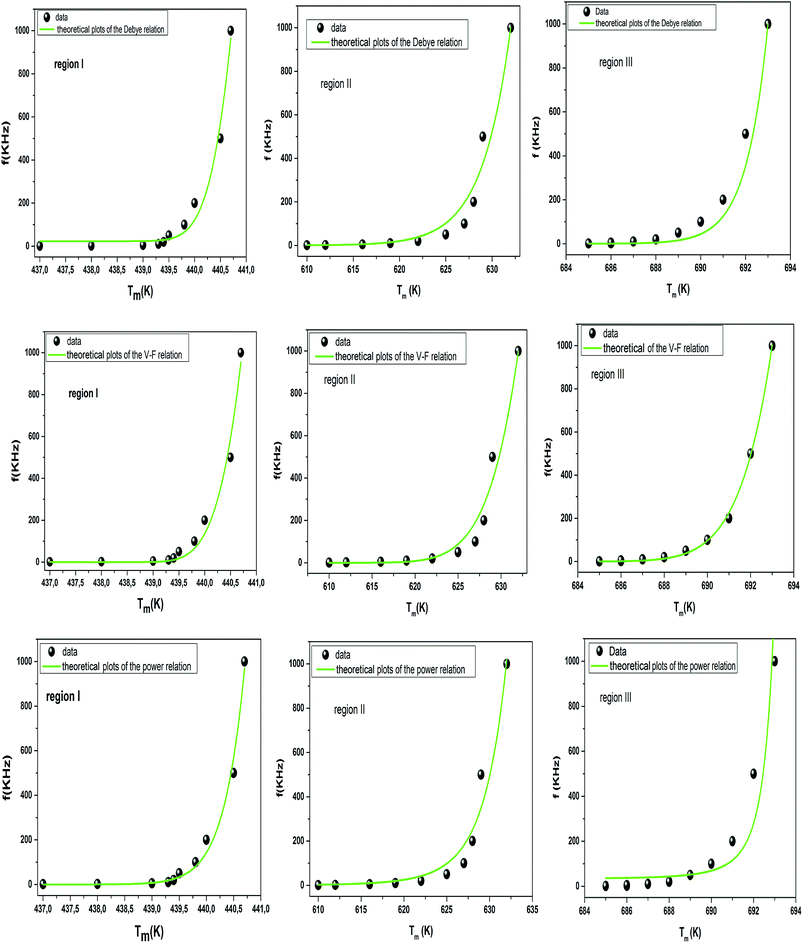 | ||
| Fig. 7 Fitting of Debye, Vogel–Fulcher and Power models to the dielectric relaxation data of the Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 ceramic. | ||
To overcome this limitation of V–F model, Cheng et al.65 proposed a power law:
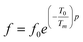 | (14) |
The fitted curves for Power model are shown in Fig. 7. The values obtained for their parameters are listed in Table 3. We notice that parameter p (Table 4) is in agreement with those of the diffuseness coefficient γ and ΔTm, which confirms the relaxor behavior of the BBTZN sample.66 The pre-exponent factor f0 provides an idea about the size of polar clusters and the degree of interaction between them. Smaller the size of the cluster, lower the interaction between them and hence the larger value of f0 and vice versa. The value of p determines the degree of relaxation and hence the rate of growth of polar clusters. The higher the relaxation is, the slower the rate of growth of polar clusters is. The observed relaxation is related to the slower rate of growth polar clusters. In this compound the Polar clusters have undergone three relaxation areas which can increase their size and this may be a source of the relatively high grain size observed by SEM.
| Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 | f0 (Hz) | Ea (eV) | TF (K) | p | χ2 | |
|---|---|---|---|---|---|---|
| Debye model | Region I | 1.186 × 1078 | 5.21 | — | — | 0.9745 |
| Region II | 4.175 × 1066 | 2.8 | — | — | 0.95583 | |
| Region III | 3.35 × 1068 | 4.23 | — | — | 0.96217 | |
| Vogel Fulcher model | Region I | 4.08 × 106 | 0.02 | 437 | — | 0.97969 |
| Region II | 6.1 × 108 | 0.052 | 586 | — | 0.99862 | |
| Region III | 1.03 × 1010 | 0.033 | 669 | — | 0.96206 | |
| Power model | Region I | 6.45 × 1013 | 0.05 | — | 16.52 | 0.98675 |
| Region II | 2.44 × 104 | 0.011 | — | 9.89 | 0.95224 | |
| Region III | 2.6 × 105 | 0.021 | — | 7 | 0.97441 | |
Comparing χ2 values, we notice the good agreement of the data with Vogel–Fulcher relationship, which suggests that the relaxor behavior in our compound is analogous to that of dipolar glass with a polarization fluctuation above a static freezing temperature.
The dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the compound BBTZN as a function of temperature up to 700 K at various frequency ranges from 1 kHz to 1 MHz is represented in Fig. 8(a). We observe a marked peak that shifts to higher frequencies with temperature, resembling the relaxor type dielectric behavior. The appearance of a broadened peak in the dielectric loss as a function of temperature is indicative of a transition from one type of relaxation process to another taking place at a characteristic temperature and may be attributed to the combined effect of the reorientation of thermally activated polar flips and loss of polarization with the rise in temperature.67 In addition, the high dielectric loss at higher temperature is supposed to be induced by the thermally activated space charge contribution (Maxwell–Wagner type).68
δ) of the compound BBTZN as a function of temperature up to 700 K at various frequency ranges from 1 kHz to 1 MHz is represented in Fig. 8(a). We observe a marked peak that shifts to higher frequencies with temperature, resembling the relaxor type dielectric behavior. The appearance of a broadened peak in the dielectric loss as a function of temperature is indicative of a transition from one type of relaxation process to another taking place at a characteristic temperature and may be attributed to the combined effect of the reorientation of thermally activated polar flips and loss of polarization with the rise in temperature.67 In addition, the high dielectric loss at higher temperature is supposed to be induced by the thermally activated space charge contribution (Maxwell–Wagner type).68
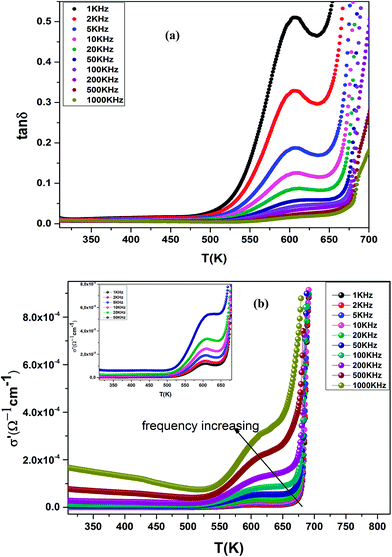 | ||
Fig. 8 (a) Temperature and frequency dependence of the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3, (b) the dielectric conductivity of this compound. δ) for Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3, (b) the dielectric conductivity of this compound. | ||
The electrical conductivity (σ′) of a dielectric material can be presented in terms of the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) by the relation:69
δ) by the relation:69
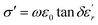 | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is dielectric loss.
δ is dielectric loss.
The temperature dependence of the electrical conductivity (σ′) for BBTZN is presented in Fig. 8(b). Results shown that σ′ increases simultaneously with increasing the temperature and frequency. Moreover, the electrical conductivity curves show a typical feature of relaxation behavior. These results are in agreement with those obtained in the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) (Fig. 8(a)).
δ) (Fig. 8(a)).
The complex electric modulus was calculated from the dielectric permittivity [ε*(ω)] using the following relation:70
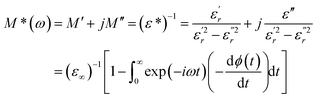 | (16) |
With
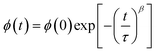 | (17) |
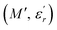 and
and 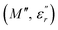 are the real and imaginary components of modulus and permittivity, respectively,
are the real and imaginary components of modulus and permittivity, respectively, 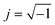 is the imaginary factor, ε∞ is the asymptotic value of real part of the dielectric constant, Φ(t) is the stretched exponential function of a material and β (0 < β < 1) is the stretching coefficient and gives the degree of correlation between ions in ionic transport corresponding to complete uncorrelated ionic motion when its value is unity.
is the imaginary factor, ε∞ is the asymptotic value of real part of the dielectric constant, Φ(t) is the stretched exponential function of a material and β (0 < β < 1) is the stretching coefficient and gives the degree of correlation between ions in ionic transport corresponding to complete uncorrelated ionic motion when its value is unity.
The temperature dependence of the electric modulus M′ and M′′ for various frequencies is shown in Fig. 9(a and b) for Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3. We observed that, at lower temperature, M′ tends to a constant value for all frequencies. This dependence indicates that the dielectric constant of the sample is thermally activated, similar to that of the dielectric constant spectrum by the presence of the phase transition with relaxor behavior (Fig. 3).
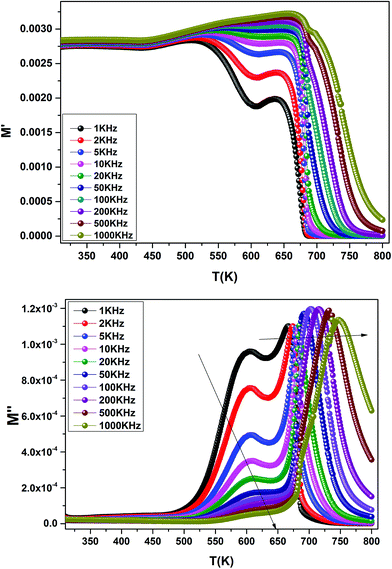 | ||
| Fig. 9 Temperature dependence of the electric modulus (M′ and M′′) for Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 at various frequencies. | ||
In addition, we see a two characteristic peaks in the temperature range. One is in the range of 300 to 600 K and the other lies between 600 and 800 K. Correspondingly, M′′ shows two peaks in the same temperature ranges. Both peaks shift to high temperature with increasing frequency indicating a thermally activated relaxation. This peaks were ascribed to the Maxwell–Wagner (M–W) space charge relaxation phenomenon, such as space charges, charged defects, and related defect complexes.71 We attribute the low temperature peak to the dielectric relaxation and the high-temperature peak to the conduction process, similar to that of the conductivity spectrum (Fig. 8(b)). A thermally activated conduction process of defects produced during high temperature sintering such as oxygen vacancies and the presence of small grain boundary. Electrical inhomogeneities could be the possible reason for these high temperature dielectric relaxations.72
The results obtained in this study indicate that our ceramics are of extreme significance as far as their technological and industrial applications are concerned.
4. Conclusion
In summary, we have synthesized a new ceramic compound of composition Ba0.97Bi0.02Ti0.9Zr0.05Nb0.04O3 by molten-salt method. Rietveld analysis indicated that this sample crystallizes in pseudocubic structure with a Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The temperature dependence of the dielectric properties was investigated in the frequency range 1 kHz to 1 MHz. Importantly, Bi3+ substitution in A site and (Zr4+, Nb5+) for Ti4+ in B site is found to induce chemical and structural inhomogeneity that leads lead to the formation of polar nanoregions, local structure distortions, and local charge imbalance reflected as increasing diffuseness in the transition. Indeed, three regions of dielectric relaxations were observed in the title perovskite at the temperature ranges of 350–500 K, 500–620 K and 620–720 K with a maximum in the dielectric permittivity that shifted to a higher temperature with increasing frequency. Moreover, to investigate the degree of the DPT, the modified Curie–Weiss law has been introduced to describe the relaxation behavior attributed to the contribution of PNRs. Using Vogel–Fulcher (V–F) model, the estimated value of parameters (Ea, TF) indicate a low barrier between two potential yield to the presence of different polarization mechanisms in this compound. These observations suggest that the present system can be considered as a potential lead-free material for the nanotechnologies applications.
m space group. The temperature dependence of the dielectric properties was investigated in the frequency range 1 kHz to 1 MHz. Importantly, Bi3+ substitution in A site and (Zr4+, Nb5+) for Ti4+ in B site is found to induce chemical and structural inhomogeneity that leads lead to the formation of polar nanoregions, local structure distortions, and local charge imbalance reflected as increasing diffuseness in the transition. Indeed, three regions of dielectric relaxations were observed in the title perovskite at the temperature ranges of 350–500 K, 500–620 K and 620–720 K with a maximum in the dielectric permittivity that shifted to a higher temperature with increasing frequency. Moreover, to investigate the degree of the DPT, the modified Curie–Weiss law has been introduced to describe the relaxation behavior attributed to the contribution of PNRs. Using Vogel–Fulcher (V–F) model, the estimated value of parameters (Ea, TF) indicate a low barrier between two potential yield to the presence of different polarization mechanisms in this compound. These observations suggest that the present system can be considered as a potential lead-free material for the nanotechnologies applications.
Conflicts of interest
There are no conflicts to declare.References
- T. Yamamoto and S. Takao, J. Appl. Phys., 1992, 31, 3120–3123 CrossRef CAS.
- R. K. Patel, P. Kumar, C. Prakash and D. K. Agrawal, Ceram. Int., 2012, 38, 1585–1589 CrossRef.
- J. Li, H. Kakemoto, S. Wada, T. Tsurumi and H. Kawaji, J. Appl. Phys., 2006, 100, 024106 CrossRef.
- H. Gong, X. Wang, S. Zhang, Z. Tian and L. Li, J. Appl. Phys., 2012, 112, 114119 CrossRef.
- G. Smolenskii and A. Agranovskaya, Soviet Physics Solid State, 1960, 1, 1429 Search PubMed.
- G. Burns and F. H. Dacol, Phys. Rev. B, 1983, 28, 2527 CrossRef CAS.
- H. Ursic, M. Santo Zarnik and M. Kosec, Smart Mater. Res., 2011, 2011, 1–6 CrossRef.
- M. T. Lanagan, N. Yang, D. C. Dube and S. J. Jang, J. Am. Ceram. Soc., 1989, 72, 481–483 CrossRef CAS.
- R. Yimnirun, Ferroelectrics, 2006, 331, 9–18 CrossRef CAS.
- J. Kuwata, K. Uchino and S. Nomura, Ferroelectrics, 1981, 37, 579–582 CrossRef CAS.
- W. Chen, Y. Li, Q. Xu and J. Zhou, J. Electroceram., 2005, 15, 229–235 CrossRef CAS.
- G. Arlt, D. Hennings and G. de With, J. Appl. Phys., 1985, 58, 1619 CrossRef CAS.
- J. Xing, Z. Tan, J. Yuan, L. Jiang, Q. Chen, J. Wu, W. Zhang, D. Xiao and J. Zhu, RSC Adv., 2016, 6, 57210–57216 RSC.
- A. J. Miller, A. Rotaru, D. C. Arnold and F. D. Morrison, Dalton Trans., 2015, 44, 10738–10745 RSC.
- W. Bai, B. Shen, J. Zhai, F. Liu and Y. Zhang, Dalton Trans., 2016, 45, 14141–14153 RSC.
- F. Bahri and H. Khemakhem, J. Alloys Compd., 2014, 593, 202–206 CrossRef CAS.
- T. Badapanda, S. K. Rout, S. Panigrahi and T. P. Sinha, Curr. Appl Phys., 2009, 9, 727 CrossRef.
- S. Mahajan, O. P. Thakur, D. K. Bhattacharya and K. Sreenivas, J. Phys. D: Appl. Phys., 2009, 42, 065413 CrossRef.
- H. Kaddoussi, N. Abdelmoula, Y. Gagou, D. Mezzane, H. Khemakhem and M. Elmarssi, Ceram. Int., 2014, 40, 10255–11026 CrossRef CAS.
- J. Li, H. Kakemoto, S. Wada and T. Tsurumi, J. Appl. Phys., 2006, 100, 024106 CrossRef.
- C. Chen, H. Zhuang, X. Zhu, K. Zhou and D. Zhang, Ceram. Int., 2015, 41, 9893–9898 CrossRef CAS.
- Ch. Rayssi, S. El Kossi, J. Dhahri and K. Khirouni, J. Alloys Compd., 2018, 759, 93–99 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65 CrossRef CAS.
- L. L. Zhang, Z. Xu, Z. Li, S. Xia and X. Yao, J. Electroceram., 2008, 21, 605–608 CrossRef CAS.
- A. Aoujgal, W. A. Gharbi, A. Outzourhit, H. Ahamdane, A. Ammar, A. Tachafine and J. C. Carru, Ceram. Int., 2011, 37, 2069–2074 CrossRef CAS.
- A. Taylor, X-Ray Metallography, Wiely, New York, 1961 Search PubMed.
- Z. Raddaoui, R. Lahouli, S. E. L. Kossi, J. Dhahri, K. Khirouni and K. Taibi, J. Alloys Compd., 2018, 765, 428–436 CrossRef CAS.
- A. Gholizadeh, Journal of Advanced Materials and Processing, 2015, 3, 71–83 Search PubMed.
- M. M. Vijatovic Petrović, R. Grigalaitis, N. Ilic, J. D. Bobi, A. Dzunuzovic, J. Banys and B. D. Stojanovi, J. Alloys Compd., 2017, 724, 959–968 CrossRef.
- C. J. Li, F. Duewer, C. Gao, H. Chang and X.-D. Xiang, Appl. Phys. Lett., 2000, 76, 769 CrossRef.
- T. Hayashi, N. Oji and H. Maiwa, J. Appl. Phys., 1994, 33, 5277 CrossRef CAS.
- T. Wang, J. Hu, H. Yang, L. Jin, X. Wei, C. Li, F. Yan and Y. Lin, J. Appl. Psychol., 2017, 121, 084103 Search PubMed.
- J. Wang, G. Rong, N. Li, C. Li, Q. Jiang and H. Cheng, Russ. J. Appl. Chem., 2015, 88, 533–537 CrossRef CAS.
- N. Haddadou, J. Belhadi, B. Manoun, K. Taïbi, B. Carcan, M. El Marssi and A. Lahmar, J. Mater. Sci.: Mater. Electron., 2018, 29, 16144–16154 CrossRef CAS.
- M. Kallel, I. Kriaa and H. Khemakhem, Ceram. Int., 2016, 42, 1379–1383 CrossRef CAS.
- B. E. Vugmeister and V. A. Stephanovich, Solid State Commun., 1987, 63, 323–327 CrossRef CAS.
- C. Mao, X. Dong, G. Wang, S. Cao and C. Yao, J. Am. Ceram. Soc., 2010, 93, 4011–4014 CrossRef CAS.
- K. Uchino, Ferroelectric Devices, Marcel Dekker, New York, 2000 Search PubMed.
- A. B. Hassen, F. I. H. Rhouma, J. Dhahri and N. Abdelmoula, J. Alloys Compd., 2016, 663, 436–443 CrossRef.
- G. A. Smolensky, J. Phys. Soc. Jpn., 1970, 28, 26 Search PubMed.
- B. Y. R. D. Shannon, Acta Crystallogr., 1976, A32, 751 CrossRef.
- F. Bahri and H. Khemakhem, Ceram. Int., 2013, 39, 7571–7575 CrossRef CAS.
- N. Haddadou, J. Belhadi, B. Manoun, K. Taïbi, B. Carcan, M. El Marssi and A. Lahmar, J. Mater. Sci.: Mater. Electron., 2018, 29, 16144–16154 CrossRef CAS.
- C. Lei, A. A. Bokov and Z. G. Ye, J. Appl. Phys., 2007, 101, 084105 CrossRef.
- S. J. Kuang, X. G. Tang, L. Y. Li, Y. P. Jiang and Q. X. Liu, Scr. Mater., 2009, 61, 68–71 CrossRef CAS.
- B. Shen, Q. Zhang, J. Zhai and Z. Xu, Ceram. Int., 2013, 39, 9–13 CrossRef.
- Y. Yanga, K. Liua, X. Liua, G. Liua, C. Xia, Z. Heb and Y. Yan, Ceram. Int., 2016, 42, 7877–7882 CrossRef.
- K. Uchino and S. Nomura, Ferroelectr. Lett., 1982, 44, 55–61 CrossRef CAS.
- L. E. Cross, Ferroelectrics, 1994, 151, 305–320 CrossRef CAS.
- Z. Sun, L. Li, J. Li, H. Zheng and W. Luo, Ceram. Int., 2016, 42, 10833–10837 CrossRef CAS.
- S. Kumar and K. B. R. Verma, J. Phys. D: Appl. Phys., 2009, 42, 075405 CrossRef.
- C. Filipic, Z. Kutnjak and R. Pirc, Phys. Rev. B, 2016, 93, 224105 CrossRef.
- F. I. H. Rhouma, A. Dhahri, J. Dhahri, M. A. Valente and K. Khirouni, Appl. Phys. A, 2013, 114, 911–917 CrossRef.
- S. Ke, H. Fan, H. Huang and H. L. W. Chan, Appl. Phys. Lett., 2008, 93, 112906 CrossRef.
- G. Smolenskii and A. Agranovskaya, Soviet Physics Solid State., 1960, 1, 1429 Search PubMed.
- C. Mao, X. Dong, G. Wang, S. Cao and C. Yao, J. Am. Ceram. Soc., 2010, 93, 4011–4014 CrossRef CAS.
- S. Ke, H. Fan, H. Huang and H. L. W. Chan, Appl. Phys. Lett., 2008, 93, 112906 CrossRef.
- W. Cai, C. Fu, J. Gao, Z. Lin and X. Deng, Ceram. Int., 2012, 38, 3367–3375 CrossRef CAS.
- Z. Y. Cheng, R. S. Katiyar, X. Yao and A. Guo, Phys. Rev. B, 1997, 55, 8165 CrossRef CAS.
- H. Vogel, Z. Phys., 1921, 22, 645–646 CAS.
- G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339–355 CrossRef CAS.
- Q. Zhang, Z. Li, F. Li and Z. Xu, J. Am. Ceram. Soc., 2011, 94, 4335–4339 CrossRef CAS.
- F. Bourguiba, A. Dhahri, F. I. H. Rhoumaa, S. Mnefgui, J. Dhahri, K. Taibi and E. K. Hlil, J. Alloys Compd., 2016, 686, 675–683 CrossRef CAS.
- D. S. Tinberg, MS thesis, The Pennsylvania State University, 2006.
- Z. Y. Cheng, R. S. Katiyar, X. Yao and A. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 8165 CrossRef CAS.
- D. Viehland, S. Jang, L. E. Cross and M. Wittig, J. Appl. Phys., 1990, 68, 2916–2921 CrossRef CAS.
- K. Li, X. L. Zhu, X. Q. Liu and X. M. Chen, Appl. Phys. Lett., 2012, 100, 012902 CrossRef.
- Y. Zhang, H. Sunn and W. Chen, Ceram. Int., 2015, 41, 8520–8532 CrossRef CAS.
- P. R. Mandal and T. K. Nath, J. Alloys Compd., 2015, 628, 379–389 CrossRef CAS.
- S. Dutta, R. N. P. Choudhary, P. K. Sinha and A. K. Thakur, J. Appl. Phys., 2004, 96, 1607 CrossRef CAS.
- B. Li, Q. X. Liu, X. G. Tang, T. F. Zhang, Y. P. Jiang, W. H. Li and J. Luo, J. Mater. Sci.: Mater. Electron., 2017, 28, 14864–14873 CrossRef CAS.
- G. Murugesan, R. Nithhya, S. Kalainathan and S. Hussain, RSC Adv., 2015, 5, 78414–78421 RSC.
| This journal is © The Royal Society of Chemistry 2019 |