Open Access Article
Open Access ArticleRedox chemistry in the pigment eumelanin as a function of temperature using broadband dielectric spectroscopy†
K. A. Motovilov *a,
V. Grinenkobc,
M. Savinovd,
Z. V. Gagkaevaa,
L. S. Kadyrova,
A. A. Pronine,
Z. V. Bedrana,
E. S. Zhukovaae,
A. B. Mostert
*a,
V. Grinenkobc,
M. Savinovd,
Z. V. Gagkaevaa,
L. S. Kadyrova,
A. A. Pronine,
Z. V. Bedrana,
E. S. Zhukovaae,
A. B. Mostert *f and
B. P. Gorshunovae
*f and
B. P. Gorshunovae
aMoscow Institute of Physics and Technology, 141701, Institutsky lane 9, Dolgoprudny, Russia. E-mail: motovilov.ka@mipt.ru
bInstitute for Solid State and Materials Physics, TU Dresden, 01069, Dresden, Germany
cInstitute for Metallic Materials, IFW Dresden, 01069, Dresden, Germany
dInstitute of Physics AS CR, Praha 8, Czech Republic
eProkhorov General Physics Institute of the Russian Academy of Sciences, 119991, Vavilov Street 38, Moscow, Russia
fDepartment of Chemistry, Swansea University, Singleton Park, SA2 8PP, Wales, UK. E-mail: a.b.mostert@swansea.ac.uk
First published on 29th January 2019
Abstract
Conductive biomolecular systems are investigated for their promise of new technologies. One biomolecular material that has garnered interest for device applications is eumelanin. Its unusual properties have led to its incorporation in a wide set of platforms including transistor devices and batteries. Much of eumelanin's conductive properties are due to a solid state redox comproportionation reaction. However, most of the work that has been done to demonstrate the role of the redox chemistry in eumelanin has been via control of eumelanin's hydration content with scant attention given to temperature dependent behavior. Here we demonstrate for the first time consistency between hydration and temperature effects for the comproportionation conductivity model utilizing dielectric spectroscopy, heat capacity measurements, frequency scaling phenomena and recognizing that activation energies in the range of ∼0.5 eV correspond to proton dissociation events. Our results demonstrate that biomolecular conductivity models should account for temperature and hydration effects coherently.
Introduction
Conductive biomaterial systems are actively being investigated for potential insights that may lead to technological applications. These biomaterial systems and their applications are quite diverse1–4 and include specific systems such as bacterial extracellular filaments,4–6 conductive protein mats7,8 and doped polysaccharides,9 to select a few. One such material that is receiving a lot of attention is the biomacromolecular system eumelanin as a model bioelectronic material.10 Eumelanin has already been tested in various devices platforms such as UV filters,11 solid-state organic electrochemical transistors,12 metal-insulator devices,13 flexible supercapacitors,14 extended gate field effect transistors,15 engineered electrodes16 and edible batteries.17Eumelanin, the archetypal melanin and referred to as melanin from now on, is part of a family of melanins primarily associated with photo-protection and pigmentation.18–20 It is also found in areas of the body, such as in the substantia nigra of the brain stem, which would suggest other roles. This has led to speculation as to other functions such as radiation protection, free radicals scavenging and heavy metal ion chelation.18–23
An additional property is a free radical signal as measured by electron paramagnetic resonance (EPR).20,24–29 The signal consists of two radicals: a carbon centered and semiquinone free radical. The most important for conductivity is the semiquinone radical (see below).26
The most relevant property for devices is melanin's hydration dependent conductivity. In the past five years it has been shown that melanin should be regarded, at minimum, as a mixed ionic/electronic conductor24,30,31 with a predominant proton component.
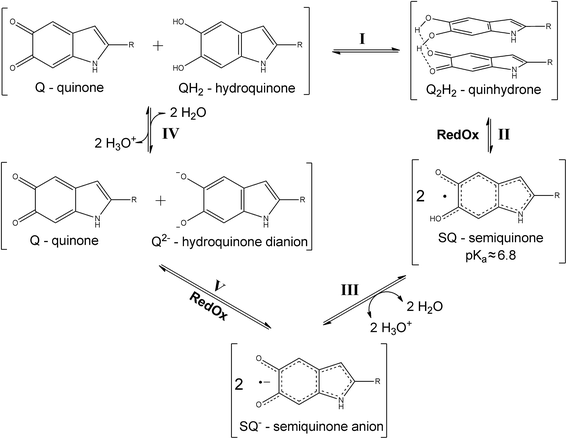
This hydration dependent effect is significant in that it can change the observed conductivity by orders of magnitude though the water content only increases linearly.24,30–33 Hence, it has become clear that any electrical study of melanin requires a degree of hydration control. The aforementioned mixed ionic/electronic viewpoint should actually be further narrowed to viewing melanin as a proton conductor exclusively based upon recent impedance work in which thin films of melanin were subject to hydration control.34 Based upon this hydration dependent behaviour, the origin of the conductivity in melanin is ascribed to a comproportionation reaction (Fig. 1, pathways IV and V) where adding water yields hydronium and semiquinone radicals for conduction. As a result, what the recent hydration dependent work shows is that the previous four decades old amorphous semiconductor model for melanin20,35–37 should be discarded.
However, even with the recent progress, there is a noticeable absence in the recent melanin work on its conductivity behavior, which is a systematic investigation of its redox chemistry as a function of temperature. Most of the recent work has focused on hydration dependent behavior. Currently, this state of affairs needs to be rectified to confirm the validity of the proposed comproportionation reaction model, since it would be expected that there should be consistency between the hydration and temperature dependent conductivity behavior.
One way to study the conductivity, hence the redox chemistry of melanin, is by performing temperature dependent direct current (DC) and broad-band dielectric/alternating current (AC) measurements. Furthermore, information of molecular and charge dynamics is provided by specific heat measurements. However, when it comes to conductive biomaterials in general, one often finds that temperature dependent studies, either on wet or dry biomaterials, are done with no concern given to properly controlling the hydration content.10 As has been demonstrated with the melanins,30 water content of a biomaterial is a first order variable for its conductive behavior. Other materials in which it is clear that water plays a significant role include the conductive bacterial filaments.38 Thus, doing a temperature dependent study without proper water content control will bring out confounding errors due to water evaporation or condensation into the sample.10 Hence, the temperature dependent work presented here are on melanin samples in which the water content has been controlled.
To date there are only a few temperature dependent, conductivity studies that have been done on melanin, which is unusual given its promise. The most thorough and consistent temperature dependent AC and DC measurements, attempting to account for hydration, were undertaken by Jastrzebska et al.32,39,40 Their data indicated that the room temperature DC conductivity of melanin rises from 10−13 to 10−5 S cm−1 depending on the hydration level32 and found DC conductivity activation energies of 0.49–0.76 eV depending on the level of vacuum and heating or cooling type of the measurement. The AC response of melanin as reported by Jastrzebska et al.40 was measured in the frequency ranges of ν = 102 to 109 Hz and39 10−2 to 107 Hz with the latter study utilizing a broader temperature interval of 253–393 K. Critically, Jastrzebska et al.'s AC studies were performed without thorough control of ambient humidity. In all their analyses, they presumed a semiconductor model, which has proven to be untenable. Thus, the interpretation of their results is now open to question.
As to specific heat measurements, there exist only few such experiments on melanin, which include work on only a narrow temperature interval of 0.3–4.2 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 (showing potential magnetic phase transitions), and on only wet samples of melanin48 with contributions assigned to melanin and water separately. However, as Fig. 1 indicates, one can't separate out water and melanin contributions since water changes the chemistry of melanin. Furthermore, if a proper comparison is going to be made with dielectric/AC and DC data, similar temperature ranges need to be covered up to and including room temperature.
47 (showing potential magnetic phase transitions), and on only wet samples of melanin48 with contributions assigned to melanin and water separately. However, as Fig. 1 indicates, one can't separate out water and melanin contributions since water changes the chemistry of melanin. Furthermore, if a proper comparison is going to be made with dielectric/AC and DC data, similar temperature ranges need to be covered up to and including room temperature.
It is clear that if the solid-state comproportionation reaction model for conductivity of melanin is to be confirmed via temperature dependent data, certain gaps will need to be filled. Hence, the work presented here addresses the outstanding problems by performing the first broad-band radio-frequency (1 Hz to 1 MHz) and terahertz (0.2–3 THz) temperature-dependent (5–325 K) measurements of complex AC conductivity and dielectric permittivity of melanin samples with different water content. These studies are supplemented by the first careful measurements of specific heat at temperatures 1.8–300 K. Furthermore, we'll show that utilizing universal scaling the data analysis and understanding of melanin can be significantly enhanced and essentially confirm the comproportionation reaction model for conductivity. Finally, all the work above we will show were done with hydration control in mind, which will demonstrate the importance of controlling not just temperature and frequency, but hydration as well.
Materials and methods
Sample preparation
Melanin was synthesized following a standard literature procedure25 utilizing as the initial starting material D,L-dopa (Sigma-Aldrich). D,L-dopa was dissolved in deionized water, subsequently adjusted to pH 8 using NH3 (28%). Air was then bubbled through the solution while being stirred for 3 days. During the 3 days synthesis the pH would naturally decrease due to the NH3 evaporation, which would necessitate the need to add ammonia periodically to bring the pH back to 8. By keeping the pH at a maximum of 8 and letting it decrease naturally ensured that ring fission of the indolquinone moieties are kept to a minimum and hence the synthesised melanin is a biomimetic material.41 The solution was then brought to pH 2 using HCl (32%) to precipitate the pigment. The solution was then filtered and washed multiple times with deionized water and dried. We also note, as per the XPS work below, that our synthetic samples, although a comparable biomimetic analogue to naturally occurring melanin, do have a higher amount of DHI (Fig. 1) moieties relative to DHICA moieties (∼7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) than what would be expected for naturally occurring melanins which usually exhibit a 1
3) than what would be expected for naturally occurring melanins which usually exhibit a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of DHI to DHICA.41 A basic elemental characterization was performed on the sample by use of X-ray Photoelectron Spectroscopy (XPS). Measurements were at the Centre for Microscopy and Microanalysis X-ray Analysis Facility (UQ) using a Kratos Axis Ultra XPS Surface Analysis System with a monochromatic Al Kα X-ray source. Survey scans were taken at a 120 eV pass energy and analysis performed using CASA XPS software. Atomic ratios for C, N and O were determined and came out at O ∼21.3%, C ∼70.9% and N ∼7.9%. These values are commensurate with a polymer based upon ∼70% DHI monomers. The powders were pressed (30 minutes at 6000 bar) into round pellets with the thickness of 1–2 mm and diameter 8–10 mm by means of LabTools hydraulic press system (Russia). To stabilize the water content the samples were placed then in hygrostats. We controlled the reference values of humidity by means of saturated solutions of LiCl, MgCl2, Na2Cr2O7, NaNO2, (NH4)2SO4, pure water and dry P2O5, corresponding to the values of relative humidity at 22 °C 11%, 33%, 55%, 65%, 98%, 100% and ∼0% respectively. Before and after each measurement procedure (either spectroscopic or specific heat) we weighed the samples and estimated the weight loss or gain against vacuum dry state. Weights measured and correspondence with hygrostats humidities yielded approximate values of water concentration in the samples commensurate with published adsorption isotherms.42
1 ratio of DHI to DHICA.41 A basic elemental characterization was performed on the sample by use of X-ray Photoelectron Spectroscopy (XPS). Measurements were at the Centre for Microscopy and Microanalysis X-ray Analysis Facility (UQ) using a Kratos Axis Ultra XPS Surface Analysis System with a monochromatic Al Kα X-ray source. Survey scans were taken at a 120 eV pass energy and analysis performed using CASA XPS software. Atomic ratios for C, N and O were determined and came out at O ∼21.3%, C ∼70.9% and N ∼7.9%. These values are commensurate with a polymer based upon ∼70% DHI monomers. The powders were pressed (30 minutes at 6000 bar) into round pellets with the thickness of 1–2 mm and diameter 8–10 mm by means of LabTools hydraulic press system (Russia). To stabilize the water content the samples were placed then in hygrostats. We controlled the reference values of humidity by means of saturated solutions of LiCl, MgCl2, Na2Cr2O7, NaNO2, (NH4)2SO4, pure water and dry P2O5, corresponding to the values of relative humidity at 22 °C 11%, 33%, 55%, 65%, 98%, 100% and ∼0% respectively. Before and after each measurement procedure (either spectroscopic or specific heat) we weighed the samples and estimated the weight loss or gain against vacuum dry state. Weights measured and correspondence with hygrostats humidities yielded approximate values of water concentration in the samples commensurate with published adsorption isotherms.42
Radiofrequency range AC measurements
The pellets with the 8–10 mm diameters and 1.2–1.3 mm thicknesses were used for the study. Au-electrodes were evaporated on plane-parallel surfaces using BAL-TEC (SCD 050) Sputter Coater. The contacts for applying the electric field were provided by silver wires fixed by a silver (Degussa) paste. Low-frequency complex dielectric permittivity, losses and conductivity were measured at frequency (1 Hz to 1 MHz) and temperature (5–295 K) ranges in a standard way using a NOVOCONTROL Alpha-AN High Performance Frequency Analyzer in conjunction with a JANIS ST-100 cryostat controlled by temperature controller Lakeshore 335. The temperature rate and applied AC electric field was about 0.2 K min−1 and 0.83–0.77 V mm−1, respectively.DC-measurements
DC conductivity was measured in a 4-point van der Pauw geometry with contacts made with silver paint. The voltage was measured with a Keithley 2002 voltmeter (input resistivity above 100 GOhm) and Keithley 6517A electrometer. The commutator leakage resistance was or the order of TOhm that allows to reliable measure sample resistance of 1–10 GOhm.Terahertz range AC measurements
Terahertz measurements were done using a commercial pulsed terahertz spectrometer TeraView TPS Spectra 3000 (UK) equipped with a home-made helium-flow optical cryostat with Mylar windows.Specific heat measurements
The specific heat data were collected by a relaxation technique in a Quantum Design physical property measurement system (PPMS) in the temperature range 1.8–300 K. The samples of a rectangular shape with the mass ∼10 mg were used. Dry samples were prepared by means of 72 hours incubation in Ar (p ∼ 1 atm). Wet samples were made from dry by means of 48 hours incubation in 100% RH atmosphere at 25 °C. Water contribution into final mass of the samples was estimated by weighing. Experiments with wet samples started with fast (20 degrees per minute) cooling aimed to minimize water evaporation in helium flow (p ∼ 5 torr) inside the cryostat.The modelling of the boson peak
We modelled the low-temperature dependences of the specific heat of our samples via a sum of the Debye contribution and the additional excess vibrational density of states due to a Lorentzian distributed boson peak:
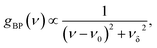 | (1) |
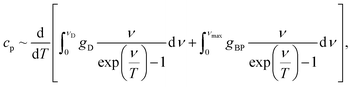 | (2) |
Experimental results
Electrical measurement results
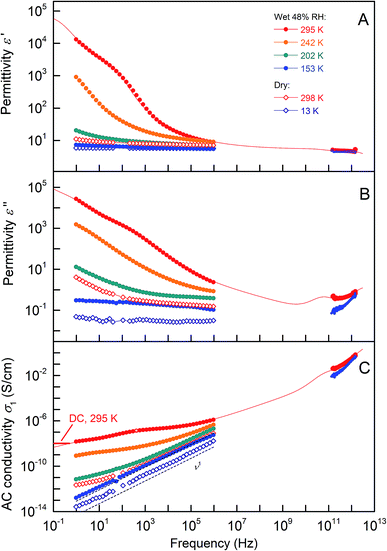
Fig. 2 depicts the radiofrequency-terahertz spectra of the real ε′(ν) and imaginary ε′′(ν) parts of the permittivity and the real component of the conductivity, σ1(ν) = νε′′/2 for two types of melanin sample – one dried in vacuum for 10 hours and another incubated at 48% RH at 22 °C, which corresponds to a mass gain of ∼13.5%. This level of hydration is sufficient for melanin to be in the conductive regime in which the comproportionation reaction is strongly exhibited.26,30,31 A strong decrease in the real and imaginary permittivity values are seen at room temperature in the spectra of the wet melanin as one increases the frequency. Such behavior is accompanied by moderate increase of the frequency dependent conductivity σ1(ν). However, when cooled down, the strong dispersion observed for ε′(ν) and ε′′(ν) weakens significantly and both spectra nearly flatten at around 150 K.The nearly constant imaginary permittivity, ε′′(ν) ≈ const, together with the corresponding conductivity σ1(ν) ∼ ε′′ν ∼ ν1 behavior indicate emergence of the nearly-constant loss regime frequently observed in biological and disordered systems.50–56 In contrast, the dry sample appears to be in a nearly constant loss regime already at room temperatures, with cooling only having a minimal effect. This indicates the clear effect that water has on melanin's electrical properties in promoting a hopping regime for conductivity (see below).
We also note that the temperature dependent features in the permittivities (including similar values and frequency features) show the same qualitative behavior as those for melanin thin films34 (see also Fig. S1†) that are successively hydrated.
The observed temperature evolution of the spectra was processed with the minimal set of appropriate terms. The pronounced dispersion in the high-temperature spectra below 1 MHz was modeled with the Havriliak–Negami relaxation expression57 commonly used to describe frequency dependent response in disordered media:
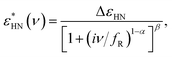 | (3) |
| σ1(ν) = Aνs. | (4) |
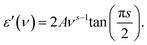 | (5) |
We also observed a second relaxation process in the room temperature permittivity and conductivity spectra with its fR estimated around 60 Hz (bump between 100 and 1000 Hz in conductivity and imaginary permittivity spectra, see Fig. 2). This second relaxation disappeared during cooling much faster than the 0.2 Hz feature and could not be observed below 250 K. The characteristic frequencies for both relaxation phenomena exhibited significant thermal stability and have activation energies of 0.43 eV ± 10% (0.2 Hz feature) and 0.39 eV ± 40% (60 Hz feature), Fig. 3A. The features have significantly different strengths (ΔεHN) of about two orders of magnitude between the 0.2 Hz and 60 Hz features at room temperature.
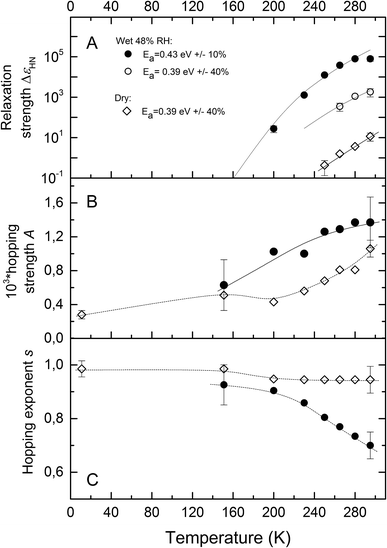 | ||
| Fig. 3 On panel (A) we present results of temperature variations of relaxation strengths and corresponding activation energies (solid lines) of two processes, observed at frequencies 0.2 Hz (Ea = 0.43 eV ± 10%) and 60 Hz (Ea = 0.39 eV ± 40%) in dry (empty rhombuses) and wet (empty and filled circles) samples of melanin. On panels (B) and (C) we fitted temperature behavior of hopping strength ΔεHN, eqn (3), and hopping exponent s, eqn (4). Dashed lines in panels B and C are guides to the eye. | ||
Example of a least-square fit of the radio-frequency and THz spectra is shown by solid lines in Fig. 2. Same procedure was used to process the spectra of dry sample that are shown in Fig. 2A–C by rhombuses. The terahertz-infrared spectra are described with a Lorentzian (infrared excitation seen as increase in ε′′ and σ1 above 1012 Hz) and Debye (terahertz response of water seen as a peak around 1011 Hz in panel B) models as explained below.
Fig. 3A–C plots the temperature dependences of the above parameters and there is clearly a hydration dependence. The hopping contribution to the radio-frequency response also freezes out while cooling (Fig. 3B). The temperature dependence of the hopping exponent s shows a crossover at 200–240 K from hopping regime (s = 0.7–0.8) to the nearly constant loss regime (s > 0.9). Usually nearly-constant loss regime in proteins is associated with the dynamics of caged water molecules.55,59
In many cases the experimental data on AC/DC conductivity and dielectric permittivity of disordered conductors, obtained at different frequencies and temperatures, can be merged on a single master curve thus signifying the frequency–temperature superposition principle.52,60 Such universal scaling can be revealed by plotting the reduced conductivity or permittivity versus reduced frequency.61 Physically, its fulfillment indicates an unchanged mechanism of electrodynamic response (in the present case conductivity) in corresponding frequency and temperature intervals. We plot such a curve in Fig. 4 for the conductivity spectra of the 13.5% wt melanin according to the relation:
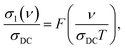 | (6) |
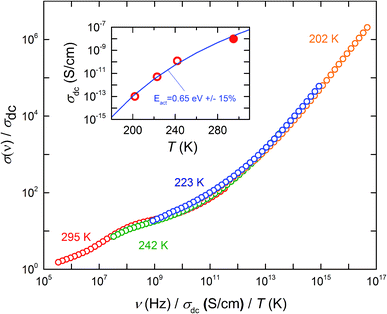 | ||
| Fig. 4 Scaling curve in accordance with eqn (6) for conductivity data of the melanin sample containing ∼13.5% wt of water. Different colors indicate different temperatures. The inset demonstrates that the DC conductivity σDC shows activating behavior with an activation energy of 0.65 eV ± 15%. Filled dot corresponds to measured value; open dots correspond to the values obtained from scaling analysis as described in the text. Experimental uncertainties are of the data points size. | ||
As a consistency check on the scaling methodology above, the AC data obtained at 1 Hz was plotted vs. 1/T, and an activation energy of 0.52 eV ± 10% was extracted (Fig. S2,† filled circles). Again, similar to our inferred DC conductivity activation energy, with discrepancies most likely being due to not operating in the DC limit. For completeness, we include the 1 Hz data obtained for the dry sample with the associated activation energy of 0.43 eV ± 10%, which is similar to the activation energies obtained for the 60 Hz feature in the vacuum level data (Fig. S2†).
It should also be noted that we do not observe any sign of relaxation processes described and interpreted by Jastrzebska et al.39 as a sign of two types of hopping phenomena. However, we did not heat our samples to as high temperatures as reported by them.39
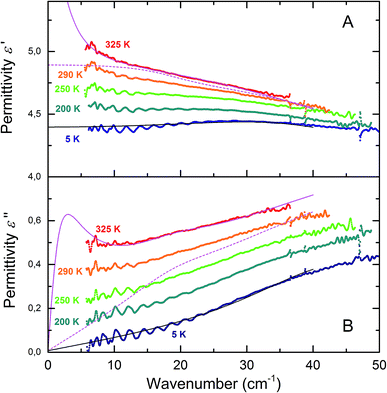
To model the terahertz spectra (included in Fig. 2) we used a Lorentzian expression that describes the resonance located above our highest frequency, and the Debye expression56 to reproduce the response of water molecules (free or bound) clearly seen at T = 325 K in the spectra of Fig. 5 (note the changes in the value is non zero). The Debye expression used is given by:
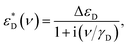 | (7) |
Heat capacity measurements results
The results of our specific heat measurements of dry and wet (15–20 wt% of water) melanin are presented in Fig. 6. As can be seen, at temperatures below 3.5 K and above ≈20 K the wet sample has a larger specific heat compared to the dry sample. This effect is more clearly demonstrated in the cP(T)/T3 vs. T presentation (Fig. 6B), where both dry and wet melanin types reveal a feature typical for classic amorphous systems – a boson peak. The boson peak is observed in disordered materials in the form of an excess contribution to the vibrational density of states (VDOS) g(ν), relative to the Debye component gD(ν) ∼ ν2. This additional contribution can be observed by inelastic neutron or Raman scattering62–67 and as a peak in the specific heat plotted as cP(T)/T3 vs. T.56,68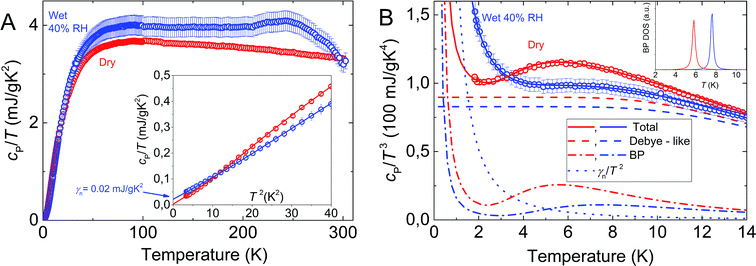 | ||
| Fig. 6 Temperature dependences of specific heat of dry and wet (15–20 wt% of water) melanin. (A) – cP/T of dry melanin (red) and wet melanin (blue). The inset shows cP/T versus T2 at low temperatures, cP/T of wet melanin does not go to zero at T = 0 K; symbols – experimental data and solid lines fits by the model eqn (2); γ is addition to Debye contribution. Experimental uncertainty is of the data points size. (B) – cP/T3 − T representation of specific heat data. Symbols – experimental data with solid lines showing the model of eqn (2). Dashed lines show Debye contribution. Dashed-dotted lines show boson peak (BP) contribution and dotted lines show linear contribution. The inset shows the BP DOS having Lorentzian distribution. BP feature (peak at ∼6 K) is clearly seen in dry melanin and its shift to a higher temperature in wet melanin. | ||
Furthermore, there is a remarkable observation which comes from the inset on Fig. 6A. Within the framework of our techniques the specific heat of dry melanin goes to zero as we approach to 0 K, unlike specific heat of wet melanin. This suggests that dry melanin has a more regular, less disordered structure. Furthermore, we also observe that at temperatures above 100 K, again unlike in wet sample, we can clearly see a gradual decrease of the dry melanin heat capacity (Fig. 6), which speaks in favor of structural reforming within the system. We will discuss this in more detail in the discussion below.
We also note that the heat capacity does not go to 0 as we approach 0 K in the case of wet melanin thus pushing us to add linear component to standard boson peak and Debye-like terms which are enough for description of dry sample behavior.
Discussion
The 0.2 Hz feature
The current study revealed several phenomenological peculiarities that have not been observed earlier. For example, two low frequency relaxations with characteristic frequencies at ∼0.2 Hz and ∼60 Hz have not been reported before. To explain the origin of these features one needs to recall both melanin's solid-state chemistry and physical structure. We will focus on the 0.2 Hz peak first and note three key features of the 0.2 Hz response, which are: (a) has a relaxation frequency of 0.2 Hz, hence the physical size/mass of the electric dipole involved must be large to account for the slow response; (b) only seen in hydrated melanin; (c) has an activation energy of 0.43 eV ± 10%. The most parsimonious explanation accounting for these observations is to assign the 0.2 Hz relaxation to the semiquinone anions within melanin. Dealing with point (a) first, the reality is that the semiquinone moieties with melanin will be part of an oligomer sheet of 4–6 monomers,20,69–73 which in turn will stack with other such sheets via the π–π interaction69,74 to form a colloidal particle. Hence, the charged electric dipole of the semiquinone, in order to align itself with the electric field, will have to rotate a relatively larger colloidal particle, leading to a slow relaxation frequency.Given that the comproportionation reaction, and hence the semiquinone, is mostly exhibited in hydrated melanins26 due to the requirement of two water molecules to generate them, it addressed point (b) and explains why this 0.2 Hz feature is not present in the dry sample.
The above leads us directly to point (c), in order to explain the origin of the activation energy, it is necessary to recall the equilibrium constant for the overall comproportionation reaction:
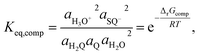 | (8) |
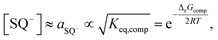 | (9) |
That the comproportionation reaction is the origin of the 0.2 Hz feature is bolstered by the fact that the temperature dependent trend of the dielectric parameters have the same behavior as the hydration dependent trend reported elsewhere34 (Fig. S1†). This argues for the same underlying mechanism i.e. the comproportionation reaction.
Indeed, if the above interpretation is adopted, unusual consistency can be obtained when inspecting the scaled DC conductivity data (Fig. 4). Since melanin is a proton conductor34 who's conductivity is due to charge density changes of protons regulated by the comproportionation reaction, one can write
| σDC ∝ nprotons ∝ [H3O+] = [SQ−]. | (10) |
Hence, one would anticipate that the conductivity would show the same order of magnitude in its activation energy as for the dielectric relaxation at 0.2 Hz. Given that 0.65 eV ± 15% is recorded for the DC conductivity, it is again confirmation of the consistency of the above interpretation.
In short, the data, both conductivity and dielectric spectra, confirms the presence of the comproportionation reaction, but for the first time is done so utilizing the temperature variable.
The 60 Hz feature
Our above explanation inclines us to believe that energies around the 0.5 eV value may be signature values for chemical equilibria. Hence, with this mind set we approached the 60 Hz relaxation feature by noting the following key features: it is higher in frequency than the 0.2 Hz feature, is present in both the dry and wet melanin forms, it is smaller in magnitude to the 0.2 Hz feature, and it has a lower energy of activation of 0.39 eV ± 40% than the 0.2 Hz feature. Considering the higher frequency of the relaxation, it implies that the electric dipole entity is spatially/mass wise smaller in magnitude. Furthermore, the smaller magnitude of the relaxation strength implies far fewer entities than the semiquinone. The best explanation for these observations is to assign the 60 Hz feature to the carboxylic acid groups present in melanin. First, they are smaller entities and hence easier to polarize, leading to a higher relaxation frequency. Furthermore, there is only a few COOH moieties present in our samples, which explains the lower dielectric strength. One can also write:
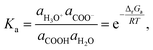 | (11) |
| [H3O+] ≈ aH3O+ ∝ Ka, | (12) |
If the above view is adopted, it can also explain why this 60 Hz feature is present in both dry and wet melanin. The first is that dry melanin usually still have trace amounts of water20,42 and since only one water molecule is required for ionization, and there is a lower activation energy involved, observing it should not be a surprise. Naturally, water is plentiful in the wet melanin sample, hence why one observed it there.
This may also explains the activation energy observed in the 1 Hz conductivity data (Fig. S2†) for the dry melanin. The lower activation energy vis-à-vis the wet sample, most likely indicates the activation energy of the carboxylic acid dissociation.
An intriguing conclusion can be drawn. The carboxylic acids present do not contribute much to the proton conductivity of melanin. They are too few in number and the conductivity is clearly dominated by a higher activation energy process (i.e. the comproportionation reaction). This has been assumed to be the case in past discussion in various works, but the data presented here confirms it experimentally.
Conductivity and terahertz results
With the 0.2 Hz, 60 Hz and conductivity data explained, we move to the nature of the conductivity mechanism. For wet melanin, the hopping exponent s (see eqn (4)) increases from ∼0.7 to ∼0.9 with decreasing temperature. These values are indicative of a hopping mechanism. In addition, as noticed in the correlation with the terahertz data in Fig. 5, liquid like water appears to be necessary for this hopping mechanism, which though slowly becomes frozen out as one passes 160 K. The conductivity mechanism, for the wet melanin sample, then enters the range of values similar to the dry melanin, implying a convergence in mechanistic behavior.Considering that melanin is a proton conductor, it is not unreasonable to assume a Grötthuss mechanism76 as the hopping mechanism observed in the wet sample. As the sample is cooled the amount of liquid, hence easily rotatable molecules, becomes less. This leads to a freezing out of the hopping mechanism at low temperature. The low temperature nearly constant loss regime can then tentatively be assumed to indicate a mass of center diffusion mechanism or a much slower hopping mechanism, which will also be present in the dry sample with characteristic activation energy of 0.026 eV ± 20%.
Heat capacity results
We discuss the boson peak behavior first (Fig. 6B). Peculiarities of boson peak behavior in proteins and other organic glass-formers have already been intensively studied by the group of Sokolov.77,78 They demonstrated that the boson peak shape should not be directly associated with specific chemical composition and chemical bond type of particular glass-former, but is related to general features common to glasses and proteins. Currently, they ascribe the universality of boson peak phenomena to nanoheterogeneity models.78 Namely, the density of states spectrum is determined by the spatial distribution of fluctuations of elastic constants of the amorphous structure. In turn, these can be considered as universalities observed in a wide class of materials. The effect of boson peak shifting to higher temperatures with increase of water content (inset in Fig. 6B) is also well known for proteins. Precise analysis of this effect for the case of lysozyme can be found in (ref. 77): increase of hydration results in shifting of the boson peak to higher temperatures, owing to an increase of contribution coming from the fast (picoseconds) relaxation processes associated with the “rattling” of amino acids within cages formed by neighboring residues and solvent molecules. In the case of melanin, carboxylic acid moieties rotation and vibration are a plausible source, especially if they are hydrated.Turning to Fig. 6A and its peculiar features. We first note the low temperature regime (inset), where the dry melanin limits to no heat capacity at 0 K, while the wet melanin sample emphatically have a non-zero intercept. Traditionally, for well ordered, non-conductive systems, the heat capacity limits to zero as one approaches 0 K since all the phonon modes are frozen out. A non-zero intercept is then indicative of free carriers. Naturally, given that melanin is an amorphous proton conducting material, this interpretation would normally give way to an alternative viewpoint: that the non-zero intercept is a common observation for disordered systems, and is related to lattice vibrations with trapped cavities included.64 However, this latter view also faces difficulties since the dry melanin sample should then also demonstrate a non-zero intercept for the heat capacity.
In short, the indirect signatures of the possible presence of free carriers in wet melanin both at high (scaling on Fig. 4) and at low (linear component of specific heat on Fig. 6) temperatures are obviously not enough to regard melanin as a system with free electrons and/or protons in a wide temperature range. Unfortunately, we were not able to measure σDC and estimate σ1 in radiofrequency range of the wet melanin (with 15–20% wt of water) at the lowest temperatures. The latter one can, possibly, give us dispersionless behavior as a clear signature of free Drude-like carriers in the system. Thus, these points indicate the need for further study to further elucidate the low temperature heat capacity behavior.
Finally, we turn to the high temperature heat capacity data for melanin. For the wet melanin above 100 K, the behavior is as expected. From 100 K to ∼200 K the heat capacity/temperature data is constant as would be expected for the Dulong–Petit law. The changes in the heat capacity afterwards is due to water melting and then evaporation. In contrast, the dry melanin data is irregular. In the 100 K and above data, there is decrease in the data line, violating the Dulong–Petit law. This may be due to a structural change within the dry melanin. It suggests that dry melanin has, as it is being heated, becoming more disordered, hence implying a more “ordered” state. Furthermore, this “ordered” state should be absent in the hydrated polymer. As such, we tentatively advance the idea that the effects seen is due to the formation of quinhydrone pairs at lower temperatures. The quinhydrone hypothesis for melanin has been discussed in the past but has fallen out of favor in recent decades (see discussion in the ESI†). On the one hand, the formation of quinhydrone dimers (as seen in Fig. 1, pathways I, II and III) should lead to greater regularity of the system at low temperature. But on the other hand it should also significantly destroy the general network of H-bonds, leading to higher energy barriers for proton conduction within material.
Implications for melanin based devices
The biomimetic synthetic analogue of melanin used in this study has potential application in bioelectronic devices as was indicated in the introduction. Since it is made synthetically, and hence there is more control, applying it to devices is a natural way to go. The present study touches on the fundamental questions of charge transport and mechanism of melanin and hence will inform what kind of devices are feasible in principle using our material. Our results clearly align with the view that the redox chemistry of melanin, via the comproportionation reaction, is responsible for the conductivity of melanin. Hence, considering melanin as a semiconductor is out of the question and thus attempting to create devices such as field effect transistors from melanin are most likely not feasible, since such devices require a semiconductor material.In contrast, melanin based devices utilising its ionic behaviour have a future, as recent work on batteries,16,17 capacitors14 and organic electrochemical transistors12 prove. Furthermore, as our work would indicate, the carboxylic acid groups do not contribute much to the charge transport, hence focus in creating different kinds of biomimetic melanins in order to control the relative DHI/DHICA content (i.e. controlling the carboxylic acid content) may not offer great advantages as far as proton charge density is concerned. However, this does not discount the importance of the ratio when it comes to secondary structural formation,79 which may still strongly influence charge transport in other aspects.
Conclusions
In conclusion, we have presented the first systematic temperature controlled DC, AC conductivity/permittivity/dielectric spectroscopy and heat capacity measurements on the synthetic melanin while controlling its hydration state appropriately.The control of these variables was key in demonstrating the potential connection between the hydration dependent behavior for melanin and the temperature dependent behavior. Consistency is achieved with the current proposed indole-quinone molecular model where the redox comproportionation reaction is believed to play a dominant role. The data shown here is the first demonstration of the self-consistency of this interpretative model in solid-state melanin using the temperature axis. Furthermore, we were able to pick up the signature of a potential mechanistic competitor in the form of the deprotonation of the carboxylic acid groups in melanin and show that it plays only a minor role. In addition, it was shown that the hopping mechanism in melanin most likely requires liquid water to operate.
Data availability
The data that support the findings of this study are available from the authors on reasonable request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge fruitful discussions with Paul Meredith, Sergei Tretiak, Andriy Zhugayevych. We thank Margarita Sheliakina for help in melanin synthesis and Barry Wood in helping obtain the XPS data. The research was supported by the project N3.9896.2017/BY and Ministry of Education and Science of the Russian Federation (Program 5 top100). ABM is a Sêr Cymru II fellow and results incorporated in this work have received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 663830.References
- A. Noy, Adv. Mater., 2011, 23, 807–820 CrossRef CAS PubMed.
- J. Rivnay, S. Inal, A. Salleo, R. M. Owens, M. Berggren and G. G. Malliaras, Nat. Rev. Mater., 2018, 3, 17086 CrossRef CAS.
- Y. Tan, R. Y. Adhikari, N. S. Malvankar, S. Pi, J. E. Ward, T. L. Woodard, K. P. Nevin, Q. Xia, M. T. Tuominen and D. R. Lovley, Small, 2016, 12, 4481–4485 CrossRef CAS PubMed.
- N. S. Malvankar and D. R. Lovley, ChemSusChem, 2012, 5, 1039–1046 CrossRef CAS PubMed.
- N. L. Ing, T. D. Nusca and A. I. Hochbaum, Phys. Chem. Chem. Phys., 2017, 19, 21791–21799 RSC.
- K. M. Leung, G. Wanger, M. Y. El-Naggar, Y. Gorby, G. Southam, W. M. Lau and J. Yang, Nano Lett., 2013, 13, 2407–2411 CrossRef CAS PubMed.
- D. D. Ordinario, L. Phan, W. G. Walkup IV, J. M. Jocson, E. Karshalev, N. Hüsken and A. A. Gorodetsky, Nat. Chem., 2014, 6, 596–602 CrossRef CAS PubMed.
- N. Amdursky, X. Wang, P. Meredith, D. D. C. Bradley and M. M. Stevens, Adv. Mater., 2016, 28, 2692–2698 CrossRef CAS PubMed.
- C. Zhong, Y. Deng, A. F. Roudsari, A. Kapetanovic, M. P. Anantram and M. Rolandi, Nat. Commun., 2011, 2, 476 CrossRef PubMed.
- P. Meredith, C. J. Bettinger, M. Irimia-Vladu, A. B. Mostert and P. E. Schwenn, Rep. Prog. Phys., 2013, 76, 034501 CrossRef CAS PubMed.
- J. M. Gallas, Optical lens system incorporating melanin as an absorbing pigment for protection against electromagnetic radiation, US Pat., US 5036115 A, 1991.
- M. Sheliakina, A. B. Mostert and P. Meredith, Mater. Horiz., 2018, 5, 256–263 RSC.
- M. Ambrico, P. F. Ambrico, A. Cardone, T. Ligonzo, S. R. Cicco, R. Di Mundo, V. Augelli and G. M. Farinola, Adv. Mater., 2011, 23, 3332–3336 CrossRef CAS PubMed.
- P. Kumar, E. Di Mauro, S. Zhang, A. Pezzella, F. Soavi, C. Santato and F. Cicoira, J. Mater. Chem. C, 2016, 4, 9516–9525 RSC.
- M. Piacenti da Silva, J. C. Fernandes, N. B. de Figueiredo, M. Congiu, M. Mulato and C. F. de Oliveira Graeff, AIP Adv., 2014, 4, 037120 CrossRef.
- Y. J. Kim, W. Wu, S.-E. Chun, J. F. Whitacre and C. J. Bettinger, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20912–20917 CrossRef CAS PubMed.
- C. J. Bettinger and J. Whitacre, A water-activated, ingestible battery, US Pat., US20150118526A1, 2015.
- G. Prota, Melanins and melanogenesis, Academic Press, 1992 Search PubMed.
- J. Y. Lin and D. E. Fisher, Nature, 2007, 445, 843–850 CrossRef CAS PubMed.
- P. Meredith and T. Sarna, Pigm. Cell Res., 2006, 19, 572–594 CrossRef CAS PubMed.
- T. Sarna, B. Pilas, E. J. Land and T. G. Truscott, Biochim. Biophys. Acta, Gen. Subj., 1986, 883, 162–167 CrossRef CAS.
- L. Panzella, G. Gentile, G. D'Errico, N. F. Della Vecchia, M. E. Errico, A. Napolitano, C. Carfagna and M. d'Ischia, Angew. Chem., Int. Ed., 2013, 52, 12684–12687 CrossRef CAS PubMed.
- L. Hong and J. D. Simon, J. Phys. Chem. B, 2007, 111, 7938–7947 CrossRef CAS PubMed.
- S. B. Rienecker, A. B. Mostert, G. Schenk, G. R. Hanson and P. Meredith, J. Phys. Chem. B, 2015, 119, 14994–15000 CrossRef CAS PubMed.
- C. C. Felix, J. S. Hyde, T. Sarna and R. C. Sealy, J. Am. Chem. Soc., 1978, 100, 3922–3926 CrossRef CAS.
- A. B. Mostert, S. B. Rienecker, C. Noble, G. R. Hanson and P. Meridith, Sci. Adv., 2018, 4, eaaq1293 CrossRef PubMed.
- S.-S. Chio, J. S. Hyde and R. C. Sealy, Arch. Biochem. Biophys., 1980, 199, 133–139 CrossRef CAS PubMed.
- S.-S. Chio, J. S. Hyde and R. C. Sealy, Arch. Biochem. Biophys., 1982, 215, 100–106 CrossRef CAS PubMed.
- A. B. Mostert, G. R. Hanson, T. Sarna, I. R. Gentle, B. J. Powell and P. Meredith, J. Phys. Chem. B, 2013, 117, 4965–4972 CrossRef CAS PubMed.
- A. B. Mostert, B. J. Powell, F. L. Pratt, G. R. Hanson, T. Sarna, I. R. Gentle and P. Meredith, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8943–8947 CrossRef CAS PubMed.
- A. Bernardus Mostert, B. J. Powell, I. R. Gentle and P. Meredith, Appl. Phys. Lett., 2012, 100, 093701 CrossRef.
- M. M. Jastrzebska, H. Isotalo, J. Paloheimo and H. Stubb, J. Biomater. Sci., Polym. Ed., 1995, 7, 577–586 CrossRef CAS PubMed.
- J. Wünsche, Y. Deng, P. Kumar, E. Di Mauro, E. Josberger, J. Sayago, A. Pezzella, F. Soavi, F. Cicoira, M. Rolandi and C. Santato, Chem. Mater., 2015, 27, 436–442 CrossRef.
- M. Sheliakina, A. B. Mostert and P. Meredith, Adv. Funct. Mater., 2018, 1805514 CrossRef.
- J. E. McGinness, P. Corry and P. Proctor, Science, 1974, 183, 853–855 CrossRef CAS PubMed.
- C. H. Culp, D. E. Eckels and P. H. Sidles, J. Appl. Phys., 1975, 46, 3658–3660 CrossRef CAS.
- J. E. McGinness, Science, 1972, 177, 896–897 CrossRef CAS PubMed.
- A. Grebenko, V. Dremov, P. Barzilovich, A. Bubis, K. Sidoruk, T. Voeikova, Z. Gagkaeva, T. Chernov, E. Korostylev, B. Gorshunov and K. Motovilov, PLoS One, 2018, 13, e0191289 CrossRef PubMed.
- M. Jastrzebska, A. Kocot, J. K. Vij, J. Zalewska-Rejdak and T. Witecki, J. Mol. Struct., 2002, 606, 205–210 CrossRef CAS.
- M. M. Jastrzebska, S. Jussila and H. Isotalo, J. Mater. Sci., 1998, 33, 4023–4028 CrossRef CAS.
- M. d'Ischia, K. Wakamatsu, A. Napolitano, S. Briganti, J.-C. Garcia-Borron, D. Kovacs, P. Meredith, A. Pezzella, M. Picardo, T. Sarna, J. D. Simon and S. Ito, Pigm. Cell Melanoma Res., 2013, 26, 616–633 CrossRef PubMed.
- A. B. Mostert, K. J. P. Davy, J. L. Ruggles, B. J. Powell, I. R. Gentle and P. Meredith, Langmuir, 2010, 26, 412–416 CrossRef CAS PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley, New York, 6th edn, 1986 Search PubMed.
- V. K. Malinovsky, V. N. Novikov, A. P. Sokolov and V. A. Bagryansky, Chem. Phys. Lett., 1988, 143, 111–114 CrossRef.
- S. Speziale, F. Jiang, C. L. Caylor, S. Kriminski, C. Zha, R. E. Thorne and T. S. Duffy, Biophys. J., 2003, 85, 3202–3213 CrossRef CAS PubMed.
- J. Griesbauer, A. Wixforth and M. F. Schneider, Biophys. J., 2009, 97, 2710–2716 CrossRef CAS PubMed.
- U. Mizutani, T. B. Massalski, J. E. McGinnes and P. M. Corry, Nature, 1976, 259, 505–507 CrossRef CAS PubMed.
- I.-S. Yang and A. C. Anderson, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34(4), 2942–2944 CrossRef CAS.
- K. Yoshida, A. Q. R. Baron, H. Uchiyama, S. Tsutsui and T. Yamaguchi, J. Chem. Phys., 2016, 144, 134505 CrossRef PubMed.
- B. Roling, C. Martiny and S. Murugavel, Phys. Rev. Lett., 2001, 87, 085901 CrossRef CAS PubMed.
- D. L. Sidebottom and C. M. Murray-Krezan, Phys. Rev. Lett., 2002, 89, 195901 CrossRef CAS PubMed.
- J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Rep. Prog. Phys., 2009, 72, 046501 CrossRef.
- K. Kämpf, B. Kremmling and M. Vogel, Phys. Rev. E, 2014, 89, 032710 CrossRef PubMed.
- S. Capaccioli, K. L. Ngai, S. Ancherbak and A. Paciaroni, J. Phys. Chem. B, 2012, 116, 1745–1757 CrossRef CAS PubMed.
- K. L. Ngai, S. Capaccioli and A. Paciaroni, Biochim. Biophys. Acta, 2016, 1861, 3553–3563 CrossRef PubMed.
- K. A. Motovilov, M. Savinov, E. S. Zhukova, A. A. Pronin, Z. V. Gagkaeva, V. Grinenko, K. V. Sidoruk, T. A. Voeikova, P. Y. Barzilovich, A. K. Grebenko, S. V. Lisovskii, V. I. Torgashev, P. Bednyakov, J. Pokorný, M. Dressel and B. P. Gorshunov, Sci. Rep., 2017, 7, 15731 CrossRef CAS PubMed.
- S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210 CrossRef CAS.
- A. K. Jonscher, Dielectric Relaxation in Solids, Chelsea Dielectrics Press Ltd, London, 1983 Search PubMed.
- S. Capaccioli, K. L. Ngai and N. Shinyashiki, J. Phys. Chem. B, 2007, 111, 8197–8209 CrossRef CAS PubMed.
- S. Murugavel and B. Roling, Phys. Rev. Lett., 2002, 89, 195902 CrossRef CAS PubMed.
- D. L. Sidebottom, Phys. Rev. Lett., 1999, 82, 3653–3656 CrossRef CAS.
- J. L. Green, J. Fan and C. A. Angell, J. Phys. Chem., 1994, 98, 13780–13790 CrossRef CAS.
- I. Iben, D. Braunstein, W. Doster, H. Frauenfelder, M. Hong, J. Johnson, S. Luck, P. Ormos, A. Schulte, P. Steinbach, A. Xie and R. Young, Phys. Rev. Lett., 1989, 62, 1916–1919 CrossRef CAS PubMed.
- F. Piazza, P. De Los Rios and Y.-H. Sanejouand, Phys. Rev. Lett., 2005, 94, 145502 CrossRef CAS PubMed.
- A. Xie, A. F. G. van der Meer and R. H. Austin, Phys. Rev. Lett., 2002, 88, 018102 CrossRef PubMed.
- H. Shintani and H. Tanaka, Nat. Mater., 2008, 7, 870–877 CrossRef CAS PubMed.
- S. Khodadadi, A. Malkovskiy, A. Kisliuk and A. P. Sokolov, Biochim. Biophys. Acta, 2010, 1804, 15–19 CrossRef CAS PubMed.
- N. V. Surovtsev, Phys. Rev. E, 2001, 64, 061102 CrossRef CAS PubMed.
- A. A. R. Watt, J. P. Bothma and P. Meredith, Soft Matter, 2009, 5, 3754 RSC.
- M. D'Ischia, A. Napolitano, V. Ball, C. T. Chen and M. J. Buehler, Acc. Chem. Res., 2014, 47(12), 3541–3550 CrossRef PubMed.
- G. W. Zajac, J. M. Gallas, J. Cheng, M. Eisner, S. C. Moss and A. E. Alvarado-Swaisgood, Biochim. Biophys. Acta, Gen. Subj., 1994, 1199, 271–278 CrossRef CAS.
- K. B. Stark, J. M. Gallas, G. W. Zajac, M. Eisner and J. T. Golab, J. Phys. Chem. B, 2003, 107, 11558–11562 CrossRef CAS.
- J. M. Gallas, K. C. Littrell, S. Seifert, G. W. Zajac and P. Thiyagarajan, Biophys. J., 1999, 77, 1135–1142 CrossRef CAS PubMed.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- L. K. Charkoudian and K. J. Franz, Inorg. Chem., 2006, 45, 3657–3664 CrossRef CAS PubMed.
- T. Miyake and M. Rolandi, J. Phys.: Condens. Matter, 2016, 28, 023001 CrossRef PubMed.
- S. Khodadadi and A. P. Sokolov, Soft Matter, 2015, 11, 4984–4998 RSC.
- S. Perticaroli, J. D. Nickels, G. Ehlers and A. P. Sokolov, Biophys. J., 2014, 106, 2667–2674 CrossRef CAS PubMed.
- R. Micillo, L. Panzella, K. Koike, G. Monfrecola, A. Napolitano and M. D'Ischia, Int. J. Mol. Sci., 2016, 17, 746 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09093a |
| This journal is © The Royal Society of Chemistry 2019 |